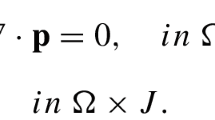Abstract
In this paper, an energy-stable Crank–Nicolson fully discrete finite element scheme is proposed for the Benjamin–Bona–Mahony–Burgers equation. Firstly, the stability of energy is proved, which leads to the boundedness of the finite element solution in \(H^{1}\)-norm. Secondly, combining with the above boundedness and the special property of bilinear element, the unconditional superclose and superconvergence results are derived. Finally, numerical examples are provided to illustrate the validity and efficiency of our theoretical analysis and method.
Similar content being viewed by others
1 Introduction
The nonlinear Benjamin–Bona–Mahony–Burgers (BBMB) equation is often used to describe the propagation of small amplitude long waves in a nonlinear dispersive medium with dissipative effect, which is considered as the following second-order partial differential equation [1]:
where \(\Omega \subset R^{2}\) is an open bounded convex polygonal domain with boundary ∂Ω, \(\alpha >0\), \(\beta >0\), \(0< T<\infty \) are given constants, \(X=(x,y)\), \(\vec{f}(u)=-(\frac{1}{2}u^{2}+u,\frac{1}{2}u^{2}+u)\), Δ and ∇⋅ denote the two-dimensional Laplace and divergence operators, respectively, \(u_{0}(X)\) is a given smooth function. It is remarkable that when \(\alpha =0\), \(\beta >0\), (1) is called Burgers’ equation, when \(\alpha >0\), \(\beta =0\), (1) is called Benjamin–Bona–Mahony (BBM) equation. Various analytical and computational methods have been proposed to solve Burgers’ and BBM equations, readers with more interests may refer to [2–7] and the references listed.
Due to the nonlinearity of BBMB equation, it is very difficult to find out the true solution. Thus, a lot of numerical methods have been considered, such as the finite difference methods [8–11], collocation method [12], meshless method [13, 14], finite element method (FEM) [15–18], and so on. For the FEM, Kadri [15] proposed semi-discrete and two kinds of fully discrete Galerkin schemes, studied the \(L^{\infty}\)-norm error estimates; Kundu [16] established the convergence of unsteady solution to steady state solution; Karakoc [17] obtained the convergence analysis by use of a cubic B-spline FEM; Gao [18] discussed the local discontinuous Galerkin FEM and derived an optimal error estimate. However, [15–18] only focus on the convergence for the one-dimensional (1D) BBMB equation, there are few works for the 2D case till now.
It is well known that the superconvergence analysis is an important approach to improve the precision of FE solution. More precisely, based on the so-called integral identity technique, the order of error in \(H^{1}\)-norm between FE approximation \(u_{h}\) and the interpolation of the exact solution \(I_{h}u\) is much better than that of u and \(I_{h}u\); this fascinating characteristic is called superclose. The global superconvergence will then be investigated by adding a postprocessing without changing the existing FE program. Meanwhile, superconvergence is critical in practical engineering numerical calculation and has always been a research hotspot. To find out more applications, readers may refer to [19–23]. As far as our knowledge is concerned, research on superconvergence for 2D BBMB equation is not yet to be found.
In this work, as a first attempt, we develop an energy-stable conforming FE scheme for problem (1) and study the superclose and superconvergence error estimates. The outline is organized as follows: in Sect. 2, the FE space and the Crank–Nicolson (C-N) fully discrete scheme are provided, then the stability of energy and the boundedness of the numerical solution in \(H^{1}\)-norm are proved; in Sect. 3, the unconditional superclose and superconvergence results are derived without the restriction of the ratio between mesh size parameter h and time step Δt; in the last section, three numerical examples are given to verify the theoretical analysis.
2 The FE space and energy-stable scheme
Assume that \(W^{k,p}(\Omega )\) is the standard Sobolev space with the norm \(\|\cdot \|_{W^{k,p}(\Omega )}\), \(H^{k}(\Omega )= W^{k,2}(\Omega )\), \(H^{0}(\Omega )= L^{2}(\Omega )\) with the norm \(\|\cdot \|_{k}\) and \(\|\cdot \|_{0}\), the inner-product in \(L^{2}(\Omega )\) is defined by \(( \cdot , \cdot )\).
Denote \(T_{h}\) to be a regular rectangular subdivision of Ω. For \(K \in T_{h}\), \(h_{K}=\operatorname{diam}K\), \(h=\max_{K\in{T}_{h}}h_{K} \). The bilinear element space \(V_{h}\) is defined by
The associated interpolation operator is defined as \(I_{h}:v\in V=H^{1}_{0}( \Omega )\rightarrow I_{h}v \in V_{h}\).
The variational form of (1) is to find \(u\in V\) such that
Let \(\{t_{n}|t_{n}=n\Delta t; n=0,1,2,\ldots , N\}\) be a uniform partition of \([0,T]\) with \(\Delta t=T/N\). For a given continuous function u on \([0,T]\), we define that \(u^{n}=u(X,t_{n})\), \(\bar{\partial}_{t}u^{n}= \frac{u^{n}-u^{n-1}}{\Delta t}\), \(t_{n-\frac{1}{2}}=(n-\frac{1}{2})\Delta t\), \({u}^{n-\frac{1}{2}}=\frac{u^{n}+u^{n-1}}{2}\). The C-N fully discrete scheme for (2) is to find \(U_{h}^{n}\in V_{h}\) such that
First of all, we achieve the following special properties of bilinear element from [19, 24].
Lemma 2.1
For all \(v_{h}\in V_{h}\), there hold
Here and later, we denote by C a generic positive constant which is independent of h and Δt and may stand for different values at different places.
Then the energy stability of (3) and the boundedness of \(\|U_{h}^{n}\|_{1}\) are proved as follows.
Theorem 2.1
Let \(E^{n}=\|U_{h}^{n}\|^{2}_{0}+\alpha |U_{h}^{n}|^{2}_{1}\) (\(n=0, 1, \ldots , N\)) be the discrete energy, \(U_{h}^{n}\) is the solution of (3), then there holds
Furthermore, we obtain
where \(M_{1}=\sqrt{\frac{\max \{1,\alpha \}}{\min \{1,\alpha \}}}\|U^{0}_{h} \|_{1}\) is a positive constant.
Proof
Taking \(v_{h}=U_{h}^{n-\frac{1}{2}}\) in (3), we can get
Firstly, the left-hand side of (8) can be rewritten as
Secondly, the right-hand side can be split as
By using the Green formula and noting that \(U^{n-\frac{1}{2}}_{h}|_{\partial \Omega}=0\), we obtain
where n⃗ is the outer normal vector, so we arrive at
Similarly, we have
substituting (11) and (12) into (10), we obtain
From (8), (9), and (13), there holds
therefore, we have
which implies \(E^{n}\leq E^{n-1}\), (6) is obtained.
Next we start to demonstrate (7). Multiplying \(2\Delta t\) on both sides of (14), replacing n with i, and summing for i from 1 to n, we have
From (15) and the triangular inequality, we have
which ends the proof. □
3 Superclose and superconvergence analysis
We first demonstrate the following unconditional superclose result.
Theorem 3.1
Let \(u^{n}\) and \(U_{h}^{n}\) be solutions of (2) and (3), respectively. Assume that \(u\in L^{\infty}(0,T;H^{3}(\Omega ))\), \(u_{t}\in L^{2}(0,T;H^{3}(\Omega ))\), \(u_{tt},u_{ttt}\in L^{2}(0,T;H^{1}(\Omega ))\), there holds
where \(\Delta t>0\) is small enough so that \(1-C\Delta t>0\).
Proof
Let \(u^{n}-U^{n}_{h}=(u^{n}-I_{h}u^{n})+(I_{h}u^{n}-U_{h}^{n}):= \xi ^{n}+ \eta ^{n}\), then the error equation can be derived by (2) and (3):
where \(R^{n}_{1}=u_{t}(t_{n-\frac{1}{2}})-\bar{\partial}_{t}u^{n}\), \(R_{2}^{n}=u(t_{n- \frac{1}{2}})-u^{n-\frac{1}{2}}\).
Taking \(v_{h}=\eta ^{n-\frac{1}{2}}\) in (17), there holds
The left-hand side of (18) can be rewritten as
Now we estimate the right-hand side: By virtue of Lemma 2.1, we arrive at
Using the Taylor expansion, the truncation error can be estimated as
the nonlinear term can be written as
By the estimation of truncation error, there holds
From the Sobolev imbedding theorem, (4) and (7), we have
and
Substituting (23)–(25) into (22), we get
Hence, from (18)–(21) and (26), we have
multiplying by \(2\Delta t\), then summing up the above inequality and noting that \(\eta ^{0}=0\), we can obtain
Choosing Δt small enough so that \(1-C\Delta t>0\) and applying discrete Gronwall’s lemma, there holds
the proof is completed. □
To obtain the global superconvergence estimate, we combine the adjacent four small elements \(K_{1}\), \(K_{2}\), \(K_{3}\), \(K_{4}\) into a big element K̃, i.e., \(\tilde{K}=\bigcup_{i=1}^{4}K_{i}\) (see Fig. 1), the corresponding subdivision is defined by \(T_{2h}\).
As in [19], we define the following interpolation postprocessing operator \(I_{2h}\):
where \(Q_{2}(\tilde{K})\) and \(C(\tilde{K})\) denote the spaces of biquadratic piecewise polynomial and continuous function on K̃, respectively, \(Z_{i}\) are all vertices of four small elements (see Fig. 1).
Meanwhile, \(I_{2h}\) has the following properties (see [19]):
Theorem 3.2
Under the assumption of Theorem 3.1, there holds the global superconvergence result as follows:
Proof
Let \(u^{n}-I_{2h}U^{n}_{h}=u^{n}-I_{2h}I_{h}u^{n}+I_{2h}I_{h}u^{n}-I_{2h}U^{n}_{h}\). By (16), (29), and the triangular inequality, we can get
the proof is completed. □
Remark 3.1
In this paper, the boundedness of \(\|U^{n}_{h}\|_{1}\) is crucial to the unconditional superclose and superconvergence results, the technique we used is more simple and direct than those in [22] and [23] ([22] applied an error splitting technique and [23] employed a complicated mathematical inductive hypothesis method to derive the boundedness of numerical solution).
4 Numerical examples
In this section, we give three examples to verify the validity of theoretical analysis, here we divide the domain Ω into \(m\times n\) rectangular meshes.
Example 1
We consider the following homogeneous BBMB equation:
Initially, the energy \(E^{n}=\|U^{n}_{h}\|^{2}_{1}\) under the initial condition \(u(x,y,0)=\sin\pi x\sin\pi y\) is plotted in Fig. 2, here \(t\in [0, 0.1]\), \(h=\frac{1}{20}\), \(\Delta t= 1.0\text{e}{-}05\).
Then a larger initial condition (\(u(x,y,0)=100\sin\pi x\sin\pi y\)) is considered, and \(E^{n}\) is displayed in Fig. 3, here t, h, and Δt are the same as above.
From Figs. 2–3 we can see that the energy is stable, which is consistent with the conclusion of Theorem 2.1.
Example 2
We consider the following inhomogeneous BBMB equation:
here \(g(x,y,t)\) could be computed by the exact solution \(u(x,y,t)=(1+e^{-t})xy(x-1)(y-1)\).
First of all, we take \(\|I_{h}u^{n}-U^{n}_{h}\|_{1}\) as an example to validate the unconditional stability. Here fix \(h=\frac{1}{100}\) and choose \(\Delta t= \frac{h}{10},\frac{h}{20},\frac{h}{40},\frac{h}{80}\), respectively, we provide the results of \(\|I_{h}u^{n}-U^{n}_{h}\|_{1}\) at \(t=0.1\), 0.5, and 1.0 in Table 1.
From Table 1, we can observe that \(\|I_{h}u^{n}-U^{n}_{h}\|_{1}\) is stable at a certain time and free from the ratio between Δt and h.
Moreover, the convergence, superclose, and superconvergence results at \(t=0.1\), 0.5, and 1.0 are listed in Tables 2–4, respectively. At the same time, we describe the error reduction results in Figs. 4–6, respectively. To confirm the convergence order, we choose \(\Delta t=h\).
From Tables 2–4 and Figs. 4–6, we can see that \(\|u^{n}-U^{n}_{h}\|_{1}\) is convergent at rate of \(O(h)\), \(\|I_{h}u^{n}-U^{n}_{h}\|_{1}\) and \(\|u^{n}-I_{2h}U^{n}_{h}\|_{1}\) are convergent at rate of \(O(h^{2})\), which coincides with the conclusions of Theorems 3.1–3.2.
Example 3
We consider the inhomogeneous BBMB equation in larger domains.
Firstly, we introduce the following equation:
where the exact solution \(u(x,y,t)=(1+e^{-t})xy(x-5)(y-5)\).
Here we take \(t=1, 2\), and 3, respectively, the unconditional stability is validated in Table 5, the convergence, superclose, and superconvergence results are listed in Tables 6–8, respectively.
Secondly, we consider the following equation:
here \(u(x,y,t)=(1+e^{-t})xy(x-8)(y-8)\).
The convergence, superclose, and superconvergence results at \(t=1, 2\), and 3 are provided in Tables 9–11, respectively.
From Tables 5–11, we can see that under the large initial condition, the numerical results are also in good agreement with our theoretical analysis.
Availability of data and materials
Not applicable.
References
Cheng, H., Wang, X.: A high-order linearized difference scheme preserving dissipation property for the 2D Benjamin-Bona-Mahony-Burgers equation. J. Math. Anal. Appl. 500, 125182 (2021)
Kutluay, S., Esen, A., Dag, I.: Numerical solutions of the Burgers’ equation by the least-squares quadratic B-spline finite element method. J. Comput. Appl. Math. 167, 21–33 (2004)
Muaz, S., Utku, E., Özis, T.: Numerical solution of Burgers’ equation with high order splitting methods. J. Comput. Appl. Math. 291, 410–421 (2016)
Chen, Y.L., Zhang, T.: A weak Galerkin finite element method for Burgers’ equation. J. Comput. Appl. Math. 348, 103–119 (2019)
Omrani, K.: The convergence of fully discrete Galerkin approximations for the Benjamin-Bona-Mahony (BBM) equation. Appl. Math. Comput. 180, 614–621 (2006)
Shi, D.Y., Yang, H.J.: A new approach of superconvergence analysis for nonlinear BBM equation on anisotropic meshes. Appl. Math. Lett. 58, 74–80 (2016)
Shi, D.Y., Jia, X.: Superconvergence analysis of two-grid finite element method for nonlinear Benjamin-Bona-Mahony equation. Appl. Numer. Math. 148, 45–60 (2020)
Omrani, K., Ayadi, M.: Finite difference discretization of the Benjamin-Bona-Mahony-Burgers equation. Numer. Methods Partial Differ. Equ. 24, 239–248 (2008)
Zhang, Q., Liu, L., Zhang, J.: The numerical analysis of two linearized difference schemes for the Benjamin-Bona-Mahony-Burgers equation. Numer. Methods Partial Differ. Equ. 36, 1790–1810 (2020)
Zhang, Q., Liu, L.: Convergence and stability in maximum norms of linearized fourth-order conservative compact scheme for Benjamin-Bona-Mahony-Burgers’ equation. J. Sci. Comput. 87, 1–31 (2021)
Haq, S., Ghafoor, A., Hussain, M.: Numerical solutions of two dimensional Sobolev and generalized Benjamin-Bona-Mahony-Burgers equations via Haar wavelets. Comput. Math. Appl. 77, 565–575 (2019)
Zarebnia, M., Parvaz, R.: On the numerical treatment and analysis of Benjamin-Bona-Mahony-Burgers equation. Appl. Math. Comput. 284, 79–88 (2016)
Dehghan, M., Abbaszadeh, M., Mohebbi, A.: The numerical solution of nonlinear high dimensional generalized Benjamin-Bona-Mahony-Burgers equation via the meshless method of radial basis functions. Comput. Math. Appl. 68, 212–237 (2014)
Dehghan, M., Abbaszadeh, M., Mohebbi, A.: The use of interpolating element-free Galerkin technique for solving 2D generalized Benjamin-Bona-Mahony-Burgers and regularized long-wave equations on non-rectangular domains with error estimate. J. Comput. Appl. Math. 286, 211–231 (2015)
Kadri, T., Khiari, N., Abidi, F.: Methods for the numerical solution of the Benjamin-Bona-Mahony-Burgers equation. Numer. Methods Partial Differ. Equ. 24, 1501–1516 (2008)
Kundu, S., Pani, A.K., Khebchareon, M.: Asymptotic analysis and optimal error estimates for Benjamin-Bona-Mahony-Burgers’ type equations. Numer. Methods Partial Differ. Equ. 34, 1053–1092 (2017)
Karakoc, S.B.G., Bhowmik, S.K.: Galerkin finite element solution for Benjamin-Bona-Mahony-Burgers equation with cubic B-splines. Comput. Math. Appl. 77, 1917–1932 (2019)
Gao, F., Qiu, J., Zhang, Q.: Local discontinuous Galerkin finite element method and error estimates for one class of Sobolev equation. J. Sci. Comput. 41, 436–460 (2009)
Lin, Q., Lin, J.F.: Finite Element Methods: Accuracy and Improvement. Bei**g Science Press, Bei**g (2006)
Lin, Q., Yan, N.N.: Efficient Finite Element Construction and Analysis. Hebei University Press, Baoding (1996)
Yang, H.J.: Superconvergence error estimate of a linearized energy-stable Galerkin scheme for semilinear wave equation. Appl. Math. Lett. 116, 107006 (2021)
Wang, J.J., Li, M., Jiang, M.P.: Superconvergence analysis of a MFEM for BBM equation with a stable scheme. Comput. Math. Appl. 93, 168–177 (2021)
Shi, X.Y., Lu, L.Z.: A new two-grid nonconforming mixed finite element method for nonlinear Benjamin-Bona-Mahoney equation. Appl. Math. Comput. 371, 124943 (2020)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problem. North-Holland, Amsterdam (1978)
Acknowledgements
The authors would like to thank the referees for their valuable suggestions, which helped to improve this work.
Funding
This work is supported by the National Natural Science Foundation of China (No.12101568), the Key Scientific Research Project of Universities in Henan Province (22A110025), and Henan Province Key Research and Development and Promotion Projects (222102210228, 222102320266).
Author information
Authors and Affiliations
Contributions
LW carried out theoretical calculation, participated in the design of the study, and drafted the manuscript. XL and HY participated in its design and helped to draft the manuscript. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, L., Liao, X. & Yang, H. Unconditional superconvergence analysis of an energy-stable finite element scheme for nonlinear Benjamin–Bona–Mahony–Burgers equation. Bound Value Probl 2022, 72 (2022). https://doi.org/10.1186/s13661-022-01651-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01651-9