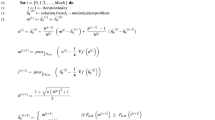Abstract
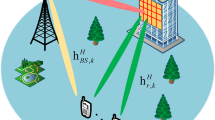
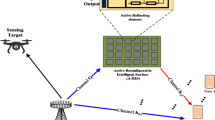
In this paper, we consider an integrated sensing and communications system assisted by a reconfigurable intelligent surface (RIS). A small number of sparsely placed active sensors are applied in the RIS to perform effective channels and, thereby, enable optimized beamforming for both communications and sensing objectives, namely, establishing reliable communication links with communication users (CUs) and effectively localize targets. The time-varying multipath channels between the RIS and the CU as well as the time-varying channel between the RIS and the targets are estimated by exploiting an interpolated Hermitian and Toeplitz covariance matrix followed by direction-of-arrival estimation using the MUSIC algorithm. Based on such results, we jointly optimize the transmit beamformer at the base station and the unit-modulus RIS passive beamformer. The RIS beamformer is optimized to maximize its minimum beam-pattern gain towards the desired sensing angles subject to the minimum signal-to-noise ratio requirement at the CU. Simulation results verify the effectiveness of the proposed approach, and the performance of different sparse array configurations is compared.
Similar content being viewed by others
1 Introduction
Next-generation wireless communication systems are required to deliver information in an extremely fast, more trustworthy, low-latency, and secure manner. Recent communications networks have emerged to use the millimeter-wave (mmWave) frequency band to provide innovative features and enable high data rate applications, such as high-quality video transmission, vehicle-to-infrastructure communications, intra-, and inter-vehicle messaging, device-to-device communications, and Internet of Things frameworks, and tactile Internet [6, 7]. ISAC can be implemented in several forms. For example, dual-function radar-communication (DRFC) systems share the same spectrum and hardware for both wireless communications and radar sensing, thereby achieving high spectral and cost efficiency [8,9,10,11].
Recently, reconfigurable intelligent surface (RIS) has emerged as a promising means for the next-generation wireless communication systems to boost the channel capacity and increase service coverage [12]. RIS is a metasurface made up of a large number of passive reflecting elements, typically in a rectangular shape, in which each element can be digitally controlled to adjust the amplitude and/or phase of the incident signal, thereby allowing optimized control of the propagation channels [13,14,15]. The capability of RIS to transform the wireless propagation environments which are traditionally considered unmanageable into controllable ones opens a new direction to change the paradigm of wireless communications and sensing with much higher capability and flexibility.
Naturally, RIS is found to be attractive in ISAC applications. For example, RIS can assist the base station (BS) to better communicate and detect communication users (CUs) and targets that are outside of the line-of-sight (LOS) region of the BS [16,17,18,\(L_u\) uncorrelated multipath. Denote the 2-D DOA of the \(l_u\)-th path from the CU and observed at the RIS as \(\{\theta _{l_u}, \phi _{l_u}\}\), \(l_u=1, \cdots , L_u\), where \(\theta _{l_u}\in [-{\pi }/2,{\pi }/2]\) and \(\phi _{l_u}\in [-{\pi }/2,{\pi }/2]\) are respectively the elevation and the azimuth angles. The 2-D steering vector \({{\textbf {a}}}(\theta _{l_u},\phi _{l_u})\) at the RIS is expressed as [36]
where
Since the CU contains a single antenna, the channel of the CU-RIS link is expressed as
where \(\beta _{l_u}\) is the path gain. The signal vector received at the RIS corresponding to the x- and the z-axes are respectively given as [35, 36]
where \({s}_u(t)\) denotes the signal transmitted by the CU, \({{\textbf {s}}}(t) = [\beta _1, \beta _2, \cdots , \beta _{L_u}]^{\textrm{T}} s_u(t)\), \({{\textbf {A}}}_x= [{{\textbf {a}}}_x(\phi _1), {{\textbf {a}}}_x(\phi _2),\cdots ,{{\textbf {a}}}_x(\phi _{L_u})]\), and \({{\textbf {A}}}_z= [{{\textbf {a}}}_z(\theta _1), {{\textbf {a}}}_z(\theta _2),\cdots ,{{\textbf {a}}}_z(\theta _{L_u})]\). In addition, \({{\textbf {n}}}_x(t) \sim {\mathcal{C}\mathcal{N}}(0, \sigma _{\textrm{n}}^2 {{\textbf {I}}}_{N_x})\) and \({{\textbf {n}}}_z(t) \sim {\mathcal{C}\mathcal{N}}(0, \sigma _{\textrm{n}}^2 {{\textbf {I}}}_{N_z})\) are the additive white Gaussian noise (AWGN) vectors observed at the x- and z-axis direction elements.
In the sensing mode, the signals are only observed at the two sparse subarrays respectively consisting of \({{{\bar{N}}}}_x\) and \({{{\bar{N}}}}_z\) elements. We define binary mask matrices for the two subarrays, \({{\textbf {U}}}_x \in {\mathbb {C}}^{W_x\times N_x}\) and \({{\textbf {U}}}_z \in {\mathbb {C}}^{W_x\times N_z}\), given as
Then, the observed signal vectors corresponding to the two subarrays become
Note that only \({{{\bar{N}}}}_x\) and \({{{\bar{N}}}}_z\) elements respectively in \({\tilde{{{\textbf {y}}}}_x}(t)\) and \({\tilde{{{\textbf {y}}}}_z}(t)\) corresponding to the active element positions are nonzero.
In Sect. 3, we will use the masked signals observed in the sparse subarrays to interpolate the missing elements within the respective subarray aperture and estimate the signal channels.
2.2.2 CU-BS channel
Similar to the CU-RIS link, we consider that the signal transmitted from the CU arriving at the BS through \(L_d\) multipath. The time-varying channel between the BS and the CU is formulated as
where \(\gamma _{l_d}\) is the \(l_d\)-th channel path gain and \({{\textbf {f}}}(\theta _{l_d})\in {\mathbb {C}}^{M \times 1}\) is the array steering vector at the BS for \(l_d=1, \cdots , L_d\). Note that we assume that the M antennas in the BS array are vertically placed so only the elevation components are considered.
2.2.3 BS-RIS channel
The channel between the BS, in which the M antennas form a vertically aligned ULA, and the RIS is assumed to be fixed and thus is known at the BS. This channel between the BS and the RIS can be decomposed into \(L_b \le \textrm{min}(M,N)\) independent paths, given as
where, for the \(l_b\)-th path, \(\alpha _b\) denotes the gain, \({{\textbf {a}}}(\theta _{l_r},\phi _{l_r}) = {{\textbf {a}}}_z(\theta _{l_r})\otimes {{\textbf {a}}}_x(\phi _{l_r})\in {\mathbb {C}}^{N\times 1}\) is the corresponding steering vector at the RIS, \({{\textbf {f}}}^{\textrm{H}}(\theta _{l_b})\in {\mathbb {C}}^{M\times 1}\) is the steering vector at the BS, and \({\varvec{\alpha }}_{{\textrm{BI}}} = [\alpha _1,\alpha _2,\cdots ,\alpha _{L_b}]^{\textrm{T}}\). The channel is decomposed into \(L_b\) independent paths with \(\alpha _b\) denoting the gain of the \(l_b\)-th path.
2.2.4 RIS-target-RIS channel
To illustrate the offerings of RIS in providing localization of targets in the NLOS region of the BS, we consider potential target locations which have LOS to the RIS but not the BS. As such, the target locations are estimated based on signals observed at the RIS.
The RIS reflects the im**ing signals from the BS to the targets and receives the signal reflected from the target. We assume \(L_t\) targets in the scene. The direction of the \(l_t\)-th target observed at the RIS is denoted as \((\theta _{l_t},\phi _{l_t})\), which is shared for both the outgoing RIS-target path and the returning target-RIS path. The round-trip channel of the RIS-target-RIS link is modeled as
where \(\delta _{l_t}\) combines the round-trip path gain and the target radar cross section (RCS), \({{\textbf {b}}}(\theta _{l_t},\phi _{l_t})= {{\textbf {b}}}_z(\theta _{l_t})\otimes {{\textbf {b}}}_x(\phi _{l_t}) \in {\mathbb {C}}^{N\times 1}\) denotes the array steering vector of the RIS from the target, and \({\varvec{\delta }}_{{\textrm{TI}}} = [\delta _1,\delta _2,\cdots ,\delta _{L_t}]^{\textrm{T}}\) corresponding to the \(l_t\)-th target for \(l_t = 1, \cdots , L_t\).
Similar to the CU-RIS channel considered in Sect. 2.2.1, the RIS only observes masked signals at the sparsely placed active element positions. The observed channel matrix corresponding to the signal received on the z-axis subarray denoted as the RIS-targets-RIS(z) link, is described as
where only \({{{\bar{N}}}}_z\) rows are nonzero. Similarly, the RIS-targets-RIS(x) link is expressed as
where only \({{{\bar{N}}}}_x\) rows are nonzero.
3 Channel estimation, joint beamforming, and target localization
In this section, we consider the channel estimation, joint beamforming at the BS and the RIS, and the target localization in terms of 2-D DOA estimation. These objectives are addressed in the following three phases. The first phase estimates the time-varying channel between the CU and the RIS using the L-shaped sparse subarrays at the RIS. In the second phase, we maximize the minimum beampattern gain of the RIS towards the desired sensing directions while ensuring the minimum SNR requirement at the CU under the maximum transmit power constraint at the BS. The objective of the third phase is to determine the target 2-D DOAs by the sparse active elements at the RIS.
3.1 Phase I: CU-RIS channel estimation
In the first phase, the signal vectors \({\tilde{{{\textbf {y}}}}}_x(t)\) and \({\tilde{{{\textbf {y}}}}}_z(t)\) observed at the two active subarrays of the RIS are used to estimate the uplink multipath channels between the CU and the RIS. The interpolation technique is applied to obtain the full covariance matrices of vectors \({{{\textbf {y}}}}_x\) and \({{{\textbf {y}}}}_z\) corresponding to all elements spanned by the active subarray aperture, namely, for elements located at positions \(p_0, p_0+1, \cdots , W_x -1\) and \(q_0, q_0+1, \cdots , W_z -1\).
3.1.1 Covariance matrix interpolation
Assuming that the noise is uncorrelated to the signals, the covariance matrices of \({\tilde{{{\textbf {y}}}}}_x(t)\) is expressed as:
where \({{\textbf {R}}}_s= \textrm{diag}(\sigma _1^2, \sigma _2^2, \cdots , \sigma _{L_u}^2)\) is the source covariance matrix, \(\sigma _{l_u}^2 = \beta _{l_u}^2 \sigma _u^2\) represents the power of the \(l_u\)-th path signal, \(\sigma _u^2 = {{\mathbb {E}}}({|s_u(t)|^2})\) is the source signal power. Because of the sparse placement of the active RIS elements, the covariance matrices \({\tilde{{{\textbf {R}}}}}_{x}\) contain missing holes. We exploit the matrix interpolation of \({\tilde{{{\textbf {R}}}}}_{x}\) to obtain an estimate of the interpolated covariance matrices \({{{\textbf {R}}}}_{x} \in {{\mathbb {C}}}^{W_x \times W_x}\).
The matrix interpolation for the x-axis subarray is formulated as the following nuclear norm minimization problem [37]:
where \({{\mathcal {T}}}({\varvec{w}}) \in {{\mathbb {C}}}^{W_x \times W_x}\) denotes the Hermitian and Toeplitz matrix with \({\varvec{w}} \in {{\mathbb {C}}}^{W_x \times 1}\) as its first column, \(\Vert {{\mathcal {T}}}({\varvec{w}}) \Vert _* = \text {tr}(\sqrt{{{\mathcal {T}}}^{\textrm{H}}({\varvec{w}}){{\mathcal {T}}}({\varvec{w}})})\) is the nuclear norm of \({{\mathcal {T}}}({\varvec{w}})\), and \(\zeta\) is a tunable regularization parameter. In addition, \({{\textbf {Q}}}_x = {{\textbf {U}}}_x{{\textbf {U}}}_x^{\textrm{T}}\) is the binary mask of the sparse covariance matrix. The obtained \({{\mathcal {T}}}({\varvec{w}})\) becomes the estimate of \({{{\textbf {R}}}}_{x}\), denotes as \({\hat{{{\textbf {R}}}}}_{x}\). We can similarly perform matrix interpolation at the z axis and obtain the estimate of the interpolated covariance matrix \({{\textbf {R}}}_{z}\), denoted as \({\hat{{{\textbf {R}}}}}_{z}\).
As the interpolated covariance matrices are full rank, subspace-based methods, such as multiple signal classification (MUSIC), can be applied to \({\hat{{{\textbf {R}}}}}_{x}\) to obtain the azimuth DOAs of the multipath signals. The elevation angles must be paired with the estimated azimuth angles and their estimation is discussed below.
3.1.2 Pair-matched 2-D DOA estimation
When there are multiple paths between the CU and the RIS, it is important to determine the correct pairing between the estimated azimuth and elevation angles. The array manifold matrix corresponding to the estimated azimuth angles \({{\hat{\phi }}}_1, {{\hat{\phi }}}_2, \cdots , {{\hat{\phi }}}_{L_u}\) can be constructed as \({\hat{{{\textbf {A}}}}}_x= [{{\textbf {a}}}_x({\hat{\phi }}_1), {{\textbf {a}}}_x({\hat{\phi }}_2),\cdots ,{{\textbf {a}}}_x({\hat{\phi }}_{L_u})]\). We will estimate the manifold matrix \({{\textbf {A}}}_z\) of the z-axis subarray from the following cross-covariance matrix between \({\tilde{{{\textbf {y}}}}}_x(t)\) and \({\tilde{{{\textbf {y}}}}}_z(t)\):
Performing the eigendecomposition of the covariance matrices \({\hat{{{\textbf {R}}}}}_{x}\) and \({\hat{{{\textbf {R}}}}}_{z}\) yields in
and
where \({\hat{{{\textbf {V}}}}}_{xs}\) and \({\hat{{{\textbf {V}}}}}_{zs}\) denote the estimated signal subspaces for the two linear arrays, whereas \({\hat{{\varvec{\Lambda }}}}_{xs}\) and \({\hat{{\varvec{\Lambda }}}}_{zs}\) are the diagonal matrices containing the eigenvalues corresponding to the signal subspaces. As the position of the active elements for x and z-axis are identical, we can write \(W_x = W_z\) and \({{\textbf {I}}}\) \(= {{\textbf {I}}}_{W_x} = {{\textbf {I}}}_{W_z} \in {\mathbb {C}}^{W_x \times W_x}\). Exploiting the relationship between the components spanning the signal subspace in the above formulations, \({{\textbf {R}}}_{{{\textbf {s}}}}\) can be estimated as [38]
Thus, an estimate of the array manifold matrix, \({\hat{{{\textbf {A}}}}}_{z}= [{{\textbf {a}}}_{z}{({\hat{\theta }}_1)}, {{\textbf {a}}}_{z}{({\hat{\theta }}_2)}, \cdots , {{\textbf {a}}}_{z}{({{\hat{\theta }}}_{L_u})}] \in {\mathbb {C}}^{W_z \times L_u}\), can be obtained from (16) as
Note that matrix \({\tilde{{{\textbf {R}}}}}_{xz}\) is not a Hermitian and Toeplitz matrix and thus cannot be directly interpolated using interpolation techniques utilizing such properties. Instead, we indirectly obtain the interpolated \({{\textbf {R}}}_{xz}\) from the following operations:
As a result, we can rewrite (20) as
For the \(l_u\)-th path, \(l_u = 1,2, \cdots , L_u\), the elevation angle can be estimated as
From the paired azimuth and elevation angle estimation, we can generate the array manifold matrix for the CU-RIS channel as \({\hat{{{\textbf {A}}}}} = \left[ {{\textbf {a}}}( {{\hat{\theta }}}_{1},{{\hat{\phi }}}_{1}), \cdots , {{\textbf {a}}}({{\hat{\theta }}}_{L_u}, {{\hat{\phi }}}_{L_u}) \right] \in {\mathbb {C}}^{N \times L_u}\).
3.1.3 Path gain estimation
Because the path gains are identical for the x- and z-axis subarrays, computation in one of these two subarrays will suffice. To estimate the path gain of the CU-RIS channel, the CU transmits pilot signal \(s_u(t)\) to the RIS. At the RIS, the received signal at the x-axis elements is given as
where \({{\textbf {g}}} = [\beta _{1}, \beta _{2}, \cdots , \beta _{L_u}]^{\textrm{T}}\) represents the path gains and can be estimated from
where \(\bar{{{\textbf {y}}}}_{x} ={\mathbb {E}}\{{{{\textbf {y}}}}_{x}(t) s_u^*(t)\}\). From the above DOAs and path gain estimation, we can reconstruct the CU-RIS multipath channel \({{\textbf {h}}}_r\).
Similarly, we can estimate the CU-BS channel at the BS which, however, does not require interpolation because all BS antennas are active. The normalized root-mean-square error (RMSE) of the CU-RIS channel at the RIS is estimated as
where \(K_\mathrm{{cu}}\) is the number of independent trials.
3.2 Phase II: joint BS and RIS beamforming optimization
In phase II, our objective is to maximize the minimum beampattern gain of the RIS towards the desired sensing angles, while ensuring the minimum SNR requirement at the CU under the maximum transmit power constraint at the BS. Let \({{\textbf {v}}} = [e^{j\psi _1},\cdots , e^{j\psi _N}]^{\textrm{T}} \in {\mathbb {C}}^{N\times 1}\) denote the reflective phase shift vector at the RIS where \(\varvec{\Phi }= \text {diag}({{\textbf {v}}})\). By combining the signals transmitted through the direct BS-CU link and the reflected BS-RIS-CU link, the received signal at the CU is expressed as
where \({{\textbf {w}}}\in {\mathbb {C}}^{M\times 1}\) denotes the transmit beamforming vector at the BS, \(\textrm{s}(t) \sim \mathcal{C}\mathcal{N}(0,\sigma _{{\textrm{s,BS}}}^2)\) is the transmitted random symbol, and \(n_c(t) \sim \mathcal{C}\mathcal{N}(0,\sigma _{{\textrm{n,CU}}}^2)\) represents the AWGN at the CU. The received SNR at the CU is computed as
Next, we consider the radar sensing towards the potential target locations which are assumed to be at the NLOS areas of the BS. In this case, we use the virtual LOS links created by the RIS reflection to sense the targets. The beampattern gain of the RIS towards the desired sensing angles are used as the sensing performance metric. The beampattern gain from the RIS towards the target angel \(({\theta _{l_t}, \phi _{l_t}})\) is given as
We are interested in sensing the prospective targets at \(L_t\) directions observed at the RIS. To achieve the aforementioned objective, i.e., maximizing the minimum beampattern gain at these \(L_t\) angles while ensuring the minimum SNR requirement at the CU under the maximum transmit power constraint at the BS, we formulate the following SNR-constrained minimum beampattern gain maximization problem,
where \({\mathcal {L}} =\{1, 2, \cdots , L_t\}\), \(P_0\) is the maximum power allowed at the BS, and \(\Gamma\) is the required SNR by the CU. \(v_n\) is the n-th element of \({{\textbf {v}}}\) and the constraint \(|v_n| =1\) ensures that the RIS weights are unit modulus, thereby achieving phase-only beamforming which is desired for convenience RIS implementations [39]. This problem is highly nonconvex and thus is difficult to be directly solved. It can be solved, however, by using the techniques of alternating optimization and semidefinite relaxation (SDR) [16]. The BS beamforming weight vector \({{\textbf {w}}}\) is first optimized with an initial value of the \(\varvec{\Phi }\) and then optimize the RIS reflecting beamforming matrix \(\varvec{\Phi }\) with optimized \({{\textbf {w}}}\). These procedures are described in the following two subsections.
3.2.1 Transmit beamforming optimization at BS
First, we optimize the transmit beamformer \({{\textbf {w}}}\) in the above problem under a presumed reflective beamformer \({\varvec{\Phi }}\). This problem is formulated as
To perform SDR, we introduce \({{\textbf {W}}} = {{\textbf {w}}}{{\textbf {w}}}^{\textrm{H}}\) with \({{\textbf {W}}}\succeq 0\) and \({\text {rank}{({{\textbf {W}}})} = 1}\). Let \({{\textbf {h}}} = {{\textbf {G}}}^{\textrm{H}}{\varvec{\Phi }}^{\textrm{H}} {{\textbf {h}}}_{r} + {{\textbf {h}}}_d\) denote the combined channel vector from the BS to the CU accounting for both BS-CU and BS-IRA-CU channels. Then, the transmit beamforming optimization in problem (31) is reformulated as,
However, this problem is still nonconvex due to the rank-one constraint on \({{\textbf {W}}}\) in (32e). Relaxing this rank-one constraint renders the SDR version of the problem (32), expressed as
This problem is a semidefinite programming (SDP) that can be efficiently solved using convex solvers, such as CVX. Once the optimal solution of \({{\textbf {W}}}\) is solved from (32) and denoted as \({{\textbf {W}}}^{{\textrm{opt}}}\), the optimized transit beamforming vector at the BS, \({{{\textbf {w}}}}\), is obtained as [16]
3.2.2 Reflective beamforming optimization at RIS
Next, we optimize the reflective beamformer \({\varvec{\Phi }}\) in problem (30) when the transmit beamformer of the BS is obtained from (33) and (34). Then, the sensing beampattern gain from the RIS towards angle \(\{ \theta _{l_t}, \phi _{l_t}\}\) is given as
where
Define
Then, by substituting (37) into (35), we have \(\rho (\theta _{l_t},\phi _{l_t})= {\bar{{\textbf {v}}}}^{\textrm{H}}{{\textbf {R}}}_2(\theta _{l_t},\phi _{l_t}){\bar{{\textbf {v}}}}\).
Let \({{\textbf {H}}} = \text {diag}({{\textbf {h}}}_r^{\textrm{H}}){{\textbf {G}}} \in {\mathbb {C}}^{N\times M}\). The received signal power at the CU can be written as \(|({{\textbf {h}}}_r^{\textrm{H}} {\varvec{\Phi }} {{\textbf {G}}}+ {{\textbf {h}}}_d^{\textrm{H}}){{\textbf {w}}}|^2= |({{\textbf {v}}}^{\textrm{H}}{{\textbf {H}}}+{{\textbf {h}}}_d^{\textrm{H}}){{\textbf {w}}}|^2\). Then, the output SNR constraint in (30b) is reformulated as,
which is equivalent to
with
As a result, the optimization of \(\varvec{\Phi }\) in problem (30) becomes the optimization of \(\bar{{\textbf {v}}}\) in the following problem:
To solve \({\bar{{\textbf {v}}}}\) using SDR, we define \(\bar{{\textbf {V}}}= {\bar{{\textbf {v}}}\bar{{\textbf {v}}}^{\textrm{H}}}\) with \({\bar{{\textbf {V}}}}\succeq 0\) and \(\text {diag}{(\bar{{\textbf {V}}})}=1\). Noting \({\bar{{\textbf {v}}}}^{\textrm{H}}{{\textbf {R}}}_2(\theta _{l_t},\phi _{l_t}){\bar{{\textbf {v}}}}= \text {tr}({{\textbf {R}}}_2(\theta _{l_t},\phi _{l_t}){\bar{{\textbf {V}}}})\) and \({\bar{{\textbf {v}}}}^{\textrm{H}}{{\textbf {R}}}_3{\bar{{\textbf {v}}}}= \text {tr}({{\textbf {R}}}_3{\bar{{\textbf {V}}}) }\), the reflective beamforming optimization in problem (41) is reformulated as
Similarly, we relax the rank-one constraint and accordingly obtain the SDR version of the problem (42) as
Let \(\bar{{\textbf {V}}}^{\textrm{opt}}\) denote the obtained optimal solution to \({\bar{{\textbf {V}}}}\) from problem (43). When it has a high rank, Gaussian randomization can be used to construct an approximate rank-one solution. At any iteration, if the updated gain is higher than the prior gain, the targets’ beampattern gain and \({{\textbf {v}}}\) are updated at the same time. If not, \({{\textbf {v}}}\) is again randomly generated.
It is noted that, with a sufficient number of randomizations, the objective value after solving the problem (42) will be monotonically non-decreasing [15]. As a result, the convergence of the proposed alternating optimization-based algorithm for solving the problem (30) is ensured.
3.3 Phase III: NLOS target localization
In this section, using the reflected RIS signal, we estimate the target 2-D DOA. The RIS has a sparse placement of the L-shaped active elements to allow for independent determination of the targets’ azimuth and elevation angles. Here, we demonstrate the estimation of the elevation angles of the targets using the RIS z-axis subarray. The signals received at the azimuth subarray can be similarly formulated and the azimuth angles of the targets can be similarly computed using the matrix interpolation and pair-matched MUSIC processes.
The echo channel reflected from the target over the RIS-reflected link, denoted as BS-RIS-targets-RIS(z), is given by
As such, the received signals at the vertical RIS subarray sensors are given by
For the estimation of the target directions, the received signal from the BS, \({{\textbf {Gw}}}s(t)\) in the above expression, act as interference. Because \({{\textbf {G}}}\) is fixed and known, we can remove this component and obtain the interference-free target echo signal as
As the active elements on the RIS are in a sparse structure, similar to (15), we can perform matrix completion to fill in the missing elements and generate the interpolated covariance matrix \({{\hat{{{\textbf {R}}}}}_Z}\). \({{\textbf {B}}}_t\) at RIS can be obtained by following the same procedures of the pair-matched MUSIC algorithm and gain estimation as described in Sect. 3.1.1.
The normalized RMSE of the target response at the RIS is estimated as
where \(K_t\) is the number of independent trials.
4 Simulation results
In this section, we provide simulation results to demonstrate the effectiveness of the proposed active RIS-assisted ISAC scheme and the superiority of the L-shaped hybrid ONRA-based sparse array structure over other L-shaped structures. The RIS contains \(N_x = N_z = 23\) elements in each dimension, rendering a total number of \(N = 529\) elements.
We use a small number of \({{\bar{N}}}=11\) active elements in all L-shaped sparse arrays and examine the channel estimation and target DOA estimation performance. Figure 2 shows the structures of different sparse active subarrays in a single axis. Each array uses 6 antenna elements. Both the x and z-axis directions use the same subarrays and they together form L-shape sparse active arrays. Note that the two subarrays share the element located at the 0-th position. For the hybrid ONRA configuration, the positions of the active elements along the x and the z axes are \({{\mathbb {X}}} = {{\mathbb {Z}}} = \{0,3,7,12,20,22\}\lambda /2\). It yields 16 nonnegative lags located as \({{\mathbb {D}}}_{\textrm{self}}^{X} = {{\mathbb {D}}}_{\textrm{self}}^{Z} = \{0,2,3,4,5,7,8,9,10,12,13,15,17,19,20,22\}\lambda /2\). It achieves the largest array aperture which coincides with the size of the RIS, rendering \(W_x = N_x = W_y = N_y = 23\) in this case.
For comparison, we compare the performance of the L-shaped hybrid ONRA-based sparse array structure with L-shaped arrays consisting of orthogonally placed ULA structures and popularly used sparse array structures, including the coprime array [30], nested array [29], coprime array with minimum lag redundancies (CAMLR) [40], and super nested array (SNA) [41]. These five sparse array configurations being compared respectively achieve 5, 9, 12, 12, and 12 unique nonnegative co-array lags and have smaller array apertures as shown in Fig. 2 [34]. The transmit array of the BS is equipped with a vertically placed ULA with \(M = 4\) antennas.
The large-scale path loss for a CU-RIS path with distance r is given as \(\textrm{PL}(r)[\text {dB}]= 10\ \text {log}_{10}(4\pi f_c/c)^2+10 \, \alpha \, \text {log}_{10}(r/r_0)\), where \(f_c\), \(\alpha\), and \(r_0\) are the carrier frequency, the path loss exponent, and the reference distance, respectively [42]. In this paper, \(f_c=28\) GHz and \(r_0=1\ \text {m}\) are assumed.
The BS and the RIS have a fixed distance of \(d_{\text {BI}}=10.2\) m, and the distance between the RIS and the CU is \(d_{\text {IC}}=120\) m. There are two targets and their 2-D angels with respect to the RIS are respectively [\(10^\circ , 30^\circ\)] and [\(30^\circ , 10^\circ\)]. The two-way complex-valued path gain is \(\delta _{l_t} = \sqrt{{\lambda ^2k}/({64\pi ^3d_{\textrm{IT}}^4})}\) denotes the signal attenuation caused by the propagation from RIS to the target and then from the target to RIS. We assumed that both targets are equally distant from the RIS, where \(d_{\text {IT}}=10.2\) m is the distance between the RIS and target, and \(k = 7\) dBm denotes the radar cross-section.
For the CU, we assume \(L_u= 2\) paths for the CU-RIS channel \({{\textbf {h}}}_r\).
We consider two distinct scenarios. In the first scenario, we intend to evaluate how well the different array structures would function, and the multipath is chosen to be closely spaced with the LOS and their DOA separation observed at the RIS is only \(2^{\circ }\) in both azimuth and elevation. In the second scenario, we consider well separated multipath whose azimuth and elevation angles both deviate from the LOS by \(20^{\circ }\). The near and far spacing between this multipath can be used to determine the performance advantages of the hybrid ONRA array construction.
Figure 3 considers the first case with closely spaced multipath and compares the normalized RMSE performance of the estimated channels with respect to the number of snapshots for different array configurations. In this case, the CU’s transmit power is 10 dBm, whereas the noise power is \(-80\) dBm. The outcomes clearly demonstrate that the RIS with L-shaped hybrid ONRA active elements achieves noticeably higher channel estimation accuracy than other sparse array structures utilizing the same number of active elements (\({\bar{N}}=11\)). In Fig. 4, we increase the transmit power from the CU to 20 dBm, and it is observed that the RMSE performance of all array configurations improves due to the increased transmit power.
In Fig. 5, we consider the second scenario with well separated multipath signals. With a \(20^{\circ }\) separation in both azimuth and elevation, the normalized RMSE of all sparse structures is much lower and the differences between different array configurations are smaller.
Figure 6 depicts the CU-RIS channel estimation results for different angular separations between the CU-IRS multipath, where the transmit power from the CU is 10 dBm and the number of snapshots is 5000. When the difference between the two azimuth angles and the two elevation angles was only \(0.1^\circ\), the channel estimation accuracy was very poor for all array configurations in this figure. For all array designs, channel estimation performance improves with increasing multipath separation, but for ONRA structures, channel estimation performance is exceptionally accurate even with a \(1^\circ\) separation when compared to other structures. This figure further highlights the superior estimate performance of the hybrid ONRA over the other array architectures.
Figure 7 depicts the normalized RMSE performance of the estimated CU-RIS channels as the transmit power varies between 0 dBm and 30 dBm, where the number of snapshots is fixed to 5000, and the two paths are closely spaced with \(2^{\circ }\) separation in both azimuth and elevation. It is observed that the normalized RMSE generally reduces as the transmit power increases and, for this closely spaced multipath scenario, the hybrid ONRA-based active RIS configuration performs much better than other sparse array structures.
In Fig. 8, we compare the normalized RMSE of the estimated CU-RIS channel versus the separation between the CU and the IRS. The number of snapshots is 5000, the transmit power is 10 dBm, and the angular separation is \(2^{\circ }\) in both azimuth and elevation. It is observed that, as the distance increases, the signal is more attenuated, yielding higher normalized RMSE results. The ONRA structure consistently outperforms the other array configurations.
Figure 9 shows the convergence performance of the minimum beampattern gain obtained in phase II based on the alternating optimization-based algorithm. Here, the transmit power from BS is 40 dBm, the noise power is \(-80\) dBm, and \(\Gamma = 10\) dB is assumed. Because the convergence performance depends on randomization, the plotted results are obtained by averaging over 5 independent trials. For comparison, we also plotted the result with true CSI of the BS-RIS channel, BS-CU channel, and CU-RIS channel to be perfectly known at the BS during optimization. We can observe that most of the array configurations achieve convergence in 6–8 iterations. Sparse subarrays using the ONRA structure achieve the highest minimum beampattern gain which is very close to that obtained under the assumption that accurate CSI is known.
In phase III, we determine the target reflected signals. Figure 10 demonstrates the normalized RMSE performance versus the number of snapshots, where the transmit power from the BS is 40 dBm and the noise power is \(-109\) dBm. It is again verified that the hybrid ONRA structure offers better performance than other sparse array configurations.
5 Conclusion
In this paper, we presented an ISAC system assisted by a RIS with partial active elements. L-shaped sparse arrays are used for channel estimation and target DOA estimation. A nuclear norm-based interpolation technique was used to fill in the gaps in the covariance matrix and achieve improved channel estimation and target DOA estimation performance. The array and RIS gains are optimized to concurrently maintain a specific SNR requirement toward the communication user and beampattern gains toward the targets which are assumed to have LOS only with the RIS. Simulation findings demonstrate that our proposed hybrid ONRA RIS structure performs better than other contemporary RIS structures.
Availability of data and materials
Data sharing is not applicable to this study.
Abbreviations
- 2-D:
-
Two-dimensional
- AWGN:
-
Additive white Gaussian noise
- BS:
-
Base station
- CAMLR:
-
Coprime array with minimum lag redundancy
- CSI:
-
Channel state information
- CU:
-
Communication user
- DOA:
-
Direction-of-arrival
- DOD:
-
Direction-of-departure
- DRFC:
-
Dual-function radar-communications
- RIS:
-
Reconfigurable intelligent surface
- ISAC:
-
Integrated sensing and communication
- LOS:
-
Line-of-sight
- MUSIC:
-
Multiple signal classification
- NLOS:
-
Non-line-of-sight
- ONRA:
-
Optimized non-redundant array
- RMSE:
-
Root-mean-square error
- SDP:
-
Semidefinite programming
- SDR:
-
Semidefinite relaxation
- SNA:
-
Super nested array
- SNR:
-
Signal-to-noise ratio
- ULA:
-
Uniform linear array
- URA:
-
Uniform rectangular array
References
A.M. Elbir, K.V. Mishra, M. Shankar, S. Chatzinotas, The rise of intelligent reflecting surfaces in integrated sensing and communications paradigms (2022), Preprint at ar**v:2204.07265
H. Elayan, O. Amin, R.M. Shubair, M.-S. Alouini, Terahertz communication: the opportunities of wireless technology beyond 5G. In: Proceeding international conference on advanced communication technologies and networking (CommNet), pp. 1–5 (2018)
Z. Pi, F. Khan, A millimeter-wave massive MIMO system for next generation mobile broadband. In: Conference record of asilomar conference on signals, systems and computers, pp. 693–698 (2012)
S.K. Sharma, I. Woungang, A. Anpalagan, S. Chatzinotas, Toward tactile internet in beyond 5G era: recent advances, current issues, and future directions. IEEE Access 8, 56948–56991 (2020)
F. Liu, Y. Cui, C. Masouros, J. Xu, T.X. Han, Y.C. Eldar, S. Buzzi, Integrated sensing and communications: towards dual-functional wireless networks for 6G and beyond. IEEE J. Sel. Areas Commun. 40(6), 1728–1767 (2022)
J.A. Zhang, F. Liu, C. Masouros, R.W. Heath, Z. Feng, L. Zheng, A. Petropulu, An overview of signal processing techniques for joint communication and radar sensing. IEEE J. Sel. Top. Signal Process. 15(6), 1295–1315 (2021)
A. Ahmed, Y.D. Zhang, Optimized resource allocation for joint radar-communications, in Signal Processing for Joint Radar-Communications. ed. by K.V. Mishra, B. Shankar, B. Ottersten, A.L. Swindlehurst (Wily-IEEE Press, New York, 2022)
A. Hassanien, M.G. Amin, Y.D. Zhang, F. Ahmad, Signaling strategies for dual-function radar communications: an overview. IEEE Aerosp. Electron. Syst. Mag. 31(10), 36–45 (2016)
A. Hassanien, M.G. Amin, Y.D. Zhang, F. Ahmad, Dual-function radar-communications: information embedding using sidelobe control and waveform diversity. IEEE Trans. Signal Process. 64(8), 2168–2181 (2015)
H. Nosrati, E. Aboutanios, D. Smith, Array partitioning for multi-task operation in dual function MIMO systems. Digit. Signal Process. 82, 106–117 (2018). https://doi.org/10.1016/j.dsp.2018.06.019
A. Ahmed, Y.D. Zhang, Y. Gu, Dual-function radar-communications using QAM-based sidelobe modulation. Digit. Signal Process. 82, 166–174 (2018). https://doi.org/10.1016/j.dsp.2018.06.018
S. Hu, F. Rusek, O. Edfors, Beyond massive MIMO: the potential of data transmission with large intelligent surfaces. IEEE Trans. Signal Process. 66(10), 2746–2758 (2018)
Q. Wu, S. Zhang, B. Zheng, C. You, R. Zhang, Intelligent reflecting surface-aided wireless communications: a tutorial. IEEE Trans. Commun. 69(5), 3313–3351 (2021)
Q. Wu, R. Zhang, Towards smart and reconfigurable environment: intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 58(1), 106–112 (2019)
Q. Wu, R. Zhang, Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wireless Commun. 18(11), 5394–5409 (2019)
X. Song, D. Zhao, H. Hua, T.X. Han, X. Yang, J. Xu, Joint transmit and reflective beamforming for IRS-assisted integrated sensing and communication. In: Proceedings of IEEE wireless communications and networking conference (WCNC), pp. 189–194 (2022)
X. Shao, C. You, W. Ma, X. Chen, R. Zhang, Target sensing with intelligent reflecting surface: architecture and performance. IEEE J. Sel. Areas Commun. 40(7), 2070–2084 (2022)
X. Wang, Z. Fei, J. Guo, Z. Zheng, B. Li, RIS-assisted spectrum sharing between MIMO radar and MU-MISO communication systems. IEEE Wirel. Commun. Lett. 10(3), 594–598 (2020)
X. Song, J. Xu, F. Liu, T.X. Han, Y.C. Eldar, Intelligent reflecting surface enabled sensing: Cramér-Rao lower bound optimization. Preprint at ar**v:2204.11071 (2022)
P. Vouras, K.V. Mishra, A. Artusio-Glimpse, S. Pinilla, A. Xenaki, D.W. Griffith, K. Egiazarian, An overview of advances in signal processing techniques for classical and quantum wideband synthetic apertures. Preprint at ar**v:2205.05602 (2022)
Z.-M. Jiang, M. Rihan, P. Zhang, L. Huang, Q. Deng, J. Zhang, E.M. Mohamed, Intelligent reflecting surface aided dual-function radar and communication system. IEEE Syst. J. 16(1), 475–486 (2021)
X. Wang, Z. Fei, Z. Zheng, J. Guo, Joint waveform design and passive beamforming for RIS-assisted dual-functional radar-communication system. IEEE Trans. Veh. Technol. 70(5), 5131–5136 (2021)
R. Liu, M. Li, A.L. Swindlehurst, Joint beamforming and reflection design for RIS-assisted ISAC systems. Preprint at ar**v:2203.00265 (2022)
Z.-Q. He, X. Yuan, Cascaded channel estimation for large intelligent metasurface assisted massive MIMO. IEEE Wirel. Commun. Lett. 9(2), 210–214 (2020)
Z. Wang, L. Liu, S. Cui, Channel estimation for intelligent reflecting surface assisted multiuser communications: framework, algorithms, and analysis. IEEE Trans. Wirel. Commun. 19(10), 6607–6620 (2020)
J. Qiao, M.-S. Alouini, Secure transmission for intelligent reflecting surface-assisted mmwave and terahertz systems. IEEE Wirel. Commun. Lett. 9(10), 1743–1747 (2020)
X. Chen, J. Shi, Z. Yang, L. Wu, Low-complexity channel estimation for intelligent reflecting surface-enhanced massive MIMO. IEEE Wirel. Commun. Lett. 10(5), 996–1000 (2021)
M.A. Haider, M.W.T. Chowdhury, Y.D. Zhang, Sparse channel estimation for IRS-aided systems exploiting 2-D sparse arrays. In: Proceedings of IEEE sensor array and multichannel signal process. Workshop (SAM), pp. 31–35 (2022)
P. Pal, P.P. Vaidyanathan, Nested arrays: a novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 58(8), 4167–4181 (2010)
P.P. Vaidyanathan, P. Pal, Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 59(2), 573–586 (2010)
S. Qin, Y.D. Zhang, M.G. Amin, Generalized coprime array configurations for direction of arrival estimation. IEEE Trans. Signal Process. 63(6), 1377–1390 (2015)
Z. Zheng, W.-Q. Wang, Y. Kong, Y.D. Zhang, MISC array: a new sparse array design achieving increased degrees of freedom and reduced mutual coupling effect. IEEE Trans. Signal Process. 67(7), 1728–1741 (2019)
A. Ahmed, Y.D. Zhang, Non-redundant sparse array with flexible aperture. In: 2020 54th Asilomar conference on signals, systems, and computers, pp. 225–229 (2020)
A. Ahmed, Y.D. Zhang, Generalized non-redundant sparse array designs. IEEE Trans. Signal Process. 69, 4580–4594 (2021)
X. Hu, R. Zhang, C. Zhong, Semi-passive elements assisted channel estimation for intelligent reflecting surface-aided communications. IEEE Trans. Wirel. Commun. 21, 1132–1142 (2022)
F. Wu, F. Cao, X. Ni, C. Chen, Y. Zhang, J. Xu, L-shaped sparse array structure for 2-D DOA estimation. IEEE Access 8, 140030–140037 (2020)
C. Zhou, Y. Gu, Z. Shi, Y.D. Zhang, Off-grid direction-of-arrival estimation using coprime array interpolation. IEEE Signal Process. Lett. 25(11), 1710–1714 (2018)
A.M. Elbir, L-shaped coprime array structures for DOA estimation. Multidimens. Syst. Signal Process. 31(1), 205–219 (2020)
R. Gooch, J. Lundell, The CM array: An adaptive beamformer for constant modulus signals. In: Proceedings of international conference on acoustics, speech, and signal processing (ICASSP), vol. 11 (IEEE, 1986), pp. 2523–2526
A. Ahmed, Y.D. Zhang, J.-K. Zhang, Coprime array design with minimum lag redundancy. In: Proceedings of international conference on acoustics, speech and signal processing (ICASSP), pp. 4125–4129 (2019)
C.-L. Liu, P. Vaidyanathan, Super nested arrays: linear sparse arrays with reduced mutual coupling-part I: fundamentals. IEEE Trans. Signal Process. 64(15), 3997–4012 (2016)
T.S. Rappaport, G.R. MacCartney, M.K. Samimi, S. Sun, Wideband millimeter-wave propagation measurements and channel models for future wireless communication system design. IEEE Trans. Commun. 63(9), 3029–3056 (2015)
Author information
Authors and Affiliations
Contributions
Mirza Asif Haider conceived of the presented idea, carried out the simulations, and prepared the original draft; Yimin D. Zhang verified the methods and edited the manuscript; Elias Aboutanios verified the methods and edited the manuscript. All authors discussed the results, contributed to the manuscript, and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Asif Haider, M., Zhang, Y.D. & Aboutanios, E. ISAC system assisted by RIS with sparse active elements. EURASIP J. Adv. Signal Process. 2023, 20 (2023). https://doi.org/10.1186/s13634-023-00977-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-023-00977-5