Abstract
We consider two nonlinear scalar delay differential equations with variable delays and give some new conditions for the boundedness and stability by means of the contraction map** principle. We obtain the differences of the two equations about the stability of the zero solution. Previous results are improved and generalized. An example is given to illustrate our theory.
Similar content being viewed by others
1. Introduction
Fixed point theory has been used to deal with stability problems for several years. It has conquered many difficulties which Liapunov method cannot. While Liapunov's direct method usually requires pointwise conditions, fixed point theory needs average conditions.
In this paper, we consider the nonlinear delay differential equations
where 
, 
, 
, 
are continuous functions. We assume the following:
(A1) 
is differentiable,
(A2) the functions 
is strictly increasing,
(A3) 
as 
.
Many authors have investigated the special cases of (1.1) and (1.2). Since Burton [1] used fixed point theory to investigate the stability of the zero solution of the equation 
, many scholars continued his idea. For example, Zhang [2] has studied the equation
Becker and Burton [3] have studied the equation
** and Luo [4] have studied the equation
Burton [5] and Zhang [6] have also studied similar problems. Their main results are the following.
Theorem 1.1 (Burton [1]).
Suppose that 
, a constant, and there exists a constant 
such that
for all 
and 
. Then, for every continuous initial function 
, the solution 
of (1.3) is bounded and tends to zero as 
.
Theorem 1.2 (Zhang [2]).
Suppose that 
is differentiable, the inverse function 
of 
exists, and there exists a constant 
such that for 
-
(i)
(1.7)
-
(ii)
(1.8)
where 
. Then, the zero solution of (1.3) is asymptotically stable if and only if
-
(iii)
(1.9)
Theorem 1.3 (Burton [7]).
Suppose that 
, a constant. Let 
be odd, increasing on 
, and satisfies a Lipschitz condition, and let 
be nondecreasing on 
. Suppose also that for each 
, one has
and there exists 
such that
Then, the zero solution of (1.4) is stable.
Theorem 1.4 (Becker and Burton [3]).
Suppose 
is odd, strictly increasing, and satisfies a Lipschitz condition on an interval 
and that 
is nondecreasing on 
. If
where 
is the unique solution of 
, and if a continuous function 
exists such that
on 
, then the zero solution of (1.5) is stable at 
. Furthermore, if 
is continuously differentiable on 
with 
and
then the zero solution of (1.4) is asymptotically stable.
In the present paper, we adopt the contraction map** principle to study the boundedness and stability of (1.1) and (1.2). That means we investigate how the stability property will be when (1.3) and (1.4) are added to the perturbed term 
. We obtain their differences about the stability of the zero solution, and we also improve and generalize the special case 
. Finally, we give an example to illustrate our theory.
2. Main Results
From existence theory, we can conclude that for each continuous initial function 
there is a continuous solution 
on an interval 
for some 
and 
on 
. Let 
denote the set of all continuous functions 
and 
. Stability definitions can be found in [8].
Theorem 2.1.
Suppose that the following conditions are satisfied:
(i)
, and there exists a constant 
so that if 
, then
(ii)there exists a constant 
and a continuous function 
such that
(iii)
Then, the zero solution of (1.1) is asymptotically stable if and only if
(iv)
Proof.
First, suppose that (iv) holds. We set
Let 
, then 
is a Banach space.
Multiply both sides of (1.1) by 
, and then integrate from 0 to 
to obtain
By performing an integration by parts, we have
or
Let
Then, 
is a complete metric space with metric 
for 
. For all 
, define the map** 
By (i) and 
,
Thus, when 
, 
.
We now show that 
as 
. Since 
and 
as 
, for each 
, there exists a 
such that 
implies 
. Thus, for 
,
Hence, 
as 
. And
By (ii) and (iv), there exists 
such that 
implies
Apply (ii) to obtain 
. Thus, 
as 
. Similarly, we can show that the rest term in (2.10) approaches zero as 
. This yields 
as 
, and hence 
.
Also, by (ii), 
is a contraction map** with contraction constant 
. By the contraction map** principle, 
has a unique fixed point 
in 
which is a solution of (1.1) with 
on 
and 
as 
.
In order to prove stability at 
, let 
be given. Then, choose 
so that 
. Replacing 
with 
in 
, we see there is a 
such that 
implies that the unique continuous solution 
agreeing with 
on 
satisfies 
for all 
. This shows that the zero solution of (1.1) is asymptotically stable if (iv) holds.
Conversely, suppose (iv) fails. Then, by (iii), there exists a sequence 
, 
as 
such that 
for some 
. We may choose a positive constant 
satisfying
for all 
. To simplify the expression, we define
for all 
. By (ii), we have
This yields
The sequence 
is bounded, so there exists a convergent subsequence. For brevity of notation, we may assume that
for some 
and choose a positive integer 
so large that
for all 
, where 
satisfies 
.
By (iii), 
in (2.5) is well defined. We now consider the solution 
of (1.1) with 
and 
for 
. We may choose 
so that 
for 
and
It follows from (2.10) with 
that for 
,
On the other hand, if the solution of (1.1) 
as 
, since 
as 
and (ii) holds, we have
which contradicts (2.22). Hence, condition (iv) is necessary for the asymptotically stability of the zero solution of (1.1). The proof is complete.
When 
, a constant, 
, we can get the following.
Corollary 2.2.
Suppose that the following conditions are satisfied:
(i)
, and there exists a constant 
so that if 
, then
-
(ii)
there exists a constant
such that for all 
, one has 
(2.25)
such that for all 
, one has 
-
(iii)
(2.26)
Then, the zero solution of (1.1) is asymptotically stable if and only if
(iv)
Remark 2.3.
We can also obtain the result that 
is bounded by 
on 
. Our results generalize Theorems 1.1 and 1.2.
Theorem 2.4.
Suppose that a continuous function 
exists such that 
and that the inverse function 
of 
exists. Suppose also that the following conditions are satisfied:
(i)there exists a constant 
such that 
,
-
(ii)
there exists a constant
such that 
satisfy a Lipschitz condition with constant 
on an interval 
,
such that 
satisfy a Lipschitz condition with constant 
on an interval 
,(iii)
and 
are odd, increasing on 
. 
is nondecreasing on 
,
(iv)for each 
, one has
Then, the zero solution of (1.2) is stable.
Proof.
By (iv), there exists 
such that
Let 
be the space of all continuous functions 
such that
where 
is a constant. Then, 
is a Banach space, which can be verified with Cauchy's criterion for uniform convergence.
The equation (1.2) can be transformed as
By the variation of parameters formula, we have
Let
then 
is a complete metric space with metric 
for 
. For all 
, define the map** 
By (i), (iii), and (2.29), we have
Thus, there exists 
such that 
and 
. Hence, 
.
We now show that 
is a contraction map** in 
. For all 
,
Since
we have 
. That means 
. Hence, 
is a contraction map** in 
with constant 
. By the contraction map** principle, 
has a unique fixed point 
in 
, which is a solution of (1.2) with 
on 
and 
.
In order to prove stability at 
, let 
be given. Then, choose 
so that 
. Replacing 
with 
in 
, we see there is a 
such that 
implies that the unique continuous solution 
agreeing with 
on 
satisfies 
for all 
. This shows that the zero solution of (1.2) is stable. That completes the proof.
When 
, a constant, we have the following.
Corollary 2.5.
Suppose that the following conditions are satisfied:
(i)there exists a constant 
such that 
,
(ii)there exists a constant 
such that 
satisfy a Lipschitz condition with constant 
on an interval 
,
(iii)
and 
are odd, increasing on 
. 
is nondecreasing on 
,
(iv)for each 
, one has
Then, the zero solution of the equation
is stable.
Corollary 2.6.
Suppose that the following conditions are satisfied:
(i)there exists a constant 
such that 
,
(ii)there exists a constant 
such that 
, 
, 
satisfy a Lipschitz condition with constant 
on an interval 
,
(iii)
and 
are odd, increasing on 
. 
is nondecreasing on 
,
(iv)for each 
, one has
Then, the zero solution of
is stable.
Remark 2.7.
The zero solution of (1.2) is not as asymptotically stable as that of (1.1). The key is that 
is not complete under the weighted metric when added the condition to 
that 
as 
.
Remark 2.8.
Theorem 2.4 makes use of the techniques of Theorems 1.3 and 1.4.
3. An Example
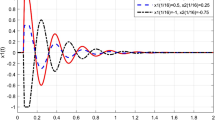
We use an example to illustrate our theory. Consider the following differential equation:
where 
, 
, 
, 
, and 
, 
. This equation comes from [4].
Choosing 
, we have
Let 
, when 
is sufficiently small, 
. Then, the condition (ii) of Theorem 2.1 is satisfied.
Let 
, then the condition (i) of Theorem 2.1 is satisfied.
And 
, then the condition (iii) and (iv) of Theorem 2.1 are satisfied.
According to Theorem 2.1, the zero solution of (3.1) is asymptotically stable.
References
Burton TA: Stability by fixed point theory or Liapunov theory: a comparison. Fixed Point Theory 2003,4(1):15–32.
Zhang B: Fixed points and stability in differential equations with variable delays. Nonlinear Analysis: Theory, Methods and Applications 2005,63(5–7):e233-e242.
Becker LC, Burton TA: Stability, fixed points and inverses of delays. Proceedings of the Royal Society of Edinburgh. Section A 2006,136(2):245–275. 10.1017/S0308210500004546
** C, Luo J: Stability in functional differential equations established using fixed point theory. Nonlinear Analysis: Theory, Methods & Applications 2008,68(11):3307–3315. 10.1016/j.na.2007.03.017
Burton TA: Stability and fixed points: addition of terms. Dynamic Systems and Applications 2004,13(3–4):459–477.
Zhang B: Contraction map** and stability in a delay-differential equation. In Dynamic Systems and Applications. Volume 4. Dynamic, Atlanta, Ga, USA; 2004:183–190.
Burton TA: Stability by fixed point methods for highly nonlinear delay equations. Fixed Point Theory 2004,5(1):3–20.
Hale JK, Verduyn Lunel SM: Introduction to Functional Differential Equations. Springer, New York, NY, USA; 1993.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ding, L., Li, X. & Li, Z. Fixed Points and Stability in Nonlinear Equations with Variable Delays. Fixed Point Theory Appl 2010, 195916 (2010). https://doi.org/10.1155/2010/195916
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/195916