Interval Type-2 Mutual Subsethood Cauchy Fuzzy Neural Inference System (IT2MSCFuNIS)

Abstract

An interval type-2 (IT2) mutual subsethood Cauchy fuzzy neural inference system has been proposed in this paper. The network architecture consists of 3-layers with all connection weights being IT2 Cauchy fuzzy membership functions (CMFs). The crisp inputs to the system are fuzzified into IT2CMFs with fixed centers and uncertain spreads. The hidden layer represents the rule-based knowledge. The firing degree of the antecedent part of each rule at the hidden layer is computed by aggregating the product of the mutual subsethood similarity measures between the inputs and the connection weights. A volume defuzzification is used to compute the numeric output. A gradient descent back-propagation algorithm is used to train the model. The novelty of the proposed model is threefold. First, is enriching the theory of the mutual subsethood fuzzy neural models by adopting the Cauchy membership function (CMF) as another powerful fuzzy basis function (FBF) rather than the classical choice of Gaussian fuzzy membership functions (GMFs). Second, is the success of computing the mutual subsethood similarity measure between the IT2CMFs and all the model parameters’ updating equations in analytic closed-form formulas, not numerically or approximately. Third, is the ability to extract the type-1 (T1) mutual subsethood Cauchy fuzzy neural inference system (T1MSCFuNIS) with all its analytic closed-form formulas directly as a special case from the general formulas of IT2MSCFuNIS model. Such a novelty makes the proposed model a concrete and effective development of the theory of mutual subsethood fuzzy neural models. Both IT2MSCFuNIS and T1MSCFuNIS models have been tested using different examples from the domains of function approximation, classification, and prediction. The results ensure the efficacy of both models compared with other models reported in the literature.

1 Introduction

Fuzzy logic has been successfully used in a wide range of real-world applications. There are mainly two different approaches for designing a Fuzzy Logic System (FLS), namely: type-1 FLS (T1FLS) and type-2 FLS (T2FLS). The primary distinction between the two types is that grades of membership functions (MFs) in T1FLS are certain, whereas they are fuzzy in T2FLS [1].

Although T1FLSs have been used in a variety of nonlinear application problems, they still cannot handle high uncertainties, which affect the accuracy and performance of the systems. Such uncertainties stem from a variety of sources, including differences in the expert estimation of the MFs of the same linguistic values, different answers to the same question, noise in measurements, and noisy data [2, 3].

On the other hand, since MFs in T2FLSs are themselves fuzzy, they can handle uncertainties better than their type-1 counterparts.

The fact that the Footprint of Uncertainty (FOU) of a type-2 fuzzy MF (T2FMF) contains arbitrary forms of type-1 fuzzy MF (T1FMF) allows handling higher levels of uncertainty, particularly in noisy environments and environments with incomplete data [4]. However, despite such a powerful capability of T2FLSs, they are highly computationally expensive and time-consuming [5]. Therefore, interval type-2 fuzzy logic system (IT2FLs) has been proposed as a simplified less computational complexity form of the general T2FLs [6, 7].

IT2 fuzzy sets (IT2FSs) have been used in a wide range of applications. In [8], Liu, and Mendel presented a practical type-2 fuzzistics methodology for obtaining IT2FS models for words. In [9], Castro et al. presented a novel homogeneous integration strategy for an IT2 fuzzy inference system and applied it to forecasting the Mackey–Glass chaotic time series. In [10], Du et al. proposed an IT2 fuzzy control for nonlinear plants with parameter uncertainty. In [11], Chen and Barman proposed an adaptive weighted fuzzy interpolative reasoning method based on representative values and similarity measures of IT2 polygonal fuzzy sets to resolve contradictions in fuzzy rule-based systems. In [12], Li et al. applied Gaussian IT2FS theory to historical traffic volume data processing to obtain a high-precision 24-h prediction of traffic volume. In [31], in dynamic systems processing, e.g. [32, 33] and in time series prediction, e.g. [34, 35].

Earlier researches emphasized the direct effect of the shape of fuzzy sets adopted for the inputs of a fuzzy system on its approximation capability [36]. Therefore, more shapes of fuzzy membership functions (FMFs) should be investigated rather than being limited to a few traditional forms [37].

Motivated by this idea, this paper presents an enhancement to the theory of MSFuNIS models by develo** a more advanced concise model. The proposed model is called: Interval type-2 Mutual Subsethood Cauchy Fuzzy Neural Inference system (IT2MSCFuNIS). For more than two decades, Gaussian fuzzy membership functions (GFMFs) were the standard selection as a FBF for develo** most FNN models, and in particular for develo** MSFuNIS models [38]. This paper has three contributions. The first is the adoption of the Cauchy fuzzy membership function (CFMF) as a new FBF for develo** an MSFuNIS model. The second is the success of computing fuzzy mutual subsethood similarity between two IT2CFMFS and all updating equations of the network parameters in analytic closed-form formulas without any need to perform several mathematical integration operations, or to make an approximation of the membership function, or to employ numeric computations as found in all previous works that adopted GFMFs. Third, is the success of extracting the type-1 mutual subsethood Cauchy fuzzy neural inference system (T1MSCFuNIS) model with all its analytic closed-form formulas directly from the general case of IT2.

The remainder of this paper is organized as follows. Section 2 presents some basic concepts of T1FSs and T2FSs. Section 3 presents a basic mathematical background of IT2 Cauchy fuzzy sets. It also presents the proposed closed-form analytic formula of mutual subsethood similarity between two Cauchy IT2MFs. Section 4 describes the architecture of the proposed model and the closed-form formulas of all updating equations of the learning parameters. Section 5 outlines the simulation results. Section 6 presents more discussions with further extensions of this work. Section 7 concludes the paper.

2 Basic Concepts

2.1 Types of Fuzzy Sets

Types of fuzzy sets are briefly defined as follows [5, 39, 40]:

Definition 1

T1FS $\widetilde{A}$ can be defined as:

$$\widetilde{A}=\left\{\left(x, {\mu }_{\widetilde{A}}\left(x\right)\right)\left|\forall x\in X\right.\right\}$$

(1)

where x is a variable with the domain X and the membership ${\mu }_{\widetilde{A}}\left(x\right)\in \left[\mathrm{0,1}\right]$.

Definition 2

The general T2FS $\widetilde{A}$ can be defined as:

$$\widetilde{A}=\left\{\left(\left(x, u\right), {\mu }_{\widetilde{A}}\left(x,u\right)\right)\left|\forall x\in X, u\in [\mathrm{0,1}]\right.\right\}$$

(2)

where x is the primary variable with the domain X, $u\in \left[\mathrm{0,1}\right]$ is the primary membership, and ${\mu }_{\widetilde{A}}\left(x,u\right)$ is the secondary membership and ${\mu }_{\widetilde{A}}\left(x,u\right)\in \left[\mathrm{0,1}\right]$.

Definition 3

The IT2FS $\widetilde{A}$ is a special case of the general T2FS wherein it always has ${\mu }_{\widetilde{A}}\left(x,u\right)=1$, can be defined as:

$$\widetilde{A}=\left\{\left(\left(x, u\right), 1\right)\left|\forall x\in X, u\in [\mathrm{0,1}]\right.\right\}$$

(3)

where x is the primary variable with the domain X and $u\in \left[\mathrm{0,1}\right]$ is the primary membership.

2.2 Cauchy Fuzzy Sets

A Cauchy fuzzy set is a special case of Bell-shaped fuzzy sets. The membership function of T1 Cauchy FS is as follows:

$${\mu }_{\widetilde{A}}\left(x\right)=\frac{1}{1+{\left(\frac{x-a}{b}\right)}^{2}}$$

(4)

The membership function of the IT2 Cauchy FS has two forms. The first form is given as:

$${\mu }_{\widetilde{A}}\left(x\right)=\frac{1}{1+{\left(\frac{x-a}{b}\right)}^{2}} ,b \in \left[ \underline{b},\overline{b }\right]$$

(5)

where a is a fixed center and b is an uncertain spread.

The second form is:

$${\mu }_{\widetilde{A}}\left(x\right)=\frac{1}{1+{\left(\frac{x-a}{b}\right)}^{2}} ,a \in \left[ \underline{a},\overline{a }\right]$$

(6)

where a is an uncertain center and b is a fixed spread.

In this paper, we will adopt the first form of the IT2 Cauchy FS where the FOU is bounded by the lower MF with lower spread bl, and the upper MF is bounded by the upper spread bu as shown in Fig. 1.

Fig. 1

IT2 Cauchy fuzzy MF with fixed center and uncertain spread

3 The Basic Mathematical Background of IT2 Cauchy Fuzzy Sets

Let $\widetilde{A}$ and $\widetilde{B}$ be two IT2 Cauchy FSs of the first form. Each of the membership functions ${\mu }_{\widetilde{A}}(x)$ and ${\mu }_{\widetilde{B}}(x)$ are formed of upper and lower membership functions. Then the upper and lower membership functions of $\widetilde{A}$ are:

$${\overline{\mu }}_{\widetilde{A}}\left(x\right)=\frac{1}{1+{\left(\frac{x-{a}_{1}}{{\overline{b}}_{1}}\right)}^{2}} ,\, {\underline{\mu }}_{\widetilde{A}}\left(x\right)=\frac{1}{1+{\left(\frac{x-{a}_{1}}{{\underline{b}}_{1}}\right)}^{2}}$$

(7)

Similarly, the upper and lower membership functions of $\widetilde{B}$

$${\overline{\mu }}_{\widetilde{B}}\left(x\right)=\frac{1}{1+{\left(\frac{x-{a}_{2}}{{\overline{b}}_{2}}\right)}^{2}} , \,{\underline{\mu }}_{\widetilde{B}}\left(x\right)=\frac{1}{1+{\left(\frac{x-{a}_{2}}{{\underline{b}}_{2}}\right)}^{2}}$$

(8)

3.1 Points of Intersection

Assuming that ${\underline{x}}_{int}$ and ${\underline{x}}_{ext }$ are the internal and external points of intersection of ${\underline{\mu }}_{\widetilde{A}}\, and\, {\underline{\mu }}_{\widetilde{B}}$, then based on [40]:

$${\underline{x}}_{int }=\frac{{\underline{b}}_{2}{a}_{1}+{\underline{b}}_{1}{a}_{2}}{{\underline{b}}_{2}+{\underline{b}}_{1}} , \,{\underline{x}}_{ext }=\frac{{\underline{b}}_{2}{a}_{1}-{\underline{b}}_{1}{a}_{2}}{{\underline{b}}_{2}-{\underline{b}}_{1}}$$

(9)

Assuming that ${\overline{x}}_{int}$ and ${\overline{x}}_{ext }$ are the internal and external points of intersection of ${\overline{\mu }}_{\widetilde{A}} \,and\, {\overline{\mu }}_{\widetilde{B}}$, respectively

$${\overline{x}}_{int }=\frac{ {\overline{b}}_{2}{a}_{1}+{\overline{b}}_{1}{a}_{2}}{ {\overline{b}}_{2}+{\overline{b}}_{1}} ,\, {\overline{x}}_{ext }=\frac{ {\overline{b}}_{2}{a}_{1}-{\overline{b}}_{1}{a}_{2}}{ {\overline{b}}_{2}-{\overline{b}}_{1}}$$

(10)

Additionally, the following set of useful relations can be obtained from (7)–(10) as follows:

$$\frac{{\underline{x}}_{int }-{a}_{1}}{{\underline{b}}_{1}}=-\left(\frac{{\underline{x}}_{int }-{a}_{2}}{{\underline{b}}_{2}}\right)=\frac{ {a}_{2}-{a}_{1}}{ {\underline{b}}_{2}+{\underline{b}}_{1}}$$

(11)

$$\frac{{\overline{x}}_{int }-{a}_{1}}{{\overline{b}}_{1}}=-\left(\frac{{\overline{x}}_{int }-{a}_{2}}{{\overline{b}}_{2}}\right)=\frac{ {a}_{2}-{a}_{1}}{ {\overline{b}}_{2}+{\overline{b}}_{1}}$$

(12)

$$\frac{{\underline{x}}_{ext }-{a}_{1}}{{\underline{b}}_{1}}=\frac{{\underline{x}}_{ext }-{a}_{2}}{{\underline{b}}_{2}}=\frac{ {a}_{1}-{a}_{2}}{ {\underline{b}}_{2}-{\underline{b}}_{1}}$$

(13)

$$\frac{{\overline{x}}_{ext }-{a}_{1}}{{\overline{b}}_{1}}=\frac{{\overline{x}}_{ext }-{a}_{2}}{{\overline{b}}_{2}}=\frac{ {a}_{1}-{a}_{2}}{ {\overline{b}}_{2}-{\overline{b}}_{1}}$$

(14)

denoting the membership degrees at ${\underline{x}}_{int }, {\underline{x}}_{ext }{\overline{x}}_{int },\,and\, {\overline{x}}_{ext}$ as$\underline{v } ,\underline{w}, \overline{ v}, and \overline{w} {\text{respectively}}$, then from (11)–(14) we have

$$\underline{v}={\underline{\mu }}_{\widetilde{A}}\left({\underline{x}}_{int }\right)={\underline{\mu }}_{\widetilde{B}}\left({\underline{x}}_{int }\right)= \frac{1}{1+{\left(\frac{ {a}_{2}-{a}_{1}}{ {\underline{b}}_{2}+{\underline{b}}_{1}}\right)}^{2}}$$

(15)

$$\underline{w}={\underline{\mu }}_{\widetilde{A}}\left({\underline{x}}_{ext }\right)={\underline{\mu }}_{\widetilde{B}}\left({\underline{x}}_{ext }\right)= \frac{1}{1+{\left(\frac{ {a}_{2}-{a}_{1}}{ {\underline{b}}_{2}-{\underline{b}}_{1}}\right)}^{2}}$$

(16)

$$\overline{v}={\overline{\mu }}_{\widetilde{A}}\left({\overline{x}}_{int }\right)={\overline{\mu }}_{\widetilde{B}}\left({\overline{x}}_{int }\right)=\frac{1}{1+{\left(\frac{{a}_{2}-{a}_{1}}{{{\overline{b}}_{2}+\overline{b}}_{1}}\right)}^{2}}$$

(17)

$$\overline{w}={\overline{\mu }}_{\widetilde{A}}\left({\overline{x}}_{ext }\right)={\overline{\mu }}_{\widetilde{B}}\left({\overline{x}}_{ext }\right)=\frac{1}{1+{\left(\frac{{a}_{2}-{a}_{1}}{{{\overline{b}}_{2}-\overline{b}}_{1}}\right)}^{2}}$$

(18)

Because of the convexity of the Cauchy fuzzy set, see Fig. 2, it is obvious from (15)–(18) that $\underline{v }$ is always greater than or equal to $\underline{w}$ and $\overline{v}$ is always greater than or equal to $\overline{w}$, i.e., $\underline{v } \ge \underline{w}\, and\, \overline{v} \ge \overline{w}$.

Fig.2

The intersection points of two IT2 Cauchy fuzzy sets

3.2 The Similarity Measure of Two IT2 Cauchy Fuzzy Sets

Wu and Mendel proposed a similarity measure for type-2 fuzzy sets that is an extension of Jaccard's similarity measure. The new similarity measure is defined as [41]:

$$S\left(\widetilde{A},\widetilde{B}\right)=\frac{{|\overline{\mu }}_{\widetilde{A}}\left(x\right)\cap {\overline{\mu }}_{\widetilde{B}}\left(x\right)|+|{\underline{\mu }}_{\widetilde{A}}\left(x\right)\cap {\underline{\mu }}_{\widetilde{B}}\left(x\right)|}{{|\overline{\mu }}_{\widetilde{A}}\left(x\right)\cup {\overline{\mu }}_{\widetilde{B}}\left(x\right)|+|{\underline{\mu }}_{\widetilde{A}}\left(x\right)\cup {\underline{\mu }}_{\widetilde{B}}\left(x\right)|}$$

(19)

where: $\widetilde{A},\widetilde{B}$ are two IT2 Cauchy FSs, $\cap$ is the fuzzy intersection operation, and $\cup$ is the fuzzy union operation. Based on our analytic closed-form formula of mutual subsethood similarity measure between two type-1 Cauchy fuzzy sets [42], we have the following generalized proposition; see the proof in Appendix A.

Proposition 1

The similarity measure of two IT2 Cauchy FSs

$$ S\left( {\tilde{A},B} \right) = \frac{{\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{min}} + \bar{b}_{{min}} } \right)\pi + (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } + \bar{\Omega })}}{{(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{max}} + \bar{b}_{{max}} )\pi - (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } + \bar{\Omega })}} $$

(20)

where,

$$ \begin{gathered} \overline{\Omega } = \left( {\overline{b}_{\max } - \overline{b}_{\min } } \right) \tan^{ - 1} \left( {\frac{{a_{\max } - a_{\min } }}{{\overline{b}_{\max } - \overline{b}_{\min } }}} \right) \hfill \\ \;\;\;\;\;\; - \left( {\overline{b}_{\max } + \overline{b}_{\min } } \right) \tan^{ - 1} \left( {\frac{{a_{\max } - a_{\min } }}{{\overline{b}_{\max } + \overline{b}_{\min } }}} \right) \hfill \\ \end{gathered} $$

(21)

$$ \begin{gathered} \underline {\Omega } = \left( {\underline {b}_{\max } - \underline {b}_{\min } } \right) \tan^{ - 1} \left( {\frac{{a_{\max } - a_{\min } }}{{\underline {b}_{\max } - \underline {b}_{\min } }}} \right) \hfill \\ \;\;\;\;\;\; - \left( {\underline {b}_{\max } + \underline {b}_{\min } } \right) \tan^{ - 1} \left( {\frac{{a_{\max } - a_{\min } }}{{\underline {b}_{\max } + \underline {b}_{\min } }}} \right) \hfill \\ \end{gathered} $$

(22)

$${\underline{b}}_{min}=\mathit{min}\left({\underline{b}}_{1},{\underline{b}}_{2}\right) , {\underline{b}}_{max}=\mathit{max}\left({\underline{b}}_{1},{\underline{b}}_{2}\right)$$

(23)

$${\overline{b}}_{min}=\mathit{min}\left({\overline{b}}_{1},{\overline{b}}_{2}\right) , {\overline{b}}_{max}=\mathit{max}\left({\overline{b}}_{1},{\overline{b}}_{2}\right)$$

(24)

$${a}_{min}=\mathit{min}\left({a}_{1},{a}_{2}\right) , {a}_{max}=\mathit{max}\left({a}_{1},{a}_{2}\right)$$

(25)

Corollary 1

The following three special cases can be obtained directly:

$$S\left(\widetilde{{\text{A}}},\widetilde{{\text{B}}}\right)=0,if \,{\underline{b}}_{min}=0, {\overline{b}}_{min}=0,$$

(26)

$$S\left(\widetilde{A},\widetilde{B}\right)=\frac{ {\underline{b}}_{min}+{\overline{b}}_{min}}{{\underline{b}}_{max}+{\overline{b}}_{max}} ,if \,{a}_{max}={a}_{min}$$

(27)

$$S\left(\widetilde{A},\widetilde{B}\right)=\frac{1-\psi }{1+\psi }, if\, {\underline{b}}_{min}= {\underline{b}}_{max}=\underline{b}$$

$$and\, {\overline{b}}_{min}={\overline{b}}_{max}=\overline{b}$$

(28)

where

$$\psi =\frac{2\left[\underline{b}\; {tan}^{-1}\left(\frac{{a}_{max}-{a}_{min}}{2\underline{b}}\right)+\overline{b}\; {tan}^{-1}\left(\frac{{a}_{max}-{a}_{min}}{2\overline{b}}\right)\right]}{( \underline{b}+\overline{b})\pi }$$

(29)

4 Architecture and Operational Details of the Proposed IT2MSCFuNIS Model

The proposed fuzzy neural model is a Mamdani-type model that represents fuzzy rules in the following form:

$${Rule}_{j}:IF\, {x}_{1}\,is\, {\widetilde{A}}_{1}^{j}\,and{\,x}_{2} \,is\, {\widetilde{A}}_{2}^{j},\, \dots , \,and\, {x}_{n}\, is\, {\widetilde{A}}_{n}^{j},$$

$$THEN\, {y}_{1}\, is\, {\widetilde{B}}_{1}^{j}\, and\,{y}_{2}\, is\, {\widetilde{B}}_{2}^{j},\, \dots , \,and\, {y}_{p}\,is\, {\widetilde{B}}_{p}^{j}$$

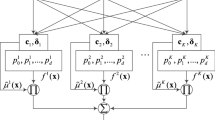
Where x_j, i = 1,…,n are the inputs, ${\widetilde{A}}_{i}^{j}$ j = 1,…, m are T2 Cauchy FSs that are defined on the input universes of discourses (UODs) to represent input linguistic values, y_k, k = 1,…, p are the outputs, and ${\widetilde{B}}_{k}^{j}$ are T2 Cauchy FSs defined on the output UODs to represent output linguistic values. Figure 3 shows the proposed architecture of a subsethood based Fuzzy neural network where x₁ to ${x}_{m}$ and ${x}_{m+1}$ to ${x}_{n}$ are linguistic and numeric inputs respectively. Domain variables or features are represented by input nodes and target variables or classes are represented by output nodes. Each hidden node represents a fuzzy rule, and connections between hidden nodes and input nodes represent fuzzy rule antecedents. Each hidden-output node connection is a result of a fuzzy rule. Fuzzy sets which correspond to linguistic labels of fuzzy if–then rules (such as SHORT, MEDIUM, and TALL), are defined on input and output UODs and represented by IT2 Cauchy MFs with a center, lower spread, and upper spread. Thus, fuzzy link weight ${w}_{ji}$ from input nodes i to rule nodes j is thus modeled by the center ${w}_{ji}^{a}$, lower spread, and upper spread ${w}_{ji}^{b}$ of a Cauchy FS and denoted by ${w}_{ji}=\left({w}_{ji}^{a},{w}_{ji}^{\underline{b}},{w}_{ji}^{\overline{b}}\right).$ In the same way, the consequent fuzzy link weight from rule node j to output node k is denoted by ${w}_{kj}=\left({w}_{kj}^{a},{w}_{kj}^{\underline{b}},{w}_{kj}^{\overline{b}}\right).$

Fig. 3

The architecture of the fuzzy neural model

This proposed model can accept both numeric and fuzzy inputs simultaneously. Numeric inputs are first fuzzified, thus all network inputs are fuzzy. Since antecedent weights are also fuzzy, a method for transmitting a fuzzy signal along with a fuzzy weight is required. In this proposed model, along with the fuzzy weight, fuzzy mutual subsethood is used to handle a signal transmission. The strength of firing at the rule node is computed by a product aggregation operator. At the output layer, the signal computation is conducted via volume defuzzification to generate numeric outputs y₁, y₂, … y_p. With the help of numerical training data, a gradient descent learning technique allows the model to fine-tune rules. Figure 3 shows the 3-layers architecture of the proposed fuzzy neural model where,

${x}_{i}$_: the crisp input (numeric or linguistic) i = 1, 2,.., n

${\widetilde{x}}_{i}$: the fuzzified form of the crisp input ${x}_{i}$

Thus, we have ${\widetilde{x}}_{i}=\left({x}_{i},{\underline{b}}_{xi},{\overline{b}}_{xi}\right)$ expressed as follows:

$${\widetilde{x}}_{i}=\frac{1}{1+{\left(\frac{x-{x}_{i}}{b{x}_{i}}\right)}^{2}} , b{x}_{i}\in \left[ {\underline{b}}_{xi},{\overline{b}}_{xi}\right]$$

(30)

$${\underline{x}}_{i}=\frac{1}{1+{\left(\frac{x-{x}_{i}}{\underline{b}{x}_{i}}\right)}^{2}} , {\overline{x}}_{i}=\frac{1}{1+{\left(\frac{x-{x}_{i}}{\overline{b}{x}_{i}}\right)}^{2}}$$

(31)

The link weight ${\widetilde{{\text{w}}}}_{ji}=\left({a}_{ji},{\underline{b}}_{ji},{\overline{b}}_{ji}\right)$ between node j in the hidden layer and input i where j = 1,2, … m is expressed as follows:

$${\widetilde{{\text{w}}}}_{ji }=\frac{1}{1+{\left(\frac{x-{a}_{ji}}{{b}_{ji}}\right)}^{2}} , {b}_{ji}\in \left[{\underline{b}}_{ji},{\overline{b}}_{ji}\right]$$

(32)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\text{w}} _{{ji}} = \frac{1}{{1 + \left( {\frac{{{\text{x}} - a_{{ji}} }}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{ji}} }}} \right)^{2} }},\bar{w}_{{ji}} = \frac{1}{{1 + \left( {\frac{{x - a_{{ji}} }}{{\bar{b}_{{ji}} }}} \right)^{2} }} $$

(33)

Similarly, the link weight ${\widetilde{w}}_{kj}=\left({a}_{kj},{\underline{b}}_{kj},\,{\overline{b}}_{kj}\right)$ between node k in the output layer and node j in the hidden layer, k = 1, 2, 3, …, p, is expressed as:

$${\widetilde{{\text{w}}}}_{kj }=\frac{1}{1+{\left(\frac{x-{a}_{kj}}{{b}_{kj}}\right)}^{2}} ,\, { b}_{kj}\in \left[{\underline{b}}_{kj},{\overline{b}}_{kj}\right]$$

(34)

$${\underline{{\text{w}}}}_{kj }=\frac{1}{1+{\left(\frac{x-{a}_{kj}}{{\underline{b}}_{kj}}\right)}^{2}} ,\, {\overline{{\text{w}}}}_{kj }=\frac{1}{1+{\left(\frac{x-{a}_{kj}}{{\overline{b}}_{kj}}\right)}^{2}}$$

(35)

From (20)–(22)

$${\upvarepsilon }_{{\text{ji}}}={{\text{S}}}_{{\text{ji}}}\left({\widetilde{x}}_{{\text{i}}},{\widetilde{{\text{w}}}}_{{\text{ji}}}\right)=\frac{\left( {\underline{b}}_{ji min}+{\overline{b}}_{ji min}\right)\pi +({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji} ) }{ ({\underline{b}}_{ji max}+{\overline{b}}_{ji max})\pi -({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji})}$$

(36)

$$ \begin{gathered} \underline {\Omega }_{ji} = \left( {\underline {b}_{ji \max } - \underline {b}_{ji \min } } \right) \tan^{ - 1} \left( {\frac{{a_{ji \max } - a_{ji \min } }}{{\underline {b}_{ji \max } - \underline {b}_{ji \min } }}} \right) \hfill \\ \;\;\;\;\;\;\;\; - \left( {\underline {b}_{ji \max } + \underline {b}_{ji \min } } \right) \tan^{ - 1} \left( {\frac{{a_{ji \max } - a_{ji \min } }}{{\underline {b}_{ji \max } + \underline {b}_{ji \min } }}} \right) \hfill \\ \end{gathered} $$

(37)

$$ \begin{gathered} \overline{\Omega }_{ji} = \left( {\overline{b}_{ji \max } - \overline{b}_{ji \min } } \right) \tan^{ - 1} \left( {\frac{{a_{ji \max } - a_{ji \min } }}{{\overline{b}_{ji \max } - \overline{b}_{ji \min } }}} \right) \hfill \\ \;\;\;\;\;\;\;\; - \left( {\overline{b}_{ji \max } + \overline{b}_{ji \min } } \right) \tan^{ - 1} \left( {\frac{{a_{ji \max } - a_{ji \min } }}{{\overline{b}_{ji \max } + \overline{b}_{ji \min } }}} \right) \hfill \\ \end{gathered} $$

(38)

where

$${a}_{ji min}=\mathit{min}\left({x}_{i},{a}_{ji}\right) ,\, {a}_{ji max}=\mathit{max}({x}_{i},{a}_{ji})$$

(39)

$${\underline{b}}_{ji min}=\mathit{min}\left(\underline{b}{x}_{i}, {\underline{b}}_{ji}\right) ,\, {\underline{b}}_{ji max}=\mathit{max}\left(\underline{b}{x}_{i}, {\underline{b}}_{ji}\right)$$

(40)

$${\overline{b}}_{ji min}=\mathit{min}(\overline{b}{x}_{i}, {\overline{b}}_{ji}) , \,{\overline{b}}_{ji max}=\mathit{max}(\overline{b}{x}_{i}, {\overline{b}}_{ji})$$

(41)

$${{\text{z}}}_{{\text{j}}}= \prod_{{\text{i}}=1}^{{\text{n}}}{\upvarepsilon }_{{\text{ji}}}=\prod_{{\text{i}}=1}^{{\text{n}}}{{\text{S}}}_{{\text{ji}}}\left({\widetilde{x}}_{{\text{i}}},{\widetilde{{\text{w}}}}_{{\text{ji}}}\right)$$

(42)

where ${S}_{ji}$ is the set-theoretic similarity measure between ${\widetilde{x}}_{i}$ and ${w}_{ji}$, ${z}_{j}$ is considered as the firing degree of the rule # j.

(i.e., hidden node #j) of the fuzzy neural model.

The model output at node k is y_k, k = 1, 2, 3, …, p, where

$${y}_{k}=\lambda {\overline{y}}_{k}+\left(1-\lambda \right){\underline{y}}_{k}$$

(43)

where $\lambda$ is the weighing constant, which is set within the range [0, 0.5].

$${\overline{y}}_{k}=\frac{\sum_{j=1}^{m}{z}_{j}{a}_{kj}{\overline{V}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\overline{V}}_{kj}} , \,{\underline{y}}_{k}=\frac{\sum_{j=1}^{m}{z}_{j}{a}_{kj}{\underline{V}}_{ kj}}{\sum_{j=1}^{m}{z}_{j}{ \underline{V}}_{ kj}}$$

(44)

In our case, the volume ${\overline{V}}_{kj}$ is simply the area of consequent weight fuzzy sets represented by IT2 Cauchy membership functions. Thus, ${\overline{V}}_{kj}$ is ${\overline{b}}_{kj}\pi$, and ${\underline{V}}_{ kj}$ is ${\underline{b}}_{kj}\pi$, then we have

$${\overline{y}}_{k}=\frac{\sum_{j=1}^{m}{z}_{j}{a}_{kj}{\overline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}} ,\, {\underline{y}}_{k}=\frac{\sum_{j=1}^{m}{z}_{j}{a}_{kj}{\underline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}$$

(45)

Thus, from (45) to (43), then we have

$${y}_{k}=\lambda \left(\frac{\sum_{j=1}^{m}{z}_{j}{a}_{kj}{\overline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}}\right)+\left(1-\lambda \right)\left(\frac{\sum_{j=1}^{m}{z}_{j}{a}_{kj}{\underline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}\right)$$

(46)

4.1 Iterative Update Equations

Based on the training data, a supervised learning approach based on a gradient descent method is used for updating the model’s parameters. The training performance criterion is taken as a squared error function:

$$E(t)=\frac{1}{2}\sum_{k=1}^{p}{({d}_{k}\left(t\right)-{y}_{k}(t))}^{2}$$

(47)

where E(t) is the error at iteration t, d_k(t) is the desired output at output node k, y_k(t) is the actual output at node k, and p is the number of nodes in the output layer. The model requires all link weights ${w}_{kj}=\left({w}_{kj}^{a},{w}_{kj}^{\underline{b}},{w}_{kj}^{\overline{b}}\right)$ at the output layer, and all link weights at the hidden layer ${w}_{ji}=\left({w}_{ji}^{a},{w}_{ji}^{\underline{b}},{w}_{ji}^{\overline{b}}\right)$ layers of the network to be IT2 Cauchy fuzzy sets. The basic update equations starting from the output layer and then the hidden layers are as follows:

$${a}_{kj}\left(t+1\right)={a}_{kj}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {a}_{kj}\left(t\right)}\right)+\alpha \Delta {a}_{kj}\left(t-1\right)$$

(48)

$${\underline{b}}_{kj}\left(t+1\right)={\underline{b}}_{kj}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {\underline{b}}_{kj}\left(t\right)}\right)+\alpha \Delta {\underline{b}}_{kj}\left(t-1\right)$$

(49)

$${\overline{b}}_{kj}\left(t+1\right)={\overline{b}}_{kj}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {\overline{b}}_{kj}\left(t\right)}\right)+\alpha \Delta {\overline{b}}_{kj}\left(t-1\right)$$

(50)

$${a}_{ji}\left(t+1\right)={a}_{ji}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {a}_{ji}\left(t\right)}\right)+\alpha \Delta {a}_{ji}\left(t-1\right)$$

(51)

$${\underline{b}}_{ji}\left(t+1\right)={\underline{b}}_{ji}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {\underline{b}}_{ji}\left(t\right)}\right)+\alpha \Delta {\underline{b}}_{ji}\left(t-1\right)$$

(52)

$${\overline{b}}_{ji}\left(t+1\right)={\overline{b}}_{ji}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {\overline{b}}_{ji}\left(t\right)}\right)+\alpha \Delta {\overline{b}}_{ji}\left(t-1\right)$$

(53)

$${\underline{b}}_{xi}\left(t+1\right)={\underline{b}}_{xi}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {\underline{b}}_{xi}\left(t\right)}\right)+\alpha \Delta {\underline{b}}_{xi}\left(t-1\right)$$

(54)

$${\overline{b}}_{xi}\left(t+1\right)={\overline{b}}_{xi}\left(t\right)-\eta \left(\frac{\partial E\left(t\right)}{\partial {\overline{b}}_{xi}\left(t\right)}\right)+\alpha \Delta {\overline{b}}_{xi}\left(t-1\right)$$

(55)

where $\eta$ is the learning rate, and $\alpha$ is the momentum parameter.

$$\Delta {a}_{kj}\left(t-1\right)={a}_{kj}\left(t\right)-{a}_{kj}\left(t-1\right)$$

(56)

$$\Delta {\underline{b}}_{kj}\left(t-1\right)={\underline{b}}_{kj}\left(t\right)-{\underline{b}}_{kj}\left(t-1\right)$$

(57)

$$\Delta {\overline{b}}_{kj}\left(t-1\right)={\overline{b}}_{kj}\left(t\right)-{\overline{b}}_{kj}\left(t-1\right)$$

(58)

$$\Delta {a}_{ji}\left(t-1\right)={a}_{ji}\left(t\right)-{a}_{ji}\left(t-1\right)$$

(59)

$$\Delta {\underline{b}}_{ji}\left(t-1\right)={\underline{b}}_{ji}\left(t\right)-{\underline{b}}_{ji}\left(t-1\right)$$

(60)

$$\Delta {\overline{b}}_{ji}\left(t-1\right)={\overline{b}}_{ji}\left(t\right)-{\overline{b}}_{ji}\left(t-1\right)$$

(61)

$$\Delta {\underline{b}}_{xi}\left(t-1\right)={\underline{b}}_{xi}\left(t\right)-{\underline{b}}_{xi}\left(t-1\right)$$

(62)

$$\Delta {\overline{b}}_{xi}\left(t-1\right)={\overline{b}}_{xi}\left(t\right)-{\overline{b}}_{xi}\left(t-1\right)$$

(63)

4.2 Evaluation of Partial Derivatives

The following are the exact closed-form formulas for the partial derivatives needed for the iterative updates in the output and the hidden layers. The proof of all formulas is given in Appendix B.

4.2.1 At the Output Layer

The exact formulas of the partial derivatives of the updating parameters at this layer are as follows:

$$\frac{\partial E}{\partial {a}_{kj}}=-\left({d}_{k}-{y}_{k}\right)\left(\frac{\lambda {z}_{j}{\overline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}}+\frac{{\left(1-\lambda \right)z}_{j}{\underline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}\right)$$

(64)

$$\frac{\partial E}{\partial {\underline{b}}_{kj}}=-\left(1-\lambda \right){ z}_{j}\left({d}_{k}-{\underline{y}}_{k}\right)\left(\frac{{a}_{kj}-{\underline{y}}_{k} }{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}\right)$$

(65)

$$\frac{\partial E}{\partial {\overline{b}}_{kj}}=-\lambda { z}_{j} \left({d}_{k}-{\overline{y}}_{k}\right)\left(\frac{{a}_{kj}-{\overline{y}}_{k} }{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}}\right)$$

(66)

4.2.2 At the Hidden Layer

The exact formulas of the partial derivatives of the updating parameters at this layer are as follows:

$$ \begin{gathered} \frac{{\partial E}}{{\partial a_{{jimin}} }} = \left( {\frac{{\varepsilon _{{ji}} + 1}}{{\varepsilon _{{ji}} }}} \right)\frac{{\left[ {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} + \bar{v}_{{ji}} } \right) - \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} + \bar{w}_{{ji}} } \right)} \right]}}{{\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} + \bar{b}_{{jimax}} } \right)\pi - \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } _{{ji}} + \bar{\Omega }_{{ji}} } \right)}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{{k = 1}}^{p} {\left( {d_{k} - y_{k} } \right)} \left[ {\frac{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{kj}} }}{{\left( {d_{k} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{y} _{k} } \right)}}\left( {\frac{{\partial E}}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{kj}} }}} \right) + \frac{{\bar{b}_{{kj}} }}{{\left( {d_{k} - \bar{y}_{k} } \right)}}\left( {\frac{{\partial E}}{{\partial \bar{b}_{{kj}} }}} \right)} \right] \hfill \\ \end{gathered} $$

(67)

$$\frac{\partial E}{\partial {a}_{ji max}}=-\left(\frac{\partial E}{\partial {a}_{ji min}}\right)$$

(68)

$$\frac{\partial E}{\partial {\underline{b}}_{ji min}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left(\frac{\left({\varepsilon }_{ji}+1\right)\left(\underline{\tau }+\underline{\rho }\right)+\pi }{\left({\varepsilon }_{ji}+1\right)\left[\left({\underline{v}}_{ji}+{\overline{v}}_{ji}\right)-\left({\underline{w}}_{ji}+{\overline{w}}_{ji}\right)\right]}\right)$$

(69)

$$\frac{\partial {\text{E}}}{\partial {\overline{{\text{b}}}}_{\mathrm{ji min}}}=\left(\frac{\partial {\text{E}}}{\partial {\underline{{\text{b}}}}_{\mathrm{ji min}}}\right)\left[\frac{\left({\upvarepsilon }_{{\text{ji}}}+1\right)\left( \overline{\uptau }+ \overline{\uprho }\right)+\uppi }{\left({\upvarepsilon }_{{\text{ji}}}+1\right)\left(\underline{\uptau }+\underline{\uprho }\right)+\uppi }\right]$$

(70)

$$\frac{\partial E}{\partial {\underline{b}}_{ji max}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left(\frac{\left({\varepsilon }_{ji}+1\right)\left(\underline{\tau }-\underline{\rho }\right)-{\varepsilon }_{ji}\pi }{\left({\varepsilon }_{ji}+1\right)\left[\left({\underline{v}}_{ji}+{\overline{v}}_{ji}\right)-\left({\underline{w}}_{ji}+{\overline{w}}_{ji}\right)\right]}\right)$$

(71)

$$\frac{\partial E}{\partial {\overline{b}}_{ji max}}=\left(\frac{\partial E}{\partial {\underline{b}}_{ji max}}\right)\left[\frac{\left({\varepsilon }_{ji}+1\right)\left( \overline{\tau }- \overline{\rho }\right)-{\varepsilon }_{ji}\pi }{\left({\varepsilon }_{ji}+1\right)\left(\underline{\tau }-\underline{\rho }\right)-{\varepsilon }_{ji}\pi }\right]$$

(72)

where

$$\underline{\tau }={\underline{v}}_{ji}\sqrt{\left(\frac{1}{{\underline{v}}_{ji}}-1\right)}-{{\text{tan}}}^{-1}\sqrt{\left(\frac{1}{{\underline{v}}_{ji}}-1\right)}$$

(73)

$$\overline{\tau }={\overline{v}}_{ji}\sqrt{\left(\frac{1}{{\overline{v}}_{ji}}-1\right)}-{tan}^{-1}\sqrt{\left(\frac{1}{{\overline{v}}_{ji}}-1\right)}$$

(74)

$$\underline{\rho }={\underline{w}}_{ji}\sqrt{\left(\frac{1}{{\underline{w}}_{ji}}-1\right)}-{{\text{tan}}}^{-1}\sqrt{\left(\frac{1}{{\underline{w}}_{ji}}-1\right)}$$

(75)

$$\overline{\rho }={\overline{w}}_{ji}\sqrt{\left(\frac{1}{{\overline{w}}_{ji}}-1\right)}-{tan}^{-1}\sqrt{\left(\frac{1}{{\overline{w}}_{ji}}-1\right)}$$

(76)

$$\tau =\left[\underline{\tau }, \overline{\tau }\right], \rho =\left[\underline{\rho }, \overline{\rho }\right]$$

(77)

It is worth mentioning that a major strength of the proposed mutual subsethood similarity measure ${\varepsilon }_{ji}$ as given in (36) is that it provides high flexibility in the derivation of the required parameters’ updating formulas as follows:

• The updating formulas of ${a}_{ji min}$ and ${a}_{ji max}$ implicitly cover the needed updates formula for a_ji in (51) based on (39).

• The updating formulas of ${\underline{b}}_{ji min}$ and ${\underline{b}}_{ji max}$ implicitly cover the needed updates formulas for ${\underline{b}}_{ji}$ and $\underline{b}{x}_{i}$ in (52) and (54) based on (40).

• The updating formulas for ${\overline{b}}_{ji min}$ and ${\overline{b}}_{ji max}$ implicitly cover the needed updates formulas for ${\overline{b}}_{ji}$ and $\overline{b}{x}_{i}$ in (53) and (55) based on (41).

Another major strength of the exact parameters updating formulas (64)–(77) is that they can be used to directly derive the exact formula for the case Cauchy Type-1 MSuFNIS (T1MSCFuNIS) as given in Appendix C.

5 Tests and Results

The proposed model is tested using four benchmark problems in the domains of function approximation, pattern classification, and prediction as follows.

5.1 Example 1: Function Approximation

In this example, the proposed model is employed to approximate the Narazaki-Ralescu function [43]:

$$ y\left( x \right) = 0.2 + 0.8\left( {x + 0.7{\text{sin}}\left( {2\pi x} \right)} \right),0 \le x \le 1 $$

(78)

21 points are generated for training at an interval of 0.05 and 101 points are generated as test data at an interval of 0.01 within the range [0, 1]. To train the network, the centers of the fuzzy weights between the input layer and hidden layer, and between the hidden layer and output layer are randomly initialized in the range [0, 1.5]. Lower spreads and upper spreads of fuzzy weights between the input layer and hidden layer are randomly initialized in the ranges [0.00001, 0.9] and [0.00001, 1.0] respectively. Lower and upper spreads of fuzzy weights between the hidden layer and the output layer are randomly initialized in the range [0, 1.5]. The model is examined to be trained for three rules, and five rules respectively. The learning rate is taken at 0.05, momentum is 0.05, and weighing constant λ is 0.5. The model’s performance is assessed using ${{\text{J}}}_{1}\mathrm{\, and\, }{{\text{J}}}_{2}$ as the following:

$${J}_{1}=\frac{100}{21}\sum_{p=1}^{21}\frac{|{y}_{p}-{y}_{p}^{\prime}|}{{y}_{p}^{\prime}}\%$$

(79)

$${J}_{2}=\frac{100}{101}\sum_{p=1}^{101}\frac{|{y}_{p}-{y}_{p}^{\prime}|}{{y}_{p}^{\prime}}\%$$

(80)

where ${{\text{y}}}_{{\text{p}}}^{\mathrm{^{\prime}}}$ is the desired output and ${{\text{y}}}_{{\text{p}}}$ is the actual output. The experiments are repeated 15 times with random initialization of the parameters each time, and the average of J₁ and J₂ is computed over 15 times. For the proposed T1MSCFuNIS model with three rules; i.e. network structure 1–3–1, J₁ = 0.039 and J₂ = 0.032, and with five rules, i.e. network structure 1–5–1, J₁ = 0.0252 and J₂ = 0.0247. For the proposed IT2MSCFuNIS model with three rules J₁ = 0.0189 and J₂ = 0.014, and with five rules J₁ = 0.0182 and J₂ = 0.0133. Figure 4 shows the actual Narzaki & Ralescu function and the simulated one using the proposed IT2MSCFuNIS model with 3 rules.

Fig. 4

Narzaki & Ralescu function approximation using three rules network of the IT2MSCFuNIS proposed model

Table 1 shows the Efficient approximation performance of the proposed models.

Table 1 Performance comparison of the proposed models with other methods for Example 1

The model SuPFuNIS in [38] is a three-layer T1 Mamdani FNN that uses symmetric T1GMFs. It is the first standard model for mutual subsethood fuzzy inference systems that appeared in 2002. The mutual subsethood similarity between two GMFs is calculated accurately, but the calculations are based on several case-wise integration operations according to the possible forms of overlap** between the two GMFs. The model uses the gradient-descent (GD) method for adjusting the network parameters. The model ASuPFuNIS in [47] is the same as [38] but with asymmetric GMFs. The model in [49] is the same as [47] but with the adoption of a Differential Evolution (DE) optimization strategy for searching for a proper number of nodes in the hidden layer as well as the network parameters.

The model ASNF in [48] is a five-layer T1 Mamdani neural fuzzy network (T1NFN) that uses asymmetric GMFs. To avoid calculating accurate mutual subsethood similarity between two T1GMFs, a triangle approximation of the MFs is employed.

The model IT2MSFuNIS in [4] is a three-layer IT2 Mamdani FNN that uses symmetric IT2GMFs with uncertain spreads. The mutual subsethood similarity between two IT2GMFs is calculated by following the same idea of the standard model in [38], having the same drawback of the complexity of calculations. To avoid more complications when develo** the parameters’ updating formulas of the network, the authors in [4] simplified their model by making a type-reduction operation at the third layer to deal with T1GMFs rather than IT2GMFs. The model adjusts the network parameters through two stages. The first is an initial adjustment using DE as a global exploration mechanism. Then, a GD is adopted as a local exploitation of the solution space. The model in [50] is the same model of [4] but the authors adopt parallel DE over 24 compute nodes to adjust all the network parameters to overcome the computationally intense calculations of the mutual subsethood similarity of IT2GMFs for each training sample in every iteration. The model in [43] is a multilayer NN with special types of neurons that perform logical operations based on different forms of activation functions. The model in [44] is a four-layer T1 Mamdani NFIS that is inappropriately denoted as FNN. The model adopts different forms of FBFs including GMF. The model in [45] is a hybrid model that mixes the techniques of Genetic Algorithms (GAs), FL, and NNs. The model uses GAs to extract fuzzy rules as a fuzzy supervised learning approach. Then, a fine-tuning stage using a hill-climbing approach via neuro-fuzzy network architecture is used. The model is a four-layer T1 Mamdani NFIS that is inappropriately called FNN. The model in [46] is similar to that in [45] with some enhancements.

It is clear from the results shown in Table 1, that the proposed model T1MSFuNIS achieves better performance than all other compared models except the model IT2MSFuNIS [4]. On the other hand, the proposed model IT2MSCFuNIS outperforms all other models.

Due to the volume of data obtained as a result of the experiments conducted on the various examples mentioned in this paper, a comprehensive and detailed presentation will be presented of the results obtained for this example only, noting that all the following examples have the same manner of detailed results.

Figure 5 shows the decaying behavior of the J2% for the case of 5-rules using the proposed model T1MSCFuNIS. The computed average values and standard deviation of the updated weights over the 15 runs are shown in Tables 2, and 3.

Fig. 5

J2% decaying behavior Example 1 using T1MSCFuNIS with 5-rules

Table 2 Average weights updates between input and hidden layer for Example 1 using T1MSCFuNIS with 5-rules

Table 3 Average weights updates of the trained features for Example 1 using T1MSCFuNIS with 5-rules

Figure 6 shows the decaying behavior of the J2% for the case of 3-rules using the proposed model IT2MSCFuNIS. The computed average values and standard deviation of the updated weights over the 15 runs are shown in Tables 4, and 5.

Fig. 6

J2% decaying behavior Example 1 using IT2MSCFuNIS with 3-rules

Table 4 Average weights updates between input and hidden layer for Example 1 using IT2MSCFuNIS with 3-rules

Table 5 Average weights updates of the trained features for Example 1 using IT2MSCFuNIS with 3-rules

5.2 Example 2: Iris Dataset Classification

Iris data involves the classification of three subspecies of the Iris flower, namely Iris sestosa, Iris versicolor, and Iris virginica based on four feature measurements of the Iris flower which are Sepal length, Sepal width, Petal length, and Petal width [51]. There are 50 patterns (of four features) for each of the three subspecies of the Iris flower. The input pattern set thus comprises 150 four-dimensional patterns. To train the network of the proposed IT2MSCFuNIS model, the centers of the fuzzy weights between the input layer and hidden layer are randomly initialized in the range of the minimum and maximum values of respective input features of Iris data, these ranges are [4.3, 7.9], [2.0, 4.4], [1.0, 6.9], and [0.1, 2.5]. The centers of fuzzy weights between the hidden layer and output layer are randomly initialized in the range [0, 1]. Lower and upper spreads of fuzzy weights between the input layer and hidden layer are randomly initialized in the ranges [0.0001, 1.0] and [0.0001, 1.1] respectively. Lower and upper spreads of fuzzy weights between the hidden layer and the output layer are randomly initialized in the range [0, 1.0]. All the 150 patterns of the Iris data are presented sequentially to the input layer of the network for training. The learning rate is taken at 0.07, momentum is 0.07, and the weighing constant is 0.5.

Once the network is trained, the test patterns (which again comprised all 150 patterns of Iris data) are presented to the trained network, and the re-substitution error is computed. The experiments are repeated 15 times with different random initializations for the parameters each time.

Table 6 compares the performance of the proposed T1MSCFuNIS and IT2MSCFuNIS models with other soft computing models in terms of the number of rules and the percentage of re-substitution accuracy. Both of the proposed models are tested using 3-rules, i.e. network structure 4–3–3, and 5-rules, i.e. network structure 4–5–3. The results show that both models can strongly classify Iris data with 100% re-substitution accuracy with either three or five rules.

Table 6 Performance comparison of the proposed models with other methods for Example 2

The model in [52] provides an algorithm for extracting fuzzy rules from a given neural-based fuzzy network. The model is a five-layer T1NFIS that uses different forms of FMFs including GMFs. The model is inappropriately denoted as FNN. The model in [53] is the same as in [52] but with an evolving capability that allows rule extraction and insertion. The model in [54] is a four-layer T1NFIS that can extract good features from the data set as well as extract a small but adequate number of classification rules. The model in [55] is a special form of multilayer perceptron network that implements Fuzzy systems. The network uses sigmoid activation functions to generate bell-shaped linguistic values. The model is considered a multi-layer T1 Mamdani NFIS that is inappropriately denoted as FNN. The model in [56] is a special form of T1 Mamdani multi-layer NFIS that uses triangular FMFs.

It is clear from the results shown in Table 6, that both proposed models T1MSFuNIS and IT2MSCFuNIS achieve better performance than most of the compared models except the model in [4]. The proposed models achieve the same performance as the models in [47] and [49].

5.3 Example 3: Miles per Gallon Prediction

This problem aims to estimate the city cycle fuel consumption in miles per gallon (MPG) [57]. There are 392 samples, 272 are randomly chosen for training and 120 for testing. The input layer of our model consists of three features which are weight, acceleration, and model year. The output layer represents the fuel consumption in MPG. To train the network, the centers of the fuzzy weights are randomly initialized in the range $[0, 1]$, and the upper spreads and the lower spreads are randomly initialized in the range [0.2, 0.9]. The model is trained for three rules and four rules. We keep the learning rate, momentum, and weighing constant $\lambda$ at 0.01 0.01, and 0.5 respectively throughout all the experiments. The model’s performance is assessed using the root mean square error as follows:

$$RMSE=\sqrt{\frac{\sum {(desired-actual)}^{2}}{number\, of\, patterns}}$$

(81)

The experiments are repeated 15 times with different random initializations for the parameters each time. Table 7 shows the performance of the proposed models compared with other methods.

Table 7 Performance Comparison of the proposed models with other methods for Example 3

For the proposed T1MSCFuNIS model with three rules; i.e. network structure 3–3–1, the average RMSE_train is 0.1795 and the average RMSE_test 0.1705, while in the case of four rules, i.e. network structure 3–4–1 the average RMSE_train is 0.1632 and the average RMSE_test is 0.1594. On the other hand, for the case of the IT2MSCFuNIS proposed model with three rules, the average RMSE_train is 0.1509 and the average RMSE_test 0.1456, while while in the case of four rules RMSE_train is 0.1404, and the average RMSE_test 0.1386.

The model SEIT2FNN is provided in [58] and tested for MPG in [59]. The model is a six-layer IT2 TSK-type self-organized NFIS that uses IT2GMF with an uncertain mean. The model is inappropriately denoted as IT2FNN. The model RIT2NFS-WB [59] is a reduced TSK-type IT2NFS that uses IT2GMFs with uncertain mean and is suitable for hardware implementation. Both models McIT2FIS-UM and McIT2FIS-US [60] are TSK-type IT2NFIS that are implemented as a five-layered network. The models adopt IT2GMF with uncertain mean and uncertain width respectively. The model eIT2FNN-LSTM in [29] is a self-evolving six-layer IT2FNIS for the synchronization and identification of nonlinear dynamics. The model uses a fuzzy LSTM neural network that can effectively deal with long-term dependence problems. eIT2FNN-LSTM uses IT2GMFs with uncertain mean.

The results given in Table 7 indicate that both proposed models T1MSFuNIS and IT2MSCFuNIS achieve better performance than all other compared models.

5.4 Example 4: Abalone Age Prediction

In this example, the abalone’s age is predicted based on its physical characteristics. The dataset is collected from the UCI machine learning repository [61]. The dataset includes 4177 samples, out of which, 3342 samples are used for training and the remaining 835 samples are used for testing. The input layer of our model consists of seven features which are Length, diameter, height, whole weight, shucked weight, viscera weight, and shell weight, the output represents the number of rings. To train the network, the centers of the fuzzy weights are randomly initialized in the range $[\mathrm{0,1}]$, and the upper spreads and the lower spreads are randomly initialized in the range [0.2, 0.9]. The model is trained for three rules and five rules we keep the learning rate to 0.01, momentum to 0.01, and weighing constant $\lambda$ to 0.5, throughout all the experiments. The model’s performance is assessed using the root mean square, the experiments are repeated 15 times with different random initialization for the parameters each time, and the average of $R{MSE}_{test}$ and $R{MSE}_{train}$ are computed for the 15 times. Table 8 shows the performance of the proposed models compared with other methods.

Table 8 Performance Comparison of the proposed models with other methods for Example 4

For the proposed T1MSCFuNIS model with three rules, i.e. network structure 7–3–1, the average of RMSE_train for the training set is 0.1047 and the average RMSE_test 0.1346, while in the case of five rules, i.e. network structure 7–5–1 the average RMSE_train is 0.1010 and the average RMSE_test is 0.1315. On the otherhand, for the case of the IT2MSCFuNIS proposed model with three rules the average RMSE_train is 0.1007 and the average RMSE_test 0.1078, while while in the case of five rules RMSE_train is 0.0962 and the average RMSE_test 0.0951.

It is clear from the results shown in Table 8 that both proposed models T1MSFuNIS and IT2MSCFuNIS outperform all other compared models.

5.5 Example 5: Corona Virus Diagnosis

In this example, a rapid diagnosis of corona virus is based on Routine Blood Tests [62]. The source of the dataset is taken from the Kaggle dataset Diagnosis of COVID-19 and its clinical spectrum created by the Hospital Israelita Albert Einstein in São Paulo, Brazil [63]. The dataset is filtered and the features were selected as mentioned in [62]. Also, the dataset is split into 80% as the training set, and 20% as the testing set. The input layer of our model consists of 16 features including WBC count, Platelet Count, Patient age, HCT, Hgb, MPV, RBC Count, Basophils count, Absolute Eosinophil Count, Lymphocyte Count, MCHC, MCH, MCV, Absolute Monocyte Count, RDW and the presence of chronic disease. The output layer consists of two nodes that represent the diagnosis state of the patient being classified as positive or negative corona virus. The centers of the fuzzy weights are randomly initialized in the range [0, 1] and both the lower spreads and the upper spreads are randomly initialized in the range [0.2, 0.9]. The model is trained for three and five rules, i.e. for network structures 16–3–2 and 16–5–2 respectively. We keep the learning rate, momentum, and weighing constant $\lambda$ at 0.7, 0.7, and 0.5 respectively throughout all the experiments. The model’s performance is assessed using the following three performance metrics:

$$sensitivity=\frac{TP}{TP+FN}*100\%$$

(82)

$${\text{Specificity}}=\frac{TN}{TN+FP}*100\%$$

(83)

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}*100\%$$

(84)

where (TP) is the number of instances that are correctly classified as positive, (FP) is the number of instances that are incorrectly classified as positive, (TN) is the number of instances that are correctly classified as negative, and (FN) is the number of incorrectly classified instances as negative. The experiments are repeated 15 times with random initialization of the parameters each time, and the averages of sensitivity, specificity, and accuracy are computed. Table 9 shows the performance comparison of the proposed model with the models given in [62].

Table 9 Performance Comparison of the proposed models with other methods in [62] for Example 5

The models k-nearest Neighbor (KNN) and Random Forest (RF) are classical machine learning classifiers. ANFIS is a popular five-layer T1FNIS [64]. It is clear from Table 9, that the proposed model IT2MSCFuNIS outperforms the three compared models. On the other hand, the proposed model T1MSCFuNIS outperforms the compared models in Accuracy and Specificity metrics and behaves very competitively with KNN in Sensitivity metrics.

6 Discussions and Further Extensions

This section presents three issues that represent potential extensions of the proposed IT2MSuFNIS model in fairly detailed discussions. The first issue deals with the candidate FBFs that can be adopted in the proposed model and the controversy surrounding the trade-off between CMF and GMF. The second issue deals with the robustness of the performance of the proposed model. The third issue discusses the applicability of IT2MSuFNIS to various domains and the possibility of integration with other models, in particular the deep learning models.

6.1 Candidate FMFs for IT2MSCFuNIS

Both Gaussian and Cauchy functions are considered well-known types of Radial Basis Functions (RBFs). Cauchy function is also called “Inverse Quadratic Function” (IQ) and is considered a special case of the family of “Bell-Shaped Functions” (BSFs) [65, 66]. As an FMF, CFMF has some interesting properties that have been observed by researchers in a number of published papers.

The computational capabilities of the Cauchy function have been addressed in previously published papers. In [67], Chandra P. et al. and in [68], Ghose U. et al. showed that Cauchy activation functions have good statistical performance better than the traditional logistic activation functions when solving regression problems using feedforward artificial neural networks. They also emphasized the fact that the Cauchy function has less computational cost as it does not involve the calculation of exponential terms.

On the other hand, when compared with GFMF, CFMF has some interesting properties that have been observed by researchers in a number of published papers. In [69, 70], Abdelbar A.M., et al. proposed a fuzzy generalization of “Particle Swarm Optimization” (PSO) called FPSO that differs from standard PSO by assigning a charisma property to some particles in the population in order to influence other particles in the neighborhood. Such a charisma property is represented by an FMF. It is found that the performance of FPSO using CFMFs outperforms the performance in the case of GFMFs. Such a difference in performance is attributed to the fact that CFMF with a certain center and a certain spread covers a wider span than GFMF with the same values of center and spread. Such a “wider-tail” property of CFMFs allows better exploration of the search space by promoting diversity.

Also, in [71], Huang W. and Li Y. showed that a probabilistic FLS gives better performance when adopting probabilistic CFMFs rather than probabilistic GFMFs.

In [42], Amer N.S. and Hefny H.A. compared the similarity/possibility monotonic characteristic of the mutual subsethood similarity between two CFMFs with that of GFMFs. They found that CFMFs are featured by preserving higher values for the monotonicity relationship between similarity and possibility which has a significant impact on better interpretability properties when adopting CFMFs rather than GFMFs when building FLS. Therefore, it is clear from the above discussion that the interest in studying CFMFs is justified and objective.

As a possible challenging extension of our proposed IT2MSuFNIS model, other forms of RBFs may be investigated by following the same style of derivations to get a closed-form analytical formula of the model parameters.

6.2 Robustness of IT2MSCFuNIS

IT2MSCFuNIS is a highly efficient modeling technique for handling vague uncertainty in the input data. The model can handle imprecision in input data in two ways. First, it can accept and learn from fuzzy data. Second, it manipulates such imprecise data using IT2FMF. Achieving excellent experimental results with minimum error, minimum standard deviation, and a high level of generalization capabilities across different benchmark datasets is a positive indication of the robustness of the model. However, this is just one aspect of robustness. Robustness is mainly concerned with maintaining good performance under probabilistic uncertainty that causes external disturbances due to noisy data.

Therefore, other factors need to be addressed to test the overall robustness of the model such as injecting random noise with arbitrary distributions to the input data before training and adopting some robust optimization algorithms to perform better in the presence of outliers or noisy data points. Also, studying the performance of the FLS with probabilistic FMFs. Several approaches are found in the literature for achieving robustness of FNN models, e.g. [71,72,73,74,75,76,77,78,79,80,81].

Based on the above discussion, enhancing the robustness of our proposed IT2MSCFuNIS model is a possible extension for future work.

6.3 Applicability of IT2MSCFuNIS

The proposed IT2MSCFuNIS is a general-purpose modeling technique that provides better handling of uncertainties in quite concise analytical formulas. Therefore, it can be applied to various practical problems in different domains as presented in this paper. However, in some situations, further research may be needed to show how it can be integrated with other practical models. In this respect, we are interested in discussing how to integrate IT2MSCFuNIS with Deep Neural Networks (DNNs) models.

The main objective of integrating fuzzy logic models with DNNs models is to allow an explanation of the generated outputs and increase the interpretability of the DNN model [82]. Recently, various forms of integrating fuzzy logic models with DL architectures’ models have appeared in the literature [83]. The commonly used approach is to inject a fuzzy layer into the DL architecture. As for examples, in [84], Yeganejou and Dick proposed a Fuzzy Deep Learning Network (FDLN) by introducing a fuzzy c-means clustering layer after the traditional convolutional neural network (CNN) layers to improve the classification of large-size data sets of hand-written digits by generating reasonably-interpretable clusters in the derived feature space of the adopted CNN. In [85], ** and Panoutsos proposed an FDLN by replacing the second fully connected dense layer in the traditional CNN with a Fuzzy Radial Basis Function Network (FRBFN). Their approach is found to maintain a high level of accuracy similar to CNN while providing linguistic interpretability to the classification layer. In [86], Sharma et al. proposed a Deep Neuro-Fuzzy approach for the healthcare recommendation system. Their approach is mainly a multilevel decision making for predicting the risk and severity of the patient diseases. They used a traditional CNN that properly classifies Heart, Liver, and Kidney diseases, and then the classified outputs of the CNN are fed into a type-2 FLS to generate the risk level linguistically. In [87], Lin et al. a novel CNN model called “Vector Deep Fuzzy Neural Network” (VDFNN) is adopted for effective automatic classification of breast cancer based on histopathological images. Their proposed VDFNN is composed of a vector convolutional layer, a pooling layer, a feature fusion layer, and an FNN layer. A global average pooling method is applied in the feature fusion layer to reduce the dimension of features. Then, the features are fed to the FNN layer instead of the traditional fully connected network.

Based on the above brief presentation of previously published approaches of DFNN, it becomes clear that our proposed IT2MSuFNIS model has promising opportunities to be adopted in various DFNN applications, e.g. [86,87,88,89]. A favorable idea in this respect is to inject the IT2MSuFNIS model as a classification layer that is proceeded by a feature fusion layer in a similar manner to [87].

7 Conclusion

This paper presents a novel model for IT2MSuFNIS. The proposed model represents a further development step of the theory of the MSuFNIS model in terms of three contributions. The first is the adoption of another bell-shaped FBF rather than the traditional choice of Gaussian MF. The second is the success of computing fuzzy mutual subsethood similarity between two IT2 Cauchy MFs as well as all weights’ updating equations of the network parameters in analytic closed-form formulas without any need to perform several mathematical integration operations, or to make an approximation of the membership function, or to employ numeric computations. The third is the success of extracting a type-1 model of the proposed IT2MSuFNIS, called T1MSuFNIS, which is an accurate and concise model with closed-form parameter updating formulas. The performance of the proposed model is tested on four benchmark problems from the domains of classification, prediction, and function approximation. Simulation experiments have shown the superiority of both the proposed IT2MSuFNIS and T1MSuFNIS when compared with other models in terms of accuracy and number of rules. As a future work, we have three directions. First, is widening the scope of the applications to other real-world problems. Second, is the development of a TSK-type version of our proposed model. Third, which is quite challenging, is to investigate other forms of FBFs to enrich the theory of the MSuFNIS model.

Appendices

Appendix A

Proof of Proposition 1

According to [42], the cardinality of T1 Cauchy fuzzy set A is

$$\left|A\right|=\left|{\mu }_{\widetilde{A}}\left(x\right)\right|=\int_{-\infty}^{\infty} \frac{1}{1+{\left(\frac{x-a}{b}\right)}^{2}}=b\pi $$

(85)

And, the cardinality of the intersection of two T1 Cauchy fuzzy sets, A and B with centers a_1, a₂ spreads b₁ and b₂. Taking $\cap$ the minimum and $\cup$ the maximum, then we have

$$\left|A \cap B\right|={b}_{min}\pi +\Omega $$

(86)

where,

$$ \begin{gathered} \Omega = \left( {b_{{max}} - b_{{min}} } \right)tan^{{ - 1}} \left( {\frac{{a_{{max}} - a_{{min}} }}{{b_{{max}} - b_{{min}} }}} \right) \hfill \\ \;\;\;\;\; - \left( {b_{{max}} + b_{{min}} } \right)tan^{{ - 1}} \left( {\frac{{a_{{max}} - a_{{min}} }}{{b_{{max}} + b_{{min}} }}} \right) \hfill \\ \end{gathered} $$

(87)

$${b}_{min}=\mathit{min}\left({b}_{1},{b}_{2}\right) , {b}_{max}=\mathit{max}\left({b}_{1},{b}_{2}\right)$$

(88)

$${a}_{min}=\mathit{min}\left({a}_{1},{a}_{2}\right), {a}_{max}=\mathit{max}\left({a}_{1},{a}_{2}\right)$$

(89)

Then, the generalized formula for mutual subsethood similarity between two T1 Cauchy fuzzy sets A and B is [42]:

$$S\left(A,B\right)=\frac{\left|A\cap B\right|}{\left|A\cup B\right|}=\frac{{b}_{min}\pi +\Omega }{{b}_{max}\pi -\Omega }$$

(90)

Now, for the case of IT2 Cauchy fuzzy sets, the similarity formula is a generalization of (90) as given in (19), see [41], then we have

$$S\left(\widetilde{A},\widetilde{B}\right)=\frac{\int {\text{min}}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx+\int {\text{min}}\left({\underline{\mu }}_{A}\left(x\right),{\underline{\mu }}_{B}\left(x\right)\right)dx}{\int {\text{max}}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx+\int {\text{max}}\left({\underline{\mu }}_{A}\left(x\right),{\underline{\mu }}_{B}\left(x\right)\right)dx}$$

(91)

For the case of two IT2 Cauchy fuzzy sets A and B, then

from (86), we have

$$\int {\text{min}}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx= {\overline{b}}_{min}\pi +\overline{\Omega }$$

(92)

$$ \begin{gathered} \bar{\Omega } = \left( {\overline{{\text{b}}} _{{max}} - \overline{{\text{b}}} _{{min}} } \right){\text{tan}}^{{ - 1}} \left( {\frac{{a_{{max}} - a_{{min}} }}{{\bar{b}_{{max}} - \bar{b}_{{min}} }}} \right) \hfill \\ \;\;\;\;\;\; - \left( {\bar{b}_{{max}} + \bar{b}_{{min}} } \right){\text{tan}}^{{ - 1}} \left( {\frac{{a_{{max}} - a_{{min}} }}{{\bar{b}_{{max}} + \bar{b}_{{min}} }}} \right) \hfill \\ \end{gathered} $$

(93)

Similarly,

$$\int \mathit{min}\left({\underline{\mu }}_{A}\left(x\right),{\underline{\mu }}_{B}\left(x\right)\right)dx= {\underline{b}}_{min}\pi +\underline{\Omega }$$

(94)

$$\underline{\Omega }=\left({\underline{{\text{b}}}}_{max}-{\underline{{\text{b}}}}_{min}\right) {{\text{tan}}}^{-1}\left(\frac{{a}_{max}-{a}_{min}}{{\underline{b}}_{max}-{\underline{b}}_{min}}\right)$$

$$-\left({\underline{b}}_{max}+{\underline{b}}_{min}\right) {{\text{tan}}}^{-1}\left(\frac{{a}_{max}-{a}_{min}}{{\underline{b}}_{max}+{\underline{b}}_{min}}\right)$$

(95)

Thus,

$$\mathit{min}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx+\int \mathit{min}\left({\underline{\mu }}_{A}\left(x\right),{\underline{\mu }}_{B}\left(x\right)\right)dx$$

$$=\left( {\underline{b}}_{min}+{\overline{b}}_{min}\right)\pi +\left(\underline{\Omega }+\overline{\Omega }\right)$$

(96)

From (85), we have

$$\left|{\overline{\mu }}_{A}\left(x\right)\right|= {\overline{b}}_{1}\pi , \left|{\underline{\mu }}_{A}\left(x\right)\right|={\underline{b}}_{1}\pi $$

(97)

$$\left|{\overline{\mu }}_{B}\left(x\right)\right|= {\overline{b}}_{2}\pi , \left|{\underline{\mu }}_{B}\left(x\right)\right|={\underline{b}}_{2}\pi $$

(98)

$$\mathit{max}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx$$

$$=\left|{\overline{\mu }}_{A}\left(x\right)\right|+ \left|{\overline{\mu }}_{B}\left(x\right)\right|-{|\overline{\mu }}_{A}\left(x\right)\cap {\overline{\mu }}_{B}\left(x\right)|$$

$$= {\overline{b}}_{1}\pi +{\overline{b}}_{2}\pi -\left({\overline{b}}_{min}\pi +\overline{\Omega }\right)$$

(99)

Since ${\overline{b}}_{min}=\mathit{min}({\overline{b}}_{1}$,${\overline{b}}_{2})$, then

$$\int \mathit{max}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx= {\overline{b}}_{max}\pi -\overline{\Omega }$$

(100)

Similarly,

$$\int \mathit{max}\left({\underline{\mu }}_{A}\left(x\right),{\underline{\mu }}_{B}\left(x\right)\right)dx= {\underline{b}}_{max}\pi -\underline{\Omega }$$

(101)

Thus

$$\int \mathit{max}\left({\overline{\mu }}_{A}\left(x\right),{\overline{\mu }}_{B}\left(x\right)\right)dx+\int \mathit{max}\left({\underline{\mu }}_{A}\left(x\right),{\underline{\mu }}_{B}\left(x\right)\right)dx$$

$$=\left({\underline{b}}_{max}+{\overline{b}}_{max}\right)\pi -\left(\underline{\Omega }+\overline{\Omega }\right)$$

(102)

From (96) and (102) in (91), we get the formula (20). ■

Appendix B

2.1 Evaluation of Partial Derivatives

2.1.1 At the Output Layer

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {{\varvec{a}}}_{{\varvec{k}}{\varvec{j}}}}\right)$:

$$\frac{\partial E}{\partial {a}_{kj}}=\left(\frac{\partial E}{\partial {y}_{k}}\right)\left(\frac{\partial {y}_{k}}{\partial {a}_{kj}}\right)$$

(103)

From (46) and (47)

$$\frac{\partial E}{\partial {y}_{k}}=-\left({d}_{k}-{y}_{k}\right)$$

(104)

$$\frac{\partial y}{\partial {a}_{kj}} =\frac{\lambda {z}_{j}{\overline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}}+\frac{{\left(1-\lambda \right)z}_{j}{\underline{b}}_{kj}}{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}$$

(105)

From (104) and (105) in (103), we get the formula (64). ■

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {\underline{{\varvec{b}}}}_{{\varvec{k}}{\varvec{j}}}}\right)$:

$$\frac{\partial E}{\partial {\underline{b}}_{kj}}=\left(\frac{\partial E}{\partial {y}_{k}}\right)\left(\frac{\partial {y}_{k}}{\partial {\underline{y}}_{k}}\right)\left(\frac{\partial {\underline{y}}_{k}}{\partial {\underline{b}}_{kj}}\right)$$

(106)

From (43) and (45) with simplification, we have

$$\frac{\partial {y}_{k}}{\partial {\underline{y}}_{k}}=\left(1-\lambda \right)$$

(107)

$$\frac{\partial {\underline{y}}_{k}}{\partial {\underline{b}}_{kj}}={z}_{j}\left(\frac{{a}_{kj}-{\underline{y}}_{k}}{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}\right)$$

(108)

From (104), (107), and (108) in (106), we get the formula (65) ■

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {\overline{{\varvec{b}}}}_{{\varvec{k}}{\varvec{j}}}}\right)$:

Similar to the derivation of $\left(\frac{\partial E}{\partial {\underline{b}}_{kj}}\right)$ we have

$$\frac{\partial E}{\partial {\overline{b}}_{kj}}=\left(\frac{\partial E}{\partial {y}_{k}}\right)\left(\frac{\partial {y}_{k}}{\partial {\overline{y}}_{k}}\right)\left(\frac{\partial {\overline{y}}_{k}}{\partial {\overline{b}}_{kj}}\right)$$

(109)

$$\frac{\partial {y}_{k}}{\partial {\overline{y}}_{k}}=\lambda $$

(110)

$$\frac{\partial {\overline{y}}_{k}}{\partial {\overline{b}}_{kj}}={z}_{j}\left(\frac{{a}_{kj}-{\overline{y}}_{k}}{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}}\right)$$

(111)

From (104), (110), and (111) in (109), we get the formula (66) ■

2.1.2 At the Hidden Layer

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {{\varvec{a}}}_{{\varvec{j}}{\varvec{i}} {\varvec{m}}{\varvec{i}}{\varvec{n}}}}\right)$:

$$ \begin{gathered} \frac{{\partial E}}{{\partial a_{{jimin}} }} = \sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right)\left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial a_{{jimin}} }}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial a_{{jimin}} }}} \right)\sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right) \hfill \\ \end{gathered} $$

(112)

From (46) with simplification, we have

$$\frac{\partial {y}_{k}}{\partial {z}_{j}}=\lambda \left(\frac{{\overline{b}}_{kj}\left({a}_{kj}-{\overline{y}}_{k}\right)}{\sum_{j=1}^{m}{z}_{j}{\overline{b}}_{kj}}\right)+\left(1-\lambda \right)\,\left(\frac{{\underline{b}}_{kj}\left({a}_{kj}-{\underline{y}}_{k}\right)}{\sum_{j=1}^{m}{z}_{j}{\underline{b}}_{kj}}\right)$$

(113)

From (65) and (66) in (113), then we have

$$\sum_{k=1}^{p}\frac{\partial E}{\partial {y}_{k}}.\frac{\partial {y}_{k}}{\partial {z}_{j}}=\sum_{k=1}^{p}\frac{\left({d}_{k}-{y}_{k}\right)}{{z}_{j}} \left[\frac{{\underline{b}}_{kj}}{\left({d}_{k}-{\underline{y}}_{k}\right)} \left(\frac{\partial E}{\partial {\underline{b}}_{kj}}\right) + \frac{{\overline{b}}_{kj}}{\left({d}_{k}-{\overline{y}}_{k}\right)} \left(\frac{\partial E}{\partial {\overline{b}}_{kj}}\right)\right]$$

(114)

From (42), then

$$\frac{\partial {z}_{j}}{\partial {\varepsilon }_{ji}}=\frac{\partial \prod_{{\text{i}}=1}^{{\text{n}}}{\upvarepsilon }_{{\text{ji}}}}{\partial {\varepsilon }_{ji}}=\prod_{\begin{array}{c}k=1\\ k\ne i\end{array}}^{{\text{n}}}{\upvarepsilon }_{{\text{jk}}}=\frac{{z}_{j}}{{\varepsilon }_{ji}}$$

(115)

From (36) by differentiation and simplification, then

$$\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}=\frac{\left[\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi +\left( {\underline{b}}_{ji min}+{\overline{b}}_{ji min}\right)\pi \right]}{ {\left[ \left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)\right]}^{2}}. \left(\frac{\partial {\underline{\Omega }}_{ji}}{\partial {a}_{ji min}}+\frac{\partial {\overline{\Omega }}_{ji}}{\partial {a}_{ji min}}\right)$$

(116)

From (37), by differentiation, simplification, and using (15) and (16), then

$$\frac{\partial {\underline{\Omega }}_{ji}}{\partial {a}_{ji min}}={\underline{v}}_{ji}-{\underline{w}}_{ji}$$

(117)

From (38), by differentiation, simplification, and using (17) and (18), then

$$\frac{\partial {\overline{\Omega }}_{ji}}{\partial {a}_{ji min}}= {\overline{v}}_{ji}-{\overline{w}}_{ji}$$

(118)

From (117) & (118) in (116) with simplification then

$$\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}= \frac{\left({\varepsilon }_{ji}+1\right)\left[\left({\underline{v}}_{ji}+{\overline{v}}_{ji}\right)-\left({\underline{w}}_{ji}+{\overline{w}}_{ji}\right)\right]}{ \left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(119)

By substituting (114), (115), and (119) in (112), we get the formula (67). ■

Derivation of $\frac{\partial {\varvec{E}}}{\partial {{\varvec{a}}}_{{\varvec{j}}{\varvec{i}} {\varvec{m}}{\varvec{a}}{\varvec{x}}}}$:

$$\frac{\partial E}{\partial {a}_{ji max}}= \sum_{k=1}^{p}\left(\frac{\partial E}{\partial {y}_{k}}\right)\left(\frac{\partial {y}_{k}}{\partial {z}_{j}}\right)\left(\frac{\partial {z}_{j}}{\partial {\varepsilon }_{ji}}\right)\left(\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji max}}\right)$$

(120)

Following a similar derivation starting from (112) up to (118), we have

$$ \begin{gathered} \frac{{\partial \varepsilon _{{ji}} }}{{\partial a_{{jimax}} }} = \frac{{\left[ {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} + \bar{b}_{{jimax}} } \right)\pi + \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimin}} + \bar{b}_{{jimin}} } \right)\pi } \right]}}{{\left[ {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} + \bar{b}_{{jimax}} } \right)\pi - \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } _{{ji}} + \bar{\Omega }_{{ji}} } \right)} \right]^{2} }}. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{{\partial \bar{\Omega }_{{ji}} }}{{\partial a_{{jimax}} }} + \frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } _{{ji}} }}{{\partial a_{{jimax}} }}} \right). \hfill \\ \end{gathered} $$

(121)

From (37) by differentiation and using (15) and (16), then

$$\frac{\partial {\underline{\Omega }}_{ji}}{\partial {a}_{ji max}}={\underline{w}}_{ji}-{\underline{v}}_{ji}=-\frac{\partial {\underline{\Omega }}_{ji}}{\partial {a}_{ji min}}$$

(122)

Also, from (38) by differentiation and using (17) and (18)

$$\frac{\partial {\overline{\Omega }}_{ji}}{\partial {a}_{ji max}}={\overline{w}}_{ji}-{\overline{v}}_{ji}=-\frac{\partial {\overline{\Omega }}_{ji}}{\partial {a}_{ji min}}$$

(123)

Thus, (122) and (123) in (121), then we have

$$\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji max}}=-\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}$$

(124)

From (124) in (120), we get the formula (68). ■

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {\underline{{\varvec{b}}}}_{{\varvec{j}}{\varvec{i}} {\varvec{m}}{\varvec{i}}{\varvec{n}}}}\right)$:

$$\frac{\partial E}{\partial {\underline{b}}_{ji min}}=\sum_{k=1}^{p}\left(\frac{\partial E}{\partial {y}_{k}}\right)\left(\frac{\partial {y}_{k}}{\partial {z}_{j}}\right)\left(\frac{\partial {z}_{j}}{\partial {\varepsilon }_{ji}}\right)\left(\frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji min}}\right)$$

$$=\left( \frac{\partial {z}_{j}}{\partial {\varepsilon }_{ji}}\right) \left(\frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji min}}\right) \sum_{k=1}^{p}\left(\frac{\partial E}{\partial {y}_{k}}\right)\left(\frac{\partial {y}_{k}}{\partial {z}_{j}}\right)$$

(125)

From (36) by differentiation and simplification

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji min}}=\frac{\left({\varepsilon }_{ji}+1\right).\frac{\partial {\underline{\Omega }}_{ji}}{\partial {\underline{b}}_{ji min}}+\pi }{\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(126)

From (37) by differentiation with simplification and using (15) and (16), then

$$ \begin{gathered} \frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } _{{ji}} }}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimin}} }} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} }} - 1} \right)} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; + \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} }} - 1} \right)} } \right] \hfill \\ \end{gathered} $$

(127)

It is suitable to rewrite (127) using the notation

$$\frac{\partial {\underline{\Omega }}_{ji}}{\partial {\underline{b}}_{ji min}}=\underline{\tau }+\underline{\rho }$$

(128)

where, $\underline{\tau }$ and $\underline{\rho }$ are defined in (73) and (75).

Substituting (128) in (126), then we have

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji min}}=\frac{\left({\varepsilon }_{ji}+1\right)\left(\underline{\tau }+\underline{\rho }\right)+\pi }{\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(129)

From (112) and (125), it is clear that

$$\frac{\partial E}{\partial {\underline{b}}_{ji min}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left[\left( \frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji min}}\right)/\left(\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}\right)\right]$$

(130)

From (119) and (129) in (130), we have the formula (69).■

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {\overline{{\varvec{b}}}}_{{\varvec{j}}{\varvec{i}} {\varvec{m}}{\varvec{i}}{\varvec{n}}}}\right)$:

Similar to the derivation of $\left(\frac{\partial E}{\partial {\underline{b}}_{ji min}}\right)$, we have

$$ \begin{gathered} \frac{{\partial E}}{{\partial \bar{b}_{{jimin}} }} = \sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right)\left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial \bar{b}_{{jimin}} }}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial \bar{b}_{{jimin}} }}} \right)\sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right) \hfill \\ \end{gathered} $$

(131)

where,

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\overline{b}}_{ji min}}=\frac{\left({\varepsilon }_{ji}+1\right).\frac{\partial {\overline{\Omega }}_{ji}}{\partial {\overline{b}}_{ji min}}+\pi }{\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(132)

$$ \begin{gathered} \frac{{\partial \bar{\Omega }_{{ji}} }}{{\partial \bar{b}_{{jimin}} }} = \left[ {\overline{{\text{w}}} _{{ji}} \sqrt {\left( {\frac{1}{{\overline{{\text{w}}} _{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\overline{{\text{w}}} _{{ji}} }} - 1} \right)} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\, + \left[ {\bar{v}_{{ji}} \sqrt {\left( {\frac{1}{{\bar{v}_{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\bar{v}_{{ji}} }} - 1} \right)} } \right] \hfill \\ \end{gathered} $$

(133)

It is suitable to rewrite (133) using the following notation

$$\frac{\partial {\overline{\Omega }}_{ji}}{\partial {\overline{b}}_{ji min}}=\overline{\tau }+\overline{\rho }$$

(134)

where $\overline{\tau }$ and $\overline{\rho }$ are defined in (74) and (76).

Substituting (134) in (132), then we have

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\overline{b}}_{ji min}}=\frac{\left({\varepsilon }_{ji}+1\right)\left(\overline{\tau }+\overline{\rho }\right)+\pi }{\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(135)

From (112) and (131), it is clear that

$$\frac{\partial E}{\partial {\overline{b}}_{ji min}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left[\left( \frac{\partial {\varepsilon }_{ji}}{\partial {\overline{b}}_{ji min}}\right)/\left(\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}\right)\right]$$

(136)

From (119) and (135) in (136) then

$$\frac{\partial E}{\partial {\overline{b}}_{ji min}} = \left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left(\frac{\left({\varepsilon }_{ji}+1\right)\left( \overline{\tau }+\overline{\rho }\right)+\pi }{\left({\varepsilon }_{ji}+1\right)\left[\left({\underline{v}}_{ji}+{\overline{v}}_{ji}\right)-\left({\underline{w}}_{ji}+{\overline{w}}_{ji}\right)\right]}\right)$$

(137)

Although formula (137) is a good closed formula, it is more suitable to get $\left(\frac{\partial E}{\partial {\overline{b}}_{ji min}}\right)$ in terms of $\left(\frac{\partial E}{\partial {\underline{b}}_{ji min}}\right)$ by dividing (137) by (69) to get the formula (70).■

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {\underline{{\varvec{b}}}}_{{\varvec{j}}{\varvec{i}} {\varvec{m}}{\varvec{a}}{\varvec{x}}}}\right)$:

$$ \begin{gathered} \frac{{\partial E}}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} }} = \sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right)\left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} }}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} }}} \right)\sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right) \hfill \\ \end{gathered} $$

(138)

From (36) by differentiation and simplification

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji max}}=\frac{\left({\varepsilon }_{ji}+1\right)\left(\frac{\partial {\underline{\Omega }}_{ji}}{\partial {\underline{b}}_{ji max}}\right)-{\varepsilon }_{ji}\pi }{ \left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(139)

From (37), by differentiation and simplification using (15) and (16), then

$$ \begin{gathered} \frac{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\Omega } _{{ji}} }}{{\partial \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} _{{jimax}} }} = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} _{{ji}} }} - 1} \right)} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{w} _{{ji}} }} - 1} \right)} } \right] \hfill \\ \end{gathered} $$

(140)

It is suitable to rewrite (140) using the following notation

$$\frac{\partial {\underline{\Omega }}_{ji}}{\partial {\underline{b}}_{ji max}}=\underline{\tau }-\underline{\rho }$$

(141)

where $\underline{\uptau }$ and $\underline{\uprho }$ are defined in (73) and (75).

Substituting (141) in (139), then we have

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji max}}=\frac{\left({\varepsilon }_{ji}+1\right)\left(\underline{\tau }-\underline{\rho }\right)-{\varepsilon }_{ji}\pi }{\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(142)

From (112) and (138), it is clear that

$$\frac{\partial E}{\partial {\underline{b}}_{ji max}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left[\left( \frac{\partial {\varepsilon }_{ji}}{\partial {\underline{b}}_{ji max}}\right)/\left(\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}\right)\right]$$

(143)

From (119) and (142) in (143), we get the formula (71).■

Derivation of $\left(\frac{\partial {\varvec{E}}}{\partial {\overline{{\varvec{b}}}}_{{\varvec{j}}{\varvec{i}} {\varvec{m}}{\varvec{a}}{\varvec{x}}}}\right)$:

Similar to the derivation of $\left(\frac{\partial E}{\partial {\underline{b}}_{ji max}}\right)$, we have

$$ \begin{gathered} \frac{{\partial E}}{{\partial \bar{b}_{{jimax}} }} = \sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right)\left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial \bar{b}_{{jimax}} }}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left( {\frac{{\partial z_{j} }}{{\partial \varepsilon _{{ji}} }}} \right)\left( {\frac{{\partial \varepsilon _{{ji}} }}{{\partial \bar{b}_{{jimax}} }}} \right)\sum\limits_{{k = 1}}^{p} {\left( {\frac{{\partial E}}{{\partial y_{k} }}} \right)} \left( {\frac{{\partial y_{k} }}{{\partial z_{j} }}} \right) \hfill \\ \end{gathered} $$

(144)

From (36) by differentiation, and simplification

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\overline{b}}_{ji max}}=\frac{\left({\varepsilon }_{ji}+1\right)\left(\frac{\partial {\overline{\Omega }}_{ji}}{\partial {\overline{b}}_{ji max}}\right)-{\varepsilon }_{ji}\pi }{ \left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(145)

From (38) by differentiation and simplification using (17) and (18)

$$ \begin{gathered} \frac{{\partial \bar{\Omega }_{{ji}} }}{{\partial \bar{b}_{{jimax}} }} = \left[ {\bar{v}_{{ji}} \sqrt {\left( {\frac{1}{{\bar{v}_{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\bar{v}_{{ji}} }} - 1} \right)} } \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left[ {\bar{w}_{{ji}} \sqrt {\left( {\frac{1}{{\bar{w}_{{ji}} }} - 1} \right)} - {\text{tan}}^{{ - 1}} \sqrt {\left( {\frac{1}{{\bar{w}_{{ji}} }} - 1} \right)} } \right] \hfill \\ \end{gathered} $$

(146)

Rewriting (146) in our new notation, then

$$\frac{\partial {\underline{\Omega }}_{ji}}{\partial {\overline{b}}_{ji max}}=\overline{\tau }-\overline{\rho }$$

(147)

Substituting (147) in (145), then we have

$$\frac{\partial {\varepsilon }_{ji}}{\partial {\overline{b}}_{ji max}}=\frac{\left({\varepsilon }_{ji}+1\right)\left(\overline{\tau }-\overline{\rho }\right)-{\varepsilon }_{ji}\pi }{\left({\underline{b}}_{ji max}+{\overline{b}}_{ji max}\right)\pi -\left({\underline{\Omega }}_{ji}+{\overline{\Omega }}_{ji}\right)}$$

(148)

From (112) and (144), it is clear that

$$\frac{\partial E}{\partial {\overline{b}}_{ji max}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left[\left( \frac{\partial {\varepsilon }_{ji}}{\partial {\overline{b}}_{ji max}}\right)/\left(\frac{\partial {\varepsilon }_{ji}}{\partial {a}_{ji min}}\right)\right]$$

(149)

From (119) and (148) in (149) then

$$\frac{\partial E}{\partial {\overline{b}}_{ji max}}=\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left(\frac{\left({\varepsilon }_{ji}+1\right)\left( \overline{\tau }-\overline{\rho }\right)-{\varepsilon }_{ji}\pi }{\left({\varepsilon }_{ji}+1\right)\left[\left({\underline{v}}_{ji}+{\overline{v}}_{ji}\right)-\left({\underline{w}}_{ji}+{\overline{w}}_{ji}\right)\right]}\right)$$

(150)

Although formula (150) is a good closed formula, it is more suitable to get $\left(\frac{\partial E}{\partial {\overline{b}}_{ji max}}\right)$ in terms of $\left(\frac{\partial E}{\partial {\underline{b}}_{ji max}}\right)$ by dividing (150) by (71) to get the formula (72).■

Appendix C

3.1 Derivation of Cauchy Type-1 MSuFNIS (T1MSCFuNIS)

3.1.1 At the Output Layer

The new settings of the parameters in the output layer when all IT2 Cauchy fuzzy sets are reduced to T1 are as follows:

$${{\text{y}}}_{{\text{k}}}={\underline{{\text{y}}}}_{{\text{k}}}={\overline{{\text{y}}}}_{{\text{k}}} ,\uplambda =1$$

(151)

$${b}_{kj}={\underline{b}}_{kj}={\overline{b}}_{kj}$$

(152)

$${w}_{kj}=\left({w}_{kj}^{a},{w}_{kj}^{\underline{b}},{w}_{kj}^{\overline{b}}\right)=\left({w}_{kj}^{a}, {w}_{kj}^{b}\right)$$

(153)

$$\frac{\partial E}{\partial {\underline{b}}_{kj}}=0 , \frac{\partial E}{\partial {b}_{kj}}=\frac{\partial E}{\partial {\overline{b}}_{kj}}$$

(154)

Then, the general partial derivatives of the parameters given in (64)–(66) are reduced to the following forms:

$$\frac{\partial E}{\partial {a}_{kj}}=-\left({d}_{k}-{y}_{k}\right)\frac{{z}_{j}{b}_{kj}}{\sum_{j=1}^{m}{z}_{j}{b}_{kj}}$$

(155)

$$\frac{\partial E}{\partial {b}_{kj}}=-{ z}_{j} \left({d}_{k}-{y}_{k}\right)\left(\frac{{a}_{kj}-{y}_{k} }{\sum_{j=1}^{m}{z}_{j}{b}_{kj}}\right)$$

(156)

3.1.2 At the Hidden Layer

The new settings of the parameters in the hidden layer when all IT2 Cauchy fuzzy sets are reduced to T1 are as follows:

$${v}_{ji}={\underline{v}}_{ji}={\overline{v}}_{ji}$$

(157)

$${w}_{ji}={\underline{w}}_{ji}={\overline{w}}_{ji}$$

(158)

$${b}_{ji max}={\underline{b}}_{ji max}={\overline{b}}_{ji max}=\mathit{max}\left({b}_{xi} ,{b}_{ji}\right)$$

(159)

$${b}_{ji min}={\underline{b}}_{ji min}={\overline{b}}_{ji min}=\mathit{min}\left({b}_{xi} ,{b}_{ji}\right)$$

(160)

$${\Omega }_{ji}={\underline{\Omega }}_{ji}={\overline{ \Omega }}_{ji}$$

(161)

$$ \begin{gathered} \Omega _{{ji}} = \left( {b_{{jimax}} - b_{{jimin}} } \right)tan^{{ - 1}} \left( {\frac{{a_{{jimax}} - a_{{jimin}} }}{{b_{{jimax}} - b_{{jimin}} }}} \right) \hfill \\ \;\;\;\;\;\;\;\; - \left( {b_{{jimax}} + b_{{jimin}} } \right)tan^{{ - 1}} \left( {\frac{{a_{{jimax}} - a_{{jimin}} }}{{b_{{jimax}} + b_{{jimin}} }}} \right) \hfill \\ \end{gathered} $$

(162)

$${\varepsilon }_{ji}={S}_{ji}=\frac{{b}_{ji min}\pi + {\Omega }_{ji}}{{b}_{ji max}\pi - {\Omega }_{ji}}$$

(163)

$${w}_{ji}=\left({w}_{ji}^{a},{w}_{ji}^{\underline{b}},{w}_{ji}^{\overline{b}}\right)=\left({w}_{ji}^{a},{w}_{ji}^{b}\right)$$

(164)

$$\uptau =\underline{\uptau }=\overline{\uptau }$$

(165)

$$\tau ={v}_{ji}\sqrt{\left(\frac{1}{{v}_{ji}}-1\right)}-{{\text{tan}}}^{-1}\sqrt{\left(\frac{1}{{v}_{ji}}-1\right)}$$

(166)

$$\uprho =\underline{\uprho }=\overline{\uprho }$$

(167)

$$\rho ={w}_{ji}\sqrt{\left(\frac{1}{{w}_{ji}}-1\right)}-{tan}^{-1}\sqrt{\left(\frac{1}{{w}_{ji}}-1\right)}$$

(168)

Then, the general partial derivatives of the parameters given in (67)–(72) are reduced to the following forms:

$$\frac{\partial E}{\partial {a}_{ji min}}=\left(\frac{{\varepsilon }_{ji}+1}{{\varepsilon }_{ji}}\right)\left(\frac{{v}_{ji}-{w}_{ji}}{{b}_{ji max} \pi -{\Omega }_{ji}}\right)\sum_{k=1}^{p}{b}_{kj}\frac{\partial E}{\partial {b}_{kj}}$$

(169)

$$\frac{\partial E}{\partial {a}_{ji max}}=-\left(\frac{\partial E}{\partial {a}_{ji min}}\right)$$

(170)

$$\frac{\partial E}{\partial {b}_{ji min}}=\frac{1}{2}\left(\frac{\partial E}{\partial {a}_{ji min}}\right)\left(\frac{\left({\varepsilon }_{ji}+1\right)\left(\tau +\rho \right)+\pi }{\left({\varepsilon }_{ji}+1\right)\left[{v}_{ji}-{w}_{ji}\right]}\right)$$

(171)

$$\frac{\partial E}{\partial {b}_{ji max}}=\frac{1}{2}\left(\frac{\partial E}{{a}_{ji min}}\right)\left(\frac{\left({\varepsilon }_{ji}+1\right)\left(\tau -\rho \right)-{\varepsilon }_{ji}\pi }{\left({\varepsilon }_{ji}+1\right)\left[{v}_{ji}-{w}_{ji}\right]}\right)$$

(172)