Stability and Time-Step Constraints of Implicit-Explicit Runge-Kutta Methods for the Linearized Korteweg-de Vries Equation

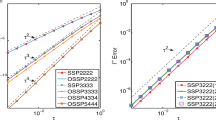
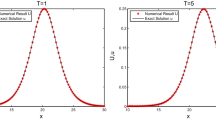
Abstract

This paper provides a study on the stability and time-step constraints of solving the linearized Korteweg-de Vries (KdV) equation, using implicit-explicit (IMEX) Runge-Kutta (RK) time integration methods combined with either finite difference (FD) or local discontinuous Galerkin (DG) spatial discretization. We analyze the stability of the fully discrete scheme, on a uniform mesh with periodic boundary conditions, using the Fourier method. For the linearized KdV equation, the IMEX schemes are stable under the standard Courant-Friedrichs-Lewy (CFL) condition $\tau \leqslant \hat{\lambda } h$. Here, $\hat{\lambda }$ is the CFL number, $\tau$ is the time-step size, and h is the spatial mesh size. We study several IMEX schemes and characterize their CFL number as a function of $\theta =d/h^2$ with d being the dispersion coefficient, which leads to several interesting observations. We also investigate the asymptotic behaviors of the CFL number for sufficiently refined meshes and derive the necessary conditions for the asymptotic stability of the IMEX-RK methods. Some numerical experiments are provided in the paper to illustrate the performance of IMEX methods under different time-step constraints.

Appendix A Proof of Lemmas 1 and 2 in the Simple Case

In this Appendix, we consider (2, 2, p) and (2, 3, p) IMEX methods coupled with an FD or a $P^1$-DG spatial discretization. We will prove Lemma 1 for the (2, 2, p) method in both cases and extend the proof to prove Lemma 2 for the (2, 3, p) method. Our analysis further enables us to adapt these proofs for (3, 3, p), (4, 3, p), and (3, 4, p) methods when combined with FD discretizations. For $P^2$-DG discretizations, the analysis becomes considerably more challenging, and we have checked both lemmas hold under the continuity assumption

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K)=\rho (\lim _{\theta \rightarrow \infty }K), \end{aligned}$$

using the software Mathematica.

Recall the tableaux for (2, 2, p) and (2, 3, p) methods take the forms (17) and (18). We will discuss the case with an FD or a $P^1$-DG spatial discretization separately.

1.1 Appendix A.1 Spectral Analysis with FD Spatial Discretization

1.1.1 Appendix A.1.1 Proof of Lemma 1 with a (2, 2, p) Method Coupled with FD

We first consider a (2, 2, p) method, and aim to prove Lemma 1. When using an FD discretization, C and D from (5) are scalars that depend on $z=\omega h$. Applying the IMEX method (17) to (19) yields the following stage equations after rearranging terms:

$$\begin{aligned} \hat{u}^{n,1}&=K_1\hat{u}^n, \qquad \hat{u}^{n,2}=K_2\hat{u}^n, \qquad \hat{u}^{n+1}=K\hat{u}^n, \end{aligned}$$

where $K_1$, $K_2$, and K are given by

$$\begin{aligned} K_1&=M_{11}, \end{aligned}$$

(A1a)

$$\begin{aligned} K_2&=M_{22}(1+\lambda \tilde{a}_{21}CK_1+\lambda \theta a_{21}DK_1), \end{aligned}$$

(A1b)

$$\begin{aligned} K&=1+\lambda \tilde{b}_1CK_1+\lambda b_1 D(\theta K_1)+\lambda \tilde{b}_2CK_2+\lambda b_2 D(\theta K_2), \end{aligned}$$

(A1c)

$$\begin{aligned} M_{ii}&= (1-\lambda \theta a_{ii} D)^{-1}, \qquad i=1,2. \end{aligned}$$

(A1d)

The goal is to show for fixed $\lambda$ and z

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K)=\lim _{\theta \rightarrow \infty }|K|= \left| \lim _{\theta \rightarrow \infty }K\right| = \left| 1- \frac{b_1}{a_{11}}- \frac{b_2}{a_{22}}+ \frac{a_{21}b_2}{a_{11}a_{22}} \right| . \end{aligned}$$

(A2)

Since K is a scalar, the first two equalities are obvious, and we focus on showing the last equality by evaluating the limit of K. For fixed $\lambda$ and z, we observe that C and D do not depend on $\theta$, and that both $K_1$ and $K_2$ are rational functions of the variable $\theta$. When $\theta \rightarrow \infty$, it is easy to observe that $M_{ii}=O(1/\theta )$. Therefore, $K_1$ is at the level of $O(1/\theta )$ and $K_2$ is at the level of $O(1/\theta +1/\theta ^2)$, which leads to

$$\begin{aligned} \lim _{\theta \rightarrow \infty }1+\lambda \tilde{b}_1CK_1+\lambda \tilde{b}_2CK_2=1. \end{aligned}$$

In addition, we have

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\lambda b_1 D(\theta K_1)= \lim _{\theta \rightarrow \infty } \frac{\lambda b_1 D \theta }{1-\lambda \theta a_{11} D} =\frac{\lambda b_1 D}{-\lambda a_{11}D}=-\frac{b_1}{a_{11}}. \end{aligned}$$

Following a similar analysis leads to the limit of the last term

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\lambda b_2 D(\theta K_2)&=\lim _{\theta \rightarrow \infty } \frac{\lambda b_2 D \theta (1-\lambda \theta a_{11} D+\lambda \tilde{a}_{21}C+\lambda \theta a_{21}D) }{(1-\lambda \theta a_{11} D)(1-\lambda \theta a_{22} D)} \\&=\frac{-\lambda ^2 a_{11}b_2D^2+\lambda ^2 a_{21}b_2D^2}{\lambda ^2 a_{11}a_{22}D^2} =-\frac{b_2}{a_{22}}+\frac{a_{21}b_2}{a_{11}a_{22}}. \end{aligned}$$

Combining all these results yields

$$\begin{aligned} \left| \lim _{\theta \rightarrow \infty }K\right| =\left| 1-\frac{b_1}{a_{11}}- \frac{b_2}{a_{22}}+ \frac{a_{21}b_2}{a_{11}a_{22}}\right| , \end{aligned}$$

which finishes the proof of (A2). The same analysis can be extended to prove Lemma 1 for (3, 3, p) and (4, 3, p) IMEX methods coupled with an FD discretization. We omit these details for brevity.

1.1.2 Appendix A.1.2 Proof of Lemma 2 with a (2, 3, p) Method Coupled with FD

Next, we consider a (2, 3, p) method (18), and aim to prove Lemma 2 by adapting the above proof. Applying this method to (5) yields the same definition of $M_{ii}$ but with $K_1$, $K_2$, and K defined as

$$\begin{aligned} K_1&=M_{22}(1+\lambda \tilde{a}_{21}C), \end{aligned}$$

(A3a)

$$\begin{aligned} K_2&=M_{33}(1+\lambda \tilde{a}_{31}C+\lambda \tilde{a}_{32}CK_1+\lambda \theta a_{32}DK_1), \end{aligned}$$

(A3b)

$$\begin{aligned} K&=1+\lambda \tilde{b}_1C+\lambda \tilde{b}_2CK_1+\lambda b_2D(\theta K_1)+\lambda \tilde{b}_3CK_2+\lambda b_3D(\theta K_2). \end{aligned}$$

(A3c)

The goal is to show for fixed $\lambda$ and z

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K) = \lim _{\theta \rightarrow \infty }|K| = \left| \lim _{\theta \rightarrow \infty }K\right| = \left| 1- \frac{b_2}{a_{22}}- \frac{b_3}{a_{33}}+ \frac{a_{32}b_3}{a_{22}a_{33}}+\lambda \alpha C\right| , \end{aligned}$$

(A4)

where

$$\begin{aligned} \alpha =\tilde{b}_1 -\frac{\tilde{a}_{21}b_2}{a_{22}} -\frac{\tilde{a}_{31}b_3}{a_{33}} +\frac{\tilde{a}_{21}a_{32}b_3}{a_{22}a_{33}}. \end{aligned}$$

(A5)

Following the same analysis as before, we observe that both $K_1$ and $K_2$ are at the level of $O(1/\theta )$, and

$$\begin{aligned} \lim _{\theta \rightarrow \infty }1+\lambda \tilde{b}_1C+\lambda \tilde{b}_2CK_1+\lambda \tilde{b}_3CK_2 =1+\lambda \tilde{b}_1C. \end{aligned}$$

Similarly, we have

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\lambda b_2D(\theta K_1)&= \lim _{\theta \rightarrow \infty } \frac{\lambda \theta b_2(1+\lambda \tilde{a}_{21}C)D}{1-\lambda \theta a_{22}D} = \frac{-b_2(1+\lambda \tilde{a}_{21}C)}{a_{22}} = \frac{-b_2}{a_{22}}+\lambda \left( \frac{-\tilde{a}_{21}b_2}{a_{22}}\right) C,\\ \lim _{\theta \rightarrow \infty }\lambda b_3D(\theta K_2)&= \frac{\lambda b_3(1+\lambda \tilde{a}_{31}C)D}{-\lambda a_{33}D}+\frac{\lambda ^2 b_3 a_{32}(1+\lambda \tilde{a}_{21}C)D^2}{\lambda ^2 a_{22}a_{33}D^2}\\&= \frac{-b_3(1+\lambda \tilde{a}_{31}C)}{a_{33}}+\frac{b_3 a_{32}(1+\lambda \tilde{a}_{21}C)}{a_{22}a_{33}}\\&= \frac{-b_3}{a_{33}}+\frac{a_{32}b_3}{a_{22}a_{33}}+\lambda \left( \frac{-\tilde{a}_{31}b_3}{a_{33}}+\frac{\tilde{a}_{21}a_{32}b_3}{a_{22}a_{33}}\right) C. \end{aligned}$$

Therefore, combining all these analyses yields

$$\begin{aligned} \begin{aligned} \left| \lim _{\theta \rightarrow \infty }K\right|&= \left| 1-\frac{b_2}{a_{22}}-\frac{b_3}{a_{33}}+\frac{a_{32}b_3}{a_{22}a_{33}} +\lambda \left( \tilde{b}_1 -\frac{\tilde{a}_{21}b_2}{a_{22}} -\frac{\tilde{a}_{31}b_3}{a_{33}} +\frac{\tilde{a}_{21}a_{32}b_3}{a_{22}a_{33}} \right) C\right| , \end{aligned} \end{aligned}$$

which finishes the proof of (A4). Again, the same analysis can be extended to prove Lemma 2 for (3, 4, p) IMEX methods coupled with an FD discretization, which is omitted for brevity.

1.2 Appendix A.2 Spectral Analysis with $P^1$-DG Spatial Discretization

1.2.1 Appendix A.2.1 Proof of Lemma 1 with a (2, 2, p) Method Coupled with $P^1$-DG

Next, we will prove Lemma 1 for a (2, 2, p) IMEX method with a $P^1$-DG discretization. Now, C and D from (5) become matrices depending on $z=\omega h$, and we denote

$$\begin{aligned} C=\begin{bmatrix} c_{11} &{}c_{12}\\ c_{21} &{}c_{22}\end{bmatrix},\qquad D=\begin{bmatrix} d_{11} &{}d_{12}\\ d_{21} &{}d_{22}\end{bmatrix}. \end{aligned}$$

Applying the IMEX method (17) to (5) yields the following stage equations after rearranging terms:

$$\begin{aligned} \hat{u}^{n,1}&=K_1\hat{u}^n, \qquad \hat{u}^{n,2}=K_2\hat{u}^n, \qquad \hat{u}^{n+1}=K\hat{u}^n, \end{aligned}$$

(A6)

where $K_1$, $K_2$, and K are given by (A1a)–(A1c), and

$$\begin{aligned} \begin{aligned} M_{ii}&=(I-\lambda \theta a_{ii}D)^{-1} = \frac{1}{\gamma _{ii}} \begin{bmatrix} 1-\lambda \theta a_{ii}d_{22} &{}\lambda \theta a_{ii}d_{12}\\ \lambda \theta a_{ii}d_{21} &{}1-\lambda \theta a_{ii}d_{11}\\ \end{bmatrix} = \frac{1}{\gamma _{ii}} \left( I-\lambda \theta a_{ii}\det (D)D^{-1} \right) \end{aligned} \end{aligned}$$

(A7)

with $\gamma _{ii}=(\lambda \theta a_{ii})^2\det (D)-(\lambda \theta )\textrm{tr}(D)+1$. The goal is to show for fixed $\lambda$ and z

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K)=\rho \left(\lim _{\theta \rightarrow \infty }K\right)=\left| 1- \frac{b_1}{a_{11}}- \frac{b_2}{a_{22}}+ \frac{a_{21}b_2}{a_{11}a_{22}}\right| . \end{aligned}$$

(A8)

To prove the first equality of (A8), namely, the continuity of $\rho (K)$ with respect to $\theta$, we assume the matrix K is a $2\times 2$ matrix with entries $k_{11}, k_{12}, k_{21}, k_{22}$. Its spectral radius $\rho (K)$ is given by

$$\begin{aligned} \rho (K)=\max \left\{ \left| \dfrac{(k_{11}+k_{22})\pm \sqrt{(k_{11}+k_{22})^2-4(k_{11}k_{22}-k_{12}k_{21})}}{2}\right| \right\} . \end{aligned}$$

Supposing the limit of K exists (as will be shown later), we have

$$\begin{aligned} \begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K)&= \lim _{\theta \rightarrow \infty }\max \left\{ \left| \dfrac{(k_{11}+k_{22})\pm \sqrt{(k_{11}+k_{22})^2-4(k_{11}k_{22}-k_{12}k_{21})}}{2}\right| \right\} \\&=\max \left\{ \left| \lim _{\theta \rightarrow \infty }\dfrac{(k_{11}+k_{22})\pm \sqrt{(k_{11}+k_{22})^2-4(k_{11}k_{22}-k_{12}k_{21})}}{2}\right| \right\} = \rho \left(\lim _{\theta \rightarrow \infty } K\right). \end{aligned} \end{aligned}$$

Now, it suffices to determine the limit of K. To simplify the calculation, we first evaluate limits of $K_1$, $\theta K_1$, $K_2$, and $\theta K_2$. It can be shown that

$$\begin{aligned} \lim _{\theta \rightarrow \infty }K_1&= \lim _{\theta \rightarrow \infty }M_{11} = \lim _{\theta \rightarrow \infty }\frac{1}{\gamma _{11}} \left( I-\lambda \theta a_{11}\det (D)D^{-1} \right) \nonumber \\&= \lim _{\theta \rightarrow \infty }\frac{I-\lambda \theta a_{11}\det (D)D^{-1}}{(\lambda \theta a_{11})^2\det (D)-(\lambda \theta )\textrm{tr}(D)+1} = 0, \end{aligned}$$

(A9)

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\theta K_1&= \lim _{\theta \rightarrow \infty }\theta M_{11} = \lim _{\theta \rightarrow \infty }\frac{\theta }{\gamma _{11}}( I-\lambda \theta a_{11}\det (D)D^{-1}) \nonumber \\&= \lim _{\theta \rightarrow \infty }\frac{\theta I-\lambda \theta ^2 a_{11}\det (D)D^{-1}}{(\lambda \theta a_{11})^2\det (D)-(\lambda \theta )\textrm{tr}(D)+1} = \frac{-D^{-1}}{\lambda a_{11}}. \end{aligned}$$

(A10)

To compute the limit of $K_2$, we will consider the limits of its three terms, $M_{22}$, $\lambda \tilde{a}_{21}M_{22}CK_1$, and $\lambda a_{21}M_{22}D\theta K_1$ separately. The limit of the first term can be computed similarly to that of $K_1$

$$\begin{aligned} \lim _{\theta \rightarrow \infty }M_{22} = \lim _{\theta \rightarrow \infty }\frac{1}{\gamma _{22}}(I-\lambda \theta a_{22}\det (D)D^{-1}) = 0. \end{aligned}$$

For the second term, we have

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\lambda \tilde{a}_{21}M_{22}CK_1 = \lambda \tilde{a}_{21}\lim _{\theta \rightarrow \infty }\frac{1}{\gamma _{11}\gamma _{22}}(I-\lambda \theta a_{22}\det (D)D^{-1})C(I-\lambda \theta a_{11}\det (D)D^{-1})=0, \end{aligned}$$

since the highest order term in the numerator is at the level of $O(\theta ^2)$ and that $\gamma _{11}\gamma _{22}$ is at the level of $O(\theta ^4)$. Similarly, we have

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\lambda a_{21}M_{22}D\theta K_1&= \lambda a_{21}\lim _{\theta \rightarrow \infty }\frac{1}{\gamma _{11}\gamma _{22}}(I-\lambda \theta a_{22}\det (D)D^{-1})(\theta D-\lambda \theta ^2 a_{11}\det (D)I)=0, \end{aligned}$$

since the highest order term in the numerator is at the level of $O(\theta ^3)$. Putting these three limits together leads to

$$\begin{aligned} \lim _{\theta \rightarrow \infty }K_2=0. \end{aligned}$$

(A11)

To determine the limit of $\theta K_2$, we can once again analyze its three terms separately. Based on our previous analysis, we can obtain

$$\begin{aligned}&\lim _{\theta \rightarrow \infty }\theta M_{22}=\frac{-D^{-1}}{\lambda a_{22}}, \qquad \qquad \lim _{\theta \rightarrow \infty }\lambda \tilde{a}_{21}M_{22}C\theta K_1=0, \\&\lim _{\theta \rightarrow \infty }\lambda a_{21}M_{22}D\theta ^2 K_1 =\frac{\lambda ^3 a_{21}a_{11}a_{22}\det (D)^2D^{-1}}{\lambda ^4(a_{11}a_{22}\det (D))^2} =\frac{a_{21}D^{-1}}{\lambda a_{11}a_{22}}. \end{aligned}$$

Collecting all three limits together yields

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\theta K_2 = \left( \frac{-1}{\lambda a_{22}}+\frac{a_{21}}{\lambda a_{11}a_{22}} \right) D^{-1}. \end{aligned}$$

Since C and D are independent of $\theta$, using the limits of $K_1$, $\theta K_1$, $K_2$, and $\theta K_2$ leads to

$$\begin{aligned} \lim _{\theta \rightarrow \infty }K&= \lim _{\theta \rightarrow \infty }(I+\lambda \tilde{b}_1CK_1+\lambda b_1 D(\theta K_1)+\lambda \tilde{b}_2CK_2+\lambda b_2 D(\theta K_2))\\&= I+0+\lambda b_1 D\frac{-D^{-1}}{\lambda a_{11}}+0+\lambda b_2 D\left( \frac{-1}{\lambda a_{22}}+\frac{a_{21}}{\lambda a_{11}a_{22}} \right) D^{-1}\\&=\left( 1-\frac{b_1}{a_{11}}-\frac{b_2}{a_{22}}+\frac{b_2a_{21}}{a_{11}a_{22}} \right) I, \end{aligned}$$

which finishes the proof of (A8), after utilizing the continuity assumption (19).

1.2.2 Appendix A.2.2 Proof of Lemma 2 with a (2, 3, p) Method Coupled with $P^1$-DG

In the end, we consider a (2, 3, p) method (18) with a $P^1$-DG discretization, and aim to prove Lemma 2 by adapting the above proof. Applying this method to (5) yields the same stage equations (A6), with $K_1$, $K_2$, and K defined in (A3) and $M_{ii}$ defined in (A7). The goal is to show for fixed $\lambda$ and z

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K) = \rho \left(\lim _{\theta \rightarrow \infty }K\right) = \max _{\kappa \in \textrm{eig}(C(z))}\left| 1-\frac{b_2}{a_{22}}-\frac{b_3}{a_{33}}+\frac{a_{32}b_3}{a_{22}a_{33}}+\lambda \alpha \kappa \right| \end{aligned}$$

(A12)

with $\alpha$ defined in (A5).

The continuity of $\rho (K)$ in $\theta$ can be verified as that in the previous section. To validate the second equality in (A12), we compute the limits of $K_1, \theta K_1, K_2, \theta K_2$ separately. Following the analysis in (A9), we have

$$\begin{aligned} \lim _{\theta \rightarrow \infty }K_1 = \left( \lim _{\theta \rightarrow \infty }M_{22}\right) (I+\lambda \tilde{a}_{21}C) = 0. \end{aligned}$$

Similarly, (A10) leads to

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\theta K_1 = \left( \lim _{\theta \rightarrow \infty }\theta M_{22}\right) (I+\lambda \tilde{a}_{21}C) = \frac{-D^{-1}}{\lambda a_{22}}(I+\lambda \tilde{a}_{21}C). \end{aligned}$$

We again determine the limit of $K_2$ by considering the limits of three terms separately. Following the same analysis in deriving (A11), we have

$$\begin{aligned} \lim _{\theta \rightarrow \infty }K_2=0. \end{aligned}$$

To determine the limit of $\theta K_2$, we can once again analyze its three terms separately. Using the results from the previous analysis, we can obtain

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\theta M_{33}(I+\lambda \tilde{a}_{31}C)&= \left( \lim _{\theta \rightarrow \infty }\theta M_{33}\right) (I+\lambda \tilde{a}_{31}C) = \frac{-D^{-1}}{\lambda a_{33}}(I+\lambda \tilde{a}_{31}C), \\ \lim _{\theta \rightarrow \infty }\lambda \tilde{a}_{32}\theta M_{33}CK_1&= \lambda \tilde{a}_{32}\left( \lim _{\theta \rightarrow \infty } M_{33}C\theta M_{22}\right) (I+\lambda \tilde{a}_{21}C) =0, \\ \lim _{\theta \rightarrow \infty }\lambda \theta ^2 a_{32}M_{33}DK_1&= \lambda a_{32}\left( \lim _{\theta \rightarrow \infty } M_{33}D\theta ^2 M_{22} \right) (I+\lambda \tilde{a}_{21}C) = \frac{a_{32}D^{-1}}{\lambda a_{22}a_{33}}(I+\lambda \tilde{a}_{21}C). \end{aligned}$$

Collecting all three limits together yields

$$\begin{aligned} \lim _{\theta \rightarrow \infty }\theta K_2 = \frac{-D^{-1}}{\lambda a_{33}}(I+\lambda \tilde{a}_{31}C)+\frac{a_{32}D^{-1}}{\lambda a_{22}a_{33}}(I+\lambda \tilde{a}_{21}C). \end{aligned}$$

Since C and D are independent of $\theta$, using the limits of $K_1$, $\theta K_1$, $K_2$, and $\theta K_2$ leads to

$$\begin{aligned} \lim _{\theta \rightarrow \infty }K&= \lim _{\theta \rightarrow \infty }(I+\lambda \tilde{b}_1C+\lambda \tilde{b}_2CK_1+\lambda b_2D(\theta K_1)+\lambda \tilde{b}_3CK_2+\lambda b_3D(\theta K_2))\\&= I+\lambda \tilde{b}_1C+0 +\frac{-b_2}{a_{22}}(I+\lambda \tilde{a}_{21}C) +0 +\frac{-b_3}{a_{33}}(I+\lambda \tilde{a}_{31}C)+\frac{b_3a_{32}}{a_{22}a_{33}}(I+\lambda \tilde{a}_{21}C)\\&= \left( 1-\frac{b_2}{a_{22}}-\frac{b_3}{a_{33}}+\frac{a_{32}b_3}{a_{22}a_{33}}\right) I+\lambda \left( \tilde{b}_1 -\frac{\tilde{a}_{21}b_2}{a_{22}} -\frac{\tilde{a}_{31}b_3}{a_{33}} +\frac{\tilde{a}_{21}a_{32}b_3}{a_{22}a_{33}} \right) C. \end{aligned}$$

With this formulation of the limit of K and the continuity of $\rho (K)$ in $\theta$, it can be shown that

$$\begin{aligned} \begin{aligned} \lim _{\theta \rightarrow \infty }\rho (K)&= \max _{\kappa \in \text {eig}(C(z))}\left| 1-\frac{b_2}{a_{22}}-\frac{b_3}{a_{33}}+\frac{a_{32}b_3}{a_{22}a_{33}}+\lambda \alpha \kappa \right| . \end{aligned} \end{aligned}$$

This finishes the proof of Lemma 2 for (2, 3, p) IMEX methods with a $P^1$-DG spatial discretization.