1 Introduction

As regional power grids become increasingly interconnected, the complexity of the power grid’s overall structure grows, accompanied by a wider array of disturbances [1]. Consequently, Automatic Generation Control (AGC) emerges as a paramount concern within interconnected power systems [2]. When a disturbance affects a segment of the interconnected power system, the resulting frequency deviation traverses tie lines, potentially impacting power flow between regional grids [3]. In power systems, AGC plays a pivotal role in restoring unit frequency and inter-regional tie line power to predefined permissible ranges during regular operation or minor disruptions [12, 13]. Additionally, advanced controllers such as sliding mode controllers [14] and robust controllers [15] have been proposed to enhance AGC. However, these methods often entail high complexity and computational burdens, fostering the application of Proportional-Integral-Derivative (PID) controllers [16]. PID controllers are commonly preferred in educational and engineering contexts due to their simplicity, cost-effectiveness, and robustness against diverse disturbances [17].

Nevertheless, the performance of PID controllers hinges on their settings [18, 19], underscoring the importance of efficient optimization models [20]. The researchers improved the Bacterial Foraging Optimization Approach (BFOA) by reducing a time-domain objective function to develop PID controllers [21]. The researchers presented a novel approach called Teaching Learning-Based Optimization (TLBO) to optimize the parameters of PID controllers in a two-region thermal system [22]. Kumar et al. [23] compared two search algorithms for PID controller design, utilizing the Imperialist Competitive Algorithm (ICA) to determine ideal parameters. Gheisarnejad [24] devised a hybrid algorithm by combining the harmony search algorithm (HSCOA) and Cuckoo Optimization Algorithm (COA) mechanisms to tune PID gains. He et al. [25] presented the Wind-Driven Butterfly Optimization Algorithm (WDBOA), which effectively balances exploration and exploitation capabilities and demonstrates superior performance in PID controller parameter optimization.

Despite scholars optimizing auxiliary controller parameters, their research typically focuses on a single objective that aligns with specific control requirements and can be addressed by a single-objective optimization algorithm. Shiva and Mukherjee [26] used Integral Squared Error (ISE) as the objective function to design a PID controller. Meanwhile, Singh et al. [5] took into account a range of performance indicators. The performance measurements were consolidated into a singular target through the utilization of the analytical hierarchy process (AHP). The inherent contradiction between these objectives presents a challenge in determining an optimal scheme for a multi-objective model that effectively addresses the trade-offs between speed, economy, and safety.

The performance of AGC primarily hinges on three factors: (a) controller structure; (b) algorithm for optimizing controller parameters; and (c) loss function performance. Facing the challenge of balancing multiple, often conflicting, control optimization objectives in nonlinear and oscillatory AGC systems, the Multi-Objective Marine Predators Algorithm (MOMPA) [27] offers an innovative solution. Inspired by the foraging behavior of marine predators, this algorithm adopts their dynamic strategies to effectively tackle multi-objective optimization problems. MOMPA is specifically designed to explore and exploit the solution space, identifying solutions that balance various objectives across the complex Pareto front [28]. Despite MOMPA’s capability in navigating complex Pareto fronts, it faces challenges in highly multi-modal environments with numerous local optima, necessitating refined exploration and exploitation strategies to prevent premature convergence on suboptimal solutions [29].

The purpose of this paper is to provide a multi-objective approach that can effectively tune PID controllers with simple designs. We construct a multi-objective model featuring the Integrated Time Squared Error (ITSE), the Integrated Time Absolute Error (ITAE), and the rate of change in deviation as objectives, comprehensively addressing convergence rate, overshoot, and system oscillation. Our approach utilizes the efficient MOMPA integrating spiral mode, Quasi-Oppositional Learning (QOL), and Q-learning (QQSMOMPA) to optimize PID controller parameters for three real-world AGC systems. The inherent variability and uncertainty present in AGC systems, including load fluctuations and parameter shifts, necessitate optimization algorithms to possess a high degree of adaptability. The augmented diversity within the QQSMOMPA guarantees that the algorithm can adjust to these fluctuations, thereby sustaining optimal or near-optimal performance across more conditions. The contributions of this paper are summarized as follows:

  1. (1)

    Introduce a novel multi-objective optimization methodology aimed at augmenting PID controller performance in nonlinear and oscillatory AGC. This methodology stands out by concurrently minimizing ITSE, ITAE, and the deviation rate of change, thereby balancing the convergence rate, overshoot, and system oscillation.

  2. (2)

    Integration of advanced optimization techniques, including spiral model and Q-learning framework, to efficiently diversify solution sets and effectively balance exploration and exploitation strategies, resulting in superior Pareto solutions for AGC systems.

  3. (3)

    Demonstration of QQSMOMPA’s efficacy through experiments, showcasing superior performance and robustness in optimizing PID controllers for AGC under various conditions. When applied to nonlinear AGC systems featuring governor dead zones, the PID controllers optimized by QQSMOMPA not only achieve 14\(\%\) reduction in the frequency settling time but also exhibit robustness against uncertainties in load disturbance inputs.

The following sections are organized in the following manner: Sect. 2 provides an overview of the AGC problem and presents a multi-objective optimization model. Section 3 elaborates on MOMPA and the proposed SMOMPA and QQSMOMPA. In Sect. 4, we employ QQSMOMPA to resolve three real-world AGC scenarios. The paper concludes in Sect. 5.

2 The Description and Solution of the Problem of AGC

2.1 The Description of AGC

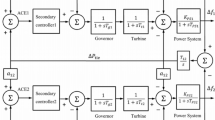
This section introduces the fundamental transfer function model of the AGC. The examination of AGC often utilizes a thermal power system with two regions and no reheat, as seen in Fig. 1, which serves as a widely adopted framework for AGC investigations. The interconnected grid system primarily consists of governors, turbines, and power systems. The inputs to the system consist of the control system signal \(\Delta P_{ref}\), changes in demand for energy \(\Delta P_{L}\), and deviations in tie-line power \(\Delta P_{tie}\). In addition, the outputs of the system encompass the frequency deviation \(\Delta f\) and the area control error (ACE), which are precisely specified by:

$$\begin{aligned} \begin{aligned} ACE_{1}&= -B \Delta f_{1} - \Delta P_{tie}, \\ ACE_{2}&= -B \Delta f_{2} + \Delta P_{tie}. \end{aligned} \end{aligned}$$
(1)

The symbol B is used to denote the frequency deviation parameter. To achieve desired goals, the control system adjusts the reference power setting of the generator set, thereby balancing the power generation and load in each region.

In previous studies [3, 30], the parameters for test system-1 were uniformly set. The parameters include \(T_{\textrm{g}}\) for the governor’s time constant, \(T_{t}\) for the non-reheat steam turbine’s time constant, B for the frequency deviation, \(T_{12}\) for the synchronous torque coefficient, \(\Delta P_{ref}\) for the reference power setting, \(\Delta P_{\textrm{g}}\) for the governor valve’s positional adjustment, \(\Delta P_{t}\) for changes in steam turbine power output, \(\Delta P_{L}\) for load demand changes, \(\Delta f\) for frequency variation, and \(\Delta P_{tie}\) for tie-line power discrepancies between regions. Per-unit values are provided for system variables: \(f=60\) Hz, \(B=0.425\) p.u MW/Hz, \(R=2.4\) Hz/p.u, \(T_{\textrm{g}}=0.03\) s, \(T_{t}=0.3\) s, \(K_{ps}=120\) Hz/p.u, \(T_{ps}=20\) s, and \(T_{12}=0.545\) p.u MW/rad.

Fig. 1
figure 1

Transfer function model of test system-1

Full size image

When affected by load changes, the frequency can still be maintained near the stable point. Therefore, each link can be approximated using a low-order transfer function, as detailed in Elgerd [31].

The transfer functions of the governor, non-reheat turbine, and power system are given by:

$$\begin{aligned} G_{\textrm{g}}(s)= & {} \frac{\Delta P_{\textrm{g}}(s)}{\Delta P_{e}(s)} = \frac{1}{s T_{\textrm{g}}+1}, \end{aligned}$$
(2)
$$\begin{aligned} G_t(s)= & {} \frac{\Delta P_{t}(s)}{\Delta P_{\textrm{g}}(s)} = \frac{1}{s T_{t}+1}, \end{aligned}$$
(3)

and

$$\begin{aligned} G_{ps}(s) = \frac{\Delta f}{\Delta P_{t}(s) - \Delta P_{L}(s) + \Delta P_{tie}(s)} = \frac{K_{p s}}{s T_{p s}+1}. \end{aligned}$$
(4)

The controller functions as a supplement to the AGC system. Despite significant advancements in advanced controllers, the traditional PID controller and its variations remain preferred due to its simple structure, high reliability, and excellent control performance. Furthermore, their ease of dynamic modeling and cost-effectiveness contribute to their effectiveness in engineering practice.

Assuming that in Fig. 1, the PID controller acts as an additional control element, the reference power settings \(\Delta P_{ref1}\) and \(\Delta P_{ref2}\) are given by:

$$\begin{aligned} \begin{aligned} \Delta P_{r e f 1}&=K_{p 1} A C E_{1}+K_{i 1} \int A C E_{1} d t+K_{d 1} \frac{d}{d t} A C E_{1}, \\ \Delta P_{r e f 2}&=K_{p 2} A C E_{2}+K_{i 2} \int A C E_{2} d t+K_{d 2} \frac{d}{d t} A C E_{2}, \end{aligned} \end{aligned}$$
(5)

where \(K_p\), \(K_i\), and \(K_d\) represent the gains of the PID controller. This paper assumes that the gains of all region controllers are the same, namely \(K_{p1} = K_{p2} = K_{p}\), \(K_{i1} = K_{i2} = K_{i}\), and \(K_{d1} = K_{d2} = K_{d}\). To achieve the control objectives, these gains must be accurately optimized, which is the motivation behind this paper.

2.2 The Construction of Multi-objective Optimization Model

As mentioned earlier, an effective AGC system for an interconnected grid aims to minimize frequency and power overshoots, guiding them to converge rapidly to zero. To achieve this goal, it is imperative to adjust the gains of the PID controller, a task that may be conceptualized as a multi-objective optimization problem (MOP). The general mathematical formulation for MOP is presented as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\text {minimize}} \\ \quad F(X)=\left\{ f_{1}(X), f_{2}(X), \ldots , f_{M}(X)\right\} \\ \text{ s.t. }\\ \quad g_{i}(X) \ge 0, \\ \quad h_{j}(X)=0, \\ \quad i=1,2, \ldots , a, j=1,2, \ldots , b, \end{array}\right. \end{aligned}$$
(6)

where X represents the candidate solution, F(X) is employed to represent the goal function, while g(X) and h(X) are utilized to express unequal and equal limitations, respectively. M represents the count of goal functions, while a and b stand for the quantities of inequality and equality constraints correspondingly.

Dominance is a notion that describes the optimality of MOP. If \(X_1\) and \(X_2\) satisfy:

$$\begin{aligned} \begin{aligned}&\forall i \in \{1, \ldots , M\}: f_{i}\left( X_{1}\right) \le f_{i}\left( X_{2}\right) , \\&\wedge \exists j \in \{1, \ldots , M\}: f_{j}\left( X_{1}\right) <f_{j}\left( X_{2}\right) , \end{aligned} \end{aligned}$$
(7)

then consider that \(X_1\) dominates \(X_2\), denoted by \(X_{1} \prec X_{2}\).

According to the retrospective research [3, 5], ITAE and ITSE are widely used in the tuning of PID controller parameters. Each of these functions has unique properties that contribute to improving the above specifications, and the formula is as follows:

$$\begin{aligned} ITAE=\int _{0}^{T} t\left( |\Delta f_{1}|+|\Delta f_{2}|+\left| \Delta P_{t i e}\right| \right) d t, \end{aligned}$$
(8)

and

$$\begin{aligned} ITSE=\int _{0}^{T} t\left( \Delta f_{1}^{2}+\Delta f_{2}^{2}+\Delta P_{t i e}^{2}\right) d t. \end{aligned}$$
(9)

When the error is big in the parameter optimization based on the ITSE, the gradient reduces quickly; when the error is small, the gradient declines slowly, which is beneficial for the convergence of the optimization. Compared with ITSE, ITAE is very effective in controlling the error amplitude, but the convergence speed is slower. Furthermore, to enhance the stability of the entire system, a third objective function given by

$$\begin{aligned} J=\int _{0}^{\textrm{T}} \textrm{t}\left( \frac{d|\Delta f_{1}|}{d t}+\frac{d|\Delta f_{2}|}{d t}+\frac{d\left| \Delta P_{t i e}\right| }{d t}\right) d t \end{aligned}$$
(10)

is proposed considering the rate of change of \(\Delta f_{1}\), \(\Delta f_{2}\) and \(\Delta P_{tie}\) which is easy to calculate.

While ITAE prioritizes long-term precision and stability, potentially resulting in slower response times, ITSE aggressively reduces large errors, favoring rapid response but risking overshoot and instability. On the other hand, the rate of change of deviation function aims to smooth system response by minimizing error fluctuations, which may hinder rapid adaptation. Due to the conflict between objective functions, this paper constructs a multi-objective optimization model to tune the PID controller parameters, which is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \textrm{minimize} \\ \quad \quad \quad ITSE=\int _{0}^{\textrm{T}} \textrm{t}\left( \Delta f_{1}^{2}+\Delta f_{2}^{2}+\Delta \textrm{P}_{\text{ tie }}^{2}\right) dt\\ \quad \quad \quad ITAE=\int _{0}^{\textrm{T}} \textrm{t}\left( \left| \Delta f_{1}\right| +\left| \Delta f_{2}\right| +\left| \Delta \textrm{P}_{\text{ tie }}\right| \right) dt \\ \quad \quad \quad J=\int _{0}^{\textrm{T}} \textrm{t}\left( \frac{d\left| \Delta f_{1}\right| }{d t}+\frac{d\left| \Delta f_{2}\right| }{d t}+\frac{d\left| \Delta P_{\text{ tie }}\right| }{d t}\right) d t \\ \text{ s.t. } \quad 0 \le K_{p} \le 2, \quad 0 \le K_{i} \le 2, \quad 0 \le K_{d} \le 2. \end{array}\right. \end{aligned}$$
(11)

In this paper, all PID gain coefficients are in the range of [0.0, 2.0]. The objective of the optimization work is to identify the Pareto optimum set of parameters for the PID controller. To accomplish this objective, this paper employs an enhanced version of the multi-objective marine predator algorithm (MOMPA), which is expounded upon in the subsequent section.

3 The Proposed Strategy

3.1 The MOMPA

The MOMPA, introduced by Chen et al. [27], stands out in the realm of multi-objective optimization for its innovative integration of dominance-based evolutionary strategies and its adeptness at balancing diversity and convergence in the Pareto frontier. Distinctively, MOMPA combines non-dominated sorting with a reference point strategy, a methodological choice that facilitates the identification and preservation of outstanding solutions, thereby ensuring a diverse set of Pareto-optimal solutions [32]. Unique to MOMPA is its adoption of a Gaussian perturbation technique, designed to enhance population diversity and bolster its global search efficacy [33].

The evolutionary strategies of MOMPA include high velocity, same velocity, and low velocity. During each phase, the updating process involves two matrices from the following options:

$$\begin{aligned} \varvec{Prey} =\left[ \begin{array}{cccc} \textit{X}_{1,1} &{} \textit{X}_{1,2} &{} \ldots &{} \textit{X}_{1, d} \\ \textit{X}_{2,1} &{} \textit{X}_{2,2} &{} \ldots &{} \textit{X}_{2, d} \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ \textit{X}_{N, 1} &{} \textit{X}_{N, 2} &{} \ldots &{} \textit{X}_{N, d} \end{array}\right] \text {,} \end{aligned}$$
(12)

and

$$\begin{aligned} \varvec{Elite} =\left[ \begin{array}{cccc} \textit{X}_{1,1}^\textit{I} &{} \textit{X}_{1,2}^\textit{I} &{} \ldots &{} \textit{X}_{1, d}^\textit{I} \\ \textit{X}_{2,1}^\textit{I} &{} \textit{X}_{2,2}^\textit{I} &{} \ldots &{} \textit{X}_{2, d}^\textit{I} \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ \textit{X}_{N, 1}^\textit{I} &{} \textit{X}_{N, 2}^\textit{I} &{} \ldots &{} \textit{X}_{N, d}^\textit{I} \end{array}\right] \text {,} \end{aligned}$$
(13)

where \(\textit{N}\) represents the number of preys and \(\textit{d}\) denotes the number of dimensions. In MOMPA, \(\varvec{Elite}\) is randomly constructed from each generation of \(\varvec{Prey}\).

The strategies used in the high-velocity phase are as follows:

$$\begin{aligned} \varvec{{stepsize}}_i=\varvec{{R_B}} \otimes \left( \varvec{{Elite}}_i-\varvec{{R_B}} \otimes \varvec{{Prey}}_i\right) \quad i=1, \ldots , N, \end{aligned}$$
(14)

and

$$\begin{aligned} \varvec{{Prey}}_i=\varvec{{Prey}}_i+P \cdot \varvec{{R}} \otimes \varvec{{stepsize}}_i, \end{aligned}$$
(15)

where the vector \(\varvec{{R_B}}\) consists of random numbers generated from a normal distribution. The variable \(\textit{N}\) represents the number of search agents, whereas \(\varvec{{R}}\) is a vector comprising random numbers generated from a uniform distribution within the range of 0 to 1. Moreover, the symbol \(\otimes\) denotes element-wise multiplications. The value of P is set to 0.5.

The strategies used in the same velocity phase are as follows:

$$\begin{aligned} \varvec{{stepsize}}_i=\varvec{{R_L}} \otimes \left( \varvec{{Elite}}_i-\varvec{{R_L}} \otimes \varvec{{Prey}}_i\right) \quad i=1, \ldots ,\left\lfloor \frac{\textit{N}}{2}\right\rfloor , \end{aligned}$$
(16)

and

$$\begin{aligned} \varvec{{Prey}}_i=\varvec{{Prey}}_i+P \cdot \varvec{{R}} \otimes \varvec{{stepsize}}_i, \end{aligned}$$
(17)

where \(\varvec{{R_L}}\) is a vector of random numbers based on Lévy distribution. The remaining half of the prey is intended for exploitation, which is indicated by:

$$\begin{aligned} \varvec{{stepsize}}_i=\varvec{{R_B}} \otimes \left( \varvec{{R_B}} \otimes \varvec{{Prey}}_i-\varvec{{Elite}}_i\right) , \quad i=\left\lfloor \frac{\textit{N}}{2}\right\rfloor +1, \ldots , \textit{N}, \end{aligned}$$
(18)

and

$$\begin{aligned} \varvec{{Prey}}_i=\varvec{{Prey}}_i+P \cdot CF \cdot \varvec{{stepsize}}_i \text {,} \end{aligned}$$
(19)

where \(CF = \left( 1-\frac{\textit{Iter}}{\textit{Iter}_{max}}\right) ^{\frac{2\textit{Iter}}{\textit{Iter}_{max}}}\) is made to regulate the \(\varvec{{stepsize}}\).

The strategies used in the low-velocity phase are as follows:

$$\begin{aligned} \varvec{{stepsize}}_i=\varvec{{R_L}} \otimes \left( \varvec{{Elite}}_i-\varvec{{R_B}} \otimes \varvec{{Prey}}_i\right) \quad i=1, \ldots , \textit{N}, \end{aligned}$$
(20)

and

$$\begin{aligned} \varvec{{Prey}}_i=\varvec{{Prey}}_i+P \cdot CF \cdot \varvec{{stepsize}}_i \text {.} \end{aligned}$$
(21)

Another significant issue, such as the effects of fish aggregating devices (FADs), has the potential to alter the behavior of marine predators. The FADs are thought of as local optimums, and their results in the search space are the discovery of these spots.

When \(\textit{r} < FADs\), the strategy is as follows:

$$\begin{aligned} \varvec{{Prey}}_i = \varvec{{Prey}}_i+CF \cdot [\varvec{{lb}}+\varvec{{R}} \otimes (\varvec{{ub}}-\varvec{{lb}})] \otimes \varvec{U}, \quad i=1, \ldots , \textit{N}. \end{aligned}$$
(22)

When \(\textit{r} \ge FADs\),

$$\begin{aligned} \varvec{{Prey}}_i =\varvec{{Prey}}_i+[FADs \cdot (1-\textit{r})+\textit{r}] \cdot \left( \varvec{{Prey}}_{\textit{r}_1}-\varvec{{Prey}}_{\textit{r}_2}\right) , \quad i=1, \ldots , \textit{N}, \end{aligned}$$
(23)

where the probability of the FADs effect is 0.2. The lower and upper bounds of the predators’ positions are \(\varvec{{lb}}\) and \(\varvec{{ub}}\), and \(\textit{r}\) is a uniform random value in the range of [0, 1]. The binary vector \(\varvec{U}\) is created by initializing a random vector in the range [0, 1] and setting its arrays to 0 if the value is less than 0.2 and 1 otherwise. Integers \(\textit{r}_1\) and \(\textit{r}_2\) are chosen at random from 1 to \(\textit{N}\).

Moreover, the MOMPA employs a Gaussian perturbation technique to enhance the diversity of the population and enhance its ability to explore the global search space. The equations of the Gaussian perturbation technique are as follows:

$$\begin{aligned} \varvec{{Prey}}_i=\varvec{{Prey}}_i+G \cdot (\varvec{{ub}}-\varvec{{lb}}), \end{aligned}$$
(24)

where G follows a normal distribution and \(i=1, \ldots , \textit{N}\).

It is worth noting that MOMPA utilizes a hybrid approach that combines the non-dominated sorting technique [34] with reference point strategy [35] to accurately and efficiently find preys of superior quality. The aforementioned procedure not only serves to improve the identification of solutions of superior quality but also plays a pivotal role in preserving the diversity present within the sets of Pareto optimal solutions. Despite the MOMPA’s efficacy in a broad spectrum of optimization scenarios, it encounters inherent limitations regarding search space complexity and susceptibility to local optima entrapment. This observation necessitates an evolution towards a more sophisticated solution, hence the development of the QQSMOMPA technique, aimed at ameliorating these constraints and augmenting the algorithm’s overall optimization capability.

3.2 The First Improvement: SMOMPA

To balance exploration and exploitation strategies and diversify the solution set, this paper integrates the spiral model from the whale optimization algorithm (WOA) into the MOMPA, thus develo** SMOMPA. The incorporation of the spiral model, initially proposed by Chen et al. [36] and based on the behavior of whales creating air bubbles to herd prey as elucidated by Gharehchopogh and Gholizadeh [37], serves as a strategic improvement. The selection of the spiral model for enhancement is motivated by its proven effectiveness in achieving a balanced interplay between the exploration and exploitation phases throughout the optimization process. Notably, the spiral model replicates the spiral bubble-net feeding strategy, which achieves a harmonious balance between encircling the prey and initiating a spiraling approach [38, 39]. This approach is akin to efficiently contracting the search area in optimization challenges while ensuring exhaustive exploration, thereby offering an effective method to navigate the delicate equilibrium between extensive global search and focused exploitation [40].

The strategy for updating the solution via the spiral model in SMOMPA is as follows:

$$\begin{aligned} \varvec{{Prey}}_i = |\varvec{{Elite}}_i - \varvec{{Prey}}_i| \cdot e^{\textit{l}\alpha } \cdot \cos {(2 \pi \alpha )} + \varvec{{Elite}}_i \quad i=1, \ldots , \textit{N}, \end{aligned}$$
(25)

where \(\textit{l}\) is a constant parameter that modifies the form of the spiral. By default, its value is set to 1. On the other hand, \(\alpha\) is a numerical value selected randomly from the interval \([-1,1]\) in each iteration.

3.3 The Second Improvement: QQSMOMPA

3.3.1 The QOL

QOL is an innovative optimization technique that draws inspiration from opposition-based learning (OBL) [41]. QOL entails evaluating potential solutions in conjunction with their quasi-opposite counterparts, which are not precise opposites but are deliberately selected to be more closely aligned with the original answers. The objective of this strategy is to improve the search for the best possible solutions within given numerical ranges. This approach aims to broaden the search scope within the solution space and facilitate the evasion of local optima [42, 43].

The quasi-opposite solution can be defined in \(\textit{d}\)-dimension as follows:

$$\begin{aligned} \varvec{{Prey}_{i}}={\text {rand}}\left( \frac{\varvec{{ub}}+\varvec{{lb}}}{2}, \varvec{{ub}}+\varvec{{lb}}-\varvec{{Prey}_{i}}\right) \quad i=1, \ldots , \textit{N}. \end{aligned}$$
(26)
figure a

3.3.2 The Q-learning

To adaptively select among numerous strategies, this paper aims to utilize Q-learning for improvement. Q-learning is a renowned algorithm in the field of Reinforcement Learning (RL) and it plays a crucial part in the methodology suggested in this work. The Q-learning method employs a reward table to provide incentives and consequences to an agent based on its behavior in various states. The \(\varvec{Q-table}\) serves as an agent’s collection of experiences, as elucidated by Zamfirache et al. [44]. The primary objective of the agent is to make well-informed judgments by consistently updating its current state, taking into account the corresponding Q-value from the \(\varvec{Q-table}\), and evaluating all possible actions. The learning process occurs through a sequence of iterations, known as iterations (referred to as Iter), where agents gain knowledge by exploring their surroundings and updating their \(Q-table\) using the Bellman equation:

$$\begin{aligned} \begin{aligned} Q\left( s, a\right) \leftarrow Q\left( s, a\right) +\lambda \left[ r_{\textit{Iter}}+\gamma \max _a\left( Q\left( s^{\prime }, a\right) \right) -Q\left( s, a\right) \right] , \end{aligned} \end{aligned}$$
(27)

where \(\lambda\) is the learning rate value and \(\gamma\) is the discount factor between 0 and 1. \(r_{\text{ Iter } }\) is the immediate reward calculated by s and a. The Algorithm 1 demonstrates the sequential process of Q-learning.

3.3.3 The QQSMOMPA

Our enhancement strategy introduces the SMOMPA algorithm and its advanced iteration, QQSMOMPA, which integrates Q-learning to refine the exploration and exploitation phases of MOMPA. This combination enhances the algorithm’s ability to remember and utilize information about the search space across iterations, effectively hel** to escape local optima and improving search efficiency.

Q-learning is a crucial component in the process of making intelligent decisions. It dynamically chooses between the fish aggregating devices and the QOL strategy, depending on the rewards obtained. The incorporation of Q-learning, QOL, and FADs provides numerous benefits. It facilitates the dynamic selection of strategies, enabling the system to modify its approach flexibly based on the present condition and past knowledge. The overarching goal of Q-learning, which is to maximize long-term rewards, is applied to the choice of position update strategy, ultimately leading to the discovery of improved solutions [45, 46].

According to our proposed QQSMOMPA, the prey assumes the function of the agent. The states represent the continuous actions of each prey, whereas action indicates the movement of each agent from one state to another. The \(\varvec{Q-table}\) contains the historical performance of the Q-learning agent in previous episodes. This information is crucial for determining the most appropriate option during the three stages. QQSMOMPA regulates the determination of the suitable phases for each agent (\(i=1, \ldots , N\)) according to a particular criterion or parameter referred to as

$$\begin{aligned} \begin{aligned} \varvec{{Prey}}_i \\&=\left\{ \begin{array}{ll} \varvec{{Prey}}_i+CF \cdot [\varvec{{lb}}+\varvec{{R}} \otimes (\varvec{{ub}}-\varvec{{lb}})] \otimes \varvec{U}, &{} if Q\left( s, a_1\right) is \max , \\ \varvec{{Prey}}_i+[FADs \cdot (1-\textit{r})+\textit{r}] \cdot \left( \varvec{{Prey}}_{\textit{r}_1}-\varvec{{Prey}}_{\textit{r}_2}\right) , &{} if Q\left( s, a_2\right) is \max , \\ {\text {rand}}\left( \frac{\varvec{{ub}}+\varvec{{lb}}}{2}, \varvec{{ub}}+\varvec{{lb}}-\varvec{{Prey}_{i}}\right) &{} if Q\left( s, a_3\right) is \max , \\ \end{array} \right. \end{aligned} \end{aligned}$$
(28)

With Q-learning assistance, the selection of actions for each prey becomes adaptive. The primary interaction between Q-learning and the three potential operations can be condensed into four steps, as outlined below:

  1. 1.

    Initialize the \(\varvec{Q-table}\) as a \(3 \times 3\) zero matrix and \(\varvec{Reward}\) is given as: \(\left[ \begin{array}{ccc}-1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1\end{array}\right] .\)

  2. 2.

    Obtain the best strategy for the current iteration to be executed based on the values contained in the \(\varvec{Q-table}\) for the current state shown in Eq. (28).

  3. 3.

    Execute the selected action and calculate the number of selected preys in \(\varvec{Prey}\) by implementing non-dominant sorting and reference point. The immediate reward is updated as follows:

    $$\begin{aligned} \varvec{Reward_{m,n}} = number \end{aligned}$$
    (29)
  4. 4.

    Update the \(\varvec{Q-table}\) using Algorithm 1.

An outstanding characteristic of the suggested method QQSMOMPA is its capacity to transition between various phases as required. Due to this particular characteristic, it can efficiently investigate both global and local optimal solutions. The Algorithm 2 demonstrates the sequential process of the proposed QQSMOMPA. Additionally, the proposed QQSMOMPA’s effectiveness is verified through its application to benchmark functions, as detailed in Supplementary Materials.

3.4 The Fuzzy Decision

After obtaining the Pareto optimal set of PID controller parameters, selecting a compromise solution becomes essential. The paper employs fuzzy set theory for a final evaluation of solutions in the Pareto optimal set. The fuzzy utility value \(\mu _{i}\) for the ith solution is determined by:

$$\begin{aligned} \mu _{i}=\frac{\sum _{j=1}^{M} \mu _{i, j}}{\sum _{i=1}^{N} \sum _{j=1}^{M} \mu _{i, j}}, \end{aligned}$$
(30)

where the variable M denotes the quantity of goal functions, whereas the variable N denotes the quantity of solutions. The formula for \(\mu _{i, j}\) is as follows:

$$\begin{aligned} \mu _{i, j}=\left\{ \begin{array}{cc} 1 &{} f_{j}\left( X_{i}\right) \le f_{j}^{\min } \\ \frac{f_{j}^{\max }-f_{j}\left( X_{i}\right) }{f_{j}^{\max }-f_{j}^{\min }} &{} f_{j}^{\min } \le f_{j}\left( X_{i}\right) \le f_{j}^{\max } \\ 0 &{} f_{j}\left( X_{i}\right) \ge f_{j}^{\max } \end{array}\right. \end{aligned}$$
(31)

where \(f_{j}^{\max }\) represents the highest value of the jth goal function within the population, whereas \(f_{j}^{\min }\) represents the smallest value. It is noteworthy to mention that this research selects the option with the highest \(\mu\) value as the ideal compromise solution.

figure b

4 Practical AGC Problem

The proposed QQSMOMPA tuning PID controller’s gains to the AGC is shown in this section using three test systems. The obtained results are contrasted with the subsequent strategy: (1) BFOA: PI [21], (2) HBFOA:PI [47], (3) TLBO: PID [22], (4) ISFS: PID [3], (5) DE: PID [48]. The tests are conducted within the Matlab R2017a environment, utilizing a computing system equipped with an i7-8750 H CPU and 8 GB RAM.

Table 1 Controller gains, settling times, and peak value for system-1 test using different methods
Full size table

4.1 Test System-1

The design of test system-1 is depicted in Fig. 1, where Table 1 lists the ideal controller parameters, peak values (p), and settling times (\(T_{s}\)). Utilizing the QQSMOMPA-tuned PID controller when introducing a 0.1 Step Load Disturbance (SLD) into region-1 at \(t = 0\) s, the peak of \(\Delta f_1\) is recorded at \(p=0.0651\) Hz (see Table 1), which is lower than the peak achieved with the ISFS-tuned PID controller (\(p=0.1226\) Hz) but slightly higher than that of the TLBO-tuned PID controller (\(p=0.0587\) Hz). In contrast, the QQSMOMPA-tuned PID controller achieves the smallest peak for \(\Delta f_2\) at \(p=0.0321\) Hz, outperforming the TLBO-tuned PID controller (\(p=0.0355\) Hz) and significantly the ISFS-tuned PID controller (\(p=0.1746\) Hz). Regarding \(\Delta P_{tie}\)’s peak value, the QQSMOMPA-tuned PID controller records the lowest at \(p=0.0123\) p.u, surpassing both the TLBO-tuned PID controller (\(p=0.0143\) p.u) and the ISFS-tuned PID controller (\(p=0.0155\) p.u). These results underline the effectiveness of our proposed method in minimizing system overshoot. Table 3 demonstrates how the QQSMOMPA framework, through the incorporation of QOL and Q-learning, adeptly balances exploration and exploitation to optimize PID controllers within nonlinear oscillatory AGC systems, yielding a diverse set of superior Pareto-optimal solutions. This balance is manifested in a spectrum of optimized PID controller gains, as evidenced by the objective function metrics, which unequivocally indicate an enhancement in performance via a comprehensive array of superior Pareto-optimal solutions.

When introducing a 0.1 SLD into region-1 at \(t = 0\) s, the resulting time-domain responses are showcased in Fig. 4. The QQSMOMPA-tuned PID controller’s responses are notably smoother, attributed to the formulation of the goal function J. Moreover, this method exhibits quicker convergence to zero for frequency deviations and tie-line power, alongside diminished peak magnitudes.

The PID controller settings, as detailed in Table 1, are kept constant to assess the controller’s stability across different operational scenarios. Furthermore, an analysis involving a concurrent 0.1 SLD in region-1 and a 0.2 SLD in region-2 has been conducted. The results for each region are depicted in Fig. 5. All evaluated strategies display adaptability to changes in the location and magnitude of load disturbances, effectively minimizing their regional discrepancies to zero. Notably, in these tests, our methodology exhibits enhanced transient response characteristics.

Table 2 Controller gains, settling times, and peak value for system-2 test using different methods
Full size table
Fig. 2
figure 2

Transfer function model of test system-2

Full size image
Table 3 Obtained controller gains and objective function values of QQSMOMPA:PID for test system-1
Full size table

4.2 Test System-2

To better align AGC with real-world conditions, we incorporate governor dead band (GDB) into a two-area no-reheat thermal power generation system, as illustrated in Fig. 2. The presence of GDB introduces system oscillations at a natural frequency of approximately 0.5 Hz. The revised governor transfer function model is presented as follows:

$$\begin{aligned} G_g(s)=\frac{0.8-s(0.2 / \pi )}{s T_{\textrm{g}}+1}. \end{aligned}$$
(32)

The per-unit values are defined as \(f=60 {\rm Hz}, B=0.425 {\rm p.u MW/Hz}, R=2.4 {\rm Hz/p.u}, T_{{\rm g}}=0.2 {\rm s}, T_{t}=0.3 {\rm s}, K_{p s}=120 {\rm Hz/p.u}, T_{p s}=20 {\rm s}, T_{12}=0.444 {\rm p.u MW/rad}\). A 0.01 SLD is introduced to region-1 at \(t = 0\) s. According to Table 2, the \(T_s\) for \(\Delta f_2\) achieved by the QQSMOMPA-tuned PID controller is \(T_s=5.56 \text { s}\), demonstrating efficiency over the DE-tuned PID controller (\(T_s=6.89 \text { s}\)) and the ISFS-tuned PID controller (\(T_s=6.48 \text { s}\)). Likewise, the peak value of \(\Delta f_1\) is lowest when using the QQSMOMPA-tuned PID controller (\(p=0.0172 \text { Hz}\)) compared to the DE-tuned PID controller (\(p=0.0196 \text { Hz}\)) and the ISFS-tuned PID controller (\(p=0.0173 \text { Hz}\)).

Fig. 3
figure 3

Random load

Full size image

The time-domain responses, derived from the gains listed in Table 2, are illustrated in Fig. 6. Characteristics such as improved responsiveness, reduced dam** oscillations, faster settling times, and decreased peak values distinguish the performance of QQSMOMPA-tuned PID controllers, enabling a swift return to equilibrium. Notably, while the ISFS-tuned PID controller emerges as a primary contender, it overlooks certain objective functions, limiting its ability to provide more feasible solutions.

Additionally, a simultaneous consideration of a 0.01 SLD in region-1 and a 0.03 SLD in region-2 is examined, to assess the resilience of each method in complex instances. The controller’s settings match those in Table 2. Figure 7 displays the matching system response. Each control scheme’s system frequency change is stable, showing the robustness of the system. In contrast, the present investigation demonstrates that the QQSMOMPA tuning PID controller exhibits enhanced anti-interference capabilities, as seen by the faster load interference suppression observed in the red track compared to previous experiments.

To verify the robustness of our proposed strategy against random disturbances under more complex conditions, a loading scenario is implemented on region-1 as depicted in Fig. 2. The loading scenario is random in duration and amplitude, and its amplitude range is \([-\,0.005,0.01]\) shown in Fig. 3.

Remaining the controller parameters unchanged, the same as Table 2, Fig. 8 shows the dynamic response of test system-2 when such a load disturbance occurs. Compared with DE: PID, QQSMOMPA has an excellent performance in optimizing PID controller parameters. From the superposition response, our scheme has better system robustness than other controllers in terms of the uncertainty of load disturbance input.

Fig. 4
figure 4

Test system-1’s time-domain responses to a 0.1 SLD in region-1

Full size image
Fig. 5
figure 5

Test system-1’s time-domain responses to a 0.1 SLD in region-1 and 0.2 SLD in region-2

Full size image
Fig. 6
figure 6

Test system-2’s time-domain responses to a 0.01 SLD in region-1

Full size image
Fig. 7
figure 7

Test system-2’s time-domain responses to a 0.01 SLD in region-1 and a 0.03 SLD in region-2

Full size image
Fig. 8
figure 8

Test system-2’s comparative time-domain responses to random load disturbance

Full size image
Fig. 9
figure 9

Transfer function model of test system-3

Full size image

4.3 Test System-3

We employ a three-region hydroelectric power system (test system-3) to evaluate the applicability of the QQSMOMPA-tuned PID controller for managing multiple generating units. The terminology used to describe this system is consistent with that of the previously mentioned test system-1 and test system-2. In test system-3, the scheduled tie-line power transmission between two adjacent regions may have indirect connections to tie lines in regions beyond the two adjacent regions it is originally scheduled to connect. The transfer function model of test system-3 is depicted in Fig. 9, and the relevant parameters are \(f=60 \mathrm {~Hz}, B=0.425\, \mathrm {p.u} \textrm{MW} / \textrm{Hz}, R=2.4 \mathrm {~Hz} / \textrm{p}. \textrm{u}, T_{\textrm{g}}=0.08 \mathrm {~s}, K_{r}=0.5 \mathrm {~s}, T_{r}=10 \mathrm {~s}\) \(T_{t}=0.3 \mathrm {~s}, K_{ep}=1.0, K_{ed}=4.0, K_{ei}=5.0, T_{w}=1 \mathrm {~s}, K_{p s}=120 \mathrm {~Hz} / \mathrm {p.u}, T_{p s}=20 \mathrm {~s}\) \(T_{12}=T_{23}=T_{13}=0.086 \, \mathrm {p.u} \textrm{MW} / \textrm{Hz}.\) The thermal systems in region-1 and region-2 make use of single-stage reheat turbines, whereas region-3 utilizes a contemporary hydraulic system that incorporates an electronic governor in place of a traditional mechanical governor.

The same optimization procedure employed in the previous test system is used to determine the optimal controller parameters for the test system-3 with Generation Rate Constraints (GRC).

The PID controller refined through the QQSMOMPA process demonstrates improved step responses in each region. It rapidly enters the specified frequency range, reducing overshoot caused by this adjustment compared to ISFS: PID, and efficiently dampens oscillations, resulting in a smoother convergence curve. Nevertheless, our algorithm is not flawless either. When comparing stability time, QQSMOMPA:PID is slightly longer than ISFS:PID, but still falls within an acceptable range. These enhancements are depicted in Figs. 10 and 11.

Table 4 Controller gains for system-3 test using different methods
Full size table
Fig. 10
figure 10

Test system-3’s time-domain responses to a 0.01 SLD in all regions

Full size image
Fig. 11
figure 11

Test system-3’s time-domain responses to a 0.01 SLD in all regions

Full size image

5 Conclusions

This paper delineates a novel framework for the optimization of PID controller gains within AGC systems for interconnected power grids, employing the QQSMOMPA algorithm. This methodology, grounded in the integration of ITAE, ITSE, and the deviation rate of change as optimization objectives, advances the state of controller tuning in AGC systems. The efficacy of this approach is substantiated through simulation analyses, evidencing the potential for improved robustness and control in AGC (Table 4).

Crucially, the auxiliary controller’s significant impact on enhancing control effectiveness highlights the imperative for continued refinement of controller structures. This underscores an emergent research trajectory that necessitates the exploration of advanced control strategies. Among these, reinforcement learning (RL) and model predictive control (MPC) stand out as pivotal areas for future investigation. RL’s adaptability and ability to optimize decision-making processes in real-time environments suggest a promising avenue for develo** dynamic control strategies that can autonomously adjust to fluctuating system dynamics. Concurrently, MPC’s foresight in anticipating system disturbances provides a compelling case for its application in preempting and mitigating control challenges. Additionally, we also notice the promising prospects of utilizing dendritic neuron models as controllers, offering another broad avenue for innovative control.