Introduction

A contagion, in a general sense, refers to the spread or transmission of diseases, behaviors, beliefs, or emotions within a population or community. Depending on the type of contagion, the observed dynamics can differ greatly. Some contagions, such as highly infectious diseases, spread throughout entire populations resulting in global pandemics, while other contagions, such as social behaviors, seem to be more constrained and spread only within certain communities [1,2,3]. To explain the difference between the contagion dynamics of a disease and the contagion dynamics of social behavior, it is usually not sufficient to look at the differences in transmission rates. Evidence from social science suggests that many contagions exhibit qualitatively different mechanisms through which they propagate throughout a population [4,5,6,7,8,9]. For example, diseases are usually spread through single connections, meaning that a susceptible individual is at risk of infection if it is in contact with a single infectious individual [4, 10,11,12]. Social behaviors, on the other hand, often spread through multiple connections, meaning that a susceptible individual is only at risk of adopting the social behavior if it is in contact with more than one infectious individual [1,2,3, 13]. This qualitative distinction has been characterized by the terms “simple” and “complex” contagion, which will be used as such throughout the remainder of this paper [4]. Note that the term ’simple’ does not in any way suggest that this type of contagion is less intricate in its dynamics. In this context it is solely used to differentiate between contagion processes that propagate through single connections and contagion processes that require multiple connections to adopting neighbors for further propagation.

Fig. 1
figure 1

Complex contagions and wide bridges. Black nodes indicate infected nodes and white nodes indicate uninfected nodes. a Shows the concept of contagion thresholds as a way to differentiate between simple and complex contagion. A node j is susceptible to simple contagion if it has a contagion threshold of \(t_j = 1\), indicating that a single connection to an infectious individual is sufficient for infection. A node j is susceptible to complex contagion if it has a contagion threshold of \(t_j > 1\), indicating that multiple connections to infectious individuals are required for infection. b Shows the concept of wide bridges as essential for the propagation of complex contagions. There exists a sufficiently wide bridge from node i to node j if there is a direct connection from node i to node j and a sufficient number of common neighbors to satisfy the common neighbor threshold \(c_j\), where \(c_j = t_j - 1\). c Shows a simple contagion path from node i to node j where every node in the network has a contagion threshold \(t = 1\). d Shows a complex contagion path from node i to node j where every node in the network has a contagion threshold of \(t = 2\)

Full size image

Simple contagions follow a threshold model where an individual is susceptible to infection if it is connected to at least a single source, and once that threshold is reached, the individual can become infected with a certain infection probability (see Fig. 1a). On the contrary, complex contagions are characterized by higher thresholds, which means that an individual is susceptible to infection only when surrounded by a certain number or proportion of others who are already infected (see Fig. 1a). Complex contagions are, thus, often associated with propagation dynamics that involve social reinforcement, such as social behaviors, beliefs, or emotions, and with the characterization of superinfections, where a second infection superimposes an earlier one [14, 15].

From a sociological perspective, the idea of a complex contagion helps us understand why it is challenging for new social behaviors or beliefs to spread widely throughout large populations and why they are more likely to catch on in smaller, clustered communities. Here, the concept of wide bridges becomes crucial, which essentially represent shared connections or common neighborhoods, that can reinforce the propagation of a complex contagion [16]. Clustered communities tend to have many of these wide bridges between their members, which then serve as the fundamental building blocks for the propagation of complex contagions [4, 16, 17] (see Fig. 1b). This is particularly relevant when considering social behaviors or beliefs for which individuals may not inherently find personal incentive or motivation to support them. However, through the reinforcement of wide bridges, or peer pressure, social behaviors and beliefs can endure and persist over time, even if individuals had not maintained them independently.

From a network perspective, the requirement of social reinforcement makes it difficult to assess and predict the spreading potential of complex contagions [16]. This is amplified by the fact that many classical network metrics, aiming to identify central nodes and important bridges, build on the notion of simple paths. Complex contagions, however, do not propagate through simple paths (see Fig. 1c). Instead, they propagate through complex paths [16], which require a certain extent of redundancy in the connections between nodes in a network (see Fig. 1d). Consequently, in the analysis of complex contagions, conventional techniques used for estimating spreading dynamics, such as the giant component, average shortest path length, or centrality measures, become uninformative and do not produce meaningful results. This underscores a considerable research gap in methods to inform about the spreading potential of complex contagions. The objective is to simplify a complex contagion system to a network that can be understood using the rules of simple paths.

In this paper, we propose a graph reduction method that reduces a given network to include only connections that are immediately relevant for a specific complex contagion process. Through repeated application, we can obtain structures that remain stable under the reduction, allowing us to define and measure for any given network and contagion, (i) strongly contagious components, (ii) weakly contagious components, and (iii) bridge components. Information about the size and location of these components can be used as a meaningful basis for assessing and preventing the potential spread of harmful contagions as well as driving the spread of beneficial contagions. The overall goal is to provide practical and computationally feasible metrics that aid in the analysis of complex contagions.

Methodology

We assume that any given contagion propagates through a network. The network represents some form of a contact network, where each node signifies an individual and each edge a contact between two individuals. The connectivity pattern is captured by the adjacency matrix of the network, denoted as \(\textbf{A}\). In this matrix, an entry \(A_{ij}\) signifies whether there is a connection from node i to node j. We specifically examine networks without multi-edges, i.e. \(A_{ij} \in [0, 1]\), and without self-loops, i.e. \(A_{ii} = 0\). Additionally, the initial contact network must be undirected, implying that connections between nodes are two-way, resulting in a symmetric adjacency matrix, i.e. \(A_{ij} = A_{ji}\). The specifics of the contagion process, that is, whether we are dealing with a simple or a complex contagion, is defined for every node, where each node i in the network is assigned its own contagion threshold \(t_i\). A threshold \(t_i = 1\) indicates that node i can be infected with simple contagion, that is, by a single infectious connection. A threshold \(t_i > 1\) indicates that to infect node i, more than one infectious connection is required. With this setup, it is possible to study contagions in which nodes have homogeneous threshold distributions, and contagions in which nodes have heterogeneous threshold distributions. In this context, “homogeneous” indicates that individuals exhibit identical thresholds and, thus, require equal social reinforcement. Conversely, “heterogeneous” indicates that individuals exhibit varying thresholds and require different strengths of social reinforcement. For example, one might consider adjusting the contagion thresholds of nodes based on their degrees, where a node with lots of contacts or friends requires more social reinforcement than a node with few contacts, to adopt a belief or social behavior. To utilize the concept of wide bridges, which is required to simplify a contact network for a given complex contagion process, we define a common neighbor threshold vector c with entries \(c_j\) for every node j in the network, where \(c_j = t_j - 1\). The common neighbor threshold \(c_j\) signifies that for a sufficient wide bridge from any node i to node j, we require \(c_j\) common neighbors between node i and node j, in addition to a direct connection between node i and node j.

Graph reduction and bride components

Given a network representation in the form of an adjacency matrix \(\textbf{A}\), and common neighbor thresholds in the form of \(c_i = t_i - 1\), we can simplify the contact network and highlight important components for the contagion. Specifically, we can obtain bridge components, using a graph reduction method, denoted as \(T_{ij}(\textbf{A}, c)\), as shown in Eq. 2, as well as strongly contagious and weakly contagious components by enforcing further stability conditions, which is shown in the following sections.

$$\begin{aligned}{} & {} \mathcal {H}(x) = {\left\{ \begin{array}{ll} 1, &{} \text {if } x\ge 0,\\ 0, &{} \text {if } x<0. \end{array}\right. }, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} T_{ij}(\textbf{A}, c) = A_{ij} \cdot \mathcal {H}\Big (-c_j + \sum _{k=1}^{N} A_{ki} A_{kj}\Big ). \end{aligned}$$
(2)

The graph reduction simplifies a network by retaining only those connections that facilitate the spread of contagion through sufficiently wide bridges [18]. The assumption being that complex contagions propagate through the assistance of social reinforcement in the form of common neighborhoods, or 2-cliques. Note that the graph reduction method does not reduce the dimension of the network N. Instead, it reduces the connections in the network by removing and altering them.

In the above equation, the term \(\sum _{k=1}^{N}A_{ki} A_{kj}\) corresponds to the number of common neighbors between nodes i and node j, where N is the number of nodes in the network. From the number of common neighbors, we subtract the common neighbor threshold \(c_j\) of node j to obtain the surplus of common neighbors over the threshold requirement. The surplus is put into the heavyside step function \(\mathcal {H}(x)\) where it is mapped to 1 if it is greater or equal to 0, or mapped to 0 if it is less than 0. Finally, the mapped surplus is multiplied with the adjacency matrix entry \(A_{ij}\). This ensures that, in addition to a sufficient surplus of common neighbors, there exists a direct connection between the nodes i and j. Thus, the simplification \(T_{ij}(\textbf{A}, c)\) yields a directed connection that signifies whether there exists a sufficient wide bridge from node i to node j. Applied to all entries i, j of the adjacency matrix \(\textbf{A}\), we obtain a directed network that holds all possible wide bridges, i.e. \(\textbf{T}(\textbf{A}, c)\). This simplification can be used as part of a process to identify additional important components, namely strongly contagious and weakly contagious components.

Strongly contagious components

Strongly contagious components are defined as groups of nodes where each node in that group can actively participate in infecting every other node in that group, and is susceptible to active infection by all other nodes in that group. Strongly contagious components, thus, follow the pattern of k-cliques where the contagion threshold t determines the configuration of the clique (see Fig. 2). Note that when working with heterogeneous contagion thresholds, the highest contagion threshold within a clique defines its dimension. To obtain strongly contagious components, we follow an iterative three-step process:

$$\begin{aligned}{} & {} U_{ij}(\textbf{A}) = \max (A_{ij}, A_{ji}), \end{aligned}$$
(3)
$$\begin{aligned}{} & {} S_{ij}(\textbf{A}) = \min (A_{ij}, A_{ji}), \end{aligned}$$
(4)
$$\begin{aligned}{} & {} \textbf{A}' = \textbf{S}(\textbf{T}(\textbf{U}(\textbf{A}), c)). \end{aligned}$$
(5)
Fig. 2
figure 2

Stable cliques. Shows strongly contagious components in the form of k-cliques. Strongly contagious components given nodes with contagion thresholds \(t_i = 1\) are made up of 1-cliques. Strongly contagious components given nodes with contagion thresholds \(t_i = 2\) are made up of 2-cliques, and strongly contagious components given nodes with contagious thresholds \(t_i = 3\) are made up of 3-cliques. The pattern continues for higher contagion thresholds. It should be noted that there exists a similar conceptual framework involving contagions through k-simplices, which utilizes hypergraphs for the representation of many-body interactions [19,20,21,22,23], as opposed to the pairwise interactions that are the focus of this study

Full size image

Initially, the network undergoes a transformation into an undirected network through the application of \(U_{ij}(\textbf{A})\) for every entry i, j. Note that in the initial application of the three-step process, converting the network to an undirected form is not necessary, but will become relevant when repeatedly applying the three-step process. Subsequently, the undirected network undergoes a simplification using the graph reduction method \(T_{ij}(\textbf{U}(\textbf{A}), c)\) for every entry i, j. Finally, the condition for a strongly contagious component is enforced using \(S_{ij}(\textbf{T}(\textbf{U}(\textbf{A}), c)))\) which keeps bridge-connections if they are two-way. Equation 5 is iteratively applied until the output remains unchanged from one iteration to the next, signifying that the process has reached equilibrium, i.e. \(\textbf{A}' = \textbf{A}\).

Weakly contagious components

Weakly contagious components are characterized as groups of nodes where each node in the group is infected by at least one other node in that group, thus, creating a weaker form of potential cyclic re-infection with other nodes in that group. To obtain weakly contagious components, we follow a similar iterative three-step process:

$$\begin{aligned}{} & {} W_{ij}(\textbf{A}) = A_{ij} \cdot \min \Big (\sum _{k=1}^{N}A_{ki}, 1\Big ), \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \textbf{A}' = \textbf{W}(\textbf{T}(\textbf{U}(\textbf{A}), c)). \end{aligned}$$
(7)

Initially, the network undergoes a transformation into an undirected form through the application of \(U_{ij}(\textbf{A})\) for every entry i, j. Subsequently, the undirected network undergoes a simplification using the graph reduction method \(T_{ij}(\textbf{U}(\textbf{A}), c)\) for every entry i, j. Finally, the condition for weak stability is enforced using \(W_{ij}(\textbf{T}(\textbf{U}(\textbf{A}), c))\) where all outward connections of a node are retained if that node has at least one inward connection. The term \(\sum _{k=1}^{N}A_{ki}\) represents the in-degree of node i which yields the number of incoming connections. We take the minimum between this number and 1, which is then multiplied with \(A_{ij}\) to keep only outgoing connections of nodes that have at least one incoming connection. The assumption behind this is that only nodes susceptible to active infection possess the potential to actively transmit infections to others in the future. Equation 7 is iteratively applied until the output remains unchanged from one iteration to the next, signifying that the process has reached equilibrium, i.e. \(\textbf{A}' = \textbf{A}\) for all entries \(A_{ij}\).

Results

In this section, we present the results of the methods discussed above applied to a sample network. Visual representations of the components obtained through these methods are provided for clarity. The identified components are evaluated through correlation against data obtained from a complex contagion SIS (susceptible, infected, susceptible) model, which simulates the propagation of a complex contagion for different seeding, infection, and recovery probabilities. Subsequently, we showcase our approach across diverse networks to illustrate its practical relevance.

Grid network analysis

We choose a representative sample network consisting of 100 nodes arranged in a grid-like structure, as shown in Fig. 3.

Fig. 3
figure 3

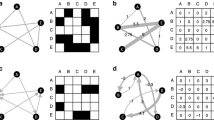
Graph reduction example for heterogeneous contagion thresholds. a Shows a grid-like example network, where the number within a node i is the contagion threshold \(t_i\) of that node. The common neighbor requirements \(c_i = t_i - 1\) are not shown. b Shows the graph reduction methods applied to the example network. Strongly contagious connections and nodes part of strongly contagious components are colored green. Weakly contagious connections and nodes part of weakly contagious components encompass all nodes and edges with colors green and yellow. Bridge connections and nodes part of bridge components encompass all nodes and edges with colors green, yellow, and white. Opaque nodes and edges show the part of the initial contact network that does not allow any sufficient wide bridges for the given complex contagion. An arrow from node i to node j indicates that there exists a sufficiently wide bridge from node i to node j given the common neighbor threshold \(c_j\) of node j

Full size image

The network’s connectivity pattern is defined by its adjacency matrix \(\textbf{A}\). For the analysis, the contagion threshold \(t_i\) of every node i is randomly assigned as either 2 or 3, i.e. \(t_i \in [2, 3]\), defining the overall contagion as a complex contagion wherein nodes require a minimum of 2 or 3 infected neighbors for infection. Note that due to the random assignment of contagion thresholds, it is possible that the threshold \(t_i\) of node i is larger than its degree \(k_i\), in which case it is not possible to spread the contagion to that node.

Bridge connections of the above network are determined by performing the initial graph reduction \(\textbf{T}(\textbf{A}, c)\). The network’s strongly contagious connections are obtained by iteratively applying \(\textbf{S}(\textbf{T}(\textbf{U}(\textbf{A}), c))\) until the result remains unchanged between successive iterations. Similarly, the network’s weakly contagious connections are obtained by iteratively applying \(\textbf{W}(\textbf{T}(\textbf{U}(\textbf{A}), c))\) until the result remains unchanged between successive iterations. Visual representations are shown in Figs. 4 and 5.

Fig. 4
figure 4

Equilibration of strongly contagious components. Starting with the example network shown in Fig. 3, we apply Eq. 5 iteratively until the output remains unchanged from one iteration to the next. For the above example network, this process takes a total of four iterations

Full size image
Fig. 5
figure 5

Equilibration of weakly contagious components. Starting with the example network shown in Fig. 3, we apply Eq. 7 iteratively until the output remains unchanged from one iteration to the next. For the above example network, this process takes a total of four iterations

Full size image
Fig. 6
figure 6

Simulation data obtained by the complex contagion SIS model. Shows the number of time-steps a node was infected in simulations of 100 time-steps, averaged over 1000 runs. The underlying network is the network shown in Fig. 3. The seeding probability \(p_{seed}\) determines the number of initially infected nodes randomly sampled from the network. The infection probability \(p_{infect}\) determines the probability with which a node becomes infected given a sufficient number of infected neighbors to satisfy its contagion threshold. The recovery probability \(p_{recovery}\) determines the probability with which a nodes recovers, where recovered nodes are again open to infection. The Pearson correlation coefficient \(r_{pearson}\) signifies the correlation among categorical values of nodes in the identified strongly contagious, weakly contagious, and bridge components, in relation to simulation data reflecting the average number of time-steps infected by the nodes. Note that we have performed the above analysis for an ensemble of 100 different grid-like networks, i.e. Moore neighborhood networks where half of the edges were randomly removed, and calculated the median Pearson correlation coefficient, the average Pearson correlation coefficient, as well as the standard deviation for the whole parameter space as depicted above. We report a median Pearson correlation coefficient of 0.58, an average Pearson correlation coefficient of 0.53, and a standard deviation of 0.18

Full size image

Strongly contagious components are indicated by nodes with the color green. They are made up of k-cliques where the highest contagion threshold t in the clique determines its dimension. Strongly contagious components mark especially strong contagion clusters, since nodes in k-cliques can all actively infect and be infected by all others. Weakly contagious components encompass nodes with the colors green and yellow. They are interesting in the sense, that if every node in the component is currently infected, the component can reinfect every part of it through at least one connection. Consequently, halting the reinfection of a weakly contagious component proves to be considerably more manageable than halting the reinfection of a strongly contagious component. The entirety of bridge components encompasses nodes with the colors white, yellow, and green, revealing the number of sufficient wide bridges in the network. Note that weakly contagious components inherently encompass strongly contagious components due to the imposition of a weaker condition. Similarly, bridge components inherently encompass weakly contagious components and strongly contagious components due to the imposition of a weaker condition. Finally, we can calculate the proportion of nodes in these components relative to the total nodes in the network. The proportion of nodes part of strongly contagious components is \(p_s = 0.15\), the proportion of nodes part of weakly contagious components is \(p_w = 0.28\), and the proportion of nodes part of bridge components is \(p_b = 0.57\).

The above results are compared with data obtained by simulations of a complex contagion SIS model. The model has three parameters, a seeding probability which determines the number of nodes that are initially infected, an infection probability which indicates the probability with which a node can be infected at each time-step if it is connected to a sufficient number of infected nodes given its contagion threshold, and a recovery probability which indicates the probability with which a node can recovery from an infection at each time-step. Note that recovered nodes can be reinfected. During simulations of 100 time-steps, we track the amount of time-step a node is infected. The simulation data is shown in Fig. 6.

The visual analysis reveals compelling alignment between our proposed components and the obtained simulation data. Specifically, we observe that the average number of time-steps a node is infected during simulation, correlates well with the three classes of components, i.e. strongly contagious, weakly contagious, and bridge components. In particular, the average number of time-steps a node is infected is in general highest in the network areas we identified as strongly contagious components, followed by weakly contagious components, and bridge components. This observation is substantiated by Pearson correlation coefficients between a nominal ranking of these components and the average number of time-steps a node is infected during simulation. Specifically, if a node is part of a strongly contagions component it is assigned a ranking of 3, if it is part of a weakly contagious component, it is assigned a ranking of 2, if it is part of bridge component it is assigned a ranking of 1, and if it is not part of any component it is assigned a ranking of 0. This is done for all nodes in the network to obtain an array of nominal component rankings. We also obtain for every node the average number of timesteps that node has been infected during simulation of the complex contagion SIS model. We standard scale both arrays and then calculate the Pearson correlation coefficient between those arrays. The correlation coefficients remain high for variations in all complex contagion SIS model parameters, that is, seeding probability, infection probability, and recovery probability. This underscores the reliability of our methods for informing about the dynamics of complex contagions propagation on networks.

Practical implementation across different networks

Our proposed methods can be applied to diverse network topologies, providing understandable and meaningful information about the contagion dynamics of a complex contagion prior to any outbreak in the form of relative component sizes. The proportion of nodes in bridge components \(p_b\), weakly contagious components \(p_w\), and strongly contagious components \(p_s\) for diverse network topologies are shown in Table 1 and Fig. 7. In addition to the relative component sizes, we also list the number of nodes in the network denoted as N, the number of edges denoted as E, the average degree of nodes in the network denoted as \(\langle k \rangle\), the average shortest path length between nodes in the network denoted as \(L_{avg}\), and the average clustering coefficient denoted as \(C_{avg}\). For the random, the small-world, the scale-free and the clustered power-law network, we assume contagion thresholds \(t_i\) randomly chosen from a uniform distribution over the interval [1, 5], corresponding to an overall contagion that has both simple and complex characteristics. For the empirical Facebook politicians network, which describe a mutual like networks among verified politician pages [24, 25] and the empirical Facebook governments network, which describes a mutual like network among verified government pages [24, 25], we assume relative contagion thresholds based on a node’s degree, i.e. \(t_i = int(round(k_i \times 0.2)) + 1\). Note that depending on the specific contagion that is subject to analysis, we can choose any distribution of contagion thresholds suitable to the contagion at hand, including any mix of thresholds corresponding to simple and thresholds corresponding to complex contagions.

Table 1 Contagious and bridge components across different networks
Full size table
Fig. 7
figure 7

Equilibration. Overview of the equilibration process for the networks of Table 1. The Figure on the left shows the equilibration for the weakly contagious graph reduction, and the Figure on the right shows the equilibration for the strongly contagious graph reduction

Full size image

The random network is generated using the Erdős-Rényi model with \(N = 1000,~p_{ER} = 0.006\), where \(p_{ER}\) is the probability for random edge creation from the set of all possible edges [26,27,28]. The small-world network is generated using the Watts-Strogatz model with \(N = 1000,~p_{WS} = 0.1,~u = 4\), where \(p_{WS}\) is the probability of rewiring each edge and u indicates that each node is joined with its u nearest neighbors in a ring topology [26, 27, 29]. The scale-free network is generated using the Barabasi-Albert model with \(N = 1000,~m = 2\), where m is the number of edges to attach from a new node to existing nodes [26, 27, 30]. The clustered power-law network is generated using the Holme-Kim model with \(N = 1000,~m = 2,~p_{HK} = 0.9\), where m is the number of edges to attach from a new node to existing nodes and \(p_{HK}\) is the probability of adding a triangle after adding a random edge [26, 31]. The large Facebook politicians network with \(N = 5908\) nodes and \(E = 41729\) edges, and the large Facebook governments network with \(N = 7057\) and \(E = 89455\) edges are obtained from a network repository [24, 25]. As depicted in Table 1, short average path lengths, which build on the notion of simple paths, cannot be utilized by complex contagions. Instead, complex contagions leverage high average clustering in the network, as indicated by higher relative bridge component sizes, as well as weakly contagious and strongly contagious component sizes, which provides further support for the validity of our proposed methodology to identify important parts of a network for a given complex contagion, as it is in good alignment with the current theory about complex contagions [4, 15,16,17, 32].

Discussion

In this paper, we propose a graph reduction method to obtain important components for the analysis and risk assessment regarding the spread of complex contagions in networks. In particular, we show how to obtain (i) strongly contagious components, which can actively infect and be actively infected by all others within the component, (ii) weakly contagious components, which are comprised of nodes which can be infected by at least one other node in that component, and (iii) bridge components, which are comprised of nodes that have sufficient wide brides between them to facilitate the spread of a complex contagion.

Analyzing the dimension of the components (i)–(iii) enables to determine their relative size in relation to the overall network size. This yields valuable metrics regarding the proportion of infectious regions within the network, allowing for comparisons with other networks and alternative contagion entities characterized by different complex contagion thresholds.

Analyzing the location of the components (i)–(iii) allows for interventions to contain the spread of an already progressing complex contagion, as well as preemptive measures to target problematic communities prior to an outbreak of a complex contagion. For example, if a specific network community exhibits patterns composed of many sufficient wide bridges with regards to a complex contagion such as adoption of a social behavior, preemptive interventions like community outreach programs or educational initiatives can be implemented to mitigate the potential impact. Additionally, since complex contagions can be both disadvantageous and advantageous, the same insights can be leveraged to identify pivotal communities for targeted promotion. For example, if a community strongly embraces a positive social behavior, such as environmental sustainable practices, leveraging that community as an example can encourage similar behaviors in neighboring areas. By incentivizing strongly contagious components, or even weakly contagious components, to adopt specific behaviors, these components can function as resilient sources for further propagation. For example, encouraging a community known for its commitment to public health practices to adopt a new health-related behavior can serve as a model for neighboring communities, fostering a broader and more stable adoption of the desired behavior.

It is worth mentioning that our findings can be integrated with other concepts, such as a complex centrality score [16]. Identifying both weakly and strongly contagious components gives us clear insights into where a contagion might persist for a longer time. However, these components can vary in how well they are connected to the rest of the network, that is, they might be isolated, poorly connected, or well-connected. Thus, identifying the components with the highest average complex centrality could provide another dimension of useful information for the assessment of the spread of a complex contagions.

Our proposed approach offers distinct advantages by being insensitive to initial seeding conditions, a critical factor in understanding the course of contagion before an outbreak occurs. Traditional methods often involve numerous simulation runs with diverse starting conditions to discern the areas susceptible to easy spread or containment of a complex contagion. In contrast, our approach effectively provides a comprehensive picture of a complex contagion dynamic by leveraging the concept of sufficient wide bridges, the fundamental building blocks for propagation. This unique feature makes our approach an invaluable tool for preemptive risk analysis and provides insightful markers for potential danger zones during an ongoing contagion.

Another notable benefit of our approach lies in its implicit insights into the effects of contagion recovery or infection stability. For instance, social beliefs and behaviors regarding community vaccination can be challenging to sustain through individual incentives alone, requiring constant social reinforcement for long-term adherence. The identification of strongly (and weakly) contagious components signifies parts in a network where such beliefs and behaviors can persist for an extended period, underscoring its resilience against the effects of recovery.

However, the method’s limitations are intricately connected to its benefits. While our approach excels in providing a holistic view of a contagion dynamic, it does not offer insights into specific outcomes or the expected variance of outcomes. Initial conditions can heavily influence whether a contagion spreads extensively or remains confined to certain network segments. Consequently, our method does not provide information on the expected propagation of a single specific spread, nor the expected variance for a given complex contagion process. To comprehensively address such aspects, additional analyses, such as multiple simulation runs, have to be included.

In summary, our method’s ability to obtain meaningful metrics regarding strongly contagious, weakly contagious, and bridge components contributes to a nuanced understanding of complex contagions. Despite limitations related to outcome variance, our approach’s insensitivity to initial conditions and implicit insights into recovery effects enhance its applicability in preemptive risk analysis and strategic interventions. This research marks a significant step toward a more comprehensive and targeted approach to managing complex contagions in networked environments.