Solution of a Two Dimensional Thermoelastic Problem Due to an Exponentially Distributed Temperature at the Boundary in Presence of a Moving Heat Source

Abstract

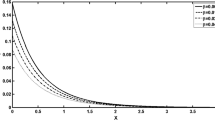
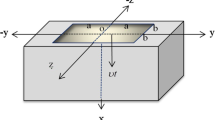
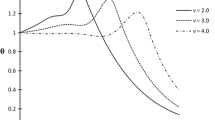
This paper presents a study on a two dimensional thermoelastic problem involving isotropic, homogeneous half-space media with a moving heat source. The problem has been constructed subject to exponentially varying temperature at the boundary. Laplace transformation and Fourier transformation are used to the governing equations and solutions are made for thermal stress distribution and temperature distribution in the Laplace–Fourier transformed domain. The inverse Laplace–Fourier transformation is obtained numerically and the results are presented graphically with discussions on different values of dam** parameter of exponentially varying temperature. It has been observed that an increment of the decaying parameter diminishes the magnitude of physical quantities. The significant effect of moving heat source velocity on stress and temperature has been noted.

Appendix 1

Inversion of the Fourier transform If $\bar{f}^{*}(x,q,p)$ Laplace–Fourier transform of the function f(x, y, t) then the inversion for Fourier transform carried out in following manners

$$\begin{aligned} \bar{f}(x,y,p)= & {} \frac{1}{\sqrt{2\pi }}\int _{-\infty }^{\infty } \bar{f}^*(x,q,p)e^{iqy}dq \\= & {} \sqrt{\frac{2}{\pi }}(\int _{0}^{\infty } \bar{f_1}^*(x,q,p) cos(qy)dq +i\int _{0}^{\infty } \bar{f_2}^*(x,q,p) sin(qy)dq) \end{aligned}$$

where $\bar{f_1}^*$ and $\bar{f_2}^*$ represent the even and odd parts of $\bar{f}^*$. Henceforth, first the transformation $z=e^{-q}$ and then the Gauss-quadrature formula for 7-point has been applied to obtain $\bar{f}(x,y,p)$.

Inversion of the Laplace transform According to Honig and Hirdes [30] The inversion formula of $\bar{f}(x,y,p)$ is

$$\begin{aligned} f(x,y,t)=\frac{e^{dt}}{2\pi }\int _{-\infty }^{\infty }\bar{f}(x,y,d+iw)dw \end{aligned}$$

where $d>$ all real parts of the singularities (for p) of $\bar{f}(x,y,p)$. Expand the function $g(x,y,d,t)=e^{-dt}f(x,y,t)$ in a Fourier series in the interval [0, 2T] for time variable. Thus the approximate formula is

$$\begin{aligned} f(x,y,t)\approx f_N(x,y,t)=\frac{c_0}{2}+\sum _{k=1}^{N}c_k \text {for } 0 \le t \le 2T \end{aligned}$$

(49)

here $c_k=\frac{e^{dt}}{T}Re[e^{ik\pi / T} \bar{f}(x,y,d+ik\pi /T)]$.

Two methods such as Korrecktur and $\varepsilon$-algorithm are used to reduce the discretization error and the truncation error and after that to accelerate the convergence. The Korrektur method is used to evaluate the function f(x, y, t) and is defined as:

$$\begin{aligned} f(x,y,t)= f_{NK}(x,y,t)= f_N(x,y,t)-e^{-2dT}f_M(x,y,t+2T) \end{aligned}$$

whereas, the $\varepsilon$-algorithm is employed to increase the rate of convergence of the series given in approximation formula (49). Let N = 2r + 1 is an odd natural number and $s_m=\sum _{k=1}^{m}c_k$ in (49). The $\varepsilon$-algorithm is:

$$\begin{aligned} {\varepsilon _{n+1}}^{(m)}={\varepsilon _{n-1}}^{(m+1)}+\frac{1}{{\varepsilon _{n}}^{(m+1)}-{\varepsilon _{n}}^{(m)}},\quad {\varepsilon _{0}}^{(m)}=0,\,\,\, {\varepsilon _{1}}^{(m)}=s_m ,\,\,\, n=1,2,3 \dots \end{aligned}$$

then the sequence ${\varepsilon _{1}}^{(1)},{\varepsilon _{3}}^{(1)},{\varepsilon _{5}}^{(1)} \dots$ converges to $f_{\infty }(x,y,t)-c_0/2$.