Modelling and analysis of a SEIQR model on COVID-19 pandemic with delay

Abstract

This paper deals with mathematical modelling and analysis of a SEIQR model to study the dynamics of COVID-19 considering delay in conversion of exposed population to the infected population. The model is analysed for local and global stability using Lyapunov method of stability followed by Hopf bifurcation analysis. Basic reproduction number is determined, and it is observed that local and global stability conditions are dependent on the number of secondary infections due to exposed as well as infected population. Our study reveals that asymptomatic cases due to exposed population play a vital role in increasing the COVID-19 infection among the population.

Introduction

Experts from Wuhan, Hubei Province of China reported an unidentified case of pneumonia in late December 2019 which was later on declared as novel coronavirus pneumonia (NCP) caused by a novel coronavirus (CoV) of coronavirus family (Huang et al. 2020). Disease caused by this coronavirus was found to be highly contagious leading to large number of deaths throughout the world. The World Health Organization (WHO) called it a pandemic and officially named the disease ‘COVID-19’ (Huang et al. 2020). Although source of the infection of this pandemic is still unclear, its initial symptoms resemble Severe Acute Respiratory Syndrome (SARS). This virus is highly infectious for it is found to be transmitted through droplets and close contact and poses a great threat to health and safety throughout the world. Whole world is looking forward to control the spread of COVID-19 and reduce the mortality rate as soon as possible. Major challenges that the world is facing in controlling the disease are the unknown mechanism of the virus spread and the absence of specific antiviral drugs. Hence, only way to control this alarming situation is to check the source of infection and block the route of transmission of infection using existing drugs (Wang et al. 2019). Prevention from exposure to virus and immunity boosting is imperative to control the disease from spreading. As a precautionary measure, most of the governmental agencies have imposed lockdown to maintain social distance. This procedure is an outstanding step to control the spread of the disease. Still, the complete lockdown may cause financial crisis for the near future. Although lockdown in high dense countries may reduce the transmission rate of infection, yet complete control may not be achieved. Hence kee** in view of economic status of a country, a full lockdown for a long tenure is not desirable at all in any circumstances (Mandal et al. 2020). Hence, government must spread awareness among the population to boost up their immunity and prevent themselves from catching the infection while working outside their homes. Strengthening of immunity may cause delay in entering into infectious stage after acquiring infection and a fairly large value of delay may even result into interruption of the disease at exposed level. Hence time delay plays a significant role in the dynamics of disease spread. We have incorporated this delay factor in our model by introducing time delay, which is novel feature of our work in studying the disease through mathematical modelling.

Mathematical modelling of infectious diseases has been used as a significant tool in understanding the dynamics of diseases and predicting the size of infectious population. A suitable mathematical model helps the government and healthcare workers in framing their policies by predicting the behavioural aspect of the disease. Bernoulli (1760), Hamer (1906), Ross (1916), Kermack and McKendrick (1927), Keeling and Rohani (2008), Wang and Zhao 2004, Buonomo et al. (2008), Zhou et al. (2014), Jana et al. (2016), Li et al. 2018 and Zegarra and Hernandez (2018) contributed the major works on mathematical epidemiology. Mathematical modelling of prevailing COVID-19 research is ongoing at a significant pace to combat the disease. Many modellers Mandal et al. (2020), Kucharski et al. (2020), Ndariou et al. (2020), Prem et al. (2020), Mizumoto and Chowell (2020), Liu et al. (2020), Fanelli and Piazza (2020), Ribeiro et al. (2020) and Chakraborty and Ghosh (2020) have proposed mathematical models on COVID-19 and disseminated their ideas to control it. Liang (2020) compared the characteristics of COVID-19 with those of SARS and MERS. They observed that the growth rate of COVID-19 is twice that of the SARS and MERS, and the doubling cycle of COVID-19 is two to three days, implying that without human intervention, the number of COVID-19 patients would double in two to three days. Marimuthu et al. (2020) studied the impact of COVID-19 on TB patients and found that on the peak of epidemic a large number of Coronavirus infectious will include TB patients. Mandal et al. (2020) formulated a mathematical model introducing a quarantine class and governmental intervention measures to mitigate disease transmission. They found that the most critical factor in achieving disease control is the reduction of the contact of exposed and susceptible humans. Ibarra-Vega (2020) studied SIR mathematical model containing COVID-19 infection and studied the effects of quarantine on the disease control. In this continuation, we propose a five-dimensional mathematical model containing susceptible, exposed, infected, quarantined and recovered population. We have also considered delay in transfer of individuals from exposed class to infected class, which is not yet considered in any of the previous models to the best of our knowledge. Time delay in entering into infectious population can be achieved by adopting healthy life style and strengthening one’s own immunity that even after getting infection individual takes some time to combat with the disease and does not enter into the infectious class rapidly. Hence time delay plays a significant role in studying the dynamics of disease spread. Effect of quarantine on the controlling the spread of disease is also incorporated and transmission of infection from both the exposed and infected class is taken into account. Since people do not acquire immunity after recovery, we have also considered the loss of immunity after recovery from quarantined and recovered population to be more realistic.

Mathematical model

COVID-19 has produced a significant burden on the healthcare system around the world leading to large number of mortality rates. Many researchers have studied mathematical models on COVID-19 to predict the dynamics of disease and help the government and health care system to frame their policies. India is also not untouched by this pandemic and already faced two waves of the pandemic. Depending on the recent condition, Indian Government has adopted quarantine strategy to stop the spread of COVID-19 virus. In this section, we presents a SEIQR compartment model of COVID-19 (Fig. 1) based on the current situation of the disease. Our model is extended form of SIR epidemic model given by Kermack and McKendrick (1927). We denote susceptible population by S(t), exposed population by E(t), infected, quarantined and recovered population are denoted by I(t), Q(t) and R(t), respectively. We assume that total population of India is N(t) and $N(t) = S(t) + E(t) + I(t) + Q(t) + R(t)$. Exposed population refers to the population in incubation period, infected population refer to the population who have got the infection and showing clinical symptoms of disease. Quarantined population refer to the population suspected to have disease and hence are separated so that they do not transmit infection among the population. Recovered population refer to the population who have recovered from the disease. We assume that there is influx of population in the system at the constant rate A. After getting COVID-19 infection, it is assumed that the population is ready to spread infection among the population after the incubation period of nearly five days. During incubation period, population does not show any symptom; therefore we assume that population in exposed class is in asymptomatic stage and after incubation period since, population starts showing symptoms of infection; therefore infected population is assumed to be in the symptomatic stage of the infection. Since COVID-19 spreads by asymptomatic as well as symptomatic infection, we assume transmission of infection among susceptible population both by exposed as well as infected class at the rate $\beta$ and $\beta _1$, respectively. After incubation period, exposed population population enter into infected population and a fraction of exposed as well as infected population is quarantined and get transferred to the quarantine population. Apart from the natural deaths of population in each compartment, disease-related deaths are also considered. While formulating the model, we assume that $\mu$ is the natural death rate of each population and $\alpha$ is the disease-related death rate of infected and quarantined population. Moreover, since population does not get permanent immunity after recovery from COVID-19, we assume that recovered population and quarantined population again are susceptible to disease at the rate $\delta$ and $\sigma$, respectively. $\eta$ is the transfer rate of exposed population to infected population and $\gamma _1$, $\gamma _2$ are the transfer rate of exposed population to infected and quarantined population, respectively. In addition, India has recovery rate of $35\%$ from COVID 19; we assume that infected and quarantined population get recovered at the rate $\theta$ and $\pi$, respectively. Furthermore, since any natural process is not instantaneous, there is some delay in manifesting clinical symptoms after getting infection; we introduce a delay term $\tau$ in the equation displaying infected population dynamics. Kee** the above facts and assumptions in mind our model may be described by the following system of nonlinear autonomous differential equations:

$$\begin{aligned} \frac{{\text {d}}S}{{\text {d}}t}= & {} A-\beta SE-\beta _1SI-\mu S+\delta R+\sigma Q, \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\text {d}}E}{{\text {d}}t}= & {} \beta SE-\eta E-\mu E-\gamma _1E, \end{aligned}$$

(2)

$$\begin{aligned} \frac{{\text {d}}I}{{\text {d}}t}= & {} \beta _1 SI+\eta E(t-\tau )-\mu I-\alpha I-\gamma _2 I-\theta I, \end{aligned}$$

(3)

$$\begin{aligned} \frac{{\text {d}}Q}{{\text {d}}t}= & {} \gamma _1 E+\gamma _2 I-\mu Q-\pi Q-\sigma Q-\alpha Q, \end{aligned}$$

(4)

$$\begin{aligned} \frac{{\text {d}}R}{{\text {d}}t}= & {} \theta I+\pi Q-\mu R-\delta R, \end{aligned}$$

(5)

with initial conditions $S(0)> 0$, $E(0)\ge 0$, $I(0)\ge 0$, $Q(0)\ge 0$ and $R(0)\ge 0$.

Fig. 1

Schematic diagram

Boundedness of the solutions

The region of attraction of the model system (1–5) with no delay is given in the following lemma:

Lemma 3.1

If assumptions of Sect. 2hold, then solutions of the model system (1–5) with no delay are bounded within following set

$$\begin{aligned} \Omega =\left\{ (S,E,I,Q,R):S+E+I+Q+R\le \frac{A}{\mu }\right\} . \end{aligned}$$

Proof

Adding all the equations of model system (1–5) and after doing some algebraic calculations, we have

$$\begin{aligned} \begin{aligned}&\frac{{\text {d}}S}{{\text {d}}t}+\frac{{\text {d}}E}{{\text {d}}t}+\frac{{\text {d}}I}{{\text {d}}t}+\frac{{\text {d}}Q}{{\text {d}}t}+\frac{{\text {d}}R}{{\text {d}}t}\\&=A-\mu S-\mu E-(\mu +\alpha )I-(\mu +\alpha )Q-\mu R, \end{aligned} \end{aligned}$$

(6)

which gives that

$$\begin{aligned} \begin{aligned}&\frac{{\text {d}}S}{{\text {d}}t}+\frac{{\text {d}}E}{{\text {d}}t}+\frac{{\text {d}}I}{{\text {d}}t}+\frac{{\text {d}}Q}{{\text {d}}t}+\frac{{\text {d}}R}{{\text {d}}t}\\&\le A-\mu (S+ E+I+Q+R), \end{aligned} \end{aligned}$$

(7)

which implies that,

$$\begin{aligned} \lim _{t\rightarrow \infty }{\text {sup}}(S(t)+E(t)+I(t)+Q(t)+R(t))\le \frac{A}{\mu }. \end{aligned}$$

This completes the proof of the Lemma 3.1.

Equilibrium analysis

Model system (1–5) has two non-negative equilibrium point in which disease-free equilibrium point $(\frac{A}{\mu },0,0,0,0)$ exists trivially and the existence of endemic equilibrium point $(S^*,E^*,I^*,Q^*,R^*)$ is discussed below.

Existence of $(S^*,E^*,I^*,Q^*,R^*)$: $S^*,E^*,\,I^*,\,Q^*$ and $R^*$ are obtained by solving the system of equations

$$\begin{aligned}&A-\beta S^*E^*-\beta _1S^*I^*-\mu S^*+\delta R^*+\sigma Q^*=0, \end{aligned}$$

(8)

$$\begin{aligned}&\beta S^*E^*-\eta E^*-\mu E^*-\gamma _1E^*=0, \end{aligned}$$

(9)

$$\begin{aligned}&\beta _1S^*I^*+\eta E^*-\mu I^*-\alpha I^*-\gamma _2 I^*-\theta I^*=0, \end{aligned}$$

(10)

$$\begin{aligned}&\gamma _1 E^*+\gamma _2 I^*-\mu Q^*-\pi Q^*-\sigma Q^*-\alpha Q^*=0, \end{aligned}$$

(11)

$$\begin{aligned}&\theta I^*+\pi Q^*-\mu R^*-\delta R^*=0. \end{aligned}$$

(12)

From Eq. (9), we get

$$\begin{aligned} S^*=\dfrac{(\eta +\mu +\gamma _1)}{\beta }. \end{aligned}$$

(13)

Further, from Eq. (10), we have

$$\begin{aligned} E^*=\left[ (\mu +\alpha +\gamma _2+\theta )-\frac{\left( \eta +\mu +\gamma _1\right) \beta _1}{\beta }\right] I^*. \end{aligned}$$

(14)

Let us take $\xi _1=\left[ (\mu +\alpha +\gamma _2+\theta )-\frac{\left( \eta +\mu +\gamma _1\right) \beta _1}{\beta }\right]$, then $E^*=\xi _1 I^*$. Now, from Eq. (11), we have

$$\begin{aligned} Q^*=\dfrac{\gamma _1 E^*+\gamma _2I^*}{\sigma +\pi +\mu +\alpha }, \end{aligned}$$

(15)

substituting the value of $E^*$, we get

$$\begin{aligned} Q^*=\dfrac{(\gamma _1 \xi _1+\gamma _2)I^*}{\sigma +\pi +\mu +\alpha }. \end{aligned}$$

(16)

Equation (12) implies that

$$\begin{aligned} \begin{aligned} R^*=&\dfrac{(\theta I^*+\pi Q^*)}{\mu +\sigma }\\ {}&=\dfrac{1}{\mu +\sigma }\left[ \theta +\frac{(\gamma _1 \xi _1+\gamma _2)}{\sigma +\pi +\mu +\alpha }\right] I^* \end{aligned} \end{aligned}$$

(17)

Let us take $\xi _2=\dfrac{1}{\mu +\sigma }\left[ \theta +\frac{(\gamma _1 \xi _1+\gamma _2)}{\sigma +\pi +\mu +\alpha }\right]$, then $R^*=\xi _2I^*$. Now, from Eq. (8), we have

$$\begin{aligned} \begin{aligned} A-(\eta +\mu +\gamma _1)\xi _1I^*-\frac{\beta _1(\eta +\mu +\gamma _1)I^*}{\beta }\\ \frac{-\mu (\eta +\mu +\gamma _1)}{\beta }+\delta \xi _2 I^*+\frac{(\gamma _1\xi _1+\gamma _2)\sigma I^*}{\mu +\pi +\sigma +\alpha }=0,\end{aligned} \end{aligned}$$

(18)

which implies that

$$\begin{aligned} I^*=\dfrac{A-\frac{\mu (\eta +\mu +\gamma _1)}{\beta }}{(\eta +\mu +\gamma _1)\xi _1+\frac{\beta _1(\eta +\mu +\gamma _1)}{\beta }-\delta \xi _2-\frac{\sigma (\gamma _1\xi _1+\gamma _2)}{(\mu +\pi +\sigma +\alpha )}}. \end{aligned}$$

(19)

Hence, interior equilibrium point of the system (1–5) exists if following inequalities hold:

$$\begin{aligned}&(\mu +\alpha +\gamma _2+\theta )>\frac{\left( \eta +\mu +\gamma _1\right) \beta _1}{\beta }, \end{aligned}$$

(20)

$$\begin{aligned}&\left[ A-\frac{\mu (\eta +\mu +\gamma _1)}{\beta }\right] \nonumber \\&\left[ (\eta +\mu +\gamma _1)\xi _1+\frac{\beta _1(\eta +\mu +\gamma _1)}{\beta } \right. \nonumber \\&\left. -\delta \xi _2-\frac{\sigma (\gamma _1\xi _1+\gamma _2)}{(\mu +\pi +\sigma +\alpha )}\right] >0. \end{aligned}$$

(21)

Basic reproduction rate by NGM method

We find reproduction ratio through use next-generation matrix approach given by Van Den Driessche and Watmough (2002). Our system can be written as ${\dot{X}}=R_1-R_2$, where ${\dot{X}}=[\frac{\text {d}S}{\text {d}t}\quad \frac{\text {d}E}{\text {d}t}\quad \frac{\text {d}I}{\text {d}t}\quad \frac{\text {d}Q}{\text {d}t}\quad \frac{\text {d}R}{\text {d}t}]$,

$$\begin{aligned}&R_1^*=\begin{bmatrix} \beta SE\\ \beta _1SI\\ 0\\ 0\\ 0 \end{bmatrix},\nonumber \\&R_2^*=\begin{bmatrix}(\eta +\mu +\gamma _1)E\\ -\eta E+(\alpha +\mu +\gamma _2+\theta )I\\ \gamma _1E-\gamma _2I+(\mu +\pi +\sigma +\alpha )Q\\ -\theta I-\pi Q+(\mu +\delta )R\\ -A+\beta SE-\beta _1SI+\mu S-\delta R -\sigma Q \end{bmatrix}. \end{aligned}$$

(22)

Now, we compute the Jacobian $R_1$ and $R_2$ from $R_1^*$ and $R_2^*$, respectively, for the classes containing infected population E, I and Q.

$$\begin{aligned}&R_1=\begin{bmatrix} \beta S &{}0 &{}0\\ 0&{}\beta _1S&{}0\\ 0&{}0&{}0 \end{bmatrix},\nonumber \\&R_2=\begin{bmatrix}(\eta +\mu +\gamma _1)&{}0&{}0\\ -\eta &{}(\alpha +\mu +\gamma _2+\theta )&{}0\\ \gamma _1&{}-\gamma _2&{}(\mu +\pi +\sigma +\alpha ) \end{bmatrix} \end{aligned}$$

(23)

$$\begin{aligned}&R_1R_2^{-1}=\frac{1}{|R_2|} \begin{bmatrix} \frac{\beta A}{\mu }(\alpha +\mu +\gamma _2+\theta )(\mu +\pi +\sigma +\alpha )&{}0&{}0\\ \frac{\beta _1 A\eta }{\mu }(\mu +\pi +\sigma +\alpha )&{}\frac{\beta _1 A}{\mu }(\eta +\mu +\gamma _1)(\mu +\pi +\sigma +\alpha )&{}0\\ 0&{}0&{}0 \end{bmatrix}, \end{aligned}$$

(24)

where $|R_2|=(\eta +\mu +\gamma _1)(\alpha +\mu +\gamma _2+\theta )(\mu +\pi +\sigma +\alpha )$.

The basic reproduction number is defined as spectral radius of $R_1R_2^{-1}$ (Driessche and Watmough 2002). Thus,

$$\begin{aligned} R_0= & {} \max \left\{ \frac{\beta A}{\mu (\eta +\mu +\gamma _1)}, \frac{\beta _1 A}{\mu (\mu +\alpha +\gamma _2+\theta )}\right\} \nonumber \\= & {} \max \{R_e, R_i \}, \end{aligned}$$

(25)

where

$$\begin{aligned} R_e= & {} \frac{\beta A}{\mu (\eta +\mu +\gamma _1)} \end{aligned}$$

(26)

$$\begin{aligned} R_i= & {} \frac{\beta _1 A}{\mu (\mu +\alpha +\gamma _2+\theta )}, \end{aligned}$$

(27)

may be defined as the number of secondary infections produced by exposed and infectious population, respectively. From this we infer that rate of spread of infection among the population is dependent on both the exposed and infected individuals in the population. Basic reproduction number is contributed by both the exposed and infected class since mathematical expression for basic reproduction number is dependent upon the transmission coefficient of infection from both the exposed and infected class. Basic reproduction number is proportional to larger transmission coefficient of infection. Hence, policy makers must take care of the density of exposed population in the system as well along with infected population.

Local stability of disease free equilibrium point

Now, we linearise the model system (1–5) about disease free equilibrium point $(\frac{A}{\mu },0,0,0,0)$ by taking $S=s+\frac{A}{\mu }$, $E=e$, $I=i$, $Q=q$ and $R=r$, where s, e, i, q and r are small perturbations about the disease-free equilibrium point. After linearisation about disease-free equilibrium point, our model takes the following form

$$\begin{aligned} \frac{\text {d}s}{\text {d}t}= & {} -\frac{A\beta }{\mu }e-\frac{A\beta _1}{\mu }i-\mu s+\delta r+\sigma q, \end{aligned}$$

(28)

$$\begin{aligned} \frac{\text {d}e}{\text {d}t}= & {} \frac{A\beta }{\mu }e-\eta e-\mu e-\gamma _1e, \end{aligned}$$

(29)

$$\begin{aligned} \frac{\text {d}i}{\text {d}t}= & {} \frac{A\beta _1}{\mu }i+\eta e-\mu i-\alpha i-\gamma _2 i-\theta i, \end{aligned}$$

(30)

$$\begin{aligned} \frac{\text {d}q}{\text {d}t}= & {} \gamma _1 e+\gamma _2 i-\mu q-\pi q-\sigma q-\alpha q, \end{aligned}$$

(31)

$$\begin{aligned} \frac{\text {d}r}{\text {d}t}= & {} \theta i+\pi q-\mu r-\delta r. \end{aligned}$$

(32)

Let us consider following semi-positive definite function

$$\begin{aligned} V=\frac{s^2}{2}+\frac{e^2}{2}+\frac{i^2}{2}+\frac{r^2}{2}+\frac{q^2}{2}, \end{aligned}$$

(33)

After differentiating it with respect to t and substituting the values of ${\dot{s}},\,{\dot{e}},\,{\dot{i}},\,{\dot{q}},\,{\dot{r}}$, we get

$$\begin{aligned} \begin{aligned} {\dot{V}}=&-\mu s^2+\left( \frac{\beta A}{\mu }-\eta -\mu -\gamma _1\right) e^2+\left( \frac{\beta _1 A}{\mu }-\alpha -\mu -\gamma _2\right) i^2\\ {}&-(\mu +\pi +\sigma )q^2-(\mu +\delta )r^2-\frac{\beta A}{\mu }se-\frac{\beta _1 A}{\mu }si\\ {}&+ \delta sr+\sigma sq+\eta ie+\gamma _1 qe+\gamma _2 qi+\theta ri+\pi rq, \end{aligned} \end{aligned}$$

(34)

If we write it as follows

$$\begin{aligned} \begin{aligned} {\dot{V}}=&-\frac{a_{11}}{4} s^2+a_{12}se-\frac{a_{22}}{3}e^2-\frac{a_{11}}{4} s^2+a_{13}si-\frac{a_{33}}{4}i^2\\ {}&-\frac{a_{11}}{4} s^2+a_{14}sq-\frac{a_{44}}{4}q^2-\frac{a_{11}}{4} s^2+a_{15}sr-\frac{a_{55}}{3}r^2\\ {}&-\frac{a_{22}}{3} e^2+a_{23}ei-\frac{a_{33}}{4}i^2-\frac{a_{22}}{3} e^2+a_{24}eq-\frac{a_{44}}{4}q^2\\ {}&-\frac{a_{33}}{4} i^2+a_{34}iq-\frac{a_{44}}{4}q^2-\frac{a_{33}}{4} i^2+a_{35}ir-\frac{a_{55}}{3}r^2\\ {}&-\frac{a_{44}}{4} q^2+a_{45}qr-\frac{a_{55}}{3}r^2, \end{aligned} \end{aligned}$$

(35)

then conditions of local stability of disease-free equilibrium point are

$$\begin{aligned} \begin{aligned} a_{12}^2<\frac{a_{11}a_{22}}{3},\qquad a_{13}^2<\frac{a_{11}a_{33}}{4},\qquad a_{14}^2<\frac{a_{11}a_{44}}{4},\\ a_{15}^2<\frac{a_{11}a_{55}}{3},\qquad a_{23}^2<\frac{a_{22}a_{33}}{4},\qquad a_{24}^2<\frac{a_{22}a_{44}}{4},\\ \qquad a_{34}^2<\frac{a_{33}a_{44}}{4},\qquad a_{35}^2<\frac{a_{33}a_{55}}{3},\qquad a_{45}^2<\frac{a_{44}a_{55}}{3}, \end{aligned} \end{aligned}$$

(36)

that is

$$\begin{aligned}&\left( \frac{\beta A}{\mu }\right) ^2<\frac{\mu }{3}(\eta +\mu +\gamma _1)(1-R_e), \end{aligned}$$

(37)

$$\begin{aligned}&\left( \frac{\beta _1 A}{\mu }\right) ^2<\frac{\mu }{4}(\alpha +\mu +\gamma _2+\theta )(1-R_i), \end{aligned}$$

(38)

$$\begin{aligned}&\sigma ^2<\frac{\mu }{4}(\mu +\pi +\sigma +\alpha ), \end{aligned}$$

(39)

$$\begin{aligned}&\delta ^2<\frac{\mu }{4}(\mu +\delta ), \end{aligned}$$

(40)

$$\begin{aligned}&\eta ^2<\frac{1}{4}(\eta +\mu +\gamma _1)(\alpha +\mu +\gamma _2+\theta )(1-R_e)(1-R_i), \end{aligned}$$

(41)

$$\begin{aligned}&\gamma _1^2<\frac{1}{4}(\eta +\mu +\gamma _1)(1-R_e)(\mu +\pi +\sigma +\alpha ), \end{aligned}$$

(42)

$$\begin{aligned}&\gamma _2^2<\frac{1}{4}(\alpha +\mu +\gamma _2+\theta )(1-R_i)(\mu +\pi +\sigma +\alpha ), \end{aligned}$$

(43)

$$\begin{aligned}&\theta ^2<\frac{1}{3}(\alpha +\mu +\gamma _2+\theta )(1-R_i)(\mu +\delta ), \end{aligned}$$

(44)

$$\begin{aligned}&\pi ^2<\frac{1}{3}(\mu +\pi +\sigma +\alpha )(\mu +\delta ). \end{aligned}$$

(45)

These conditions infer that the disease-free equilibrium point is locally asymptotically stable if above conditions are satisfied and $R_e<1$, $R_i<1$.

Global stability of disease-free equilibrium point

Theorem 7.1

The disease-free equilibrium of the model is globally asymptotically stable whenever $R_e<1$, $R_i<1$.

Proof

Consider the following Lyapunov function

$$\begin{aligned} L=m_1E+m_2I+m_3Q, \end{aligned}$$

(46)

where $m_1=\frac{1}{\eta +\mu +\gamma _1}$, $m_2=\frac{1}{\mu +\alpha +\gamma _2+\theta }$ and $m_3=1$. Differentiating Eq. (32) with respect to t, we get

$$\begin{aligned} {\dot{L}}=m_1{\dot{E}}+m_2{\dot{I}}+m_3{\dot{Q}}, \end{aligned}$$

(47)

after substituting the values of $m_1,\,m_2,\,m_3,\, {\dot{E}},\,{\dot{I}},\,{\dot{Q}}$ and doing some algebraic manipulations, we get

$$\begin{aligned} \begin{aligned} {\dot{L}}&\le 2\left[ R_e-1+\gamma _1+\frac{\eta }{\mu +\alpha +\gamma _2+\theta }\right] E\\&\quad +2\left[ R_i-1+\gamma _2\right] I, \end{aligned} \end{aligned}$$

(48)

which implies that ${\dot{L}}\le 0$, if following inequalities hold

$$\begin{aligned}&R_e<1-\gamma _1-\frac{\eta }{\mu +\alpha +\gamma _2+\theta }, \end{aligned}$$

(49)

$$\begin{aligned}&R_i<1-\gamma _2 \end{aligned}$$

(50)

and ${\dot{L}}=0$ if and only if $E=I=Q=0$. Hence L is a Lyapunov function on R if inequalities (49) and (50) satisfied by the parameters.

Therefore, the largest compact invariant subset of the set where ${\dot{L}}=0$ is the singleton set $\{(E,I,Q)=(0,0,0)\}$. Thus, it follows by the LaSalle’s invariance principle (LaSalle 1976) that $(E,I,Q)\rightarrow (0,0,0)$ as $t\rightarrow \infty$. Thus, this proves the statement of the theorem.

Local stability of interior equilibrium point

If s, e, i, q and r are small perturbations given to S, E, I, Q and R, respectively, such that $S=S^*+s$, $E=E^*+e$, $I=I^*+i$, $Q=Q*+q$ and $R=R^*+r$, then linearised form of system (1–5) about interior equilibrium point ($S^*$, $E^*$, $I^*$, $Q*$, $R^*$) is

$$\begin{aligned} \frac{{\text {d}}s}{{\text {d}}t}= & {} -\beta S^*e-\beta E^*s-\beta _1S^*i-\beta _1I^*s-\mu s+\delta r+\sigma q, \end{aligned}$$

(51)

$$\begin{aligned} \frac{{\text {d}}e}{{\text {d}}t}= & {} \beta S^*e+\beta E^*s-\eta e-\mu e-\gamma _1e, \end{aligned}$$

(52)

$$\begin{aligned} \frac{{\text {d}}i}{{\text {d}}t}= & {} \beta _1S^*i+\beta _1I^*s+\eta e(t-\tau )-\mu i-\alpha i-\gamma _2 i-\theta i, \end{aligned}$$

(53)

$$\begin{aligned} \frac{{\text {d}}q}{{\text {d}}t}= & {} \gamma _1 e+\gamma _2 i-\mu q-\pi q-\sigma q-\alpha q, \end{aligned}$$

(54)

$$\begin{aligned} \frac{{\text {d}}r}{{\text {d}}t}= & {} \theta i+\pi q-\mu r-\delta r, \end{aligned}$$

(55)

The variational matrix of this linearised system has the following characteristic equation,

$$\begin{aligned} \begin{aligned}&e^{-\uplambda \tau }\left[ B_1\uplambda ^2+B_2\uplambda +B_3\right] +\uplambda ^5+B_4\uplambda ^4+B_5\uplambda ^3\\&+B_6\uplambda ^2+B_7\uplambda +B_8=0, \end{aligned} \end{aligned}$$

(56)

where

$$\begin{aligned} B_1= & {} \eta \beta \xi _1\beta _1I^*S^*, \end{aligned}$$

(57)

$$\begin{aligned} B_2= & {} \eta \beta \xi _1I^*(\beta _1S^*(A_{44}+A_{55})-\delta \theta -\sigma \gamma _2), \end{aligned}$$

(58)

$$\begin{aligned} B_3= & {} \eta \beta \xi _1I^*(\beta _1S^*A_{44}A_{55}-\sigma \gamma _2A_{55}-\delta (\gamma _2\pi +\theta A_{44})), \end{aligned}$$

(59)

$$\begin{aligned} B_4= & {} A_{11}+A_{44}+A_{55}-A_{22}-A_{33}, \end{aligned}$$

(60)

$$\begin{aligned} B_5=&A_{44}A_{55}+A_{11}A_{55}+A_{11}A_{44}-A_{33}A_{55} \nonumber \\&-A_{33}A_{44}-A_{11}A_{33} \nonumber \\&+A_{22}(A_{33}-A_{11}-A_{44}-A_{55})+I^*S^*\beta _1^2+\xi _1I^*S^*\beta ^2, \end{aligned}$$

(61)

$$\begin{aligned} B_6=&A_{11}A_{44}A_{55}-A_{33}A_{44}A_{55}-A_{33}A_{11}A_{55}-A_{33}A_{11}A_{44}\nonumber \\&-A_{22}(A_{44}A_{55}+A_{11}A_{55}+A_{11}A_{44}\nonumber \\&-A_{33}A_{55}-A_{33}A_{44}-A_{11}*A_{33})\nonumber \\&-\beta _1I^*(A_{22}\beta _1S^*-\beta _1S^*(A_{44}+A_{55})+\sigma \gamma _2+\delta \theta )\nonumber \\&-\beta \xi _1I^*(A_{33}\beta S^*+\sigma \gamma _1-\beta S^*(A_{44}+A_{55})), \end{aligned}$$

(62)

$$\begin{aligned} B_7=&A_{22}(A_{33}A_{44}A_{55}-A_{11}A_{44}A_{55}\nonumber \\&+A_{33}A_{11}A_{55}+A_{33}A_{11}A_{44})\nonumber \\&-A_{11}A_{33}A_{44}A_{55}-\beta _1I^*(A_{22}(\beta _1S^*(A_{44}\nonumber \\&+A_{55})-\sigma \gamma _2-\delta \theta )-\beta _1S^*A_{44}*A_{55}\nonumber \\&+\sigma \gamma _2A_{55}+\delta (\gamma _2\pi +\theta A_{44})) \nonumber \\&-\beta \xi _1I^*(A_{33}(\beta S^*(A_{44}+A_{55}-\sigma \gamma _1)\nonumber \\&+\sigma \gamma _1A_{55}+\delta \gamma _1\pi -\beta S^*A_{44}A_{55})), \end{aligned}$$

(63)

$$\begin{aligned} B_8=&A_{22}(\beta _1I^*(-\beta _1S^*A_{44}A_{55}+\sigma \gamma _2A_{55}+\delta (\gamma _2\phi +\theta A_{44}))\nonumber \\&+A_{11}A_{33}A_{44}A_{55})\nonumber \\&-\beta \xi _1I^*A_{33}(\beta S^*A_{44}A_{55}-\sigma \gamma _1A_{55}-\delta \gamma _1\phi ), \end{aligned}$$

(64)

here $A_{11}=\beta \xi _1+\beta _1I^*$, $A_{22}=\beta S^*-\eta -\mu -\gamma _1$, $A_{33}=\beta _1S^*-\mu -\alpha -\gamma _2-\theta$, $A_{44}=\mu +\phi +\sigma +\alpha$ and $A_{55}=\mu +\delta$.

Case 1: In absence of delay $(\tau =0)$, Eq. (56) can be written as follows

$$\begin{aligned} \begin{aligned} \uplambda ^5+B_4\uplambda ^4+B_5\uplambda ^3+(B_1+B_6)\uplambda ^2+(B_2+B_7)\uplambda +B_3+B_8=0. \end{aligned} \end{aligned}$$

(65)

Routh Hurwitz criterion deduce that interior equilibrium point will be locally asymptotically stable if following hold,

$$\begin{aligned}&B_4>0,\, B_5>0,\,B_1+B_6>0,\,B_2+B_7>0,\, B_3+B_8>0, \end{aligned}$$

(66)

$$\begin{aligned}&B_4B_5>B_1+B_6 \end{aligned}$$

(67)

$$\begin{aligned}&(B_4B_5-B_1-B_6)(B_1+B_6)>(B_4B_2+B_4B_7-B_3-B_8)B_4 \end{aligned}$$

(68)

$$\begin{aligned}&(B_4B_5-B_1-B_6)(B_1B_2+B_1B_7+B_6B_2+B_6B_7-B_5B_3-B_5B_8)>(B_4B_2+B_4B_7-B_3-B_8)^2 \end{aligned}$$

(69)

Case 2: In presence of delay $(\tau \ne 0)$, the stability switch may occur if the characteristic Eq. (56) has purely imaginary root. Let $\uplambda =i\omega$ be a root of Eq. (56). By substituting this value of $\uplambda$ and comparing real and imaginary parts Eq. (56) will give following equations,

$$\begin{aligned}&(B_3-B_1\omega ^2)\cos \omega \tau +B_2\omega \sin \omega \tau =-B_4 \omega ^4+B_6\omega ^2-B_8 \end{aligned}$$

(70)

$$\begin{aligned}&B_2\omega \cos \omega \tau -(B_3-B_1\omega ^2)\sin \omega \tau = -\omega ^{5}+B_5\omega ^3-B_7\omega . \end{aligned}$$

(71)

Now, squaring and adding these equations, we get

$$\begin{aligned} \begin{aligned}&\omega ^{10}+(B_4^2-2B_5)\omega ^{8}+(B_5^2+2B_7-2B_4B_6)\omega ^{6}\\&+(B_6^2+2B_4B_8-2B_5B_7-B_1)\omega ^{4}\\&+(B_7^2-2B_6B_8+2B_1B_3-B_2^2)\omega ^{2}+B_8^2-B_3^2=0. \end{aligned} \end{aligned}$$

(72)

If we take $\omega ^2 =X$, then Eq. (72) can be written as

$$\begin{aligned} \begin{aligned}&X^{5}+(B_4^2-2B_5)X^{4}+(B_5^2+2B_7-2B_4B_6)X^{3}\\&+(B_6^2+2B_4B_8-2B_5B_7-B_1)X^{2}\\&+(B_7^2-2B_6B_8+2B_1B_3-B_2^2)X+B_8^2-B_3^2=0. \end{aligned} \end{aligned}$$

(73)

If we take, $F(X)=X^{5}+(B_4^2-2B_5)X^{4}$ $+ (B_5^2+2B_7-2B_4B_6)X^{3}$ $+(B_6^2+2B_4B_8-2B_5B_7-B_1)X^{2}$ $+(B_7^2-2B_6B_8$ $+2B_1B_3-B_2^2)X+B_8^2-B_3^2$ and if $B_3^2<B_8^2$, then $F(0) < 0$ and because F(X) is a polynomial function with leading coefficient positive, so there will be at least one positive root of Eq. (73) and from this root we can find a positive root of Eq. (72), say $\omega _0$. Hence, if $B_3^2<B_8^2$ holds then the interior equilibrium point will experience a stability switch for some $\tau >0$ and by solving Eqs. (70) and (71) we get the following critical value for the time lag

$$\begin{aligned} \begin{aligned}&\tau _{n}=\frac{1}{\omega _0}\sin ^{-1}\\&\left[ \frac{B_2\omega _0(-B_4\omega _0^4+B_6\omega _0^2-B_8)-(B_3-B_1\omega _0^2 )(-\omega _0^5+B_5\omega _0^3-B_7\omega _0)}{B_2^2\omega _0^2+(B_3-B_1\omega _0)^2}\right] \\&+\frac{2n\pi }{\omega _0},\qquad n=0,1, \ldots . \end{aligned} \end{aligned}$$

(74)

Existence and direction of Hopf bifurcation

In this section, we will investigate the conditions of the existence of Hopf bifurcation at the critical point of the delay. Differentiating Eq. (56) with respect to $\tau$, we get

$$\begin{aligned}&\dfrac{{\text {d}}\uplambda }{{\text {d}}\tau }|_{\tau =\tau _{n}}\nonumber \\&=\dfrac{\uplambda (B_1\uplambda ^2+B_2\uplambda +B_3)e^{-\tau _{0}\uplambda }-B_7}{e^{-\tau _{0}\uplambda }[\tau B_1\uplambda ^2+(\tau B_2+2B_1)\uplambda +\tau B_3+B_2]+5\uplambda ^4+4B_4\uplambda ^3+3B_5\uplambda ^2+2B_6\uplambda }. \end{aligned}$$

(75)

If $\dfrac{{\text {d}}(Re\uplambda )}{{\text {d}}\tau }|_{\tau =\tau _n}\ne 0$, then the transversality condition for the existence of Hopf bifurcation at critical value $\tau _{n}$ of the delay holds and system will experience stability switch at that point. Now, we will use normal form method and centre manifold theory (Hassard et al. 1981) to investigate the quality of Hopf Bifurcation. After re-scaling the time t by $\frac{t}{\tau }$ and linearising the system (1–5) by transforming $S=S^*+u_1$, $E=E^*+u_2$, $I=I^*+u_3$, $Q=Q^*+u_4$ and $R=R^*+u_5$, we get the following linearised form:

$$\begin{aligned} \frac{{\text {d}}u_1}{{\text {d}}t}= & {} \tau [-\beta s^*u_2-\beta e^*u_1-\beta _1s^*u_3-\beta _1i^*u_1 \nonumber \\&-\mu u_1+\delta u_5+\sigma u_4, \end{aligned}$$

(76)

$$\begin{aligned} \frac{{\text {d}}u_2}{{\text {d}}t}= & {} \tau [\beta s^*u_2+\beta e^*u_1-\eta u_2-\mu u_2-\gamma _1u_2], \end{aligned}$$

(77)

$$\begin{aligned} \frac{{\text {d}}u_3}{{\text {d}}t}= & {} \tau [\beta _1s^*u_3+\beta _1i^*u_1+\eta u_2(t-1)\nonumber \\&-\mu u_3-\alpha u_3-\gamma _2 u_3-\theta u_3], \end{aligned}$$

(78)

$$\begin{aligned} \frac{{\text {d}}u_4}{{\text {d}}t}= & {} \tau [\gamma _1 u_2+\gamma _2 u_3-\mu u_4-\pi u_4-\sigma u_4-\alpha u_4], \end{aligned}$$

(79)

$$\begin{aligned} \frac{{\text {d}}u_5}{{\text {d}}t}= & {} \tau [\theta u_3+\pi u_4-\mu u_5-\delta u_5], \end{aligned}$$

(80)

and remaining nonlinear terms are

$$\begin{aligned} f(u_1,u_2,u_3,u_4,u_5)=\tau \begin{pmatrix}-\beta u_1u_2-\beta _1u_1u_3\\ \beta u_1u_2\\ \beta _1u_1u_3\\ 0\\ 0 \end{pmatrix}. \end{aligned}$$

(81)

Let us take $\tau =\tau _n+\mu _0$, $\mu _0\in {\mathbb {R}}$, now for $\phi =(\phi _1,\phi _2,\phi _3,\phi _4,\phi _5)^{T}\in C([-1,\,0],{\mathbb {R}}^{5})$ let us define

$$\begin{aligned} L_{\mu _0}(\phi )=(\tau _{n}+\mu _0)[F_1\phi (0)+F_2\phi (-1)], \end{aligned}$$

(82)

where

$$\begin{aligned} F_1=\begin{pmatrix} -A_{11} &{} -\beta S^* &{} -\beta _1S^* &{} \delta &{} \sigma \\ \beta E^* &{} A_{22} &{}0 &{}0 &{}0\\ \beta _1I^* &{}0 &{} A_{33} &{} 0 &{}0\\ 0&{} \gamma _1 &{} \gamma _2 &{} -A_{44} &{}0\\ 0&{} 0 &{} \theta &{} \pi &{} A_{55} \end{pmatrix} \end{aligned}$$

(83)

and

$$\begin{aligned} F_2= \begin{pmatrix} 0 &{} 0 &{}0 &{}0 &{}0\\ 0 &{} 0 &{}0 &{}0 &{}0\\ 0 &{} \eta &{}0 &{}0 &{}0\\ 0 &{} 0 &{}0 &{}0 &{}0\\ 0 &{} 0 &{}0 &{}0 &{}0 \end{pmatrix}. \end{aligned}$$

(84)

Application of Riesz representation theorem implies that there exists a matrix having functions of bounded variation as its component, say $\eta _0(\xi ,\mu _0)$ for $\xi \in [-1,\,\,0]$, such that for $\phi \in C$

$$\begin{aligned} L_{\mu _0}\phi =\int _{-1}^{0}{\text {d}}\eta _0(\xi ,\mu _0)\phi (\xi ). \end{aligned}$$

(85)

We take

$$\begin{aligned} \eta _0(\xi ,\mu _0)=(\tau _{0}+\mu _0)[F_1\delta (\xi )-F_2\delta (\xi +1)], \end{aligned}$$

(86)

where $\delta$ is a Dirac delta function. Now, we define

$$\begin{aligned} P(\mu _0)(\phi )(\xi )={\left\{ \begin{array}{ll} \dfrac{{\text {d}}\phi (\xi )}{{\text {d}}\xi }\qquad \qquad \qquad {\text {if}} \quad \xi \in \left[ -1,\quad 0\right) ,\\ \int _{-1}^{0}{\text {d}}\eta _0(y,\mu _0)\phi (y)\quad {\text {if}}\quad \xi =0, \end{array}\right. } \end{aligned}$$

(87)

for $\phi \in C^1([-1,\,0],{\mathbb {R}}^{5})$ and for $\phi \in C([-1,\,0],{\mathbb {R}}^{5})$, we take

$$\begin{aligned}&f_{\mu _0}(\phi )=f(\mu _0,\phi )=(\tau _{0}+\mu _0)\nonumber \\&\begin{pmatrix} -\beta \phi _1(0) \phi _2(0)-\beta _1\phi _1(0) \phi _3(0)\\ \beta \phi _1(0) \phi _2(0)\\ \beta _1\phi _1(0) \phi _3(0)\\ 0\\ 0 \end{pmatrix}. \end{aligned}$$

(88)

Let us define

$$\begin{aligned} R(\mu _0)(\phi )(\xi )={\left\{ \begin{array}{ll} 0 \qquad \qquad {\text {if}}\,\quad \xi \in \left[ -1,\,\,0 \right) ,\\ f(\xi ,\mu _0) \qquad {\text {if}}\, \xi =0. \end{array}\right. } \end{aligned}$$

(89)

Then model system (1–5) will be equivalent to following operator equation

$$\begin{aligned} \dfrac{{\text {d}}u_{t}}{{\text {d}}t}=P(\mu _0)u_{t}+R(\mu _0)u_t, \end{aligned}$$

(90)

where $u_t(\xi )=u(t+\xi )$ for $\xi \in [-1,0]$. Further, for $\psi \in C^{1}([0,\,\,1],({\mathbb {C}}^{5})^{*})$, we define

$$\begin{aligned} P^*\psi (y)={\left\{ \begin{array}{ll} -\dfrac{{\text {d}}\psi (y)}{{\text {d}}y} \qquad \qquad {\text {if}} \quad y\in \left( 0,\,\,1\right] ,\\ \int _{-1}^{0}d\eta _0^{T}(t,0)\psi (-t)\qquad {\text {if}}\quad y=0. \end{array}\right. } \end{aligned}$$

(91)

and a bilinear inner product

$$\begin{aligned} \langle \psi ,\phi \rangle =\overline{\psi (0)}\phi (0)-\int _{-1}^{0}\int _{\xi _2}^{0}\overline{\psi (\xi _2-\xi )}{\text {d}}\eta _0(\xi )\phi (\xi _2){\text {d}}\xi _2, \end{aligned}$$

(92)

where $\eta _0(\xi )=\eta _0(\xi ,0)$. Since $\pm i\omega _0\tau _{n}$ are eigenvalues of P(0) and P and $P^*$ are adjoint operators, so $\pm i\omega _0\tau _{n}$ will also be the eigenvalues of $P^*$. We can easily check that vectors $h(\xi )=(1,h_{1},h_{2},h_{3},h_{4})^{T}e^{i\omega _0\tau _{n}\xi }$ and $h^{*}(y)=K(1,h_{1}^{*},h_{2}^{*},h_{3}^{*},h_{4}^{*})^{T}e^{i\omega _0\tau _{n}y}$ are the eigenvectors of P(0) and $P^*$ corresponding to the eigenvalue $i\omega _0\tau _{n}$ and $-i\omega _0\tau _{n}$, respectively, where

$$\begin{aligned} h_1= & {} \dfrac{\beta E^*}{\omega _0 i-A_{22}}\qquad h_2=\dfrac{\beta _1 I^*+\eta e^{-\omega _0\tau _n i}h_1}{\omega _0 i-A_{33}} \end{aligned}$$

(93)

$$\begin{aligned} h_3= & {} \dfrac{\gamma _1 h_1+\gamma _2 h_2}{A_{44}+\omega _0 i},\qquad h_4=\dfrac{\theta h_2+\pi h_3}{\omega _0 i-A_{55}}, \end{aligned}$$

(94)

$$\begin{aligned} h_1^*= & {} \dfrac{\beta S^*-\eta e^{-\omega _0\tau _n i}h_2^*-\gamma _1h_3^*}{A_{22}+\omega _0i},\qquad h_2^*=\dfrac{\beta _1S^*-\gamma _2h_3^*-\theta h_4^*}{A_{33}+\omega _0i}, \end{aligned}$$

(95)

$$\begin{aligned} h_3^*= & {} \dfrac{\delta +\pi h_4^*}{A_{44}-\omega _0i},\qquad h_4^*=\dfrac{-\sigma }{A_{55}+\omega _0i}, \end{aligned}$$

(96)

$$\begin{aligned} K= & {} [1+h_1^*\overline{h_1}+h_2^*\overline{h_2}+h_3^*\overline{h_3}+h_4^*\overline{h_4}+\eta h_2^*\overline{h_1}\tau _n e^{\omega _0\tau _n i}]^{-1} \end{aligned}$$

(97)

We can easily verify that $\langle h^*(y),h(\xi ) \rangle =1$ and $\langle h^*(y),{\overline{h}}(\xi ) \rangle =0$. Using the algorithm given by Hassard et al. (1981) for the analysis of Hopf bifurcation and following the computational process as done by Devi and Gupta (2019), we can calculate following coefficients to compute important quantities describing the quality of Hopf bifurcation:

$$\begin{aligned}&g_{20}=2\tau _{n}{\overline{K}}[\beta h_1(\overline{h_1^*}-1)+\beta _1 h_2(\overline{h_2^*}-1)], \end{aligned}$$

(98)

$$\begin{aligned}&g_{02}=2\tau _{n}{\overline{K}}[\beta \overline{h_1}(\overline{h_1^*}-1)+\beta _1 \overline{h_2}(\overline{h_2^*}-1)], \end{aligned}$$

(99)

$$\begin{aligned}&g_{11}=\tau _{n}{\overline{K}}[\beta (h_1+\overline{h_1})(\overline{h_1^*}-1)+\beta _1 (h_2+\overline{h_2})(\overline{h_2^*}-1)], \end{aligned}$$

(100)

$$\begin{aligned} g_{21}= & {} 2\tau _{n}{\overline{K}}\left[ \beta (\overline{h_1^*}-1)\left( \frac{h_1W_{20}^{1}(0)}{2}+h_1W_{11}^{1}(0) \right. \right. \nonumber \\&\quad \left. \left. +W_{11}^{2}(0)+\frac{W_{20}^{2}(0)}{2}\right) \right. \nonumber \\&\quad \left. +\beta _1(\overline{h_2^*}-1)\left( \frac{\overline{h_2}W_{20}^{1}(0)}{2}+h_2W_{11}^{1}(0)+W_{11}^{3}(0)+\frac{W_{20}^{3}(0)}{2}\right) \right] , \end{aligned}$$

(101)

where

$$\begin{aligned}&W_{20}(\xi )=\dfrac{ig_{20}}{\omega \tau _{n}}h(0)e^{i\omega _0\tau _{n}\xi }+\dfrac{i\overline{g_{20}}}{3\omega _0\tau _n}\overline{h(0)}e^{-i\omega _0\tau _{n}\xi }+E_1e^{2i\omega _0\tau _{n}\xi }, \end{aligned}$$

(102)

$$\begin{aligned}&W_{11}(\xi )=-\dfrac{ig_{11}}{\omega _0\tau _{n}}h(0)e^{i\omega _0\tau _{n}\xi }+\dfrac{i\overline{g_{11}}}{\omega _0\tau _n}\overline{h(0)}e^{-i\omega _0\tau _{n}\xi }+E_2, \end{aligned}$$

(103)

$$\begin{aligned}&M_2=\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&\beta _1S^*&-\delta&-\sigma \\ -\beta E^*&-A_{22}+2\omega _0 i&0&0&0\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&0&0\\ 0&-\gamma _1&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(104)

$$\begin{aligned}&E_{1}^{(1)}=\dfrac{1}{M_2}\begin{vmatrix} -\beta h_1-\beta _1h_2&\beta S^*&-\delta&-\sigma \\ \beta h_1&-A_{22}+2\omega _0 i&0&0&0\\ \beta _1 h_2&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&0&0\\ 0&-\gamma _1&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(105)

$$\begin{aligned}&E_{1}^{(2)}=\dfrac{1}{M_2}\begin{vmatrix} A_{11}+2\omega _0 i&-\beta h_1-\beta _1h_2&\beta _1S^*&-\delta&-\sigma \\ -\beta E^*&\beta h_1&0&0&0\\ -\beta _1 I^*&\beta _1 h_2&-A_{33}+2\omega _0i&0&0\\ 0&0&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(106)

$$\begin{aligned}&E_{1}^{(3)}=\dfrac{1}{M_2}\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&-\beta h_1-\beta _1h_2&-\delta&-\sigma \\ -\beta E^*&-A_{22}+2\omega _0 i&\beta h_1&0&0\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&\beta _1 h_2&0&0\\ 0&-\gamma _1&0&A_{44}+2\omega _0i&0\\ 0&0&0&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(107)

$$\begin{aligned}&E_{1}^{(4)}=\dfrac{1}{M_2}\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&\beta _1 S^*&-\beta h_1-\beta _1h_2&-\sigma \\ -\beta E^*&-A_{22}+2\omega _0 i&0&\beta h_1&0\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&\beta _1 h_2&0\\ 0&-\gamma _1&-\gamma _2&0&0\\ 0&0&-\theta&0&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(108)

$$\begin{aligned}&E_{1}^{(5)}=\dfrac{1}{M_2}\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&\beta _1 S^*&-\delta&-\beta h_1-\beta _1h_2\\ -\beta E^*&-A_{22}+2\omega _0 i&0&0&\beta h_1\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&0&\beta _1 h_2\\ 0&-\gamma _1&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&0 \end{vmatrix}, \end{aligned}$$

(109)

$$\begin{aligned}&M_4=\begin{vmatrix} A_{11}&\beta S^*&\beta _1S^*&-\delta&-\sigma \\ -\beta E^*&-A_{22}&0&0&0\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}&0&0\\ 0&-\gamma _1&-\gamma _2&A_{44}&0\\ 0&0&-\theta&-\pi&-A_{55} \end{vmatrix}, \end{aligned}$$

(110)

$$\begin{aligned}&E_{2}^{(1)}=\dfrac{2}{M_4}\begin{vmatrix} -{\text {Re}}(\beta h_1-\beta _1h_2)&\beta S^*&-\delta&-\sigma \\ -{\text {Re}}(\beta h_1)&-A_{22}+2\omega _0 i&0&0&0\\ -{\text {Re}}(\beta _1 h_2)&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&0&0\\ 0&-\gamma _1&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(111)

$$\begin{aligned}&E_{2}^{(2)}=\dfrac{2}{M_4}\begin{vmatrix} A_{11}+2\omega _0 i&-{\text {Re}}(-\beta h_1-\beta _1h_2)&\beta _1S^*&-\delta&-\sigma \\ -\beta E^*&-{\text {Re}}(\beta h_1)&0&0&0\\ -\beta _1 I^*&-{\text {Re}}(\beta _1 h_2)&-A_{33}+2\omega _0i&0&0\\ 0&0&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(112)

$$\begin{aligned}&E_{2}^{(3)}=\dfrac{2}{M_4}\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&-{\text {Re}}(-\beta h_1-\beta _1h_2)&-\delta&-\sigma \\ -\beta E^*&-A_{22}+2\omega _0 i&-{\text {Re}}(\beta h_1)&0&0\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-{\text {Re}}(\beta _1 h_2)&0&0\\ 0&-\gamma _1&0&A_{44}+2\omega _0i&0\\ 0&0&0&-\pi&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(113)

$$\begin{aligned}&E_{2}^{(4)}=\dfrac{2}{M_4}\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&\beta _1 S^*&-{\text {Re}}(-\beta h_1-\beta _1h_2)&-\sigma \\ -\beta E^*&-A_{22}+2\omega _0 i&0&-{\text {Re}}(\beta h_1)&0\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&-{\text {Re}}(\beta _1 h_2)&0\\ 0&-\gamma _1&-\gamma _2&0&0\\ 0&0&-\theta&0&-A_{55}+2\omega _0i \end{vmatrix}, \end{aligned}$$

(114)

$$\begin{aligned}&E_{2}^{(5)}=\dfrac{2}{M_4}\begin{vmatrix} A_{11}+2\omega _0 i&\beta S^*&\beta _1 S^*&-\delta&-{\text {Re}}(-\beta h_1-\beta _1h_2)\\ -\beta E^*&-A_{22}+2\omega _0 i&0&0&-{\text {Re}}(\beta h_1)\\ -\beta _1 I^*&-\eta e^{2\omega _0\tau _{n}i}&-A_{33}+2\omega _0i&0&-{\text {Re}}(\beta _1 h_2)\\ 0&-\gamma _1&-\gamma _2&A_{44}+2\omega _0i&0\\ 0&0&-\theta&-\pi&0 \end{vmatrix}. \end{aligned}$$

(115)

Now, we can calculate following quantities to investigate the direction, stability and period of bifurcating periodic solutions at critical value of delay:

$$\begin{aligned} C_1(0)= & {} \dfrac{i}{2\omega _0\tau _{n}}\left( g_{20}g_{11}-2|g_{11}|^2-\dfrac{|g_{02}|^2}{3}\right) + \dfrac{g_{21}}{2}, \end{aligned}$$

(116)

$$\begin{aligned} \mu _2= & {} -\dfrac{{\text {Re}}(C_1(0))}{{\text {Re}}\left( \dfrac{{\text {d}}\uplambda (\tau _{n})}{{\text {d}}\tau }\right) }, \end{aligned}$$

(117)

$$\begin{aligned} \beta _2= & {} 2{\text {Re}}(C_1(0)), \end{aligned}$$

(118)

and

$$\begin{aligned} T_2=\dfrac{-{\text {Im}}(C_1(0))+\mu _2{\text {Im}}\left( \dfrac{{\text {d}}\uplambda (\tau _{n})}{{\text {d}}\tau }\right) }{\omega _0\tau _{n}}. \end{aligned}$$

(119)

From classical bifurcation theorem (Hassard et al. (1981)), we deduce that bifurcation periods exist for $\tau >\tau _{n}(\tau <\tau _{n})$ and Hopf bifurcation is supercritical (subcritical) if sign of $\mu _2$ is positive (negative) and if $\beta _2<0$ ($\beta _2>0$), then these bifurcating periodic solutions are stable (unstable). Further, their period increases (decreases) if $T_2>0\,(T_2<0)$.

Simulation

In this section, we justify the analytical findings by a set of parameters as given below (Table 1):

Table 1 Parameter values for simulation

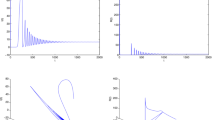
With the above set of parameters, we observe that conditions of local and global asymptotic stability are satisfied. In addition, value of basic reproductions number due to exposed population was found to be 1.8418 and that due to infected population was observed to be 1.002. Further, we draw the graphs between various population with time for different parameter values. Figure 2 confirms the local asymptotic stability of the system and displays variation of each population with time. Figure 2 displays variation of infected population with time for different rate of transmission of infection from exposed population, $\beta$. Figure 3 shows variation of infected population size for different transmission rate of coefficient of infection from infected population, $\beta _1$. Figure 4 displays variation of infected population with time for different rate of loss of immunity after infection, $\delta$. Figure 5 displays variation of infected population with time for different rate of quarantining exposed and infected population, $\gamma _1$ and $\gamma _2$. This graph also displays that when we are failed to quarantine asymptomatic exposed population, infected population rises even though infected population are quarantined. Further, as $\gamma _1$ and $\gamma _2$ rise, infected population decrease.

Moreover, we computed the model for delay term $\tau$ and observed that infected population start showing prominent oscillation in the equilibrium value after $\tau =14$. Figure 5 shows oscillations in the equilibrium value of infected population for $\tau = 14$. In Fig. 6, we observe that as value of $\tau$ increases, oscillations become more prominent and also it is found that as $\tau$ increase, infected population decrease.

Discussion

Numerical simulation is done for some hypothetical parameter values to determine the behaviour of exposed and infected population with time for different values of parameters. It is observed that behaviour of population with parameters is consistent with the model formulated. Graphs for infected and exposed population with time for different values of rate of transmission of infection show that as transmission rate increases, both the population rise as formulated by our model. Further, it is observed that as $\delta$ increases, infected population also rises. This implies that more and more population will become infected if reinfection occurs rapidly after recovery from the disease. Significance of quarantining the exposed and infected population is depicted through the graphs. It is observed that quarantining the population reduce the exposed and infected population as depicted by the model. Moreover, simulation confirms that quarantining the population in exposed stage will play a major role in controlling the spread of infection. We have two different forms of basic reproduction number, one due to exposed population and the other due to infected population. It is observed that basic reproduction number due to exposed population in asymptomatic stage is greater than that due to infected population in the symptomatic stage. This supports the fact that number of secondary infections of COVID-19 are contributed more by the exposed population. Time delay in conversion of population from exposed stage to infected stage is studied through numerical simulation. Prominent oscillation in the infected population is observed if delay is 14 days or more. This may be interpreted by stating that as time delay increases although people recover but at the mean time oscillations signify that number of active cases due to exposed or asymptomatic population are more as compared to the infected population; therefore, number of secondary infections are significant as represented by oscillations in the graph (Figs. 7, 8).

Conclusion

We present a mathematical model on COVID-19 with the assumption that infection spread among the population by both asymptomatic(exposed) class and symptomatic (infected) class. We further assume that there is time delay in entering in to the symptomatic stage from the asymptomatic stage. We have studied the model by performing equilibrium analysis and numerical simulation. Numerical simulation results are found to be consistent with the model formulated. Basic reproduction number is computed by next-generation matrix approach. It is observed that basic reproduction number is contributed by both the exposed and infected classes. In addition, local and global stability analysis of the disease free equilibrium point is determined. It is observed that system is globally asymptotically stable if basic reproduction number due exposed class and infected class are less than unity. Furthermore, local stability of endemic equilibrium point is studied with and without delay. Conditions of existence and direction of Hopf bifurcation are determined. Critical value of delay is determined analytically at which stability switch occurs. Moreover to justify the analytical findings and to depict the behaviour of exposed and infected population with variation in different parameters, we have performed numerical simulation with a set of hypothetical parameter values. Numerical study reveals that number of secondary infections caused by asymptomatic population are higher as compared to symptomatic or infected population. It also displays that quarantining of asymptomatic class must be done on priority basis as quarantining asymptomatic population decreases the infected population at higher rate as compared to only quarantining infected or symptomatic class. Further, it is observed that time delay plays a significant role in determining the infected population size. If time delay increases, i.e. if a person remains in asymptomatic stage for a longer time, recovery takes place instead of going to infected stage if immunity of the person is strong enough that is why infected population size reduces with the increase in delay. However, oscillation observed in the infected population size indicates that in the asymptomatic stage population produce more infected population along with increase in recovered population, thereby causing oscillations in the number of infected population with time.

Fig. 2

Variation of all population with time

Fig. 3

Variation of infected population with time for different $\beta$

Fig. 4

Variation of infected population with time for different $\beta _1$

Fig. 5

Variation of infected population with time for different values of $\delta$

Fig. 6

Variation of infected population with time for different $\gamma _1$ and $\gamma _2$

Fig. 7

Variation of infected populations with time for $\tau = 14$

Fig. 8

Variation of infected population with time for different values of $\tau$