Introduction

Robot can walk in a variety of ways. Up to now, the movement forms can be roughly divided into wheeled [1], tracked [2], wheel-foot compound [3], snake-like [4] and bionic leg [5], etc. Compared with other types of robots, bionic legged robot adopts the similar structure with the creatures which have legs, so, it has the characteristics of discontinuous support. Especially when combined with hydraulic drive which has a high power to weight ratio, it not only adapts well to unknown, unstructured environments, but also can pass through the barrier. Therefore, this type of robot is particularly suitable to use in the complex environment in the field [6].

In order to improve the adaptability of legged robot to complex environment, the foot end is generally designed as semi-cylindrical structure [7, 8]. However, in the process of robot walking, the semi-cylindrical foot end will lead to the real-time change of the contact point between the foot end and ground, which will lead to a certain deviation in the kinematics based on D-H coordinate transformation and the statics based on virtual work principle. This will cause the robot to produce the wrong posture and the wrong calculated force, thus affecting the movement control of the whole robot.

Regarding the phenomenon that the robot has wrong posture in the process of movement, Guardabrazo et al. [9] quantitatively analyzed the influence of the hemispherical foot end on the hip joint trajectory of Silo6 walking robot, aiming at the problem of hip joint trajectory deviation. Meanwhile, the kinematics was modified by adding nonlinear equations, and the validity of the proposed method was verified by using a two-dimensional insect-like leg test platform. Based on the inverse velocity kinematics of the legged robot, Chen Gang [10] divided the position-posture closed-loop control into position closed-loop control and posture closed-loop control to realize the precise position-posture control of the robot. Through co-simulation, the validity of using the closed-loop control method based on position-posture to solve the position-posture deviation problem was verified. Chen Weihai et al. [11] proposed a method to correct the trajectory of robot foot end through force feedback information, and verified the validity of this method by testing hexapod robots. Zhu Yaguang et al. [12] proposed a semi-cylindrical foot end trajectory correction algorithm based on LS-SVM, and verified the validity of the method on a hexapod robot prototype. To solve the problem of robot motion parameter deviation, Lin Peng et al. [13] firstly established the kinematics model of the mobile robot, and then estimated the motion parameters by using the multiple linear regression mathematical model based on least squares. Finally, the validity of the proposed method was verified by the omnidirectional robot. Li **g et al. [14] proposed a numerical method for solving the inverse kinematics of a six degree of freedoms (6-DOF) robot with a non-spherical wrist. By compensating the end position deviation between the actual robot end posture and the target posture calculated by the simplified inverse kinematics solution, the inverse solution of the simplified robot gradually approached the expected solution. Finally, the validity of the proposed algorithm was verified by a robot prototype.

Regarding the phenomenon that the robot has the wrong calculated force in the process of movement, Hawley Louis et al. [15] proposed an external force observer construction method based on Kalman filtering equation by using the force sensing resistance (FSR) under the foot of humanoid robot and the robot inertial measurement unit (IMU), which could keep the deviation range of external force estimation within a reasonable range. Kresimir Turkovic et al. [16] proposed an end-force estimation method based on the manipulator dynamics model, Jacobian matrix and joint torques, which assumed that there was a connection between the forces acting on the end-effector and the torques of the manipulator joints. The validity of the method was verified by the manipulator arm experiments on the aircraft. Li Dongyi et al. [17] proposed a calculation method of equivalent Jacobian inverse matrix, aiming at the phenomenon that the traditional virtual work principle in 3-RPS parallel robot could not solve the driving force because the Jacobian matrix was not full rank matrix, and the validity of the method was verified by simulation model.

In the above control algorithm of robot body posture deviation compensation and foot end force deviation compensation, although the adjustment of robot body posture and foot end force deviation is realized, most of the algorithms are too complex and do not take into account the situation that body and contact surface are at different angles. However, the situation that body and contact surface are at different angles always occurs in the actual movement process of the robot.

Based on the above situation, this paper mainly carries out the following research work:

The kinematics and statics correction algorithm proposed in this paper is based on the control algorithm as shown in Fig. 1. As can be seen from Fig. 1, the implementation of the control algorithm requires the following two steps:

Fig. 1
figure 1

Control algorithm

Full size image

Step 1 is environmental parameters identification algorithm for the whole leg. This step is mainly used to solve the equivalent angle \(\vartheta\) between the robot body and the contact surface.

Step 2 is kinematics and statics correction algorithm. This step is the core research content of this paper and the main contribution of this paper. As long as the equivalent angle \(\vartheta\) between the robot body and the contact surface can be accurately identified, the control algorithm proposed in this paper can effectively reduce the calculation deviation of kinematics and statics, thus improve the motion control precision of the whole robot.

Regarding Step 1, environmental parameter identification has been extensively studied in the field of robot control, and relevant algorithms have been relatively mature. For example, methods such as foot end six-dimensional force sensor, robot body IMU [18], machine vision [19] and lidar [20] can be used for environmental identification. The identification of complex environment, such as beach, jungle, snow and grass, is also the difficulty and hotspot of current research.

Regarding Step 2, the control algorithm shown in Fig. 1 is to set the equivalent angle \(\vartheta\) identified in Step 1 as the input quantity, and on this basis, to correct the kinematics and statics algorithms, effectively making up for the fact that the existing research correction algorithms in this field seldom take into account the different angles (take \(\vartheta\) as different equivalent values) between the robot body and the ground.

Based on the above ideas, the organizations of the paper are organized as follows:

“Sampling system” describes the sampling system in this paper, namely the composition of the 3-DOF leg hydraulic drive system (LHDS). In “Mathematical modeling of kinematics and statics of LHDS”, the kinematics of leg based on D-H coordinate transformation and the statics calculation method based on virtual work principle are derived. “Deviation analysis of kinematics and statics” analyzes the reasons for the calculation deviation caused by the rolling effect of the semi-cylindrical foot end, and calculates the kinematics and statics deviation respectively under common working conditions. In “Kinematics and statics correction algorithm”, the semi-cylindrical foot end is treated as a rod perpendicular to the ground, and a kinematics correction algorithm based on virtual DOF is proposed. The actual contact point between the foot end and the ground is translated to the ideal modeling point, and a statics correction method based on the translation theorem of forces is proposed. The statics correction algorithm is the main contribution of this paper, and kinematics correction algorithm is the supplement of sampling system 2 in Ref. [21]. In addition, these two algorithms are general and can be extended to different leg structure with similar foot end. In “Experiment”, the validity of the proposed kinematics and statics correction algorithms are verified experimentally by using the LHDS performance test platform under different working conditions.

Sampling system

The study content of this paper is a sampling system based on 3-DOF LHDS, and its real model and three-dimensional model are shown in Fig. 2.

Fig. 2
figure 2

3-DOF LHDS of legged robot

Full size image

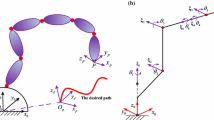
LHDS is mainly composed of the following five parts: Base (For connecting leg with aluminum alloy guide rail), hip joint, knee joint, ankle joint, and three sets of hydraulic drive unit (HDU). The LHDS can move up and down along aluminum alloy support through guide rail.

As can be seen from Fig. 2b, LHDS contains a total of 3-DOF, which are represented by O, E and G successively. A and B are the connecting positions of the HDU in the hip joint. C and D are the connecting positions of the HDU in the knee joint. F and H are the connecting positions of the HDU in the ankle joint, and I is the mid-point of the semi-cylindrical foot end.

The HDU of the leg is a highly integrated valve-controlled cylinder independently designed and developed by the authors’ team, as shown in Fig. 3. It is mainly composed of valve block, servo cylinder, servo valve, position sensor and one-dimensional force sensor. The one-dimensional force sensor is installed on the end of the piston rod of the servo cylinder, and the position sensor is installed on the side of the servo cylinder, which is used for the force closed-loop control and position closed-loop control of the HDU. Servo valve and valve block are installed on the upper part of the servo cylinder. The valve-controlled cylinder has the advantages of compact structure and large power-to-weight ratio, which reduces the connection pipeline between the servo valve and the servo cylinder. Besides, it can effectively reduce the probability of leakage and pipe joint damage and improve its dynamic performance.

Fig. 3
figure 3

Real model of HDU

Full size image

Mathematical modeling of kinematics and statics of LHDS

Kinematics modeling

The forward kinematics solution is to use the known angles of each joint to solve the position of the foot end relative to the hip joint. D–H coordinate transformation is a commonly used kinematics modeling method of robot. During the D–H transformation, the length of each rod should be determined. However, due to the special structure of the semi-cylindrical foot end, the length of the foot is uncertain; therefore, the line between the mid-point I of the semi-cylindrical foot end and the ankle joint G is selected as the length of the foot in this paper. Considering the complexity of the mechanical structure of the leg and for the convenience of modeling and analysis, the three-dimensional LHDS diagram in Fig. 2 is simplified to Fig. 4 in this paper.

Fig. 4
figure 4

Diagram of leg kinematics model

Full size image

In Fig. 4, O is the origin of the coordinates of the hip joint, \(x_{0}\) is the positive direction of the horizontal axis, and \(y_{0}\) is the positive direction of the vertical axis, \(l_{1}\) is the OE length of thigh, \(l_{2}\) is the EG length of shank, and \(l_{3}\) is the GI length of foot Specify the direction of joint rotation counterclockwise to be positive. \(\theta_{1}\) is the included angle between thigh and the positive direction of \(x_{0}\) axis, which is set as the rotation angle of hip joint. \(\theta_{2}\) is the included angle between EG and OE extension line, which is set as the rotation angle of knee joint. \(\theta_{3}\) is the included angle between EG extension line and GI, which is set as the rotation angle of ankle joint. \(\alpha\) is the included angle between EG and ED, \(\beta\) is the included angle between OA and the positive direction of \(x_{0}\) axis. AB, CD, and FH are the total length of the hip, knee, and ankle joint HDUs, respectively.

The main structure dimension parameters of LHDS are shown in Table 1.

Table 1 Main structure dimension parameters of LHDS
Full size table

In Table 2, \(a_{i - 1}\) is the measured distance from \(z_{i - 1}\) to \(z_{i}\) (the zi axis is perpendicular to the \(x_{i}\) and \(y_{i}\) axis, the positive direction of the zi axis satisfies the Cartesian right-handed coordinate system) along \(x_{i - 1}\); \(\alpha_{i - 1}\) is the rotation angle from \(z_{i - 1}\) to \(z_{i}\) around \(x_{i - 1}\); \(d_{i}\) is the measured distance from \(x_{i - 1}\) to \(x_{i}\) along \(z_{i}\); \(\theta_{i}\) is the rotation angle from \(x_{i - 1}\) to \(x_{i}\) around \(z_{i}\).

Table 2 D–H parameters of LHDS mechanical structure
Full size table

In the D–H coordinate system as shown in Fig. 4, the relative position relation can be expressed by the general transformation equation \({}_{i}^{i - 1} T\) of connecting rod.

$$ {}_{i}^{i - 1} T = \left[ {\begin{array}{*{20}c} {\cos \theta_{i} } &\quad { - \sin \theta_{i} } & \quad0 & \quad{a_{i - 1} } \\ {\sin \theta_{i} \cos \alpha_{i - 1} } & \quad{\cos \theta_{i} \cos \alpha_{i - 1} } & \quad{ - \sin \alpha_{i - 1} } & \quad{ - d_{i} \sin \alpha_{i - 1} } \\ {\sin \theta_{i} \sin \alpha_{i - 1} } & \quad{\cos \theta_{i} \sin \alpha_{i - 1} } & \quad{\cos \alpha_{i - 1} } & \quad{d_{i} \cos \alpha_{i - 1} } \\ 0 & \quad0 & \quad0 & \quad1 \\ \end{array} } \right]. $$
(1)

By substituting the parameters in Table 2 into Eq. (1), the transformation matrix between adjacent connecting rods can be obtained as follows:

$$ {}_{1}^{0} T = \left[ {\begin{array}{*{20}c} {\cos \theta_{1} } & \quad{ - \sin \theta_{1} } & \quad0 & \quad0 \\ {\sin \theta_{1} } & \quad{\cos \theta_{1} } & \quad0 & \quad0 \\ 0 & \quad0 & \quad1 & \quad0 \\ 0 & \quad0 & \quad0 & \quad1 \\ \end{array} } \right], $$
(2)
$$ {}_{2}^{1} T = \left[ {\begin{array}{*{20}c} {\cos \theta_{2} } & \quad{ - \sin \theta_{2} } & \quad0 & \quad{l_{1} } \\ {\sin \theta_{2} } & \quad{\cos \theta_{2} } & \quad0 & \quad0 \\ 0 & \quad0 & \quad1 & \quad0 \\ 0 & \quad0 & \quad0 & \quad1 \\ \end{array} } \right], $$
(3)
$$ {}_{3}{^{2}} T = \left[ {\begin{array}{*{20}c} {\cos \theta_{3} } & \quad{ - \sin \theta_{3} } & \quad0 & \quad{l_{2} } \\ {\sin \theta_{3} } & \quad{\cos \theta_{3} } & \quad0 & \quad0 \\ 0 & \quad0 & \quad1 & \quad0 \\ 0 & \quad0 & \quad0 & \quad1 \\ \end{array} } \right], $$
(4)
$$ {}_{4}^{3} T = \left[ {\begin{array}{*{20}c} {\cos \theta_{4} } & \quad{ - \sin \theta_{4} } & \quad0 & \quad{l_{3} } \\ {\sin \theta_{4} } & \quad{\cos \theta_{4} } & \quad0 & \quad0 \\ 0 & \quad0 & \quad1 & \quad0 \\ 0 & \quad0 & \quad0 & \quad1 \\ \end{array} } \right]. $$
(5)

By multiplying Eqs. (2), (3), (4), and (5) in turn, \({}_{4}^{0} T\) can be obtained as follows:

$$ {}_{4}^{0} T{ = }\left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{1} + \theta_{2} + \theta_{3} + \theta_{4} } \right)} & \quad{ - \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} + \theta_{4} } \right)} &\quad 0 &\quad \begin{gathered} l_{1} \cos \theta_{1} + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \\ {\sin \left( {\theta_{1} + \theta_{2} + \theta_{3} + \theta_{4} } \right)} &\quad {\cos \left( {\theta_{1} + \theta_{2} + \theta_{3} + \theta_{4} } \right)} &\quad 0 & \begin{gathered} l_{1} \sin \theta_{1} + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]. $$
(6)

Then the relative position relationship between the foot end position I \(\left( {X_{{{\text{foot}}}}^{X} ,X_{{{\text{foot}}}}^{Y} } \right)\) and the hip joint O can be obtained from Eq. (6), so the forward kinematics solution is obtained as follows:

$$ \left\{ {\begin{array}{*{20}c} {X_{{{\text{foot}}}}^{X} = l_{1} \cos \theta_{1} + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \\ {X_{{{\text{foot}}}}^{Y} = l_{1} \sin \theta_{1} + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \\ \end{array} } \right.. $$
(7)

The inverse kinematics solution is to find the angle of each joint by the position of the foot end relative to the hip joint. Because LHDS is 3-DOF and has a redundant DOF, if only the position of the foot end to the hip joint is given, it will become an indefinite solution problem because use two equations solve for three unknown numbers when analyzing the inverse kinematics. Therefore, a constraint should be added to the inverse kinematics solution of this kind of 3-DOF leg structure. There are many forms of such constraints; the constraint used in this paper is when LHDS at stance phase, making the hip joint O, ankle joint G, and foot end I collinear, as shown in Fig. 5. The above method can effectively solve the problem of indeterminate solution in inverse kinematics analysis.

Fig. 5
figure 5

Diagram of leg inverse kinematics model

Full size image

In Fig. 5, the included angle θ0 between the line where OGI is located and the positive direction of x0 axis is as follows:

$$ \theta_{0} = \arctan 2(X_{{{\text{foot}}}}^{Y} ,X_{{{\text{foot}}}}^{X} ). $$
(8)

In \(\Delta OEG\), \(\angle EOG\) is:

$$ \begin{aligned} & \angle EOG = \arccos \left( {\frac{{OE{^{2}} + OG{^{2}} - EG{^{2}} }}{2 \cdot OE \cdot OG}} \right)\\ &\quad = \arccos \left( {\frac{{OE{^{2}} + \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right){^{2}} - EG{^{2}} }}{{2 \cdot OE \cdot \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right)}}} \right). \hfill \\ \end{aligned} $$
(9)

According to Fig. 5, the rotation angle of hip joint θ1 is as follows:

$$ \begin{aligned} \theta_{1} & = \theta_{0} + \angle EOG = \arctan 2(X_{{{\text{foot}}}}^{Y} ,X_{{{\text{foot}}}}^{X} ) \\ & \quad + \arccos \left( {\frac{{OE{^{2}} + \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right){^{2}} - EG{^{2}} }}{{2 \cdot OE \cdot \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right)}}} \right)\end{aligned} $$
(10)

In \(\Delta OEG\), \(\angle OEG\) is as follows:

$$ \begin{aligned} & \angle OEG = \arccos \left( {\frac{{OE{^{2}} + EG{^{2}} - OG{^{2}} }}{2 \cdot OE \cdot EG}} \right) \\ &\quad = \arccos \left( {\frac{{OE{^{2}} + EG{^{2}} - \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right){^{2}} }}{2 \cdot OE \cdot EG}} \right). \hfill \\ \end{aligned} $$
(11)

According to Fig. 5, the rotation angle of knee joint θ2 is as follows:

$$ \begin{gathered} \theta_{2} = \angle OEG - \pi \hfill \\ = \arccos \left( {\frac{{OE{^{2}} + EG{^{2}} \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right){^{2}} }}{2 \cdot OE \cdot EG}} \right) - \pi \hfill \\ \end{gathered} $$
(12)

In \(\Delta OEG\), \(\angle OEG\) is as follows:

$$ \begin{gathered} \angle OGE = \arccos \left( {\frac{{OG{^{2}} + EG{^{2}} - OE{^{2}} }}{2 \cdot OG \cdot EG}} \right) \hfill \\ = \arccos \left( {\frac{{\left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right){^{2}} + EG{^{2}} - OE{^{2}} }}{{2 \cdot \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right) \cdot EG}}} \right). \hfill \\ \end{gathered} $$
(13)

According to Fig. 5, the rotation of angle ankle joint θ3 is as follows:

$$ \begin{gathered} \theta_{3} = \angle OGE \hfill \\ = \arccos \left( {\frac{{\left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right){^{2}} + EG{^{2}} - OE{^{2}} }}{{2 \cdot \left( {\sqrt {X_{{{\text{foot}}}}^{Y}{^{2}} + X_{{{\text{foot}}}}^{X}{^{2}} } - GI} \right) \cdot EG}}} \right). \hfill \\ \end{gathered} $$
(14)

During LHDS actual motion control, the variable that can be directly controlled are the elongation of the hip, knee, and ankle joint HDUs. It is necessary to obtain the relation between angle of each joint and elongation of HDU. The triangular relationship of each joint is shown in Fig. 6.

Fig. 6
figure 6

Relation diagram between each joint angle and each elongation of HDU

Full size image

The total elongation of the hip joint HDU AB, the knee joint HDU CD, and the ankle joint HDU FH respectively is as follows:

$$ \begin{gathered} AB = l_{01} + \Delta x_{p1} \hfill \\ CD = l_{02} + \Delta x_{p2} \hfill \\ FH = l_{03} + \Delta x_{p3} , \hfill \\ \end{gathered} $$
(15)

where \(l_{01}\) is the initial length of the hip joint HDU, \(l_{02}\) is the initial length of the knee joint HDU, and \(l_{03}\) is the initial length of the ankle joint HDU.

In \(\Delta AOB\) of Fig. 6a, \(\angle AOB\) can be obtained by the law of cosines as follows:

$$ \angle AOB = \arccos \left( {\frac{{OA{^{2}} + OB{^{2}} - AB{^{2}} }}{2 \cdot OA \cdot OB}} \right). $$
(16)

According to the geometric relation in Fig. 6a, the rotation angle θ1 of hip joint can be obtained as follows:

$$ \begin{aligned} \theta_{1} &= \beta - \angle AOB - \angle BOE \hfill \\ & = \beta - \arccos \left( {\frac{{OA{^{2}} + OB{^{2}} - \left( {l_{01} + \Delta x_{p1} } \right){^{2}} }}{2 \cdot OA \cdot OB}} \right) - \angle BOE \hfill \\ \end{aligned} $$
(17)

According to the above equation, the extension length \(\Delta x_{p1}\) of the hip joint is as follows:

$$ \Delta x_{p1} = \sqrt {OA{^{2}} + OB{^{2}} - 2 \cdot OA \cdot OB \cdot \cos (\beta - \angle BOE - \theta_{1} )} - l_{01} . $$
(18)

In \(\Delta CDE\) of Fig. 6b, \(\angle CED\) can be obtained by the law of cosines as follows:

$$ \angle CED = \arccos \left( {\frac{{EC{^{2}} + ED{^{2}} - CD{^{2}} }}{2 \cdot EC \cdot ED}} \right). $$
(19)

According to the geometric relation in Fig. 6b, the rotation angle θ2 of knee joint can be obtained as follows:

$$ \begin{aligned} \theta_{2} &= \angle CED - \pi - \alpha + \angle OEC \hfill \\ &= \arccos \left( {\frac{{EC{^{2}} + ED{^{2}} - \left( {l_{02} + \Delta x_{p2} } \right){^{2}} }}{2 \cdot EC \cdot ED}} \right) - \pi - \alpha + \angle OEC \hfill \\ \end{aligned} $$
(20)

According to the above equation, the extension length \(\Delta x_{p2}\) of the knee joint is as follows:

$$ \Delta x_{p2} = \sqrt {EC{^{2}} + ED{^{2}} - 2 \cdot EC \cdot ED \cdot \cos (\angle OEC - \theta_{2} - \pi - \alpha )} - l_{02} . $$
(21)

In \(\Delta FGH\) of Fig. 6c, \(\angle FGH\) can be obtained by the law of cosines as follows:

$$ \angle FGH = \arccos \left( {\frac{{GF{^{2}} + GH{^{2}} - FH{^{2}} }}{2 \cdot GF \cdot GH}} \right) $$
(23)

According to the geometric relation in Fig. 6c, the rotation angle θ3 of ankle joint can be obtained as follows:

$$ \begin{aligned} \theta_{3} &= \pi - \angle FGH - \angle IGH - \angle EGF \hfill \\ &= \pi - \arccos \left( {\frac{{GF{^{2}} + GH{^{2}} - (l_{03} + \Delta x_{p3} ){^{2}} }}{2 \cdot GF \cdot GH}} \right) \!-\! \angle IGH \!-\! \angle EGF. \hfill \\ \end{aligned} $$
(23)

According to the above equation, the extension length \(\Delta x_{p3}\) of the ankle joint is as follows:

$$ \Delta x_{p3} = \sqrt {GF{^{2}} + GH{^{2}} - 2 \cdot GF \cdot GH \cdot \cos (\theta_{3} - \pi + \angle IGH + \angle EGF)} - l_{03} . $$
(24)

Statics modeling

The inverse statics solution is to use the known foot end contact force to solve out the torque of each joint. The statics model diagram of LHDS is shown in Fig. 7, and the forces of the hip, knee, and ankle joint HDUs are, respectively, denoted as \(\Delta F_{s1}\), \(\Delta F_{{s{2}}}\) and \(\Delta F_{s3}\).

Fig. 7
figure 7

Diagram of leg statics model

Full size image

According to the virtual work principle, the forward statics solution can be obtained as follows:

$$ {\varvec{\tau}} = J^{\text{T}} \left( {\varvec{q}} \right){\varvec{F}}, $$
(25)

where \({\varvec{F}}\) is contact force applied to the foot end, \(J^{\text{T}} \left( {\varvec{q}} \right)\) is force Jacobi of leg, \({\varvec{\tau}}\) is torques applied to the hip, knee, and ankle joints.

In Eq. (25), the joint force vector \({\varvec{\tau}}\) is as follows:

$$ \user2{\tau = }\left[ {\tau_{1} ,\tau_{2} ,\tau_{3} } \right]^{\text{T}} $$
(26)

In Eq. (25), the contact force \({\varvec{F}}\) on the foot end is as follows:

$$ \user2{F = }\left[ {F_{{{\text{foot}}}}^{x} ,F_{{{\text{foot}}}}^{y} } \right]^{\text{T}} $$
(27)

In Eq. (25), the force Jacobi \(J^{\text{T}} \left( {\varvec{q}} \right)\) of the leg is as follows:

$$ \begin{gathered} J^{\text{T}} \left( {\varvec{q}} \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial X_{{{\text{foot}}}}^{X} }}{{\partial \theta_{1} }}}\quad {\frac{{\partial X_{{{\text{foot}}}}^{Y} }}{{\partial \theta_{1} }}} \\ {\frac{{\partial X_{{{\text{foot}}}}^{X} }}{{\partial \theta_{2} }}}\quad {\frac{{\partial X_{{{\text{foot}}}}^{Y} }}{{\partial \theta_{2} }}} \\ {\frac{{\partial X_{{{\text{foot}}}}^{X} }}{{\partial \theta_{3} }}}\quad{\frac{{\partial X_{{{\text{foot}}}}^{Y} }}{{\partial \theta_{3} }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \begin{gathered} - l_{1} \sin \left( {\theta_{1} } \right) - l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) - \hfill \\ l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \begin{gathered} l_{1} \cos \left( {\theta_{1} } \right) + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \\ { - l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) - l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)}{l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \\ { - l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)}{l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \\ \end{array} } \right]. \hfill \\ \end{gathered} $$
(28)

Substituting Eqs. (26), (27), and (28) into Eq. (25), the following can be obtained:

$$ \left\{ \begin{gathered} \tau_{1} = - F_{{{\text{foot}}}}^{x} \left( \begin{gathered} l_{1} \sin \left( {\theta_{1} } \right) + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \right) \hfill \\ + F_{{{\text{foot}}}}^{y} \left( \begin{gathered} l_{1} \cos \left( {\theta_{1} } \right) + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \right) \hfill \\ \tau_{2} = - F_{{{\text{foot}}}}^{x} \left( {l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( \begin{gathered} \theta_{1} + \hfill \\ \theta_{2} + \theta_{3} \hfill \\ \end{gathered} \right)} \right) \hfill \\ + F_{{{\text{foot}}}}^{y} \left( {l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( \begin{gathered} \theta_{1} + \hfill \\ \theta_{2} + \theta_{3} \hfill \\ \end{gathered} \right)} \right) \hfill \\ \tau_{3} = - F_{{{\text{foot}}}}^{x} l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) + F_{{{\text{foot}}}}^{y} l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \right.. $$
(29)

The forward statics solution is to use the known torque of each joint to solve out the foot end contact force. According to Eq. (29), it is only needed to know the torque on any two joints to obtain the contact force on the foot end. In this paper, the contact force on the foot end can be obtained through the torque on the knee and ankle joints, and the forward statics solution can be obtained as follows:

$$ \left\{ \begin{gathered} F_{{{\text{foot}}}}^{x} = \frac{{\tau_{2} l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) - \tau_{3} \left( {l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \right)}}{{l_{2} l_{3} \sin \left( {\theta_{3} } \right)}} \hfill \\ F_{{{\text{foot}}}}^{y} = \frac{{\tau_{2} l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) - \tau_{3} \left( {l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right)} \right)}}{{l_{2} l_{3} \sin \left( {\theta_{3} } \right)}} \hfill \\ \end{gathered} \right.. $$
(30)

During LHDS actual motion control, the variables that can be directly collected are measured signals of hip, knee, and ankle joint HDUs’ one-dimensional force sensors. Therefore, it is necessary to clarify the relationship between each joint torque and the measured signal of each joint HDU one-dimensional force sensor. The relationship between torque of each joint and the force of each joint HDU is shown in Fig. 8.

Fig. 8
figure 8

Relationship between each joint torque and each joint HDU force

Full size image

In \(\Delta AOB\) of Fig. 8a, \(\angle ABO\) can be obtained by using the law of cosines and Eq. (15) as follows:

$$ \angle ABO = \arccos \left( {\frac{{(l_{01} + \Delta x_{p1} ){^{2}} + OB{^{2}} - OA{^{2}} }}{{2 \cdot (l_{01} + \Delta x_{p1} ) \cdot OB}}} \right). $$
(31)

According to Eq. (31), the map** relationship between the signal \(\Delta F_{s1}\) detected by the one-dimensional force sensor of the hip joint HDU and the torque \(\tau_{1}\) of the hip joint is as follows:

$$ \tau_{1} = \Delta F_{s1} \cdot OB \cdot \sin \left( {\arccos \left( {\frac{{(l_{01} + \Delta x_{p1} ){^{2}} + OB{^{2}} - OA{^{2}} }}{{2 \cdot (l_{01} + \Delta x_{p1} ) \cdot OB}}} \right)} \right). $$
(32)

In \(\Delta CDE\) of Fig. 8b, \(\angle DCE\) can be obtained by using the following law of cosines:

$$ \angle DCE = \arccos \left( {\frac{{(l_{02} + \Delta x_{p2} ){^{2}} + EC{^{2}} - ED{^{2}} }}{{2 \cdot (l_{02} + \Delta x_{p2} ) \cdot EC}}} \right). $$
(33)

According to Eq. (33), the map** relationship between the signal \(\Delta F_{s2}\) detected by the one-dimensional force sensor of the knee joint HDU and the torque \(\tau_{2}\) of the knee joint is as follows:

$$ \tau_{2} = \Delta F_{s2} \cdot EC \cdot \sin \left( {\arccos \left( {\frac{{(l_{03} + \Delta x_{p2} ){^{2}} + EC{^{2}} - ED{^{2}} }}{{2 \cdot (l_{02} + \Delta x_{p2} ) \cdot EC}}} \right)} \right). $$
(34)

In \(\Delta FGH\) of Fig. 8c, \(\angle GFH\) can be obtained by using the following law of cosines:

$$ \angle GFH = \arccos \left( {\frac{{(l_{03} + \Delta x_{p3} ){^{2}} + GF{^{2}} - GH{^{2}} }}{{2 \cdot (l_{03} + \Delta x_{p3} ) \cdot GF}}} \right). $$
(35)

According to Eq. (35), the map** relationship between the signal \(\Delta F_{s3}\) detected by the one-dimensional force sensor of the ankle joint HDU and the torque \(\tau_{3}\) of the ankle joint is as follows:

$$ \tau_{3} = \Delta F_{s3} \cdot GF \cdot \sin \left( {\arccos \left( {\frac{{(l_{03} + \Delta x_{p3} ){^{2}} + GF{^{2}} - GH{^{2}} }}{{2 \cdot (l_{03} + \Delta x_{p3} ) \cdot GF}}} \right)} \right). $$
(36)

Deviation analysis of kinematics and statics

Quantitative analysis of kinematics solving deviation

When the leg of the robot in stance phase, the phenomenon of hip joint deviation caused by the rolling of the semi-cylindrical foot end is shown in Fig. 9. The dotted line in Fig. 9 is the position of the leg when the foot end is regarded as the point, and the solid line is the position of the leg caused by the rolling of the semi-cylindrical foot end.

Fig. 9
figure 9

The hip joint deviation caused by the rolling of the semi-cylindrical foot end when the leg of the robot in stance phase

Full size image

In Fig. 9, the hip joint trajectory deviation \(\overrightarrow {{O^{\prime}O}} = \left( {\Delta x,\Delta y} \right)\) is as follows:

$$ \left\{ \begin{gathered} \Delta x = R\left( {\sin \varphi - \varphi } \right) \hfill \\ \Delta y = R\left( {1 - \cos \varphi } \right) \hfill \\ \end{gathered} \right.. $$
(37)

The included angle \(\gamma\) between \(\overrightarrow {{IO_{r} }}\) and \(\overrightarrow {IG}\), the rotation angle \(\theta_{1}\) of the hip joint, the rotation angle \(\theta_{2}\) of the knee joint, the rotation angle \(\theta_{3}\) of the ankle joint, included angle \(\varphi\) between \(\overrightarrow {{O_{r} P}}\) and \(\overrightarrow {{O_{r} I}}\), included angle \(\gamma\) between \(\overrightarrow {{IO_{r} }}\) and \(\overrightarrow {IG}\), and included angle \(\vartheta\) between the robot body and contact surface are parallel transported to the G of the ankle joint in this paper, as shown in Fig. 10.

Fig. 10
figure 10

The hip joint deviation caused by the rolling of the semi-cylindrical foot end after parallel transport the angle

Full size image

In Fig. 10, the included angle \(\varphi\) between \(\overrightarrow {{O_{r} P}}\) and \(\overrightarrow {{O_{r} I}}\) is as follows:

$$ \varphi = \frac{\pi }{2} + \theta_{1} + \theta_{2} + \theta_{3} + \gamma - \vartheta . $$
(38)

Substituting Eq. (38) into Eq. (37), the hip joint trajectory deviation \(\overrightarrow {{O^{\prime}O}} = \left( {\Delta x,\Delta y} \right)\) can be obtained as follows:

$$ \left\{ \begin{gathered} \Delta x = R\left( {\cos \left( {\theta_{1} + \theta_{2} + \theta_{3} + \gamma - \vartheta } \right) - \frac{\pi }{2} - \theta_{1} - \theta_{2} - \theta_{3} - \gamma + \vartheta } \right) \hfill \\ \Delta y = R\left( {1 + \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} + \gamma - \vartheta } \right)} \right) \hfill \\ \end{gathered} \right.. $$
(39)

According to Eq. (39), the hip joint trajectory deviation is not only related to the rotation angle \(\theta_{1}\), \(\theta_{2}\), \(\theta_{3}\) of hip, knee, and ankle joints, but also related to the included angle \(\vartheta\) between the robot body and the contact surface.

Quantitative analysis of statics solving deviation

In the movement process of the robot, the contact force between the semi-cylindrical foot end and ground is shown in Fig. 11. In Fig. 11, \(F_{{{\text{foot}}}}^{x}\) and \(F_{{{\text{foot}}}}^{y}\) are the components in the horizontal and vertical directions of contact forces between the foot end and ground (The positive direction of \(F_{{{\text{foot}}}}^{x}\) is vertical upward, the positive direction of \(F_{{{\text{foot}}}}^{y}\) is horizontal to the right), and \(\delta\) is the angle formed by \(\overrightarrow {{IO_{r} }}\) and \(\overrightarrow {IP}\).

Fig. 11
figure 11

Schematic diagram of semi-cylindrical foot end in contact with the ground

Full size image

From Fig. 11, under ideal circumstances, there is a rigid contact between the foot end and the ground, and the contact point is P. However, the statics modeling point based on virtual work principle is I, so it is necessary to simplify the contact point from P to I. According to the translation theorem of forces, the contact point can be directly translated to point I, but additional torque will be generated. The distance \(PI\) is as follows:

$$ \begin{aligned} PI &= \sqrt {R{^{2}} + R{^{2}} - 2R{^{2}} \cos \varphi } \hfill \\ \, &= \sqrt 2 R\sqrt {1 - \cos \varphi } . \hfill \\ \end{aligned} $$
(40)

In Fig. 11, the torque \(\tau_{y}\) generated by \(F_{{{\text{foot}}}}^{y}\) on point I is as follows:

$$ \begin{aligned} \tau_{y} & = F_{{{\text{foot}}}}^{y} \times PI \times \cos \left( {\frac{\pi - \varphi }{2} - \delta } \right) \hfill \\ \, &= F_{{{\text{foot}}}}^{y} \sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right). \hfill \\ \end{aligned} $$
(41)

In Fig. 11, the torque \(\tau_{x}\) generated by \(F_{{{\text{foot}}}}^{x}\) on point I is as follows:

$$ \begin{aligned} \tau_{x} & = F_{{{\text{foot}}}}^{x} \times AI \times \sin \left( {\frac{\pi - \varphi }{2} - \delta } \right) \hfill \\ &= F_{{{\text{foot}}}}^{x} \sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right). \hfill \\ \end{aligned} $$
(42)

Combined with Eq. (38) and Fig. 11, angle \(\delta\) can be obtained as as follows:

$$ \delta { = } - \theta_{1} - \theta_{2} - \theta_{3} - \gamma . $$
(43)

As can be seen from Fig. 11, the contact point P may be located to the left or right of ideal contact point I. Different positions will produce completely opposite torque effect, so it needs to be discussed in two cases. The position of contact point P can be determined by angle \(\varphi\). When angle \(\varphi\) is greater than zero, contact point P is located to the left of ideal contact point I. When angle \(\varphi\) is less than zero, contact point P is located to the right of ideal contact point I.

When angle \(\varphi\) is greater than zero, the actual torque of each joint is as follows:

$$ \left\{ \begin{gathered} \tau_{1c} = \tau_{1} - \tau_{y} + \tau_{x} \hfill \\ \tau_{2c} = \tau_{2} - \tau_{y} + \tau_{x} \hfill \\ \tau_{3c} = \tau_{3} - \tau_{y} + \tau_{x} \hfill \\ \end{gathered} \right. $$
(44)

When angle \(\varphi\) is less than zero, the actual torque of each joint is as follows:

$$ \left\{ \begin{gathered} \tau_{1c} = \tau_{1} + \tau_{y} - \tau_{x} \hfill \\ \tau_{2c} = \tau_{2} + \tau_{y} - \tau_{x} \hfill \\ \tau_{3c} = \tau_{3} + \tau_{y} - \tau_{x} \hfill \\ \end{gathered} \right. $$
(45)

It can be seen from Eqs. (44) and (45) that the expression of the actual torque of each joint will be appended with a correction term. These correction terms are the root causes of deviations in the statics calculation method based on the virtual work principle. The expression of the correction terms of each joint is as follows:

$$ \left\{ \begin{gathered} \tau_{1c}^{\prime } = F_{{{\text{foot}}}}^{x} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ - F_{{{\text{foot}}}}^{y} {\text{ sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \tau_{2c}^{\prime } = F_{{{\text{foot}}}}^{x} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ - F_{{{\text{foot}}}}^{y} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \tau_{3c}^{\prime } = F_{{{\text{foot}}}}^{x} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ - F_{{{\text{foot}}}}^{y} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right.. $$
(46)

According to Eq. (46), it can be known that

$$ \tau_{3c}^{\prime } { = }\tau_{2c}^{\prime } { = }\tau_{1c}^{\prime } . $$
(47)

Substituting the Eqs. (46) and (47) into Eq. (30), the calculation deviation \(\Delta F = \left( {\Delta F_{x} ,\Delta F_{y} } \right)^{\text{T}}\) of the statics can be obtained as follows:

$$ \left\{ \begin{gathered} \Delta F_{x} { = }\frac{{ - \tau_{2}^{\prime } l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right)}}{{l_{2} l_{3} \sin \left( {\theta_{3} } \right)}} \hfill \\ \Delta F_{y} { = }\frac{{ - \tau_{2}^{\prime } l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right)}}{{l_{2} l_{3} \sin \left( {\theta_{3} } \right)}} \hfill \\ \end{gathered} \right., $$
(48)

where

$$ \begin{aligned} \tau_{2}^{\prime } &= F_{{{\text{foot}}}}^{x} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ & \quad - F_{{{\text{foot}}}}^{y} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{aligned} $$
(49)

Also select the included angle \(\vartheta\) between the robot body and the contact surface are − 10°, 0° and 10°, control the foot end of the robot body to remain stationary at the initial position. \(F_{foot}^{x}\) in the x direction changes within the range of \(\pm \;500\;{\text{N}}\), and \(F_{{{\text{foot}}}}^{y}\) end in the y direction changes within the range of \(\pm \;1000\;{\text{N}}\). Then, the statics calculation deviation \(\Delta F = \left( {\Delta F_{x} ,\Delta F_{y} } \right)^{{\text{T}}}\) caused by the semi-cylindrical foot end is shown in Fig. 12.

Fig. 12
figure 12

Statics calculation deviation caused by the semi-cylindrical foot end

Full size image

It can be seen from Fig. 12 that the statics calculation deviation caused by the semi-cylindrical foot end exists in the direction perpendicular and parallel to the contact surface. When the included angle between the robot body and the contact surface are 10°, 0°, and 10°, the maximum absolute values of the statics calculation deviations in the positive direction of x axis are 52.89, 37.72, and 21.09 N, respectively, the maximum absolute values of the statics calculation deviations in the positive direction of y axis are 86.92, 63.48, and 36.37 N, respectively. These deviations will cause the foot end contact force detected by the sensor to deviate from the actual contact force, thus weakening the control effect of control algorithms such as impedance control and contact force control. Therefore, it is very necessary to propose a statics correction algorithm for the special structure of semi-cylindrical foot end.

Kinematics and statics correction algorithm

Kinematics correction algorithm based on virtual DOF

The kinematics correction algorithm proposed in this paper is shown in Fig. 13. Considering that the semi-cylindrical foot end is always tangent to the contact surface, the method of virtual DOF is adopted in this paper. The semi-cylindrical foot end is virtualized as a rod \(O_{r} P\) which is always perpendicular to the contact surface.

Fig. 13
figure 13

Schematic diagram of leg kinematics correction algorithm of robot with semi-cylindrical foot end

Full size image

In Fig. 13, the relationship between \(\overrightarrow {OI}\) and \(\overrightarrow {OP}\) can be obtained as follows:

$$ \overrightarrow {OP} = \overrightarrow {OI} + \overrightarrow {IP} . $$
(50)

In Eq. (50), \(\overrightarrow {OI}\) is as follows:

$$ \overrightarrow {OI} = \left[ \begin{gathered} l_{1} \cos \theta_{1} + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ l_{1} \sin \theta_{1} + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \right]. $$
(51)

In Eq. (50), \(\overrightarrow {IP}\) is the following:

$$ \overrightarrow {IP} = \left[ \begin{gathered} - R\sin \varphi \hfill \\ - R\left( {1 - \cos \varphi } \right) \hfill \\ \end{gathered} \right]. $$
(52)

According to Eqs. (38), (50), (51), and (52), \(\overrightarrow {OP}\) in the coordinate system of hip joint can be written as follows:

$$ \overrightarrow {OP} = \left[ \begin{gathered} l_{1} \cos \theta_{1} + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ - R\cos \left( {\theta_{1} + \theta_{2} + \theta_{3} + \gamma - \vartheta } \right) \hfill \\ l_{1} \sin \theta_{1} + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ - R\sin \left( {\theta_{1} + \theta_{2} + \theta_{3} + \gamma - \vartheta } \right) - R \hfill \\ \end{gathered} \right]. $$
(53)

According to Eq. (53), the forward kinematics solution of the leg with semi-cylindrical foot end can be written as follows:

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} X_{{{\text{foot}}}}^{X} = l_{1} \cos \theta_{1} + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) \hfill \\ + \left( {l_{3} - R\cos \left( {\gamma - \vartheta } \right)} \right)\cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ + R\sin \left( {\gamma - \vartheta } \right)\sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \\ \begin{gathered} X_{{{\text{foot}}}}^{Y} = l_{1} \sin \theta_{1} + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) \hfill \\ + \left( {l_{3} - R\cos \left( {\gamma - \vartheta } \right)} \right)\sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ - R\sin \left( {\gamma - \vartheta } \right)\cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) - R \hfill \\ \end{gathered} \\ \end{array} } \right.. $$
(54)

Statics correction algorithm for semi-cylindrical foot end

From Eq. (46), it can be seen that the additional correction term in the joint moment expression is the root cause of the statics calculation deviation. Therefore, the core idea of the statics correction algorithm proposed in this paper is to compensate the torque of each joint by using the additional correction term of each joint.

By substituting Eqs. (44) and (45) into Eq. (29), the inverse statics solution of the robot leg with a semi-cylindrical foot end can be obtained as follows:

$$ \left\{ \begin{gathered} \tau_{1c} = - F_{{{\text{foot}}}}^{x} \left[ \begin{gathered} \left( \begin{gathered} l_{1} \sin \left( {\theta_{1} } \right) + l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \right) \hfill \\ - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right] \hfill \\ { + }F_{{{\text{foot}}}}^{y} \, \left[ \begin{gathered} \left( \begin{gathered} l_{1} \cos \left( {\theta_{1} } \right) + l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + \hfill \\ l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ \end{gathered} \right) \hfill \\ - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right] \hfill \\ \tau_{2c} = - F_{{{\text{foot}}}}^{x} \left[ \begin{gathered} l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( \begin{gathered} \theta_{1} + \hfill \\ \theta_{2} + \theta_{3} \hfill \\ \end{gathered} \right) \hfill \\ - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right] \hfill \\ { + }F_{{{\text{foot}}}}^{y} \left[ \begin{gathered} l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( \begin{gathered} \theta_{1} + \hfill \\ \theta_{2} + \theta_{3} \hfill \\ \end{gathered} \right) \hfill \\ - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right] \hfill \\ \tau_{3c} = - F_{{{\text{foot}}}}^{x} \left[ \begin{gathered} l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right] \hfill \\ + F_{{{\text{foot}}}}^{y} \left[ \begin{gathered} l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) \hfill \\ - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right. $$
(55)

By substituting Eq. (55) into Eq. (30), the forward statics solution of the robot leg with a semi-cylindrical foot end can be obtained as follows:

$$ \left\{ \begin{gathered} F_{{{\text{foot}}}}^{x} = \frac{\begin{gathered} \tau_{2c} \left[ {l_{3} \cos \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right)} \right] \hfill \\ - \tau_{3c} \left[ {l_{2} \cos \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \cos \left( \begin{gathered} \theta_{1} + \hfill \\ \theta_{2} + \theta_{3} \hfill \\ \end{gathered} \right) - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \sin \left( {\frac{\varphi }{2} + \delta } \right)} \right] \hfill \\ \end{gathered} }{{l_{2} l_{3} \sin \left( {\theta_{3} } \right) - l_{2} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\theta_{1} + \theta_{2} + \frac{\varphi }{2} + \delta } \right)}} \hfill \\ F_{{{\text{foot}}}}^{y} = \frac{\begin{gathered} \tau_{2c} \left[ {l_{3} \sin \left( {\theta_{1} + \theta_{2} + \theta_{3} } \right) - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right)} \right] \hfill \\ - \tau_{3c} \left[ {l_{2} \sin \left( {\theta_{1} + \theta_{2} } \right) + l_{3} \sin \left( \begin{gathered} \theta_{1} + \hfill \\ \theta_{2} + \theta_{3} \hfill \\ \end{gathered} \right) - {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\frac{\varphi }{2} + \delta } \right)} \right] \hfill \\ \end{gathered} }{{l_{2} l_{3} \sin \left( {\theta_{3} } \right) - l_{2} {\text{sign}}(\varphi )\sqrt 2 R\sqrt {1 - \cos \varphi } \cos \left( {\theta_{1} + \theta_{2} + \frac{\varphi }{2} + \delta } \right)}} \hfill \\ \end{gathered} \right. $$
(56)

Experiment

Introduction of the experimental system

The validity of the kinematics and statics correction algorithm proposed in this paper was verified experimentally by using the LHDS performance test platform. The experimental test site is shown in Fig. 14.

Fig. 14
figure 14

LHDS loading experiment diagram

Full size image

By controlling the load simulation experimental platform to perform impedance control in the vertical direction, the load simulation experimental platform is guaranteed to be in close contact with the foot end during the verification process of the kinematics correction algorithm, and constantly moves with the deviation of the foot end in the vertical direction. During the validation of the statics correction algorithm, the foot end position of the LHDS keeps unchanged. By changing the extension length of the load simulation experimental platform, different contact forces can be loaded on the foot end. The specific experimental principle is shown in Fig. 15.

Fig. 15
figure 15

Schematic diagram of LHDS loading experiment

Full size image

Kinematics correction experiment

From Eq. (39), it can be concluded that if the vertical deviation of the hip joint is improved, then the horizontal displacement also can be improved. Therefore, the vertical deviation of the hip joint trajectory was used as the evaluation index to test the validity of the proposed kinematics correction algorithm. In this paper, the sinusoidal signal input from the foot end parallel to the contact surface is \(150\sin \left( {0.5t} \right)\). The position sensor in the vertical movement plane of the load simulation platform detects the deviation in the vertical direction during the movement of the foot end. The specific experimental plan is shown in Table 3.

Table 3 Experimental plan
Full size table

In Table 3, plans 1 and 2 aim to test the correction effect of kinematics correction algorithm when the robot body at the same angle with the contact surface and the foot end is at different positions. Plans 2 and 3 aim to test the correction effect of kinematics correction algorithm when the robot body at the different angles with the contact surface and the foot end at the same position.

The relationship between theoretical deviation, uncorrected deviation, corrected deviation of hip joint trajectory is, respectively, shown in Figs. 16, 17, 18 [21]. The theoretical deviation curves are the deviation in the positive direction of the \(y_{0}\) axis of the hip joint obtained by inserting the real-time extension length of each hydraulic driving unit into Eq. (39). The uncorrected deviation curves are the deviation in the positive direction of the \(y_{0}\) axis of the hip joint obtained by inverse kinematics solution when the foot end is regarded as a point. The corrected deviation curves are the deviation in the positive direction of the \(y_{0}\) axis of the hip joint obtained by using the kinematics correction algorithm proposed in this paper.

Fig. 16
figure 16

Hip joint trajectory deviation in plan 1

Full size image
Fig. 17
figure 17

Hip joint trajectory deviation in plan 2

Full size image
Fig. 18
figure 18

Hip joint trajectory deviation in plan 3

Full size image

In Figs. 16, 17, 18, it can be seen that the theoretical deviation of the hip joint trajectory and the uncorrected deviation almost coincide, indicating that the theoretical calculation of the hip joint trajectory deviation in Eq. (39) is correct. In plans 1 to 3, the trajectory deviation of the hip joint is greatly reduced by adding the correction algorithm proposed in this paper, which indicates that the kinematics algorithm proposed in this paper is applicable when the foot end is located at different positions and the robot body is at different angles to the contact surface. However, it can be seen from the experimental curves of plan 1 to 3 that the corrected deviation of hip joint has been stable within the range of about 2 mm. It is assumed that the deviation is caused by the compression deformation of the foot end rubber, the wear of the foot end rubber, the measurement deviation, the deviation of the position control system of the HDU, and the installation deviation of the experimental platform.

In order to quantitatively analyze the experimental results, the experimental curves obtained in Figs. 16a, 17a, and 18a are processed in this paper, as shown in Table 4, where \(R\) represents the maximum deviation rate of hip trajectory in the whole period, and \(R_{{\text{a}}}\) represents the average deviation rate of hip trajectory in the whole period. The equations are as follows:

$$ R = \left( {E_{1} - E_{2} } \right)/E_{1} , $$
(57)
$$ R_{{\text{a}}} = \left( {E_{{{\text{a1}}}} - E_{{{\text{a2}}}} } \right)/E_{{{\text{a1}}}} , $$
(58)

where \(E_{1}\) represents the absolute value of the maximum deviation of hip joint trajectory under ideal kinematics, and \(E_{{{\text{a1}}}}\) represents the average value of absolute deviation of hip joint trajectory under ideal kinematics. \(E_{2}\) represents the absolute value of the maximum deviation of hip trajectory by using the kinematics correction algorithm, and \(E_{{{\text{a2}}}}\) represents the average value of absolute deviation of hip trajectory by using the kinematics correction algorithm.

Table 4 Trajectory deviation of hip joint under each plan
Full size table

The larger the value of \(R\), the better the reduction effect of the correction algorithm on the maximum deviation. The larger the value of \(R_{{\text{a}}}\), the better the reduction effect of the correction algorithm on the average deviation in the whole movement period.

From Table 4, the following conclusions can be drawn: both the maximum and average deviation rates of hip trajectory in the whole period are more than 60%, indicating that the hip trajectory deviation phenomenon has been significantly reduced after the application of the correction algorithm proposed in this paper. Because the maximum deviation and average deviation of the ideal kinematics in plan 3 are small, and the correction effect is always affected by compression, deformation, wear and other factors of the foot end rubber, the correction effect is worse than that in plan 1 and 2.

Statics correction experiments

In order to directly measure the contact force between the foot end and the load simulation test platform, considering that the LHDS only moves in the vertical plane, this paper fixed the two-dimensional force sensor on the load simulation test platform to realize the accurate measurement of the contact force. The experimental equipment is shown in Fig. 19.

Fig. 19
figure 19

The experimental equipment

Full size image

The LHDS is fixed on the base and controlled by the upper computer to keep the initial position unchanged during the experiment. The load simulation test platform at the bottom is used for impedance control. By changing the impedance input position and placement angle of the load simulation test platform, the force loading of different positions and angles of the foot end can be realized. Since the LHDS remains stationary during the experiment, no inertial forces are generated. When the statics correction algorithm proposed in this paper is used to solve the foot end force, the detection value of the one-dimensional force sensor of each joint is directly subtracted from the initial value of the one-dimensional force sensor when the foot end is not loaded, so as to eliminate the influence of the gravity term in dynamics on the experimental results.

The specific experimental plans are shown in Table 5:

Table 5 Experimental plan
Full size table

The purpose of plans 1, 3 and 5 is to test the validity of correction algorithm when the body of the LHDS is at different angles to the contact surface and the foot end is at the initial position. The purpose of plans 2, 4 and 6 is to test the validity of correction algorithm when the body of the LHDS is at different angles to the contact surface and the foot end is at other positions. The purpose of plans 1 and 2, plans 3 and 4, and plans 5 and 6 is to test the validity of correction algorithm when the body of LHDS is at the different angle to the contact surface and the foot end is in different positions.

In plans 1–6, both the foot end contact force and the solution deviation related to the time are shown in Figs. 20, 21, 22, 23, 24, 25. The force sensor measured value is the actual contact force detected by the two-dimensional force sensor. The uncorrected statics solution force is the value of the statics solution when the foot end is regarded as a point. The corrected statics solution force is the calculated value of the foot end contact force after applying the statics correction algorithm. The theoretical deviation is the deviation in x/y direction of the foot end contact force obtained by substituting the real-time detection value of position sensor and one-dimensional force sensor of each joint HDU into Eq. (48). The uncorrected deviation is the difference between the calculated value of statics and the detected value of two-dimensional force sensor in the x/y direction when the foot end is regarded as a point. The corrected deviation is the difference between the calculated value of the foot end contact force and the detected value of the two-dimensional force sensor in x/y direction when applying the correction algorithm.

Fig. 20
figure 20

Foot end contact force and calculation deviation curves of plan 1

Full size image
Fig. 21
figure 21

Foot end contact force and calculation deviation curves of plan 2

Full size image
Fig. 22
figure 22

Foot end contact force and calculation deviation curves of plan 3

Full size image
Fig. 23
figure 23

Foot end contact force and calculation deviation curves of plan 4

Full size image
Fig. 24
figure 24

Foot end contact force and calculation deviation curves of plan 5

Full size image
Fig. 25
figure 25

Foot end contact force and calculation deviation curves of plan 6

Full size image

From Figs. 20, 21, 22, 23, 24, 25, it can be seen that the theoretical deviation and the uncorrected deviation of the foot end contact force almost coincide, indicating that the theoretical calculation of the foot end contact force deviation in Eq. (48) is correct. In plans 1–6, after adding the correction algorithm proposed in this paper, the foot end contact force deviation is greatly reduced, indicating that the statics correction algorithm proposed in this paper is applicable when the foot end is located at different positions and the robot body is at different angles with the contact surface.

This paper uses the same evaluation index as Eqs. (57) and (58) to evaluate the effect of statics correction. Then, the meanings of each symbol are as follows:

\(R\) is the maximum deviation rate of foot end contact force in the whole period, \(R_{{\text{a}}}\) is the average deviation rate of foot end contact force in the whole period, \(E_{1}\) is the absolute value of the maximum deviation of foot end contact force under ideal statics calculation, \(E_{{{\text{a1}}}}\) is the average value of the absolute value of foot end contact force deviation under ideal statics calculation, \(E_{2}\) is the absolute value of the maximum deviation of foot end contact force after using the correction algorithm, \(E_{{{\text{a2}}}}\) is the average value of the absolute value of the foot end contact force deviation after using the correction algorithm; the data processing results are shown in Tables 6 and 7 as follows.

Table 6 Deviation of foot end contact force in the direction of x axis
Full size table
Table 7 Deviation of foot end contact force in the direction of y axis
Full size table

From Tables 6, 7, the following conclusions can be drawn: In the direction of x/y axis, the maximum deviation rate and average deviation rate of foot end contact force in the whole cycle reached more than 42%. The results show that the foot end contact force deviation is obviously reduced by using the correction algorithm proposed in this paper. In plan 3, the maximum deviation and average deviation of ideal statics along the y axis are small, and the deviation of foot end contact force after correction along the y axis is always maintained at about 11 N, so the correction effect is the worst.

Conclusion

First, because the kinematics based on D-H coordinate transformation and the static based on virtual work principle are simplified in the modeling process, the actual contact point of the foot end deviates from the ideal modeling point. So, it will inevitably produce a certain deviation, which will affect the motion control performance of the whole robot.

Second, after applying the kinematics correction algorithm proposed in this paper, the trajectory deviation of the hip joint is greatly reduced. The experimental results show that, in plan 1 to 3, after applying the kinematics correction algorithm proposed in this paper, the maximum deviation reduction rate reaches 71.69%, 87.16%, and 65.00%, respectively. And the average deviation reduction rate in the whole motion period reaches 80.56%, 90.99%, and 67.68%, respectively.

Third, after applying the statics correction algorithm proposed in this paper, the deviation of foot end contact force is greatly reduced. The experimental results show that, in plan 1 to 6, after applying the proposed statics correction algorithm, the maximum deviation reduction rate in the x axis direction reaches 88.80%, 77.15%, 85.09%, 53.75%, 86.71%, and 70.10%, respectively. The average deviation reduction rate in the whole movement period reaches 89.51%, 76.54%, 77.15%, 61.78%, 77.59%, and 58.36%, respectively. The maximum deviation reduction rate in the y axis direction reaches 55.92%, 70.77%, 44.53%, 62.73%, 71.36%, and 79.69%, respectively. The average deviation reduction rate in the whole movement period reaches 58.63%, 80.99%, 43.37%, 63.65%, 73.39%, and 77.57%, respectively.

Future work: although the kinematics and statics correction algorithm proposed in this paper can achieve obvious correction effect, they cannot completely eliminate the deviation. It is assumed that this is due to the wear of the rubber particles wrapped around the semi-cylindrical foot end and the deformation of the rubber during contact with the foot end. In future, it is planned to design the corresponding compensation algorithm according to the above phenomenon to further improve the control accuracy of the robot leg.