SpringerLink
Log in

Survey on Multi-period Mean–Variance Portfolio Selection Model

  • Published:
Journal of the Operations Research Society of China Aims and scope Submit manuscript

Abstract

Due to the non-separability of the variance term, the dynamic mean–variance (MV) portfolio optimization problem is inherently difficult to solve by dynamic programming. Li and Ng (Math Finance 10(3):387–406, 2000) and Zhou and Li (Appl Math Optim 42(1):19–33, 2000) develop the pre-committed optimal policy for such a problem using the embedding method. Following this line of research, researchers have extensively studied the MV portfolio selection model through the inclusion of more practical investment constraints, realistic market assumptions and various financial applications. As the principle of optimality no longer holds, the pre-committed policy suffers from the time-inconsistent issue, i.e., the optimal policy computed at the intermediate time t is not consistent with the optimal policy calculated at any time before time t. The time inconsistency of the dynamic MV model has become an important yet challenging research topic. This paper mainly focuses on the multi-period mean–variance (MMV) portfolio optimization problem, reviews the essential extensions and highlights the critical development of time-consistent policies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. The filtration \({\mathcal {F}}_t\) represents the information available at time t (see [10] for detail of discrete-time market model).

  2. If the first asset is the benchmark, the wealth dynamic becomes \(x_{t+1} = r^1_t x_t + {\hat{\varvec{r}}}_t^{\top } {\hat{\varvec{u}}}_t\), where \({\hat{\varvec{r}}}_t=(r^2_t - r^1_t, r^3_t - r^1_t,\cdots , r^n_t- r^1_t)^{\top }\) is the excess return vector and \({\hat{\varvec{u}}}_t \in {\mathbb {R}}^{n-1}\) is the truncated decision vector of \(\varvec{u}_t\).

  3. Similar model is also considered in [11].

  4. Reader may refer [5, 12] for the detailed discussion of three models.

  5. If the risk-free rate is random, then it becomes the similar model with all assets being risky.

  6. In this paper, we define the boundary of the product term as \(\prod _{k=t_1}^{t_2} a_k =1\) if \(t_1>t_2\).

  7. The detail derivation of policy (5) is given in [13]. Note that the policy (5) is different from the one given in [5], as the problem formulations are different.

  8. We re-calibrate the date given in Example 1 in [5] from yearly based statistics to the monthly based ones. Then, \(T=12\) means that the investment horizon is 12 months.

  9. We adopt the similar data for Fig. 1(a) and set \(T=12\) months. As for the static MV model, we regard the whole horizon \(T=12\) as a single period and solve the static MV portfolio selection for the buy and hold policy. We then simulate 5000 sample paths of the return vector and compute the terminal wealth for different policies.

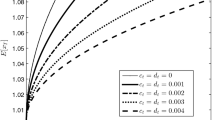
  10. Comparing with [9], one important extension given in [22] is that it drops the nonnegative assumption \(\text {E}[\varvec{p}_t\varvec{p}_t^{\top }]^{-1}\text {E}[\varvec{p}_t]\geqslant 0\) for \(t=0,\cdots ,T-1\). The new setting fits the fact that the expected value of premium vectors may be negative in the time-varying market.

  11. Take the practice of AIS as an example. For investors with assets under management (AUM) between US$100,000 and US$250,000, the annual fee charged by AIS is 0.80% of AUM or US$1,500, whichever is greater.

  12. Note that \(T_s\) is related to the management fee, which can be fixed by the method given in Sect. 3 in [12].

  13. The time-consistent mean–variance policies in the market with all risky assets can be found in [56].

  14. A more detailed comparison between the pre-committed policy and different types of time-consistent policies can be found in [60].

References

  1. Markowitz, H.M.: Portfolio selection. J. Financ. 7(1), 1063–1070 (1952)

    Google Scholar 

  2. Ao, M.M., Li, Y.Y., Zheng, X.H.: Approaching mean-variance efficiency for large portfolios. Rev. Financ. Stud. 32(7), 2890–2919 (2019)

    Article  Google Scholar 

  3. Kolm, P.N., Tütüncü, R.: 60 years of portfolio optimization: practical challenges and current trends. Eur. J. Oper. Res. 234(2), 356–371 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Mencarelli, L., Ambrosio, C.D.: Complex portfolio selection via convex mixed-integer quadratic programming: a survey. Int. Trans. Oper. Res. 26(2), 389–414 (2019)

    Article  MathSciNet  Google Scholar 

  5. Li, D., Ng, W.L.: Optimial dynamic portfolio selection: multiperiod mean-variance formulation. Math. Finance 10(3), 387–406 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  6. Zhou, X.Y., Li, D.: Continuous-time mean-variance portfolio selection: a stochastic LQ framework. Appl. Math. Optim. 42(1), 19–33 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  7. Gârleanu, N., Pedersen, L.H.: Dynamic trding with predictable returns and transaction cost. J. Financ. 68(6), 2309–2340 (2013)

    Article  Google Scholar 

  8. Li, B., Hoi, S.C.H.: Online portfolio selection: a survey. ACM Comput. Surev. 46(3), 1–36 (2014)

    MATH  Google Scholar 

  9. Cui, X.Y., Gao, J.J., Li, X., Li, D.: Optimal multi-period mean-variance policy under no-shorting constraint. Eur. J. Oper. Res. 234(2), 459–468 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Föllmer, H., Schied, A.: Stochastic Finance: An Introduction in Discrete Time. De Gruyter Studies in Mathematics. Walter De Gruyter, Berlin (2004)

    Book  MATH  Google Scholar 

  11. Yao, H.X., Li, Z.F., Li, X.Y.: The premium of dynamic trading in a discrete-time setting. Quant. Financ. 16(8), 1237–1257 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gao, J.J., Li, D., Cui, X.Y., Wang, S.Y.: Time cardinality constrained mean-variance dynamic portfolio selection and market timing: a stochastic control approach. Automatica 54, 91–99 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Gao, J.J., Li, D.: Multiperiod mean-variance portfolio optimization with general correlated returns. IFAC Proc. 47, 9007–9012 (2014)

    Article  Google Scholar 

  14. Chiu, C.H., Zhou, X.Y.: The prmium of dynamic trading. Quant. Financ. 11, 115–123 (2011)

    Article  Google Scholar 

  15. van Staden, P.M., Dang, D.M., Forsyth, P.A.: On the distribution of terminal wealth under dynamic mean-variance optimal investment strategies. SIAM. J. Financ. Math 12(2), 566–603 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. van Staden, P.M., Dang, D., Forsyth, P.A.: The surprising robustness of dynamic mean-variance portfolio optimization to model misspecification error. Eur. J. Oper. Res. 289, 774–792 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  17. Yao, H., Lai, Y., Ma, Q., Jian, M.: Asset allocation for a dc pension fund with stochastic income and mortality risk: a multi-period mean-variance framework. Insur. Math. Econ. 54, 84–92 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Chiu, M.C., Wong, H.Y.: Mean-variance asset-liability management with asset correlation risk and insurance liabilities. Insur. Math. Econ. 59, 300–310 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Yao, H., Chen, P., Li, X.: Multi-period defined contribution pension funds investment management with regime-switching and mortality risk. Insur. Math. Econ. 71, 103–113 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  20. Zhang, L., Zhang, H., Yao, H.: Optimal investment management for a defined contribution pension fund under imperfect information. Insur. Math. Econ. 79, 210–224 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  21. Sun, Z., Zhang, X., Yuen, K.C.: Mean-variance asset-liability management with affine diffusion factor process and a reinsurance option. Scand. Actuar. J. 2020(3), 218–244 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  22. Wu, W.P., Gao, J.J., Li, D., Shi, Y.: Explicit solution for constrained scalar-state stochastic linear-quadratic control with multiplicative noise. IEEE Trans. Autom. Control 64, 1999–2012 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  23. Li, X., Zhou, X.Y., Lim, A.E.B.: Dynamic mean-variance portfolio selection with no shorting constraints. SIAM J. Control Optim. 40(5), 1540–1555 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  24. Hu, Y., Zhou, X.Y.: Constrained stochastic LQ control with random coefficients, and application to portfolio selection. SIAM J. Control Optim. 44(2), 444–466 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  25. Cui, X.Y., Li, D., Li, X.: Mean-variance policy for discrete-time cone constrained markets: the consistency in efficiency and minimum-variance signed supermartingale measure. Math. Financ. 27(2), 471–504 (2017)

    Article  MathSciNet  Google Scholar 

  26. Costa, O.L.V., Oliveira, A.D.: Optimal mean-variance control for discrete-time systems with Markovian jumps and multiplicative noises. Automatica 48(2), 304–315 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  27. Zhu, S.S., Li, D., Wang, S.Y.: Risk control over bankruptcy in dynamic portfolio selection: a generalized mean-variance formulation. IEEE Trans. Autom. Control 49(3), 447–457 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  28. Li, C., Li, Z.: Multi-period portfolio optimization for asset-liability management with bankrupt control. Appl. Math. Comput. 218, 11196–11208 (2012)

    MathSciNet  MATH  Google Scholar 

  29. Costa, O., Nabholz, R.: Multiperiod mean-variance optimization with intertemporal restrictions. J. Optim. Theory Appl. 134(2), 257–274 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  30. Xu, Y., Li, Z.F.: Dynamic portfolio selection based on serially correlated return-dynamic mean-variance formulation. Syst. Eng. Theory Pract. 18(8), 123–131 (2008)

    Google Scholar 

  31. Dokuchaev, N.: Discrete time market with serial correlations and optimal myopic strategies. Eur. J. Oper. Res. 177, 1090–1104 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  32. Çakmak, U., Özekici, S.: Portfolio optimization in stochastic markets. Math. Methods Oper. Res. 63, 151–168 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  33. Wu, H., Li, Z.F.: Multi-period mean-variance portfolio selection with regime switching and a stochastic cash flow. Insur. Math. Econ. 50(3), 371–384 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Yao, H., Lai, Y., Hao, Z.: Uncertain exit time multi-period mean-variance portfolio selection with dndogenous liabilities and markov jumps. Automatica 49(11), 3258–3269 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  35. Wu, H., Zeng, Y., Yao, H.X.: Multi-period Markowtiz’s mean-variance portfolio selection with state-dependent exit probability. Econ. Model. 36, 69–78 (2014)

    Article  Google Scholar 

  36. Herzog, F., Dondi, G., Geering, H.P.: Stochastic model predictive control and portfolio optimization. Int. J. Theor. Appl. Finance 10(2), 981–1000 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  37. Boyd, S., Busseti, E., Diamond, S., Kahn, R.N., Koh, K., Nystrup, P.: Multi-period trading via convex optimization. Found. Trends Opt. 3(1), 1–76 (2017)

    Article  Google Scholar 

  38. Nystrup, P., Boyd, S., Lindström, E., Madsen, H.: Multi-period portfolio selection with drawdown control. Ann. Oper. Res. 282, 245–271 (2017)

    Article  MATH  Google Scholar 

  39. Cong, F., Oosterlee, C.W.: Multi-period mean-variance portfolio optimization based on Monte–Carlo simulation. J. Econ. Dyn. Control 64, 23–38 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  40. Basak, S., Chabakauri, G.: Dynamic mean-variance asset allocation. Rev. Financ. Stud. 23(8), 2970–3016 (2010)

    Article  Google Scholar 

  41. Strotz, R.H.: Myopia and inconsistency in dynamic utility maximization. Rev. Econ. Stud. 23(3), 165–180 (1955)

    Article  Google Scholar 

  42. O’Donoghue, T., Rabin, M.: Doing it now or later. Am. Econ. Rev. 89(1), 103–124 (1999)

    Article  Google Scholar 

  43. Grenadier, S.R., Wang, N.: Investment under uncertainty and time-inconsistent preferences. J. Financ. Econ. 84(1), 2–39 (2007)

    Article  Google Scholar 

  44. Wu, H.: Time-consistent strategies for a multiperiod mean-variance portfolio selection problem. J. Appl. Math., Article ID , 841627 (2013)

  45. Wu, H., Chen, H.: Nash equilibrium strategy for a multi-period mean-variance portfolio selection problem with regime switching. Econ. Model. 46, 79–90 (2015)

    Article  Google Scholar 

  46. Wang, L., Chen, Z.: Nash equilibrium strategy for a dc pension plan with state-dependent risk aversion: a multiperiod mean-variance framework. Discrete. Dyn. Nat. Soc., Article ID , 7581231 (2018)

  47. **ao, H., Ren, T., Bai, Y., Zhou, Z.: Time-consistent investment-reinsurance strategies for the insurer and the reinsurer under the generalized mean-variance criteria. Mathematics 7(9), 857 (2019)

    Article  Google Scholar 

  48. Zeng, Y., Li, Z., Lai, Y.: Time-consistent investment and reinsurance strategies for mean-variance insurers with jumps. Insur. Math. Econ. 52(3), 498–507 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  49. Lin, X., Qian, Y.: Time-consistent mean-variance reinsurance-investment strategy for insurers under CEV model. Scand. Actuar. J. 2016(7), 646–671 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  50. Zhang, Y., Wu, Y., Li, S., Wiwatanapataphee, B.: Mean-variance asset liability management with state-dependent risk aversion. N. Am. Actuar. J. 21(1), 87–106 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  51. Chen, K., Wong, H.Y.: Time-consistent mean-variance hedging of an illiquid asset with a cointegrated liquid asset. Financ. Res. Lett. 29, 184–192 (2019)

    Article  Google Scholar 

  52. Zhang, L., Li, D., Lai, Y.: Equilibrium investment strategy for a defined contribution pension plan under stochastic interest rate and stochastic volatility. J. Comput. Appl. Math. 368, 112536 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  53. Zhao, Q., Shen, Y., Wei, J.: Mean-variance investment and contribution decisions for defined benefit pension plans in a stochastic framework. J. Ind. Manag. Optim. 17(3), 1147–1171 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  54. Björk, T., Murgoci, A., Zhou, X.Y.: Mean-variance portfolio optimization with state-dependent risk aversion. Math. Financ. 24(1), 1–24 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  55. Hu, Y., **, H., Zhou, X.Y.: Time-inconsistent stochastic linear-quadratic control. SIAM J. Control. Optim. 50(3), 1548–1572 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  56. Pun, C.S.: Time-consistent mean-variance portfolio selection with only risky assets. Econ. Model. 75, 281–292 (2018)

    Article  Google Scholar 

  57. Cui, X.Y., Li, X., Li, D., Shi, Y.: Time consistent behavioral portfolio policy for dynamic mean-variance formulation. J. Oper. Res. Soc. 68(12), 1647–1660 (2017)

    Article  Google Scholar 

  58. Wang, J., Forsyth, P.A.: Continuous time mean variance asset allocation: a time-consistent strategy. Eur. J. Oper. Res. 209(2), 184–201 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  59. Cong, F., Oosterlee, C.W.: On pre-committed aspects of a time-consistent strategy for a mean-variance investor. J. Econ. Dyn. Control 70, 178–193 (2016)

    Article  MATH  Google Scholar 

  60. Van Staden, P.M., Dang, D.-M., Forsyth, P.A.: On the distribution of terminal wealth under dynamic mean-variance optimal investment strategies. SIAM. J. Financ. Math 12(2), 566–603 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  61. Cui, X.Y., Li, D., Shi, Y.: Self-coordination in time inconsistent stochastic decision problems: a planner-doer game framework. J. Econ. Dyn. Control 75, 91–113 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  62. Ni, Y.-H., Si, B., Zhang, X.: Yet the game between precommitted policy and time-consistent policy. ar**v preprint ar**v:1908.03728 (2019)

  63. Cui, X.Y., Li, D., Wang, S., Zhu, S.: Better than dynamic mean-variance: time inconsistency and free cash flow stream. Math. Financ. 22(2), 346–378 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  64. Zhu, S., Li, D., Wang, S.: Myopic Efficiency in Multi-period Portfolio Selection with a Mean-variance Formulation, pp. 53–74. Global-Link Publisher, Hong Kong (2003)

    Google Scholar 

  65. Bäuerle, N., Grether, S.: Complete markets do not allow free cash flow streams. Math. Methods Oper. Res. 81(2), 137–146 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  66. Dang, D.-M., Forsyth, P.A.: Better than pre-committed mean-variance portfolio allocation strategies: a semi-self-financing Hamilton–Jacobi–Bellman equation approach. Eur. J. Oper. Res. 250(3), 827–841 (2016)

    Article  MATH  Google Scholar 

  67. Bengen, W.P.: Determining withdrawal rates using historical data. J. Financ. Plan. 7(4), 171–180 (1994)

    Google Scholar 

  68. Dang, D.-M., Forsyth, P.A., Vetzal, K.R.: The 4% strategy revisited: a pre-commitment mean-variance optimal approach to wealth management. Quant. Financ. 17(3), 335–351 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  69. Cui, X.Y., Gao, J.J., Shi, Y., Zhu, S.S.: Time-consistent and self-coordination strategies for multi-period mean-Conditional Value-at-Risk portfolio selection. Eur. J. Oper. Res. 276(2), 781–789 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  70. Gao, J.J., Zhou, K., Li, D.: Dynamic mean-LPM and mean-CVaR portfolio optimization in continuous time. SIAM J. Control. Optim. 55(3), 1377–1397 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  71. Huang, X., Li, D.: A two-level reinforcement learning algorithm for ambiguous mean-variance portfolio selection problem. In: IJCAI, pp. 4527–4533 (2020)

  72. Wang, H.R., Zhou, X.Y.: Continuous-time mean-variance portfolio selection: A reinforcement learning framework. Math. Financ. 30(4), 1273–1308 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  73. Wang, H., Zariphopoulou, T., Zhou, X.Y.: Reinforcement learning in continuous time and space: a stochastic control approach. J. Mach. Learn. Res. 21(198), 1–24 (2020)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

All the authors of this paper would like to thank Professor Duan Li for his guidance, help and encouragement during their Ph.D. and postdoctoral time at the Chinese University of Hong Kong.

Author information

Authors and Affiliations

  1. School of Statistics and Management, Shanghai University of Finance and Economics, Shanghai, 200433, China

    **ang-Yu Cui

  2. School of Information Management and Engineering, Shanghai University of Finance and Economics, Shanghai, 200433, China

    Jian-Jun Gao

  3. Department of Applied Mathematics, The Hong Kong Polytechnic University, Hong Kong, China

    Xun Li

  4. Academy of Statistics and Interdisciplinary Sciences, Faculty of Economics and Management, East China Normal University, Shanghai, 200062, China

    Yun Shi

Authors
  1. **ang-Yu Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jian-Jun Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xun Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yun Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian-Jun Gao.

Additional information

This paper is dedicated to the late Professor Duan Li in commemoration of his contributions to optimization, financial engineering, and risk management.

This work is partially supported by the National Natural Science Foundation of China (Nos. 71971132, 61573244, 71671106, 71971083 and 72171138), by the Key Program of National Natural Science Foundation of China (No. 71931004), by Shanghai Institute of International Finance and Economics, by Program for Innovative Research Team of Shanghai University of Finance and Economics and by the Open Research Fund of Key Laboratory of Advanced Theory and Application in Statistics and Data Science-MOE.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cui, XY., Gao, JJ., Li, X. et al. Survey on Multi-period Mean–Variance Portfolio Selection Model. J. Oper. Res. Soc. China 10, 599–622 (2022). https://doi.org/10.1007/s40305-022-00397-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40305-022-00397-6

Keywords

Mathematics Subject Classification

Search

Navigation