Abstract
Within the framework of Riehl–Shulman’s synthetic \((\infty ,1)\)-category theory, we present a theory of two-sided cartesian fibrations. Central results are several characterizations of the two-sidedness condition à la Chevalley, Gray, Street, and Riehl–Verity, a two-sided Yoneda Lemma, as well as the proof of several closure properties. Along the way, we also define and investigate a notion of fibered or sliced fibration which is used later to develop the two-sided case in a modular fashion. We also briefly discuss discrete two-sided cartesian fibrations in this setting, corresponding to \((\infty ,1)\)-distributors. The systematics of our definitions and results closely follows Riehl–Verity’s \(\infty \)-cosmos theory, but formulated internally to Riehl–Shulman’s simplicial extension of homotopy type theory. All the constructions and proofs in this framework are by design invariant under homotopy equivalence. Semantically, the synthetic \((\infty ,1)\)-categories correspond to internal \((\infty ,1)\)-categories implemented as Rezk objects in an arbitrary given \((\infty ,1)\)-topos.













Similar content being viewed by others
Notes
Even though this cannot be expressed in our theory yet, cf. [98, Chapter 7].
Note the parallel to axiomatic homotopy theory where a Quillen equivalence between “homotopy theories” presented through model categories lifts to an equivalence of their associated homotopy categories.
Though we will soon also consider certain fibered functors (between fibrations placed in the vertical direction) that can be regarded as fibrations themselves (placed in the horizontal direction).
Generalizing to arbitrary shape inclusions or type maps again this gives rise to the notion of j-LARI cell.
We obtain a formally analogue characterization via Chevalley criteria in the context of j-LARI cells and j-LARI-cell-preserving functors, cf.[98, Theorem A.2.6].
This is a proposition because being a cocartesian arrow is a proposition.
All three objectwise limit notions satisfying the expected universal properties w.r.t. to cocartesian functors.
Recall the uniqueness of cocartesian lifts, cf. [17, Proposition 5.1.3].
Note that for the codomain of the equivalence we have identified the type of morphisms \(\Big (\langle e,f,x\rangle \longrightarrow \langle e',{{\,\textrm{id}\,}}_{e'}, x'\rangle \Big )\) (in the fiber \(\sum _{g:P\,b \mathbin {\downarrow } e'} Q(b,\partial _0\,g)\)) with simply \((x \rightarrow ^{b^*Q}_f x')\).
Again, identifying \(\langle d,f,x\rangle \longrightarrow _{\langle {v},{g}\rangle } \langle e',{{\,\textrm{id}\,}}_{e'}, x'\rangle \) with \(x \rightarrow ^K_{\langle {v},{gf}\rangle } x'\).
Suppressing the repeated data in the lower layers.
For the official naming we prefer the fibrational variant since it is closer to its semantic counterpart, but of course by the typal Grothendieck construction there exists an indexed variant as well.
Note that all the cocartesian lifts exist because they are over P-vertical arrows.
As can e.g. be checked by projection equivalence.
Here, we write
 , giving rise to the comma object \(\sum _{a:A} (a \rightarrow _A a') \times P(a,b)\).
, giving rise to the comma object \(\sum _{a:A} (a \rightarrow _A a') \times P(a,b)\).We are grateful to Emily Riehl for pointing out this example.
We are indebted to Emily Riehl for helpful explanations and discussions about [74, Thm. 7.1.4].
In particular, again the types of each of these identities is a proposition, hence so is their product.
Here, and in the following we will not formally spell out the universal properties, but they are analogous to the respective propositions in [17, Subsection 5.3.3]. The addition/generalization is that the base types are binary products, and the fibrations and functors are two-sided cartesian.
Note in particular that we have an equivalence \(A''' \times B''' \simeq (A' \times B') \times _{A \times B} (A'' \times B'')\).
Where a : A, \(a':A'\) lies strictly over a via \(k'\) etc .
We thank Ulrik Buchholtz for initially suggesting this proof in [17] because it circumvents dealing with unwieldy coherence data that would occur in different presentations of the sequential limit.
All three objectwise limit notions satisfying the expected universal properties w.r.t. to cocartesian functors.
In contrast to the current version of [17, Proposition B.2.3]: one only needs the fibrations involved to be isoinner, and not cocartesian, which in any case becomes clear from the given proof.
This could have also been used as a more direct argument to prove “2 \(\implies \) 1” as well.
By Segal-ness, the witnesses for the triangle identities are actually unique up to contractibility.
This justifies the ensuing list of logical equivalences.
We thank Ulrik Buchholtz for pointing out the subsequent argument.
References
Ahrens, B., Kapulkin, K., Shulman, M.: Univalent categories and the Rezk completion. Math. Struct. Comput. Sci. 25(5), 1010–1039 (2015). https://doi.org/10.1017/S0960129514000486
Ahrens, B., North, P.R., Shulman, M., Tsementzis, D.: The univalence principle (2021). ar**v:2102.06275
Ahrens, B., North, P.R., van der Weide, N.: Bicategorical type theory: semantics and syntax. Math. Struct. Comput. Sci. 33(10), 868–912 (2023). https://doi.org/10.1017/S0960129523000312
Annenkov, D., Capriotti, P., Kraus, N., Sattler, C.: Two-level type theory and applications. Math. Struct. Comput. Sci. (2023). https://doi.org/10.1017/S0960129523000130
Awodey, S.: Type theory and homotopy. In: Epistemology Versus Ontology: Essays on the Philosophy and Foundations of Mathematics in Honour of Per Martin-Löf, pp. 183–201. Springer, Berlin (2012)
Awodey, S., Warren, M.A.: Homotopy theoretic models of identity types. Math. Proc. Camb. Philos. Soc. 146(1), 45–55 (2009). https://doi.org/10.1017/S0305004108001783
Ayala, D., Francis, J.: Fibrations of \(\infty \)-categories. High. Struct. 4(1) (2020). http://journals.mq.edu.au/index.php/higher_structures/article/view/29
Bakovic, I.: Fibrations of bicategories. Preprint available at http://www.irb.hr/korisnici/ibakovic/groth2fib.pdf (2011)
Bardomiano Martínez, C.: Limits and exponentiable functors in simplicial homotopy type theory (2022). https://arxiv.org/abs/2202.12386
Barwick, C., Dotto, E., Glasman, S., Nardin, D., Shah, J.: Parametrized higher category theory and higher algebra: Exposé I—elements of parametrized higher category theory (2016). https://arxiv.org/abs/1608.03657
Barwick, C., Shah, J.: Fibrations in \(\infty \)-category theory. In: 2016 MATRIX annals, pp. 17–42. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-72299-3_2. https://www.matrix-inst.org.au/wp_Matrix2016/wp-content/uploads/2017/08/BarwickShah.pdf
Bénabou, J.: Les distributeurs, rapport 33, inst. de math. Pure et Appl. Univ. Cath. Louvain la Neuve (1973)
Bénabou, J.: Distributors at work (2000). https://www2.mathematik.tu-darmstadt.de/%7Estreicher/FIBR/DiWo.pdf. Notes from lectures at TU Darmstadt taken by Thomas Streicher
Borceux, F.: Handbook of Categorical Algebra: Volume 2, Categories and Structures, vol. 2. Cambridge University Press, Cambridge (1994)
Boavida de Brito, P.: Segal objects and the Grothendieck construction. In: An Alpine Bouquet of Algebraic Topology, Contemporary Mathematics, vol. 708, pp. 19–44. American Mathematical Society, Providence, RI (2018).https://doi.org/10.1090/conm/708/14271
Buchholtz, U.: Higher Structures in Homotopy Type Theory, pp. 151–172. Springer International Publishing, Cham (2019). https://doi.org/10.1007/978-3-030-15655-8_7 . ar**v:1807.02177
Buchholtz, U., Weinberger, J.: Synthetic fibered \((\infty ,1)\)-category theory. High. Struct. 7, 74–165 (2023). https://doi.org/10.21136/HS.2023.04
Capriotti, P.: Models of type theory with strict equality. Ph.D. thesis, The University of Nottingham (2016). ar**v:1702.04912
Capriotti, P., Kraus, N.: Univalent higher categories via complete semi-segal types. Proc. ACM Program. Lang. (2017). https://doi.org/10.1145/3158132
Cavallo, E., Riehl, E., Sattler, C.: On the directed univalence axiom (2018). http://www.math.jhu.edu/~eriehl/JMM2018-directed-univalence.pdf. Talk at AMS Special Session on Homotopy Type Theory, Joint Mathematics Meething, San Diego
Cigoli, A.S., Mantovani, S., Metere, G., Vitale, E.M.: Fibered aspects of Yoneda’s regular span. Adv. Math. 360, 106899 (2020). https://doi.org/10.1016/j.aim.2019.106899. (https://www.sciencedirect.com/science/article/pii/S0001870819305146)
Cisinski, D.C.: Univalent universes for elegant models of homotopy types (2014). ar**v:1406.0058
Cisinski, D.C.: Higher Categories and Homotopical Algebra. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2019). https://doi.org/10.1017/9781108588737
Cisinski, D.C., Nguyen, H.K.: The universal cocartesian fibration (2022). ar**v:2210.08945
Clementino, M.M., Nunes, F.L.: Lax comma \(2\)-categories and admissible \(2\)-functors. Theory Appl. Categ. 40(6), 180–26 (2024). (http://www.tac.mta.ca/tac/volumes/40/6/40-06.pdf)
Cohen, C., Coquand, T., Huber, S., Mörtberg, A.: Cubical type theory: a constructive interpretation of the univalence axiom. In: 21st International Conference on Types for Proofs and Programs (TYPES 2015), LIPIcs. Leibniz Int. Proc. Inform. Schloss Dagstuhl. Leibniz-Zent. Inform., Wadern (2018). https://doi.org/10.4230/LIPIcs.TYPES.2015.5
Cruttwell, G.S.H., Shulman, M.A.: A unified framework for generalized multicategories. Theory Appl. Categ. 24(21), 580–655 (2010)
Di Liberti, I., Loregian, F.: On the unicity of formal category theories. ar**v preprint ar**v:1901.01594 (2019)
Gálvez-Carrillo, I., Kock, J., Tonks, A.: Decomposition spaces and restriction species. Int. Math. Res. Not. 2020(21), 7558–7616 (2020)
Gepner, D., Haugseng, R., Nikolaus, T.: Lax colimits and free fibrations in \(\infty \)-categories. Doc. Math. 22, 1225–1266 (2017). https://doi.org/10.25537/dm.2017v22.1225-1266
Gray, J.W.: Fibred and cofibred categories. In: Eilenberg, S., Harrison, D.K., MacLane, S., Röhrl, H.: (eds.) Proceedings of the Conference on Categorical Algebra, pp. 21–83. Springer, Berlin (1966). https://doi.org/10.1007/978-3-642-99902-4_2
Grayson, D.: An introduction to univalent foundations for mathematicians. Bull. Am. Math. Soc. 55(4), 427–450 (2018). https://doi.org/10.1090/bull/1616
Haugseng, R.: The higher Morita category of \(\mathbb{E} _n\)-algebras. Geom. Topol. 21(3), 1631–1730 (2017)
Haugseng, R., Hebestreit, F., Linskens, S., Nuiten, J.: Two-variable fibrations, factorisation systems and-categories of spans. In: Forum of Mathematics, Sigma, vol. 11, p. e111. Cambridge University Press, Cambridge (2023)
Hermida, C.: On fibred adjunctions and completeness for fibred categories. In: Recent Trends in Data Type Specification, pp. 235–251. Springer (1992). https://doi.org/10.1007/3-540-57867-6_14
Hofmann, M., Streicher, T.: The groupoid model refutes uniqueness of identity proofs. In: Proceedings Ninth Annual IEEE Symposium on Logic in Computer Science, pp. 208–212 (1994).https://doi.org/10.1109/LICS.1994.316071
Hofmann, M., Streicher, T.: Lifting Grothendieck universes. Unpublished note (1997). https://www2.mathematik.tu-darmstadt.de/~streicher/NOTES/lift.pdf
Joyal, A.: Quasi-categories and Kan complexes. J. Pure Appl. Algebra 175(1–3), 207–222 (2002). https://doi.org/10.1016/S0022-4049(02)00135-4. (Special volume celebrating the 70th birthday of Professor Max Kelly)
Joyal, A.: Notes on quasi-categories (2008). http://www.math.uchicago.edu/~may/IMA/Joyal.pdf
Kapulkin, K., Lumsdaine, P.L.: The simplicial model of univalent foundations (after Voevodsky). J. Eur. Math. Soc. 23(6), 2071–2126 (2021)
Kavvos, A.: A quantum of direction (2019). https://www.lambdabetaeta.eu/papers/meio.pdf. Preprint
Kock, A., Kock, J.: Local fibred right adjoints are polynomial. Math. Struct. Comput. Sci. 23(1), 131–141 (2013). https://doi.org/10.1017/S0960129512000217
Kudasov, N.: Rzk. An experimental proof assistant based on a type theory for synthetic \(\infty \)-categories. https://github.com/rzk-lang/rzk
Kudasov, N., Riehl, E., Weinberger, J.: Formalizing the \(\infty \)-categorical Yoneda lemma. In: Proceedings of the 13th ACM SIGPLAN International Conference on Certified Programs and Proofs, pp. 274–290 (2024). https://doi.org/10.1145/3636501.3636945
Li-Bland, D.: The stack of higher internal categories and stacks of iterated spans (2015). ar**v:1506.08870
Licata, D.R., Harper, R.: 2-dimensional directed type theory. In: Twenty-Seventh Conference on the Mathematical Foundations of Programming Semantics (MFPS XXVII), Electronic Notes on Theoretical and Computer Science, vol. 276, pp. 263–289. Elsevier Sci. B. V., Amsterdam (2011). https://doi.org/10.1016/j.entcs.2011.09.026
Loregian, F., Riehl, E.: Categorical notions of fibration. Expo. Math. 38(4), 496–514 (2020). https://doi.org/10.1016/j.exmath.2019.02.004
Lurie, J.: Higher Topos Theory. No. 170 in Annals of Mathematics Studies. Princeton University Press, Princeton (2009)
Lurie, J.: Higher algebra (2017). https://www.math.ias.edu/~lurie/papers/HA.pdf
Martini, L.: Yoneda’s lemma for internal higher categories (2021). https://arxiv.org/abs/2103.17141
Martini, L.: Cocartesian fibrations and straightening internal to an \(\infty \)-topos (2022). ar**v:2204.00295
Martini, L., Wolf, S.: Limits and colimits in internal higher category theory (2022). ar**v:2111.14495
Martini, L., Wolf, S.: Internal higher topos theory (2023). ar**v:2303.06437
McCloskey, E.: Relative weak factorization systems. Master’s thesis, ILLC, Universiteit van Amsterdam (2022). https://eprints.illc.uva.nl/id/eprint/2220/1/MoL-2022-20.text.pdf
Metere, G.: Distributors and the comprehensive factorization system for internal groupoids. Theor. Appl. Categ. Struct. 34(5), 109–120 (2019)
Nguyen, H.K.: Theorems in higher category theory and applications. Ph.D. thesis, Universität Regensburg (2019). https://epub.uni-regensburg.de/38448/
North, P.R.: Towards a directed homotopy type theory. In: Proceedings of the Thirty-Fifth Conference on the Mathematical Foundations of Programming Semantics. Electronic Notes in Theoretical Computer Science, vol. 347, pp. 223–239 (2019)
Nuyts, A.: Towards a directed homotopy type theory based on 4 kinds of variance. Ph.D. thesis, Master Thesis, KU Leuven (2015). https://anuyts.github.io/files/mathesis.pdf
Orton, I., Pitts, A.M.: Axioms for modelling cubical type theory in a topos. In: 25th EACSL Annual Conference and 30th Workshop on Computer Science Logic, CSL’16, Marseille, France, August 29–September 1, 2016. Proceedings, p. 19. Schloss Dagstuhl – Leibniz Zentrum für Informatik, Wadern (2016). https://doi.org/10.4230/LIPIcs.CSL.2016.24. Id/No 24
Penon, D., Penon, J.: 2-catégories réductibles. In: Theory and Applications of Categories Reprints (no. 19, 2010) (1978)
Rasekh, N.: Cartesian fibrations and representability. Homol. Homotopy Appl. 24(2), 135–161 (2022)
Rasekh, N.: Cartesian fibrations of complete segal spaces. High. Struct. 7, 40–73 (2023). https://doi.org/10.21136/HS.2023.03
Rezk, C.: Toposes and homotopy toposes (2010). Unpublished note. http://www.math.uiuc.edu/~rezk/homotopy-topos-sketch.pdf
Rezk, C.: Stuff about quasicategories (2017). https://faculty.math.illinois.edu/~rezk/quasicats.pdf
Riehl, E.: Math 721: homotopy type theory (2021). https://github.com/emilyriehl/721/blob/master/721lectures.pdf. Course notes
Riehl, E.: Could \(\infty \)-category theory be taught to undergraduates? Not. Am. Math. Soc. 70(5) (2023)
Riehl, E., Shulman, M.: A type theory for synthetic \(\infty \)-categories. High. Struct. 1(1), 147–224 (2017). (https://higher-structures.math.cas.cz/api/files/issues/Vol1Iss1/RiehlShulman)
Riehl, E., Verity, D.: The \(2\)-category theory of quasi-categories. Adv. Math. 280, 549–642 (2015). https://doi.org/10.1016/j.aim.2015.04.021
Riehl, E., Verity, D.: Homotopy coherent adjunctions and the formal theory of monads. Adv. Math. 286, 802–888 (2016). https://doi.org/10.1016/j.aim.2015.09.011
Riehl, E., Verity, D.: Fibrations and Yoneda’s lemma in an \(\infty \)-cosmos. J. Pure Appl. Algebra 221(3), 499–564 (2017). https://doi.org/10.1016/j.jpaa.2016.07.003
Riehl, E., Verity, D.: Kan extensions and the calculus of modules for \(\infty \)-categories. Algebr. Geom. Topol. 17(1), 189–271 (2017). https://doi.org/10.2140/agt.2017.17.189
Riehl, E., Verity, D.: Infinity category theory from scratch. High. Struct. 4(1) (2020)
Riehl, E., Verity, D.: Cartesian exponentiation and monadicity. Cah. Topol. Géom. Différ. Catég. (to appear) (2021). ar**v:2101.09853
Riehl, E., Verity, D.: Elements of \(\infty \)-Category Theory. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2022)
Rijke, E.: Introduction to Homotopy Type Theory. Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (2022). ar**v:2212.11082
Ruit, J.: Formal category theory in \(\infty \)-equipments I. ar**v preprint ar**v:2308.03583 (2023)
sHoTT Community, T.: sHoTT library in Rzk (2024). https://rzk-lang.github.io/sHoTT/
Shulman, M.: An explicit description of cocomma-categories? MathOverflow. https://mathoverflow.net/q/247311. Version: 2016-08-11
Shulman, M.: The univalence axiom for elegant Reedy presheaves. Homol. Homotopy Appl. 17(2), 81–106 (2015). https://doi.org/10.4310/HHA.2015.v17.n2.a6
Shulman, M.: Univalence for inverse diagrams and homotopy canonicity. Math. Struct. Comput. Sci. 25(5), 1203–1277 (2015). https://doi.org/10.1017/S0960129514000565
Shulman, M.: Univalence for inverse EI diagrams. Homol. Homotopy Appl. 19(2), 219–249 (2017). https://doi.org/10.4310/HHA.2017.v19.n2.a12
Shulman, M.: All \((\infty ,1)\)-toposes have strict univalent universes (2019). ar**v:1904.07004
Stenzel, R.: Univalence and completeness of segal objects. J. Pure Appl. Algebra 227(4), 107254 (2023)
Stevenson, D.: Model structures for correspondences and bifibrations. ar**v preprint ar**v:1807.08226 (2018)
Street, R.: Elementary Cosmoi. I. Category Seminars, Proceedings, Sydney 1972/1973, Lecture Notes in Mathematics, vol. 420, pp. 134–180 (1974)
Street, R.: Fibrations and Yoneda’s lemma in a \(2\)-category. In: Category Seminar (Proceedings Seminars, Sydney, 1972/1973), pp. 104–133. Lecture Notes in Mathematics, vol. 420 (1974). https://doi.org/10.1007/BFb0063102
Street, R.: Fibrations in bicategories. Cah. Topol. Géom. Différ. 21(2), 111–160 (1980). (http://www.numdam.org/article/CTGDC_1980__21_2_111_0.pdf)
Street, R.: Correction to: “Fibrations in bicategories’’ [Cahiers Topologie Géom. Différentielle 21 (1980), no. 2, 111–160; MR0574662 (81f:18028)]. Cah. Topol. Géom. Différ. Catég. 28(1), 53–56 (1987)
Streicher, T.: A model of type theory in simplicial sets: a brief introduction to Voevodsky’s homotopy type theory. J. Appl. Log. 12(1), 45–49 (2014). https://doi.org/10.1016/j.jal.2013.04.001
Streicher, T.: Fibered categories à la Jean Bénabou (2023). ar**v:1801.02927
Swan, A.: Separating path and identity types in presheaf models of univalent type theory (2018). ar**v:1808.00920
Univalent Foundations Program, T.: Homotopy Type Theory: Univalent Foundations of Mathematics. https://homotopytypetheory.org/book, Institute for Advanced Study (2013)
Voevodsky, V.: Notes on type systems (2009). Unpublished https://www.math.ias.edu/vladimir/sites/math.ias.edu.vladimir/files/expressions_current.pdf
Voevodsky, V.: A simple type system with two identity types (2013). Unpublished note. https://www.math.ias.edu/vladimir/sites/math.ias.edu.vladimir/files/HTS.pdf
Von Glehn, T.: Polynomials, fibrations and distributive laws. Theory Appl. Categ. 33(36), 1111–1144 (2018)
Warren, M.: Directed type theory. Lecture at IAS, Princeton (2013). https://www.youtube.com/watch?v=znn6xEZUKNE
Weaver, M.Z., Licata, D.R.: A constructive model of directed univalence in bicubical sets. In: Proceedings of the 35th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS ’20, pp. 915–928. Association for Computing Machinery, New York, NY, USA (2020). https://doi.org/10.1145/3373718.3394794
Weinberger, J.: A synthetic perspective on \((\infty ,1)\)-category theory: fibrational and semantic aspects. Ph.D. thesis, Technische Universität, Darmstadt (2022). http://tuprints.ulb.tu-darmstadt.de/20716/
Weinberger, J.: Strict stability of extension types (2022). ar**v:2203.07194
Weinberger, J.: Internal sums for synthetic fibered \((\infty ,1)\)-categories. J. Pure Appl. Algebra 228(9), 107659 (2024). https://doi.org/10.1016/j.jpaa.2024.107659
Yoneda, N.: On Ext and exact sequences. J. Fac. Sci. Univ. Tokyo Sect. I 8(507–576), 1960 (1960)
Acknowledgements
I am grateful to the US Army Research Office for the support of some stages of this work under MURI Grant W911NF-20-1-0082. I also thank the Max Planck Institute for Mathematics Bonn for its hospitality and financial support during some work on this project. I wish to thank Ulrik Buchholtz, Emily Riehl, and Thomas Streicher for many helpful discussions, valuable feedback, and steady guidance. The anonymous referee has provided detailed and valuable corrections and suggestions to significantly improve the presentation of the paper, which I am highly grateful for. I am thankful to Tim Campion and Sina Hazratpour for further discussions. Furthermore, I am indebted to Ulrik Buchholtz for his collaboration on synthetic fibered \((\infty ,1)\)-category theory that made the work at hand possible in the first place.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Bjørn Ian Dundas.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Fibered equivalences
We state some expected and useful closure properties of fibered equivalences.
Lemma A.1
(Right properness) Pullbacks of weak equivalences are weak equivalences again, i.e. , given a pullback diagram

then, as indicated if the right vertical map is a weak equivalence, then so is the left hand one.
Proof
Denote by \(P: A \rightarrow \mathcal {U}\) the straightening of \(k:B \rightarrow A\), so that \(B \simeq \sum _{a:A} P\,a\), and \(D \simeq \sum _{c:C} P(j\,c)\). The map \(k:B \rightarrow A\) (identified with its projection equivalence) is a weak equivalence if and only if \(\prod _{a:A} {{\,\textrm{isContr}\,}}(P\,a)\). This implies \(\prod _{c:C} P(j\,c)\) which is equivalent to \(k' = j^*k\) being a weak equivalence, as desired. \(\square \)
Proposition A.1
(Homotopy invariance of homotopy pullbacks) Given a map between cospans of types

where the vertical arrows are weak euivalences the induced map
is an equivalence as well.
Proof
By right properness and 2-out-of-3 the mediating map  is an equivalence as can be seen from the diagram:
is an equivalence as can be seen from the diagram:

This gives the following cube

and by the Pullback Lemma we know that the back face is a pullback, too. Then again, by right properness
is an equivalence. \(\square \)
Proposition A.2
Given a fibered equivalence as below

and a map \(k:A \rightarrow B\) the fibered equivalence \(\varphi \) pulls back as shown below:

Proof
By projection equivalence, we can consider families \(R:B \rightarrow \mathcal {U}\), \(P: F \equiv \widetilde{R} \rightarrow \mathcal {U}\), \(Q : E \equiv \widetilde{P} \rightarrow \mathcal {U}\), with \(F \equiv \widetilde{Q}\). The fibered equivalence \(\varphi \) is given by a family of equivalences
The induced family

also constitutes a fibered equivalence. Commutation of all the diagrams is clear since, after projection equivalence, all the vertical maps are given by projections. \(\square \)
Lemma A.2
(Closedness of fibered equivalences under dependent products) Let I be a type. Suppose given a family \(B:I\rightarrow \mathcal {U}\) and indexed families \(P,Q:\prod _{i:I} B_i \rightarrow \mathcal {U}\) together with a fiberwise equivalence \(\varphi : \prod _{i:I} \prod _{b:B} P_i\,b {\mathop {\longrightarrow }\limits ^{\simeq }} Q_i\,b\). Then the map
induced by taking the dependent product over I is a fiberwise equivalence, too.
Proof
For i : I, we fibrantly replace the given fiberwise equivalence \(\varphi _i\) by projections, giving rise to (strictly) commutative diagrams:

Now, \(\varphi \) being a fiberwise equivalence is equivalent to
By (weak) function extensionality,Footnote 30 this implies
wich yields the desired statement. Note, that the latter equivalence follows by projection equivalence of the diagram obtained by applying \(\prod _{i:I}(-)\):

\(\square \)
Lemma A.3
(Closedness of fibered equivalences under sliced products) Given indexed families \(P,Q:I \rightarrow B \rightarrow \mathcal {U}\) and a family of fibered equivalences \(\prod _{i:I} \prod _{b:B} P_i \,b {\mathop {\longrightarrow }\limits ^{\simeq }} Q_i \,b\). Then the induced fibered functor
between the sliced products over B is also a fibered equivalence.
Proof
As usual, denote for i : by  and
and  the unstraightenings of the given fibered families, giving rise to a (strict) diagram:
the unstraightenings of the given fibered families, giving rise to a (strict) diagram:

Since weak equivalences are closed under taking dependent products, the induced fibered map \(\prod _{i:I} \varphi _i: \prod _{i:I} E_i \rightarrow _{I \rightarrow B} \prod _{i:I} F_i\) is also a weak equivalence, and by right properness Lemma A.1 the desired mediating map is as well:

\(\square \)
Proposition A.3
For an indexing type I and a base Rezk type B, families of fibered equivalences between Rezk types over B are closed under taking sliced products, i.e. : Given a family of isoinner fibrations over B together with a fibered equivalence as below left, the induced maps on the right make up a fibered equivalence as well:

Proof
This is a consequence of Lemmas A.2 and A.3, considering the following diagram:

\(\square \)
Fibered (LARI) adjunctions
Building on previous work [67, Section 11] and [17, Appendix B] we provide a characterization of fibered LARI adjunctions along similar lines.
Theorem B.1
(Characterizations of fibered adjunctions, cf. [67, Theorem 11.23], [17, Theorem B.1.4]) Let B be a Rezk type. For \(P,Q:B \rightarrow \mathcal {U}\) isoinner families we write  and
and  . Given a fibered functor \(\varphi : E \rightarrow _B F\) such that (strictly)
. Given a fibered functor \(\varphi : E \rightarrow _B F\) such that (strictly)

the following are equivalent propositions:
-
1.
The type of fibered left adjoints of \(\varphi \), i.e. , fibered functors \(\psi \) which are ordinary (transposing) left adjoints of \(\varphi \) whose unit, moreover, is vertical.
-
2.
The type of fibered functors \(\psi :F \rightarrow _B E\) together with a vertical 2-cell \(\eta : {{\,\textrm{id}\,}}_F \Rightarrow _B \varphi \psi \) s.t.

is a fiberwise equivalence.
-
3.
The type of sliced (or fiberwise) left adjoints (over B) to \(\varphi \), i.e. , fibered functors \(\psi :F \rightarrow _B E\) together with a fibered equivalence
$$\begin{aligned} \psi \mathbin {\downarrow }_{B} E \simeq _{F \times _B E} F \mathbin {\downarrow }_{B} \varphi . \end{aligned}$$ -
4.
The type of bi-diagrammatic fibered (or fiberwise) left adjoints, i.e. , fibered functors \(\psi \) together with:
-
a vertical natural transformation \(\eta : {{\,\textrm{id}\,}}_F \Rightarrow _B \varphi \psi \)
-
two vertical natural transformations \(\varepsilon , \varepsilon ': \psi \varphi \Rightarrow _B {{\,\textrm{id}\,}}_E\)
-
homotopiesFootnote 31\(\alpha : \varphi \varepsilon \circ \eta \varphi =_{E \rightarrow F} {{\,\textrm{id}\,}}_\varphi , ~\beta : \varepsilon ' \psi \circ \psi \eta =_{F \rightarrow E} {{\,\textrm{id}\,}}_\psi \)
-
-
5.
The type of fibered functors \(\psi \) together with:
-
a vertical natural transformation \(\eta : {{\,\textrm{id}\,}}_F \Rightarrow _B \varphi \psi \)
-
two natural transformations \(\varepsilon , \varepsilon ': \psi \varphi \Rightarrow {{\,\textrm{id}\,}}_E\)
-
homotopies \(\alpha : \varphi \varepsilon \circ \eta \varphi =_{E \rightarrow F} {{\,\textrm{id}\,}}_\varphi , ~\beta : \varepsilon ' \psi \circ \psi \eta =_{F \rightarrow E} {{\,\textrm{id}\,}}_\psi \)
-
Proof
At first, we prove that, given a fixed and fibered functor \(\psi :F \rightarrow _B E\) the respective witnessing data are propositions.Footnote 32
- 1 \(\iff \) 5:
-
This follows from the equivalence between transposing left adjoint and bi-diagrammatic left adjoint data, cf. [67, Theorem 11.23].
- 4 \(\implies \) 5:
-
This is clear since the latter is a weakening of the former.
- 5 \(\implies \) 4:
-
Denoting the base component of \(\varepsilon \) by \(v:\varDelta ^1 \rightarrow (B \rightarrow B) \simeq B \rightarrow (\varDelta ^1 \rightarrow B)\), projecting down from \(\alpha \) via \(\xi \) we obtain the identity \(\xi \alpha : v \circ {{\,\textrm{id}\,}}_B = {{\,\textrm{id}\,}}_B\). Thus \(\varepsilon \) is vertical, and similarly one argues for \(\varepsilon '\).
- 3 \(\iff \) 4:
-
Given the fibered functor \(\psi \), both lists of data witness that for every b : B the components \(\psi _b \dashv \varphi _b: P\,b \rightarrow Q\,b\) define an adjunction between the fibers, again by [67, Theorem 11.23].
- 2 \(\implies \) 3:
-
The latter is an instance of the former.
- 4 \(\implies \) 2:
-
Using naturality and the triangle identities, we show that the fiberwise conditions (vertical case) can be lifted to the case of arbitrary arrows in the base.Footnote 33 Consider the transposing maps:

The first roundtrip yields:

The result yields back k using a triangle identity in the triangle on the left, and naturality of \(\varepsilon \) in the square on the right:

In addition, we have also used naturality of \(\varepsilon \) for \(\psi _a \varepsilon _d \equiv \varepsilon _{\psi _a\,d}\). An analogous argument proves the other roundtrip.
We have proven, that relative to a fixed fibered functor \(\psi : F \rightarrow _B E\) the different kinds of witnesses that this is a fibered left adjoint to \(\varphi \) are equivalent propositions, giving rise to a predicate \({\textrm{isFibLAdj}}_\varphi : (F \rightarrow _B E) \rightarrow {\textrm{Prop}}\). What about the \(\varSigma \)-type  as a whole? E.g. using the data from Item 3 (after conversion via [67, Theorem 11.23]), said type is equivalent to
as a whole? E.g. using the data from Item 3 (after conversion via [67, Theorem 11.23]), said type is equivalent to
Finally, one shows that this is indeed a proposition, completely analogously to the argument given in the proof of [67, Theorem 11.23] for the non-dependent case. \(\square \)
Definition B.1
(Fibered (LARI) adjunction) Let B be a Rezk type and \(\pi : E \twoheadrightarrow B\), \(\xi :F \twoheadrightarrow B\) be isoinner fibrations, with  and
and  . Given a fibered functor \(\varphi : E \rightarrow _B F\), the data of a fibered left adjoint right inverse (LARI) adjunction is given by
. Given a fibered functor \(\varphi : E \rightarrow _B F\), the data of a fibered left adjoint right inverse (LARI) adjunction is given by
-
a fibered functor \(\psi : F \rightarrow _B E\),
-
and an equivalence \(\varPhi : \psi \mathbin {\downarrow }_{B} E \simeq _{F \times _B E} F \mathbin {\downarrow }_{B} \varphi \) s.t. the fibered unit

is a componentwise homotopy.
Together, this defines the data of a fibered LARI adjunction. Diagrammatically, we represent this by:

In fact, as established in the previous works of [67, Section 11] the unit of a coherent adjunction is determined uniquely up to homotopy. Hence, using the characterizations of a (coherent) LARI adjunction, the type of fibered LARI adjunctions in the above sense is equivalent to the type of LARI adjunctions which are also fibered adjunctions. This implies the validity of the familiar closure properties for this restricted class as well.
Sliced commas and products
We record here explicitly some closure properties involving sliced commas and products that are often used, especially in the treatise of two-sided fibrations and related notions.
Proposition C.1
(Dependent products of sliced commas) For a type I and i : I, given fibered cospans
of Rezk types, taking the dependent product fiberwisely commutes with forming sliced comma types:

Proof
We denote by \(P_i, Q_i, R_i: B_i \rightarrow \mathcal {U}\) the straightenings of the given maps \(E_i \twoheadrightarrow B_i\), \(F_i \twoheadrightarrow B_i\), and \(G_i \twoheadrightarrow B_i\), resp. Using projection equivalence, the sliced commas are computed as
From this and the type-theoretic axiom of choice, we obtain as projection equivalence for
the type
This yields the desired fibered equivalence. \(\square \)
Corollary C.1
(Products of commas in a slice) Fix a base Rezk type B be and an indexing type I. Given for i : I an isoinner fibration \(\pi _i:E_i \twoheadrightarrow B\) consider a cospan of isoinner fibrations \(\psi _i: F_i \rightarrow E_i \leftarrow G_i: \varphi \). Then we have a fibered equivalence:

Proposition C.2
(Fibered (LARI) adjunctions are preserved by sliced products) For an indexing type I and a base Rezk type B, families of fibered (LARI) adjunctions between Rezk types over B are closed under taking sliced products, i.e. : Given a family of isoinner fibrations over B together with a fibered (LARI) adjunction as below left, the induced maps on the right make up a fibered (LARI) adjunction as well:

Proof
Given a family of fibered adjunctions as indicated amounts to a family of fibered equivalences, themselves fibered over B, for i : I:

Taking the dependent product over i : I produces a fibered equivalence, itself fibered over \(B^I\). Pullback along \(\textrm{cst}: B \rightarrow B^I\) yields the sliced products and again preserves the fibered equivalence:

Since sliced products canonically commute with both sliced commas and fiber products, this gives a fibered equivalence

which exactly yields the desired fibered adjunction of the sliced products. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Weinberger, J. Two-sided cartesian fibrations of synthetic \((\infty ,1)\)-categories. J. Homotopy Relat. Struct. (2024). https://doi.org/10.1007/s40062-024-00348-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40062-024-00348-3
Keywords
- \((\infty , 1)\)-categories
- Two-sided cartesian fibrations
- Segal spaces
- Rezk spaces
- Fibered Yoneda lemma
- Homotopy type theory
- Simplicial type theory



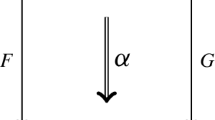
 , giving rise to the comma object
, giving rise to the comma object 



