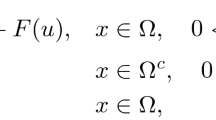Abstract
The main objective of this paper is analysis of the initial-boundary value problems for the linear time-fractional diffusion equations with a uniformly elliptic spatial differential operator of the second order and the Caputo type time-fractional derivative acting in the fractional Sobolev spaces. The boundary conditions are formulated in form of the homogeneous Neumann or Robin conditions. First we discuss the uniqueness and existence of solutions to these initial-boundary value problems. Under some suitable conditions on the problem data, we then prove positivity of the solutions. Based on these results, several comparison principles for the solutions to the initial-boundary value problems for the linear time-fractional diffusion equations are derived.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we deal with a linear time-fractional diffusion equation in the form
where \(\partial _t^{\alpha }\) is the Caputo fractional derivative of order \(\alpha \in (0,1)\) defined on the fractional Sobolev spaces (see Section 2 for the details) and \(\varOmega \subset {\mathbb {R}}^d, \ d=1,2,3\) is a bounded domain with a smooth boundary \(\partial \varOmega \). All the functions under consideration are supposed to be real-valued.
In what follows, we always assume that the following conditions are satisfied:
Using the notations \(\partial _j = \frac{\partial }{\partial x_j}\), \(j=1, 2,\ldots , d\), we define a conormal derivative \(\partial _{\nu _A}w\) with respect to the differential operator \(\sum _{i,j=1}^d\partial _j(a_{ij}\partial _i)\) by
where \(\nu = \nu (x) =: (\nu _1(x),\ldots , \nu _d(x))\) is the unit outward normal vector to \(\partial \varOmega \) at the point \(x := (x_1,\ldots , x_d) \in \partial \varOmega \).
For the equation (1.1), we consider the initial-boundary value problems with the homogeneous Neumann boundary condition
or the more general homogeneous Robin boundary condition
where \(\sigma \) is a sufficiently smooth function on \(\partial \varOmega \) that satisfies the condition \(\sigma (x) \ge 0,\ x\in \partial \varOmega \).
For partial differential equations of the parabolic type that correspond to the case \(\alpha =1\) in the equation (1.1), several important qualitative properties of solutions to the corresponding initial-boundary value problems are known. In particular, we mention a maximum principle and a comparison principle for the solutions to these problems ([28, 29]).
The main purpose of this paper is the comparison principles for the linear time-fractional diffusion equation (1.1) with the Neumann or the Robin boundary conditions.
For the equations of type (1.1) with the Dirichlet boundary conditions, the maximum principles in different formulations were derived and used in [3, 17,18,19,20,21,22,23, 33]. For a maximum principle for the time-fractional transport equations we refer to [24]. In [12], a maximum principle for more general space- and time-space-fractional partial differential equations has been derived.
Because any maximum principle involves the Dirichlet boundary values, its formulation in the case of the Neumann or Robin boundary conditions requires more cares. For this kind of the boundary conditions, both positivity of solutions and the comparison principles can be derived under some suitable restrictions on the problem data. One typical result of this sort says that the solution u to the equation (1.1) with the boundary condition (1.4) or (1.5) and an appropriately formulated initial condition is non-negative in \(\varOmega \times (0,T)\) if the initial value a and the non-homogeneous term F are non-negative in \(\varOmega \) and in \(\varOmega \times (0,T)\), respectively. Such positivity properties and their applications have been intensively discussed and used for the partial differential equations of parabolic type (\(\alpha =1\) in the equation (1.1)), see, e.g., [4, 5, 25], or [29].
However, to the best knowledge of the authors, no results of this kind have been published for the time-fractional diffusion equations in the case of the Neumann or Robin boundary conditions. The main subject of this paper is in derivation of a positivity property and the comparison principles for the linear equation (1.1) with the boundary condition (1.4) or (1.5) and an appropriately formulated initial condition. In the subsequent paper, these result will be extended to the case of the semilinear time-fractional diffusion equations. The arguments employed in these papers rely on an operator theoretical approach to the fractional integrals and derivatives in the fractional Sobolev spaces that is an extension of the theory well-known in the case \(\alpha =1\), see, e.g., [10, 26, 30]. We also refer to the recent publications [2] and [16] devoted to the comparison principles for solutions to the fractional differential inequalities with the general fractional derivatives and for solutions to the ordinary fractional differential equations, respectively.
The rest of this paper is organized as follows. In Section 2, some important results regarding the unique existence of solutions to the initial-boundary value problems for the linear time-fractional diffusion equations are presented. Section 3 is devoted to a proof of a key lemma that is a basis for the proofs of the comparison principles for the linear and semilinear time-fractional diffusion equations. The lemma asserts that each solution to (1.1) is non-negative in \(\varOmega \times (0,T)\) if \(a\ge 0\) and \(F \ge 0\), provided that u is assumed to satisfy some extra regularity. In Section 4, we prove a comparison principle that is our main result for the problem (1.1) for the linear time-fractional diffusion equation. Moreover, we establish the order-preserving properties for other problem data (the zeroth-order coefficient c of the equation and the coefficient \(\sigma \) of the Robin condition). Finally, a detailed proof of an important auxiliary statement is presented in an Appendix.
2 Well-posedness results
For \(x \in \varOmega , 0<t<T\), we define an operator
and assume that the conditions (1.2) for the coefficients \(a_{ij}, b_j, c\) are satisfied.
In this section, we deal with the following initial-boundary value problem for the linear time-fractional diffusion equation (1.1) with the time-fractional derivative of order \(\alpha \in (0,1)\)
along with the initial condition (2.3) formulated below.
To appropriately define the Caputo fractional derivative \(d_t^{\alpha }w(t)\), \(0<\alpha <1\), we start with its definition on the space
that reads as follows:
Then we extend this operator from the domain \({\mathcal {D}}(d_t^{\alpha }) := {_{0}C^1[0,T]}\) to \(L^2(0,T)\) taking into account its closability ( [32]). As have been shown in [13], there exists a unique minimum closed extension of \(d_t^{\alpha }\) with the domain \({\mathcal {D}}(d_t^{\alpha }) = {_{0}C^1[0,T]}\). Moreover, the domain of this extension is the closure of \({_{0}C^1[0,T]}\) in the Sobolev-Slobodeckij space \(H^{\alpha }(0,T)\). Let us recall that the norm \(\Vert \cdot \Vert _{H^{\alpha } (0,T)}\) of the Sobolev-Slobodeckij space \(H^{\alpha }(0,T)\) is defined as follows ( [1]):
By setting
we obtain ( [13])
and
In what follows, we also use the Riemann-Liouville fractional integral operator \(J^{\beta }\), \(\beta > 0\) defined by
Then, according to [9] and [13],
Next we define
As have been shown in [9] and [13], there exists a constant \(C>0\) depending only on \(\alpha \) such that
Now we can introduce a suitable form of initial condition for the problem (2.2) as follows
and write down a complete formulation of an initial-boundary value problem for the linear time-fractional diffusion equation (1.1):
It is worth mentioning that the term \(\partial _t^{\alpha }(u(x,t) - a(x))\) in the first line of (2.4) is well-defined due to inclusion formulated in the third line of (2.4). In particular, for \(\frac{1}{2}< \alpha < 1\), the Sobolev embedding leads to the inclusions \(H_{\alpha }(0,T) \subset H^{\alpha }(0,T)\subset C[0,T]\). This means that \(u\in H_{\alpha }(0,T;L^2(\varOmega ))\) implies \(u \in C([0,T];L^2(\varOmega ))\) and thus in this case the initial condition can be formulated as \(u(\cdot ,0) = a\) in \(L^2\)-sense. Moreover, for sufficiently smooth functions a and F, the solution to (2.4) can be proved to satisfy the initial condition in a usual sense: \(\lim _{t\rightarrow 0} u(\cdot ,t) = a\) in \(L^2(\varOmega )\) (see Lemma 4 in Section 4). Consequently, the third line of (2.4) can be interpreted as a generalized initial condition.
In the following theorem, a fundamental result regarding the unique existence of the solution to the initial-boundary value problem (2.4) is presented.
Theorem 1
For \(a\in H^1(\varOmega )\) and \(F \in L^2(0,T;L^2(\varOmega ))\), there exists a unique solution \(u(F,a) = u(F,a)(x,t) \in L^2(0,T;H^2(\varOmega ))\) to the initial-boundary value problem (2.4) such that \(u(F,a)-a \in H_{\alpha }(0,T;L^2(\varOmega ))\).
Moreover, there exists a constant \(C>0\) such that
Before starting with the proof of Theorem 1, we introduce some notations and derive several helpful results needed for the proof.
For an arbitrary constant \(c_0>0\), we define an elliptic operator \(A_0\) as follows:
We recall that in the definition (2.5), \(\sigma \) is a smooth function, the inequality \(\sigma (x)\ge 0,\ x\in \partial \varOmega \) holds true, and the coefficients \(a_{ij}\) satisfy the conditions (1.2).
Henceforth, by \(\Vert \cdot \Vert \) and \((\cdot ,\cdot )\) we denote the standard norm and the scalar product in \(L^2(\varOmega )\), respectively. It is well-known that the operator \(A_0\) is self-adjoint and its resolvent is a compact operator. Moreover, for a sufficiently large constant \(c_0>0\), by Lemma 6 in Section 1, we can verify that \(A_0\) is positive definite. Therefore, by choosing the constant \(c_0>0\) large enough, the spectrum of \(A_0\) consists entirely of discrete positive eigenvalues \(0 < \lambda _1 \le \lambda _2 \le \cdots \), which are numbered according to their multiplicities and \(\lambda _n \rightarrow \infty \) as \(n\rightarrow \infty \). Let \(\varphi _n\) be an eigenvector corresponding to the eigenvalue \(\lambda _n\) such that \(A\varphi _n = \lambda _n\varphi _n\) and \((\varphi _n, \varphi _m) = 0\) if \(n \ne m\) and \((\varphi _n,\varphi _n) = 1\). Then the system \(\{ \varphi _n\}_{n\in {\mathbb {N}}}\) of the eigenvectors forms an orthonormal basis in \(L^2(\varOmega )\) and for any \(\gamma \ge 0\) we can define the fractional powers \(A_0^{\gamma }\) of the operator \(A_0\) by the following relation (see, e.g., [26]):
where
and
We note that \({\mathcal {D}}(A_0^{\gamma }) \subset H^{2\gamma }(\varOmega )\).
Our proof of Theorem 1 is similar to the one presented in [9, 13] for the case of the homogeneous Dirichlet boundary condition. In particular, we employ the operators S(t) and K(t) defined by ( [9, 13])
and
In the above formulas, \(E_{\alpha ,\beta }(z)\) denotes the Mittag-Leffler function defined by a convergent series as follows:
It follows directly from the definitions given above that \(A_0^{\gamma }K(t)a = K(t)A_0^{\gamma }a\) and \(A_0^{\gamma }S(t)a = S(t)A_0^{\gamma }a\) for \(a \in {\mathcal {D}} (A_0^{\gamma })\). Moreover, the inequality (see, e.g., Theorem 1.6 (p. 35) in [27])
implicates the estimations ( [9])
In order to shorten the notations and to focus on the dependence on the time variable t, henceforth we sometimes omit the variable x in the functions of two variables x and t and write, say, u(t) instead of \(u(\cdot ,t)\).
Due to the inequalities (2.8), the estimations provided in the formulation of Theorem 1 can be derived as in the case of the fractional powers of generators of the analytic semigroups ( [10]). To do this, we first formulate and prove the following lemma:
Lemma 1
Under the conditions formulated above, the following estimates hold true for \(F\in L^2(0,T;L^2(\varOmega ))\) and \(a \in L^2(\varOmega )\):
-
(i)
$$\begin{aligned} \left\| \int ^t_0 A_0K(t-s)F(s) ds \right\| _{L^2(0,T;L^2(\varOmega ))} \le C\Vert F\Vert _{L^2(0,T;L^2(\varOmega ))}, \end{aligned}$$
-
(ii)
$$\begin{aligned} \left\| \int ^t_0 K(t-s)F(s) ds \right\| _{H_{\alpha }(0,T;L^2(\varOmega ))} \le C\Vert F\Vert _{L^2(0,T;L^2(\varOmega ))}, \end{aligned}$$
-
(iii)
$$\begin{aligned} \Vert S(t)a - a\Vert _{H_{\alpha }(0,T;L^2(\varOmega ))} + \Vert S(t)a\Vert _{L^2(0,T;H^2(\varOmega ))} \le C\Vert a\Vert . \end{aligned}$$
Proof
We start with proving the estimate (i). By (2.7), we have
Therefore, using the Parseval equality and the Young inequality for the convolution, we obtain
Then we employ the representation
and the complete monotonicity of the Mittag-Leffler function ( [8])
to get the inequality
Hence,
Now we proceed with proving the estimate (ii). For \(0<t<T, \, n\in {\mathbb {N}}\) and \(f\in L^2(0,T)\), we set
Then
in \(L^2(\varOmega )\) for any fixed \(t \in [0,T]\).
First we prove that
In order to prove this, we apply the Riemann-Liouville fractional integral \(J^{\alpha }\) to \(L_nf\) and get the representation
By direct calculations, using (2.9), we obtain the formula
Therefore, we have the relation
that is,
Hence, \(L_nf \in H_{\alpha }(0,T) = J^{\alpha }L^2(0,T)\). By definition, \(\partial _t^{\alpha }= (J^{\alpha })^{-1}\) ( [13]) and thus the last formula can be rewritten in the form
Using the inequality (2.10), we obtain
Therefore,
Thus, the estimate (2.11) is proved.
Now we set \(f_n(s) := (F(s), \, \varphi _n)\) for \(0<s<T\) and \(n\in {\mathbb {N}}\). Since
we obtain
By applying (2.11), we get the following chain of inequalities and equations:
Thus, the proof of the estimate (ii) is completed.
The estimate (iii) from Lemma 1 follows from the standard estimates of the operator S(t). It can be derived by the same arguments as those that were employed in Section 6 of Chapter 4 in [13] for the case of the homogeneous Dirichlet boundary condition and we omit here the technical details. \(\square \)
Now we proceed to the proof of Theorem 1.
Proof
In the first line of the problem (2.4), we regard the expressions \(\sum _{j=1}^d b_j(x,t)\partial _ju\) and c(x, t)u as some non-homogeneous terms. Then this problem can be rewritten in terms of the operator \(A_0\) as follows
In its turn, the first line of (2.12) can be represented in the form ( [9, 13])
Moreover, it is known that if \(u\in L^2(0,T;H^2(\varOmega ))\) satisfies the initial condition \(u-a \in H_{\alpha }(0,T;L^2(\varOmega ))\) and the equation (2.13), then u is a solution to the problem (2.12). With the notations
the equation (2.13) can be represented in form of a fixed point equation \(u = Ru + G\) on the space \(L^2(0,T;H^2(\varOmega ))\).
Lemma 1 yields the inclusion \(G \in L^2(0,T;H^2(\varOmega ))\). Moreover, since \(\Vert A_0^{\frac{1}{2}}a\Vert \le C\Vert a\Vert _{H^1(\varOmega )}\) and \({\mathcal {D}}(A_0^{\frac{1}{2}}) = H^1(\varOmega )\) (see, e.g., [6]), the estimate (2.8) implies
and thus
Consequently, the inclusion \(S(t)a \in L^2(0,T;H^2(\varOmega ))\) holds valid.
For \(0<t<T\), we next estimate \(\Vert Rv(\cdot ,t)\Vert _{H^2(\varOmega )}\) for \(v(\cdot ,t) \in {\mathcal {D}}(A_0)\) as follows:
For derivation of this estimate, we employed the inequalities
and \(\Vert (c(s)+c_0)v(s)\Vert _{H^1(\varOmega )} \le C\Vert v(s)\Vert _{H^2(\varOmega )}\) that are valid because of the inclusions \(b_j \in C^1(\overline{\varOmega }\times [0,T])\)) and \(c+c_0\in C([0,T];C^1(\overline{\varOmega }))\).
Since \((J^{\frac{1}{2}\alpha }w_1)(t) \ge (J^{\frac{1}{2}\alpha }w_2)(t)\) if \(w_1(t) \ge w_2(t)\) for \(0\le t\le T\), and \(J^{\frac{1}{2}\alpha }J^{\frac{1}{2}\alpha }w = J^{\alpha }w\) for \(w_1, w_2, w \in L^2(0,T)\), we have
Repeating this argumentation m-times, we obtain
Applying the Young inequality to the integral at the right-hand side of the last estimate, we arrive to the inequality
Employing the known asymptotic behavior of the gamma function, we obtain the relation
that means that for sufficiently large \(m\in {\mathbb {N}}\), the map**
is a contraction. Hence, by the Banach fixed point theorem, the equation (2.13) possesses a unique fixed point. Therefore, by the first equation in (2.4), we obtain the inclusion \(\partial _t^{\alpha }(u-a) \in L^2(0,T;L^2(\varOmega ))\). Since \(\Vert \eta \Vert _{H_{\alpha }(0,T)} \sim \Vert \partial _t^{\alpha }\eta \Vert _{L^2(0,T)}\) for \(\eta \in H_{\alpha }(0,T)\) ( [13]), we finally obtain the estimate
The proof of Theorem 1 is completed. \(\square \)
3 Key lemma
For derivation of the comparison principles for solutions to the initial-boundary value problems for the linear and semilinear time-fractional diffusion equations, we need some auxiliary results that are formulated and proved in this section.
In addition to the operator \(-A_0\) defined by (2.5), we define an elliptic operator \(-A_1\) with a positive zeroth-order coefficient:
where \(b_0 \in C^1([0,T];C^1(\overline{\varOmega })) \cap C([0,T];C^2(\overline{\varOmega }))\), \(b_0(x,t) > 0,\ (x,t)\in \overline{\varOmega }\times [0,T]\), and \(\min _{(x,t)\in \overline{\varOmega }\times [0,T]} b_0(x,t)\) is sufficiently large.
We also recall that for \(y\in W^{1,1}(0,T)\), the pointwise Caputo derivative \(d_t^{\alpha }\) is defined by
In what follows, we employ an extremum principle for the Caputo fractional derivative formulated below.
Lemma 2
([17]) Let the inclusions \(y\in C[0,T]\) and \(t^{1-\alpha }y' \in C[0,T]\) hold true.
If the function \(y=y(t)\) attains its minimum over the interval [0, T] at the point \(t_0 \in (0, \,T]\), then
In Lemma 2, the assumption \(t_0>0\) is essential. This lemma was formulated and proved in [17] under a weaker regularity condition posed on the function y, but for our arguments we can assume that \(y\in C[0,T]\) and \(t^{1-\alpha }y' \in C[0,T]\).
Employing Lemma 2, we now formulate and prove our key lemma that is a basis for further derivations in this paper.
Lemma 3
(Positivity of a smooth solution) For \(F\in L^2(0,T;L^2(\varOmega ))\) and \(a\in H^1(\varOmega )\), let \(F(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\), \(a(x)\ge 0,\ x\in \varOmega \), and \(\min _{(x,t)\in \overline{\varOmega }\times [0,T]} b_0(x,t)\) be a sufficiently large positive constant. Furthermore, we assume that there exists a solution \(u\in C([0,T];C^2(\overline{\varOmega }))\) to the initial-boundary value problem
and u satisfies the condition \(t^{1-\alpha }\partial _tu \in C([0,T];C(\overline{\varOmega }))\).
Then the solution u is non-negative:
For the partial differential equations of parabolic type with the Robin boundary condition (\(\alpha =1\) in (3.3)), a similar positivity property is well-known (see, e.g., [11]). However, it is worth mentioning that the regularity of the solution to the problem (3.3) at the point \(t=0\) is a more delicate question compared to the one in the case \(\alpha =1\). In particular, we cannot expect the inclusion \(u(x,\cdot ) \in C^1[0,T]\). This can be illustrated by a simple example of the equation \(\partial _t^{\alpha }y(t) = y(t)\) with \(y(t)-1 \in H_{\alpha }(0,T)\) whose unique solution \(y(t) = E_{\alpha ,1}(t^{\alpha })\) does not belong to the space \(C^1[0,T]\).
Proof
First we introduce an auxiliary function \(\psi \in C^1([0,T];C^2(\overline{\varOmega }))\) that satisfies the conditions
Proving existence of such function \(\psi \) is non-trivial. In this section, we focus on the proof of the lemma and then come back to the problem (3.4) in Appendix.
Now, choosing \(M>0\) sufficiently large and \(\varepsilon >0\) sufficiently small, we set
For a fixed \(x\in \varOmega \), by the assumption on the regularity of u, we have the inclusion
Then, \(\partial _tu(x,\cdot ) \in L^1(0,T)\), that is, \(u(x,\cdot ) \in W^{1,1}(0,T)\). Moreover,
On the other hand, for \(w\in H_{\alpha }(0,T) \cap W^{1,1}(0,T)\) and \(w(0) = 0\), the equality
holds true with any constant c (see, e.g., Theorem 2.4 of Chapter 2 in [13]).
Since \(u(x,\cdot ) - a \in H_{\alpha }(0,T)\) and \(u(x,\cdot ) \in W^{1,1}(0,T)\), by (3.7), the relations \(\partial _t^{\alpha }(u-a) = d_t^{\alpha }(u-a) = d_t^{\alpha }u\) hold true for almost all \(x\in \varOmega \).
Furthermore, since \(\varepsilon (M+\psi (\cdot ,t)+t^{\alpha }) \in W^{1,1}(0,T)\), we obtain
and
Now we choose a constant \(M>0\) such that \(M + \psi (x,t) \ge 0\) and \(d_t^{\alpha }\psi (x,t) + b_0(x,t)M > 0\) for \((x,t) \in \overline{\varOmega } \times [0,T]\), so that
Moreover, because of the relation \(\partial _{\nu _A}w = \partial _{\nu _A}u + \varepsilon \partial _{\nu _A}\psi \), we obtain the following estimate:
Evaluation of the representation (3.5) at the point \(t=0\) immediately leads to the formula
Let us assume that the inequality
does not hold valid, that is, there exists a point \((x_0,t_0) \in \overline{\varOmega }\times [0,T]\) such that
Since \(M>0\) is sufficiently large and u(x, 0) is non-negative, we obtain the inequality
and thus \(t_0\) cannot be zero.
Next, we show that \(x_0 \not \in \partial \varOmega \). Indeed, let us assume that \(x_0 \in \partial \varOmega \). Then the estimate (3.9) yields that \(\partial _{\nu _A}w(x_0,t_0) + \sigma (x_0)w(x_0,t_0) \ge \varepsilon \). By (3.10) and \(\sigma (x_0)\ge 0\), we obtain
which implies
Here \({\mathcal {A}}(x) = (a_{ij}(x))_{1\le i,j\le d}\) and \([b]_i\) means the i-th element of a vector b.
For sufficiently small \(\varepsilon _0>0\) and \(x_0\in \partial \varOmega \), we now verify the inclusion
Indeed, since the matrix \({\mathcal {A}}(x_0)\) is positive-definite, the inequality
holds true. In other words, the inequality
is satisfied. Because the boundary \(\partial \varOmega \) is smooth, the domain \(\varOmega \) is locally located on one side of \(\partial \varOmega \). In a small neighborhood of the point \(x_0\in \partial \varOmega \), the boundary \(\partial \varOmega \) can be described in the local coordinates composed of its tangential component in \({\mathbb {R}}^{d-1}\) and the normal component along \(\nu (x_0)\). Consequently, if \(y \in {\mathbb {R}}^d\) satisfies the inequality \(\angle (\nu (x_0), y-x_0) > \frac{\pi }{2}\), then \(y\in \varOmega \). Therefore, for a sufficiently small \(\varepsilon _0>0\), the point \(x_0-\varepsilon _0{\mathcal {A}}(x_0)\nu (x_0)\) is located in \(\varOmega \) and we have proved the inclusion (3.12).
Moreover, for sufficiently small \(\varepsilon _0>0\), we can prove that
Indeed, the inequality (3.10) yields
Then, by the mean value theorem, we obtain the inequality
where \(\theta \) is a number between 0 and \(\xi \in (0,\varepsilon _0)\). Thus, the inequality (3.13) is verified.
By combining (3.13) with (3.12), we conclude that there exists a point \(\widetilde{x_0} \in \varOmega \) such that the inequality \(w(\widetilde{x_0},t_0) < w(x_0,t_0)\) holds true, which contradicts the assumption (3.10). Thus, we have proved that \(x_0 \not \in \partial \varOmega \).
According to (3.10), the function w attains its minimum at the point \((x_0,t_0)\). Because \(0 < t_0 \le T\), Lemma 2 yields the inequality
Since \(x_0 \in \varOmega \), the necessary condition for an extremum point leads to the equality
Moreover, because the function w attains its minimum at the point \(x_0 \in \varOmega \), in view of the sign of the Hessian, the inequality
holds true (see, e.g., the proof of Lemma 1 in Section 1 of Chapter 2 in [5]).
The inequalities \(b(x_0,t_0)>0\), \(w(x_0,t_0) < 0\), and (3.14)-(3.16) lead to the estimate
which contradicts the inequality (3.8).
Thus, we have proved that
Since \(\varepsilon >0\) is arbitrary, we let \(\varepsilon \downarrow 0\) to obtain the inequality \(u(x,t) \ge 0\) for \((x,t) \in \varOmega \times (0,T)\) and the proof of Lemma 3 is completed. \(\square \)
Let us finally mention that the positivity of the function \(b_0\) from the definition of the operator \(-A_1\) is an essential condition for validity of our proof of Lemma 3. However, in the next section, we remove this condition while deriving the comparison principles for the solutions to the initial-boundary value problem (2.4).
4 Comparison principles
According to the results formulated in Theorem 1, in this section, we consider the solutions to the initial-boundary value problem (2.4) that belong to the following space of functions:
In what follows, by u(F, a) we denote the solution to the problem (2.4) with the initial data a and the source function F.
Our first result concerning the comparison principles for the solutions to the initial-boundary value problems for the linear time-fractional diffusion equation is presented in the next theorem.
Theorem 2
Let the functions \(a \in H^1(\varOmega )\) and \(F \in L^2(\varOmega \times (0,T))\) satisfy the inequalities \(F(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\) and \(a(x) \ge 0,\ x\in \varOmega \), respectively.
Then the solution \(u(F,a) \in {\mathcal {Y}}_\alpha \) to the initial-boundary value problem (2.4) is non-negative, e.g., the inequality
holds true.
Let us emphasize that the non-negativity of the solution u to the problem (2.4) holds true for the space \( {\mathcal {Y}}_\alpha \) and thus u does not necessarily satisfy the inclusions \(u \in C([0,T];C^2(\overline{\varOmega }))\) and \(t^{1-\alpha }\partial _tu \in C([0,T]; C(\overline{\varOmega }))\). Therefore, Theorem 2 is widely applicable. Before presenting its proof, let us discuss one of its corollaries in form of a comparison property:
Corollary 1
Let \(a_1, a_2 \in H^1(\varOmega )\) and \(F_1, F_2 \in L^2(\varOmega \times (0,T))\) satisfy the inequalities \(a_1(x) \ge a_2(x),\ x\in \varOmega \) and \(F_1(x,t) \ge F_2(x,t), \ (x,t)\in \varOmega \times (0,T)\), respectively.
Then the inequality
holds true.
Proof
Setting \(a:= a_1-a_2\), \(F:= F_1 - F_2\) and \(u:= u(F_1,a_1) - u(F_2,a_2)\), we immediately obtain the inequalities \(a(x)\ge 0,\ x\in \varOmega \) and \(F(x,t)\ge 0, \ (x,t)\in \varOmega \times (0,T)\) and
Therefore, Theorem 2 implies that \(u(x,t)\ge 0, \ (x,t)\in \varOmega \times (0,T)\), that is, \(u(F_1, a_1)(x,t) \ge u(F_2,a_2)(x,t), \ (x,t)\in \varOmega \times (0,T)\). \(\square \)
In its turn, Corollary 1 can be applied for derivation of the lower and upper bounds for the solutions to the initial-boundary value problem (2.4) by suitably choosing the initial values and the source functions. Let us demonstrate this technique on an example.
Example 1
Let the coefficients \(a_{ij}, b_j\), \(1\le i,j\le d\) of the operator
from the initial-boundary value problem (2.4) satisfy the conditions (1.2). Now we consider the homogeneous initial condition \(a(x)=0,\ x\in \varOmega \) and assume that the source function \(F \in L^2(0,T;L^2(\varOmega ))\) satisfies the inequality
with certain constants \(\beta \ge 0\) and \(\delta >0\).
Then the solution u(F, 0) can be estimated from below as follows:
Indeed, it is easy to verify that the function
is a solution to the following problem:
Due to the inequality \(F(x,t) \ge \delta t^{\beta },\ (x,t) \in \varOmega \times (0,T)\), we can apply Corollary 1 to the solutions u and \({\underline{u}}\) and the inequality (4.2) immediately follows.
In particular, for the spatial dimensions \(d \le 3\), the Sobolev embedding theorem leads to the inclusion \(u \in L^2(0,T;H^2(\varOmega )) \subset L^2(0,T;C(\overline{\varOmega }))\) and thus the strict inequality \(u(F,0)(x,t) > 0\) holds true for almost all \(t>0\) and all \(x\in \overline{\varOmega }\).
Now we proceed to the proof of Theorem 2.
Proof
In the proof, we employ the operators Qv(t) and G(t) defined by (2.14). In terms of these operators, the solution \(u(t):= u(F,a)(t)\) to the initial-boundary problem (2.4) satisfies the integral equation
For readers’ convenience, we split the proof into three parts.
I. First part of the proof: existence of a smoother solution
In the formulation of Lemma 3, we assumed existence of a solution \(u\in C([0,T];C^2(\overline{\varOmega }))\) to the initial-boundary value problem (3.3) satisfying the inclusion \(t^{1-\alpha }\partial _tu \in C([0,T];C(\overline{\varOmega }))\). On the other hand, Theorem 1 asserts the unique existence of solution u to the initial-boundary value problem (2.4) from the space \({\mathcal {Y}}_\alpha \), i.e., of the solution u that satisfies the inclusions \(u\in L^2(0,T;H^2(\varOmega ))\) and \(u - a \in H_{\alpha }(0,T;L^2(\varOmega ))\).
In this part of the proof, we show that for \(a \in C^{\infty }_0(\varOmega )\) and \(F \in C^{\infty }_0(\varOmega \times (0,T))\), the solution to the problem (2.4) satisfies the regularity assumptions formulated in Lemma 3.
More precisely, we first prove the following lemma:
Lemma 4
Let \(a_{ij}\), \(b_j\), c satisfy the conditions (1.2) and the inclusions \(a\in C^{\infty }_0(\varOmega )\), \(F \in C^{\infty }_0(\varOmega \times (0,T))\) hold true.
Then the solution \(u=u(F,a)\) to the problem (2.4) satisfies the inclusions
and \(\lim _{t\rightarrow 0} \Vert u(t) - a\Vert _{L^2(\varOmega )} = 0\).
Proof
We recall that \(c_0>0\) is a positive fixed constant and
Then \({\mathcal {D}}(A_0^{\frac{1}{2}}) = H^1(\varOmega )\) and \(\Vert A_0^{\frac{1}{2}}v\Vert \sim \Vert v\Vert _{H^1(\varOmega )}\) ( [6]). Moreover, for the operators S(t) and K(t) defined by (2.6) and (2.7), the estimates (2.8) hold true.
In what follows, we denote \( \frac{\partial u}{\partial t}(\cdot ,t)\) by \(u'(t) = \frac{du}{dt}(t)\) if there is no fear of confusion.
The solution u to the integral equation (4.3) can be constructed as a fixed point of the equation
As already proved, this fixed point satisfies the inclusion \(u\in L^2(0,T;H^2(\varOmega ))\) \( \cap \) \( (H_{\alpha }(0,T;L^2(\varOmega )) + \{ a\}).\)
Now we derive some estimates for the norms \(\Vert A_0^{\kappa }u(t)\Vert \), \(\kappa =1,2\) and \(\Vert A_0u'(t)\Vert \) for \(0<t<T\). First we set
Since \(F\in C^{\infty }_0(\varOmega \times (0,T))\), we obtain the inclusion \(F\in L^{\infty }(0,T;{\mathcal {D}}(A_0^2))\) and the inequality \(D < +\infty \). Moreover, in view of (2.8), for \(\kappa =1,2\), we get the estimates
The regularity conditions (1.2) lead to the estimates
Moreover,
by using the inequalities (2.8). Then
The generalized Gronwall inequality yields the estimate
which implies the inequality
Next, for the space \(C([0,T]; L^2(\varOmega ))\), we can repeat the same arguments as the ones employed for the iterations \(R^n\) of the operator R in the proof of Theorem 1 and apply the fixed point theorem to the equation (4.3) that leads to the inclusion \(A_0u \in C([0,T];L^2(\varOmega ))\). The obtained results implicate
Choosing \(\varepsilon _0 > 0\) sufficiently small, we have the equation
Next, according to [6], the inclusion
holds true. Now we proceed to the proof of the inclusion \(Q(s)u(s) \in {\mathcal {D}}(A_0^{\frac{3}{4}-\varepsilon _0})\). By (2.8), we obtain the inequality
which leads to the estimate
because of the inequality
which follows from the regularity conditions (1.2) posed on the coefficients \(b_j, c\).
For \(0<t<T\), the generalized Gronwall inequality applied to the integral inequality (4.8) yields the estimate
For the relation (4.7), we repeat the same arguments as the ones employed in the proof of Theorem 1 to estimate \(A_0^{\frac{3}{2}}u(t)\) in the norm \(C([0,T];L^2(\varOmega ))\) by the fixed point theorem arguments and thus we obtain the inclusion \(A_0^{\frac{3}{2}}u \in C([0,T];L^2(\varOmega ))\).
Summarising the estimates derived above, we have shown that
Next we estimate the norm \(\Vert Au'(t)\Vert \). First, \(u'(t)\) is represented in the form
so that
Similarly to the arguments applied for derivation of (4.5), we obtain the inequality
The inclusion \(Q(0)u(0) = Q(0)a \in C^2_0(\varOmega ) \subset {\mathcal {D}}(A_0)\) follows from the regularity conditions (1.2) and the inclusion \(a \in C^{\infty }_0(\varOmega )\). Furthermore, by (2.7) and (2.8), we obtain
and
Hence, the representation (4.10) leads to the estimate
Now we consider a vector space
with the norm
It is easy to verify that \(\widetilde{X}\) with the norm \(\Vert v\Vert _{\widetilde{X}}\) defined above is a Banach space.
Arguing similarly to the proof of Theorem 1 and applying the fixed point theorem in the Banach space \(\widetilde{X}\), we conclude that \(A_0u \in \widetilde{X}\), that is, \(t^{1-\alpha }A_0u' \in C([0,T];L^2(\varOmega ))\). Using the inclusion \({\mathcal {D}}(A_0) \subset C(\overline{\varOmega })\) in the spatial dimensions \(d=1,2,3\), the Sobolev embedding theorem yields
Now we proceed to the estimation of \(A_0^2u(t)\). Since \(\frac{d}{ds}(-A_0^{-1}S(s)) = K(s)\) for \(0<s<T\) by (2.7), the integration by parts yields
Applying the Lebesgue convergence theorem and the estimate \(\vert E_{\alpha ,1}(\eta )\vert \le \frac{C}{1+\eta },\ \eta >0\) (Theorem 1.6 in [27]), we readily reach
as \(t \rightarrow \infty \) for \(a \in L^2(\varOmega )\).
Hence, \(u \in C([0,T];L^2(\varOmega ))\) and \(\lim _{t\downarrow 0} \Vert (S(t)-1)a\Vert = 0\) and thus
and
which justify the last equality in the formula (4.12).
Thus, in terms of (4.12), the representation (2.13) can be rewritten in the form
Since \(u(0) = a \in C^{\infty }_0(\varOmega )\) and \(F \in C^{\infty }_0(\varOmega \times (0,T))\), in view of (1.2) we have the inclusions
Now we use the conditions (1.2) and (2.8) and repeat the arguments employed for derivation of (4.5) by means of (4.6) and (4.11) to obtain the estimates
and the inclusion
Therefore,
that is,
On the other hand, the estimate (4.9) implies \(Q(t)u(t) \in C([0,T];H^2(\varOmega ))\) and we obtain
For further arguments, we define the Schauder spaces \(C^{\theta }(\overline{\varOmega })\) and \(C^{2+\theta }(\overline{\varOmega })\) with \(0<\theta <1\) (see, e.g., [7, 14]) as follows: A function w is said to belong to the space \(C^{\theta }(\overline{\varOmega })\) if
For \(w \in C^{\theta }(\overline{\varOmega })\), we define the norm
and for \(w\in C^{2+\theta }(\overline{\varOmega })\), the norm is given by
In the last formula, the notations \(\tau := (\tau _1,\ldots , \tau _d) \in ({\mathbb {N}}\cup \{0\})^d\), \(\partial _x^{\tau }:= \partial _1^{\tau _1}\cdots \partial _d^{\tau _d}\), and \(\vert \tau \vert := \tau _1 + \cdots + \tau _d\) are employed.
For \(d=1,2,3\), the Sobolev embedding theorem says that \(H^2(\varOmega ) \subset C^{\theta }(\overline{\varOmega })\) with some \(\theta \in (0,1)\) ( [1]).
Therefore, in view of (4.14), we obtain the inclusion \(h:= A_0u(\cdot ,t) \in C^{\theta }(\overline{\varOmega })\) for each \(t \in [0,T]\). Now we apply the Schauder estimate (see, e.g., [7] or [14]) for solutions to the elliptic boundary value problem
with the boundary condition \(\partial _{\nu _A}u(\cdot ,t) + \sigma (\cdot )u(\cdot ,t) = 0\) on \(\partial \varOmega \) to reach the inclusion
This inclusion and (4.11) yield the conclusion \(u \in C([0,T];C^2(\overline{\varOmega }))\) and \(t^{1-\alpha }\partial _tu \in C([0,T];C(\overline{\varOmega }))\) of the lemma.
Finally we prove that \(\lim _{t\rightarrow 0} \Vert u(t) - a \Vert = 0\). By (2.8), we have
and so
for each \(h \in L^{\infty }(0,T;L^2(\varOmega ))\). Therefore by the regularity \(u \in C([0,T];C^2(\overline{\varOmega }))\), we see that
where R is defined in (2.14). Moreover, for justifying (4.12), we have already proved \(\lim _{t\rightarrow 0} \Vert S(t)a - a\Vert = 0\) for \(a \in L^2(\varOmega )\). Thus the proof of Lemma 4 is complete. \(\square \)
II. Second part of the proof.
In this part, we weaken the regularity conditions posed on the solution u to (3.3) in Lemma 3 and prove the same results provided that \(u\in L^2(0,T;H^2(\varOmega ))\) and \(u-a \in H_{\alpha }(0,T;L^2(\varOmega ))\), under the assumption that \(\min \limits _{(x,t)\in \overline{\varOmega }\times [0,T]} b_0(x,t) > 0\) is sufficiently large.
Let \(F \in L^2(0,T;L^2(\varOmega ))\) and \(a\in H^1(\varOmega )\) satisfy the inequalities \(F(x,t)\ge 0,\ (x,t)\in \varOmega \times (0,T)\) and \(a(x)\ge 0,\ x\in \varOmega \).
Now we apply the standard mollification procedure (see, e.g., [1]) and construct the sequences \(F_n \in C^{\infty }_0(\varOmega \times (0,T))\) and \(a_n \in C^{\infty }_0(\varOmega )\), \(n\in {\mathbb {N}}\) such that \(F_n(x,t)\ge 0,\ (x,t)\in \varOmega \times (0,T)\) and \(a_n(x)\ge 0,\ x\in \varOmega \), \(n\in {\mathbb {N}}\) and \(\lim _{n\rightarrow \infty } \Vert F_n-F\Vert _{L^2(0,T;L^2(\varOmega ))} = 0\) and \(\lim _{n\rightarrow \infty }\Vert a_n-a\Vert _{H^1(\varOmega )} = 0\). Then Lemma 4 yields the inclusion
and thus Lemma 3 ensures the inequalities
Since Theorem 1 holds true for the initial-boundary value problem (3.3) with F and a replaced by \(F-F_n\) and \(a-a_n\), respectively, we have
as \(n\rightarrow \infty \). Therefore, we can choose a subsequence \(m(n)\in {\mathbb {N}}\) such that \(u(F,a)(x,t) = \lim _{m(n)\rightarrow \infty } u(F_{m(n)},a_{m(n)})(x,t)\) for almost all \((x,t) \in \varOmega \times (0,T)\). Then the inequality (4.16) leads to the desired result, namely, to the inequality \(u(F,a)(x,t) \ge 0\) for almost all \((x,t) \in \varOmega \times (0,T)\).
III. Third part of the proof.
Let the inequalities \(a(x)\ge 0,\ x\in \varOmega \) and \(F(x,t)\ge 0,\ (x,t)\in \varOmega \times (0,T)\) hold true for \(a\in H^1(\varOmega )\) and \(F \in L^2(0,T;L^2(\varOmega ))\) and let \(u=u(F,a) \in L^2(0,T;H^2(\varOmega ))\) is a solution to the problem (2.4). In order to complete the proof of Theorem 2, we have to demonstrate the non-negativity of the solution without any assumptions on the sign of the zeroth-order coefficient.
First, the zeroth-order coefficient \(b_0(x,t)\) in the definition (3.1) of the operator \(-A_1\) is set to a constant \(b_0>0\) that is assumed to be sufficiently large. In this case, the initial-boundary value problem (2.4) can be rewritten as follows:
In what follows, we choose sufficiently large \(b_0>0\) such that \(b_0 \ge \Vert c\Vert _{C(\overline{\varOmega } \times [0,T])}\).
In the previous parts of the proof, we already interpreted the solution u as a unique fixed point for the equation (4.3). Now let us construct an appropriate approximating sequence \(u_n\), \(n\in {\mathbb {N}}\) for the fixed point u. First we set \(u_0(x,t) := 0\) for \((x,t) \in \varOmega \times (0,T)\) and \(u_1(x,t) = a(x) \ge 0, \ (x,t) \in \varOmega \times (0,T)\). Then we define a sequence \(u_{n+1},\ n\in {\mathbb {N}}\) of solutions to the following initial-boundary value problems with the given \(u_n\):
First we show that
Indeed, the inequality (4.19) holds for \(n=1\). Now we assume that \(u_n(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\). Then \((b_0+c(x,t))u_n(x,t) + F(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\), and thus by the results established in the second part of the proof of Theorem 2, we obtain the inequality \(u_{n+1}(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\). By the principle of mathematical induction, the inequality (4.19) holds true for all \(n\in {\mathbb {N}}\).
Now we rewrite the problem (4.18) as
where \(A_0\) and Q(t) are defined by (2.5) and (2.14), respectively. Next we estimate \(w_{n+1}:= u_{n+1} - u_n\). By the relation (4.18), \(w_{n+1}\) is a solution to the problem
In terms of the operator K(t) defined by (2.7), acting similarly to our analysis of the fixed point equation (4.3), we obtain the integral equation
which leads to the inequalities
For their derivation, we used the norm estimates
and
that hold true under the conditions (1.2). Thus we arrive at the integral inequality
The generalized Gronwall inequality yields now the estimate
The second term at the right-hand side of the last inequality can be represented as follows:
Thus, we can choose a constant \(C>0\) depending on \(\alpha \) and T, such that
Recalling that
and setting \(\eta _n(t):= \Vert A_0^{\frac{1}{2}}w_n(t)\Vert \), we can rewrite (4.20) in the form
Since the Riemann-Liouville integral \(J^{\frac{1}{2}\alpha }\) preserves the sign and the semi-group property \(J^{\beta _1}(J^{\beta _2}\eta )(t) = J^{\beta _1+\beta _2}\eta (t)\) is valid for any \(\beta _1, \beta _2 > 0\), applying the inequality (4.21) repeatedly, we obtain the estimates
The known asymptotic behavior of the gamma function justifies the relation
Thus we have proved that the sequence \(u_N = w_0 + \cdots + w_N\) converges to the solution u in \(L^{\infty }(0,T;H^1(\varOmega ))\) as \(N \rightarrow \infty \). Therefore, we can choose a subsequence \(m(n)\in {\mathbb {N}}\) such that \(\lim _{m(n)\rightarrow \infty } u_{m(n)}(x,t) = u(x,t)\) for almost all \((x,t) \in \varOmega \times (0,T)\). This statement in combination with the inequality (4.19) means that \(u(x,t) \ge 0\) for almost all \((x,t) \in \varOmega \times (0,T)\). The proof of Theorem 2 is completed. \(\square \)
Now let us fix a source function \(F = F(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\) and an initial value \(a \in H^1(\varOmega )\) in the initial-boundary value problem (2.4) and denote by \(u(c,\sigma ) = u(c,\sigma )(x,t)\) the solution to the problem (2.4) with the functions \(c=c(x,t)\) and \(\sigma = \sigma (x)\). Then the following comparison property regarding the coefficients c and \(\sigma \) is valid:
Theorem 3
Let \(a\in H^1(\varOmega )\) and \(F \in L^2(\varOmega \times (0,T))\) and the inequalities \(a(x)\ge 0,\ x\in \varOmega \) and \(F(x,t)\ge 0,\ (x,t)\in \varOmega \times (0,T)\) hold true.
-
(i)
Let \(c_1, c_2 \in C^1([0,T]; C^1(\overline{\varOmega })) \cap C([0,T];C^2(\overline{\varOmega }))\) and \(c_1(x,t) \ge c_2(x,t)\) for \((x,t)\in \varOmega \). Then \(u(c_1,\sigma )(x,t) \ge u(c_2,\sigma )(x,t)\) in \(\varOmega \times (0,T)\).
-
(ii)
Let \(c(x,t) < 0,\ (x,t) \in \varOmega \times (0,T)\) and a constant \(\sigma _0>0\) be arbitrary and fixed. If the smooth functions \(\sigma _1, \sigma _2\) on \(\partial \varOmega \) satisfy the conditions
$$\begin{aligned} \sigma _2(x) \ge \sigma _1(x) \ge \sigma _0,\ x\in \partial \varOmega , \end{aligned}$$then the inequality \(u(c,\sigma _1) \ge u(c, \sigma _2),\ x\in \varOmega \times (0,T)\) holds true.
Proof
We start with a proof of the statement (i). Because \(a(x)\ge 0,\ x\in \varOmega \) and \(F(x,t)\ge 0,\ (x,t)\in \varOmega \times (0,T)\), Theorem 2 yields the inequality \(u(c_2,\sigma )(x,t)\ge 0,\ (x,t)\in \varOmega \times (0,T)\). Setting \(u(x,t):= u(c_1,\sigma )(x,t) - u(c_2,\sigma )(x,t)\) for \((x,t) \in \varOmega \times (0,T)\), we obtain
Since \(u(c_2,\sigma )(x,t) \ge 0\) and \((c_1-c_2)(x,t) \ge 0\) for \((x,t) \in \varOmega \times (0,T)\), Theorem 2 leads to the estimate \(u(x,t)\ge 0\) for \((x,t) \in \varOmega \times (0,T)\), which is equivalent to the inequality \(u(c_1,\sigma )(x,t) \ge u(c_2,\sigma )(x,t)\) for \((x,t) \in \varOmega \times (0,T)\) and the statement (i) is proved.
Now we proceed to the proof of the statement (ii). Similarly to the procedure applied for the second part of the proof of Theorem 2, we choose the sequences \(F_n \ge 0\), \(F_n \in C^{\infty }_0(\varOmega \times (0,T))\) and \(a_n \ge 0\), \(a_n \in C^{\infty }_0(\varOmega )\), \(n\in {\mathbb {N}}\) such that \(F_n \rightarrow F\) in \(L^2(\varOmega \times (0,T))\) and \(a_n \rightarrow a\) in \(H^1(\varOmega )\). Let \(u_n\), \(v_n\) be the solutions to the initial-boundary value problem (2.4) with \(F=F_n\), \(a=a_n\) and the coefficients \(\sigma _1\) and \(\sigma _2\) in the boundary condition, respectively. According to Lemma 4, the inclusions \(v_n, u_n \in C(\overline{\varOmega } \times [0,T])\) and \(t^{1-\alpha }\partial _tv_n, \, t^{1-\alpha }\partial _tu_n \in C([0,T];C(\overline{\varOmega }))\), \(n\in {\mathbb {N}}\) hold true and thus Theorem 2 yields
Moreover, the relation
follows from Theorem 1. Let us now define an auxiliary function \(w_n:= u_n - v_n\). For this function, the inclusions
hold true. Furthermore, it is a solution to the initial-boundary value problem
The inequalities (4.22) and \(\sigma _2(x) \ge \sigma _1(x), \ x\in \partial \varOmega \) lead to the estimate
To finalize the proof of the theorem, a variant of Lemma 3 formulated below will be employed.
Lemma 5
Let the elliptic operator \(-A\) be defined by (2.1) and the conditions (1.2) be satisfied. Moreover, let the inequality \(c(x,t) < 0\) for \(x \in \overline{\varOmega }\) and \(0\le t \le T\) hold true and there exist a constant \(\sigma _0>0\) such that
For \(a \in H^1(\varOmega )\) and \(F\in L^2(\varOmega \times (0,T))\), we further assume that there exists a solution \(u\in C([0,T];C^2(\overline{\varOmega }))\) to the initial-boundary value problem
that satisfies the inclusion \(t^{1-\alpha }\partial _tu \in C([0,T];C(\overline{\varOmega }))\). Then the inequalities \(F(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\) and \(a(x)\ge 0, \ \varOmega \) implicate the inequality \(u(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\).
In the formulation of this lemma, at the expense of the extra condition \(\sigma (x) > 0\) on \(\partial \varOmega \), we do not assume that \(\min \limits _{(x,t)\in \overline{\varOmega }\times [0,T]} (-c(x,t))\) is sufficiently large. This is the main difference between the conditions supposed in Lemma 5 and in Lemma 3. The proof of Lemma 5 is much simpler compared to the one of Lemma 3; it will be presented at the end of this section.
Now we complete the proof of Theorem 3. Since \(c(x,t) < 0\) for \((x,t)\in \varOmega \times (0,T)\) and \(\sigma _1(x) \ge \sigma _0 > 0\) on \(\partial \varOmega \) and taking into account the conditions (4.24) and (4.26), we can apply Lemma 5 to the initial-boundary value problem (4.25) and deduce the inequality \(w_n(x,t) \ge 0,\ (x,t)\in \varOmega \times (0,T)\), that is, \(u_n(x,t) \ge v_n(x,t),\ (x,t)\in \varOmega \times (0,T)\) for \(n\in {\mathbb {N}}\). Due to the relation (4.23), we can choose a suitable subsequence of \(w_n,\ n\in {\mathbb {N}}\) and pass to the limit as n tends to infinity thus arriving at the inequality \(u(c,\sigma _1)(x,t) \ge u(c,\sigma _2)(x,t)\) in \(\varOmega \times (0,T)\). The proof of Theorem 3 is completed. \(\square \)
At this point, let us mention a direction for further research in connection with the results formulated and proved in this sections. In order to remove the negativity condition posed on the coefficient \(c=c(x,t)\) in Theorem 3 (ii), one needs a unique existence result for solutions to the initial-boundary value problems of type (2.4) with non-zero Robin boundary condition similar to the one formulated in Theorem 1. There are several works that treat the case of the initial-boundary value problems with non-homogeneous Dirichlet boundary conditions (see, e.g., [31] and the references therein). However, to the best of the authors’ knowledge, analogous results are not available for the initial-boundary value problems with the non-homogeneous Neumann or Robin boundary conditions. Thus, in Theorem 3 (ii), we assumed the condition \(c(x,t)<0,\ (x,t)\in \varOmega \times (0,T)\), although our conjecture is that this result holds true for an arbitrary coefficient \(c=c(x,t)\).
We conclude this section with a proof of Lemma 5 that is simple because in this case we do not need the function \(\psi \) defined as in (3.4).
Proof
First we introduce an auxiliary function as follows:
The inequalities \(c(x,t)<0,\ (x,t)\in \overline{\varOmega } \times [0,T]\) and \(\sigma (x) \ge \sigma _0>0,\ x\in \partial \varOmega \) and the calculations similar to the ones done in the proof of Lemma 3 implicate the inequalities
and
Based on these inequalities, the same arguments that were employed after the formula (3.10) in the proof of Lemma 3 readily complete the proof of Lemma 5. \(\square \)
Change history
15 November 2023
A Correction to this paper has been published: https://doi.org/10.1007/s13540-023-00222-8
References
Adams, R.A.: Sobolev Spaces. Academic Press, New York (1975)
Al-Refai, M., Luchko, Yu.: Comparison principles for solutions to the fractional differential inequalities with the general fractional derivatives and their applications. J. Differ. Equ. 319(2), 312–324 (2022)
Borikhanov, M., Kirane, M., Torebek, B.T.: Maximum principle and its application for the nonlinear time-fractional diffusion equations with Cauchy-Dirichlet conditions. Appl. Math. Lett. 81, 14–20 (2018)
Evans, L.C.: Partial Differential Equations. American Math. Soc, Providence, Rhode Island (1998)
Friedman, A.: Partial Differential Equations of Parabolic Type. Dover Publications, New York (2008)
Fujiwara, D.: Concrete characterization of the domains of fractional powers of some elliptic differential operators of the second order. Proc. Japan Acad. 43(2), 82–86 (1967)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer-Verlag, Berlin (2001)
Gorenflo, R., Kilbas, A.A., Mainardi, F., Rogosin, S.V.: Mittag-Leffler Functions. Related Topics and Applications. Springer-Verlag, Berlin (2014)
Gorenflo, R., Luchko, Yu., Yamamoto, M.: Time-fractional diffusion equation in the fractional Sobolev spaces. Fract. Calc. Appl. Anal. 18(2), 799–820 (2015). https://doi.org/10.1515/fca-2015-0048
Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Springer-Verlag, Berlin (1981)
Ilyin, A.M., Kalashnikov, A.S., Oleynik, O.A.: Linear second-order partial differential equations of the parabolic type. J. Math. Sci. 108(4), 435–542 (2002)
Kirane, M., Torebek, B.T.: Maximum principle for space and time-space fractional partial differential equations. Z. Anal. Anwend. 40(3), 277–301 (2021)
Kubica, A., Ryszewska, K., Yamamoto, M.: Introduction to a Theory of Time-fractional Partial Differential Equations. Springer Nature Singapore, Singapore (2020)
Ladyzhenskaya, O.A., Ural’tseva, N.N.: Linear and Quasilinear Elliptic Equations. Academic Press, New York (1968)
Lions, J.-L., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications, vol. I. Springer-Verlag, Berlin (1972)
Lu, Z., Zhu, Y.: Comparison principles for fractional differential equations with the Caputo derivatives. Adv. Differ. Equ., 237 (2018)
Luchko, Yu.: Maximum principle for the generalized time-fractional diffusion equation. J. Math. Anal. Appl. 351(1), 218–223 (2009)
Luchko, Yu.: Boundary value problems for the generalized time-fractional diffusion equation of distributed order. Fract. Calc. Appl. Anal. 12(4), 409–422 (2009)
Luchko, Yu.: Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation. Comput. Math. Appl. 59(5), 1766–1772 (2010)
Luchko, Yu.: Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation. J. Math. Anal. Appl. 374(2), 538–548 (2011)
Luchko, Yu., Yamamoto, M.: On the maximum principle for a time-fractional diffusion equation. Fract. Calc. Appl. Anal. 20(5), 1131–1145 (2017). https://doi.org/10.1515/fca-2017-0060
Luchko, Yu., Yamamoto, M.: A survey on the recent results regarding maximum principles for the time-fractional diffusion equations. In: Bhalekar, S. (ed.) Frontiers in Fractional Calculus, pp. 33–69. Bentham Science Publishers, Sharjah, United Arab Emirates (2018)
Luchko, Yu., Yamamoto, M.: Maximum principle for the time-fractional partial differential equations. In: Kochubei, A., Luchko, Yu. (eds.) Handbook of Fractional Calculus with Applications: Fractional Differential Equations, vol. 2, pp. 299–325, Walter de GruyterGmbH, Berlin (2019). https://doi.org/10.1515/9783110571660
Luchko, Yu., Suzuki, A., Yamamoto, M.: On the maximum principle for the multi-term fractional transport equation. J. Math. Anal. Appl. 505(1), 125579 (2022)
Pao, C.V.: Nonlinear Parabolic and Elliptic Equations. Plenum Press, New York (1992)
Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer-Verlag, Berlin (1983)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Protter, M.H., Weinberger, H.F.: Maximum Principles in Differential Equations. Springer-Verlag, Berlin (1999)
Renardy, M., Rogers, R.C.: An Introduction to Partial Differential Equations. Springer-Verlag, New York (1993)
Tanabe, H.: Equations of Evolution. Pitman, London (1979)
Yamamoto, M.: Weak solutions to non-homogeneous boundary value problems for time-fractional diffusion equations. J. Math. Anal. Appl 460(1), 365–381 (2018)
Yosida, K.: Functional Analysis. Springer-Verlag, Berlin (1971)
Zacher, R.: Boundedness of weak solutions to evolutionary partial integro-differential equations with discontinuous coefficients. J. Math. Anal. Appl. 348(1), 137–149 (2008)
Acknowledgements
The second author was supported by Grant-in-Aid for Scientific Research Grant-in-Aid (A) 20H00117 and Grant-in-Aid for Challenging Research (Pioneering) 21K18142 of Japan Society for the Promotion of Science.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In the proof of Lemma 3 that is a basis for all other derivations presented in this paper, we essentially used an auxiliary function that satisfies the conditions (3.4). Thus, ensuring existence of such function is an important problem worth for detailed considerations. In this appendix, we present a solution to this problem.
For the readers’ convenience, we split our existence proof into three parts.
I. First part of the proof
In this part, we prove the following lemma:
Lemma 6
Let the conditions (1.2) be satisfied and the constant
is sufficiently large.
Then there exists a constant \(\kappa _1>0\) such that
for all \(v \in H^2(\varOmega )\) satisfying \(\partial _{\nu _A}v + \sigma v = 0\) on \(\partial \varOmega \) for each \(t \in [0,T]\).
In particular, Lemma 6 implies that all of the eigenvalues of the operator \(A_0\) defined by (2.5) are positive if the constant \(c_0>0\) is sufficiently large. Henceforth we employ the notation \(b=(b_1,\ldots , b_d)\).
Proof
By using the conditions (1.2) and the boundary condition \(\partial _{\nu _A}v + \sigma v = 0\) on \(\partial \varOmega \), integration by parts yields
Here and henceforth \(C>0\), \(C_{\varepsilon }, C_{\delta } > 0\), etc. denote generic constants which are independent of the function v.
By the trace theorem (Theorem 9.4 (pp. 41-42) in [15]), for \(\delta \in (0, \frac{1}{2}]\), there exists a constant \(C_{\delta }>0\) such that
Now we fix \(\delta \in \left( 0, \, \frac{1}{2}\right) \). The interpolation inequality for the Sobolev spaces implicates that for any \(\varepsilon >0\) there exists a constant \(C_{\varepsilon ,\delta } > 0\) such that the following inequality holds true (see, e.g., Chapter IV in [1] or Sections 2.5 and 11 of Chapter 1 in [15]):
Therefore, we obtain the estimate
for all \(v \in H^1(\varOmega )\). Substituting this inequality into (5.2), we obtain
Choosing a sufficiently small \(\varepsilon > 0\) such that \(\kappa - 2C(\varepsilon C_{\delta })^2> 0\) and a sufficiently large \(M>0\) such that
completes the proof of Lemma 6. \(\square \)
II. Second part of the proof
Due to the estimate (5.1), we can apply Theorem 3.2 (p. 137) in [14] that implicates existence of a constant \(\theta \in (0,1)\) such that for each \(t \in [0,T]\), a solution \(\psi (\cdot ,t) \in C^{2+\theta }(\overline{\varOmega })\) to the problem (3.4) exists uniquely, where \(C^{2+\theta }(\overline{\varOmega })\) is the Schauder space defined in the proof of Lemma 4 in Section 4.
Now we introduce an auxiliary function
Because of the inclusion \(\psi (\cdot ,t) \in C^{2+\theta }(\overline{\varOmega })\), the value of the function \(\eta (t)\) is finite for each \(t \in [0,T]\).
Furthermore, for an arbitrary \(G \in C^{\theta }(\overline{\varOmega })\), there exists a unique solution \(w=w(\cdot ,t)\) to the problem
for each \(t \in [0,T]\).
Now we prove that for each \(t\in [0,T]\) there exists a constant \(C_t > 0\) such that
for all solutions w of the problem (5.4). In the inequality (5.5), the constant \(C_t>0\) depends on the norms \(\Vert a_{ij}\Vert _{C^1(\overline{\varOmega })}\), \(1\le i,j\le d\), \(\Vert b_k\Vert _{C([0,T];C^2(\overline{\varOmega }))}\), \(0\le k\le d\) of the coefficients, but not on the coefficients by themselves.
Indeed, for each \(t \in [0,T]\), the inequality
holds true (see, e.g., the formula (3.7) on p. 137 in [14]). To obtain the desired estimate we have to eliminate the term \(\Vert w(\cdot ,t)\Vert _{C(\overline{\varOmega })}\) on the right-hand side of the last inequality. This can be done by the standard compactness-uniqueness arguments. More precisely, let us assume that (5.5) does not hold. Then there exist the sequences \(w_n\in C^{2+\theta }(\overline{\varOmega }),\ n\in {\mathbb {N}}\) and \(G_n\in C^{\theta }(\overline{\varOmega }),\ n\in {\mathbb {N}}\) such that \(\Vert w_n\Vert _{C^{2+\theta }(\overline{\varOmega })} = 1\) and \(\lim _{n\rightarrow \infty }\Vert G_n\Vert _{C^{\theta }(\overline{\varOmega })} = 0\). By the Ascoli-Arzelà theorem, we can extract a subsequence \(w_{k(n)}\) from the sequence \(w_n\) such that \(w_{k(n)} \longrightarrow \widetilde{w}\) in \(C(\overline{\varOmega })\) as \(n\rightarrow \infty \). Applying the estimation (5.6) to the equation
equipped with the homogeneous boundary condition \(\partial _{\nu _A}(w_{k(n)} - w_{k(m)}) + \sigma (w_{k(n)} - w_{k(m)}) = 0\) on \(\partial \varOmega \), we we arrive at the relation
as \(n,m \rightarrow \infty \). Hence, there exists a function \(w_0 \in C^{2+\theta }(\overline{\varOmega })\) such that \(w_{k(n)} \rightarrow w_0\) in \(C^{2+\theta }(\overline{\varOmega })\). Moreover, we obtain the relations
and \(G_{k(n)} = A_1(t)w_{k(n)} \rightarrow A_1(t)w_0\) in \(C^{\theta }(\overline{\varOmega })\).
Since \(\lim _{n\rightarrow \infty } \Vert G_{k(n)}\Vert _{C^{\theta }(\overline{\varOmega })} = 0\), we obtain \(A_1(t)w_0 = 0\) in \(\varOmega \) with \(\partial _{\nu _A}w_0 + \sigma w_0 = 0\) on \(\partial \varOmega \). Then Lemma 6 yields \(w_0(x,t)=0\) in \(\varOmega \) that contradicts the relation \(\Vert w_0\Vert _{C^{2+\theta }(\overline{\varOmega })} = 1\) that we established above. The obtained contradiction implicates the desired norm estimate (5.5).
III. Third part of the proof
The last missing detail of the proof is the inclusion \(\psi \in C^1([0,T];C^2(\overline{\varOmega }))\) for the function \(\psi \) constructed in the previous part of the proof.
To show this inclusion, we first verify that for an arbitrarily but fixed \(t\in [0,T]\) the function \(d(x,s):= \psi (x,t) - \psi (x,s)\) satisfies the equations
For an arbitrarily but fixed \(\delta >0\) we set \(I_{\delta ,t}:= [0,T] \cap \{s;\, \vert t-s\vert \le \delta \}\).
Applying the relation (5.3) and the estimate (5.5) to the solution d of (5.7) yields
For the function
the inclusions \(b_j \in C([0,T];C^1(\overline{\varOmega }))\), \(0\le j \le d\) imply \(\lim _{\delta \downarrow 0} h(\delta ) = 0\).
Now we rewrite the estimate (5.8) in terms of the function \(\eta \) defined by (5.3) as
and thus obtain the inequality
Choosing \(\delta : =\delta (t)>0\) sufficiently small, for a given \(t \in [0,T]\), the estimate \(\sup _{s\in I_{\delta (t),t}} \eta (s) \le C_1\eta (t)\) holds true. Varying \(t \in [0,T]\), we now choose a finite number of the intervals \(I_{\delta (t),t}\) that cover the whole interval [0, T] and thus obtain the norm estimate
with some constant \(C_2>0\).
For \(s \in I_{\delta (t),t}\), substitution of (5.9) into (5.8) yields the estimate
Consequently, \(\lim _{s\rightarrow t} \Vert \psi (\cdot ,s) - \psi (\cdot ,t)\Vert _{C^{2+\theta }(\overline{\varOmega })} = 0\) and we have shown the inclusion
To complete the proof, the now verify the inclusion \(\psi \in C^1([0,T];C^{2+\theta }(\overline{\varOmega }))\). Since \(-A_1(\xi )\psi (x,\xi ) = 1\) in \(\varOmega \), differentiating this formula with respect to \(\xi \) leads to the representation
By subtracting the equation (5.11) with \(\xi =s\) from the one with \(\xi =t\), we deduce that the function \(d_1(x,s):= (\partial _t\psi )(x,t) - (\partial _t\psi )(x,s)\) satisfies the relation
and the boundary condition \(\partial _{\nu _A}d_1 + \sigma d_1 = 0\) on \(\partial \varOmega \) for all \(s,t \in [0,T]\). Thus, the inclusion \(\psi \in C^1([0,T];C^{2+\theta }(\overline{\varOmega }))\) will follow from the relation \(\lim _{s\rightarrow t} \Vert d_1(\cdot ,s)\Vert _{C^{2+\theta }(\overline{\varOmega })} = 0\) that we now prove. To this end, by applying Theorem 3.2 (p. 137) in [14] to the equation (5.12), it suffices to prove that
Applying Theorem 3.2 in [14] to the equation (5.11), in view of the regularity conditions (1.2) and the equation (5.11), we obtain the estimates
The inequalities (5.9) and (5.14) lead to the norm estimate
By employing the arguments similar to those used above, the estimate
can be derived. Since \(\partial _t^kb_j \in C([0,T];C^1(\overline{\varOmega }))\) for \(k=0,1\) and \(0\le j \le d\) by the conditions (1.2) and \(\nabla ^k\psi \in C([0,T];C^{1+\theta } (\overline{\varOmega }))\) with \(k=0,1\) by the inclusion (5.10), the relation \(\lim _{s\rightarrow t} \Vert H_{\ell }(\cdot ,t,s)\Vert _{C^{\theta }(\overline{\varOmega })} = 0\) with \(\ell =1,2\) immediately follows from the norm estimates (5.15) and (5.16). Thus, we showed existence of a function satisfying the conditions (3.4).
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Luchko, Y., Yamamoto, M. Comparison principles for the time-fractional diffusion equations with the Robin boundary conditions. Part I: Linear equations. Fract Calc Appl Anal 26, 1504–1544 (2023). https://doi.org/10.1007/s13540-023-00182-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13540-023-00182-z
Keywords
- Fractional calculus (primary)
- Fractional diffusion equation
- Positivity of solutions
- Comparison principle