SpringerLink
Log in

A market- and time-consistent extension for the EIOPA risk-margin

  • Original Research Paper
  • Published:
European Actuarial Journal Aims and scope Submit manuscript

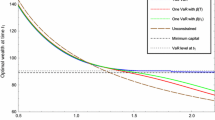
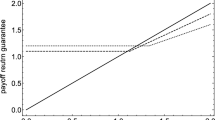
Abstract

In this paper, we investigate market- and time-consistent valuation of life-insurance liabilities, which are long-dated by nature. To obtain a market- and time-consistent value, the “two-step market evaluation” introduced by Pelsser and Stadje (Math Finance 24:25–65, 2014) is used to evaluate a hybrid payoff with underlying hedgeable financial and (partially) unhedgeable actuarial risks. The resulting time-consistent and market-consistent (TCMC) price captures the dynamics of the risk drivers over the lifetime of the contract. We show that the EIOPA standard-formula for the risk-margin is not time-consistent, and we construct a time-consistent version of the risk-margin that captures the extra uncertainties from the process dynamics. EIOPA’s standard-formula for the Risk-Margin is compared to the TCMC price for a simple unit-linked contract and we show that the effects of time-inconsistency are increasing with maturity and are significant for long-dated contracts.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. See example (3.4) in Pelsser and Stadje [37] for examples of two-step actuarial operators under the previously described representation.

  2. Also called the “risk-neutral” probability.

  3. The EIOPA Technical Specification [21] and in specific articles https://www.asf.com.pt/NR/rdonlyres/359F79DF-586C-42D0-8064-97811541C23F/0/A__Technical_Specification_for_the_Preparatory_Phase__Part_I_.pdf released by the European Insurance and Occupational Pension Authority (EIOPA) provides advice and formulations on the calculation of the risk-margin on top of the best-estimate for long-term liabilities in a multi-period setting.

  4. A one-year discount should be applied to the pay-off \(h(y_{t+k})\) under \(\mathbb {V}\text {aR}\) operator.

  5. Note that all \(y_t\) values may also be represented by the “discounted” quantities relative to the money-market account process B(t) defined in Sect. 3.1 with which the discount factors can be taken off from the formula.

  6. Note that the conditional expectation is time-consistent.

  7. The discount factor is omitted due to use of \(x_t\) as the discounted financial risk driver. Further explanation is in Sect. 3.1

  8. Considering the stochastic evolution of mortality risk through time, a more precise concept is “the remaining lifetime at the beginning of the calendar year t” for which the notation is \(T_{x}(t)\).

  9. In the notation, if we assume the present \(t=0\), the notation t is representative of the past “calendar times” \(\{t_0, t_0 +1, \dots , 0\}\) in the model.

  10. In case the function f is non-increasing, then any probability p under \(\mathbb {V}\text {aR}\) function will be turned into \(1-p\).

  11. These parameters are estimated on the basis of mortality data aggregated for “men and women” of the Netherlands during the calendar years 1960–2006 (47 years).

  12. Accessible via ECB web-page, https://www.ecb.europa.eu/stats/money/yc/html/index.en.html.

References

  1. Acciaio B, Penner I (2011) Dynamic risk measures. Adv Math Methods Fin pp 1–34

  2. Artzner P, Delbaen F, Eber J, Heath D, Ku H (2007) Coherent multiperiod risk adjusted values and bellman’s principle. Ann Oper Res 152(1):5–22

    Article  MathSciNet  MATH  Google Scholar 

  3. Assa H, Gospodinov N (2018) Market consistent valuations with financial imperfection. Decis Econ Financ 41:65–90

    Article  MathSciNet  MATH  Google Scholar 

  4. Barigou K, Chen Z, Dhaene J (2019) Fair dynamic valuation of insurance liabilities: merging actuarial judgement with market- and time-consistency. Insur Math Econ 88:19–29

    Article  MathSciNet  MATH  Google Scholar 

  5. Barigou K, Dhaene J (2019) Fair valuation of insurance liabilities via mean-variance hedging in a multi-period setting. Scand Actuar J 2019(2):163–187

    Article  MathSciNet  MATH  Google Scholar 

  6. Barrieu P, El Karoui N (2009) Pricing, hedging, and designing derivatives with risk measures. Princeton University Press, Princeton

    MATH  Google Scholar 

  7. Bion-Nadal J (2009) Time consistent dynamic risk processes. Stoch Process Appl 119(2):633–654

    Article  MathSciNet  MATH  Google Scholar 

  8. Carriere J (1996) Valuation of the early-exercise price for options using simulations and nonparametric regression. Insur Math Econom 19(1):19–30

    Article  MathSciNet  MATH  Google Scholar 

  9. Chen Z, Chen B, Dhaene J (2020) Fair dynamic valuation of insurance liabilities: a loss averse convex hedging approach. Scand Actuar J 0(0):1–27

  10. Cheridito P, Delbaen F, Kupper M (2006) Coherent and convex monetary risk measures for unbounded cadlag processes. Financ Stoch 9(3):369–387

    Article  MATH  Google Scholar 

  11. Cheridito P, Stadje M (2009) Time-inconsistency of var and time-consistent alternatives. Financ Res Lett 6(1):40–46

    Article  Google Scholar 

  12. Cvitanic J, Karatzas I (1992) Convex duality in constrained portfolio optimization. Ann Appl Probab 2(4):767–818

    Article  MathSciNet  MATH  Google Scholar 

  13. Deelstra G, Devolder P, Gnameho K, Hieber P (2019) Valuation of hybrid financial and actuarial products in life insurance: a universal 3-step method. Available at SSRN: https://ssrn.com/abstract=3307061

  14. Delbaen F, Schachermayer W (1994) A general version of the fundamental theorem of asset pricing. Math Ann 300(3):463–520

    Article  MathSciNet  MATH  Google Scholar 

  15. Delbaen F, Schachermayer W (1996) The variance-optimal martingale measure for continuous processes. Bernoulli 2(1):81–105

    Article  MathSciNet  MATH  Google Scholar 

  16. Delong L, Dhaene J, Barigou K (2019) Fair valuation of insurance liability cash-flow streams in continuous time: applications. ASTIN Bull 49(2):299–333

    Article  MathSciNet  MATH  Google Scholar 

  17. Delong L, Dhaene J, Barigou K (2019) Fair valuation of insurance liability cash-flow streams in continuous time: theory. Insur Math Econom 88:196–208

    Article  MathSciNet  MATH  Google Scholar 

  18. Dhaene J, Denuit M, Goovaerts M, Kaas R, Vyncke D (2002) The concept of comonotonicity in actuarial science and finance: theory. Insur Math Econ 31(1):3–33. Special Issue: Papers presented at the 5th IME Conference, Penn State University, University Park, PA, 23-25 July 2001

  19. Dhaene J, Stassen B, Barigou K, Linders D, Chen Z (2017) Fair valuation of insurance liabilities: merging actuarial judgement and market-consistency. Insur Math Econom 76:14–27

    Article  MathSciNet  MATH  Google Scholar 

  20. EC Delegated Regulation 2015/35 (2015) Commission delegated regulation (EU) 2015/35. Technical report, European Parliament and of the Council on the taking-up and pursuit of the business of Insurance and Reinsurance (Solvency II)

  21. EIOPA Technical Specification (2014) Technical specifications for the preparatory phase (part 1). Technical report, European Insurance and Occupational Pensions Authority

  22. Follmer H, Penner I (2006) Convex risk measures and the dynamics of their penalty functions. Stat Decis 24(1):61–96

    MathSciNet  MATH  Google Scholar 

  23. Föllmer H, Schweizer M (1989) Hedging by sequential regression: an introduction to the mathematics of option trading. ASTIN Bull 18(2):147–160

    Article  Google Scholar 

  24. Frittelli M, Gianin ER (2004) Dynamic convex risk measures, risk measures for the 21st century. Wiley, New York

    Google Scholar 

  25. Goovaerts M, Laeven R (2008) Actuarial risk measures for financial derivative pricing. Insur Math Econom 42(2):540–547

    Article  MathSciNet  MATH  Google Scholar 

  26. Hodges S, Neuberger A (1989) Optimal replication of contingent claims under transaction costs. Rev Futures Mark 8(2):222–239

    Google Scholar 

  27. Jobert A, Rogers L (2008) Valuations and dynamic convex risk measures. Math Financ 18(1):1–22

    Article  MathSciNet  MATH  Google Scholar 

  28. Kramkov D, Schachermayer W (1999) The asymptotic elasticity of utility functions and optimal investment in incomplete markets. Ann Appl Probab 9(3):904–950

    Article  MathSciNet  MATH  Google Scholar 

  29. Kupper M, Cheridito P, Filipovic D (2008) Dynamic risk measures, valuations and optimal dividends for insurance. In: Mini-workshop, mathematics of solvency. Mathematisches Forschungsinstitut Oberwolfach

  30. Lee RD, Carter LR (1992) Modeling and forecasting US mortality. J Am Stat Assoc 87(419):659–671

    MATH  Google Scholar 

  31. Longstaff FA, Schwartz ES (2001) Valuing American options by simulation: a simple least-squares approach. Rev Financ Stud 14(1):113–147

    Article  MATH  Google Scholar 

  32. Maccheroni F, Marinacci M, Rustichini A (2006) Ambiguity aversion, robustness, and the variational representation of preferences. Econometrica 74(6):1447–1498

    Article  MathSciNet  MATH  Google Scholar 

  33. Malamud S, Trubowitz E, Wüthrich M (2008) Market consistent pricing of insurance products. ASTIN Bull 38(2):483–526

    Article  MathSciNet  MATH  Google Scholar 

  34. Møller T (2002) On valuation and risk management at the interface of insurance and finance. Br Actuar J 8(4):787–827

    Article  Google Scholar 

  35. Musiela M, Zariphopoulou T (2004) A valuation algorithm for indifference prices in incomplete markets. Financ Stoch 8(3):399–414

    Article  MathSciNet  MATH  Google Scholar 

  36. Pelsser A (2011) Pricing in incomplete market. Netspar Panel Paper (25)

  37. Pelsser A, Stadje M (2014) Time-consistent and market-consistent evaluations. Math Financ 24(1):25–65

    Article  MathSciNet  MATH  Google Scholar 

  38. Peng S (2004) Filtration consistent nonlinear expectations and evaluations of contingent claims. Acta Mathematicae Applicatae Sinica (English Series) 20(2):191–214

    Article  MathSciNet  MATH  Google Scholar 

  39. Rosazza Gianin E (2006) Risk measures via \(g\)-expectations. Insur Math Econom 39(1):19–34

    Article  MathSciNet  MATH  Google Scholar 

  40. Salahnejhad A, Pelsser A (2016) Time-consistent actuarial valuation. Insur Math Econom 66:97–112

    Article  MathSciNet  MATH  Google Scholar 

  41. Salahnejhad Ghalehjooghi A, Pelsser A (2021) Time-consistent and market-consistent actuarial valuation of the participating pension contract. Scand Actuar J 2021(4):266–294

    Article  MathSciNet  MATH  Google Scholar 

  42. Schweizer M (1995) On the minimal martingale measure and the Föllmer–Schweizer decomposition. Stoch Anal Appl 13(5):573–600

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. KU Leuven-Faculty of Economics and Business (FEB), Leuven, Belgium

    Ahmad Salahnejhad Ghalehjooghi

  2. Maastricht University (UM), Maastricht, The Netherlands

    Antoon Pelsser

  3. University of Amsterdam (UvA), Netspar and Risk At Work, Amsterdam, The Netherlands

    Antoon Pelsser

Authors
  1. Ahmad Salahnejhad Ghalehjooghi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Antoon Pelsser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmad Salahnejhad Ghalehjooghi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors are grateful for the constructive and helpful comments and directions given by Prof. Dr. Jan Dhaene (KU Leuven) on this paper.

The research leading to these results has received funding from the European Union Seventh Framework Programme ([FP7/2007-2013] [FP7/2007-2011]) under Grant agreement \(n^\circ\) 289032.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Salahnejhad Ghalehjooghi, A., Pelsser, A. A market- and time-consistent extension for the EIOPA risk-margin. Eur. Actuar. J. 13, 517–539 (2023). https://doi.org/10.1007/s13385-023-00343-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13385-023-00343-7

Search

Navigation