1 Introduction

Electromagnetic (EM) logging while drilling (LWD) has been widely used in high-angle and horizontal (HA/HZ) wells for real-time geosteering and formation evaluation (Netto et al. 2013; Hu et al. 2017; Yuan et al. 2018; Lai et al. 2018). A fast and accurate EM LWD modeling algorithm is required for the pre-drilling forward simulation, the real-time inversion and the post-drilling evaluation in directional wells (Tan et al. 2012; Shao et al. 2013; Wang et al. 2019). The simulation of EM LWD in HA/HZ wells is essentially a 3D modeling problem (Deng et al. 2010, 2015; Zhang et al. 2019a, b). A variety of accurate 3D EM LWD modeling algorithms, e.g., finite difference method, finite element method and finite volume method (Gao et al. 2010; Rumpf et al. 2014; Zhang et al. 2019a, b), are therefore developed to address the 3D problem associated with tool structures, borehole and mud invasion. However, the model constructions and solutions of the 3D algorithms are quite complicated and time-consuming (Bensdorp et al. 2016), which restrict their applications in real-time data processing (Li and Wang 2016; Wu et al. 2017). To solve this problem, the formation is simplified to a 1D layered model through the sliding-window strategy in practice (Wang et al. 2018; Hu and Fan 2018), and the coils are modeled by the magnetic dipoles (Hong et al. 2014). The real-time geosteering requirement can then be satisfied with the use of EM fields’ closed form. This technique, however, lacks for feasibility and accuracy analysis toward complex structures, e.g., folds, faults, which can be formed under the in situ stress in realistic subsurface formation (Tan et al. 2019).

For some geological structures, the rock properties are continuous in strike but discontinuous in lateral direction within the well logging scope. Therefore, the structures like folds and faults can normally be simplified to 2D models in LWD modeling and simulated effectively and efficiently by the 2.5D algorithm (Dyatlov et al. 2015; Rodríguez-Rozas et al. 2018; Thiel et al. 2018). The basic principle of the 2.5D algorithm is to apply the Fourier transform to convert a 3D problem in spatial domain into a series of 2D problems in spectral domain, solve the fields in spectral domain and convert it back to the spatial domain through the inverse Fourier transform (Xu and Li 2018; Liu et al. 2012; Wu et al. 2019). To satisfy the real-time data processing and geosteering requirement, the key issues for the 2.5D modeling to answer are (1) how to rapidly solve the electric and magnetic fields in 2D spectral domain with arbitrary oriented dipoles; (2) how to improve the IFT efficiency based on the characteristics of the fields in spectral domain.

In this paper, a 2.5D finite difference method is proposed to model the EM LWD and applied to analyze the tool responses in complex geological structures. First, the dipoles in spatial domain are converted into incident fields in spectral domain as the effective sources. Second, the scattered field wave equations in spectral domain are derived from Maxwell’s equations and then solved by the direct solvers. Finally, we propose a truncated Gauss–Hermite quadrature to accelerate the IFT, which transforms the solution in spectral domain to spatial domain. The 2.5D algorithm is then applied to compare the tool responses in complex reservoirs (folds, faults and sandstone pinch-outs) with those from the 1D model and analyze the 1D simplification’s feasibility. Note that in this paper, we focus on modeling the complex geological structures while ignoring the borehole environment, tool structure and mud resistivity; the neglected effects are either negligible or can be corrected by calibration (Kang et al. 2018; Rosa et al. 2018).

2 2.5D modeling of the EM LWD

2.1 Physics of EM LWD and formation model

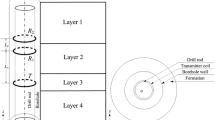
The EM LWD provides measurements of multiple investigation depths by using multi-frequency and multi-spacing configurations. Figure 1a-I shows the basic structures of one transmitter—two receivers; Fig. 1a-II presents the tool structure of ARC675 introduced by Schlumberger, which includes five basic measurement units (five axial transmitters and two coaxial receivers) and works at 2 MHz and 400 kHz. For an arbitrary basic measurement unit, the phase shift resistivity (PSR) (attenuation resistivity (ATR)) can then be obtained according to its single-value relationship with the phase shift (PS) (attenuation (AT)) of the voltages at the receivers, as shown in Fig. 1b, c. The PS and AT are defined as (Li and Wang 2016)

$$\begin{aligned} {\text{PS}} & = \arctan \left( {\frac{{\text{Im} \left( {V_{\text{R2}} } \right)}}{{{\text{Re}}\left( {V_{\text{R2}} } \right)}}} \right) - \arctan \left( {\frac{{\text{Im} \left( {V_{\text{R1}} } \right)}}{{{\text{Re}}\left( {V_{\text{R1}} } \right)}}} \right) \\ {\text{AT}} & = 10\lg \left( {\frac{{\left[ {\text{Im} \left( {V_{\text{R1}} } \right)} \right]^{2} + \left[ {{\text{Re}}\left( {V_{\text{R1}} } \right)} \right]^{2} }}{{\left[ {\text{Im} \left( {V_{\text{R2}} } \right)} \right]^{2} + \left[ {{\text{Re}}\left( {V_{\text{R2}} } \right)} \right]^{2} }}} \right). \\ \end{aligned}$$
(1)
Fig. 1
figure 1

Tool configuration of the EM LWD and the relationship between the phase shift (attenuation) and the formation resistivity: a basic structure with one transmitter and two receivers (I) and the tool structure of ARC675 developed by Schlumberger (II), b phase shift and c attenuation

Full size image

2.2 2.5D modeling of electric logging

Generally, electric logging modeling requires 3D model since the complex borehole and geological structures should be taken into account. In LWD modeling, the borehole and invasion effects are usually neglected; therefore, the model selection is highly dependent on the depth of investigation (DOI) of the tool and the shape of formation structure. (1) If the formation structure is complex within the tool detection ranges, a 3D model should be used (Fig. 2a). (2) If the formation properties keep invariant along one direction within the tool detection ranges, a 2D model can be chosen (Fig. 2b). (3) If the bed boundaries are parallel to each other within the tool detection ranges, a 1D model can be a good choice (Fig. 2c). The 1D models have been widely used in real-time geosteering and fast inversion since the tool responses can be computed analytically with low CPU time and memory requirement. However, the application of the 1D model in complex formation reconstruction is restricted due to the over simplification. Therefore, the forward modeling and inversion of EM LWD in the 2D models gain more and more attentions. In this paper, we focus on the fast modeling of EM LWD in 2D formations, e.g., folds and faults, to provide technology supports for EM LWD evaluation in complex formations.

Fig. 2
figure 2

Formation models

Full size image

The EM LWD modeling can be converted to the EM field computation problem with magnetic dipoles since the EM wavelengths are much larger than the coil sizes. For a lossy medium, the time harmonic Maxwell’s equations can be expressed as

$$\begin{aligned} & \nabla \times {\mathbf{E}} - {\text{i}}\omega \mu {\mathbf{H}} = - {\mathbf{M}} \\ & \nabla \times {\mathbf{H}} + {\text{i}}\omega \varepsilon {\mathbf{E}} = {\mathbf{J}} \\ \end{aligned}$$
(2)

where ε = (ε′ + iσ/ω) is the complex permittivity, M (J) is the magnetic (electric) current density. The EM fields in spatial domain can be split into background fields and scattered fields. Assuming a homogeneous isotropic background with permeability μb and permittivity εb, the background Eb and Hb field will follow

$$\begin{aligned} & \nabla \times {\mathbf{E}}^{\text{b}} - {\text{i}}\omega \mu_{\text{b}} {\mathbf{H}}^{\text{b}} = - {\mathbf{M}} \\ & \nabla \times {\mathbf{H}}^{\text{b}} + {\text{i}}\omega \varepsilon_{\text{b}} {\mathbf{E}}^{\text{b}} = {\mathbf{J}} \\ \end{aligned}$$
(3)

Eliminating the source term by subtracting Eq. 3 from Eq. 2, we can obtain

$$\begin{aligned} & \nabla \times {\mathbf{E}}^{\text{sct}} - {\text{i}}\omega \mu {\mathbf{H}}^{\text{sct}} = {\mathbf{M}}^{\text{sct}} \\ & \nabla \times {\mathbf{H}}^{\text{sct}} + {\text{i}}\omega \varepsilon {\mathbf{E}}^{\text{sct}} = {\mathbf{J}}^{\text{sct}} \\ \end{aligned}$$
(4)

where the equivalent sources Msct and Jsct are defined as

$$\begin{aligned} {\mathbf{M}}^{\text{sct}} = {\text{i}}\omega \left( {\mu - \mu_{\text{b}} } \right){\mathbf{H}}^{\text{inc}} \hfill \\ {\mathbf{J}}^{\text{sct}} = - {\text{i}}\omega \left( {\varepsilon - \varepsilon_{\text{b}} } \right){\mathbf{E}}^{\text{inc}} \hfill \\ \end{aligned}$$
(5)

The EM wave equations can then be obtained as

$$\begin{aligned} \nabla \times \left( {\frac{{\nabla \times {\mathbf{E}}^{\text{sct}} }}{\mu }} \right) - \omega^{2} \varepsilon {\mathbf{E}}^{\text{sct}} & = \nabla \times \left( {\frac{{{\mathbf{M}}^{\text{sct}} }}{\mu }} \right) + \omega^{2} \left( {\varepsilon - \varepsilon_{\text{b}} } \right){\mathbf{E}}^{\text{b}} \\ \nabla \times \left( {\frac{{\nabla \times {\mathbf{H}}^{sct} }}{\varepsilon }} \right) - \omega^{2} \mu {\mathbf{H}}^{\text{sct}} & = \nabla \times \left( {\frac{{{\mathbf{J}}^{\text{sct}} }}{\varepsilon }} \right) + \omega^{2} \left( {\mu - \mu_{\text{b}} } \right){\mathbf{H}}^{\text{b}} \\ \end{aligned}$$
(6)

If the formation properties keep invariant along y direction, we can obtain the wave equations in spectral domain by applying the FT to Eq. 6 (Wu et al. 2019):

$$\begin{aligned} \tilde{\nabla } \times \left( {\frac{{\tilde{\nabla } \times {\tilde{\mathbf{E}}}^{\text{sct}} }}{\mu }} \right) - \omega^{2} \varepsilon {\tilde{\mathbf{E}}}^{\text{sct}} & = \tilde{\nabla } \times \left( {\frac{{{\tilde{\mathbf{M}}}^{\text{sct}} }}{\mu }} \right) + \omega^{2} \left( {\varepsilon - \varepsilon_{\text{b}} } \right){\tilde{\mathbf{E}}}^{\text{b}} \\ \tilde{\nabla } \times \left( {\frac{{\tilde{\nabla } \times {\tilde{\mathbf{H}}}^{\text{sct}} }}{\varepsilon }} \right) - \omega^{2} \mu {\tilde{\mathbf{H}}}^{\text{sct}} & = \tilde{\nabla } \times \left( {\frac{{{\tilde{\mathbf{J}}}^{\text{sct}} }}{\varepsilon }} \right) + \omega^{2} \left( {\mu - \mu_{\text{b}} } \right){\tilde{\mathbf{H}}}^{\text{b}} \\ \end{aligned}$$
(7)

where the right-hand side term is the equivalent source in spectral domain. At the working frequency of the well logging problems, electric fields and magnetic fields are coupled together. Therefore, either the electric wave equation or the magnetic wave equation can be selected to solve the EM fields accordingly. The selected wave equation is then discretized using a staggered finite difference grid and generates a linear system:

$${\tilde{\mathbf{A}}} \cdot {\tilde{\mathbf{x}}} = {\tilde{\mathbf{b}}}$$
(8)

where \({\tilde{\mathbf{A}}}\) is the coefficient matrix obtained from the finite difference scheme, \({\tilde{\mathbf{x}}}\) is the electric or magnetic field vector to be solved, and \({\tilde{\mathbf{b}}}\) is the source term. Note that the 2.5D finite difference scheme and matrix assembly process are similar to the 3D method except that \(\nabla = \left( {\partial x,\partial y,\partial z} \right)\) should be replaced by \(\nabla = \left( {\partial x,{\text{i}}k_{y} ,\partial z} \right)\). Finally, the field counterparts in spatial domain can be obtained by applying the IFT to the solved EM fields in spectral domain (Dyatlov et al. 2015):

$${\mathbf{H}}\left( {x,y,z} \right) = \text{F}^{ - 1} \left( {{\tilde{\mathbf{H}}}\left( {x,\tilde{k}_{y} ,z} \right)} \right) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {{\tilde{\mathbf{H}}}\left( {x,\tilde{k}_{y} ,z} \right)e^{{ - {\text{i}}\tilde{k}_{y} y}} {\text{d}}\tilde{k}_{y} } .$$
(9)

2.3 Inverse Fourier transform

The 2.5D algorithm convert a 3D problem into a series of 2D problems of different wave numbers, and the number of 2D problem determines the simulation efficiency. The straightforward way to address the IFT is the IFFT, which can be accelerated by reducing the number of sampling points through the linear interpolation in spectral domain. Another class of approaches is to use numerical integration methods including Gauss–Legendre (GL) and Gauss–Hermite (GH), by viewing the IFT as an integral problem. GL quadrature is appropriate for definite integral, and therefore, the integration intervals should be determined first. GH demands the integrand decaying as exp(− x2), but do not have to determine the integration ranges. In this paper, we propose a truncated GH quadrature method according to the decaying property of the fields in spectral domain.

  1. 1.

    Interpolation-fast Fourier transform

The sample density can be improved with cheap time cost by applying the linear interpolation in spectral domain. Assuming that the interval between the ith and the (i + 1)th sampling point is split into (m + 1) segments, the field at the interpolation point can then be expressed as

$${\tilde{\mathbf{H}}}_{j} = {\tilde{\mathbf{H}}}_{i} + \left( {{\tilde{\mathbf{H}}}_{i + 1} - {\tilde{\mathbf{H}}}_{i} } \right)\frac{{\left( {K_{j} - k_{i} } \right)}}{{\left( {k_{i + 1} - k_{i} } \right)}}\quad K_{j} = 1,2,3, \ldots ,\left({m + 1}\right)\cdot\left({N - 1}\right) + 1;\,i=1,2,3, \ldots ,N-1$$
(10)
  1. 2.

    Gauss–Legendre quadrature

Equation 9 shows that the integral interval of IFT ranges from negative infinity to positive infinity, but it can be truncated into [kmin, kmax] since the magnetic fields in spectral domain will approach to 0 as the wave number increases (see Sect. 3). The magnetic fields in spatial domain can be approximated as

$${\mathbf{H}}\left( {x,y,z} \right) = \frac{{k_{\max} - k_{\min} }}{4\pi } \cdot \sum\limits_{i = 1}^{N} {\omega_{i} \cdot {\tilde{\mathbf{H}}}\left( {x,\frac{{k_{\max} - k_{\min} }}{2}k_{yi} + \frac{{k_{\max} + k_{\min} }}{2},z} \right)\cdot e^{{ - i\left( {\frac{{k_{\max} - k_{\min} }}{2}k_{yi} + \frac{{k_{\max} + k_{\min} }}{2}} \right)y}}}$$
(11)

where kmin and kmax are the cutoff wave numbers.

  1. 3.

    Gauss–Hermite quadrature

Different from GL, the integration interval of GH quadrature is from negative infinity to positive infinity. Since the decaying properties of the magnetic fields in spectral domain are similar to the requirement of GH integrand, GH can be applied to the IFT of the magnetic fields with a slight modification as

$${\mathbf{H}}\left( {x,y,z} \right) \approx \frac{1}{2\pi }\sum\limits_{i = 1}^{N} {\omega_{i} \cdot {\tilde{\mathbf{H}}}\left( {x,k_{yi} ,z} \right)e^{{\left( {k_{yi}^{2} - {\text{i}}k_{yi} y} \right)}} }$$
(12)
  1. 4.

    Truncated Gauss–Hermite quadrature

However, the magnetic fields in spectral domain do not decay as exp(− x2), which will lead to the inaccurate results if the GH quadrature is used directly. To address this problem, we truncate the integration into [− km, km] for GH just as we did for GL rule. Define a cutoff coefficient:

$$C = \frac{{k_{\text{m}} }}{{\hbox{max} \left\{ {n_{i} } \right\}}},\quad i = 1,2,3, \ldots ,N$$
(13)

where ni is the ith Gauss node and km is the truncation value of ky. The spatial magnetic fields can then be approximated as:

$${\mathbf{H}}\left( {x,y,z} \right) \approx \frac{1}{2\pi }\sum\limits_{i = 1}^{N} {\omega_{i} \cdot {\tilde{\mathbf{H}}}\left( {x,k_{yci} ,z} \right)e^{{\left( {{{k_{yci}^{2} } \mathord{\left/ {\vphantom {{k_{yci}^{2} } {C^{2} }}} \right. \kern-0pt} {C^{2} }} - {\text{i}}k_{yci} y} \right)}} \cdot C}$$
(14)

where kyc = ky·C is the Gaussian quadrature after the truncation and ωi is the weight of the ith GH node.

3 Characteristics of fields in spectral domain and analysis of IFT

3.1 Analysis of fields in spectral domain

In this section, we analyze the characteristics of fields in spectral domain by taking magnetic dipoles-induced magnetic fields as example. We assume a z-oriented magnetic dipole located at (0,0) m inside a 10 Ω m homogeneous model radiates 400 kHz EM fields. Figure 3 shows the magnetic fields at z = 2.0 m (x is from − 10 to 10 m) vary with wave numbers and lateral distances in spectral domain, from which we can conclude that magnitude of the magnetic fields decay along both spatial direction (x) and wave number direction (ky). Note that only one 2D problem on x–z plane needs to solve per wave numbers.

Fig. 3
figure 3

Magnetic fields generated by a z-oriented magnetic dipole in a homogeneous medium. Imaginary parts of aHxz, bHyz, cHzz, real parts of dHxz, eHyz and fHzz

Full size image

Figure 4 shows the magnitude of Hzz component on y = 0 plane. From the spatial perspective, magnetic fields attenuate along both x and z directions rapidly. From the wave number’s perspective, the magnetic fields show similar distributions with different wave numbers, but the magnitude decays as the wave number increases. Aforementioned examples indicate that magnetic fields have good decaying properties in spectral domain. Note that this property is also valid for formations with complex structures. In sum, the wave number can be cut off when applying the IFT since the magnetic fields will reduce to 0 if the absolute of the wave number is large enough. The procedure to truncate the wave numbers is (1) determine the maximum magnitude value of the magnetic fields Hm; (2) find a minimum wave number k0 to ensure the magnetic fields less than one thousandth of Hm when the absolute of wave number is larger than |k0|; (3) choose the cutoff wave number km as k0.

Fig. 4
figure 4

Magnitude of Hzz component under different wave numbers

Full size image

3.2 Fast solver for IFT

The EM fields in x–z plane can be obtained by solving the linear equations in spectral domain; the spatial domain fields can be further obtained by applying the IFT. To evaluate the efficiency of the IFT methods, we calculate the relative errors with different numbers of sampling points as

$$\delta = \frac{{\left| {{\mathbf{H}}_{\text{IFT}} \left( {x,:,z} \right) - {\mathbf{H}}_{0} \left( {x,:,z} \right)} \right|}}{{\left| {{\mathbf{H}}_{0} \left( {x,:,z} \right)} \right|}} \times 100\%$$
(15)

where H0 is the analytical solution of magnetic field tensor in spatial domain, HIFT is the magnetic field tensor obtained by IFT and (x, z) are the coordinate values. The resistivity of the formation is fixed at 5 Ω m, and the frequency of the tool is set to 24 kHz. Without loss of generality, an arbitrary point x = 0 and z = 9.56 m is chosen as an example to analyze the efficiency of the IFT methods. Figure 5a shows the relative errors of interpolation IFFT (IFFTI) decrease as the number of samples and number of interpolation points increase, indicating that the linear interpolation is a feasible way to improve the IFFT. Figure 5b shows the relative error comparison among IFFT, IFFTI, GL and GHT. The relative errors decrease as the number of samples increases for all four methods, where the slope of IFFT (GL) closes to IFFTI (GHT). Table 1 presents the fewest samples for all methods with the relative error lower than 1.0%, which shows that the efficiency of the different IFT methods follows GHT > GL > IFFTI > IFFT. The efficiency of GHT proposed in this paper is 45 times faster than the traditional IFFT because the number of samples decreases to 1/45. To further verify the conclusion, we test the IFT methods in another scenario. In this case, the formation resistivity and tool frequency are 10 Ω m and 400 kHz, and the observation point locates at (0, 2.0 m). The IFT results are shown in Fig. 5c, and the same conclusion as aforementioned can be obtained.

Fig. 5
figure 5

Comparisons of IFT methods: relative errors with respect to the number of interpolation points in spectral domain for IFFT (a); relative errors respect to the number of samples (the formation resistivity is 5 Ω m, the tool frequency is 24 kHz, and the observation point is x = 0, z = 9.56 m) (b) and the formation resistivity is 10 Ω m, the tool frequency is 400 kHz, and the observation point is x = 0, z = 2.0 m (c)

Full size image
Table 1 Comparison among sample numbers of different IFT methods
Full size table

4 Examples for complex structures

4.1 Responses in fold model

Fold is one of the most common geological structures that is difficult to be modeled by 1D methods due to its lateral discontinuity. In practice, the formation is split into a series of 1D model by using the sliding-window method: (1) assume a rectangular window with a tiny width along the direction vertical to the tool (Fig. 6b); (2) the bed boundaries within the window can be viewed as a bunch of straight line segments; (3) extend the segments to obtain the simplified 1D model (red dash lines in Fig. 6b). To investigate the feasibility of the simplification of fold, we build a three-layered model as shown in Fig. 6b. The middle bed is resistive of 1-m thickness, and the boundaries vary with cosine function of 20 m period (L). The EM LWD responses with 2 MHz–28 in (0.71 m) configuration are presented in Fig. 6a as the tool penetrates the fold horizontally. The red solid (dashed) curve and blue solid (dashed) curve represent, respectively, the apparent resistivity of attenuation, and the apparent resistivity of phase shift, while the black solid curve is the true model resistivity. We can see that the curves of PSR and model resistivity completely overlap within the horizontal section (0–2 m, 22–24 m). By contrast, ATR is larger than model resistivity, indicating that the ATR is significantly affected by the shoulder bed. The different behavior of PSR and ATR is because the investigation depth of the attenuation is much larger than the phase shift. Besides, both PSR and ATR from simplified 1D model agree well with the original 2D fold model, indicating that the simplification by using the sliding-window method is feasible. Another comparison of tool responses and simplified results for L = 10 m is shown in Fig. 7, from which we can also observe that 1D results agree well with 2D results.

Fig. 6
figure 6

Comparison between the apparent resistivity curves from original fold model and simplified 1D model (L = 20 m)

Full size image
Fig. 7
figure 7

Comparison between the apparent resistivity curves from original fold model and simplified 1D model (L = 10 m)

Full size image

4.2 Responses in fault model

Fault plays an important role in oil and gas reservoir; for one thing, hydrocarbons migrate along faults; for another, the fault sealing by mud daubing protects the reservoir. Three kinds of dip-slip fault models, vertical fault (Fig. 8b), reverse fault (Fig. 9b) and normal fault (Fig. 10b), are built in this case. The resistivity, thickness and fault throw are fixed at 20 Ω m, 1 m and 1.5 m. The fault dip angles of the normal and inverse faults are 45°. The EM LWD responses with 2 MHz–28 in (0.71 m) configuration are compared between original 2D faults and simplified 1D models in Figs. 8, 9 and 10, from which we can observe: (1) the results from 1D model agree well with the original formation if the tool is far away from the fault because the fault is out of the detection range of the tool and makes no impacts on the tool responses. (2) The shape and amplitude of the resistivity curve of simplified model become inaccurate when the tool approaching the fault. (3) The fault will affect the EM LWD responses significantly and therefore induce large 1D simplification errors if the well trajectory is parallel to the dip direction.

Fig. 8
figure 8

Apparent resistivity curves of EM LWD in a vertical fault model

Full size image
Fig. 9
figure 9

Apparent resistivity curves of EM LWD in a reverse fault model

Full size image
Fig. 10
figure 10

Apparent resistivity curves of EM LWD in a normal fault model and simplified 1D model

Full size image

4.3 Responses in sandstone pinch-out

Sandstone pinch-out can be observed as hydrocarbon accommodation space. The main characteristic of the trap is the sedimentary bed thinning along the basin margin direction. A sandstone pinch-out in Fig. 11 includes a 20-Ω m oil/gas layer and a 3-Ω m water layer. A horizontal well penetrates the reservoir from the left to the right, 0.5 m from both the oil/gas layer’s top boundary of the oil/gas layer and the oil/water interface. The EM LWD tool responses (400 kHz–40 in (1.02 m) and 2 MHz–28 in (0.71 m)) between original sandstone pinch-out and simplified 1D model are compared in Fig. 11a, b. Obvious curve separation can be observed when the tool penetrates the sandstone pinch-out, which demonstrates that the simplification introduces large errors.

Fig. 11
figure 11

Apparent resistivity curves of EM LWD in a sandstone pinch-out model

Full size image

5 Conclusions

In this paper, a 2.5D algorithm for arbitrary 2D models is applied to model the EM LWD efficiently in complex geological structures. Based on the decaying properties of the EM fields in spectral domain, we propose the GHT to truncate the integration of wave numbers self-adaptively; the efficiency can be improved several tens of times compared to the traditional IFT.

For the geological fold with smooth lateral changes in formation properties and bed boundaries, the 1D simplification with sliding windows can ensure both the modeling speed and accuracy for EM LWD modeling. By contrast, for the formation structures with drastic property changes or sharp boundaries like faults and sandstone pinch-outs, the simplified 1D model can cause large errors, and therefore, 2.5D algorithms should be applied to secure the accuracy. Besides, when the fault dip is identical with the well trajectory, the fault effects on EM LWD are larger than those when the fault dip is opposite to the well trajectory.

We also observe that when the tool is far away from the faults or non-parallel boundaries, the results from the simplified model can agree well with the original model. Therefore, it is a feasible way to simulate the EM LWD using the cross-dimensional method by combining the 1D and 2.5D algorithm to ensure both efficiency and accuracy.