Residual Stress Analysis of Orthotropic Materials by the Through-hole Drilling Method

Abstract

The present study deals with the development and the application of the through-hole drilling method for the residual stress analysis in orthotropic materials. Through a systematic theoretical study of the stress field present on orthotropic plates with a circular hole, the relationships between the relaxed strains measured by a rectangular strain gauge rosette and the Cartesian components of the unknown residual stresses are obtained. The theoretical formulas of each influence coefficient allow the user an easy application of the method to the analysis of uniform-residual stresses on a generic homogeneous orthotropic material. Furthermore, to extend the method to the analysis of the residual stresses on orthotropic laminates, caused by initial in-plane loadings, an alternative formulation is implemented. The accuracy of the proposed method has been assessed through 3D numerical simulations and experimental tests carried out on unidirectional, cross-ply and angle-ply laminates.

Appendices

Appendix A

1.1 Conformal Map** and Superposition Principle

Using the Lekhnitskii approach [17], the complex functions $\Phi ^{\prime }_{1}$ and $\Phi ^{\prime }_{2}$ related to a generic uniaxial stress σ _φ applied at the hole edge and oriented at an angle φ from the longitudinal material direction L, is given by:

$$ \begin{array}{*{20}c} {\Phi ^{\prime }_{1} {\left( {x,y} \right)} = \frac{{\sigma _{\varphi } }} {{2{\left( {\mu _{1} - \mu _{2} } \right)}}} \cdot \frac{{i{\left( {i + \mu _{1} } \right)}}} {{f_{1} {\left( {x,y} \right)}}} \cdot {\left( {Sin\varphi - i \cdot Cos\varphi } \right)}{\left( {Cos\varphi + \mu _{2} Sin\varphi } \right)}} \\ {\Phi ^{\prime }_{2} {\left( {x,y} \right)} = - \frac{{\sigma _{\varphi } }} {{2{\left( {\mu _{1} - \mu _{2} } \right)}}} \cdot \frac{{i{\left( {i + \mu _{2} } \right)}}} {{f_{2} {\left( {x,y} \right)}}} \cdot {\left( {Sin\varphi - i \cdot Cos\varphi } \right)}{\left( {Cos\varphi + \mu _{1} Sin\varphi } \right)}} \\ \end{array} $$

(33)

In equations (33) f _k (x,y) (k = 1,2) functions are obtained by the conformal map** [17–19, 22, 23] of the complex plane $z_{k} = {\left( {x + \mu _{k} y} \right)}$ in the region around the hole; indicating with r _a the hole radius, it follows:

$$ f_{k} {\left( {x,y} \right)} = \left\{ {\begin{array}{*{20}c} {{\frac{{x + \mu _{k} y}} {{r_{a} }}{\sqrt {\frac{{{\left( {x + \mu _{k} y} \right)}^{2} }} {{r^{2}_{a} }} - {\left( {1 + \mu ^{2}_{k} } \right)}} } + \frac{{{\left( {x + \mu _{k} y} \right)}^{2} }} {{r^{2}_{a} }} - {\left( {1 + \mu ^{2}_{k} } \right)}\quad {\left| {\zeta _{k} } \right|} \geqslant 1}} \\ {{ - \frac{{x + \mu _{k} y}} {{r_{a} }}{\sqrt {\frac{{{\left( {x + \mu _{k} y} \right)}^{2} }} {{r^{2}_{a} }} - {\left( {1 + \mu ^{2}_{k} } \right)}} } + \frac{{{\left( {x + \mu _{k} y} \right)}^{2} }} {{r^{2}_{a} }} - {\left( {1 + \mu ^{2}_{k} } \right)}\quad {\left| {\zeta _{k} } \right|} < 1}} \\ \end{array} } \right. $$

(34)

where ζ _k (k  = 1,2) are:

$$ \zeta _{k} = \frac{{{\left( {x + \mu _{k} y} \right)} + {\sqrt {{\left( {x + \mu _{k} y} \right)}^{2} - r^{2}_{a} {\left( {1 + \mu ^{2}_{k} } \right)}} }}} {{r_{a} {\left( {1 - i \cdot \mu _{k} } \right)}}}\quad {\left( {k = 1,\;2} \right)}. $$

(35)

In the previous equations, only the roots with positive real part should be considered.

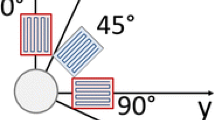
For the superposition principle, the components $\sigma ^{{{\left( r \right)}}}_{L}$, $\sigma ^{{{\left( r \right)}}}_{T}$, $\tau ^{{{\left( r \right)}}}_{{LT}}$ of the residual stresses relaxed after drilling a hole in a component subjected to a residual stress distribution characterized by the generic Cartesian components σ _L , σ _T , τ _LT , can be obtained by adding the contributions due to the three residual stress components σ _L (φ = 0°), σ _T (φ = 90°) and τ _LT (φ = 45°) present before drilling the hole. Substituting into equation (33) φ=0°, 90° and ±45° (the contribution of τ _LT is obtained by considering a tensile stress at +45° and a compressive stress at −45°) and adding the corresponding expressions so obtained, the general formulation of the complex functions represented by equation (3) is obtained.

Appendix B

1.1 Generalized Hooke’s Law in Terms of Dimensionless Constants and Derivation of Equations (5)

Considering a generic orthotropic material, for a plane stress state the relationship between the Cartesian strain components and corresponding stress components is expressed by the well known generalized Hooke’s law [24]; in particular, considering the Cartesian reference axes constituted by the material axes L–T, it can be written as [24]:

$${\left\{ {\begin{array}{*{20}c} {{\varepsilon _{L} }} \\ {{\varepsilon _{T} }} \\ {{\gamma _{{LT}} }} \\ \end{array} } \right\}} = {\left[ {\begin{array}{*{20}c} {{\frac{1}{{E_{L} }}}} & {{\frac{{ - \nu _{{LT}} }}{{E_{L} }}}} & {0} \\ {{\frac{{ - \nu _{{LT}} }}{{E_{L} }}}} & {{\frac{1}{{E_{T} }}}} & {0} \\ {0} & {0} & {{G_{{LT}} }} \\ \end{array} } \right]} \cdot {\left\{ {\begin{array}{*{20}c} {{\sigma _{L} }} \\ {{\sigma _{T} }} \\ {{\tau _{{LT}} }} \\ \end{array} } \right\}}$$

(36)

Therefore, considering the relaxed stress components $\sigma ^{{{\left( r \right)}}}_{L}$, $\sigma ^{{{\left( r \right)}}}_{T}$, $\tau ^{{{\left( r \right)}}}_{{LT}}$ and introducing the dimensionless elastic constant $\overline{E}$, $\overline{G}$ and $\overline{\nu }$ [20, 21] into equation (36), it becomes:

$$ {\left\{ {\begin{array}{*{20}c} {{\varepsilon _{L} }} \\ {{\varepsilon _{T} }} \\ {{\gamma _{{LT}} }} \\ \end{array} } \right\}} = \frac{1} {{E_{L} }}{\left[ {\begin{array}{*{20}c} {1}&{{ - \overline{\nu } }}&{0} \\ {{ - \overline{\nu } }}&{{\overline{E} }}&{0} \\ {0}&{0}&{{{\overline{E} } \mathord{\left/ {\vphantom {{\overline{E} } {\overline{G} }}} \right. \kern-\nulldelimiterspace} {\overline{G} }}} \\ \end{array} } \right]} \cdot {\left\{ {\begin{array}{*{20}c} {{\sigma ^{{{\left( r \right)}}}_{L} }} \\ {{\sigma ^{{{\left( r \right)}}}_{T} }} \\ {{\tau ^{{{\left( r \right)}}}_{{LT}} }} \\ \end{array} } \right\}} $$

(37)

Finally, substituting equation (4) into equation (37), equations (5) are obtained after simple algebra.

Appendix C

1.1 Relationship Between ${\left[ {\widetilde{E}} \right]}_{k}$ and [E] _k

The stiffness matrix [E] _k of an orthotropic ply in the principal coordinate system 1–2 (see Fig. 5), is given by [24]:

$$ {\left[ E \right]}_{k} = {\left[ {\begin{array}{*{20}c} {{{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}}&{{\nu _{{12}} {E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}}&{0} \\ {{\nu _{{12}} {E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}}&{{{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {1 - \nu _{{12}} \nu _{{21}} } \right)}}}}&{0} \\ {0}&{0}&{{G_{{12}} }} \\ \end{array} } \right]} $$

(38)

where E ₁, E ₂, G ₁₂, ν ₁₂ and ν ₂₁ are the ply elastic properties in the coordinate system 1–2.

Indicating with α _k the angle between the laminate longitudinal direction L and the principal direction 1 of the kth ply, the stiffness matrix ${\left[ {\widetilde{E}} \right]}_{k}$ of the ply in the coordinate system L–T is given by [24]:

$${\left[ {\widetilde{E}} \right]}_{k} = {\left[ {T{\left( {\alpha _{k} } \right)}} \right]} \cdot {\left[ {E^{ * } } \right]}_{k} \cdot {\left[ {\overline{T} {\left( {\alpha _{k} } \right)}} \right]}^{{ - 1}} $$

(39)

where ${\left[ {E^{ * } } \right]}_{k}$ is the matrix that is obtained by substituting into the matrix [E] _k the term G ₁₂ with 2G ₁₂, and [T(α _k )] is the in-plane transformation matrix given by:

$$ {\left[ {T{\left( {\alpha _{k} } \right)}} \right]} = {\left[ {\begin{array}{*{20}c} {{\cos ^{2} \alpha _{k} }}&{{sen^{2} \alpha _{k} }}&{{2\cos \alpha _{k} \sin \alpha _{k} }} \\ {{\sin ^{2} \alpha _{k} }}&{{\cos ^{2} \alpha _{k} }}&{{ - 2\cos \alpha _{k} \sin \alpha _{k} }} \\ {{ - \cos \alpha _{k} \sin \alpha _{k} }}&{{\cos \alpha _{k} \sin \alpha _{k} }}&{{\cos ^{2} \alpha _{k} - \sin ^{2} \alpha _{k} }} \\ \end{array} } \right]} $$

(40)

Moreover, ${\left[ {\overline{T} {\left( {\alpha _{k} } \right)}} \right]}$ is the matrix obtained by multiplying by two the term of the third row of the matrix [T(α _k )].