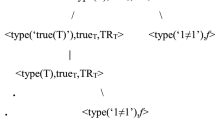Abstract
We extend the Embracing Revenge account of the semantic paradoxes by constructing two distinct consequence relations that reflect, in different ways, the transfinitely-many-valued semantics developed in earlier work. In particular, we adapt the underlying ideas of “gappy” approaches based on K3, and “glutty” approaches based on LP, to the Embracing Revenge framework, by treating the infinitely many non-classical truth values as infinitely many ways that a sentence might fail to receive a classical truth value in the former case, and as infinitely many ways that a sentence might receive both classical truth values in the latter. In order to obtain deductive systems that are very nearly classical, we need to utilize different conditionals (and different negations) in each logic.
Similar content being viewed by others
Notes
Of course, the Curry Paradox, in full generality, concerns the fact that we can prove any sentence \(\Phi \) via running the argument rehearsed here on any sentence \(\** me to see this much-simplified version of the rather inelegant construction provided in earlier drafts of this essay.
In more detail: \(\Phi _\Sigma (\ulcorner \Psi \urcorner )\) is \(\top \) if the semantic value of \(\Psi \) is in \(\Sigma \) and is not identical to \(\bot \), and \(\Phi _\Sigma (\ulcorner \Psi \urcorner )\) is \(\bot \) otherwise.
On is the proper class of all ordinals. See Hellman and Cook (2018a) for an in-depth discussion of the role that indefinite extensibility plays in the Embracing Revenge view, and an examination of the connections between the resulting open-endedness of the concept Semantic Value and the indefinite extensibility of the set-theoretic heirarchy.
For mathematical convenience we represent the linguistic hierarchy as an increasing sequence of distinct languages, although philosophically we prefer to interpret the formalism as describing a single, ever-growing language. See Cook (2008) and Hellman and Cook (2018a) for more detailed discussions of the need for a transfinite hierarchy of languages, and for an argument against the existence of a ‘super-language’ consisting of the union of the languages in the hierarchy.
All of these expressions in each \(\mathcal {L}_\alpha \) are extensional. Tourville and Cook (2020) contains a detailed exploration of an extension of the Embracing Revenge framework obtained via the inclusion of intensional operators. There are interesting and important questions regarding how such intensional operators behave in the various logics introduced below. We leave the investigation of these issues for another time (or to the ambitious reader).
Note, however, that we allow for infinite conjunctions in order to ‘simulate’ universal quantification (and hence, in combination with negation, existential quantification).
One should take care not to confuse the pathological predicates \(\textsf {P}_\beta (\xi )\) and the propositional letters \(\textsf {P}_\beta \).
Note that negation does not invert or otherwise rearrange the pathological values.
A similar construction is sketched in Schlenker (2010).
It is important to note the limitation of this theorem: There are many connectives defined on all semantic values in \(\{\top , \bot \} \cup \{\rho _\alpha : \alpha \in \textsf {On}\}\) (i.e., on the entire proper class of semantic values) that are not expressible in terms of the resources of any \(\mathcal {L}_\alpha \).
When making semantic claims such as \(\Delta \vDash \Gamma \) we have been treating \(\Delta \) and \(\Gamma \) as sets. In sequents such as \(\Delta \vdash \Gamma \) occurring in sequent calculus rules and derivations, however, we will treat \(\Delta \) and \(\Gamma \) as multisets, in order to make applications of contraction explicit.
Thanks are owed to an anonymous referee for pointing out the connection between Quine’s maxim and the present project.
This sharply distinguishes the Maximal Deducibility Maxim from Quine’s Maxim of Minimal Multilation, or at least Quine’s applications of the latter maxim, which take classical logic to be the un-mutilated standard.
See Cook (2012) for an argument that, although perhaps analytic or (metaphysically) necessary, the T-schema is not a logical truth (nor is the intersubstitutivity of a sentence and the claim that it is true logically valid).
The fact that both ERK3 and ERLP satisfy the standard structural rules is a trivial consequence of the definitions of ERK3 and ERLP consequence.
Given the manner in which we are interpreting the Maximum Deducibility Maxim (i.e., as demanding a logic as close to classical logic as possible), we restrict our attention here to those operators that correspond to notions in classical logic. In other words, determining what rules govern the constants \(\textsf {C}_\beta \) is left for another time (or to the ambitious reader).
It is worth noting that, on the standard definition of disjunction in terms of conjunction and negation:
$$\begin{aligned} \Phi \vee \Psi =_{df} \lnot (\lnot \Phi \wedge \lnot \Psi ) \end{aligned}$$The standard sequent calculus rules for disjunction:

and:

are also logically ERK3 valid and logically ERLP valid.
We leave the task of formulating such rules and verifying this fact to the interested reader.
The upshot of these truth tables is perhaps easier to grasp if we reorder the arguments as follows:

Note that these definitions of relativized strong and weak negations, as well as the definitions of the Frege and Anti-Frege conditionals in the sections that follow, are not the only ones possible. The definitions that appear here have been chosen based on their simplicity and clarity (in the authors’ opinion, at least—the reader’s mileage may vary).
Thanks are owed to an anonymous referee who suggested reformulating the rules in this manner.
This is a claim about the identity of the two truth functions in question.
Interestingly, the remainder of the proof is correct in ERLP—that is, it shows that the sequent \(\textsf {T}(\ulcorner \** \urcorner ) \vdash \bot \) leads to a contradiction:

References
Beall, J. (Ed.). (2008). Revenge of the liar: New essays on the paradox. Oxford University Press.
Beal, J. (2011). Multiple-conclusion LP and default classicality. Review of Symbolic Logic, 4(2), 326–336.
Beall, J. (2013). LP+, K3+, FDE+, and their classical collapse. The Review of Symbolic Logic, 6(4), 742–754.
Berg, E., & Cook, R. (2017). The propositional logic of Frege’s Grundgesetze: Semantics and expressiveness. Journal for the History of Analytical Philosophy, 5(6), 1–34.
Cobreros, P., Égré, P., Ripley, D., & van Rooij, R. (2012). Tolerant, classical, strict. Journal of Philosophical Logic, 41(2), 347–385.
Cook, R. (2008). Embracing revenge: On the indefinite extensibility of language. In (Beall 2008): 31–52
Cook, R. (2009). What is a truth value, and how many are there? Studia Logica, 92, 183–201.
Cook, R. (2012). The T-schema is a not a logical truth. Analysis, 72, 231–239.
Cook, R. (2013). Key concepts in philosophy: Paradoxes. Polity Press.
Curry, H. (1942). The inconsistency of certain formal logics. Journal of Symbolic Logic, 7(3), 115–117.
Frege, G. (1893/1903/2014), Grundgesetze der Arithmetik, Vols. I & II, P. Ebert & M. Rossberg (eds. & trans.). Oxford University Press.
Hellman, G., & Cook, R. (2018a). Extendibility and paradox. In (Hellman & Cook 2018b): 51–73.
Hellman, G., & Cook, R. (Eds.). (2018). Hilary Putnam on logic and mathematics. Springer.
Kleene, S. (1952). Introduction to metamathematics. Van Nostrand.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72, 690–716.
Murzi, J., & Rossi, L. (2020). Generalized revenge. Australasian Journal of Philosophy, 98(1), 153–177.
Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8, 219–241.
Quine, W. (1986). Philosophy of logic (2nd ed.). Harvard University Press.
Restall, G. (1999). An introduction to substructural logics. Routledge.
Rosenblatt, J. (2022). Should the non-classical logician be embarrassed? Philosophy and Phenomenological Research. https://doi.org/10.1111/phpr.12770
Schlenker, P. (2010). Super-liars. Review of Symbolic Logic, 3(3), 374–414.
Tarski, A. (1933). The concept of truth in the languages of the deductive sciences. In (Tarki 1984): 252–278.
Tarki, A. (1984). Logic, semantics, metamathematics: Papers from 1923 to 1938. J. Corcoran (Ed.). Hackett Publishing.
Tourville, N., & Cook, R. (2016). Embracing the technicalities: Expressive completeness and revenge. Review of Symbolic Logic, 9(2), 325–358.
Tourville, N., & Cook, R. (2020). Embracing intensionality: Paradoxicality and semi-truth operators in fixed point models. Logic Journal of the IGPL, 8(5), 747–770.
van Rooij, R. (2010). Vagueness, Tolerance, and Non-transitive Entailment (manuscript).
Acknowledgements
We would like to thank the audiences at the 2018 Semantic Paradox and Revenge Conference at the University of Salzburg, Austria; the 2016 International Conference on Paradoxes, Logic, and Philosophy at the Department of Philosophy and Institute of Foreign Philosophy, Peking University, China; the 2016 5\(^{th}\) Workshop on Philosophical Logic at SADAF, Buenos Aires, Argentina; and the 2016 ASL Logic Colloquium at the University of Leeds, England for helpful and generous feedback. Thanks are also owed to a number of extremely helpful referees.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts of interest, funding information, or other disclosures relevant to this work.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Non-Classical Approaches to Paradox.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Tourville, N., Cook, R.T. Conditionals, curry, and consequence: embracing deduction. Synthese 201, 52 (2023). https://doi.org/10.1007/s11229-022-04013-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11229-022-04013-1