1 Introduction

Accurate detection of physical interference between two or more bodies is crucial in the design of many engineering systems. Non-interference constraints appear in numerical optimization problems that manipulate an object within an environment containing other objects such that there is no collision. Many numerical optimization problems must enforce non-interference constraints manipulate an object within an environment containing other objects such that there is no collision. Prior literature on these problems describe these constraints using inconsistent terminology, e.g., anatomical constraints (Bergeles et al. 2015; Lin et al. 2022), spatial integration constraints (Brelje et al. 2020; Brelje 2021), boundary constraints (Criado Risco et al. 2023; Stanley and Ning 2019), and interference checks (Fadel et al. 2015). We observe that these terms represent the same underlying concept applied to different problem settings; therefore, we propose a common term, geometric non-interference constraints, since they are employed in design optimization to ensure a design where there exists no interference between two or more geometric shapes or paths of motion.

In our study, a geometric shape is associated with the design configuration of an engineering system at a particular instance of time. The geometric shapes of interest in this paper are curves in two dimensions, or orientable surfaces in three dimensions. We assume that the geometric shapes are non-self-intersecting but make no assumptions on whether they are open or closed. A path of motion or trajectory is the set of points that traces the motion of a point on the engineering system as the system changes configuration over time. The paths considered in this paper are simply curves in two or three dimensions. We use the term layout to refer to a set of geometric shapes.

Based on the definitions above, we identify three major classes of optimization problems with geometric non-interference constraints: layout optimization, shape optimization, and optimal path planning. All three classes are within the scope of problems we address in this paper.

Layout optimization optimizes the positions of design shapes via translation subject to geometric non-interference, with or without additional boundary constraints. For example, the wind farm layout optimization problem (WFLOP) consists of positioning wind turbines within a wind farm in an optimal way while ensuring that interference between turbines and the boundary of the wind farm is avoided (Cazzaro and Pisinger 2022; Guirguis et al. 2016; Reddy 2021; Criado Risco et al. 2023). Another example of a layout optimization problem is the packing problem. Packing problems consist in positioning objects within a domain while minimizing the amount of space occupied or maximizing the number of objects placed without geometric interference (Fadel et al. 2015; Brandt 2017).

Shape optimization seeks to optimize geometric shapes subject to geometric non-interference, with or without additional boundary constraints. For example, shape optimization of an aircraft fuselage optimizes the shape of a fuselage with constraints ensuring that the passengers, crew, payload, and all the subsystems fit inside the fuselage (Brelje et al. 2020; Brelje 2021).

Optimal path planning optimizes the trajectory of a point or a set of points subject to geometric non-interference, with or without additional boundary constraints. The design optimization of surgical robots is an example of a problem involving robot motion planning—a class of problems within optimal path planning—that has attracted recent attention (Bergeles et al. 2015; Lin et al. 2022). In the design optimization of surgical robots, non-interference constraints are imposed such that the robot does not collide with the anatomy of a patient during operation. Additionally, it is desirable for the robot to maintain a safe distance from the anatomy, motivating the use of a distance-based non-interference constraint formulation in such problems. An example of an aerospace application is the representation of complex no-fly zone shapes in trajectory optimization (Kim and Liem 2022; Orndorff et al. 2023).

The problems just mentioned are solved using numerical optimization algorithms. Historically, gradient-free algorithms have been more commonly used to solve such problems, e.g., in layout optimization (Lodi et al. 2002; Cagan et al. 2002; Fasano 2014) and in robot motion planning (Bergeles et al. 2015). A major reason behind this was the difficulty in efficiently computing the derivatives for a complex model. As models become more complex, that is, with more disciplines and design variables, solutions become impracticable with gradient-free algorithms since these algorithms scale poorly with the number of design variables. However, the recent emergence of modeling frameworks such as OpenMDAO (Gray et al. 2019) has enabled efficient design of large-scale and multidisciplinary systems using gradient-based optimization, including some of the aforementioned problems with geometric non-interference constraints (Brelje et al. 2020; Guirguis et al. 2016; Criado Risco et al. 2023; Lin et al. 2022).

Geometric non-interference constraint functions for gradient-based optimization require special consideration. These functions must be continuously differentiable or smooth in order to be used with a gradient-based optimization algorithm. They should also be efficient to compute because optimization algorithms evaluate constraint functions and their derivatives repeatedly over many optimization iterations. During some iterations, the optimizer may violate an interference constraint, and useful gradient information in such iterations is still required despite it being infeasible. Consequently, any non-interference constraint function must be defined in the event of an overlap between objects and provide necessary gradient information.

Fig. 1
figure 1

An ideal constraint function \(\phi \) indicates geometric interferences using signed distances of representative points \({\textbf{x}}^{(i)}\) on a body from the boundary \(\Gamma \) defining the feasible space \(\Omega \)

Full size image

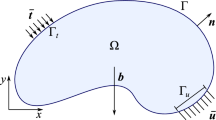
Figure 1 shows a diagram with two iterations of a design body in an optimization problem. One of the designs shown is feasible while the other is not. The feasible design is the one where the design body is completely inside the feasible space whereas the infeasible design has at least one point on the design body lying outside the feasible space. For the \(\phi \) defined in Fig. 1, enforcing the optimization constraint \(\phi ({\textbf{x}}^{(i)})\ge \epsilon \) for certain representative points \({\textbf{x}}^{(i)}\) chosen on the surface of the design body guarantees non-interference by ensuring that all \({\textbf{x}}^{(i)}\) stay within the feasible region for the final optimized design. The constant \(\epsilon \) can be any small positive value appropriate for a given problem.

The formulation of the constraint function \(\phi \), and consequently its derivatives, is inherently defined by the shape of the boundary \(\Gamma \) of the feasible space. It cannot always be assumed that the boundary \(\Gamma \) is a fixed shape across all optimization iterations, as many problems will consider the design body and the constraining boundary \(\Gamma \) both as variables within an overarching design problem. For example, the simultaneous shape and layout optimization problem in Brelje (2021) optimizes the shape of a wing while also considering the packing of internal batteries. We acknowledge that \(\phi \) is dependent on variations in \(\Gamma \) within the context of an outer loop design problem; however, we do not consider the sensitivity of \(\phi \) to variations in \(\Gamma \) to be within the scope of this paper. For our study, we focus on the formulation of a non-interference constraint function \(\phi \) with respect to a fixed boundary \(\Gamma \).

Existing non-interference constraint formulations suffer from various limitations. The formulation of quasi-phi-functions by Stoyan et al. (2015) provides an analytical form to represent an interference for simple geometric shapes. Quasi-phi-functions are continuous but only piecewise continuously differentiable. These functions are also not generalized to represent any arbitrary shape. The formulation by Brelje et al. (2020) is generalized to any triangulated 3D geometric shape, but has computational limitations. The computational complexity of their method is \({\mathcal {O}}(N_\Gamma )\), where \(N_\Gamma \) is the number of elements in the triangulation. They are able to overcome this scaling issue by making use of graphics processing units (GPUs) but demonstrate their formulation on a geometric shape with only 626 elements in the triangulation. In their recent work on the WFLOP, Criado Risco et al. (2023) formulate a generic explicit method for geometric shapes in 2D, but the method suffers from the same scaling issues as in Brelje et al. (2020) and contains discontinuous derivatives. The formulation by Bergeles et al. (2015) employs a distance potential function that is calculated with the k-nearest neighbors of poinst that lie on the boundary. With the use of a k-d tree structure, the computational complexity of the k-nearest neighbor search scales better than linearly (\({\mathcal {O}}(k\log (N_\Gamma ))\), on average) but the structure is not suitable for gradient-based optimization because the derivatives are discontinuous when the set of k-nearest neighbors changes.

Outside the domain of non-interference constraint formulations currently employed in optimization, we discovered a significant body of research conducted on a remarkably similar problem by the computer graphics community. Surface reconstruction in the field of computer graphics is the process of converting a set of points into a surface for graphical representation. A common approach for surface reconstruction is the representation of surfaces by an implicit function. Implicit surface reconstruction methods such as Poisson (Kazhdan et al. 2006), Multi-level Partition of Unity (MPU) (Ohtake et al. 2003), and Smooth Signed Distance (SSD) (Calakli and Taubin 2011), to name a few, construct an implicit function from a point cloud to represent a surface. We observed that some of these distance-based formulations can be applied to overcome prior limitations in enforcing geometric non-interference constraints in gradient-based optimization.

The objective of this work is to devise a general methodology based on an appropriate surface reconstruction method to generate a smooth and fast-to-evaluate geometric non-interference constraint function from an oriented point cloud. It is desired that the function locally approximates the signed distance to a geometric shape and that its evaluation time is independent of the number of points sampled over the geometric shape \(N_\Gamma \). The function must also be an accurate implicit representation of the surface implied by the given point cloud. The contribution of this paper is a new formulation for representing geometric non-interference constraints in gradient-based optimization. We investigate various properties of the proposed formulation, its efficiency compared to existing non-interference constraint formulations, and its accuracy compared to state-of-the-art surface reconstruction methods. Additionally, we demonstrate the computational speedup of our formulation in an experiment with a path planning and shape optimization problem.

The remainder of this paper proceeds as follows. Section 2 reviews existing geometric non-interference constraint formulations for optimization. In this section, we also provide a thorough survey of implicit surface reconstruction methods in order to identify methodologies to be brought into our formulation. Section 3 presents our methodology to generate a level set function for representing geometric non-interference constraints. Section 4 provides numerical results that quantify the accuracy and efficiency of our formulation. We demonstrate our accuracy on common benchmarking models from the computer graphics community and also on geometries with aerospace applications. We finally demonstrate the application of our method using a surgical robot design optimization problem. In Sect. 5, we summarize our approach, its potential impact, and avenues for future work.

2 Related work

This section presents an overview of related work to the defined research problem. We begin by reviewing prior methods for enforcing non-interference constraints in gradient-based optimization in Sect. 2.1. We then review the problem of surface reconstruction and its complexities in Sect. 2.2. Various methods for dividing up the domain for the implicit function are introduced in Sect. 2.2.1. In Sect. 2.2.2, we present a literature review for methods that approximate the signed distance function.

2.1 Previous methods for enforcing non-interference constraints in gradient-based optimization

We identify two preexisting methods for enforcing geometric non-interference constraints in gradient-based optimization that are both continuous and differentiable. Previous constraint formulations that are explicitly defined by the set of nearest neighbors (e.g., work by Criado Risco et al. (2023) and Bergeles et al. (2015)) have been used in optimization, but we note that they are non-differentiable and may incur numerical difficulties in gradient-based optimization.

Brelje et al. (2020) implement a general mesh-based constraint formulation for non-interference constraints between two triangulations of objects. Two nonlinear constraints define their formulation. The first constraint is that the minimum distance of the design shape to the geometric shape is greater than zero, and the second constraint is that the intersection length between the two bodies is zero—i.e., there is no intersection. A binary check, e.g., ray tracing, must be used to reject optimization iterations where the design shape is entirely in the infeasible region, where the previous two constraints are satisfied. As noted by Brelje et al., this formulation may make the optimizer susceptible to getting stuck in an infeasible part of the domain for nonconvex shapes. Additionally, the constraint function has an evaluation time complexity of \({\mathcal {O}}(N_\Gamma )\). They initially addressed this scaling by using parallel processing with graphics processing units (GPUs). Further improvements, e.g., a more efficient FORTRAN-based implementation, bounding box testing, only using the minimum value in triangle tests, and load balancing, accelerated their derivative computation by a factor of 500 in one example (Brelje 2021).

Lin et al. (2022) implement a modified signed distance function, making it differentiable throughout. Using an oriented set of points to represent the bounds of the feasible region, the constraint function is a distance-based weighted sum of signed distances between the points and a set of points on the design shape. This representation is inexact and is found to compromise accuracy to achieve smoothness in the constraint representation. Additionally, their formulation also has a time complexity of \({\mathcal {O}}(N_\Gamma )\) for evaluation, which we improve upon through the proposed method.

2.2 Surface reconstruction

Our research goal—to derive a smooth level set function from a set of oriented points—closely aligns with the problem of surface reconstruction in computer graphics. Surface reconstruction is done in many ways, and we refer the reader to Berger et al. (2017), Huang et al. (2022) for a full survey on surface reconstruction methods from point clouds. We, in particular, focus on implicit surface reconstruction, which constructs an implicit function whose zero level set represents the smooth surface implied by the point cloud.

Surface reconstruction begins with a representation of a geometric shape. Geometric shape representations (e.g., point clouds, triangulations, meshes containing general polygons) can be sampled and readily converted into an oriented point cloud and posed as a surface reconstruction problem. When working with point clouds, there can be many practical difficulties, e.g., the precision of 3D scanners which will introduce error into scans. As a result, implicit surface reconstruction methods often take into consideration nonuniform sampling, noise, outliers, misalignment between scans, and missing data in point clouds. Implicit surface reconstruction methods have been shown to address these issues well, including hole-filling (Carr et al. 1997; Hong-Kai et al. 2001; Davis et al. 2002), reconstructing surfaces from noisy samples (Dinh et al. 2001; Kazhdan et al. 2006; Pan et al. 2017), reconstructing sharp corners and edges (Dinh et al. 2001), and reconstructing surfaces without normal vectors in the point cloud (Hoppe et al. 1992; Pan et al. 2017).

2.2.1 Approaches for constructing implicit functions from points

Implicit surface reconstruction methods construct an implicit function from a set of points, that is not necessarily the original point cloud defining the geometric shape. We identify three classes of approaches for selecting these points.

One approach for selecting the points for constructing the implicit function is to adaptively subdivide the implicit function’s domain using an octree structure. Octrees, as used by Calakli and Taubin (2011), Zhou et al. (2010), Kazhdan et al. (2006), Pan et al. (2017), Ohtake et al. (2003), Tang and Feng (2018), recursively subdivide the domain into octants using various heuristics in order to form neighborhoods of control points near the surface. Heuristics include point density (Calakli and Taubin 2011), error-controlled (Ohtake et al. 2003), and curvature-based (Tang and Feng 2018) subdivisions. The error of the surface reconstruction decays with the sampling width between control points, which decreases exponentially with respect to the octree depth (Kazhdan et al. 2006). Additionally, the neighborhoods of control points from octrees can be solved for and evaluated in parallel using graphics processing units (GPUs), which allows for fast, on-demand surface reconstruction as demonstrated in Zhou et al. (2010).

Another approach is to construct the implicit function by directly using the point cloud defining the geometric shape. A chosen subset of points in the point cloud and points projected in the direction of the normal vectors are used to place the radial basis function (RBF) centers in Carr et al. (2001). This approach results in fewer points than octrees that are still distributed near the surface. The explicit formulation by Hicken and Kaur (Hicken and Kaur 2022) uses all points in the point cloud to define the implicit function and shows favorable decay in surface reconstruction error as the number of points in the point cloud \(N_\Gamma \) increases. This structure has been used in combination with RBFs for hole-filling in Carr et al. (1997) and anisotropic basis functions for representing sharp corners in Dinh et al. (2001).

Another approach is to construct a uniform grid of points to control the implicit function. Unlike the aforementioned approaches, the distribution of points is decoupled from the resolution of the point cloud. As a result, deformations to the geometric shape can be represented without loss in accuracy near the surface as shown by Hong-Kai et al. (2001). This makes it a popular structure in partial differential equation (PDE) based reconstruction methods that evolve the surface during reconstruction, such as in Tasdizen et al. (2002), Jakobsen et al. (2007). In general, more points representing the implicit function are required to achieve the same level of accuracy to other approaches. As a result, implicit functions defined by a uniform grid are more computationally expensive to solve for in both time and memory usage than the aforementioned approaches, as experienced by Sibley and Taubin (2005), but can be reduced by a GPU-based multigrid approach as implemented by Jakobsen et al. (2007).

2.2.2 Approaches for signed distance function approximation

Another way to classify the implicit function generated in surface reconstruction is as an indicator function or as a continuous function that (in some cases) provides a measure of distance to the boundary. In these cases, we use the term, signed distance function (SDF). SDFs are commonly used because it is often useful to know the distance to the boundary. Often, the implicit function only locally approximates the SDF near the boundary, as is the case with our method. We identify four approaches for locally approximating the SDF, which are described below.

2.2.3 Explicit formulations

Explicit formulations use the point cloud data to define an explicit formula representing the implicit function. These methods formulate local linear approximations to the SDF, then interpolate between these approximations. Criado Risco et al. (2023) present the simplest approach which uses the nearest edge and normal vector to define the function explicitly. The resultant constraint function is piecewise continuous but non-differentiable at points where the nearest edge switches. Belyaev et al. (2013) derive a special smoothing method for defining signed \(L_p\)-distance functions, which is a continuous and smooth transition between piecewise functions. Hicken and Kaur (2022) use a modified constraint aggregation method that defines a basis function with basis weights that exponentially decay with distance. The resultant formulation is a smooth and differentiable approximation to the SDF, which we identify as a strong candidate for enforcing non-interference constraints with good accuracy.

Given an oriented point cloud which is a set of ordered pairs \({\mathcal {P}}= \{(P_i,\mathbf {{\textbf{n}}}_i):i=1,\dots , N_\Gamma \}\), where \({\textbf{p}}_i\) is the location of the points sampled over the geometric shape, and \(\mathbf {{\textbf{n}}}_i\) are the unit normal vectors at \({\textbf{p}}_i\), the explicit level set function defined by Hicken and Kaur (2022) is

$$\begin{aligned} \phi _{H}({\textbf{x}})&= \frac{\sum ^{N_\Gamma }_{i=1} d_i({\textbf{x}})e^{-\rho (\Delta _i({\textbf{x}}) - \Delta _{\text {min}})}}{\sum ^{N_\Gamma }_{j=1} e^{-\rho (\Delta _j({\textbf{x}}) - \Delta _{\text {min}})}}, \end{aligned}$$
(1)

where \(d_i({\textbf{x}})\) is the signed distance to the hyperplane defined by the point and normal vector pair in the point cloud \(({\textbf{p}}_i,\mathbf {{\textbf{n}}}_i)\), \(\Delta _i({\textbf{x}})\) is the Euclidean distance from \({\textbf{x}}\) to \({\textbf{p}}_i\), \(\Delta _\text {min}\) is the Euclidean distance to the nearest neighbor, and \(\rho \) is a smoothing parameter.

To improve accuracy, Hicken and Kaur suggest modifications to make the linear approximation to a quadratic approximation by using the principal curvatures of the surface. Unless readily provided by a smooth geometric representation, the principal curvatures must be approximated from the point cloud, such as the approximation method by Tang and Feng (2018). To reduce the computational complexity, Hicken and Kaur suggest only evaluating the k-nearest neighbors, since the basis weights exponentially decay with distance. However, using the k-nearest neighbors will remove the function’s differentiability as the set of k-nearest neighbors changes. As a result, the evaluation time scales by \({\mathcal {O}}(N_\Gamma )\) to be differentiable. While not originally purposed for geometric non-interference constraints, the formulation by Hicken and Kaur is on par in computational complexity with other currently used non-interference constraint formulations (Lin et al. 2022; Criado Risco et al. 2023; Brelje et al. 2020). Note that explicit formulations rely heavily on the accuracy of the point cloud data and will be susceptible to inaccuracies when provided with point clouds containing poor data, such as noise and outliers.

2.2.4 Interpolation formulations with radial basis functions

Another method to construct the level set function is to solve an interpolation problem given an oriented point cloud \({\mathcal {P}}\). Because the data points of \({\mathcal {P}}\) always lie on the zero contour, nonzero interpolation points for the implicit function can be defined on the interior and exterior, as originally done by Turk and O’Brien (2002). Radial basis functions (RBFs) are then formulated to interpolate the data. To avoid overfitting, thin-plate splines can be used to formulate the smoothest interpolator for the data, as noted in Carr et al. (2001, 1997). Solving for the weights of an RBF involves solving a linear system, which is often dense and very computationally expensive due to their global support. Turk and O’Brien (2002) solve up to 3,000 RBF centers, and improvements by Carr et al. (2001) allow up to 594,000 RBF centers to be constructed in reasonable time (hours). On top of the significant computational expense, interpolating RBFs have been criticized for having blobby reconstructions (Turk and O’Brien 2002; Dinh et al. 2001) which poorly represent sharp features in the geometric shapes.

2.2.5 PDE-based formulations

Another approach is to construct the level set function as a vector field that smoothly approximates the normal vectors \(\mathbf {{\textbf{n}}}_i\) given by the point cloud \({\mathcal {P}}\). The vector field is then integrated and fit, usually by a least squares fitting, to make the zero level set fit the point cloud. We classify the methods that solve for the vector field as a solution to a partial differential equations (PDEs) as PDE-based methods. Poisson’s method (Kazhdan et al. 2006) uses variational techniques to Poisson’s equation to construct a vector field. Improvements to this method add penalization weights to better fit the zero contour to the point cloud in Kazhdan and Hoppe (2013). Tasdizen et al. (2002) prioritize minimal curvature and minimal error in the vector field by solving a set of coupled second order PDEs to derive their level set function. Hong-Kai et al. (2001) use the level set method, originally introduced by Osher and Sethian Osher and Sethian (1988), for surface reconstruction, with the advantage of modeling deformable shapes. In the aformentioned PDE-based methods, the setup for the implicit function reduces to solving a PDE by time-step** (Hong-Kai et al. 2001; Tasdizen et al. 2002) or a sparse linear system (Kazhdan et al. 2006; Kazhdan 2005) in the case of Poisson’s equation. Kazhdan et al. (2006) note that care should be taken when choosing a smoothing filter for the normal field defined by \(\mathbf {{\textbf{n}}}_i\), especially for nonuniformly sampled points. In the analysis done by Calakli and Taubin (2011), they found that Poisson’s method often over-smooths some surfaces. We also note that solutions to PDEs are more difficult to implement than other methods in practice.

2.2.6 Energy minimization formulations

Another methodology is to solve an optimization problem that minimizes some energy function with respect to the values of the basis function directly. The smooth signed distance (SSD) surface reconstruction method (Calakli and Taubin 2011) minimizes an energy function with three terms. Minimizing these three terms maximizes smoothness and minimizes the approximation error of the zero level set and the gradient field to the data in \({\mathcal {P}}\), all in a least squares sense. Alternative forms, such as in Tang and Feng (2018), Ohtake et al. (2003), propose a different energy term to this formulation, which does a direct least squares fit to the approximate signed distance function. We perform a more thorough discussion of the four energy terms in Sect. 3, as our method also poses an energy minimization problem.

Table 1 Signed distance approximations and their basis function representations
Full size table

The energy minimization problem proposed in these papers is a well-posed unconstrained quadratic programming (QP) problem. The solution to these unconstrained QP problems reduces to the solution of a linear system. Making use of hierarchical structures, such as octrees, and compactly supported basis functions, the linear system is sparse and recursively solved at increasing depths of the structure. These advantages allow for fast solutions on the order of minutes as reported by Calakli and Taubin (2011), Tang and Feng (2018). It should be noted that the time and space (memory) consumed by hierarchical approaches grows exponentially with the depth of the octree, so many implementations limit the depth up to 11. The resultant number of control points in Tang and Feng (2018) is on the order of \(10^6\).

2.2.7 Summary

We note that interpolation formulations with RBFs, PDE-based formulations, and energy minimization formulations are different approaches to the same problem of approximating the SDF. The primary differences lie within the derivation and implementation of such methods. The energy minimization formulation by Calakli and Taubin (2011) performs a least squares fit to the data in the point cloud. Thin-plate spline RBFs are an exact solution to an equivalent least squares energy minimization problem, as derived by Buhmann (2003). The two-step energy minimization formulation by Sibley and Taubin (2005) follows the same approach as PDE-based methods in which a vector field is solved for and then a least squares fit is done to fit the surface. We refer interested readers to Calakli and Taubin (2011) which discuss the similarities and differences between their energy minimization method, SSD, and the Poisson’s method.

We summarize the context for all the methods in Table 1, highlighting the main differences in their formulation, basis function representation, and distribution of points controlling the function. We note that our method is an energy minimization formulation, which uses the same energy terms as Calakli and Taubin (2011), but with a different basis function and different distribution of control points.

3 Methodology

3.1 Signed distance function

The approach to our methodology is to compute a level set function \(\phi \) by approximating the signed distance function (SDF) of a geometric shape. We assume that the geometric shape partitions its neighboring space into a feasible region and an infeasible region as shown in Fig. 2. Our goal is to generate a level set function such that the zero contour of the function approximates the boundary between the feasible and infeasible regions, i.e., the geometric shape. We also require that evaluating the implicit function at any point in the domain of interest will determine if the point is located on the boundary or within one of the two regions, as indicated by the signed distance of the point from the boundary. We follow the convention of denoting distances in the feasible region as positive and those in the infeasible region as negative. The signed distance function in the neighborhood \({\mathcal {N}} \subset {\mathbb {R}}^n\) of a point on the geometric shape can then be defined as

$$\begin{aligned} d_{\Gamma }({\textbf{x}}) = {\left\{ \begin{array}{ll} + D({\textbf{x}}) &{} \text {if} \;\; {\textbf{x}} \in \Omega \\ - D({\textbf{x}}) &{} \text {if} \;\; {\textbf{x}} \in {\mathcal {N}}\setminus \Omega \end{array}\right. } \end{aligned}$$
(2)

where \(D:{\mathbb {R}}^n \rightarrow {\mathbb {R}}_{\ge 0}\) measures the shortest distance of a point \({\textbf{x}}\) to the boundary \(\Gamma \). The local feasible region \(\Omega \subset {\mathcal {N}}\) and the local infeasible region \({\mathcal {N}}\setminus \Omega \) are separated by the local boundary \(\Gamma _l = \Gamma \cap {\mathcal {N}}\) within the neighborhood, and \(\Gamma _l \subset \Omega \). Note that \(n=2\) or \(n=3\) for geometric shapes: \(n=2\) implies \(\Gamma \) is a curve in two dimensions while \(n=3\) implies \(\Gamma \) is an orientable surface in three dimensions. We assume that \(\Gamma \) is always a connected set. We make no assumptions on the surface or curve being open or closed. However, we assume that \(\Gamma \) does not contain the boundary points or curves if the curve or surface is open to ensure the existence of a neighborhood where the definition of \(d_\Gamma \) is valid. We also note that for closed geometric shapes, the definition of a local neighborhood is not necessary, as the feasible and infeasible regions can be simply defined as the inside and outside of the closed boundary \(\Gamma \) (see Fig. 1), or vice versa. This is identical to the standard definition of the signed distance function.

Fig. 2
figure 2

A 2D open funnel partitions the neighborhood of a point \({\textbf{p}}_i\) into a feasible region \(\Omega \) and an infeasible region \({\mathcal {N}} {\setminus } \Omega \)

Full size image

3.2 B-spline functions

Our desired level set function is a smooth approximation to the signed distance function of a geometric shape and is defined as a map** \(\phi : \mathbb {V} \subset {\mathbb {R}}^n\rightarrow {\mathbb {R}}\), where \(\mathbb {V}\) is the space where we wish to evaluate the level set function as a non-interference constraint function during optimization. This means that the zero level set \(S=\{{\textbf{x}}:\phi ({\textbf{x}})=0\}\) implicitly approximates the given geometric shape. To achieve such an approximation, we utilize tensor product B-splines. A B-spline volume \({\textbf{P}}: [0,1]^3 \rightarrow {\mathbb {R}}^3\) is defined as

$$\begin{aligned} {\textbf{P}}(u,v,w) = \sum _{i,j,k=0}^{n_i,n_j,n_k} {\textbf{C}}_{i,j,k} {\textbf{B}}_{i,d_1}(u) {\textbf{B}}_{j,d_2}(v) {\textbf{B}}_{k,d_3}(w), \end{aligned}$$
(3)

where \((u,v,w) \in [0,1]^3\) are the normalized parametric coordinates, \({\textbf{B}}_{i,d_1}(u)\), \({\textbf{B}}_{j,d_2}(v)\), \({\textbf{B}}_{k,d_3}(w)\) are the B-spline basis functions of degrees \(d_1,d_2,d_3\) in the i, j, k directions respectively, and \({\textbf{C}}_{i,j,k}\) are the control points that form the \((n_i+1)\times (n_j+1)\times (n_k+1)\) control net in the physical coordinate system. Equation (3) is essentially a tensor product, and hence \({\textbf{P}}\) is also called a tensor product B-spline.

A B-spline volume maps a volumetric space in the parametric coordinate system (u, v, w) to the physical coordinate system (x, y, z) by translating and deforming the volumetric space according to the control net \({\textbf{C}}_{i,j,k}\). The volumetric space we wish to represent in the physical coordinate system is a rectangular prism \(\mathbb {V}\). This is the physical space where geometric non-interference constraints need to be evaluated; therefore, we refer to \(\mathbb {V}\) as the domain of interest. We require that \(\mathbb {V}\) encompasses the minimum bounding box for a given point cloud. The minimum bounding box is the smallest closed box in \({\mathbb {R}}^n\) that contains the input point cloud representing a geometric shape. We space the control points \({\textbf{C}}_{i,j,k}\) across \(\mathbb {V}\) in a uniform grid and consider them to be constant. The domain of interest is not always a cube; therefore, parametric coordinates may be scaled differently along different directions. To compensate for this, some directions may contain more control points than others depending on the dimensions of \(\mathbb {V}\).

The B-spline basis functions \({\textbf{B}}_{i,d_1}(u)\), \({\textbf{B}}_{j,d_2}(v)\), and \({\textbf{B}}_{k,d_3}(w)\) are generated by the de Boor’s recursion formula (De Boor 1972). The formulas for all three directions are identical, and \({\textbf{B}}_{i,d_1}(u)\) along the i direction is computed by recursion

$$\begin{aligned} \begin{aligned} {\textbf{B}}_{i,0}(u)&= {\left\{ \begin{array}{ll} 1 &{} \text {if} \; t_i \le u < t_{i+1}\\ 0 &{} \text {otherwise} \end{array}\right. },\\ {\textbf{B}}_{i,k}(u)&= \frac{u-t_i}{t_{i+k}-t_i}{\textbf{B}}_{i,k-1}(u) + \frac{t_{i+k+1}-u}{t_{i+k+1}-t_{i+1}}{\textbf{B}}_{i+1,k-1}(u), \end{aligned} \end{aligned}$$
(4)

where \(t_i\) denotes the knots in the i direction. The basis functions corresponding to \({\textbf{C}}_{i,j,k}\) provides support only for \((u,v,w) \in [u_i,u_{i+d_1+1}] \times [v_j,v_{j+d_2+1}] \times [w_k,w_{k+d_3+1}]\); thus the basis functions are sparse. This also means that the number of nonzero terms in the summation of Eq. (3) is proportional to the degrees \(d_1\), \(d_2\), and \(d_3\).

We define the B-splines for our formulation using uniform knot vectors and a uniform grid of control points \({\textbf{C}}_{i,j,k}\) across \(\mathbb {V}\). This makes the map** \((u,v,w) \rightarrow (x,y,z)\) a linear, one-to-one relationship with \((u,v,w) \in [0,1]^3\) spanning the entire volumetric space of \(\mathbb {V}\). Thus, \(\frac{\partial u}{\partial x}\), \(\frac{\partial v}{\partial y}\), and \(\frac{\partial w}{\partial z}\) are constants that depend only on the dimensions of the rectangular prism \(\mathbb {V}\). Since we are using a standard uniform knot vector, it should be noted that the control points \({\textbf{C}}_{i,j,k}\) must lie beyond \(\mathbb {V}\) in order for the domain of the B-spline to be \(\mathbb {V}\). With this setup, we define our desired function \(\phi \) as

$$\begin{aligned} \phi (x,y,z) = \sum _{i,j,k=0}^{n_i,n_j,n_k} {\textbf{C}}^{(\phi )}_{i,j,k} {\textbf{B}}_{i,d_1}(u(x)) {\textbf{B}}_{j,d_2}(v(y)) {\textbf{B}}_{k,d_3}(w(z)), \end{aligned}$$
(5)

where u(x), v(y),  and w(z) map the physical coordinates to parametric coordinates, and \({\textbf{C}}^{(\phi )}_{i,j,k}\) are the values of the function \(\phi \) at the control points. The derivatives with respect to the spatial coordinates and derivatives with respect to the control points are easily derived from this form. The sparsity of the basis functions over the entire domain and the use of uniform knot vectors make the computation of \(\phi \) at any given point (x, y, z) in the domain highly efficient.

Note that for a level set function \(\phi \) for a curve in two dimensions, \(\mathbb {V}\) is a rectangle, \({\textbf{P}}\) reduces to a B-spline surface, and we omit terms along the k direction in Eq. (5). In all of the remaining discussion, we assume that the geometric shape is a surface in three dimensions.

3.3 Energies for B-spline fitting

The core of our methodology lies in computing appropriate \({\textbf{C}}^{(\phi )}_{i,j,k}\) values on the control net so that the level set function \(\phi \) approximates the signed distance function with favorable properties for gradient-based optimization. Note that since our approximation uses B-splines, the resulting function will already be smooth and fast-to-evaluate. Therefore, the remaining task is to formulate an approach for reliably estimating \({\textbf{C}}^{(\phi )}_{i,j,k}\) using the data from an oriented point cloud.

An oriented point cloud is a set of ordered pairs \({\mathcal {P}}= \{({\textbf{p}}_i,\mathbf {{\textbf{n}}}_i):i=1,\dots , N_\Gamma \}\), where \({\textbf{p}}_i\) are the physical coordinates of the points sampled over the geometric shape, and \(\mathbf {{\textbf{n}}}_i\) are the unit normal vectors to the surface (or curve) at \({\textbf{p}}_i\) oriented towards the infeasible region. Our method always requires an oriented point cloud as its input. However, we note that in cases where only a point cloud without normal information is available, Principal Component Analysis (PCA) along with a Minimum Spanning Tree (MST) algorithm can be used for estimating normals and their orientation (Hoppe et al. 1992). Edge-Aware Resampling (EAR) (Huang et al. 2013) is another method that can be used for generating noise-free normals that also preserves sharp features.

We calculate \({\textbf{C}}^{(\phi )}_{i,j,k}\) values by minimizing an energy function consisting of multiple energies. The terms in the energy function are adopted from existing surface reconstruction methods (Calakli and Taubin 2011; Ohtake et al. 2003; Pan et al. 2017; Tang and Feng 2018). Since the zero contour of our desired level set function \(\phi \) should approximate the geometric shape represented by the point cloud, it is straightforward to see that we should minimize energies to approximately satisfy \(\phi ({\textbf{p}}_i)=0\) and \(\nabla \phi ({\textbf{p}}_i) = -\mathbf {{\textbf{n}}}_i\). Hence we first define energies

$$\begin{aligned} {\mathcal {E}}_p = \frac{1}{N_\Gamma } \sum ^{N_\Gamma }_{i=1} \phi ({\textbf{p}}_i)^2 \quad \text {and} \quad {\mathcal {E}}_n = \frac{1}{N_\Gamma } \sum ^{N_\Gamma }_{i=1}\left\| \nabla \phi ({\textbf{p}}_i) + \mathbf {{\textbf{n}}}_i\right\| ^2, \end{aligned}$$
(6)

where \({\mathcal {E}}_p\) estimates the approximation error as the average of squared distances of the point cloud from the zero contour of \(\phi \), and \({\mathcal {E}}_n\) measures the average of squared alignment errors of the level set function’s gradient when compared to the negative of the unit normal vectors in the point cloud. Note that we take the negative of the normals (oriented toward the infeasible region) from the point cloud since we want distances given by \(\phi \) to be positive inside the feasible region. Minimizing \({\mathcal {E}}_p\) forces the zero contour of \(\phi \) to pass through all the points in the point cloud, and minimizing \({\mathcal {E}}_n\) tries to orient the function’s direction of steepest increase \(\nabla \phi \) along the normal to the geometric shape while pointing toward the feasible direction, both in the least squares sense. Minimizing \({\mathcal {E}}_n\) is important since the derivatives of the exact signed distance function \(d_\Gamma \) on the boundary of a geometric shape is along the normal to the boundary, and \(d_\Gamma \) always satisfies the eikonal equation, i.e., \(\Vert \nabla d_\Gamma \Vert =1\).

If we perform a direct minimization of energies \({\mathcal {E}}_p\) and \({\mathcal {E}}_n\), the resulting function attempts to accurately fit the point data on the geometric shape, and since these energies do not control the behavior of \(\phi \) away from the geometric shape, it could create superfluous zero contours away from the point cloud as reported in previous studies (Calakli and Taubin 2011). To overcome this issue, we define the regularization energy

$$\begin{aligned} {\mathcal {E}}_r = \frac{1}{|V|} \int _\mathbb {V} \left\| \nabla ^2 \phi ({\textbf{x}}) \right\| _F^2 d\mathbb {V}, \end{aligned}$$
(7)

where \(\nabla ^2 \phi ({\textbf{x}})\) is the Hessian matrix of \(\phi \) evaluated at \({\textbf{x}}\), \(\left\| \cdot \right\| _F\) represents the Frobenius norm, and \(|V|=\int _\mathbb {V} d\mathbb {V}\) is the total volume of \(\mathbb {V}\). The regularization energy \({\mathcal {E}}_r\) is interpreted as the aggregate curvature of \(\phi \) over the entire volumetric space of \(\mathbb {V}\). The minimization of \({\mathcal {E}}_r\) smooths the function \(\phi \) since forcing the Hessian to be zero forces the variations in the gradient field \(\nabla \phi \) to a minimum. Since the gradient of \(\phi \) is approximately aligned with the unit normals on the point cloud when minimizing \({\mathcal {E}}_n\), trying to maintain a constant \(\nabla \phi \) by minimizing \({\mathcal {E}}_r\) also helps satisfy the eikonal equation \(\Vert \nabla \phi \Vert =1\) for points further away from the point cloud. We evaluate the integral in \({\mathcal {E}}_r\) using the B-spline control points \({\textbf{C}}_{i,j,k}\) lying inside \(\mathbb {V}\) as quadrature points with unit quadrature weights. Therefore, the regularization energy is approximated as a discrete sum is given by

$$\begin{aligned} {\mathcal {E}}_r = \frac{1}{|V|} \int _\mathbb {V} \left\| \nabla ^2 \phi ({\textbf{x}}) \right\| _F^2 d\mathbb {V} \approx \frac{1}{N} \sum ^N_{i=1} \left\| \nabla ^2 \phi ({\textbf{x}}_{i}) \right\| _F^2, \end{aligned}$$
(8)

where N is total number of quadrature points, typically about the same as the number of control points \(N_{cp}=(n_i+1)\times (n_j+1)\times (n_k+1)\).

Some surface reconstruction techniques employ another energy term \({\mathcal {E}}_d\), which attempts to fit the signed distance function over the entire domain \(\mathbb {V}\). However, minimizing this energy was found to create overfitting issues and produce high frequency oscillations in the level set function \(\phi \) in our investigation and previous studies (Tang and Feng 2018). As a result, we neglect this energy in our formulation. Nevertheless, we present it here for the sake of completeness. The signed distance energy is given by

$$\begin{aligned} {\mathcal {E}}_d = \frac{1}{N} \sum ^{N}_{i=1} \left( \phi ({\textbf{x}}_{i}) - d_\Gamma ({\textbf{x}}_{i})\right) ^2, \end{aligned}$$
(9)

where signed distances \(d_\Gamma ({\textbf{x}}_{i})\) are evaluated at the control points within \(\mathbb {V}\) (same as quadrature points in \({\mathcal {E}}_r\)). The signed distances \(d_\Gamma ({\textbf{x}}_{i})\) can be approximated using distances to the nearest neighbor in the point cloud and its normal (Tang and Feng 2018), or by evaluating the explicit Eq. (1). Note that minimizing \({\mathcal {E}}_r\) can act as a regularization to avoid overfitting caused by \({\mathcal {E}}_d\) but careful weighting of the four energies according to the geometric shape is necessary.

3.4 Final energy minimization problem

Finally, we define the total energy function f as

$$\begin{aligned} f = \underbrace{\frac{1}{N_\Gamma } \sum ^{N_\Gamma }_{i=1} \phi ({\textbf{p}}_i)^2}_{{\mathcal {E}}_p} + \underbrace{\frac{\lambda _n}{N_\Gamma } \sum ^{N_\Gamma }_{i=1} \Vert \nabla \phi ({\textbf{p}}_i) + \mathbf {{\textbf{n}}}_i\Vert ^2}_{\lambda _n {\mathcal {E}}_n} + \underbrace{\frac{\lambda _r}{N} \sum ^{N}_{i=1} \Vert \nabla ^2 \phi ({\textbf{x}}_{i}) \Vert _F^2}_{\lambda _r {\mathcal {E}}_r}, \end{aligned}$$
(10)

where \(\lambda _n\) and \(\lambda _r\) are the relative penalization weights for \({\mathcal {E}}_n\) and \({\mathcal {E}}_r\) with respect to \({\mathcal {E}}_p\). The energy minimization problem that yields the desired level set function \(\phi \) is then given by

$$\begin{aligned} \begin{aligned} \text {minimize}&\quad f = {\mathcal {E}}_p + \lambda _n {\mathcal {E}}_n + \lambda _r {\mathcal {E}}_r\\ \text {with respect to}&\quad {\textbf{C}}^{(\phi )}_{i,j,k}. \end{aligned} \end{aligned}$$
(11)

Note that the function values at the control points \({\textbf{C}}^{(\phi )}_{i,j,k}\) directly affect \({\mathcal {E}}_p, {\mathcal {E}}_n,\) and \({\mathcal {E}}_r\) through the definition of \(\phi \) using B-splines (see Eq. (5)). If the geometric shape is a curve in two dimensions, then the optimization variables are \({\textbf{C}}^{(\phi )}_{i,j}\). The choice of penalization weights is not obvious. Penalization weights may require tuning on a case-by-case basis depending on the geometric shape. In general, we recommend \(\lambda _n\sim 10^{-2}\) and \(\lambda _r\sim 10^{-4}\) based on the parameter study presented in Sec. 4.

We provide a summary of our methodology in Algorithm 1 for geometric shapes that are surfaces in three dimensions. The algorithm is easily adapted for curves in two dimensions by simply omitting terms along the k direction.

figure a

3.5 Implementation details

We initialize \({\textbf{C}}_{i,j,k}^{(\phi )}\) for the energy minimization problem (11) by evaluating the explicit equation (1) at each control point \({\textbf{C}}_{i,j,k}\). This initialization gives an overall good initial guess for the signed distance function with relatively small \({\mathcal {E}}_p\) and \({\mathcal {E}}_n\) values. While the initialized B-spline function \(\phi \) is always differentiable for degree two or more, points of non-differentiability in the exact signed distance function will create regions of high curvatures in \(\phi \). Hence, this initialization may result in a large \({\mathcal {E}}_r\) term, even for smooth geometric shapes.

The minimization of \({\mathcal {E}}_r\) is thus necessary to smooth these regions of high curvatures, although compromising the accuracy at representing the exact SDF in these regions. Thus, \(\lambda _r\) should be large enough to enable smoothing of high curvatures that exist in the exact signed distance initialization but small enough so that it does not induce a large error in representing signed distances near the geometric shape. This is essential for better convergence in the overarching optimization problem when solved using a gradient-based algorithm.

In our implementation, we define the B-spline domain \(\mathbb {V}\) by extending the minimum bounding box for the point cloud along its diagonal by \(15\%\). The choice of \(15\%\) is purely empirical, and it can be lower or higher depending on the optimization problem requirements. The additional margin allows optimization algorithms to evaluate the constraint function at locations that are away from the geometric shape.

Higher order B-splines are computationally expensive. However, they improve the local degrees of freedom and the ability to control the function. In our experiments with the Stanford Bunny model shown in Fig. (5), we found no significant reduction in error for B-spline degrees higher than three. Hence, we recommend cubic B-splines for reasonable accuracy and computational efficiency.

Additionally, it is often too computationally expensive to express a non-interference constraint for an optimization problem by representing all optimization constraints \(\phi ({\textbf{x}}^{(i)})\ge 0\) individually, especially for a large number of points on the design. Instead, we recommend implementing a smooth minimum or maximum function such as KS-aggregation (Kreisselmeier and Steinhauser 1979) to reduce the number of constraints in the optimization problem.

As an additional note, we consider an extension to the current problem in which the boundary \(\Gamma \) of the feasible space, which is discretized and represented by a point cloud \({\mathcal {P}}\), is also varying during an optimization problem. In such a case, Algorithm 1 must be completed at every optimization iteration and the derivatives of the constraint values {\(\phi ({\textbf{x}}^{(i)})\), for \(i=1,2,\ldots ,N_d\)} with respect to \({\mathcal {P}}\) must be computed. For computing these derivatives, we would apply the direct or adjoint method where the states are the control point values \({\textbf{C}}^{(\phi )}_{i,j,k}\) computed as a solution to the energy minimization problem. Therefore, to compute the derivatives, we have to solve M systems of linear equations where M is the lower between the number of points representing the boundary (\(N_\Gamma \)) or the number of points representing the engineering design system (\(N_d\)). Note that this operation will scale at a minimum of \({\mathcal {O}}(M)\) and may be impractical to perform at every iteration of a large optimization problem. We hope for this problem to be addressed in a future work.

Lastly, we note that the energy minimization problem (11) is inherently an unconstrained quadratic programming (QP) problem, and we follow the derivation from Calakli and Taubin (Calakli and Taubin 2011) to reduce problem 11 to the solution of a sparse, symmetric, positive definite linear system. Using a conjugate gradient solver, the solution to this problem is able to be completed on the order of seconds, depending on the number of control points. We release the python package to perform the energy minimization and evaluation of the non-interference constraint in an open-source package (https://github.com/LSDOlab/lsdo_genie). Further numerical studies are presented in the next section.

Fig. 3
figure 3

The \(-1\), 0, 1, and 2 contours of the initialized (left) and the energy minimized (right) level set function \(\phi \)

Full size image

4 Numerical study

This section presents the results of various numerical studies using our formulation. We begin by studying our method using simple two-dimensional geometric shapes in Sect. 4.1. In Sect. 4.2, we investigate the dependence of our method on various parameters using the Stanford Bunny dataset. Sect. 4.3 then compares our method to previous non-interference constraint formulations using the Stanford Bunny, and other surface reconstruction methods using three datasets from the Stanford 3D Scanning Repository. We demonstrate the accuracy of our method in representing geometric shapes for aerospace optimization applications in Sect. 4.4. We conclude the section by demonstrating the application of our method by solving a medical robot design optimization problem with non-interference constraints in Sect. 4.5.

We implement the proposed method in a Python environment, and run all experiments on a desktop with an 8-core Ryzen 7 @ 3.6 GHz processor and 32 GB of RAM. We do not implement multi-threading or parallelization with GPUs in any of our numerical experiments.

Fig. 4
figure 4

The exact SDF (top) and the energy minimized LSF \(\phi \) along a 1D slice (bottom) for multiple geometric shapes

Full size image

4.1 Investigations using simple geometric shapes in two dimensions

We begin by applying our formulation to curves in two dimensions. Because our formulation is generic, no modifications are required to Eq. (10), and the terms in the k direction are simply ignored for 2D geometric shapes.

For 2D curves, the isocontours from the level set function (LSF) \(\phi \) can be readily visualized to facilitate a better understanding of the function both near and far from the curve. Figure 3 visualizes the isocontours of the initialized and energy minimized LSF for a rectangle using our formulation. We initialize \({\textbf{C}}^{(\phi )}_{i,j}\) using the explicit Eq. (1). Neglecting the sharp corners in this example, the contours of the initialized function closely match the exact signed distance function (SDF). Thus, the explicit method provides an excellent approximation of the SDF. We observe that the contours of the LSF are more rounded near the corners after energy minimization. Minimizing \({\mathcal {E}}_r\) smooths sharp corners on all isocontours, however, not to a degree that compromises \({\mathcal {E}}_n\) and \({\mathcal {E}}_p\) near the zero contour. We note that \({\mathcal {E}}_n\) and \({\mathcal {E}}_p\) have less influence compared to \({\mathcal {E}}_r\) on the isocontours corresponding to 1 and 2, hence these contours are even more rounded.

A LSF representing multiple geometric shapes may also be obtained using a single B-spline. Figure 4 shows the exact SDF and a one-dimensional slice of our energy minimized LSF \(\phi \) along the x axis for a domain containing multiple circles. We note that the non-differentiable points in the exact SDF can lie inside or outside of a geometric shape. This example illustrates how our energy minimization formulation balances the trade-off between minimizing the curvature of \(\phi \) and maximizing the accuracy at representing the SDF near points of non-differentiability and high curvature. Our energy minimized LSF \(\phi \) poorly approximates the SDF near points of non-differentiability and high curvature. However, in regions without any non-differentiabilities or high curvatures, the zero level set preserves a good approximation to the exact SDF. For the remainder of the numerical results section, we only consider a single geometric shape within the domain of interest \(\mathbb {V}\), because the error of our formulation increases with the minimum bounding box diagonal.

4.2 Investigations using a complex geometric shape in three dimensions

We use the well known Stanford Bunny scanned dataset (shown in Fig. 5) to analyze our formulation’s performance on three-dimensional geometric shapes. This dataset contains a large point cloud which we consider as an exact surface. We coarsely sample this point set and apply our method, measuring the accuracy of the resultant energy minimized LSF. The Stanford Bunny contains small scale features, sharp corners, flat surfaces, and smooth surfaces which will test the accuracy of our formulation in representing different geometric features. The sampled point set is free of noise, missing data, and nonuniformity, which are challenges not investigated in this paper.

Fig. 5
figure 5

The Stanford Bunny model

Full size image

We use the root-mean-squared (RMS) error and max error to evaluate the accuracy of our energy minimized LSF in approximating the signed distance function. The errors are normalized by the minimum bounding box diagonal L to ensure that they are independent of the size of a geometric shape. This allows for a common metric for comparing accuracies across different geometric shapes. The errors are defined as

$$\begin{aligned} \text {RMS error}&= \frac{1}{L}\sqrt{\frac{\sum _{i=1}^{N_e} (\phi ({\textbf{x}}_i) - d_{\Gamma }({\textbf{x}}_i))^2}{N_e}}, \; \; \text {and} \end{aligned}$$
(12)
$$\begin{aligned} \text {max error}&= \max _{i=1,2,\ldots ,N_e} \frac{1}{L}|\phi ({\textbf{x}}_i)- \text {d}_{\Gamma }({\textbf{x}}_i)|, \end{aligned}$$
(13)

where \(N_e\) is the number of points \({\textbf{x}}_i\) used to calculate the error, and the signed distances are approximated using explicit Eq. (1) on the large point cloud. We define the on-surface error by evaluating points that lie on the geometric shape where the true value is zero. The off-surface error is computed by evaluating points that are near but do not lie on the geometric shape. To acquire these sample points, we take the original sample points and move them in the direction of the normal vectors by specified distances.

Fig. 6
figure 6

The RMS errors for on- and off-surface points while varying \(\lambda _n\) and \(\lambda _r\) about 1. This result uses the Stanford Bunny sampled at \(N_\Gamma =25,000\), and a control point grid of \(31\times 31\times 26\)

Full size image

The energy minimization problem has two different resolution scales: the resolution of the point cloud data and the resolution of the B-spline control grid. The energy minimized LSF’s ability to approximate the signed distance is best when both resolutions are very fine. Unlike hierarchical structures or explicit methods, the control grid resolution for our method is independent of the point cloud resolution. As a result, we conduct an experiment to highlight the effects of varying the two resolution scales. Table 2 tabulates the results of our nine experiments, in which on-surface error and fitting times from of our experiments are shown. Fitting time is the time to solve energy minimization problem (11). We show averaged the fitting times across \(N_\Gamma \) resolutions because it does not influence the fitting time given a constant number of control points \(N_{cp}\). In terms of the on-surface error, increasing both resolutions correlates to a decrease in both RMS and maximum error. In our results, the maximum error of our function monotonically decreases with increasing \(N_{cp}\), however, does not monotonically decrease with increasing \(N_\Gamma \). The source of this comes from the fact that the optimal solution will compromise regions it can not fit in order to get a better overall solution (a decrease in RMS error). In terms of the fitting time, increasing the number of control points \(N_{cp}\) increases the time to solve the energy minimization problem. We note that for each application of our method, a compromise between accuracy and fitting time must be made when selecting the resolutions.

Table 2 The relative on-surface error for our method applied to the Stanford Bunny model. Penalization weights used were \(\lambda _n=10^{-2}\), and \(\lambda _r=5\times 10^{-4}\)
Full size table

While we do not propose an exact method for selecting the penalization weights \(\lambda _n\) and \(\lambda _r\), we provide a fixed point parameter study on each weight. Figure 6 shows the resulting errors from varying each penalization weight about the fixed point \(\lambda _n=\lambda _r=1\) using the Stanford Bunny dataset. The study on \(\lambda _r\) shows that small values (\(\lambda _r<1\)) have very little effect on the RMS error, and large values (\(\lambda _r>1\)) significantly reduce the energy minimized function’s accuracy. The study on \(\lambda _n\) suggests that for a given geometric shape, there exists an optimum value of \(\lambda _n\) that minimizes the energy minimized function’s error. In all studies, we observed an increase in the minimization time as the corresponding weight increased (not visualized in the figure). These observations lead us to recommend the use of \(\lambda _n\sim 10^{-2}\) and \(\lambda _r\sim 10^{-4}\) for reasonable accuracy for this particular geometry.

The ability of our function to represent nonzero level sets of the Stanford Bunny is visualized in Fig. 7. The level sets form good approximations of the offset surfaces, with a maximum relative distance error of \(9.8\times 10^{-3}\). In these visualizations, we observe the region of highest error to be near the neck and feet of the model, where sharp edges and corners exist. Most notably, the 0.005 and 0.01 level sets remove the ears of the model, despite them being in the exact SDF representation. As a thin feature, the removal of the ears in the 0.005 and 0.01 level sets is consistent with similar observations by Tang and Feng (2018).

Fig. 7
figure 7

Isocontours of the energy minimized LSF for the Stanford Bunny. The colors represent the error of the isocontour to the true signed distance value. The isocontours and error are normalized by the minimum bounding box diagonal

Full size image
Fig. 8
figure 8

Evaluation time per point (left), on-surface root-mean-square error (center), and off-surface root-mean-square error (right) varying the sampling (\(N_\Gamma \)) of the Stanford Bunny model. Our method was applied using a control point grid of (\(31\times 31\times 26\)) and \(\lambda _n=10^{-2}, \lambda _r=5\times 10^{-4}\)

Full size image

4.3 Comparison to other methods using complex geometric shapes in three dimensions

We show the computation time and accuracy of our method compared to explicit non-interference constraint formulations in Fig. 8, varying the sample size \(N_\Gamma \) of the Stanford Bunny. We observe that the method presented by Lin et al. (2022) and the explicit method presented by Hicken and Kaur (2022) scale in evaluation time with \({\mathcal {O}}(N_\Gamma )\), while our method scales independently of \(N_\Gamma \). We note that formulation from Lin et al. is not an attempt at approximating the signed distance function, thus is neglected from the RMS error comparisons. In terms of on-surface error, the explicit method has a steady decay in RMS error with respect to increasing \(N_\Gamma \), suggesting a power law relationship. Our method has a similar decay up to \(N_\Gamma =10^4\), where the RMS error decays slower for larger \(N_\Gamma >10^4\). Similarly, the off-surface RMS error of the explicit method steadily decays for both the \(\pm 0.005\) and \(\pm 0.01\) contours, and our method decays until \(N_\Gamma =10^4\). For \(N_\Gamma >10^4\), the off-surface error of our method decays slowly. Our method’s \(\pm 0.01\) contours have significantly more error than the \(\pm 0.005\) contours, while the explicit method has similar error for both sets of isocontours. For both on-surface and off-surface error, our method performs better in terms of accuracy up until the \(\pm 0.005\) contours and \(N_\Gamma <2\times 10^4\). From this information, we conclude that the explicit method will outperform in terms of accuracy and underperform in terms evaluation time compared to our method for most very finely sampled geometries. We note that our method can achieve better accuracy than shown in Fig. 8 by a trade-off in fitting time as shown in Table 2. Additionally, we note that the explicit method requires a noise-free, uniform sampling to achieve the presented results, which is not always feasible.

We apply our method using two additional scanned datasets from the Stanford 3D Scanning Repository. Table 3 records the results of the on-surface error of our method, as well as the reported on-surface error from four notable surface reconstruction methods for necessary context. The methods are smooth signed distance (SSD) reconstruction (Calakli and Taubin 2011), Multi-Level Partition of Unity (MPU) (Ohtake et al. 2003), wavelets (Manson et al. 2008), and screened Poisson (SP) (Kazhdan and Hoppe 2013). The results for the surface reconstruction methods were obtained from Kazhdan and Hoppe (2013), Ohtake et al. (2003), Pan et al. (2017), Tang and Feng (2018) and were not reproduced in our investigation, resulting in missing data in the table. Of the three scanned datasets, our energy minimized LSF maintains on-surface RMS error and max error on the same order of magnitude compared to the four other methods.

Table 3 Reported on-surface error of surface reconstruction methods and our method for three benchmarking datasets. We reconstruct using \(N_{cp}=25,000\), \(\lambda _n=10^{-2}\), and \(\lambda _r=5\times 10^{-4}\)
Full size table

4.4 Application to aircraft design problems

We now apply our formulation to a number of geometric shapes involved in novel aircraft design. Aircraft design optimization is a long standing problem and has been the subject of recent interest in problems involving geometric non-interference constraints, e.g., the layout optimization of air cargo (Brandt 2017), trajectory optimization with complex no-fly zone shapes (Kim and Liem 2022; Orndorff et al. 2023), aerodynamic shape optimization (Brelje et al. 2020), and joint battery layout and wing shape optimization (Brelje 2021). To enable gradient-based design optimization involving these constraints, a new generic method is required to represent numerous components within an aircraft’s design. We recognize the potential for our formulation and demonstrate its capabilities by conducting an experiment.

In this experiment, we apply our formulation and quantify the resultant errors of five geometric shapes commonly associated with aircraft design. The geometries we model include a fuselage and a wing from a novel electric vertical take-off and landing (eVTOL) concept vehicle (Silva et al. 2018), a human avatar (Reed et al. 2014), a luggage case, and a rectangular prism representing a battery pack within the wing. A visualization of these components in a feasible design configuration is illustrated in Fig. 9.

Table 4 Relative on-surface error of our method on various components of engineering systems. All geometries were sampled at \(N_\Gamma =25,000\). The optimization weights \(\lambda _n=10^{-2}\) and \(\lambda _r=5\times 10^{-4}\) were used
Full size table
Fig. 9
figure 9

Components necessary for spatial integration in aircraft design optimization. A cross section view is shown for an aircraft fuselage, wing, battery pack, human avatar, and luggage

Full size image

Table 4 tabulates the on-surface error of the energy minimized LSF for each geometry. We observe that the smallest relative on-surface error is of the smooth fuselage shape, while the largest relative error is of the human avatar. We note from this example that geometries with features well proportioned to their minimum bounding box diagonal are better fit using our method. For example, the small scale features (e.g. hands and feet) of the human avatar produce large relative error, yet the smooth fuselage with no small-scale features has very low relative error. We observe that the bounding boxes of the fuselage, wing, and battery pack are poorly proportioned between each dimension, yet do not result in an increase of relative error compared to other geometries. Geometries with longer minimum bounding box diagonals will result in larger absolute errors.

4.5 Application to medical robot design optimization

We now apply our method for enforcing geometric non-interference constraints to a medical robot design problem involving concentric tube robots (CTRs). CTRs are composed of two or more long and slender pre-curved tubes made of superelastic materials. They can be designed to reach points in a large region of interest by rotating and translating the tubes relative to each other at their bases. These characteristics make them ideal for minimally invasive surgeries where a surgeon can operate on a small region of interest with high dexterity through actuation at the base.

In the foundational works of Sears and Dupont (2006) and Webster et al. (2006), expressions for the shape and tip position of the CTR are derived with respect to the robot’s geometric and control variables. Bergeles et al. (2015) use these expressions to perform gradient-free optimization of the CTR’s geometric and control variables with anatomical constraints. These anatomical constraints, i.e., geometric non-interference constraints, enforce that the CTR does not interfere with the anatomy (e.g., the right ventricle of the heart shown in Fig. 10) during operation. Recent work by Lin et al. (2022) shows that gradient-based optimization enables an efficient and scalable solution to simultaneously optimize the large set of the tube’s geometric and control variables while enforcing anatomical constraints. The experiment we now present follows the workflow of (Lin et al. 2022), however, using our new formulation for representing the anatomical constraint function.

The presented workflow involves the solution of multiple optimization problems, including an initial path planning problem, and the geometric design and control of the CTR (the ‘simultaneous optimization problem’ described by Lin et al. (2022)). The path planning problem solves for a parametric 3D curve that represents an optimal collision-free path to the surgical site within the anatomy. Then, points along this path serve as inputs to the geometric design and control optimization of the CTR, which involve a kinematic model of the robot. In both subproblems, the non-interference constraints are enforced by evaluating a discrete set of points along the path or physical CTR to ensure that no points lie outside of the anatomy.

We begin our experiment with an investigation in the heart anatomy which represents the non-interference constraint of the problem. The initial oriented point cloud of the heart is obtained from segmentation and 3D reconstruction by magnetic resonance imaging (MRI) scans. Due to the limited machine accuracy, error introduced by aligning multiple scans, and normal approximation, the oriented point cloud is noisy, nonuniform, and contains poorly oriented normals. We perform a simple and necessary smoothing step on this point cloud as illustrated in Fig. 10. Although less precise at capturing small scale features, the smoothing step assists our method in reconstructing a smooth zero contour for constraint representation.

Fig. 10
figure 10

Preprocessing the raw scanned data (left) to a smooth approximate model (right)

Full size image
Table 5 Accuracy of our method in representing a smoothed heart model. Minimum bounding box diagonal is 244.75 mm. The anatomy is sampled at \(N_\Gamma =100,000\), and our method uses a control point discretization of (\(28\times 23\times 37\)), \(\lambda _n=10^{-2}\), and \(\lambda _r=10^{-4}\)
Full size table

The smooth representation has relative errors \(3.1\times 10^{-3}\) (RMS) and \(1.9\times 10^{-2}\) (max) compared to the original noisy representation. The error in our energy minimized function obtained from the smoothed heart model is tabulated in Table 5. We observe that the on-surface RMS and max error of our representation is an order of magnitude less than the error introduced by the smoothing step. This implies that our representation of the smooth model is no worse than the smoothing step itself. We see that our method generates a function with a reliable zero level set of the smooth heart geometry, with an on-surface RMS error of \(2.1\times 10^{-4}\). This error is lower compared to all the other examples in Table 3, and we attribute this to the smoothness of the heart geometry. We also note that the max on- and off-surface absolute errors of our representation are of the same order as the diameter of the CTR itself, typically 0.5\(-\)2.0 mm.

We now solve the two optimization subproblems using our energy minimized LSF of the smoothed heart model to enforce the geometric non-interference constraint. In the model from Lin et al. (2022), the non-interference constraint was imposed using a penalization function \(g({\textbf{x}})\), where it was defined as negative for the feasible region, and positive for the infeasible region. In our implementation, we represent this function with our energy minimized LSF in the form \(g({\textbf{x}})=-\phi ({\textbf{x}})\). The results from this experiment are shown in Table 6, where the number of function evaluations and optimization time are tabulated for each subproblem and non-interference constraint method. The time to solve the energy minimization problem for our method is denoted as the fitting time. Between the two subproblems, the number of function evaluations and optimization time is significantly more for the design subproblem due to the inclusion of the kinematics models. Between the two non-interference constraint methods, we observe a significant decrease in optimization time by using our new method for both subproblems. Even when accounting for the fitting time, our method provides a significant speedup for the design subproblem. However, we note that the speedup provided by our method for computationally inexpensive optimization problems, such as the path planning subproblem, may be negated by the fitting time to solve for the energy minimized LSF. For geometries with larger \(N_\Gamma \) and more complex optimization problems requiring more function evaluations, we expect the speedup in optimization time to be more pronounced.

Table 6 Constraint function evaluations and optimization time for the concentric tube robot’s path planning and design optimization. The anatomy is represented using \(N_\Gamma =1,842\)
Full size table

5 Conclusion

In this paper, we presented a new method for modeling interference between geometric shapes in gradient-based optimization. In Sec. 1, we consolidated the terminology used in prior literature and call this category of constraints ‘geometric non-interference constraints’. Additionally, we framed the set of optimization problems with geometric non-interference constraints into three groups: layout optimization, shape optimization, and optimal path planning problems. Section 2 reviewed the existing geometric non-interference constraint formulations in gradient-based optimization and contextualized our formulation within the field of surface reconstruction. Section 3 presented our new constraint formulation, which approximates the signed distance function using B-splines computed by solving an energy minimization problem. Section 4 presented accuracy and scaling studies with our formulation. We also solved a path planning and shape optimization problem using our new formulation.

The contribution of this paper is a new formulation for representing geometric non-interference constraints in gradient-based optimization. This formulation involves a scalable, smooth, and fast-to-evaluate constraint function that approximates the local signed distance to a geometric shape. The use of B-spline functions is key to our formulation being scalable, smooth, and fast-to-evaluate. We showed that our formulation achieves a level of accuracy on the same order of magnitude as surface reconstruction methods used in computer graphics. Additionally, our formulation yields better accuracy, up to a certain limit, and scales better in evaluation time with respect to the number of points sampled on the geometric shape \(N_\Gamma \) compared to previous non-interference constraint formulations used by the optimization community. The fitting time for our formulation is on the order of seconds and scales with the number of B-spline control points. To accurately represent small-scale features under our new formulation, we must perform uniform refinement of the B-spline control points, which will increase the number of control points and, consequently, the fitting time required to achieve the level of accuracy desired. Evaluation times are on the order of \(10^{-6}\) seconds per point as measured on a modern desktop workstation, entirely independent of the number of sample points \(N_\Gamma \). The method results in a 78% and 56% speedup in optimization time for a path planning and design subproblem, respectively, for an existing concentric tube robot (CTR) gradient-based design optimization problem.

We identify multiple directions for future work. Adaptive octrees with B-splines can represent small-scale features such as edges and sharp corners more accurately. Using octrees for discretization instead of using a uniform grid can clearly yield faster and more accurate solutions in problems where any of the modeled geometries remain constant during optimization iterations, e.g., the CTR or wind farm layout optimization problems. However, it is worth restating that when geometries evolve during optimization, rediscretizing surfaces using octrees in each optimization iteration becomes unreasonably expensive, and we only recommend a uniform discretization in such cases. Even when using a uniform discretization, the computational cost to compute the total derivatives of the constraints with respect to the changing geometries with our new formulation may still be impractical for such an optimization problem. In its current state, our formulation is relatively well-suited for a fixed-boundary with detailed geometric features that require a fine discretization (\(N_\Gamma \) large), because existing explicit formulations have evaluation times that increase with the number of points. However, for geometries that can be represented with coarse meshes, we expect the evaluation times of our formulation and explicit formulations to be comparable. Acceleration with multi-threading or graphics processing units (GPUs) is another possible direction for future research.