Low-dimensional behavior of generalized Kuramoto model

Abstract

We study the global bifurcation of a generalization of the Kuramoto model in the fully connected network in which the connections are weighted by the frequency of the oscillators. By driving the low dimensional manifold of this infinite-dimensional dynamical system, we obtain bifurcation boundaries for different types of transitions to the synchronized state. Using this analytic framework, we obtain the characteristic flow field of the system for each dynamical region in parameter space. To check the effect of nonzero-centered frequency distribution, we consider bimodal Lorentzian distribution as an example. In this case, the system shows three types of transitions to the synchronized state, depending on the parameters of the frequency distribution: (1) a two-step transition with Bellerophon state, (2) a continuous transition, as in the classical Kuramoto model, and (3) a first-order, explosive, transition with hysteresis.

Appendices

Appendix A: Frequency distribution

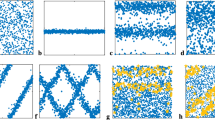
To shed more light on the system’s dynamics, in Figs. 4 and 5, we plot the steady-state average frequency distribution, $P(\dot{\langle \theta \rangle })$, in the network for forward and backward transitions. To understand the difference between explosive and two-step transition, we compare the frequency distribution for two values of $\Delta$. The first row corresponds to $\Delta =0.8$ and the second row to $\Delta =2$. We look at the frequency distribution in the system at different values of $\lambda$. Given that for small coupling strength, frequencies are symmetric, as shown in Fig. 4a, b, the overall frequency distribution has an average around zero; until becoming asymmetric at (c). This is the point where the frequency distribution loses its symmetry. By further increasing the coupling strength, one cluster becomes stronger than the other. Finally, at (d), $\lambda =2.04$, one cluster takes over. While in the $\Delta =2$ case, the distribution remains symmetric until a critical point in Fig. 4k. A similar dynamic also happens for the backward transition (Fig. 5).

Fig. 4

Probability density function of the frequency $P(\dot{\langle \theta \rangle })$ in forward transition. The first row corresponds to the case of $\Delta =0.8$, and second row for the last row $\Delta =2$. Each column corresponds to a single value of $\lambda$. (a), (g): $\lambda =0.02$, (b), (h): $\lambda =1.8$, (c), (i): $\lambda =1.98$, (d), (j): $\lambda =2.04$, (e), (k): $\lambda =2.98$, (f), (l): $\lambda =3$

Fig. 5

Probability density function of the frequency $P(\dot{\langle \theta \rangle })$ in backward transition. The first row corresponds to the case of $\Delta =0.8$, and the second row to $\Delta =2$. Each column corresponds to a single value of $\lambda$. (a), (g): $\lambda =3$, (b), (h): $\lambda =2.1$, (c), (i): $\lambda =2.08$, (d), (j): $\lambda =2$, (e), (k): $\lambda =1.8$, (f), (l): $\lambda =1$

Fig. 6

Correlation matrix $(D_{ij})$ in forward transition. The first row corresponds to the case of $\Delta =0.8$, and the second row to $\Delta =2$. Each column corresponds to a single value of $\lambda$. (a), (g): $\lambda =0.02$, (b), (h): $\lambda =1.8$, (c), (i): $\lambda =1.98$, (d), (j): $\lambda =2.04$, (e), (k): $\lambda =2.98$, (f), (l): $\lambda =3$

Fig. 7

Correlation matrix $(D_{ij})$ in backward transition. The first row corresponds to the case of $\Delta =0.8$, and the second row to $\Delta =2$. Each column corresponds to a single value of $\lambda$. (a), (g): $\lambda =3$, (b), (h): $\lambda =2.1$, (c), (i): $\lambda =2.08$, (d), (j): $\lambda =2$, (e), (k): $\lambda =1.8$, (f), (l): $\lambda =1$

Appendix B: Correlation matrix

To study the collective dynamics in more detail, we look at the correlation matrix. The local phase configurations of the system can be determined by the correlation matrix D, which is defined as:

$$\begin{aligned} D_{ij}= \lim _{\Delta t \rightarrow \infty }\frac{1}{\Delta t}\int ^{\Delta t+t_s}_{t_s}\cos (\theta _i(t)-\theta _j(t))dt. \end{aligned}$$

(B1)

where $t_s$ is the time needed for reaching a stationary state. The correlation matrix element $D_{ij}$ is a measure of coherency between the pair of oscillators at i and j positions and takes a value in the interval $1\le D \le -1$. $D_{ij}=1$ when there is a full synchrony between nodes i and j ($\theta _i=\theta _j$), and $D_{ij}=-1$ when they are in the anti-phase state ($\theta _i=\theta _j \pm \pi$). Here, we used $5\times 10^5$ time steps for the stationary time $t_s$ and $3\times 10^4$ time steps for the averaging window $\Delta t$.

We calculate the time-averaged correlation matrices $(D_{ij})$ in Fig. 6. To compare the dynamics of the two-step transition, which happens for $\Delta <1$, and the explosive transition, happening for $\Delta >1$, we look at the correlation matrices of $\Delta =0.8,2$. The first row in Fig. 6 shows the results of $\Delta =0.8$, and the second row corresponds to the case of $\Delta =2$. Each row shows how the correlation between the oscillators changes by a progressive increase in the coupling constant. There is an obvious difference between the nature of transition for $\Delta <1$ and $\Delta >1$. For the narrow distribution, the first row in Figs. 4, 6 the system first goes into a two-cluster state, and then these clusters get closer to being synchronized. For very small $\lambda$, (a), there is no correlation in the system the frequency distribution being symmetric. By increase in $\lambda$, two clusters appear in the system (Fig. 6b–c), the oscillators inside each cluster are synchronized but not in sync with the other cluster. So, the increase in the coupling strength does not affect the order parameter. Further increase in the coupling constant, $\lambda$, makes the frequency distribution asymmetric, and more oscillators from one cluster join the other. The probability density, $P(D_{ij})$, shifts toward zero. On the other hand, for the wide distribution (second row in Fig. 6), the system stays totally out of sync up to a threshold point (Fig. 6k) ($\lambda =2.98$) and does an explosive transition to the synchronized state (Fig. 6l) ($\lambda =3$) as shown in Fig. 2d.

To see the difference between the dynamics in forward and backward transition, we present the frequency distribution and correlation matrix in Figs. 5, 7, respectively, similar to the forward plots (Figs. 4, 6 ). The first row corresponds to the case of $\Delta =0.8$, and the second row $\Delta =2$. For $\Delta =0.8$, we observe three types of dynamics. For $\lambda \ge 2.08$, (a–c), the system is in the high-order parameter state, with a large population of oscillators being in a frequency-locked state, which shows itself as an asymmetric distribution in frequency (Fig. 5). By increasing the coupling constant, the system goes to a full unsynchronized state (Fig. 5d). For $\Delta =2$, on the other hand, there is no intermediate state, and the system shows a sudden transition to the unsynchronized state.