SpringerLink
Log in

Fundamental weight systems are quantum states

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

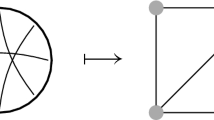
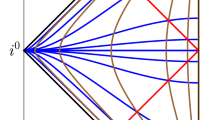
Abstract

Weight systems on chord diagrams play a central role in knot theory and Chern–Simons theory; and more recently in stringy quantum gravity. We highlight that the noncommutative algebra of horizontal chord diagrams is canonically a star-algebra and ask which weight systems are positive with respect to this structure; hence, we ask: Which weight systems are quantum states, if horizontal chord diagrams are quantum observables? We observe that the fundamental \({\mathfrak {g}}{\mathfrak {l}}(n)\)-weight systems on horizontal chord diagrams with N strands may be identified with the Cayley distance kernel at inverse temperature \(\beta = \textrm{ln}(n)\) on the symmetric group on N elements. In contrast to related kernels like the Mallows kernel, the positivity of the Cayley distance kernel had remained open. We characterize its phases of indefinite, semi-definite and definite positivity, in dependence of the inverse temperature \(\beta \); and we prove that the Cayley distance kernel is positive (semi-)definite at \(\beta = \text {ln}(n)\) for all \(n = 1,2,3, \ldots \). In particular, this proves that all fundamental \({\mathfrak {g}}{\mathfrak {l}}(n)\)-weight systems are quantum states, and hence, so are all their convex combinations. We close with briefly recalling how, under our “Hypothesis H”, this result impacts on the identification of bound states of multiple M5-branes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data availability

There is no further data associated with this work.

References

  1. Altschuler, D., Freidel, L.: Vassiliev knot invariants and Chern-Simons perturbation theory to all orders. Commun. Math. Phys. 187, 261–287 (1997). ar**v:q-alg/9603010

    Article  ADS  MathSciNet  Google Scholar 

  2. Babai, L.: Spectra of Cayley graphs. J. Combin. Theor. B 27, 180–189 (1979). https://doi.org/10.1016/0095-8956(79)90079-0

    Article  MathSciNet  Google Scholar 

  3. Balachandran, A.P., Govindarajan, T.R., de Queiroz, A.R., Reyes-Lega, A.F.: Algebraic approach to entanglement and entropy. Phys. Rev. A 88, 022301 (2013). ar**v:1301.1300

    Article  ADS  Google Scholar 

  4. Bar-Natan, D.: Perturbative aspects of the Chern–Simons topological quantum field theory. PhD thesis, Princeton University (1991). https://ncatlab.org/nlab/files/BarNatanPerturbativeCS91.pdf

  5. Bar-Natan, D.: On the Vassiliev knot invariants. Topology 34(2), 423–472 (1995). https://doi.org/10.1016/0040-9383(95)93237-2

    Article  MathSciNet  Google Scholar 

  6. Bar-Natan, D.: Vassiliev and Quantum Invariants of Braids. The interface of knots and physics (San Francisco, CA, 1995), 129–144, Proc. Sympos. Appl. Math., vol. 51. AMS Short Course Lecture Notes, Amer. Math. Soc., Providence, RI (1996). ar**v:q-alg/9607001

  7. Bar-Natan, D., Stoimenow, A.: The Fundamental Theorem of Vassiliev Invariants. In: Geometry and Physics, Lecture Notes in Pure & App. Math., vol. 184, Marcel Dekker Inc. (1996). ar**v:q-alg/9702009

  8. Bar-Natan, D.: The Cayley distance kernel following ar**v:2105.0287 by Corfield, Sati, and Schreiber, https://drorbn.net/AcademicPensieve/2021-05/nb/CayleyDistanceKernel.pdf

  9. Berkooz, M., Narayan, P., Simón, J.: Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction. J. High Energy Phys. 08, 192 (2018). ar**v:1806.04380

    Article  ADS  MathSciNet  Google Scholar 

  10. Berkooz, M., Isachenkov, M., Narovlansky, V., Torrents, G.: Towards a full solution of the large N double-scaled SYK model. J. High Energy Phys. 03, 079 (2019). ar**v:1811.02584

    Article  ADS  MathSciNet  Google Scholar 

  11. Chmutov, S., Duzhin, S., Mostovoy, J.: Introduction to Vassiliev Knot Invariants. Cambridge University Press (2012). ISBN:9781139107846, ar**v:1103.5628

  12. Collari, C.: A note on weight systems which are quantum states. Can. Math. Bull. (2023) https://doi.org/10.4153/S0008439523000206ar**v:2210.05399

  13. Diaconis, P.: Group representations in Probability and Statistics. Institute of Mathematical Statistics Lecture Notes Monogr. Ser. 11 (1988). jstor:i397389, https://jdc.math.uwo.ca/M9140a-2012-summer/Diaconis.pdf

  14. Diaconis, P., Hanlon, P.: Eigen Analysis for Some Examples of the Metropolis Algorithm. In: Richards, D. (ed.) Hypergeometric Functions on Domains of Positivity, Jack Polynomials, and Applications. Contemporary Mathematics 138, Amer. Math. Soc. (1992), https://doi.org/10.1090/conm/138

  15. Diaconis, P., Shahshahani, M.: Generating a random permutation with random transpositions. Z. Wahrscheinlichkeitsth. verw. Gebiete 57, 159–179 (1981). https://doi.org/10.1007/BF00535487

    Article  MathSciNet  Google Scholar 

  16. Drutu, C., Kapovich, M.: Geometric Group Theory. Colloquium Publications, vol. 63. Amer. Math. Soc. (2018) ISBN:978-1-4704-1104-6

  17. Fiorenza, D., Sati, H., Schreiber, U.: Twisted Cohomotopy implies M-theory anomaly cancellation on 8-manifolds. Commun. Math. Phys. 377, 1961–2025 (2020). https://doi.org/10.1007/s00220-020-03707-2. ar**v:1904.10207

  18. Fiorenza, D., Sati, H., Schreiber, U.: Twisted Cohomotopy implies M5 WZ term level quantization. Commun. Math. Phys. 384, 403–432 (2021). https://doi.org/10.1007/s00220-021-03951-0. ar**v:1906.07417

  19. Fligner, M.A., Verducci, J.S.: Distance based ranking models. J. R. Stat. Soc. B 48(3), 359–369 (1986) jstor:2345433

  20. Fligner, M.A., Verducci, J.S. (eds.): Probability Models and Statistical Analyses for Ranking Data, Lecture Notes in Statistics, vol. 80. Springer (1993). https://doi.org/10.1007/978-1-4612-2738-0

  21. Foster-Greenwood, B., Kriloff, C.: Spectra of Cayley graphs of complex reflection groups. J. Algebraic Combin. 44(1), 33–57 (2016). https://doi.org/10.1007/s10801-015-0652-8. ar**v:1502.07392

  22. Fulton, W.: Young Tableaux, with Applications to Representation Theory and Geometry. Cambridge University Press, Cambridge (1997). https://doi.org/10.1017/CBO9780511626241

    Book  Google Scholar 

  23. Fulton, W., Harris, J.: Representation Theory: A First Course. Springer, Berlin (1991). https://doi.org/10.1007/978-1-4612-0979-9

    Book  Google Scholar 

  24. Gnedin, A., Gorin, V., Kerov, S.: Block characters of the symmetric groups. J. Algebraic Comb. 38(1), 79–101 (2013). ar**v:1108.5044

    Article  MathSciNet  Google Scholar 

  25. Hofmann, T., Schölkopf, B., Smola, A.J.: Kernel methods in machine learning. Ann. Stat. 36(3), 1171–1220 (2008). ar**v:math/0701907

    Article  MathSciNet  Google Scholar 

  26. Hwang, S.-G.: Cauchy’s interlace theorem for eigenvalues of Hermitian matrices. Am. Math. Mon. 111(2), 157–159 (2004) jstor:4145217

  27. Jahn, A., Eisert, J.: Holographic tensor network models and quantum error correction: a topical review. Quantum Sci. Technol. 6, 033002 (2021). ar**v:2102.02619

    Article  ADS  Google Scholar 

  28. Jahn, A., Gluza, M., Pastawski, F., Eisert, J.: Majorana dimers and holographic quantum error-correcting code. Phys. Rev. Res 1, 033079 (2019). ar**v:1905.03268

    Article  Google Scholar 

  29. Jiao, Y., Vert, J.-P.: The Kendall and Mallows Kernels for permutations. IEEE Trans. Pattern Anal. Mach. Intell. 40(7), 1755–1769 (2018). https://doi.org/10.1109/TPAMI.2017.2719680

    Article  Google Scholar 

  30. Jucys, A.-A.: Factorization of Young projection operators for the symmetric group. Lietuvos Fizikos Rinkinys 11(1), 1–10 (1971). https://ncatlab.org/nlab/files/Jucys-1971.pdf

  31. Jucys, A.-A.: Symmetric polynomials and the center of the symmetric group ring. Rep. Math. Phys. 5(1), 107–112 (1974). https://doi.org/10.1016/0034-4877(74)90019-6

    Article  ADS  MathSciNet  Google Scholar 

  32. Kadison, R.V., Ringrose, J.R.: Fundamentals of the theory of operator algebras I: Elementary Theory. Graduate Studies in Mathematics, vol. 15. Amer. Math. Soc. (1997). ISBN:978-0-8218-0819-1

  33. Kaski, P.: Eigenvectors and spectra of Cayley graphs, Lecture notes, Postgraduate Course in Theoretical Computer Science, Helsinki (2002). www.tcs.hut.fi/Studies/T-79.300/2002S/esitelmat/kaski_paper_020506.pdf

  34. Kohno, T.: Loop spaces of configuration spaces and finite type invariants. Geom. Topol. Monogr. 4, 143–160 (2002). ar**v:math/0211056

    Article  MathSciNet  Google Scholar 

  35. Kontsevich, M.: Vassiliev’s knot invariants. Adv. Sov. Math. 16, 2 (1993). http://pagesperso.ihes.fr/~maxim/TEXTS/VassilievKnot.pdf

  36. James, G.D.: The Representation Theory of the Symmetric Groups. Lecture Notes in Mathematics, vol. 682. Springer, Berlin (1978)

    Google Scholar 

  37. Landsman, K.: Foundations of quantum theory: From classical concepts to Operator algebras. Springer Open (2017). https://doi.org/10.1007/978-3-319-51777-3

    Article  ADS  Google Scholar 

  38. Lovász, L.: Spectra of graphs with transitive groups. Period. Math. Hung. 6, 191–195 (1975). https://doi.org/10.1007/BF02018821

    Article  MathSciNet  Google Scholar 

  39. Mairal, J., Vert, J.-P.: Machine Learning with Kernel Methods. Lecture Notes (2017). http://members.cbio.mines-paristech.fr/~jvert/svn/kernelcourse/course/2021mva

  40. McNamara, S.: Twistor Inspired Methods in Perturbative Field Theory and Fuzzy Funnels, PhD thesis, Queen Mary, U. of London (2006). spire:1351861

  41. Meyer, P.-A.: Quantum Probability for Probabilists. Lecture Notes in Mathematics, vol. 1538. Springer (1995). https://doi.org/10.1007/BFb0084701

  42. Milnor, J., Moore, J.: On the structure of Hopf algebras. Ann. Math. 81, 211–264 (1965). https://doi.org/10.2307/1970615

    Article  MathSciNet  Google Scholar 

  43. McNamara, S., Papageorgakis, C., Ramgoolam, S., Spence, B.: Finite N effects on the collapse of fuzzy spheres. J. High Energy Phys. 0605, 060 (2006). ar**v:hep-th/0512145

    Article  ADS  MathSciNet  Google Scholar 

  44. Murphy, G.E.: A new construction of Young’s seminormal representation of the symmetric groups. J. Algebra 69(2), 287–297 (1981). https://doi.org/10.1016/0021-8693(81)90205-2

    Article  MathSciNet  Google Scholar 

  45. Narovlansky, V.: Towards a Solution of Large N Double-Scaled SYK. Seminar Notes (2019). https://ncatlab.org/nlab/files/NarovlanskySYK19.pdf

  46. Selinger, P.: A survey of graphical languages for monoidal categories. In: Coecke, B. (ed.) New Structures for Physics. Lecture Notes Phys., vol. 813. Springer, Berlin (2010). https://doi.org/10.1007/978-3-642-12821-9_4, ar**v:0908.3347

  47. Ramgoolam, S., Spence, B., Thomas, S.: Resolving brane collapse with 1/N corrections in non-Abelian DBI. Nucl. Phys. B 703, 236–276 (2004). ar**v:hep-th/0405256

    Article  ADS  MathSciNet  Google Scholar 

  48. Rockmore, D., Kostelec, P., Hordijk, W., Stadler, P.F.: Fast Fourier transform for fitness landscapes. Appl. Comput. Harmon. Anal. 12, 57–76 (2002). https://doi.org/10.1006/acha.2001.0346

    Article  MathSciNet  Google Scholar 

  49. Sagan, B.: The Symmetric Group. Springer, Berlin (2001). https://doi.org/10.1007/978-1-4757-6804-6

    Book  Google Scholar 

  50. Sati, H.: Framed M-branes, corners, and topological invariants. J. Math. Phys. 59, 062304 (2018). https://doi.org/10.1063/1.5007185. ar**v:1310.1060]

    Article  ADS  MathSciNet  Google Scholar 

  51. Sati, H., Schreiber, U.: Equivariant Cohomotopy implies orientifold tadpole cancellation. J. Geom. Phys. 156, 103775 (2020). https://doi.org/10.1016/j.geomphys.2020.103775. ar**v:1909.12277

  52. Sati, H., Schreiber, U.: Differential Cohomotopy implies intersecting brane observables via configuration spaces and chord diagrams. Adv. Theor. Math. Phys. 26(4), 957–1051 (2022). https://doi.org/10.4310/ATMP.2022.v26.n4.a4. ar**v:1912.10425

  53. Sati, H., Schreiber, U.: Twisted Cohomotopy implies M5-brane anomaly cancellation. Lett. Math. Phys. 111, 120 (2021). https://doi.org/10.1007/s11005-021-01452-8. ar**v:2002.07737

  54. Sati, H., Schreiber, U.: The character map in equivariant twistorial Cohomotopy implies the Green-Schwarz mechanism with heterotic M5-branes, ar**v:2011.06533

  55. Sati, H., Schreiber, U.: M/F-Theory as Mf-Theory. Rev. Math. Phys. (2023, in print) ar**v:2103.01877

  56. Stanley, R.: Theory and application of plane partitions 2. Stud. Appl. Math. 50(3), 259–279 (1971)

    Article  MathSciNet  Google Scholar 

  57. Stanley, R.: Enumerative combinatorics, vol. 1. Cambridge University Press 2011 (1986). ISBN:9781107602625, http://www-math.mit.edu/~rstan/ec/ec1.pdf

  58. Stanley, R.: Enumerative combinatorics, vol. 2. Cambridge University Press (1999). https://doi.org/10.1017/CBO9780511609589

  59. Sternberg, S.: Group Theory and Physics. Cambridge University Press, Cambridge (1994). ISBN:9780521558853

  60. Yan, H.: Geodesic string condensation from symmetric tensor gauge theory: a unifying framework of holographic toy models. Phys. Rev. B 102, 161119 (2020). ar**v:1911.01007

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank Abdelmalek Abdesselam, Dror Bar-Natan, Carlo Collari, Jean-Philippe Vert and David Speyer for comments and discussion. Collari has meanwhile built on our result in [12].

Author information

Authors and Affiliations

  1. Centre for Reasoning, University of Kent, Kent, UK

    David Corfield

  2. Mathematics Division of Science and Center for Quantum and Topological Systems, New York University Abu Dhabi, Abu Dhabi, UAE

    Hisham Sati & Urs Schreiber

Authors
  1. David Corfield
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hisham Sati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Urs Schreiber
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Urs Schreiber.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors acknowledge support by Tamkeen under the NYU Abu Dhabi Research Institute Grant CG008.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Corfield, D., Sati, H. & Schreiber, U. Fundamental weight systems are quantum states. Lett Math Phys 113, 112 (2023). https://doi.org/10.1007/s11005-023-01725-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11005-023-01725-4

Keywords

Mathematics Subject Classification

Search

Navigation