SpringerLink
Log in

Stochastic Perturbation of Integrable Systems: A Window to Weakly Chaotic Systems

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

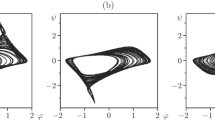
Integrable non-linear Hamiltonian systems perturbed by additive noise develop a Lyapunov instability, and are hence chaotic, for any amplitude of the perturbation. This phenomenon is related, but distinct, from Taylor’s diffusion in hydrodynamics. We develop expressions for the Lyapunov exponents for the cases of white and colored noise. The situation described here being ‘multi-resonance’—by nature well beyond the Kolmogorov–Arnold–Moser regime, it offers an analytic glimpse on the regime in which many near-integrable systems, such as some planetary systems, find themselves in practice. We show with the aid of a simple example, how one may model in some cases weakly chaotic deterministic systems by a stochastically perturbed one, with good qualitative results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

  1. The exponent \(\frac{1}{3}\) is also familiar in the theory of products of random matrices, see: [1, 2]. This is not surprising considering that the noise has in this approximation no impact on the dynamical system but only on the tangent dynamics, and since (18) end up being random linear transformations.

  2. For the treatment of the diffusion away from a torus (in the case of the Standard Map), see: [15].

References

  1. Anteneodo, C., Vallejos, R.O.: Scaling laws for the largest Lyapunov exponent in long-range systems: a random matrix approach. Phys. Rev. E 65(1), 016210, 2001

  2. Anteneodo, C., Vallejos, R. O.: Generalized Lyapunov exponents of the random harmonic oscillator: cumulant expansion approach. Phys. Rev. E. 85(2), 021124 (2012)

  3. Aris, R.: On the dispersion of a solute in a fluid flowing through a tube. Royal Soc. London Proc. Ser. A 235, 67–77 (1956)

    Article  ADS  Google Scholar 

  4. Benettin, G., Ponno, A.: Time-scales to equipartition in the Fermi–Pasta–Ulam problem: finite-size effects and thermodynamic limit. J. Statist. Phys. 144(4), 793–812 (2011)

  5. Cépas, O., Kurchan, J.: Canonically invariant formulation of Langevin and Fokker–Planck equations. EPJ B 2(2), 221–223 (1998)

    Article  ADS  Google Scholar 

  6. Chertkov, M., Kolokolov, I., Lebedev, V., Turistin, K.: Polymer statistics in a random flow with mean shear. J. Fluid Mech. 531, 251–260 (2005)

  7. de Wijn, A.S., Hess, B., Fine, B.V.: Largest lyapunov exponents for lattices of interacting classical spins. Phys. Rev. Lett. 109, 034101 (2012). ar**v:1209.1468

  8. Derrida, B., Gardner, E.: Lyapounov exponent of the one dimensional anderson model: weak disorder expansions. J. de Physique 45, 1283–1295 (1984)

    Article  MathSciNet  Google Scholar 

  9. Fishman, S., Grempel, D.R., Prange, R.E.: Chaos, quantum recurrences and Anderson localization. Phys. Rev. Lett. 49, 509–512 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  10. Froeschlé, C., Guzzo, M., Lega, E.: Graphical evolution of the arnold web: from order to chaos. Science 289(5487), 2108–2110 (2000)

    Article  ADS  Google Scholar 

  11. Gardiner, C.W.: Handbook of Stochastic Methods, 2nd edn. Springer, Berlin (1985)

    Google Scholar 

  12. Guyon, É., Hulin, J.-P., Petit, L.: Hydrodynamique physique, 3rd edn. EDP Sciences, Paris (2012)

    Google Scholar 

  13. Halperin, B.I.: Green’s functions for a particle in a one-dimensional random potential. Phys. Rev. 139, 104–117 (1965)

    Article  ADS  MathSciNet  Google Scholar 

  14. http://en.wikipedia.org/wiki/Pendulum. Accessed 1 June 2014

  15. Kruscha, A., Ketzmerick, R., Kantz, H.: Biased diffusion inside regular islands under random symplectic perturbations. Phys. Rev. E 85(6), 066210 (2012)

    Article  ADS  Google Scholar 

  16. Landau, L.D., Lifshitz, E.M.: Quantum mechanics. In: A Course of Theoretical Physics, vol. 3, Pergamon Press (1965)

  17. Laskar, J.: A numerical experiment on the chaotic behaviour of the solar system. Nature 338, 237–238 (1989)

    Article  ADS  Google Scholar 

  18. Livi, R., Pettini, M., Ruffo, S., Sparpaglione, M., Vulpiani, A.: Equipartition threshold in nonlinear large Hamiltonian systems: the Fermi–Pasta–Ulam model. Phys. Rev. A 31, 1039–1045 (1985)

    Article  ADS  Google Scholar 

  19. Mallick, K., Marcq, P.: Anomalous diffusion in nonlinear oscillators with multiplicative noise. Phys. Rev. E 66(4), 041113 (2002)

    Article  ADS  Google Scholar 

  20. Risken, H.: The Fokker–Planck Equation: Methods of Solution and Applications, 2nd edn. Springer-Verlag, Berlin (1989)

    Book  MATH  Google Scholar 

  21. Schomerus, H., Titov, M.: Statistics of finite-time Lyapunov exponents in a random time-dependent potential. Phys. Rev. E 66, 066207 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  22. See for example the discussion in: Morbidelli, A., Froeschlé, C.: On the relationship between Lyapunov times and macroscopic instability times. Celest. Mech. Dyn. Astron. 63, 227–239 (1996)

  23. Sussman, G.J., Wisdom, J.: Numerical evidence that the motion of Pluto is chaotic. Science 241, 433–437 (1988)

    Article  ADS  Google Scholar 

  24. Sussman, G.J., Wisdom, J.: Chaotic evolution of the solar system. Science 257(5066), 56–62 (1992)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  25. Tailleur, J., Kurchan, J.: Probing rare physical trajectories with Lyapunov weighted dynamics. Nat. Phys. 3, 203–207 (2007)

    Article  Google Scholar 

  26. Tannor, D.J.: Introduction to quantum mechanics. University Science Books, Sausalito (2007)

    Google Scholar 

  27. Taylor, G.: Dispersion of soluble matter in solvent flowing slowly through a tube. Royal Soc. London Proc. Ser. A 219, 186–203 (1953)

    Article  ADS  Google Scholar 

  28. Tessieri, L., Izrailev, F.M.: Anderson localization as a parametric instability of the linear kicked oscillator. Phys. Rev. E 62(3), 3090 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  29. Wisdom, J.: Urey Prize lecture: Chaotic dynamics in the solar system. Icarus 72, 241–275 (1987)

  30. Zwanzig, R.: Nonlinear generalized Langevin equations. J. Stat. Phys. 9, 215–220 (1973)

    Article  ADS  Google Scholar 

  31. Zwanzig, R.: Nonequilibrium Statistical Mechanics. Oxford University Press, Oxford (2001)

    MATH  Google Scholar 

Download references

Acknowledgments

We wish to thank G. Benettin, M. Chertkov, A. Politi, S. Ruffo, S. Tremaine and A. deWijn for clarifying remarks and suggestions.

Author information

Authors and Affiliations

  1. PMMH-ESPCI, Paris, France

    Khanh-Dang Nguyen Thu Lam

  2. Laboratoire de Physique Statistique, École Normale Supérieure, CNRS UMR 8550, UPMC, UDD, 24 Rue Lhomond, 75231 , Paris, France

    Jorge Kurchan

Authors
  1. Khanh-Dang Nguyen Thu Lam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jorge Kurchan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jorge Kurchan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lam, KD.N.T., Kurchan, J. Stochastic Perturbation of Integrable Systems: A Window to Weakly Chaotic Systems. J Stat Phys 156, 619–646 (2014). https://doi.org/10.1007/s10955-014-1030-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-014-1030-y

Keywords

Search

Navigation