1 Introduction

Mathematical Modeling is a predominant decision tool that can be efficacious to evaluate the transmission of a disease and apply the necessary control measures [1,2,3]. Analysis of changes in transmission rates helps to identify the effectiveness of the control measures and promote alternate interventions [4]. Phenomenological models were presented in [5], to predict the dynamics of COVID-19. Artificial intelligence (AI) techniques play an important role in finding high-quality prognostic models for the analysis of infectious diseases [6]. Through Social Internet of Things (SIoT) Wang et al. [7] obtained risk-awareness for suspected COVID-19 cases using a graph embedding technique.

Graph theory deals with the mathematical study and analysis of networks. These networks play a vital role in the environment and public health, and as a result ecological and epidemiological researchers have now drawn their attention to network analysis [8]. In biomedical research, graphs can capture the underlying connectivity relations among biological entities such as genes, DNA and proteins [9,10,11,12]. Topological analysis of large-scale protein interaction networks can provide insights into redundancies which can in turn result in predictions of protein functions [13]. Moreover, the control strategies for infectious diseases often relies on graph theoretical networks [14]. It has been shown that the early diagnosis of neurological disorders can be made possible through the detection of abnormal patterns of neural synchronization in specific brain regions [15].

Trees are connected graphs that do not contain a cycle. The vertices of a rooted tree could represent a variety of biological entities such as DNA sequences or various species and the edges could represent their mutations or inter connections with other species. Such rooted trees of biological interest are called phylogenetic trees or evolutionary trees. A hypertree is an interconnection topology which is a combination of the binary tree and hypercube concept. Hypertrees are applicable in a scenario where there are interactions among certain vertices at a given level of the binary trees, and hence one can model such interactions through the use of hypertrees. Machine learning and AI techniques have shown that when contact tracing is fully utilized, one can mitigate the eruption of the pandemic by breaking the current chain of proliferation of the corona virus, and thus hel** to reduce the rate of recent epidemics [16].

Topological indices of a chemical compound are molecular descriptors. Several topological indices have been defined and utilised in QSPR/QSAR studies to understand the relationship between molecular structure and potential physicochemical properties [16,17,18,19]. Stimulated by such varied applications of biological networks, we have in this paper obtained a number of topological indices of these networks and we have also verified the expressions using computer codes. In this process we have also identified several logical flaws found in Gao et al. [20], in the computation of certain topological indices for some of the trees and we have provided corrected expressions.

2 Mathematical preliminaries and techniques

The distance d(u,v) between two vertices u and v in a connected graph G is the length of the shortest path between them. If \( l \ge 1, \) then the set \( \left\{ {1, \ldots ,l} \right\} \) will be denoted by \( \left[ l \right]. \) For any vertex \( v \in V\left( G \right) \), the eccentricity of v is defined as \( \eta \left( v \right) = \hbox{max} \{d\left( {u, v} \right) |u \in V\left( G \right)\} \).

Ghorbani and Khaki [18] introduced the eccentric version of geometric-arithmetic index as fourth geometric-arithmetic eccentricity index which is stated as

$$ GA_{4} \left( G \right) = \mathop \sum \limits_{st \in E\left( G \right)} \frac{{2\sqrt {\eta \left( s \right)\eta \left( t \right)} }}{\eta \left( s \right) + \eta \left( t \right)}. $$

Further, the fourth Zagreb index, the fourth multiplicative Zagreb index, the sixth Zagreb index, the sixth multiplicative Zagreb index, and the fourth and sixth Zagreb polynomial index [19, 20] are defined as follows:

$$ Zg_{4} \left( G \right) = \mathop \sum \limits_{st \in E\left( G \right)} \left( {\eta \left( s \right) + \eta \left( t \right)} \right); $$
$$ {{\Pi }}_{4}^{*} \left( G \right) = \mathop \prod \limits_{st \in E\left( G \right)} \left( {\eta \left( s \right) + \eta \left( t \right)} \right); $$
$$ Zg_{6} \left( G \right) = \mathop \sum \limits_{st \in E\left( G \right)} \eta \left( s \right) \eta \left( t \right); $$
$$ {{\Pi }}_{6}^{*} \left( G \right) = \mathop \prod \limits_{st \in E\left( G \right)} \eta \left( s \right) \eta \left( t \right); $$
$$ Zg_{4} \left( {G, x} \right) = \mathop \sum \limits_{st \in E\left( G \right)} x^{\eta \left( s \right) + \eta \left( t \right)} ; $$
$$ Zg_{6} \left( {G, x} \right) = \mathop \sum \limits_{st \in E\left( G \right)} x^{\eta \left( s \right) \eta \left( t \right)} . $$

In addition, the fifth multiplicative atom bond connectivity index [20] is defined by

$$ ABC_{5} {{\Pi }}\left( {\text{G}} \right) = \mathop \prod \limits_{st \in E\left( G \right)} \sqrt {\frac{\eta \left( s \right) + \eta \left( t \right) - 2}{\eta \left( s \right) \eta \left( t \right)}} . $$

3 Error corrections of previous techniques and results

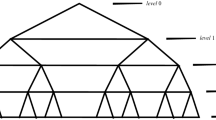
A hypertree HT(l) [21] is a complete binary tree \( T_{l} \) (a binary tree with l levels where level a, \( 0 \le a \le l \) contains \( 2^{a} \) vertices) and the vertices of \( T_{l} \) are labeled as follows: The root node has label 1 and is said to be at level 0. The children of the vertex x are labeled with 2x and 2x + 1. Additional edges in a hypertree are horizontal, where two vertices in the same level a, \( 1 \le a \le l \), are joined by an edge if their label difference is \( 2^{a - 1} , \) see Fig. 1.

Fig. 1
figure 1

Hypertree HT(3) of dimension 3

Full size image

Gao et al. [20] have obtained various topological indices defined above in the form of Theorem 1 for the hypertree, HT(l) with l-levels. As their results are erroneous as shown here, we provide the corrected results for various topological indices reported by Gao et al. [20].

Consider the hypertree HT (3) in Fig. 1 as an example to derive the correct expressions for HT.

By manual calculation of the eccentricities for the various vertices in Fig. 1 we obtain for HT(3):

$$ \begin{aligned} \eta \left( 1 \right) & = \eta \left( 2 \right) = \eta \left( 3 \right) = 3; \\ \eta \left( 4 \right) & = \eta \left( 5 \right) = \eta \left( 6 \right) = \eta \left( 7 \right) = 4; \\ \eta \left( 8 \right) & = \eta \left( 9 \right) = \eta \left( {10} \right) = \eta \left( {11} \right) = \eta \left( {12} \right) = \eta \left( {13} \right) = \eta \left( {14} \right) = \eta \left( {15} \right) = 5. \\ \end{aligned} $$

Hence for HT(3) with 21 edges upon substation of the eccentricity values, we obtain:

$$ Zg_{4} \left( {HT\left( 3 \right)} \right) = \mathop \sum \limits_{st \in E\left( G \right)} \left( {\eta \left( s \right) + \eta \left( t \right)} \right) = 174 $$
(1)

and likewise,

$$ {{\Pi }}_{4}^{*} \left( {HT\left( 3 \right)} \right) = \mathop \prod \limits_{st \in E\left( G \right)} \left( {\eta \left( s \right) + \eta \left( t \right)} \right) = 14,287,819,685,207,040,000 $$
(2)

However, the application of the derived formulae in Ref [20] yield:

$$ \begin{aligned} Zg_{4} \left( {HT\left( 3 \right)} \right) & = 6\left( 3 \right) + \left( {9\left( 3 \right) - 2} \right)\left( {2^{3} - 2} \right)\left( {3 - 1} \right) = 318 \end{aligned} $$
(3)
$$ \Pi _{4}^{*} (HT( 3 )) = 6( 3)\mathop \prod \limits_{a = 1}^{3 - 1} \mathop \prod \limits_{q = 3}^{2( 3 ) - 2} 2^{2a}( {4q + 2})( {2q + 2} ) = 18\mathop \prod \limits_{a = 1}^{2} 2^{2a} \left[ {\left( {4\left( 3 \right) + 2} \right)\left( {2\left( 3 \right) + 2} \right) {\text{x}} \left( {4\left( 4 \right) + 2} \right)\left( {2\left( 4 \right) + 2} \right)} \right] = 23,224,320 $$
(4)

The expression obtained manually in Eq. (1) is in disagreement with Eq. (3) obtained by the application of the expression derived for \( Zg_{4} \left( {HT\left( l \right)} \right) \) by Gao et al. [20]. Similarly, Eqs. (2) and (4) imply that the expression obtained in Ref [20] for \( {{\Pi }}_{4}^{*} \left( {HT\left( l \right)} \right) \) is also not correct. More comparisons are given in Table 1 for all of the indices for the hypertrees. We have also used TopoChemie-2020 [22], a suite of Fortran’95 codes to compute all of the topological indices considered here to validate the results. The results obtained from TopoChemie-2020 are shown in Table 1 for comparison with the results obtained from present work and those from Ref [20].

Table 1 Results obtained for hypertree HT(l), with the computer code compared with the results from the expressions derived here and those from Ref [20]
Full size table

The corrected result for HT(l) is as follows.

Theorem 3.1

(Corrected Theorem 1 of [20]) Let HT(l) be the l–level hypertree network with \( l \ge 3. \) Then we have the following results:

$$ \begin{aligned} GA_{4} \left( {HT\left( l \right)} \right) & = 3 + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {\frac{{4\sqrt {\left( {l + a - 1} \right)\left( {l + a} \right)} }}{{2\left( {l + a} \right) - 1}} + 1} \right); \\ Zg_{4} \left( {HT\left( l \right)} \right) & = 2^{l + 1} \left( {6l - 7} \right) - 6l + 16; \\ {{\Pi }}_{4}^{*} \left( {HT\left( l \right)} \right) & = 8l^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) - 1} \right)^{2a + 1} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right)} \right)^{2a} ; \\ Zg_{6} \left( {HT\left( l \right)} \right) & = 2^{l + 1} \left( {6l^{2} - 14l + 11} \right) - 3l^{2} + 16l - 22; \\ {{\Pi }}_{6}^{*} \left( {HT\left( l \right)} \right) & = l^{6} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\left( {l + a - 1} \right)^{2} + l + a - 1} \right)^{2a + 1} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {l + a} \right)^{{2^{a + 1} }} ; \\ Zg_{4} \left( {HT\left( l \right), x} \right) & = 3x^{2l} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a + 1} x^{{2\left( {l + a} \right) - 1}} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} x^{{2\left( {l + a} \right)}} ; \\ Zg_{6} \left( {HT\left( l \right), x} \right) & = 3x^{{l^{2} }} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a + 1} x^{{\left( {l + a - 1} \right)\left( {l + a} \right)}} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} x^{{\left( {l + a} \right)^{2} }} ; \\ ABC_{5} {{\Pi }}\left( {HT\left( l \right)} \right) & = \left( {\frac{{\sqrt {2l - 2} }}{l}} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \begin{array}{*{20}c} {\left( {\frac{{2\left( {l + a} \right) - 3}}{{\left( {l + a - 1} \right)\left( {l + a} \right)}}} \right)^{{2^{a} }} } \\ \\ \end{array} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{2\left( {l + a - 1} \right)}}{{\left( {l + a} \right)^{2} }}} \right)^{{2^{a - 1} }} . \\ \end{aligned} $$

Proof

First, we partition the edge set of HT(l) as follows:

  • \( E_{ll} = \left\{ {e = st \in E\left( {HT\left( l \right)} \right)| \eta \left( s \right) = \eta \left( t \right) = l} \right\} \) and \( n_{ll} = \left| {E_{ll} } \right| = 3; \)

  • \( E_{{\left( {l + a - 1} \right)\left( {l + a} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right)} \right)| \eta \left( s \right) = l + a - 1\,{\text{and}}\,\eta \left( t \right) = l + a} \right\} \) and \( n_{{\left( {l + a - 1} \right)\left( {l + a} \right)}} = \left| {E_{{\left( {l + a - 1} \right)\left( {l + a} \right)}} } \right| = 2\left( {2^{a} } \right), \) where \( a \in \left[ {l - 1} \right]; \)

  • \( E_{{\left( {l + a} \right)\left( {l + a} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right)} \right)| \eta \left( s \right) = \eta \left( t \right) = l + a} \right\} \) and \( n_{{\left( {l + a} \right)\left( {l + a} \right)}} = \left| {E_{{\left( {l + a} \right)\left( {l + a} \right)}} } \right| = 2^{a} , \) where \( a \in \left[ {l - 1} \right]. \)

By the definition, we have

$$ \begin{aligned} GA_{4} \left( {HT\left( l \right)} \right) & = 3 + \mathop \sum \limits_{a = 1}^{l - 1} 2 \times 2^{a} \left( {\frac{{2\sqrt {\left( {l + a - 1} \right)\left( {l + a} \right)} }}{{2\left( {l + a} \right) - 1}}} \right) + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \\ & = 3 + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {\frac{{4\sqrt {\left( {l + a - 1} \right)\left( {l + a} \right)} }}{{2\left( {l + a} \right) - 1}} + 1} \right); \\ Zg_{4} \left( {HT\left( l \right)} \right) & = 3 \times 2l + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {6\left( {l + a} \right) - 2} \right) \\ & = 2^{l + 1} \left( {6l - 7} \right) - 6l + 16; \\ {{\Pi }}_{4}^{*} \left( {HT\left( l \right)} \right) & = \left( {2l} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) - 1} \right)^{{2^{a + 1} }} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right)} \right)^{{2^{a} }} \\ & = 8l^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) - 1} \right)^{2a + 1} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right)} \right)^{{2^{a} }} \\ Zg_{6} \left( {HT\left( l \right)} \right) & = 3 \times l^{2} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {3\left( {l + a - 1} \right)^{2} + 4\left( {l + a - 1} \right) + 1} \right) \\ & = 2^{l + 1} \left( {6l^{2} - 14l + 11} \right) - 3l^{2} + 16l - 22. \\ \end{aligned} $$

Proceeding along the same lines, we prove the remaining equations. □

4 Certain distance and degree based topological indices

In this section, we compute certain distance and degree based topological indices of hypertrees that have not been obtained before. We begin with the following definitions.

Definition 4.1

The first Zagreb index M1(G) was introduced by Gutman [23] and it is defined as

$$ M_{1} (G) = \mathop \sum \limits_{{v_{i} \in V\left( G \right)}} d_{i}^{2} $$

where \( d_{i} = d_{G} \left( {v_{i} } \right) \) is denoted by the degree of vertex \( v_{i} \) for i =1,2,…,n such that \( d_{1} \ge d_{2} \ge \cdots \ge d_{n} \).

Definition 4.2

The second Zagreb index M2(G) [23] of graph G is defined as

$$ M_{2} (G) = \mathop \sum \limits_{{v_{i} v_{j} \in E\left( G \right)}} d_{i} d_{j} $$

Definition 4.3

Let G = (V(G), E(G)) be a graph with n = |V(G)| vertices and m = |E(G)| edges. The edge connecting the vertices i and j is denoted by ij. Then Atom-bond Connectivity Index (ABC) [24] is defined as

$$ ABC\left( G \right) = \mathop \sum \limits_{ij\in E\left( G \right) } \sqrt {\frac{{d_{i} + d_{j} - 2}}{{d_{i} d_{j} }}} $$

Definition 4.4

The Padmakar-Ivan Index [25] is given by

$$ PI\left( G \right) = \mathop \sum \limits_{{e = \left( {uv} \right) \in E\left( G \right) }} [ {n_{u} (e) + n_{v} (e)}] $$

where nu(e) denotes the number of vertices lying closer to the vertex u than the vertex v and nv(e) denotes the number of vertices lying closer to the vertex v than the vertex u.

Definition 4.5

The Szeged Index [26] is defined as

$$ Sz\left( G \right) = \mathop \sum \limits_{{e = \left( {uv} \right) \in E\left( G \right) }} [n_{u} (e) \times n_{v} (e)] $$

Definition 4.6

The Schultz index [27] is defined as

$$ S\left( G \right) = 1/2\mathop \sum \limits_{{\left( {u,v} \right) \in V\left( G \right) \times V\left( G \right) }} [d(u) + d(v)]d(u,v) $$

where d(u,v) is the number of edges in a minimum path connecting the vertices u and v in G, d(u) represents the degree of the vertex u.

Definition 4.7

The Gutman index [28] denoted by Gut(G) is defined as

$$ Gut\left( G \right) = 1/2\mathop \sum \limits_{{\left( {u,v} \right) \in V\left( G \right) \times V\left( G \right) }} [d(u) \times d(v)] d(u,v) $$

4.1 Hypertree

Theorem 4.1.1

Let HT(l) be the \( l \)-level hypertree network, \( l \ge 2 \). Then the atom bond connectivity index \( ABC\left( {HT\left( l \right)} \right) = 1.97921882532 \times 2^{l} - 1.64764861611 \).

Proof

First, we partition the edge set of HT(l) as follows:

\( E_{24} = \left\{ {e = uv \in E\left( {HT\left( l \right)} \right) | d\left( u \right) = 2 \;and\; d\left( v \right) = 4{{\} }} \;and\; \left| {E_{24} } \right| = 2}. \right. \)

\( E_{22} = \left\{ {e = uv \in E\left( {HT\left( l \right)} \right) | d\left( u \right) = d\left( v \right) = 2{{\} }} \;and\; \left| {E_{22} } \right| = 2^{l - 1} }. \right. \)

\( E_{42} = \left\{ {e = uv \in E\left( {HT\left( l \right)} \right) | d\left( u \right) = 4 \;and \;d\left( v \right) = 2{{\} }} and \left| {E_{42} } \right| = 2^{l} } \right. \).

\( E_{44} = \left\{ {e = uv \in E\left( {HT\left( l \right)} \right) | d\left( u \right) = 4\; and\; d\left( v \right) = 4{{\} }} \;and\; \left| {E_{44} } \right| = 2^{l + 1} - 2^{l - 1} - 5^{{}} } \right. \).

By the definition, we have

$$ \begin{aligned} ABC\left( {HT\left( l \right)} \right) & = \mathop \sum \limits_{{e\in E_{24} }} \sqrt {\frac{d\left( u \right) + d\left( v \right) - 2}{d\left( u \right)d\left( v \right)}} + \mathop \sum \limits_{{e\in E_{22} }} \sqrt {\frac{d\left( u \right) + d\left( v \right) - 2}{d\left( u \right)d\left( v \right)}} \\ & \quad + \mathop \sum \limits_{{e\in E_{42} }} \sqrt {\frac{d\left( u \right) + d\left( v \right) - 2}{d\left( u \right)d\left( v \right)}} + \mathop \sum \limits_{{e\in E_{44} }} \sqrt {\frac{d\left( u \right) + d\left( v \right) - 2}{d\left( u \right)d\left( v \right)}} \\ & = 2\sqrt {\frac{1}{2}} + 2^{l - 1} \sqrt {\frac{1}{2}} + 2^{l} \sqrt {\frac{1}{2}} + (2^{l + 1} - 2^{l - 1} - 5)\sqrt {\frac{3}{8}} \\ & = 1.97921882532 \times 2^{l} - 1.64764861611.\;\;\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 4.1.2

Let HT(l) be the \( l \)-level hypertree network, \( l \ge 2 \). Then the first Zagreb index

$$ M_{1} \left( {HT\left( l \right)} \right) = 20 \times 2^{l} - 28. $$

Proof

First, we partition the vertex set of HT(l) as follows:

\( P_{1} = \left\{ {v | d\left( v \right) = 2{{\} }} \;and\; \left| {P_{1} } \right| = 2^{l} + 1} \right. \).

\( P_{2} = \left\{ {v | d\left( v \right) = 4{{\} }} \;and\; \left| {P_{2} } \right| = 2^{l + 1} - 2^{l} - 2} \right. \).

By the definition, we have

$$ \begin{aligned} M_{1} \left( {HT\left( l \right)} \right) & = \mathop \sum \limits_{{v\in P_{1} }} (d(v))^{2} + \mathop \sum \limits_{{v\in P_{2} }} (d(v))^{2} \\ & = (2^{l} + 1)\left( {2^{2} } \right) + (2^{l + 1} - 2^{l} - 2)\left( {4^{2} } \right) = 20 \times 2^{l} - 28.\,\,\,{\square } \\ \end{aligned} $$

Theorem 4.1.3

Let HT(l) be the \( l \)-level hypertree network, \( l \ge 2 \). Then the second Zagreb index \( M_{2} \left( {HT\left( l \right)} \right) = 34 \times 2^{l} - 64 \).

The proof runs analogous to that of Theorem 4.1.1. □

Theorem 4.1.4

Let \( HT\left( l \right) \) be the \( l \)-level hypertree with \( l \ge 2. \) Then the szeged index

$$ Sz\left( {HT\left( l \right)} \right) = 2^{3l} - 27 \times 2^{2l} + 12l \times 2^{l} + 21 \times 2^{l} + 8l \times 2^{2l} + 5. $$

Proof

Let \( B_{e} = \left\{ {e|e \in E\left( {T_{l} } \right)\} } \right. \) and \( H_{e} = \left\{ {e|e } \right. \) is horizontal} be the partition of the edge set of HT(\( l \)) as edges of the associated binary tree \( T_{l} \) and horizontal edges respectively. Let \( e = \left( {uv} \right) \in B_{e} \) where u and v are in level i and i + 1 respectively, \( 1 \le i \le l - 1 \). Then by the symmetric structure of the hypertree, we have \( n\left( v \right) = 2^{l - i + 1} - 2. \) For example, the hypertree HT(\( 4 \)) with \( n\left( v \right) = 14 \) is shown in Fig. 2. Note that the number of edges between level i and i + 1, \( 1 \le i \le l - 1 \) is \( 2^{i + 1} \). Further, \( n\left( u \right) = \left| {V\left( { HT\left( l \right)} \right)} \right| - n\left( v \right) = 2^{l + 1} - 2^{l - i + 1} + 1 \). It is easy to verify that \( n\left( u \right) = 1 \) and \( n\left( v \right) = 2^{l} - 1 \), when \( \left( {uv} \right) \in B_{e} \), u is in level 0 and v is in level 1.

Fig. 2
figure 2

The hypertree HT(\( 4 \)) with \( n\left( v \right) = 14 \)

Full size image

For any level i, \( 1 \le i \le l \), if \( e = \left( {uv} \right) \in H_{e} \), then \( n\left( u \right) = n\left( v \right) = 2^{l} - 1. \) Hence

$$ \begin{aligned} Sz\left( {HT\left( l \right)} \right) & = \mathop 2(1)(2^{l} - 1) + \mathop \sum \limits_{i = 1}^{l - 1} \left( {n\left( u \right) n\left( v \right)} \right)2^{i + 1} + ( 2^{l} - 1)\left( {n\left( u \right) n\left( v \right)} \right) \\ & = \mathop 2(1)(2^{l} - 1) + \mathop \sum \limits_{i = 1}^{l - 1} 2^{i + 1} (2^{l + 1} - 2^{l - i + 1} + 1)\left( { 2^{l - i + 1} - 2} \right) + \left( {2^{l} - 1} \right)(2^{l} - 1)^{2} \\ & = 2^{3l} - 27 \times 2^{2l} + 12l \times 2^{l} + 21 \times 2^{l} + 8l \times 2^{2l} + 5.\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 4.1.5

Let HT(\( l \)) be the \( l \)-level hypertree with \( l \ge 2. \) Then the PI index

$$ PI\left( {HT\left( l \right)} \right) = 6 \times \left( {2^{l} - 1} \right)^{2} . $$

Proof

Let \( B_{e} = \left\{ {e|e \in E\left( {T_{l} } \right)\} } \right. \) and \( H_{e} = \left\{ {e|e } \right. \) is horizontal} be the partition of the edge set of HT(\( l \)) as binary tree edges and horizontal edges respectively. Let \( e = \left( {uv} \right) \in V_{e} \) where u and v are in level i and i + 1 respectively, \( 1 \le i \le l - 1 \). Then by the symmetric structure of the hypertree, we have \( n\left( v \right) = 2^{l - i + 1} - 2. \) For example, the hypertree HT(\( 4 \)) with \( n\left( v \right) = 14 \) is shown in Fig. 2. Note that the number of edges between level i and i + 1, \( 1 \le i \le l - 1 \) is \( 2^{i + 1} \). Further, \( n\left( u \right) = \left| {V\left( { HT\left( l \right)} \right)} \right| - n\left( v \right) = 2^{l + 1} - 2^{l - i + 1} + 1 \). It is easy to verify that \( n\left( u \right) = 1 \) and \( n\left( v \right) = 2^{l} - 1 \), when \( \left( {uv} \right) \in B_{e} \), u is in level 0 and v is in level 1.

For any level i, \( 1 \le i \le l \), if \( e = \left( {uv} \right) \in H_{e} \), then \( n\left( u \right) = n\left( v \right) = 2^{l} - 2. \) Hence

$$ \begin{aligned} PI\left( {HT\left( l \right)} \right) & = 2(1+(2^{l} -1)) + \mathop \sum \limits_{i = 1}^{l - 1} \left( {n\left( u \right) + n\left( v \right)} \right)(2^{i + 1} ) + ( 2^{l} - 1)\left( {n\left( u \right) + n\left( v \right)} \right) \\ & = 2^{l+1} + \mathop \sum \limits_{i = 1}^{l - 1} (2^{l + 1} )[(2^{l + 1} - 2^{l - i + 1} + 1) + \left( { 2^{l - i + 1} - 2} \right)] \\ & \quad + (2^{l} - 1)((2^{l} - 1) + (2^{l} - 1)) = 6 \times (2^{l} - 1)^{2} .\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 4.1.6

Let HT(l) be the \( l \)-level hypertree network, \( l \ge 2. \) Then Schultz index

$$ S\left( {HT\left( l \right)} \right) = 38l \times 2^{l} - 70 \times 2^{2l} + 50 \times 2^{l} + 24l \times 2^{2l} + 20 $$

Proof

Since HT(l) is bi-regular with degree 2 and degree 4 vertices, we partition the vertices (ordered pairs) of HT(l) as follows:

\( V_{22} = \left\{ {\left( {x,y} \right)/d\left( x \right) = d\left( y \right) = 2} \right.\} \; and\; \left| {V_{22} } \right| = 2^{l} + (2^{l} - 1)(2^{l - 1} ) \),

\( V_{24} = \left\{ {\left( {x,y} \right)/d\left( x \right) = 2 \;and\; d\left( y \right) = 4} \right.\} \) \( and\; \left| {V_{24} } \right| = (2^{l} + 1) (2^{l} - 2) \), and

\( V_{44} = \left\{ {\left( {x,y} \right)/d\left( x \right) = d\left( y \right) = 4} \right.\} \;and\; \left| {V_{44} } \right| = (2^{l} - 2)(2^{l} - 3)/2 \). Hence,

$$ \begin{aligned} S\left( {HT\left( l \right)} \right) & = \mathop \sum \limits_{{\left( {u,v} \right)\in V_{22} }} \left( {d\left( u \right) + d\left( v \right)} \right) d\left( {u,v} \right) + \mathop \sum \limits_{{\left( {u,v} \right)\in V_{24} }} \left( {d\left( u \right) + d\left( v \right)} \right) d\left( {u,v} \right) \\ & \quad + \mathop \sum \limits_{{\left( {u,v} \right)\in V_{44} }} \left( {d\left( u \right) + d\left( v \right)} \right) d\left( {u,v} \right) \\ & = l \times 2^{l + 2} + 2^{l + 1} \left[ {\left( {\mathop \sum \limits_{i = 1}^{l - 1} 2^{i - 1} \left( {4i + 1} \right)} \right) + 1} \right] \\ & \quad + \left( {2 + 4} \right)\left[ {\mathop \sum \limits_{i = 2}^{i - 1} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j} \right)2^{l + j - 1} } \right)} \right. \\ & \quad + \left. {\mathop \sum \limits_{i = 1}^{l - 1} \left( {l - i} \right)2^{l} + \mathop \sum \limits_{i = 2}^{l - 1} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j + 1} \right)2^{l + j - 1} } \right) + \mathop \sum \limits_{i = 1}^{l - 1} \left( {l - i + 1} \right)2^{l} + \mathop \sum \limits_{i = 1}^{l - 1} i \times 2^{i} } \right] \\ & \quad+ \left( {4 + 4} \right)\left[ {\mathop \sum \limits_{k = 1}^{l - 2} \left[ {\mathop \sum \limits_{i = 2}^{l - 1 - k} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j - k} \right)2^{l + j - k - 1} } \right)} \right]} \right. \\ & \quad + \mathop \sum \limits_{k = 1}^{l - 2} \left( {\mathop \sum \limits_{i = 1}^{l - 1 - k} \left( {l - i - k} \right)2^{l - k} } \right) \\ & \quad + \mathop \sum \limits_{k = 1}^{l - 2} \mathop \sum \limits_{i = 2}^{l - 1 - k} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j - k + 1} \right)2^{l + j - k - 1} } \right) \\ & \quad \left. { + \mathop \sum \limits_{k = 1}^{l - 2} \left( {\mathop \sum \limits_{i = 1}^{l - 1 - k} \left( {l - i - k + 1} \right)2^{l - k} } \right) + \mathop \sum \limits_{i = 1}^{l - 1} \left[ {\mathop \sum \limits_{j = 1}^{i - 1} 2^{j - 1} \times 2j + \mathop \sum \limits_{j = 1}^{i - 1} 2^{j - 1} \times \left( {2j + 1} \right) + 1} \right]2^{i - 1} } \right] \\ &\quad = 38l \times 2^{l} - 70 \times 2^{2l} + 50 \times 2^{l} + 24l \times 2^{2l} + 20.\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 4.1.7

Let HT(l) be the \( l \)-level hypertree network, \( l \ge 2 \). Then Gutman index

$$ Gut\left( {HT\left( l \right)} \right) = 60l \times 2^{l} - 111 \times 2^{2l} + 80 \times 2^{l} + 36l \times 2^{2l} + 32. $$

Proof

Since HT(l) is bi-regular with degrees 2 and 4, we partition the vertices (ordered pairs) of HT(l) as follows:

\( V_{22} = \left\{ {\left( {x,y} \right)/d\left( x \right) = d\left( y \right) = 2} \right.\} \;and\; \left| {V_{22} } \right| = 2^{l} + (2^{l} - 1)(2^{l - 1} ) \),

\( V_{24} = \left\{ {\left( {x,y} \right)/d\left( x \right) = 2 \; and\; d\left( y \right) = 4} \right.\} \;and\; \left| {V_{24} } \right| = (2^{l} + 1) (2^{l} - 2) \), and

\( V_{44} = \left\{ {\left( {x,y} \right)/d\left( x \right) = d\left( y \right) = 4} \right.\} \;and\; \left| {V_{44} } \right| = (2^{l} - 2)(2^{l} - 3)/2 \). Hence,

$$ \begin{aligned} Gut\left( {HT\left( l \right)} \right) & = \mathop \sum \limits_{{\left( {u,v} \right)\in V_{22} }} \left( {d\left( u \right) \times d\left( v \right)} \right) d\left( {u,v} \right) + \mathop \sum \limits_{{\left( {u,v} \right)\in V_{24} }} \left( {d\left( u \right) \times d\left( v \right)} \right) d\left( {u,v} \right) \\ & \quad + \mathop \sum \limits_{{\left( {u,v} \right)\in V_{44} }} \left( {d\left( u \right) \times d\left( v \right)} \right) d\left( {u,v} \right) \\ & = l \times 2^{l + 2} + 2^{l + 1} \left[ {\left( {\mathop \sum \limits_{i = 1}^{l - 1} 2^{i - 1} \left( {4i + 1} \right)} \right) + 1} \right] \\ &\quad +(2\times 4) \left[ {\mathop \sum \limits_{i = 2}^{l - 1} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j} \right)2^{l + j - 1} } \right)} \right. \\ & \quad + \left. {\mathop \sum \limits_{i = 1}^{l - 1} \left( {l - i} \right)2^{l} + \mathop \sum \limits_{i = 2}^{l - 1} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j + 1} \right)2^{l + j - 1} } \right) + \mathop \sum \limits_{i = 1}^{l - 1} \left( {l - i + 1} \right)2^{l} + \mathop \sum \limits_{i = 1}^{l - 1} i \times 2^{i} } \right] \\ & \quad +(4\times 4) \left[ {\mathop \sum \limits_{k = 1}^{l - 2} \left[ {\mathop \sum \limits_{i = 2}^{l - 1 - k} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j - k} \right)2^{l + j - k - 1} } \right)} \right]} \right. \\ & \quad + \mathop \sum \limits_{k = 1}^{l - 2} \left( {\mathop \sum \limits_{i = 1}^{l - 1 - k} \left( {l - i - k} \right)2^{l - k} } \right) \\ & \quad + \mathop \sum \limits_{k = 1}^{l - 2} \left[ {\mathop \sum \limits_{i = 2}^{l - 1 - k} \left( {\mathop \sum \limits_{j = 1}^{i - 1} \left( {l - i + 2j - k + 1} \right)2^{l + j - k - 1} } \right)} \right] \\ & \quad \left. { + \mathop \sum \limits_{k = 1}^{l - 2} \left( {\mathop \sum \limits_{i = 1}^{l - 1 - k} \left( {l - i - k + 1} \right)2^{l - k} } \right) + \mathop \sum \limits_{i = 1}^{l - 1} \left[ {\mathop \sum \limits_{j = 1}^{i - 1} 2^{j - 1} \times 2j + \mathop \sum \limits_{j = 1}^{i - 1} 2^{j - 1} \times \left( {2j + 1} \right) + 1} \right]2^{i - 1} } \right] \\ & \quad \quad \quad \quad \quad \quad = 60l \times 2^{l} - 111 \times 2^{2l} + 80 \times 2^{l} + 36l \times 2^{2l} + 32.\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Remark 4.1.8

The results obtained from TopoChemie-2020 are shown in Table 2 for comparison with the results obtained from Theorems 4.1.1–4.1.7.

Table 2 Results obtained for hypertree HT(l), with the computer code compared with the results from the expressions in Theorems 4.1.1–4.1.7
Full size table

5 Corona product of hypertree and a path

In this section, we consider the topological indices of hypertrees generated through corona products that have not been considered before.

Definition 5.1

[29] The corona product \( G_{1} \odot G_{2} \) of two graphs \( G_{1} \) with \( n_{1} \) vertices and \( m_{1} \) edges and \( G_{2} \) with \( n_{2} \) vertices and \( m_{2} \) edges is defined as the graph obtained by taking one copy of \( G_{1} \) and \( n_{1} \) copies of \( G_{2} \), and then joining the \( i{\text{th}} \) vertex of \( G_{1} \) with an edge to every vertex in the \( i{\text{th}} \) copy of \( G_{2} \).

It follows from the definition of the corona that \( G_{1} \odot G_{2} \) has \( n_{1} + n_{1} n_{2} \) vertices and \( m_{1} + n_{1} m_{2} + n_{1} n_{2} \) edges. It is easy to see that \( G_{1} \odot G_{2} \) is not in general isomorphic to \( G_{2} \odot G_{1} \). For illustration, the corona product of hypertree HT(3) and path \( P_{3} \) is given in Fig. 3.

Fig. 3
figure 3

The corona product HT(3)\( \odot P_{3} \) of hypertree HT(3) and path \( P_{3} \)

Full size image

Theorem 5.2

Let \( HT\left( l \right) \odot P_{r} , l,r \ge 2 \) be the corona product of hypertree and a path network on r vertices. Then we have the following:

$$ \begin{aligned} GA_{4} \left( {HT\left( l \right) \odot P_{r} } \right) & = \left( {2 + r} \right)\mathop \sum \limits_{a = 1}^{l - 1} 2^{a + 1} \frac{{\sqrt {\left( {l + a} \right)\left( {l + a + 1} \right)} }}{{\left( {2l + 2a + 1} \right)}} + r2^{l + 1} \frac{{\sqrt {4l^{2} + 2l} }}{4l + 1} + 2r\frac{{\sqrt {\left( {l + 1} \right)\left( {l + 2} \right)} }}{2l + 3} \\ & \quad + \left( {r - 1} \right)\left( {2^{l + 1} - 2} \right) + 2^{l} + r; \\ \end{aligned} $$
$$ \begin{aligned} Zg_{4} \left( {HT\left( l \right) \odot P_{r} } \right) & = 6\left( {l + 1} \right) + \left( {r + 2} \right)\left( {2^{l} \left( {4l - 3} \right) - 4l + 2} \right) + 2^{l} \left( r \right)\left( {4l + 1} \right) + r\left( {2l + 3} \right) \\ & \quad - \left( {2r - 2} \right)\left( {2l - 4l 2^{l} } \right) + 2^{l + 1} \left( {2l - 1} \right) - 4l + 2\left( {r - 1} \right)\left( {l + 2} \right); \\ \end{aligned} $$
$$ \begin{aligned} {{\Pi }}_{4}^{*} \left( {HT\left( l \right) \odot P_{r} } \right) & = \left( {2l + 2} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) + 1} \right)^{{2^{a} \left( {2 + r} \right)}} \times \left( {4l + 1} \right)^{{r2^{l} }} \times \left( {2l + 3} \right)^{r} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l} \left( {2\left( {l + a} \right) + 2} \right)^{{2^{a} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) + 2} \right)^{{2^{a} }} \times \left( {2l + 4} \right)^{r - 1} ; \\ \end{aligned} $$
$$ \begin{aligned} & Zg_{6} \left( {HT\left( l \right) \odot P_{r} } \right) \\ & = 3\left( {l + 1} \right)^{2} + \left( {r + 2} \right)\left( {2^{l} + 2.2^{l} \left( {2l^{2} - 3l + 2} \right) - 2l^{2} - 4} \right) + 2^{l} r\left( {4l^{2} + 2l} \right) \\ & \quad + r(l + 1)(l + 2) + (r - 1)(4 \times 2^{l} - 2l^{2} + 8 \times 2^{l} l^{2} - 4) \\ & \quad + 2^{l} \left( {4l^{2} - 4l + 3} \right) - 2l^{2} - 4 + \left( {r - 1} \right)\left( {l + 2} \right)^{2} ; \\ \end{aligned} $$
$$ \begin{aligned} {{\Pi }}_{6}^{*} \left( {HT\left( l \right) \odot P_{r} } \right) & = \left( {l + 1} \right)^{6} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\left( {l + a} \right)^{2} + l + a} \right)^{{2^{a} \left( {2 + r} \right)}} \times \left( {4l^{2} + 2l} \right)^{{r2^{l} }} \times \left( {l^{2} + 3l + 2} \right)^{r} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l} \left( {l + a + 1} \right)^{{2^{a + 1} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {l + a + 1} \right)^{{2^{a + 1} }} \times \left( {l + 2} \right)^{{2\left( {r - 1} \right)}} ; \\ \end{aligned} $$
$$ \begin{aligned} Zg_{4} \left( {HT\left( l \right) \odot P_{r} ,x} \right) & = 3x^{{2\left( {l + 1} \right)}} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)x^{{2\left( {l + a} \right) + 1}} + r2^{l} x^{4l + 1} + rx^{2l + 3} \\ & \quad + \left( {r - 1} \right)\mathop \sum \limits_{a = 1}^{l} 2^{a} x^{{2\left( {l + a + 1} \right)}} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} x^{{2\left( {l + a + 1} \right)}} + \left( {r - 1} \right)x^{{2\left( {l + 2} \right)}} ; \\ \end{aligned} $$
$$ \begin{aligned} Zg_{6} \left( {HT\left( l \right) \odot P_{r} ,x} \right) & = 3x^{{\left( {l + 1} \right)^{2} }} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)x^{{\left( {l + a} \right)\left( {l + a + 1} \right)}} + r2^{l} x^{{4l^{2} + 2l}} + rx^{{\left( {l + 1} \right)\left( {l + 2} \right)}} \\ & \quad + \left( {r - 1} \right)\mathop \sum \limits_{a = 1}^{l} 2^{a} x^{{\left( {l + a + 1} \right)^{2} }} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} x^{{\left( {l + a + 1} \right)^{2} }} + \left( {r - 1} \right)x^{{\left( {l + 2} \right)^{2} }} ; \\ \end{aligned} $$
$$ \begin{aligned} ABC_{5} {{\Pi }}\left( {HT\left( l \right) \odot P_{r} } \right) & = \left( {\frac{{\sqrt {2l} }}{l + 1}} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{2\left( {l + a} \right) - 1}}{{\left( {l + a} \right)^{2} + l + a}}} \right)^{{2^{a - 1} \left( {2 + r} \right)}} \times \left( {\frac{4l - 1}{{4l^{2} + 2l}}} \right)^{{2^{l - 1} r}} \\ & \quad \times \left( {\sqrt {\frac{2l + 1}{{l^{2} + 3l + 2}}} } \right)^{r} \times \mathop \prod \limits_{a = 1}^{l} \left( {\frac{{\sqrt {2\left( {l + a} \right)} }}{l + a + 1}} \right)^{{2^{a} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{\sqrt {2\left( {l + a} \right)} }}{l + a + 1}} \right)^{{2^{a} }} \times \left( {\frac{{\sqrt {2\left( {l + 1} \right)} }}{l + 2}} \right)^{r - 1} . \\ \end{aligned} $$

Proof

We prove the result based on the structure analysis and edge partition method. By analyzing the structure \( HT\left( l \right) \odot P_{r} \) its edge set \( E\left( {HT\left( l \right) \odot P_{r} } \right) \) can be divided into seven partitions based on the eccentricities of associated vertices:

  • \( E_{{\left( {l + 1} \right)\left( {l + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = \eta \left( t \right) = l + 1} \right\} \) and \( n_{{\left( {l + 1} \right)\left( {l + 1} \right)}} = \left| {E_{{\left( {l + 1} \right)\left( {l + 1} \right)}} } \right| = 3; \)

  • \( E_{{\left( {l + a} \right)\left( {l + a + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = l + a\; {\text{and}}\, \eta \left( t \right) = l + a + 1} \right\} \) and \( n_{{\left( {l + a} \right)\left( {l + a + 1} \right)}} = \left| {E_{{\left( {l + a} \right)\left( {l + a + 1} \right)}} } \right| = 2^{a} \left( {2 + r} \right), \) where \( a \in \left[ {l - 1} \right]; \)

  • \( E_{{2l\left( {2l + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = 2l \;{\text{and}}\; \eta \left( t \right) = 2l + 1} \right\} \) and \( n_{{2l\left( {2l + 1} \right)}} = \left| {E_{{2l\left( {2l + 1} \right)}} } \right| = 2^{l} r \);

  • \( E_{{\left( {l + 1} \right)\left( {l + 2} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = l + 1 \;{\text{and}}\; \eta \left( t \right) = l + 2} \right\} \) and \( n_{{\left( {l + 1} \right)\left( {l + 2} \right)}} = \left| {E_{{\left( {l + 1} \right)\left( {l + 2} \right)}} } \right| = r; \)

  • \( E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = \eta \left( t \right) = l + a + 1} \right\} \) and \( n_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = \left| {E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} } \right| = 2^{a} \left( {r - 1} \right), \) where \( a \in \left[ l \right]; \)

  • \( E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = \eta \left( t \right) = l + a + 1} \right\} \) and \( n_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = \left| {E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} } \right| = 2^{a} , \) where \( a \in \left[ {l - 1} \right] \) \( ; \)

  • \( E_{{\left( {l + 2} \right)\left( {l + 2} \right)}} = \left\{ {e = st \in E\left( {HT\left( l \right) \odot P_{r} } \right)| \eta \left( s \right) = \eta \left( t \right) = l + 2} \right\} \) and \( n_{{\left( {l + 2} \right)\left( {l + 2} \right)}} = \left| {E_{{\left( {l + 2} \right)\left( {l + 2} \right)}} } \right| = r - 1. \)

Let the edge colors green, blue, sky blue, yellow, black, red and brown in Fig. 3 represent the edge partitions \( E_{44} , E_{{\left( {l + a} \right)\left( {l + a + 1} \right)}} , E_{{6\left( {6 + 1} \right)}} , E_{{4\left( {4 + 1} \right)}} , E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} , _{ } E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right) }} , \) and \( E_{{\left( {4 + 1} \right)\left( {4 + 1} \right)}} \) respectively. That is, the edge partition of \( HT\left( 3 \right) \odot P_{3} \) is given as follows:

  • \( E_{44} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = \eta \left( t \right) = 4} \right\} \) and \( n_{44} = \left| {E_{44} } \right| = 3; \)

  • \( E_{{\left( {l + a} \right)\left( {l + a + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = l + a \;{\text{and}}\; \eta \left( t \right) = l + a + 1} \right\} \) and \( n_{{\left( {l + a} \right)\left( {l + a + 1} \right)}} = 2^{a} \left( {2 + 3} \right) = 5\left( {2^{a} } \right), \) where \( a \in \left[ 2 \right]; \)

  • \( E_{{6\left( {6 + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = 6\; {\text{and}}\; \eta \left( t \right) = 6 + 1} \right\} \) and \( n_{{6\left( {6 + 1} \right)}} = 2^{3} {\text{x }}3 = 24; \)

  • \( E_{{4\left( {4 + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = 4 \;{\text{and}} \;\eta \left( t \right) = 4 + 1} \right\} \) and \( n_{{4\left( {4 + 1} \right)}} = 3; \)

  • \( E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = \eta \left( t \right) = l + a + 1} \right\} \) and \( n_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = 2^{a} \left( {r - 1} \right) = 2\left( {2^{a} } \right), \) where \( a \in \left[ 3 \right]; \)

  • \( E_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = \eta \left( t \right) = l + a + 1} \right\} \) and \( n_{{\left( {l + a + 1} \right)\left( {l + a + 1} \right)}} = 2^{a} , \) where \( a \in \left[ 2 \right] \);

  • \( E_{{\left( {4 + 1} \right)\left( {4 + 1} \right)}} = \left\{ {e = st \in E\left( {HT\left( 3 \right) \odot P_{3} } \right)| \eta \left( s \right) = \eta \left( t \right) = 4 + 1} \right\} \) and \( n_{{\left( {4 + 1} \right)\left( {4 + 1} \right)}} = 2. \)

From the definitions of eccentricity-based topological indices, we get

$$ \begin{aligned} & GA_{4} \left( {HT\left( l \right) \odot P_{r} } \right) \\ & = 3 + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)\frac{{2\sqrt {\left( {l + a} \right)\left( {l + a + 1} \right)} }}{{2\left( {l + a} \right) + 1}} + r \times 2^{l} \times \frac{{2\sqrt {2l\left( {2l + 1} \right)} }}{4l + 1} \\ & \quad + r\frac{{2\sqrt {\left( {l + 1} \right)\left( {l + 2} \right)} }}{2l + 3} + \mathop \sum \limits_{a = 1}^{l} 2^{a} \left( {r - 1} \right) + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} + \left( {r - 1} \right) \\ & = \left( {2 + r} \right)\mathop \sum \limits_{a = 1}^{l - 1} 2^{a + 1} \frac{{\sqrt {\left( {l + a} \right)\left( {l + a + 1} \right)} }}{{\left( {2l + 2a + 1} \right)}} + r2^{l + 1} \frac{{\sqrt {4l^{2} + 2l} }}{4l + 1} + 2r\frac{{\sqrt {\left( {l + 1} \right)\left( {l + 2} \right)} }}{2l + 3} \\ & \quad + \left( {r - 1} \right)\left( {2^{l + 1} - 2} \right) + 2^{l} + r; \\ \end{aligned} $$
$$ \begin{aligned} & Zg_{4} \left( {HT\left( l \right) \odot P_{r} } \right) \\ & = 3 \times \left( {2l + 2} \right) + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)\left( {2l + 2a + 1} \right) + r \times 2^{l} \left( {4l + 1} \right) + r\left( {2l + 3} \right) \\ & \quad + (r - 1)\sum_{a=1}^{l}2^{a} (2l + 2a + 2) + \sum_{a=1}^{l-1}2^{a} (2l + 2a + 2) + 2(r - 1)(l + 2) \\ & = 6\left( {l + 1} \right) + \left( {r + 2} \right)\left( {2^{l} \left( {4l - 3} \right) - 4l + 2} \right) + 2^{l} \left( r \right)\left( {4l + 1} \right) + r\left( {2l + 3} \right) \\ & \quad - (2r - 2)(2l - 4l2^{l} ) + 2^{(l + 1)} (2l - 1) - 4l + 2(r - 1)(l + 2); \\ \end{aligned} $$
$$ \begin{aligned} {{\Pi }}_{4}^{*} \left( {HT\left( l \right) \odot P_{r} } \right) & = \left( {2l + 2} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) + 1} \right)^{{2^{a} \left( {2 + r} \right)}} \times \left( {4l + 1} \right)^{{r \times 2^{l} }} \times \left( {2l + 3} \right)^{r} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l} \left( {2\left( {l + a} \right) + 2} \right)^{{2^{a} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) + 2} \right)^{{2^{a} }} \left( {2l + 4} \right)^{r - 1} \\ & = \left( {2l + 2} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) + 1} \right)^{{2^{a} \left( {2 + r} \right)}} \times \left( {4l + 1} \right)^{{r2^{l} }} \times \left( {2l + 3} \right)^{r} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l} \left( {2\left( {l + a} \right) + 2} \right)^{{2^{a} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {2\left( {l + a} \right) + 2} \right)^{{2^{a} }} \times \left( {2l + 4} \right)^{r - 1} ; \\ \end{aligned} $$
$$ \begin{aligned} Zg_{6} \left( {HT\left( l \right) \odot P_{r} } \right) & = 3\left( {l + 1} \right)^{2} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)\left( {l + a} \right)\left( {l + a + 1} \right) + r \times 2^{l} \times 2l\left( {2l + 1} \right) + r \\ & \quad \times \left( {l + 1} \right) \times \left( {l + 2} \right) + \left( {r - 1} \right)\mathop \sum \limits_{a = 1}^{l} 2^{a} \left( {l + a + 1} \right)^{2} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {l + a + 1} \right)^{2} + \left( {r - 1} \right)\left( {l + 2} \right)^{2} \\ & = 3\left( {l + 1} \right)^{2} + \left( {r + 2} \right)\left( {2l + 2 \times 2^{l} \left( {2l^{2} - 3l + 2} \right) - 2l^{2} - 4} \right) + 2^{l} r\left( {4l^{2} + 2l} \right) \\ & \quad + r\left( {l + 1} \right)\left( {l + 2} \right) + \left( {r - 1} \right)\left( {4 \times 2^{l} - 2l^{2} + 8 \times 2^{l} l^{2} - 4} \right) + 2^{l} \left( {4l^{2} - 4l + 3} \right) - 2l^{2} \\ & \quad - 4 + \left( {r - 1} \right)\left( {l + 2} \right)^{2} ; \\ \end{aligned} $$
$$ \begin{aligned} {{\Pi }}_{6}^{*} \left( {HT\left( l \right) \odot P_{r} } \right) & = \left( {l + 1} \right)^{6} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\left( {l + a} \right)^{2} + l + a} \right)^{{2^{a} \left( {2 + r} \right)}} \\ & \quad \times \left( {\left( {2l} \right)^{2} + 2l} \right)^{{r \times 2^{l} }} \times \left( {\left( {l + 1} \right)^{2} + \left( {l + 1} \right)} \right)^{r} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l} \left( {l + a + 1} \right)^{{2^{a + 1} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {l + a + 1} \right)^{{2^{a + 1} }} \times \left( {l + 2} \right)^{{2\left( {r - 1} \right)}} \\ & = \left( {l + 1} \right)^{6} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\left( {l + a} \right)^{2} + l + a} \right)^{{2^{a} \left( {2 + r} \right)}} \times \left( {4l^{2} + 2l} \right)^{{r2^{l} }} \times \left( {l^{2} + 3l + 2} \right)^{r} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l} \left( {l + a + 1} \right)^{{2^{a + 1} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {l + a + 1} \right)^{{2^{a + 1} }} \times \left( {l + 2} \right)^{{2\left( {r - 1} \right)}} ; \\ \end{aligned} $$
$$ \begin{aligned} & Zg_{4} \left( {HT\left( l \right) \odot P_{r} , x} \right) \\ & = 3x^{{2\left( {l + 1} \right)}} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)x^{{2\left( {l + a} \right) + 1}} + r2^{l} x^{4l + 1} + rx^{2l + 3} + \left( {r - 1} \right)\mathop \sum \limits_{a = 1}^{l} 2^{a} x^{{2\left( {l + a + 1} \right)}} \\ & \quad + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} x^{{2\left( {l + a + 1} \right)}} + \left( {r - 1} \right)x^{{2\left( {l + 2} \right)}} ; \\ \end{aligned} $$
$$ \begin{aligned} & Zg_{6} \left( {HT\left( l \right) \odot P_{r} , x} \right) \\ & = 3x^{{\left( {l + 1} \right)^{2} }} + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} \left( {2 + r} \right)x^{{\left( {l + a} \right)\left( {l + a + 1} \right)}} + r2^{l} x^{{4l^{2} + 2l}} + rx^{{\left( {l + 1} \right)\left( {l + 2} \right)}} + \left( {r - 1} \right)\mathop \sum \limits_{a = 1}^{l} 2^{a} x^{{\left( {l + a + 1} \right)^{2} }} \\ & \quad + \mathop \sum \limits_{a = 1}^{l - 1} 2^{a} x^{{\left( {l + a + 1} \right)^{2} }} + \left( {r - 1} \right)x^{{\left( {l + 2} \right)^{2} }} ; \\ \end{aligned} $$
$$ \begin{aligned} & ABC_{5} {{\Pi }}\left( {HT\left( l \right) \odot P_{r} } \right) \\ & = \left( {\sqrt {\frac{{2\left( {l + 1} \right) - 2}}{{\left( {l + 1} \right)^{2} }}} } \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{2\left( {l + a} \right) - 1}}{{\left( {l + a} \right)^{2} + l + a}}} \right)^{{2^{a - 1} \left( {2 + r} \right)}} \times \left( {\sqrt {\frac{4l - 1}{{2l\left( {2l + 1} \right)}}} } \right)^{{r\left( {2^{l} } \right)}} \\ & \quad \times \left( {\sqrt {\frac{{2\left( {l + 1} \right) - 1}}{{\left( {l + 1} \right)\left( {l + 2} \right)}}} } \right)^{r} \times \mathop \prod \limits_{a = 1}^{l} \left( {\frac{{\sqrt {2\left( {l + a} \right)} }}{l + a + 1}} \right)^{{2^{a} \left( {r - 1} \right)}} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{\sqrt {2\left( {l + a} \right)} }}{l + a + 1}} \right)^{{2^{a} }} \times \left( {\sqrt {\frac{{2\left( {l + 1} \right)}}{{\left( {l + 2} \right)^{2} }}} } \right)^{{\left( {r - 1} \right)}} \\ & = \left( {\frac{{\sqrt {2l} }}{l + 1}} \right)^{3} \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{2\left( {l + a} \right) - 1}}{{\left( {l + a} \right)^{2} + l + a}}} \right)^{{2^{a - 1} \left( {2 + r} \right)}} \left( {\frac{4l - 1}{{4l^{2} + 2l}}} \right)^{{2^{l - 1} r}} \\ & \quad \times \left( {\sqrt {\frac{2l + 1}{{l^{2} + 3l + 2}}} } \right)^{r} \times \mathop \prod \limits_{a = 1}^{l} \left( {\frac{{\sqrt {2\left( {l + a} \right)} }}{l + a + 1}} \right)^{{2^{a} \left( {r - 1} \right)}} \\ & \quad \times \mathop \prod \limits_{a = 1}^{l - 1} \left( {\frac{{\sqrt {2\left( {l + a} \right)} }}{l + a + 1}} \right)^{{2^{a} }} \times \left( {\frac{{\sqrt {2\left( {l + 1} \right)} }}{l + 2}} \right)^{r - 1} .\;\;\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 5.3

Let \( HT\left( k \right) \odot P_{n} , k,n \ge 2 \) be the corona product of hypertree and a path network on n vertices. Then the atom bond connectivity index

$$ \begin{aligned} ABC\left( {HT\left( k \right) \odot P_{n} } \right) & = \frac{{2^{k - 1} \sqrt {2\left( {n + 1} \right)} }}{n + 2} + \left( {2 + 2^{k} } \right)\sqrt {\frac{2}{n + 4}} + \left( {\left( {2^{k - 1} - 1} \right) + \left( {2^{k} - 4} \right)} \right)\frac{{\sqrt {2n + 6} }}{n + 4} + (2^{k} + 1)\sqrt 2 \\ & \quad + \left( {n - 2} \right)\left( {2^{k} + 1} \right) \sqrt {\frac{n + 3}{{3\left( {n + 2} \right)}}} + \left( {2^{k} - 2} \right)\sqrt 2 + \left( {n - 2} \right)\left( {2^{k} - 2} \right)\sqrt {\frac{n + 5}{{3\left( {n + 4} \right)}}} \\ & \quad + \sqrt {2 } \left( {2^{k + 1} - 1} \right) + \frac{{2\left( {2^{k + 1} - 1} \right)\left( {n - 3} \right)}}{3} \\ \end{aligned} $$

Proof

First, we partition the edge set of \( HT\left( k \right) \odot P_{n} \) as follows:

\( E_{{\left( {n + 2} \right)\left( {n + 2} \right)}} = \bigg\{ {e = uv\in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = d\left( v \right) = n + 2{{\bigg\} }} \;and \;\left| {E_{{\left( {n + 2} \right)\left( {n + 2} \right)}} } \right| = 2^{k - 1} } \).

\( E_{{\left( {n + 2} \right)\left( {n + 4} \right)}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 2 \;and\; d\left( v \right) = n + 4{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 2} \right)\left( {n + 4} \right)}} } \right| = 2 + 2^{k} } \).

\( E_{{\left( {n + 4} \right)\left( {n + 4} \right)}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = d\left( v \right) = n + 4{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 4} \right)\left( {n + 4} \right)}} } \right| = (2^{k - 1} - 1}) + \mathop \sum \limits_{i = 1}^{k - 2} 2^{i + 1} \)

\( E_{{\left( {n + 2} \right)2}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 2\; and\; d\left( v \right) = 2{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 2} \right)2}} } \right| = 2(2^{k} + 1)} \)

\( E_{{\left( {n + 2} \right)3}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 2 \;and \;d\left( v \right) = 3{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 2} \right)3}} } \right| = \left( {n - 2} \right)(2^{k} + 1)} \)

\( E_{{\left( {n + 4} \right)2}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 4 \;and\; d\left( v \right) = 2{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 4} \right)2}} } \right| = \mathop \sum \limits_{i = 1}^{k - 1} 2^{i + 1} }\)

\( E_{{\left( {n + 4} \right)3}} = \bigg\{ {e = uv\in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 4\; and\; d\left( v \right) = 3{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 4} \right)3}} } \right| = \left( {n - 2} \right)\mathop \sum \limits_{i = 1}^{k - 1} 2^{i} } \)

\( E_{23} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = 2\; and\; d\left( v \right) = 3{{\bigg\} }} and \left| {E_{23} } \right| = 2^{k + 2} - 2} \)

\( E_{33} = \bigg\{ {e = uv\in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = d\left( v \right) = 3{{\bigg\} }} \;and\; \left| {E_{33} } \right| = \left( {n - 3} \right)(2^{k + 1} - 1)} \)

By the definition, we have

$$ \begin{aligned} ABC\left( {HT\left( k \right) \odot P_{n} } \right) & = 2^{k - 1} \sqrt {\frac{{\left( {n + 2} \right) + \left( {n + 2} \right) - 2}}{{\left( {n + 2} \right)^{2} }}} + \left( {2 + 2^{k} } \right)\sqrt {\frac{{\left( {n + 2} \right) + \left( {n + 4} \right) - 2}}{{\left( {n + 2} \right).\left( {n + 4} \right)}}} \\ & \quad + \left( {\left( {2^{k - 1} - 1} \right) + \mathop \sum \limits_{i = 1}^{k - 2} 2^{i + 1} } \right)\sqrt {\frac{{\left( {n + 4} \right) + \left( {n + 4} \right) - 2}}{{\left( {n + 4} \right)^{2} }}} + 2\left( {2^{k} + 1} \right)\sqrt {\frac{{\left( {n + 2} \right) + 2 - 2}}{{\left( {n + 2} \right).2}}} \\ & \quad + \left( {n - 2} \right)\left( {2^{k} + 1} \right)\sqrt {\frac{{\left( {n + 2} \right) + 3 - 2}}{{\left( {n + 2} \right).3}}} + \mathop \sum \limits_{i = 1}^{k - 1} 2^{i + 1} \sqrt {\frac{{\left( {n + 4} \right) + 2 - 2}}{{\left( {n + 4} \right).2}}} \\ & \quad + \left( {n - 2} \right)\mathop \sum \limits_{i = 1}^{k - 1} 2^{i} \sqrt {\frac{{\left( {n + 4} \right) + 3 - 2}}{{\left( {n + 4} \right).3}}} + \left( {2^{k + 2} - 2} \right)\sqrt {\frac{2 + 3 - 2}{2.3}} \\ & \quad + \left( {n - 3} \right)\left( {2^{k + 1} - 1} \right)\sqrt {\frac{3 + 3 - 2}{3.3}} \\ & = \frac{{2^{k - 1} \sqrt {2\left( {n + 1} \right)} }}{n + 2} + \left( {2 + 2^{k} } \right)\sqrt {\frac{2}{n + 4}} + \left( {\left( {2^{k - 1} - 1} \right) + \left( {2^{k} - 4} \right)} \right)\frac{{\sqrt {2n + 6} }}{n + 4} \\ & \quad + \left( {2^{k} + 1} \right)\sqrt 2 + \left( {n - 2} \right)\left( {2^{k} + 1} \right) \sqrt {\frac{n + 3}{{3\left( {n + 2} \right)}}} + \left( {2^{k} - 2} \right)\sqrt 2 \\ & \quad + \left( {n - 2} \right)\left( {2^{k} - 2} \right)\sqrt {\frac{n + 5}{{3\left( {n + 4} \right)}}} + \sqrt {2 } \left( {2^{k + 1} - 1} \right) + \frac{{2\left( {2^{k + 1} - 1} \right)\left( {n - 3} \right)}}{3}.\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 5.4

Let \( HT\left( k \right) \odot P_{n} , k,n \ge 2 \) be the corona product of hypertree and a path network on n vertices. Then the first Zagreb index

$$ M_{1} \left( {HT\left( k \right) \odot P_{n} } \right) = 30n 2^{k} - 21n - n^{2} + 2n^{2} 2^{k} - 18. $$

Proof

First, we partition the vertex set of \( HT\left( k \right) \odot P_{n} \) as follows:

\( P_{1} = \left\{ {v | d\left( v \right) = \left( {n + 2} \right){{\} }}\; and\; \left| {P_{1} } \right| = 2^{k} + 1} \right. \)

\( P_{2} = \left\{ {v | d\left( v \right) = \left( {n + 4} \right){{\} }} \;and\; \left| {P_{2} } \right| = 2^{k} - 2} \right. \)

\( P_{3} = \left\{ {v | d\left( v \right) = 2{{\} }}\; and\; \left| {P_{3} } \right| = 4 \times 2^{k} - 2} \right. \)

\( P_{4} = \left\{ {v | d\left( v \right) = 3{{\} }} \;and\; \left| {P_{4} } \right| = \left( {n - 2} \right)(2^{k + 1} - 1} \right.) \)

By the definition, we have

$$ \begin{aligned} M_{1} \left( {HT\left( k \right) \odot P_{n} } \right) & = (2^{k} + 1)\left( {n + 2} \right)^{2} + \left( {2^{k} - 2} \right)\left( {n + 4} \right)^{2} + \left( {4 \times 2^{k} - 2} \right)2^{2} + \left( {n - 2} \right)(2^{k + 1} - 1)3^{2} \\ & = 30n 2^{k} - 21n - n^{2} + 2n^{2} 2^{k} - 18.\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Theorem 5.5

Let \( HT\left( k \right) \odot P_{n} , k,n \ge 2 \) be the corona product of hypertree and a path network on n vertices. Then the second Zagreb index

$$ M_{2} \left( {HT\left( k \right) \odot P_{n} } \right) = 52n \times 2^{k} - 53n - 8 \times 2^{k} - 6n^{2} + 9n^{2} 2^{k} - 37. $$

Proof

First, we partition the edge set of \( HT\left( k \right) \odot P_{n} \) as follows:

\( E_{{\left( {n + 2} \right)\left( {n + 2} \right)}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = d\left( v \right) = n + 2{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 2} \right)\left( {n + 2} \right)}} } \right| = 2^{k - 1} }\).

\( E_{{\left( {n + 2} \right)\left( {n + 4} \right)}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 2 \;and\; d\left( v \right) = n + 4{{\bigg\} }}\; and\; \left| {E_{{\left( {n + 2} \right)\left( {n + 4} \right)}} } \right| = 2 + 2^{k} }\).

\( E_{{\left( {n + 4} \right)\left( {n + 4} \right)}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = d\left( v \right) = n + 4{{\bigg\} }}\; and\; \left| {E_{{\left( {n + 4} \right)\left( {n + 4} \right)}} } \right| = (2^{k - 1} - 1}) + \mathop \sum \limits_{i = 1}^{k - 2} 2^{i + 1} \)

\( E_{{\left( {n + 2} \right)2}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 2 \;and\; d\left( v \right) = 2{{\bigg\} }}\; and\; \left| {E_{{\left( {n + 2} \right)2}} } \right| = 2(2^{k} + 1)}\)

\( E_{{\left( {n + 2} \right)3}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 2\; and \;d\left( v \right) = 3{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 2} \right)3}} } \right| = \left( {n - 2} \right)(2^{k} + 1)}\)

\( E_{{\left( {n + 4} \right)2}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 4 \;and\; d\left( v \right) = 2{{\bigg\} }} \;and\; \left| {E_{{\left( {n + 4} \right)2}} } \right| = \mathop \sum \limits_{i = 1}^{k - 1} 2^{i + 1} }\)

\( E_{{\left( {n + 4} \right)3}} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = n + 4 \;and\; d\left( v \right) = 3{{\bigg\} }}\; and\; \left| {E_{{\left( {n + 4} \right)3}} } \right| = \left( {n - 2} \right)\mathop \sum \limits_{i = 1}^{k - 1} 2^{i} }\)

\( E_{23} = \bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = 2\; and\; d\left( v \right) = 3{{\bigg\} }}\; and\; \left| {E_{23} } \right| = 2^{k + 2} - 2}\)

\( E_{33} =\bigg\{ {e = uv \in E\left( {HT\left( k \right) \odot P_{n} } \right) | d\left( u \right) = d\left( v \right) = 3{{\bigg\} }} \;and\; \left| {E_{33} } \right| = \left( {n - 3} \right)(2^{k + 1} - 1)}\)

By the definition, we have

$$ \begin{aligned} M_{2} \left( {HT\left( k \right) \odot P_{n} } \right) & = 2^{k - 1} [ {(n + 2) \left( {n + 2} \right)}] + (2 + 2^{k} )[ {(n + 2)(n + 4)} ] + [ {(2^{k - 1} - 1)} \\ & \quad + {\mathop \sum \limits_{i = 1}^{k - 2} 2^{i + 1} }]\left( {n + 4} \right)^{2} + 2(2^{k} + 1)[( n + 2)2] + \left( {n - 2} \right)(2^{k} + 1) \\ & \quad \times[ {\left( {n + 2} \right) \cdot 3} ] + \mathop \sum \limits_{i = 1}^{k - 1} 2^{i + 1} [(n + 4)2] + \left( {n - 2} \right)\mathop \sum \limits_{i = 1}^{k - 1} 2^{i} [ {\left( {n + 4} \right)3} ] \\ & \quad + 6(2^{k + 2} - 2) + 9\left( {n - 3} \right)(2^{k + 1} - 1) \\ & = 52n \times 2^{k} - 53n - 8 \times 2^{k} - 6n^{2} + 9n^{2} 2^{k} - 37.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\square } \\ \end{aligned} $$

Remark 5.6

The results obtained from TopoChemie-2020 are shown in Table 3 for comparison with the results obtained from Theorems 5.2–5.5.

Table 3 Results obtained for the corona product of hypertree and a path network with n vertices \( HT\left( k \right) \odot P_{n} \) with the computer code compared with the results from the expressions in Theorems 5.2–5.5
Full size table

6 Chemical applications and conclusion

The recursive hypertree networks considered in this study could have several applications to chemical problems such as recursive molecular networks that occur in chemical applications, for example, dendrimers [30]. The QSAR studies of dendrimers could then be benefited by the various topological indices derived in this work for hypertrees. Furthermore, recent extension of topological indices to relativistic topological indices considered in [31] could have significant ramifications in the prediction of relativistic chemical properties of complex network of molecular and material systems when heavier atoms such as Pt, Pd and other heavy elements are present [32,33,34,35]. For such systems relativistic effects are quite important [32,33,34,35]. It is anticipated that when the expressions derived here for the topological indices of hypertrees are generalized to encompass such relativistic corrections [32,33,34,35] then the generalized relativistic expressions could have important applications in the prediction of topological properties of dendrimeric metal–organic networks containing very heavy atoms. Moreover, graph products such as the corona products and other products have been recently considered for the computation of Mostar indices of nanomaterials [36], and thus we expect more research along these lines employing graph products in the future.

Biological processes are well interpreted by reliable models for interaction networks. The structure of social networks has to be studied along with the spread of infectious diseases like corona virus [8]. In this paper we have considered certain biochemical networks such as k-level hypertrees and corona product of hypertrees and several topological indices have been obtained for the same.