SpringerLink
Log in

Arrangement rule of stability regions and single-electron transfer in common-gate quadruple-dot devices for the real ratio of gate capacitances

  • Published:
Journal of Computational Electronics Aims and scope Submit manuscript

Abstract

For single-electron transfer in common-gate multidot devices, the arrangement of stability regions along the gate voltage (Vg) axis is important because single-electron transfer occurs around the overlap of stability regions. The stability regions along the Vg axis are well known to have periodicity when the device has an integer ratio of gate capacitances (Cg). However, the arrangement rule for the real Cg ratio is unclear. In this paper, stability regions for quadruple-dot devices with symmetric Cg are exhaustively examined. The arrangement of stability regions along the Vg axis is drawn as a map of the real Cg ratio in a newly proposed diagram. Here, the arrangement for a particular Cg ratio is drawn along a straight line that passes through the origin and has a slope depending on the Cg ratio. In the diagram, stability regions are arranged two-dimensionally, and the abovementioned periodicity for integer Cg ratios clearly appears. How neighboring stability regions interrelate with each other in the diagram is mathematically examined and described in detail. Next, the sequences of tunneling events around the overlap of stability regions are investigated, and eight kinds of tunneling sequences for single-electron transfer are determined.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Germany)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data availability

This paper has no associated dataset.

Notes

  1. Energies such as the charging energy and thermal energy can also be normalized by a standard energy e2/Cgt. The thermal effect on CB is unchanged if the temperature and Cgt are changed such that the normalized thermal energy E’th is kept constant, that is, the thermal energy Eth is inversely proportional to Cgt.

References

  1. Likharev, K.K.: Single-electron transistors: electrostatic analogs of the DC SQUIDS. IEEE Trans. Magn. 23, 1142–1145 (1987)

    Article  ADS  Google Scholar 

  2. Geerligs, L.J., Anderegg, V.F., Holweg, P.A.M., Mooij, J.E., Pothier, H., Esteve, D., Urbina, C., Devoret, M.H.: Frequency-locked turnstile device for single electrons. Phys. Rev. Lett. 64, 2691–2694 (1990)

    Article  ADS  CAS  PubMed  Google Scholar 

  3. Pothier, H., Lafarge, P., Urbina, C., Esteve, D., Devoret, M.H.: Single-electron pump based on charging effects. Europhys. Lett. 17, 249–254 (1992)

    Article  ADS  Google Scholar 

  4. Kouwenhoven, L.P., Johnson, A.T., van der Vaart, N.C., Harmans, C.J.P.M., Foxon, C.T.: Quantized current in a quantum-dot turnstile using oscillating tunnel barriers. Phys. Rev. Lett. 67, 1626–1629 (1991)

    Article  ADS  CAS  PubMed  Google Scholar 

  5. Yano, K., Ishii, T., Hashimoto, T., Kobayashi, T., Murai, F., Seki, K.: Room-temperature single-electron memory. IEEE Trans. Electron Devices 41, 1628–1638 (1994)

    Article  ADS  Google Scholar 

  6. Takahashi, Y., Namatsu, H., Kurihara, K., Iwadate, K., Nagase, M., Murase, K.: Size dependence of the characteristics of Si single-electron transistors on SIMOX Substrates. IEEE Trans. Electron Devices 43, 1213–1217 (1996)

    Article  ADS  CAS  Google Scholar 

  7. Ishikuro, H., Fujii, T., Saraya, T., Hashiguchi, G., Hiramoto, T., Ikoma, T.: Coulomb blockade oscillations at room temperature in a Si quantum wire metal-oxide-semiconductor field-effect transistor fabricated by anisotropic etching on a silicon-on-insulator substrate. Appl. Phys. Lett. 68, 3585–3587 (1996)

    Article  ADS  CAS  Google Scholar 

  8. Pashkin, Y.A., Nakamura, Y., Tsai, J.S.: Room-temperature Al single-electron transistor made by electron-beam lithography. Appl. Phys. Lett. 76, 2256–2258 (2000)

    Article  ADS  CAS  Google Scholar 

  9. Saitoh, M., Takahashi, N., Ishikuro, H., Hiramoto, T.: Large electron addition energy above 250 meV in a silicon quantum dot in a single-electron transistor. Jpn. J. Appl. Phys.. J. Appl. Phys. 40, 2010–2012 (2001)

    Article  ADS  CAS  Google Scholar 

  10. Waugh, F.R., Berry, M.J., Crouch, C.H., Livermore, C., Mar, D.J., Westervelt, R.M., Campman, K.L., Gossard, A.C.: Measuring interactions between tunnel-coupled quantum dots. Phys. Rev. B 53, 1413–1420 (1996)

    Article  ADS  CAS  Google Scholar 

  11. Nuryadi, R., Ikeda, H., Ishikawa, Y., Tabe, M.: Ambipolar Coulomb blockade characteristics in a two-dimensional Si multidot device. IEEE Trans. Nanotechnol. 2, 231–235 (2003)

    Article  ADS  Google Scholar 

  12. Nuryadi, R., Ikeda, H., Ishikawa, Y., Tabe, M.: Current fluctuation in single-hole transport through a two-dimensional Si multidot. Appl. Phys. Lett. 86, 133106 (2005)

    Article  ADS  Google Scholar 

  13. Gyakushi, T., Asai, Y., Tsurumaki-Fukuchi, A., Arita, M., Takahashi, Y.: Periodic Coulomb blockade oscillations observed in single-layered Fe nanodot array. Thin Solid Films 704, 138012 (2020)

    Article  ADS  CAS  Google Scholar 

  14. Nakazato, K., Blaikle, R.J., Ahmed, H.: Single-electron memory. J. Appl. Phys. 75, 5123–5134 (1994)

    Article  ADS  CAS  Google Scholar 

  15. Ikeda, H., Tabe, M.: Numerical study of turnstile operation in random-multidot-channel field-effect transistor. J. Appl. Phys. 99, 073705 (2006)

    Article  ADS  Google Scholar 

  16. Moraru, D., Ono, Y., Inokawa, H., Tabe, M.: Quantized electron transfer through random multiple tunnel junctions in phosphorus-doped silicon nanowires. Phys. Rev. B 76, 075332 (2007)

    Article  ADS  Google Scholar 

  17. Yokoi, K., Moraru, D., Ligowski, M., Tabe, M.: Single-gated single-electron transfer in nonuniform arrays of quantum dots. Jpn. J. Appl. Phys. 48, 024503 (2009)

    Article  ADS  Google Scholar 

  18. Jo, M., Uchida, T., Tsurumaki-Fukuchi, A., Arita, M., Fujiwara, A., Ono, Y., Nishiguchi, K., Inokawa, H., Takahashi, Y.: Fabrication and single-electron-transfer operation of a triple-dot single-electron transistor. J. Appl. Phys. 118, 214305 (2015)

    Article  ADS  Google Scholar 

  19. Azuma, Y., Yasutake, Y., Kono, K., Kanehara, M., Teranishi, T., Majima, Y.: Single-electron transistor fabricated by two bottom-up processes of electroless Au plating and chemisorption of Au nanoparticle. Jpn. J. Appl. Phys. 49, 090206 (2010)

    Article  ADS  Google Scholar 

  20. Okabayashi, N., Maeda, K., Muraki, T., Tanaka, D., Sakamoto, M., Teranishi, T., Majima, Y.: Uniform charging energy of single-electron transistors by using size-controlled Au nanoparticles. Appl. Phys. Lett. 100, 033101 (2012)

    Article  ADS  Google Scholar 

  21. Kano, S., Maeda, K., Tanaka, D., Sakamoto, M., Haranishi, T., Majima, Y.: Chemically assembled double-dot single-electron transistor analyzed by the orthodox model considering offset charge. J. Appl. Phys. 118, 134304 (2015)

    Article  ADS  Google Scholar 

  22. Urbina, C., Pothier, H., Lafarge, P., Orfila, P.F., Esteve, D., Devoret, M., Geerligs, L.J., Anderegg, V.F., Holweg, P.A.M., Mooij, J.E.: Controlled transfer of single charge carriers. IEEE Trans. Magn. 27, 2578–2580 (1987)

    Article  ADS  Google Scholar 

  23. Esteve, D.: Chap 3. In: Grabert, H., Devoret, M.H. (eds.) Single Charge Tunneling: Coulomb Blockade Phenomena in Nanostructures, pp. 109–137. Plenum, New York (1992)

    Chapter  Google Scholar 

  24. Imai, S., Moriguchi, S.: Single-common-gate triple-dot single-electron devices with side gate capacitances larger than the central one. Jpn. J. Appl. Phys. 53, 094002 (2014)

    Article  ADS  Google Scholar 

  25. Imai, S., Ito, M.: Anomalous single-electron transfer in common-gate quadruple-dot single-electron devices with asymmetric junction capacitances. Jpn. J. Appl. Phys. 57, 064001 (2018)

    Article  ADS  Google Scholar 

  26. Devoret, M.H., Grabert, H.: Chap 1. In: Grabert, H., Devoret, M.H. (eds.) Single Charge Tunneling: Coulomb Blockade Phenomena in Nanostructures, pp. 1–19. Plenum, New York (1992)

    Google Scholar 

  27. Yokoi, K., Moraru, D., Mizuno, T., Tabe, M.: Electrical control of capacitance dispersion for single-electron turnstile operation in common-gated junction arrays. J. Appl. Phys. 108, 053710 (2010)

    Article  ADS  Google Scholar 

  28. Imai, S., Ito, Y.: Single-electron pum** in single-common-gate quadruple-dot devices with asymmetric gate capacitances. Jpn. J. Appl. Phys. 58, 034001 (2019)

    Article  ADS  CAS  Google Scholar 

  29. Imai, S., Kato, H., Hiraoka, Y.: Stability diagrams of single-common-gate double-dot single-electron transistors with arbitrary junction and gate capacitances. Jpn. J. Appl. Phys. 51, 124301 (2012)

    Article  ADS  Google Scholar 

  30. Imai, S., Kawamura, D.: Analytical study on a single-electron device with three islands connected to one gate electrode. Jpn. J. Appl. Phys. 48, 124502 (2009)

    Article  ADS  Google Scholar 

  31. Imai, S.: Stability diagrams of triple-dot single-electron device with single common gate. Jpn. J. Appl. Phys. 50, 034302 (2011)

    Article  ADS  Google Scholar 

Download references

Funding

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

Author information

Authors and Affiliations

  1. Department of Electrical and Electronic Engineering, Ritsumeikan University, Kusatsu, Shiga, 525-8577, Japan

    Shigeru Imai & Yusuke Watanabe

Authors
  1. Shigeru Imai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yusuke Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the study conception and design. Analysis were performed by Shigeru Imai and Yusuke Watanabe. The first draft of the manuscript was written by Shigeru Imai, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Shigeru Imai.

Ethics declarations

Competing interests

The authors have no relevant financial or nonfinancial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

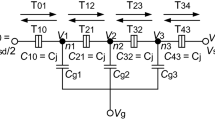
The general formulas of the CB conditions as linear inequalities of Vsd, Vg, and n1 to n4 are described in Appendices A and B of Ref. [25]. In this paper, the junction capacitances are uniform and have a value of Cj. The outer and inner gate capacitances are equal to Cgs and Cgc, respectively. The bias voltages are V0 = −Vsd/2 and V4 = Vsd/2. Then, the formulas are rewritten as follows:

The left side of Eq. (1) is presented as follows:

$$C_{{{\text{T}}10}} (V_{1} - V_{{0}} ) = Q_{1} + r_{{{\kern 1pt} {\text{3S}}}} \left\{ {Q_{2} + r_{{{\kern 1pt} {\text{2S}}}} \left( {Q_{3} + r_{{{\text{1S}}}} Q_{4} } \right)} \right\} + C_{{{\text{T}}10}} \frac{{V_{{{\text{sd}}}} }}{2},$$
(15)
$$C_{{{\text{T}}21}} (V_{2} - V_{{1}} ) = - r_{{{\kern 1pt} {\text{S3}}}} Q_{1} + r_{{{\kern 1pt} {\text{S1}}}} \left\{ {Q_{2} + r_{{{\kern 1pt} 2{\text{S}}}} \left( {Q_{3} + r_{{{\kern 1pt} {\text{1S}}}} Q_{4} } \right)} \right\},$$
(16)
$$C_{{{\text{T3}}2}} (V_{3} - V_{{2}} ) = r_{{{\kern 1pt} {\text{S2}}}} \left( { - r_{{{\kern 1pt} {\text{1S}}}} Q_{1} - Q_{2} + Q_{3} + r_{{{\kern 1pt} {\text{1S}}}} Q_{4} } \right),$$
(17)
$$C_{{{\text{T43}}}} (V_{{4}} - V_{{3}} ) = - r_{{{\kern 1pt} {\text{S1}}}} \left\{ {r_{{{\kern 1pt} {\text{2S}}}} \left( {r_{{{\kern 1pt} {\text{1S}}}} Q_{1} + Q_{2} } \right) + Q_{3} } \right\} + r_{{{\kern 1pt} {\text{S3}}}} Q_{4} ,$$
(18)
$$C_{{{\text{T54}}}} (V_{{5}} - V_{{4}} ) = C_{{{\text{T54}}}} \frac{{V_{{{\text{sd}}}} }}{2} - r_{{{\kern 1pt} 3{\text{S}}}} \left\{ {r_{{{\kern 1pt} {\text{2S}}}} \left( {r_{{{\kern 1pt} {\text{1S}}}} Q_{1} + Q_{2} } \right) + Q_{3} } \right\} - Q_{4} .$$
(19)

Here, Q1, Q2, Q3, and Q4 are defined as follows:

$$Q_{{{\kern 1pt} 1}} = - n_{1} e - C_{{\text{j}}} \frac{{V_{{{\text{sd}}}} }}{2} + C_{{{\text{gs}}}} V_{{\text{g}}} ,$$
(20)
$$Q_{{{\kern 1pt} 2}} = - n_{2} e + C_{{{\text{gc}}}} V_{{\text{g}}} ,$$
(21)
$$Q_{{{\kern 1pt} 3}} = - n_{3} e + C_{{{\text{gc}}}} V_{{\text{g}}} ,$$
(22)
$$Q_{{{\kern 1pt} 4}} = - n_{4} e + C_{{\text{j}}} \frac{{V_{{{\text{sd}}}} }}{2} + C_{{{\text{gs}}}} V_{{\text{g}}} .$$
(23)

The total capacitances are presented as follows, although CT21, CT32, and CT43 are not used in the right-hand sides of Eqs. (16), (17), and (18).

$$C_{{{\text{T}}10}} = C_{{{\text{T54}}}} = \frac{{C_{{{\text{Sg1}}}} C_{{\text{j}}} + C_{{{\text{Sg1}}}} C_{{{\text{Sg3}}}} + C_{{\text{j}}} C_{{{\text{Sg3}}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg3}}}} }},$$
(24)
$$C_{{{\text{T21}}}} = C_{{{\text{T43}}}} = \frac{{C_{{\text{j}}} C_{{{\text{Sg1}}}} + C_{{\text{j}}} C_{{{\text{Sg3}}}} + C_{{{\text{Sg1}}}} C_{{{\text{Sg3}}}} }}{{C_{{{\text{Sg1}}}} + C_{{{\text{Sg3}}}} }}.$$
(25)
$$C_{{{\text{T32}}}} = \frac{{2C_{{\text{j}}} + C_{{{\text{Sg2}}}} }}{2}.$$
(26)

By substituting Eqs. (20)–(24) into Eqs. (15)–(19), the total effective charges are expressed as linear combinations of Vsd, Vg, and n1 to n4. The coefficients in Eqs. (15)–(19) are presented as follows:

$$r_{{{\kern 1pt} 1{\text{S}}}} = \frac{{C_{{\text{j}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg1}}}} }},\quad r_{{{\kern 1pt} 2{\text{S}}}} = \frac{{C_{{\text{j}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg2}}}} }},\quad r_{{{\kern 1pt} 3{\text{S}}}} = \frac{{C_{{\text{j}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg3}}}} }},\quad$$

\(r_{{{\kern 1pt} {\text{S1}}}} = \frac{{C_{{{\text{Sg1}}}} }}{{C_{{{\text{Sg1}}}} + C_{{{\text{Sg3}}}} }},\quad r_{{{\kern 1pt} {\text{S2}}}} = \frac{{C_{{{\text{Sg2}}}} }}{{C_{{{\text{Sg2}}}} + C_{{{\text{Sg2}}}} }} = \frac{1}{2},\quad r_{{{\kern 1pt} {\text{S3}}}} = \frac{{C_{{{\text{Sg3}}}} }}{{C_{{{\text{Sg3}}}} + C_{{{\text{Sg1}}}} }}.\)

The capacitances CSgi (i = 1–4) in the coefficients are defined as follows, although CSg4 is not used in this paper.

$$C_{{{\text{Sg1}}}} = C_{{{\text{gs}}}} + C_{{\text{j}}} ,C_{{{\text{Sg2}}}} = C_{{{\text{gc}}}} + \frac{{C_{{\text{j}}} C_{{{\text{Sg1}}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg1}}}} }},$$
$$C_{{{\text{Sg3}}}} = C_{{{\text{gc}}}} + \frac{{C_{{\text{j}}} C_{{{\text{Sg2}}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg2}}}} }},C_{{{\text{Sg4}}}} = C_{{{\text{gs}}}} + \frac{{C_{{\text{j}}} C_{{{\text{Sg3}}}} }}{{C_{{\text{j}}} + C_{{{\text{Sg3}}}} }}.$$

Note that r21R, r32R, r43R, r21L, r32L, r43L, rR21, rR32, rR43, rL12, rL23, and rL34 in Ref. [25] correspond to r3S, r2S, r1S, r1S, r2S, r3S, rS3, rS2, rS1, rS1, rS2, and rS3, respectively. Additionally, CLgi and CRgi in Ref. [25] correspond to CSgi and CSg(5-i), respectively.

Appendix 2

Assume that the bias voltage Vsd = 0. Charges Q1, Q2, Q3, and Q4 can be rewritten by using V′g and V′r as follows because CgtVg = V′g e and 2CgcVg = V′r e:

$$Q_{{{\kern 1pt} 1}} = - n_{1} e + \frac{{C_{{{\text{gt}}}} - 2C_{{{\text{gc}}}} }}{2}V_{{\text{g}}} = \left( { - n_{1} + \frac{{V^{\prime}_{{\text{g}}} }}{2} - \frac{{V^{\prime}_{r} }}{2}} \right)e,$$
(27)
$$Q_{{{\kern 1pt} 2}} = \left( { - n_{2} + \frac{{V^{\prime}_{r} }}{2}} \right)e,$$
(28)
$$Q_{{{\kern 1pt} 3}} = \left( { - n_{3} + \frac{{V^{\prime}_{r} }}{2}} \right)e,$$
(29)
$$Q_{{{\kern 1pt} 4}} = - n_{4} e + \frac{{C_{{{\text{gt}}}} - 2C_{{{\text{gc}}}} }}{2}V_{{\text{g}}} = \left( { - n_{4} + \frac{{V^{\prime}_{{\text{g}}} }}{2} - \frac{{V^{\prime}_{r} }}{2}} \right)e.$$
(30)

Then, the effective total charges in Eqs. (15)–(19) are rewritten as follows:

$$\begin{gathered} C_{{{\text{T}}10}} (V_{1} - V_{{0}} ) = Q_{1} + r_{{{\kern 1pt} {\text{3S}}}} Q_{{2}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} Q_{{3}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} Q_{{4}} \hfill \\ = \frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {Q_{1} + Q_{{2}} + Q_{{3}} + Q_{{4}} } \right) - \left( {\frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2} - \frac{{r_{{{\kern 1pt} {\text{3S}}}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}} \right)\left( {Q_{{2}} + Q_{{3}} } \right) \hfill \\ \quad + \frac{{1 - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {Q_{1} - Q_{{4}} } \right) + \frac{{r_{{{\kern 1pt} {\text{3S}}}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {Q_{{2}} - Q_{{3}} } \right) \hfill \\ = \frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right)e - \left( {\frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2} - \frac{{r_{{{\kern 1pt} {\text{3S}}}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}} \right)\left( {V^{\prime}_{r} - n_{23} } \right)e \hfill \\ \quad + \frac{{1 - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {n_{4} - n_{1} } \right)e + \frac{{r_{{{\kern 1pt} {\text{3S}}}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {n_{3} - n_{2} } \right)e \hfill \\ \end{gathered}$$
$$= \left\{ {c_{1} \left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right) - c_{2} \left( {V^{\prime}_{r} - n_{23} } \right) + \left( {1 - c_{1} } \right)\left( {n_{4} - n_{1} } \right) + c_{3} \left( {n_{3} - n_{2} } \right)} \right\}e,$$
(31)
$$\begin{gathered} C_{{{\text{T}}21}} (V_{2} - V_{{1}} ) = - r_{{{\kern 1pt} {\text{S3}}}} Q_{1} + r_{{{\kern 1pt} {\text{S1}}}} Q_{2} + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} Q_{3} + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} Q_{4} \hfill \\ = - \frac{{r_{{{\kern 1pt} {\text{S3}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {Q_{1} + Q_{2} + Q_{3} + Q_{4} } \right) + \left( {\frac{{1 + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}} \right)\left( {Q_{2} + Q_{3} } \right) \hfill \\ - \frac{{r_{{{\kern 1pt} {\text{S3}}}} + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {Q_{1} - Q_{4} } \right) + \frac{{r_{{{\kern 1pt} {\text{S1}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {Q_{2} - Q_{3} } \right) \hfill \\ = - \frac{{r_{{{\kern 1pt} {\text{S3}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right)e + \left( {\frac{{1 + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}} \right)\left( {V^{\prime}_{r} - n_{23} } \right)e \hfill \\ - \frac{{r_{{{\kern 1pt} {\text{S3}}}} + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {n_{4} - n_{1} } \right)e + \frac{{r_{{{\kern 1pt} {\text{S1}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {n_{3} - n_{2} } \right) \hfill \\ \end{gathered}$$
$$= \left\{ { - c_{4} \left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right) + c_{5} \left( {V^{\prime}_{r} - n_{23} } \right) - \left( {1 - c_{5} - c_{6} } \right)\left( {n_{4} - n_{1} } \right) + c_{6} \left( {n_{3} - n_{2} } \right)} \right\}e,$$
(32)
$$\begin{gathered} C_{{{\text{T3}}2}} (V_{3} - V_{{2}} ) = r_{{{\kern 1pt} {\text{S2}}}} r_{{{\kern 1pt} {\text{1S}}}} Q_{4} + r_{{{\kern 1pt} {\text{S2}}}} Q_{3} - r_{{{\kern 1pt} {\text{S2}}}} Q_{2} - r_{{{\kern 1pt} {\text{S2}}}} r_{{{\kern 1pt} {\text{1S}}}} Q_{1} \hfill \\ = - r_{{{\kern 1pt} {\text{S2}}}} r_{{{\kern 1pt} {\text{1S}}}} \left( {Q_{1} - Q_{4} } \right) - r_{{{\kern 1pt} {\text{S2}}}} \left( {Q_{2} - Q_{3} } \right) \hfill \\ = - r_{{{\kern 1pt} {\text{S2}}}} r_{{{\kern 1pt} {\text{1S}}}} \left( {n_{4} - n_{1} } \right)e - r_{{{\kern 1pt} {\text{S2}}}} \left( {n_{3} - n_{2} } \right)e \hfill \\ = - \frac{{r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {n_{4} - n_{1} } \right)e - \frac{1}{2}\left( {n_{3} - n_{2} } \right)e \hfill \\ \end{gathered}$$
$$= \left\{ { - c_{7} \left( {n_{4} - n_{1} } \right) - \frac{1}{2}\left( {n_{3} - n_{2} } \right)} \right\}e,$$
(33)
$$\begin{gathered} C_{{{\text{T43}}}} (V_{4} - V_{{3}} ) = r_{{{\kern 1pt} {\text{S3}}}} Q_{4} - r_{{{\kern 1pt} {\text{S1}}}} Q_{3} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} Q_{2} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} Q_{1} \hfill \\ = \frac{{r_{{{\kern 1pt} {\text{S3}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {Q_{4} + Q_{3} + Q_{2} + Q_{1} } \right) - \left( {\frac{{1 + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}} \right)\left( {Q_{3} + Q_{2} } \right) \hfill \\ - \frac{{r_{{{\kern 1pt} {\text{S3}}}} + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {Q_{1} - Q_{4} } \right) + \frac{{r_{{{\kern 1pt} {\text{S1}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {Q_{2} - Q_{3} } \right) \hfill \\ = \frac{{r_{{{\kern 1pt} {\text{S3}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right)e - \left( {\frac{{1 + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}} \right)\left( {V^{\prime}_{r} - n_{23} } \right)e \hfill \\ - \frac{{r_{{{\kern 1pt} {\text{S3}}}} + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2}\left( {n_{4} - n_{1} } \right)e + \frac{{r_{{{\kern 1pt} {\text{S1}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {n_{3} - n_{2} } \right)e \hfill \\ \end{gathered}$$
$$= \left\{ {c_{4} \left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right) - c_{5} \left( {V^{\prime}_{r} - n_{23} } \right) - \left( {1 - c_{5} - c_{6} } \right)\left( {n_{4} - n_{1} } \right) + c_{6} \left( {n_{3} - n_{2} } \right)} \right\}e,$$
(34)
$$\begin{gathered} C_{{{\text{T54}}}} (V_{{5}} - V_{{4}} ) = - Q_{4} - r_{{{\kern 1pt} {\text{3S}}}} Q_{{3}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} Q_{{2}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} Q_{{1}} \hfill \\ = - \frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {Q_{4} + Q_{3} + Q_{{2}} + Q_{{1}} } \right) + \left( {\frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2} - \frac{{r_{{{\kern 1pt} {\text{3S}}}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}} \right)\left( {Q_{{3}} + Q_{{2}} } \right) \hfill \\ \quad + \frac{{1 - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {Q_{1} - Q_{{4}} } \right) + \frac{{r_{{{\kern 1pt} {\text{3S}}}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {Q_{{2}} - Q_{{3}} } \right) \hfill \\ = - \frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right)e + \left( {\frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2} - \frac{{r_{{{\kern 1pt} {\text{3S}}}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}} \right)\left( {V^{\prime}_{r} - n_{23} } \right)e \hfill \\ \quad + \frac{{1 - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2}\left( {n_{4} - n_{1} } \right)e + \frac{{r_{{{\kern 1pt} {\text{3S}}}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2}\left( {n_{3} - n_{2} } \right)e \hfill \\ \end{gathered}$$
$$= \left\{ { - c_{1} \left( {V^{\prime}_{{\text{g}}} - n_{{\text{t}}} } \right) + c_{2} \left( {V^{\prime}_{r} - n_{23} } \right) + \left( {1 - c_{1} } \right)\left( {n_{4} - n_{1} } \right) + c_{3} \left( {n_{3} - n_{2} } \right)} \right\}e.$$
(35)

Here, rS1 + rS3 = 1 and rS2 = 1/2 are used to derive Eqs. (32), (33), and (34). The coefficients are presented by using rc as follows:

$$c_{1} = \frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2} = \frac{{\left( {2 + r_{{\text{c}}} } \right)\left( {26 - r_{{\text{c}}} - r_{c}^{2} } \right)}}{{2\left( {44 + 24r_{{\text{c}}} - 3r_{c}^{2} - r_{c}^{3} } \right)}},$$

\(c_{2} = \frac{{1 + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\text{1S}}}} }}{2} - \frac{{r_{{{\kern 1pt} {\text{3S}}}} + r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2} = \frac{{\left( {26 - r_{{\text{c}}} - r_{c}^{2} } \right)r_{{\text{c}}} }}{{2\left( {44 + 24r_{{\text{c}}} - 3r_{c}^{2} - r_{c}^{3} } \right)}},\)

$$c_{3} = \frac{{r_{{{\kern 1pt} {\text{3S}}}} - r_{{{\kern 1pt} {\text{3S}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2} = \frac{{6 + 3r_{{\text{c}}} - r_{c}^{2} }}{{44 + 24r_{{\text{c}}} - 3r_{c}^{2} - r_{c}^{3} }},$$

\(c_{4} = \frac{{r_{{{\kern 1pt} {\text{S3}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2} = \frac{{\left( {26 - r_{{\text{c}}} - r_{{\text{c}}}^{2} } \right)r_{{\text{c}}} }}{{2\left( {60 + 9r_{{\text{c}}} - 5r_{{\text{c}}}^{2} } \right)}},\)

$$c_{5} = \frac{{1 + r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} r_{{{\kern 1pt} {\text{1S}}}} }}{2} = \frac{{3\left( {26 - r_{{\text{c}}} - r_{{\text{c}}}^{2} } \right)}}{{2\left( {60 + 9r_{{\text{c}}} - 5r_{{\text{c}}}^{2} } \right)}},$$

\(c_{6} = \frac{{r_{{{\kern 1pt} {\text{S1}}}} - r_{{{\kern 1pt} {\text{S1}}}} r_{{{\kern 1pt} {\text{2S}}}} }}{2} = \frac{{\left( {3 - r_{{\text{c}}} } \right)\left( {6 + 3r_{{\text{c}}} - r_{{\text{c}}}^{2} } \right)}}{{2\left( {60 + 9r_{{\text{c}}} - 5r_{{\text{c}}}^{2} } \right)}},\)

$$c_{7} = \frac{{r_{{{\kern 1pt} {\text{1S}}}} }}{2} = \frac{1}{{5 - r_{{\text{c}}} }}.$$

Equation (33) shows that CT32(V3 − V2) is independent of V′g and V′r, and therefore, only the electron state n determines whether the CB conditions CB23 and CB32 are satisfied at V′sd = 0. When CB23 and CB32 are satisfied at V′sd = 0, the SRR and TSRR exist, and the boundary lines bk(k + 1) and b(k + 1)k for k = 0, 1, 3, and 4 are expressed as follows:

$$b_{{k(k + { 1})}} :C_{{{\text{T}}\left( {k + 1} \right)k}} \left( {V_{{\left( {k + 1} \right)}} - V_{k} } \right) = \frac{e}{2}.$$
(36)
$$b_{{(k + { 1})k}} : - C_{{{\text{T}}k\left( {k + 1} \right)}} \left( {V_{k} - V_{{\left( {k + 1} \right)}} } \right) = C_{{{\text{T}}\left( {k + 1} \right)k}} \left( {V_{{\left( {k + 1} \right)}} - V_{k} } \right) = - \frac{e}{2}.$$
(37)

By substituting Eqs. (31)–(35) into Eqs. (36) and (37), Eqs. (7)–(14) are obtained.

For example, when n1 = n4 and n2 = n3, CB23 and CB32 are satisfied because CT32(V3 − V2) = 0. Then, CT10(V1 − V0) =  −CT54(V5 − V4) and CT21(V2 − V1) =  −CT43(V4 − V3) are satisfied because the third and fourth terms of Eqs. (31), (32), (34), and (35) are zero. Thus, b01(nA) = b54(nA), b45(nA) = b10(nA), b12(nA) = b43(nA), and b34(nA) = b21(nA) are confirmed, and their expressions have been derived.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Imai, S., Watanabe, Y. Arrangement rule of stability regions and single-electron transfer in common-gate quadruple-dot devices for the real ratio of gate capacitances. J Comput Electron 23, 51–64 (2024). https://doi.org/10.1007/s10825-023-02119-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10825-023-02119-4

Keywords

Search

Navigation