1 Introduction

The 2008 global financial crisis, triggered by the US housing market crash, caused a dramatic fall in the home-ownership rate in housing markets. Following the crisis, large investors, such as private equity firms, institutional investors, and real estate investment trusts, developed a new business type that relies on constructing a portfolio of single-family housing units for rental income purposes. These large investors are especially the biggest buyers in struggling local housing markets where, generally, housing prices increase faster than in healthy housing markets Yilmaz et al. (2023). Consequently, after the sub-prime mortgage crisis, large investors have dominated local housing markets in return for benefiting from the leading edge of rising house prices and the rental income in their portfolio Allen et al. (2018).

Modeling of housing price evolution is an essential research area in the literature on real estate and financial markets. Over the years, numerous modeling approaches have been developed to understand, predict, and forecast housing price evolution. These approaches can be broadly categorized into traditional econometric models, machine learning techniques, and behavioral models. The traditional econometric models are based on economic theory and statistical methods. One widely used approach is the hedonic pricing model, which decomposes the house price into various attributes such as location, size, and amenities. Regression analysis is commonly employed in hedonic models to estimate the impact of each attribute on the housing price (see the review **ao and **ao (2017)). Time-series models like autoregressive integrated moving average (ARIMA) and vector autoregression (VAR) are also used to capture the temporal dynamics of housing prices (e.g., Tse (1997); Chin and Fan (2005); Yilmaz (2020); Crawford and Fratantoni (2003)). With the advent of big data and advancements in computing power, machine learning techniques have gained popularity in housing price modeling. Techniques like decision trees, random forests, support vector machines (SVM), and neural networks are used to analyze vast datasets and identify complex patterns and non-linear relationships affecting housing prices (e.g., Chen et al. (2017a, 2017b); Selim (2009)). These models can handle many variables and interactions, making them suitable for capturing intricate price movements. Behavioral models have introduced new perspectives into housing price modeling by considering the impact of psychological and behavioral factors on housing markets Filatova (2015). Behavioral models aim to incorporate human biases and heuristics into price predictions, enhancing understanding housing market dynamics. Spatial and spatiotemporal models consider the spatial nature of housing markets, and spatial econometrics has emerged as a specialized field. Geographically weighted regression (GWR) and spatial autoregressive models rely on spatial heterogeneity and dependence on housing price changes (e.g., Fotheringham et al. (2015); Huang et al. (2010). Spatio-temporal models further extend these approaches by considering both spatial and temporal aspects to capture the evolution of housing prices over space and time. Hybrid modeling approaches combine elements of different methodologies to exploit their respective strengths (e.g., Pinter et al. (2020); Zhan et al. (2023). For instance, researchers may integrate econometric models with machine learning techniques to harness interpretability and predictive power. Hybrid models aim to comprehensively analyze housing price dynamics, incorporating both macroeconomic factors and micro-level attributes.

Even though many housing price modeling approaches have been developed, it becomes evident that despite advancements in financial theory and sophisticated portfolio optimization methods, there are inherent limitations when making educated investment decisions. Various unpredictable factors, including economic fluctuations, geopolitical events, and local market dynamics, influence housing markets. While valuable in other asset classes, traditional portfolio optimization approaches struggle to capture the complexity and uncertainty that characterize housing markets fully. The illiquidity of real estate assets and the challenges in accurately assessing future house prices further compound the limitations. While educated strategies can mitigate risk, investors must recognize that no algorithm or mathematical model can shield them from housing markets’ inherent volatility and idiosyncrasies. Despite these, housing prices are assumed to follow a geometric Brownian motion in classical calendar times in many studies (e.g., Kau et al. (1993, 1995); Yilmaz and Selcuk-Kestel (2018, 2019); Yilmaz et al. (2023, 2022); Sharp et al. (2009); Azevedo-Pereira et al. (2003)). However, these studies neglect sudden price falls by an unknown factor during crash times. This unknown factor is assumed to be bounded by a known constant. However, the size of the crash, the time, and the number of crashes in a given time horizon are unknown and not included in the stochastic models in a probabilistic way. This framework allows to use the worst-case scenario portfolio optimization approach and apply it to housing markets. This is the first study to apply the worst-case portfolio optimization problem to housing markets, which allows constructing robust and resilient portfolios to extreme market conditions. Large investors can make informed decisions and manage their portfolio risk effectively by considering stress scenarios and utilizing mathematical techniques such as convex optimization and semidefinite programming. This methodology helps us to construct robust and resilient housing portfolios for extreme housing market conditions. More precisely, it can be applied to housing markets for the following purposes:

  • Incorporating stress scenarios: Worst-case portfolio optimization can be used to construct portfolios that can withstand stress scenarios in housing markets. Investors can construct robust and resilient portfolios by considering worst-case scenarios, e.g., a housing market crash or a recession.

  • Minimizing potential losses: The worst-case approach aims to minimize the maximum possible loss a portfolio can incur. This can be achieved in housing markets by constructing portfolios prioritizing downside protection and minimizing potential losses in extreme housing market conditions.

  • Utilizing mathematical techniques: The worst-case portfolio optimization utilizes techniques such as convex optimization and semidefinite programming to compute the worst-case risk and construct optimal portfolios. These techniques can be applied constructing robust and resilient housing portfolios.

  • Managing risk effectively: By incorporating stress scenarios into the optimization process, investors can make educated decisions and manage risk effectively in housing markets. The worst-case portfolio optimization offers a valuable perspective for investors who prioritize downside protection and seek to minimize potential losses in extreme housing market conditions.

Korn and Menkens (2005) propose a new stochastic control approach to determine portfolio processes maximizing worst-case bounds for expected utility from final wealth in the presence of uncertain downward stock price jumps, particularly focusing on crash scenarios. Their analysis considers uncertain yet bounded crash occurrences and adjusts portfolio strategies to accommodate changing market coefficients post-crash, utilizing solutions derived from nonlinear differential equations. This approach offers a novel investment strategy allowing indifference towards crash occurrences by diversifying investments between bonds and stocks. Rebonato and Denev (2014) emphasizes causal explanations over association-based measures like correlations in asset allocation under market distress or specific scenarios. Leveraging insights from choice theory under ambiguity aversion, Rebonato and Denev (2014) employs Bayesian-net methodology to derive stable allocation results, thereby enhancing the robustness of portfolio allocation strategies. Departing from traditional portfolio theories, Bernard et al. (2014) introduce a novel framework that accommodates additional constraints on final wealth in stressed financial markets, aligning with the diverse needs of investors. Their study not only enhances dependence modeling by addressing full dependence between risks but also offers insights into better modeling portfolio losses under partial information, crucial for regulatory assessments like Solvency II. By develo** strategies that mitigate losses without solely focusing on worst-case states,  Bernard et al. (2014) contribute to reducing systemic risk and enhancing diversification in tail-risk scenarios. The worst-case portfolio approach, proposed by Korn and Müller (2022), provides a robust framework for modeling investment decision problems amidst stress scenarios, thereby inherently subjecting resulting portfolios to stress testing. Korn and Müller (2022) establish the efficacy of this approach in addressing severe yet plausible stress scenarios, which can significantly impact the balance sheets and solvency positions of insurance undertakings. Their work demonstrates the existence of a minimum constant portfolio process optimal for multi-stress worst-case problems, alongside a verification theorem delineating conditions on Lagrange multipliers and nonlinear ordinary differential equations essential for constructing optimal worst-case portfolio strategies.

Optimal portfolio allocations for large investors in housing markets under stress scenarios can be designed using various approaches. One approach is the worst-case portfolio approach, which models investment decision problems that include stress scenarios and constructs stress test-prone portfolios Korn and Müller (2022). An alternative approach is to consider the emotional component of investors’ financial goals and incorporate financially efficient anxiety reduction into portfolio theory Sarpong (2019). Additionally, the optimal design of stress scenarios can be achieved by a risk-averse principal who seeks to learn about exposures of agents to risk factors and intervenes if excessive exposures are uncovered Parlatore and Philippon (2022). Furthermore, a customized scenario design based on historical data can be used to determine plausible market changes that would adversely impact portfolio performance Nagpal (2017). Finally, a framework that maintains the stylized features of portfolio theory while considering the goal of security in stressed financial markets can be used to construct optimal strategies for investors Bernard et al. (2014). This study incorporates the worst-case scenario portfolio optimization problem introduced by Korn and Müller (2022) into housing markets. This study departs from previous studies and traditional portfolio theories for housing markets concerning a framework that considers additional constraints on final wealth in stressed housing markets, addressing the needs of large investors. The study also contributes to dependence modeling by providing a way to cope with the problem of full dependence between risks, which are severe but plausible hypothetical situations that can adversely affect the total wealth, which represents the worst possible situation for portfolio loss. It assesses the impact of state-dependent preferences on trading decisions and constructs optimal strategies explicitly, showing their outperformance compared to traditional diversified strategies under worst-case scenarios.

In this study, introducing a new worst-case portfolio optimization approach is not our main concern. Instead, it analyzes optimal portfolios of large investors when the market is faced with a crash before the time horizon. The study aims to present large investors with an educated investment in housing markets, which might be more profitable than investing all savings in the money market account. It presents a novel mathematical framework tailored for housing markets capable of enduring significant catastrophic events or crashes. This framework introduces the notion of worst-case scenario portfolio optimization, departing from conventional stochastic models that typically neglect abrupt declines in housing prices during market crashes. To bridge this conceptual gap, the study integrates considerations of the timing, frequency, and severity of market crashes into housing market models. The objective is to develop portfolios that are both robust and resilient, particularly catering to the needs of large investors amidst extreme housing market conditions. Thus, rather than focusing solely on housing markets that consistently perform well, there is often an emphasis on identifying housing markets that performs poorly. Accordingly, as Rotella Junior et al. (2023) emphasize, we incorporate the importance of incorporating worst-case housing market data into our model to attain robustness.

The study is organized as four sections. Section 2 introduces the housing market environment and the worst-case scenario method we consider in our empirical analysis. Section 3 presents scenarios and and empirical analysis by considering simulated datasets, and Sect. 4 concludes the study and presents possible extension of the study.

2 Housing Market Environment

This study classifies the investors into two groups, large and individual investors. However, it analyzes housing markets by considering only large investors. Here, the large investor corresponds to the investors who are assumed to use houses in their portfolios for only business purposes. More clearly, they are traders who intend to lease and resell houses in their portfolio without leasing or occupying them. The large investor context includes “corporate" as investors. On the other hand, individual investors are not corporations, and their legal mailing address appears for at least three transactions Mills et al. (2019). From now on, we will use “investors" instead of “large investors".

Consider a market that contains only two possible assets available to invest: a riskless asset and a risky asset corresponding to the housing vulnerable to housing market crashes (e.g., high-inflationary and low-interest rate business cycles, catastrophic events, etc.). Suppose we are given a complete filtered probability space \((\Omega ,\mathcal {F}_t,\mathbb {F},\mathbb {P})\) in which the corresponding processes are defined and a fixed time horizon \(0<T<\infty\). In this probability space, let us denote the riskless asset by the standard money market account or bond formula given as

$$\begin{aligned} dB(t)=B(t)rdt,\; B(0)=1 \end{aligned}$$
(1)

with a constant interest rate r.

Before introducing housing price dynamics and establishing the appropriate filtration on the provided probability space, it is essential to introduce the concept of a stress scenario. By following Korn and Müller (2022); Seifried (2010), we propose a non-probabilistic model of crashes as stress scenarios as follows:

Definition 1

Let a housing market crash scenario be defined by \(z\in [0,1)\), where \(z\in \mathbb {R}\) is called stress. A pair \((z,\xi )\), consisting of a stress z and a stochastic process \(\xi \in [0,T]\cup \{\infty \}\), where \(0<T<\infty\) unless otherwise stated, is called a stress scenario. We refer to \(\xi\) as the time of occurrence of stress z. We define \(\{\xi =\infty \}\) if the market does not face stress. We assign a jump process for stress scenario \((z, \xi )\) given as

$$\begin{aligned} J_z(t):=\mathbbm {1}_{\xi \le t},\quad t\in [0, T]. \end{aligned}$$

Without loosing generality, we assume that there are n number of stress scenarios with tuples \((z^{(1)},\xi _1),\ldots ,(z^{(n)},\xi _n)\) having jump processes \(J_j(t):=J_{z^j}(t)\), where \(j=1,\ldots ,n\). Furthermore, assume that the filtered probability space we work in satisfies the usual conditions and includes the filtration generated by Brownian motion W(t) and jump processes \(J_1(t),\ldots , J_n(t)\). Also, we have to extend the filtration \(\mathbb {F}\) to \([0, T]\cup \{\infty \}\) by assuming \(\mathcal {F}_\infty :=\mathcal {F}_T\) to include the no stress scenario \(\xi _j=\infty\) for \(j\in \{1,\ldots , n\}\). In this setting, \(\xi _j\) are stop** times concerning the extended filtration. We denote the stop** times by \(\xi _j\in \Theta\), where \(\Theta\) is the set of all \([0,T]\cup \{\infty \}\)-valued stop** times.

Now, we can introduce the housing price process. Suppose housing price dynamics are driven by a Brownian motion and a jump process, which obeys the stochastic differential equation (SDE) given as

$$\begin{aligned} dH(t)=H(t^-)\Big ((\mu +\delta -m)dt+\sigma dW(t)-\sum _{j=1}^n{z^{(j)}dJ_j(t)}\Big ),\; H(0)=h, \end{aligned}$$
(2)

where \(\mu\) is the change in the housing price and represents the average growth rate of housing prices in the market and it captures the tendency of housing prices to increase over time due to factors such as demand, population growth, economic conditions, and other market-specific influences. Hence, contributes to the overall drift term that drives the expected change in housing prices. The parameter \(\delta >0\) is the constant continuous rental income yield and reflects the income of the investor receives from renting out a property. The parameter \(m>0\) is the constant continuous maintenance cost yield and captures the ongoing costs associated with property upkeep, repair, and maintenance. These costs are subtracted from the potential returns generated by the property’s rental income and price appreciation. The parameters \(\sigma >0\) is the volatility of the housing price, W(t) is a Brownian motion, \(z^{(j)}\) denotes the stress scenarios, and \(H(0)=h>0\) is the initial housing price.

The housing market may face stress, and thus, we can observe jump \(J_j(t)\), \((j\in \{1,\ldots ,n\})\). However, investors have no information about the possibility of the appearance of the stress or jumps. More precisely, investors lack any information regarding the dynamic characteristics of the jump processes, including their potential intensities. In this study, for the sake of simplicity, each stress is allowed to occur at most once on the fixed time horizon [0, T].

The housing price evaluation process described in (2) has the potential for further extension by introducing additional parameters, as outlined in Remark 1. However, for the purposes of this study, the inclusion of the extra term is not being considered here but will be considered in a future study.

Remark 1

Suppose, the housing market satisfies the condition give in (2). Then, it can be extended further by considering an SDE for the dynamics of housing market that incorporates market liquidity as

$$\begin{aligned} dH(t)=H(t^-)\Big ((\mu +\delta -m)dt+\sigma dW(t)-\sum _{j=1}^n{z^{(j)}dJ_j(t)},\Big )+\lambda (H(t^-),t)dt,\; H(0)=h, \end{aligned}$$

where \(\lambda (H(t),t)\) is the liquidity factor that captures the effect of market liquidity on housing price dynamics. It can be defined in different ways depending on the specific modeling assumptions and market conditions. For instance, one way to incorporate liquidity is to use the time on the market as a proxy for liquidity. The longer a house remains on the market, the lower its liquidity. In this case, the liquidity term can be defined as:

$$\begin{aligned} \lambda (H(t),t)=-\psi (H(t),t)T(t), \end{aligned}$$

where \(\psi ((H(t),t)\) is a liquidity factor that captures the sensitivity of housing price to time on the market, and T(t) is the average number of days properties spent on the market up to selling time t. A negative value of \(\psi ((H(t),t)\) implies that the longer a house remains on the market, the lower its price.

Remark 2

During housing market booms, the rapid increase in housing prices attracts a larger number of investors to the market, including new investors seeking potentially high returns. Consequently, the liquidity of the housing market tends to deteriorate, especially as the market becomes increasingly dominated by less experienced investors. Such an influx of unsophisticated agents can lead to less efficient market dynamics and hinder liquidity. Several factors contribute to the degradation of market liquidity during housing market booms:

  1. 1.

    Reduced time-on-market: Booms are associated with shorter property listing duration, indicative of faster property sales. This reduced time-on-market can lead to diminished market liquidity due to fewer available properties and heightened buyer competition.

  2. 2.

    Increased price dispersion: Booms often result in greater variability in housing prices, leading to higher price dispersion. This heightened dispersion can complicate price negotiations between buyers and sellers, further impacting market liquidity.

  3. 3.

    Influx of new market participants: Booms attract a surge of individuals to the market, including new agents seeking lucrative commissions. However, the increased presence of new agents does not necessarily translate to higher success rates. Studies suggest lower agent productivity in high-cost housing markets during booms, contributing to market inefficiencies and exacerbated liquidity challenges.

The housing market may experience stress, which results in jumps \(J_j(t)\), where \(j\in \{1,\ldots ,n\}\). However, investors lack information about potential occurrence of stress or jumps, including their dynamic characteristics and potential intensities. For simplicity, this study assumes that each stress can occur at most once within the fixed horizon [0, T].

Suppose the housing market contains enough housing units and an investor with an initial wealth of \(x>0\) willing to invest only in housing and the money market account. If the market faces a stress, the investor observes the stress scenario and adjust its portfolio accordingly after the occurrence of the stress. The investor has a self-financing portfolio process denoted by \(\pi \ge 0\), which is the fraction of the investor’s wealth invested in housing. The portfolio process \(\pi\) assumed to be predictable to model a reallocation of holdings is not possible when the stress occurs. Nevertheless, adopting a prudent investment approach must also ensure protection against financial ruin. Consequently, let us reorganize the definition of admissible wealth process given in Korn and Müller (2022) and introduce the following definition.

Definition 2

Suppose an investor endowed with an initial wealth \(x>0\) at \(t\in [0, T]\) can observe a possible stress in the housing market and responses accordingly. Let the pairs \((z^{(1)},\xi _1),\ldots ,(z^{(n)},\xi _n)\) be the possible stress scenarios in the housing market. Then, the set for \(s\in [t,T]\) the admissible portfolio process \(\pi\) corresponding to the investor’s initial wealth, denoted by \(\mathbb {A}(t,x)\) satisfies

  1. (i)

    The investor’s wealth process \(X^\pi (t)\) corresponding to the admissible portfolio process \(\pi\) is the unique solution of the wealth process SDE

    $$\begin{aligned} dX^\pi (s)= & {} X^\pi (s^-)\Big ((r+\pi (s)[\mu +\delta -m-r])ds+\pi (s)\sigma dW(s)-\sum _{j=1}^n{\pi (s)z^{(j)}dJ_j(s)}\Big ),\\ X^\pi (t)= & {} x. \end{aligned}$$
  2. (ii)

    The admissible portfolio process \(\pi (s)\) has a form

    $$\begin{aligned} \pi (s)=\sum _{u\in \{0,1\}^n}\mathbbm {1}_{\{\bar{u}(s)=u\}\pi _u(s)}, \end{aligned}$$

    where \(\pi _u(s)\) are predictable and right continuous with left limits on a fixed time interval [0, T], \(\forall u=(u_1\ldots ,u_n)\in \{0,1\}^n\), and \(\bar{u}(s)=(\bar{u}_1(s),\ldots ,\bar{u}_n(s))\in \{0, 1\}^n\). Here, \(\bar{u}_i=1\) if and only if \(s\le \xi _i\) for \(i\in \{1,\ldots ,n\}\).

  3. (iii)

    Moreover, the wealth process satisfies

    $$\begin{aligned} X^\pi (s)> & {} 0,\quad \forall s\in [t, T],\\ \int _t^T{\pi ^2_{u}(s)ds}< & {} \infty , \; \mathbb {P}-\text { a.s. for}\; u\in \{0,1\}^n. \end{aligned}$$

In Definition 2, observe that the portfolio process is valid during the crash. We can introduce the following remark to adjust the portfolio process after the crash.

Remark 3

  1. (i)

    If the market faces stress \(z^{(j)}\) at stop** time \(\xi _j\in \Theta\) for \(j\in \{1,\ldots ,n\}\) and \(\xi _j<\infty\), \(X^\pi\) changes at stress time \(\xi _j\) with regard to Korn and Müller (2022)

    $$\begin{aligned} X^\pi (\xi )=\Big (1-\pi (\xi _j)z^{(j)}\Big )X^\pi (\xi _j^-). \end{aligned}$$

    The definition of the portfolio process ensures that a change to the appropriate \(\pi _u(\cdot )\) sub-strategy follows right after the jump in the housing price.

  2. (ii)

    The positivity condition, ensures that an investor does not suffer a total loss as a consequence of any stress. Namely, an admissible portfolio process \(\pi\) for n remaining stresses \(z^{(1)},\ldots , z^{(n)}\) should satisfy the following

    $$\begin{aligned} \max \Big \{\pi (t)z^{(j)}\mid j=1,\ldots ,n\Big \}<1, \quad t\in [0,T]. \end{aligned}$$
  3. (iii)

    For n stress scenarios, \(X^\pi\) before the first stress has occurred often denoted by \(X^{\pi _{(1,\ldots ,1)}}\). This holds special significance because our approach to solving the worst-case problem involves a recursive construction of the solution, beginning with the established optimal portfolio process under the assumption of no crashes.

Now, suppose that the investor wants to maximize its expected terminal utility under the worst-case scenario \((z^{(1)},\xi _1),\ldots ,(z^{(n)},\xi _n)\). Let \(U:(0,\infty )\mapsto \mathbb {R}\) be the utility function of the investor, which assumed to be strictly concave, increasing, and continuously differentiable. Then, the investor has an optimization problem organized as

$$\begin{aligned} \sup _{\pi \in \mathbb {A}(x)}\inf _{\xi _1,\ldots ,\xi _n\in \Theta }\mathbb {E}_{0,x,(u_1,\ldots ,,u_n)}[U(X^\pi (T))],\; u_1=\ldots =u_n=1, \end{aligned}$$

where \(\mathbb {A}(x)=\mathbb {A}(0,x)\), \(\Theta\) is the set of stop** times, \(\mathbb {E}_{0,x,(u_1,\ldots ,,u_n)}\) is the conditional expectation given that \(X^\pi (t)=x\), and \(u_j\in \{0, 1\}\), \(j=1,\ldots ,n\) with \(u_j=1\) if and only if \(\xi _j\ge t\). However, we omit these indices if \(t=0\) or \(u_1=\ldots =u_n=0\).

In the further analysis, the study considers a constant relative risk aversion (CRRA) utility function given as

$$\begin{aligned} U(x)=\frac{1}{1-\gamma }x^{1-\gamma }, \end{aligned}$$

where \(\gamma >0\), and \(\gamma \ne 1\).

2.1 Deconstructing Terminal Utility: Analyzing the Post-Stress Dilemma

Define \(\xi _k=\max \{\xi _1,\xi _2\}\) where \(\xi _k<\infty\) and focus on the optimal strategy after the last stress. Suppose the notation is denoted \(\pi _{(0)}=\pi _{(0,0)}\) for the admissible self-financing portfolio \(\pi \in \mathbb {A}(x)\). Then, the post-stress problem becomes

$$\begin{aligned} \max _{\pi \in \mathbb {A}(\xi _k,x)}\mathbb {E}\left[ U(X^\pi (T))\right] , \end{aligned}$$
(3)

yielding the standard Merton problem with random initial time \(\xi _k\).

Proposition 1

(Terminal utility decomposition Korn and Müller (2022)) Let \(z^{(1)}\) and \(z^{(2)}\) be two stresses with corresponding stop** times \(\xi _1,\; \xi _2<\infty\). Then, for any \(\pi \in \mathbb {A}(x)\) the investor has a decomposition

$$\begin{aligned} U(X^\pi (T)=U(X^\pi (\xi _k))e^{(1-\gamma )\int _{\xi _k}^T{\phi _\gamma (\pi (t))dt}Y^\gamma _T(\pi )}, \end{aligned}$$

where

$$\begin{aligned} \phi _\gamma (\pi )=r+\pi [\mu +\delta -m-r]-\frac{1}{2}\gamma \pi ^2\sigma ^2 \end{aligned}$$

and \(Y^\gamma (\pi )=(Y^\gamma _t(\pi ))_{t\in [\xi _k,T]}\) is an \(\mathcal {F}_t\)-martingale that satisfies \(Y^\gamma _{\xi _k}(\pi )=1\).

Proof

The proof can be obtained using the change of measure device given by Theorem 4.1 (Change-of-Measure Device) in Seifried (2010) and Theorem 3.1 in Korn and Müller (2022), respectively.

Remark 4

Proposition 1 illustrates that investing in housing in inflationary business cycle periods may not be favorable since the interest rate is usually high. However, if central banks are slow to stabilize interest rates against inflation, investing in housing may be more favorable.

In a stress-free market environment, we have to solve the Merton problem with random initial time. The terminal wealth utility decomposition can solve this problem by maximizing the functional \(\phi _\gamma\). For instance, an admissible portfolio process \(\bar{\pi }\in \mathbb {A}(\xi _k,x)\) is optimal for the post-stress problem (3) if \(\bar{\pi }_{(0)}=\pi ^*\), where

$$\begin{aligned} \pi ^*=\arg \max _{\pi \in \mathbb {R}}\phi _\gamma \left( \pi \right) . \end{aligned}$$

Notice that \(\pi ^*\) is constant independent of random time \(\xi _k\) and initial wealth x Korn and Müller (2022).

Proposition 2

(Solution of the post-stress portfolio problem Korn and Müller (2022)) Let \(\phi _\gamma\) as in Proposition 1. Then, the optimal portfolio strategy \(\pi ^*\) and the corresponding value function \(v(\xi _k;x)\) in the post-stress problem (3) with random initial time \(\xi _k\in \Theta\) and \(\xi _k<\infty\), are

$$\begin{aligned} \pi ^*=\frac{1}{\gamma \sigma ^2}[\mu +\delta -m-r] \end{aligned}$$

and

$$\begin{aligned} v(\xi _k;x)=\frac{x^{1-\gamma }}{1-\gamma }e^{(1-\gamma )\int _{\xi _k}^T{\phi ^\gamma (\pi ^*)ds}}, \end{aligned}$$

respectively.

Proof

Using Itô’s lemma to CRRA utility function, the proof can be achieved using a similar method given in Korn and Menkens (2005).

Henceforth, to perceive a stress as a potential threat, we require

$$\begin{aligned} 0<\pi ^*z,\ \quad \forall z \end{aligned}$$
(4)

since the optimal portfolio process in a stress-free market should suffer a loss as a consequence of stress z.

Remark 5

Proposition 2 shows that the crash is unfavorable to the investor who decides to ignore the crash, and therefore, a priory, the crash is perceived as a threat.

The problem presented in (3) reflects an extremely cautious approach to dealing with market uncertainty surrounding a crash. Specifically, the investor chooses not to assign numerical probabilities to the occurrence of a stress event. However, focusing on the worst-case scenario is a reasonable strategy when faced with catastrophic disasters that lack reliable mathematical and statistical models.

2.2 The Worst-Case Problem for One-Stress

First, let us examine a portfolio problem under the most unfavorable conditions, where a single stress scenario \((z,\xi )\) is considered. Additionally, let \(v_0(t;x)\) represent the value function for the optimal portfolio problem after the stress period.

Definition 3

Let \((z,\xi )\) and \(v_0(t;x)\) be a single stress scenario and the value function for the optimal portfolio problem after the stress period, respectively. If there is an admissible portfolio process \(\pi \in \mathbb {A}(x)\) such that the process satisfies the following condition

$$\begin{aligned} v_0\Big (t;(1-\pi _{(1)}(t)z)X^{\pi _{(1)}}(t^-)\Big ),\quad t\in [0,T]\cup \{\infty \} \end{aligned}$$

is a martingale for

$$\begin{aligned} v_0\Big (\infty ;(1-\pi _{(1)}(\infty )z)X^{\pi _{(1)}(\infty ^-)}\Big )=U(X^{\pi _{(1)}}(T)), \end{aligned}$$

where \(\pi \in \mathbb {A}(x)\) is called an indifference strategy for the investor.

Proposition 3

(Indifference-optimality principle Korn and Müller (2022)) Let \(\bar{\pi }\) be an indifference strategy and suppose \(\forall \pi \in \mathbb {A}(x)\) there is at least a single stress time \(\tilde{\xi }\in \Theta\) satisfying

$$\begin{aligned} \mathbb {E}\left[ v_0\left( t;\left( 1-\pi _{(1)}(\bar{\xi }z)\right) X^{\pi _{(1)}}(\tilde{\xi }^-)\right) \right] \le \mathbb {E}\left[ v_0\left( t;\left( 1-\bar{\pi }_{(1)}(\tilde{\xi })z\right) X^{\bar{\pi }_{(1)}}(\tilde{\xi }^-)\right) \right] . \end{aligned}$$

Then, the portfolio process \(\bar{\pi }\) is an optimal worst-case portfolio process.

Proposition 4

(Indifference frontier Korn and Müller (2022)) Let inequality (4) be valid and let \(\pi \in \mathbb {A}(x)\) be an admissible portfolio process for the one-stress worst-case portfolio problem with stress scenario \((z,\xi )\). Further, let \(\bar{\pi }\) be an indifference strategy. Define

$$\begin{aligned} \tau =\inf \Big \{t:\pi _{(1)}(t)z>\bar{\pi }_{(1)}(t)z\Big \}, \end{aligned}$$

and

$$\begin{aligned} \tilde{\pi }_{(1)}(t)=\pi _{(1)}(t)\quad \text {if}\quad t<\tau \quad \text {and}\quad \tilde{\pi }_{(1)}(t)=\bar{\pi }_{(1)}(t)\quad \text {if}\quad t\ge \tau . \end{aligned}$$

Then, we have \(\tilde{\pi }\in \mathbb {A}(x)\) and the worst-case bound attained by \(\tilde{\pi }\) is at least as big as that achieved by \(\pi\).

Hence, only a portfolio process that does not exceed the indifference frontier of an indifference strategy \(\bar{\pi }\), i.e., which does not exceed the indifference level \(\bar{\pi }_{(1)}z\) for \(t\in [0, T]\), can be a worst-case optimal portfolio process.

Theorem 1

(Solution of the one-stress worst-case problem Korn and Müller (2022)) Let (4) be satisfied and assume a single stress scenario \((z,\xi\). The optimal portfolio process is the indifference strategy \(\bar{\pi }\), given by

$$\begin{aligned} \bar{\pi }_{(1)}(t)=\pi ^*-\frac{z\pi ^*-N(t)}{z^2\sigma ^{-2}}\sigma ^{-2}z, \end{aligned}$$

where N(t) is the unique solution of the ODE

$$\begin{aligned} N^\prime (t)=-\frac{1}{2z^2\sigma ^{-2}}\gamma \left( 1-N(t)\right) \left( z\pi ^*-N(t)\right) ^2 \end{aligned}$$

with final condition \(N(T) = 0\). The corresponding value function \(v_1(t;x)\) is

$$\begin{aligned} v_1(t;x)= & {} \sup _{\pi \in \mathbb {A}(t,x)\inf _{\xi \in \Theta _t}}\mathbb {E}_{t,x,(1)}\Big [U(X^\pi (T))\Big ]=v_0\left( t;\left( 1-\bar{\pi }_{(1)}(t)z\right) x\right) \\= & {} \mathbb {E}_{t,x}\Big [U\left( X^{\bar{\pi }_{(1)}}(T)\right) \Big ] \end{aligned}$$

for \(t \in [0, T ]\), where \(\Theta _t\) denotes the class of \([t, T ]\cup \{\infty \}\)-valued stop** times.

Proof

The proof can be achieved by following Korn and Leoff (2019).

Lemma 1

(Decreasing wealth loss Korn and Müller (2022)) Assume a single stress scenario \((z,\xi )\) and let \(\bar{\pi }\) be given as in Theorem 1. Then, we have

$$\begin{aligned} 0\le \bar{\pi }_{(1)}(t)z<\min \left\{ \pi ^*z,1\right\} \end{aligned}$$

and as a consequence particularly \((\bar{\pi }_{(1)}z)^\prime <0\) and \((\bar{\pi }_{(1)}z)^{\prime \prime }<0\), \(\forall t\in [0,T]\).

Proof

See Korn and Müller (2022).

3 Empirical Analysis

In the housing market context, worst-case scenarios can include various factors affecting housing prices, such as natural catastrophes, economic downturns, interest rate fluctuations, housing bubbles, and local economic decline. An economic downturn can lead to a decrease in demand for housing and a drop in prices. Natural catastrophes, such as hurricanes, earthquakes, and floods, can damage homes and infrastructure, leading to a decrease in demand and a drop in prices. A natural catastrophe can be severe and widespread, leading to a prolonged period of low demand and falling prices. The economic downturn can be severe, leading to a prolonged period of low demand and falling prices. Interest rate fluctuations can affect the affordability of mortgages and the demand for housing. Interest rates can rise sharply, leading to a decrease in demand and a price drop. A housing bubble occurs when prices rise rapidly and unsustainably, fueled by speculative behavior and unrealistic expectations. The housing bubble can burst, leading to a sudden and significant price drop. Changes in government policies, such as tax laws and regulations, can affect housing markets significantly. In the worst-case scenario, policy changes can be unfavorable to the housing market, leading to a decrease in demand and a drop in prices. Local housing markets that are heavily dependent on a single industry or company can experience severe downturns if that industry or company faces financial troubles or closures. However, in this study, we avoid introducing a specific reason for the price decrease. We only consider a significant price change as a worst-case since the scenarios may trigger each other, and we assume that the market is faced with stress before the portfolio adjustment.

As a numerical illustration, the study presents simulations considering the market parameters as \(\mu =0.03\), \(\delta =0.001\), \(m = 0.0009\), \(\sigma = 0.09\), \(\# of stress scenerio=1\), \(h = 80\), \(r = 0.02\), \(x = 100\), and \(T = 10\) with a daily basis with a stress \(z=0.04\). The simulations rely on an initial portfolio weight of \(\pi =0.8\) invested in the housing and the remaining wealth \((1-\pi =0.20)\) invested in the bank account as a riskless asset. The investor considers a CRRA utility function with \(\gamma =2\), indicating increasing relative risk aversion. Hence, the investor becomes more risk-averse as its wealth increases.

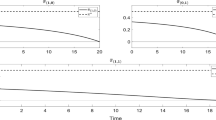
Figure 1 illustrates the simulation of the worst-case portfolio effect on the wealth process with the above mentioned parameters. The figure comprises two panels: the upper panel depicts the evaluation of investor wealth, contrasting scenarios with and without adjustments following a market crash. The solid blue line represents the wealth trajectory when adjustments are made, while the dashed gray line illustrates the scenario without adjustments. Additionally, a horizontal dashed red line denotes the time of the market crash. In the lower panel, portfolio adjustments in response to the market crash are showcased. The dashed line represents the portfolio weight allocated to housing before and after the crash, while the blue line signifies the adjusted portfolio weight. Initially, the housing investment constitutes \(80\%\) of the portfolio, but post-crash optimization leads to a revised optimal weight of \(60\%\). Notably, the investor’s wealth remains unchanged before the crash for both adjusted and non-adjusted portfolios. However, a substantial disparity emerges between the portfolios’ performance post-crash. As the figure reveals, the investor’s wealth is decreasing after the crash occurred since house prices are decreasing. However, if the investor adjusts its portfolio considering the worst-case portfolio, the wealth loss is less than kee** the portfolio without any change. Hence, adjusting the portfolio after the crash makes it possible to protect against the portfolio’s downside risk. The figure also reveals the change in the weight of investment in housing. It is clear that when the market is faced with a crash, the investment in housing is decreasing. In Appendix 3, we present additional simulations, which indicate the benefit of using the worst-case scenario to protect our wealth against the downside risk.

Fig. 1
figure 1

A numerical illustration of worst-case portfolio effect on housing market portfolio

Full size image

Figures 2 and 3, showcase simulation results utilizing the parameters outlined previously. Figure 2 specifically delves into the impact of crash magnitude on investor portfolios. It elucidates that when the crash magnitude is relatively minor, its repercussions on portfolio wealth are likewise limited. However, regardless of the crash magnitude, adjusting the portfolio emerges as a superior strategy compared to adhering to the initial portfolio composition. Notably, this figure also underscores the versatility of our methodology, as it proves effective even in housing markets experiencing downturns, where property prices are declining. Contrastingly, Fig. 3 presents a scenario where the crash occurs earlier compared to the preceding cases. Here, it becomes evident that if the crash transpires earlier, there exists a possibility of market recovery prior to the maturity T. Moreover, adjusting the portfolio post-crash results in higher gains for the investor compared to maintaining the initial portfolio composition. Thus, the efficacy of portfolio adjustment in conjunction with worst-case scenario analysis is starkly evident, mitigating potential losses in investor wealth.

Fig. 2
figure 2

Numerical illustration of worst-case portfolio effect on housing market portfolio (crash time\(=8\), z=0.4)

Full size image
Fig. 3
figure 3

Numerical illustration of worst-case portfolio effect on housing market portfolio (crash time\(=5\), z=0.8)

Full size image

4 Conclusion

This study has comprehensively examined the potential worst-case scenarios affecting the housing market. By scrutinizing various factors, including economic downturns, natural catastrophes, interest rate fluctuations, housing bubbles, government policy changes, and localized economic decline, the study has laid a strong foundation for understanding the risks housing market investors face.

The numerical illustration presented in this research demonstrates the real-world implications of worst-case scenarios on investor wealth, focusing on the importance of portfolio adjustments to mitigate these risks. We observed that reacting to these scenarios by adjusting one’s portfolio can effectively safeguard against the downside risk of housing market investments.

However, this study acknowledges that risk management in the housing market is a complex and ongoing challenge, particularly when considering an infinite time horizon. As wealth accumulates and evolves, the dynamics of risk aversion change, emphasizing the importance of continuous portfolio reassessment. Future work in this field should delve deeper into the dynamics of risk aversion over extended time horizons, exploring how investor behavior adapts and strategies evolve as wealth accumulates. Furthermore, it is essential to consider the interplay between these various worst-case scenarios. Future research can focus on assessing how these factors interact and amplify each other over extended periods. Additionally, examining more intricate portfolio adjustment strategies and investigating alternative asset classes that can act as hedges against housing market risks would be a valuable avenue for further inquiry.