Abstract
We study the homotopy right Kan extension of homotopy sheaves on a category to its free cocompletion, i.e. to its category of presheaves. Any pretopology on the original category induces a canonical pretopology of generalised coverings on the free cocompletion. We show that with respect to these pretopologies the homotopy right Kan extension along the Yoneda embedding preserves homotopy sheaves valued in (sufficiently nice) simplicial model categories. Moreover, we show that this induces an equivalence between sheaves of spaces on the original category and colimit-preserving sheaves of spaces on its free cocompletion. We present three applications in geometry and topology: first, we prove that diffeological vector bundles descend along subductions of diffeological spaces. Second, we deduce that various flavours of bundle gerbes with connection satisfy \((\infty ,2)\)-categorical descent. Finally, we investigate smooth diffeomorphism actions in smooth bordism-type field theories on a manifold. We show how these smooth actions allow us to extract the values of a field theory on any object coherently from its values on generating objects of the bordism category.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Main Results
Local-to-global properties are ubiquitous in topology, geometry, and quantum field theory. The prototypical example of a local-to-global, or descent, property is the gluing of local sections of a sheaf: given a manifold M with an open covering \(\{U_i\}_{i \in I}\), global sections of a sheaf F on M are in bijection with families \(\{f_i \in F(U_i)\}_{i \in I}\) such that \(f_{i|U_{ij}} = f_{j|U_{ij}}\) for all \(i,j \in I\), with \(U_{ij} {:}{=}U_i \cap U_j\).
Geometric structures on manifolds are, in general, not described by sheaves of sets; instead, one needs to pass to sheaves of higher categories. For example, complex vector bundles form a sheaf on the site of manifolds and open coverings which is valued in categories rather than sets. In the works of Schreiber [\(\underline{{\mathscr {H}}}_{\infty ,0}(Q\underline{M},F)\). Here, \(\underline{M}\) is the presheaf on \({{\mathscr {C}}\text {art} }\) consisting of smooth maps to M, the functor Q is a cofibrant replacementFootnote 2 in \({\mathscr {H}}_{\infty ,0}\), and \(\underline{{\mathscr {H}}}_{\infty ,0}(-,-)\) denotes the  -enriched hom functor in \({\mathscr {H}}_{\infty ,0}\). If F is the simplicial presheaf on cartesian spaces which describes G-bundles or n-gerbes, for instance, then the Kan complex \(\underline{{\mathscr {H}}}_{\infty ,0}(Q\underline{M},F)\) is the \(\infty \)-groupoid of G-bundles or n-gerbes on M, respectively. In fact, we could use any presheaf X on \({{\mathscr {C}}\text {art} }\) in place of \(\underline{M}\) and thus study geometries on any such X. (Later we will even allow X to be a presheaf of \(\infty \)-groupoids itself.)
-enriched hom functor in \({\mathscr {H}}_{\infty ,0}\). If F is the simplicial presheaf on cartesian spaces which describes G-bundles or n-gerbes, for instance, then the Kan complex \(\underline{{\mathscr {H}}}_{\infty ,0}(Q\underline{M},F)\) is the \(\infty \)-groupoid of G-bundles or n-gerbes on M, respectively. In fact, we could use any presheaf X on \({{\mathscr {C}}\text {art} }\) in place of \(\underline{M}\) and thus study geometries on any such X. (Later we will even allow X to be a presheaf of \(\infty \)-groupoids itself.)
We write \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}},{{\mathscr {S}}\text {et} })\) for the category of (small) presheaves of sets on \({\mathscr {C}}\). Motivated by the above discussion, we pose the following two questions for sheaves on a generic site \(({\mathscr {C}},\tau )\):
-
(1)
If F satisfies descent with respect to the pretopology \(\tau \), does the assignment \(X \mapsto \underline{{\mathscr {H}}}_{\infty ,0}(QX,F)\) satisfy descent with respect to a related pretopology \({{\widehat{\tau }}}\) on \({{\widehat{{\mathscr {C}}}}}\)?
-
(2)
If so, can we understand which \({{\widehat{\tau }}}\)-sheaves on \({{\widehat{{\mathscr {C}}}}}\) arise as extensions \(\underline{{\mathscr {H}}}_{\infty ,0}(Q(-),F)\) of some ordinary sheaf F on \(({\mathscr {C}},\tau )\)?
We answer both of these questions in this paper, working over general Grothendieck sites \(({\mathscr {C}},\tau )\): any pretopology \(\tau \) on \({\mathscr {C}}\) induces a pretopology \({{\widehat{\tau }}}\) of generalised coverings on \({{\widehat{{\mathscr {C}}}}}\). We prove that with respect to such a pair of pretopologies, the answer to the first question is always ‘yes’. One way of saying this is that the process of extending any geometric structure from objects of \({\mathscr {C}}\) to objects of \({{\widehat{{\mathscr {C}}}}}\) does not destroy the descent property; we can still think of the extended structure as having geometric flavour and perform local-to-global constructions.
In concrete terms, the induced Grothendieck pretopology \({{\widehat{\tau }}}\) on \({{\widehat{{\mathscr {C}}}}}\) consists of the \(\tau \)-local epimorphisms, also called generalised coverings [17], which are defined as follows. Let \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {{\widehat{{\mathscr {C}}}}}\) denote the Yoneda embedding of \({\mathscr {C}}\). A morphism \(\pi :Y \rightarrow X\) in \({{\widehat{{\mathscr {C}}}}}\) is a \(\tau \)-local epimorphism if, for every \(c \in {\mathscr {C}}\) and every map \({{\mathscr {Y}}}_c \rightarrow X\), there exists a covering \(\{c_i \rightarrow c\}_{i \in I}\) in the site \(({\mathscr {C}},\tau )\) such that each composition \({{\mathscr {Y}}}_{c_i} \rightarrow {{\mathscr {Y}}}_c \rightarrow X\) factors through \(\pi \); this is an abstract way of saying that the morphism \(\pi \) has local sections.
Let \({{\mathscr {M}}}\) be a left proper cellular or combinatorial simplicial model category. We consider the projective model structures on \(\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\) and \(\textrm{Fun}({{\widehat{{\mathscr {C}}}}}{}^{\text {op}}, {{\mathscr {M}}})\), and their left Bousfield localisations \(\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})^{loc}\) and \(\textrm{Fun}({{\widehat{{\mathscr {C}}}}}{}^{\text {op}}, {{\mathscr {M}}})^{loc}\) at the \(\tau \)-coverings and \({{\widehat{\tau }}}\)-coverings, respectively. That is, the fibrant objects in these localised model categories are \({{\mathscr {M}}}\)-valued homotopy sheaves on \(({\mathscr {C}}, \tau )\) and \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\), respectively. We show the following result (see Theorems 3.30, 3.37 and Proposition 3.38 below):
Theorem 1.1
Let \({{\mathscr {M}}}\) be a left proper simplicial model category which is cellular or combinatorial and \({\mathscr {C}}\) a category. Let \(\tau \) be a Grothendieck coverage on \({\mathscr {C}}\), and \({{\widehat{\tau }}}\) the induced Grothendieck coverage of \(\tau \)-local epimorphisms on \({{\widehat{{\mathscr {C}}}}}\). There is a Quillen adjunction

whose right adjoint restricts on fibrant objects to the homotopy right Kan extension along the Yoneda embedding \({{\mathscr {Y}}}:{\mathscr {C}}\hookrightarrow {{\widehat{{\mathscr {C}}}}}\),
A prime application is the case of homotopy sheaves of higher categories: denoting by \(\mathscr {C}\mathscr {S}\mathscr {S}_n\) the model category of n-fold complete spaces [2, 9, 41], let \({\mathscr {H}}_{\infty ,n}^{loc}\) be the left Bousfield localisation of the projective model structure on \(\textrm{Fun}({\mathscr {C}}^{\text {op}}, \mathscr {C}\mathscr {S}\mathscr {S}_n)\) at the Čech nerves of coverings in \(({\mathscr {C}},\tau )\). Similarly, we let \({{\widehat{{\mathscr {H}}}}}_{\infty ,n}^{loc}\) denote the left Bousfield localisation of \(\textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, \mathscr {C}\mathscr {S}\mathscr {S}_n)\) at the Čech nerves of the \(\tau \)-local epimorphisms. As a direct corollary to Theorem 1.1 we obtain:
Corollary 1.2
Let \(n \in {\mathbb {N}}_0\), and let \({\mathscr {C}}\) be a small category.
-
(1)
For any fibrant \({\mathscr {F}}\in {\mathscr {H}}_{\infty ,n}\), the presheaf \(\underline{{\mathscr {H}}}_{\infty ,n} \big ( Q(-), {\mathscr {F}}\big )\) is equivalent to the homotopy right Kan extension \({\textrm{hoRan}}_{{{\mathscr {Y}}}} {\mathscr {F}}\) of \({\mathscr {F}}\) along the Yoneda embedding \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {{\widehat{{\mathscr {C}}}}}\). In particular, \(\underline{{\mathscr {H}}}_{\infty ,n} \big ( Q(-), {\mathscr {F}}\big )\) presents the \(\infty \)-categorical right Kan extension of presheaves of \((\infty ,n)\)-categories along \({{\mathscr {Y}}}\).
-
(2)
If \(({\mathscr {C}},\tau )\) is a Grothendieck site, there is a Quillen adjunction

This answers our first question affirmatively since \(\underline{{\mathscr {H}}}_{\infty ,n} (Q(-), -)\) preserves fibrant objects.
In Sect. 4.1 we deduce the following strictification and descent result (Theorem 4.18 and Theorem 4.12, respectively), thereby filling significant gaps in the literature on diffeological spaces:
Theorem 1.3
Let \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}:{{\mathscr {D}}{\textrm{fg}}}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }\) be the pseudo-functor which assigns to a diffeological space its category of diffeological vector bundles. The following statements hold true:
-
(1)
There is a strict functor \(\iota ^* {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) (which we construct explicitly) and an objectwise equivalence of pseudo-functors \({{\mathscr {D}}{\textrm{fg}}}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \),
$$\begin{aligned} {\mathcal {A}}:\iota ^* {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} \overset{\sim }{\longrightarrow }{{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\,. \end{aligned}$$ -
(2)
Diffeological vector bundles satisfy descent along subductions of diffeological spaces.
Here we use Rezk’s classifying diagram functor to deduce a 1-categorical analogue of Corollary 1.2 for \(n=1\). This readily provides the desired descent result; the main remaining work in proving Theorem 1.3 goes into the strictification of \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\).
Further, we deduce from Corollary 1.2 that various flavours of the 2-category of bundle gerbes with connection as introduced by Waldorf [4.34 and 4.35).
In Sect. 5 we answer the second question above. To do so, we pass to quasi-categorical language: let \({\textsf {C}}\) be a quasi-category with a Grothendieck (pre)topology \(\tau \). Let \({\widehat{{\textsf {C}}}_\infty }\) denote the quasi-category of (small) presheaves of spaces on \({\textsf {C}}\). We write \({\textsf {Sh}}({\textsf {C}},\tau )\) for the quasi-category of \(\tau \)-sheaves on \({\textsf {C}}\) and \({\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}})\) for the quasi-category \({{\widehat{\tau }}}\)-sheaves on \({\widehat{{\textsf {C}}}_\infty }\) whose underlying functor \({\widehat{{\textsf {C}}}_\infty }\rightarrow {\textsf {S}}^{\text {op}}\) preserves colimits.
Theorem 1.4
Let \(({\textsf {C}},\tau )\) be as above, and let \({{\mathscr {Y}}}_*\) denote the \(\infty \)-categorical right Kan extension of presheaves along the Yoneda embedding \({{\mathscr {Y}}}:{\textsf {C}}^{\text {op}}\rightarrow {\widehat{{\textsf {C}}}_\infty }^{\text {op}}\). The adjunction \({{\mathscr {Y}}}^* \dashv {{\mathscr {Y}}}_*\) restricts to an equivalence of quasi-categories

Finally, to make contact with the first part of this paper, we prove a similar result where \({\textsf {C}}= {\textsf {N}}{\mathscr {C}}\) is an ordinary category; this relates quasi-categorical \(\tau \)-sheaves of spaces on \({\textsf {N}}{\mathscr {C}}\) to \({{\widehat{\tau }}}\)-sheaves of spaces on the 1-category of set-valued presheaves \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {L} )\) (Theorem 5.14).
1.1 Conventions
Sizes and universes Throughout, we choose and fix a nested triple of Grothendieck universes \(\text {S} \in \text {L} \in \text {XL} \),Footnote 3 and we assume that \(\text {S} \) contains the natural numbers. We write \({{\mathscr {S}}\text {et} }_\text {S} \) and  for the categories of \(\text {S} \)-small sets and \(\text {S} \)-small simplicial sets, respectively, and analogously for the universes \(\text {L} \) and \(\text {XL} \). As is common in the literature, we refer to the elements in \({{\mathscr {S}}\text {et} }_\text {S} \) simply as small sets, those of \({{\mathscr {S}}\text {et} }_\text {L} \) as large sets and those of \({{\mathscr {S}}\text {et} }_\text {XL} \) as extra large sets. All indexing sets will be assumed to be \(\text {S} \)-small.
for the categories of \(\text {S} \)-small sets and \(\text {S} \)-small simplicial sets, respectively, and analogously for the universes \(\text {L} \) and \(\text {XL} \). As is common in the literature, we refer to the elements in \({{\mathscr {S}}\text {et} }_\text {S} \) simply as small sets, those of \({{\mathscr {S}}\text {et} }_\text {L} \) as large sets and those of \({{\mathscr {S}}\text {et} }_\text {XL} \) as extra large sets. All indexing sets will be assumed to be \(\text {S} \)-small.
Let \({\mathscr {C}}\) be a small category. Consider the category \({{\widehat{{\mathscr {C}}}}}{:}{=}\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\) of \({{\mathscr {S}}\text {et} }_\text {S} \)-valued presheaves on \({\mathscr {C}}\). Observe that \({{\widehat{{\mathscr {C}}}}}\) is no longer small, since \({{\mathscr {S}}\text {et} }_\text {S} \) is not small. However, since \({{\mathscr {S}}\text {et} }_\text {S} \) is a large category (its objects and morphisms each form sets in \(\text {L} \)), it follows that \({{\widehat{{\mathscr {C}}}}}\) is a large category.
The Yoneda embedding \({{\widehat{{{\mathscr {Y}}}}}}:{{\widehat{{\mathscr {C}}}}}\rightarrow \textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {L} )\) is fully faithful; observing that an object of \({{\mathscr {S}}\text {et} }_\text {S} \) is also an object of \({{\mathscr {S}}\text {et} }_\text {L} \), the standard proof applies. Further, the Yoneda Lemma holds true for both \({{\mathscr {Y}}}\) and \({{\widehat{{{\mathscr {Y}}}}}}\) (again by the usual method of proof). Finally, observe for any \(c \in {\mathscr {C}}\) and for any \(X \in {{\widehat{{\mathscr {C}}}}}\), by the Yoneda Lemma, there are canonical isomorphisms
Categories and higher categories In this article we use two different models for higher categories. Section 2 and Appendix A do not make use of higher categories. In Sects. 3 and 4 we use n-fold complete Segal spaces (introduced in [2]) as a model for \((\infty ,n)\)-categories. In particular, the term ‘\(\infty \)-groupoid’ shall always refer to a Kan complex, and ‘\((\infty ,n)\)-category’ shall always mean a n-fold complete Segal space. In Sect. 5, and only there, all higher categories are modelled as quasi-categories in the sense of [12, 27, 34]. In order to make clear the distinction between ordinary categories (possibly endowed with model structures), n-fold complete Segal spaces, and quasi-categories, we denote ordinary categories by script letters \({\mathscr {C}}, {\mathscr {D}}, \ldots \), n-fold complete Segal spaces (or presheaves thereof) by ordinary capitals \(F, G, \ldots \), and quasi-categories by sans-serif capitals \({\textsf {C}}, {\textsf {D}}, \ldots \). In particular, the quasi-categories of small spaces is denoted \({\textsf {S}}_\text {S} \), and analogously for the universes \(\text {L} \) and \(\text {XL} \). The term ‘small space’ (used on its own, as opposed to ‘Segal space’, for instance) shall always mean an object in the quasi-category \({\textsf {S}}_\text {S} \) of small spaces, and analogously for the terms ‘large space’ and ‘extra large space’ and the universes \(\text {L} \) and \(\text {XL} \), respectively.
Enriched categories If \({{\mathscr {V}}}\) is a monoidal category and \({\mathscr {C}}\) is a \({{\mathscr {V}}}\)-enriched category (or \({{\mathscr {V}}}\)-category), we denote the \({{\mathscr {V}}}\)-enriched hom-objects of \({\mathscr {C}}\) by \(\underline{{\mathscr {C}}}^{{\mathscr {V}}}(-,-)\). If  is the category of simplicial sets, we also write
is the category of simplicial sets, we also write  . If \({{\mathscr {V}}}\) is a symmetric monoidal model category and \({\mathscr {C}}\) is a \({{\mathscr {V}}}\)-enriched model category (in the sense of [23, Sec. 4]), we will equivalently say that \({\mathscr {C}}\) is a model \({{\mathscr {V}}}\)-category.
. If \({{\mathscr {V}}}\) is a symmetric monoidal model category and \({\mathscr {C}}\) is a \({{\mathscr {V}}}\)-enriched model category (in the sense of [23, Sec. 4]), we will equivalently say that \({\mathscr {C}}\) is a model \({{\mathscr {V}}}\)-category.
Tractability We recall from [3, Def. 1.21] that a large model category \({{\mathscr {M}}}\) is tractable if there exists a regular \(\text {L} \)-small cardinal \(\lambda \) such that the category underlying \({{\mathscr {M}}}\) is locally \(\lambda \)-presentable, and there exist \(\text {L} \)-small sets I, J of morphisms with the following properties: the source and target of the morphisms in I and J are \(\lambda \)-presentable and cofibrant, the fibrations (resp. trivial fibrations) in \({{\mathscr {M}}}\) are precisely those morphisms satisfying the right lifting property with respect to J (resp. I). In particular, \({{\mathscr {M}}}\) is combinatorial. For further details and background on the formalism of enriched Bousfield localisation, we refer the reader to [3].
Diagrams For \({\mathscr {J}}\) a large category and \({\mathscr {C}}\) a \(\text {L} \)-tractable or \(\text {L} \)-combinatorial model category (cf. [2, 3]), the projective and the injective model structures on \(\textrm{Fun}({\mathscr {J}}, {\mathscr {C}})\) exist and are again \(\text {L} \)-tractable (resp. \(\text {L} \)-combinatorial); we denote them by \(\textrm{Fun}({\mathscr {J}}, {\mathscr {C}})_{proj}\) and \(\textrm{Fun}({\mathscr {J}}, {\mathscr {C}})_{inj}\), respectively. If \({\mathscr {J}}\) is a Reedy category, we denote the Reedy model structure on \(\textrm{Fun}({\mathscr {J}}, {\mathscr {C}})\) by \(\textrm{Fun}({\mathscr {J}}, {\mathscr {C}})_{Reedy}\).
Left Bousfield localisation. We recall that if \({{\mathscr {M}}}\) is a large simplicial model category with a chosen collection of morphisms A, then
-
\(z \in {{\mathscr {M}}}\) is A-local if it is fibrant in \({{\mathscr {M}}}\) and for every morphism \(f :x \rightarrow y\) in A the induced morphism
$$\begin{aligned} \underline{{{\mathscr {M}}}}(Qy, z) \xrightarrow {(Qf)^*} \underline{{{\mathscr {M}}}}(Qx,z) \end{aligned}$$is a weak homotopy equivalence in
 , and
, and -
\(f \in {{\mathscr {M}}}(x,y)\) is an A-local weak equivalence if for every A-local object \(z \in {{\mathscr {M}}}\) the morphism
$$\begin{aligned} \underline{{{\mathscr {M}}}}(Qy, z) \xrightarrow {(Qf)^*} \underline{{{\mathscr {M}}}}(Qx,z) \end{aligned}$$is a weak equivalence in
 .
.
In that case, the left Bousfield localisation \(L_A {{\mathscr {M}}}\), provided it exists, is a large simplicial model category with a simplicial left Quillen functor \({{\mathscr {M}}}\rightarrow L_A {{\mathscr {M}}}\) which is universal among simplicial left Quillen functors out of \({{\mathscr {M}}}\) that send A-local weak equivalences to weak equivalences (cf. for instance [3, Def. 4.42, Def. 4.45]).
2 Grothendieck Sites and Local Epimorphisms
We recall the definition of a Grothendieck pretopology and a site. Throughout this article, we assume that \({\mathscr {C}}\) is a small category.
Definition 2.1
We write \({{\widehat{{\mathscr {C}}}}}{:}{=}\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\) for the large category of small presheaves on \({\mathscr {C}}\).
Let \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {{\widehat{{\mathscr {C}}}}}\), \(c \mapsto {{\mathscr {Y}}}_c\), denote the Yoneda embedding of \({\mathscr {C}}\).
Definition 2.2
([26, Def. 2.1.9]) Let \({\mathscr {C}}\) be a small category.
-
(1)
A coverage, or Grothendieck pretopology, on \({\mathscr {C}}\) is given by assigning to every object \(c \in {\mathscr {C}}\) a small set \(\tau (c)\) of families of morphisms \(\{f_i :c_i \rightarrow c\}_{i \in I}\) (with \(I \in {{\mathscr {S}}\text {et} }_\text {S} \)) satisfying the following properties: \(\{1_c\} \in \tau (c)\) for each \(c \in {\mathscr {C}}\), and for every family \(\{f_i :c_i \rightarrow c\}_{i \in I} \in \tau (c)\) and any morphism \(g :c' \rightarrow c\) in \({\mathscr {C}}\) there exists a family \(\{f'_j :c'_j \rightarrow c'\}_{j \in J} \in \tau (c')\) such that for every \(j \in J\) we find some \(i \in I\) and a commutative diagram

-
(2)
The families in \(\{f_i :c_i \rightarrow c\}_{i \in I} \in \tau (c)\) are called covering families for c.
-
(3)
A (Grothendieck) site is a category \({\mathscr {C}}\) equipped with a coverage \(\tau \).
Later we will use the following technical condition:
Definition 2.3
We call a site \(({\mathscr {C}},\tau )\) closed if it satisfies the following condition: let \(\{c_i \rightarrow c\}_{i \in I}\) be any covering family in \(({\mathscr {C}}, \tau )\). Further, for each \(i \in I\), let \(\{c_{i,j} \rightarrow c_i\}_{j \in J_i}\) be a covering family in \(({\mathscr {C}},\tau )\). Then, there exists a covering family \(\{d_k \rightarrow c\}_{k \in K}\) such that every morphism \(d_k \rightarrow c\) factors through one of the composites \(c_{i,j} \rightarrow c_i \rightarrow c\).
Example 2.4
Let \({{\mathscr {C}}\text {art} }\) be the category of cartesian spaces, i.e. of sub-manifolds of \({\mathbb {R}}^\infty \) that are diffeomorphic to some \({\mathbb {R}}^n\), with smooth maps between these manifolds as morphisms. This category is small and has finite products. A coverage on \({{\mathscr {C}}\text {art} }\) is defined by calling a family \(\{\iota _i :c_i \rightarrow c\}_{i \in I}\) a covering family if it satisfies
-
(1)
all \(\iota _i\) are open embeddings (in particular \(\dim (c_i) = \dim (c)\) for all \(i \in I\)),
-
(2)
the \(\iota _i\) cover c, i.e. \(c = \bigcup _{i \in I} \iota _i(c_i)\), and
-
(3)
every finite intersection \(\iota _{i_0}(c_{i_0}) \cap \cdots \cap \iota _{i_m}(c_{i_m})\), with \(i_0, \ldots , i_m \in I\), is a cartesian space.
Coverings \(\{\iota _i :c_i \rightarrow c\}_{i \in I}\) with these properties are called differentiably good open coverings of c. They induce a coverage \(\tau _{dgop}\) on \({{\mathscr {C}}\text {art} }\), which turns \(({{\mathscr {C}}\text {art} },\tau _{dgop})\) into a site. This site is even closed, because every open cover of \(c \in {{\mathscr {C}}\text {art} }\) admits a differentiably good refinement [19, Cor. A.1]. There is a canonical embedding \({{\mathscr {C}}\text {art} }\hookrightarrow {{\mathscr {M}}{\text {fd}}}\) of \({{\mathscr {C}}\text {art} }\) into the category of all smooth manifolds. Thereby, any manifold M defines a presheaf \(\underline{M}\) on \({{\mathscr {C}}\text {art} }\), defined by \(\underline{M}(c) = {{\mathscr {M}}{\text {fd}}}(c,M)\). \(\triangleleft \)
Example 2.5
Let \({{\mathscr {O}}\text {p} }\) be the small category whose objects are open subsets of \({\mathbb {R}}^n\) for any (varying) \(n \in {\mathbb {N}}_0\) and whose morphisms are all smooth maps between such open subsets. The category \({{\mathscr {O}}\text {p} }\) has finite products and carries a coverage whose covering families are the open coverings. The resulting site is denoted \(({{\mathscr {O}}\text {p} },\tau _{op})\); observe that it is closed. \(\triangleleft \)
Definition 2.6
Let \(({\mathscr {C}},\tau )\) be a site. A morphism \(\pi :Y \rightarrow X\) in \({{\widehat{{\mathscr {C}}}}}\) is a \(\tau \)-local epimorphism if for every \(c \in {\mathscr {C}}\) and each morphism \(\varphi :{{\mathscr {Y}}}_c \rightarrow X\) there exists a covering \(\{f_j :c_j \rightarrow c\}_{j \in J} \in \tau (c)\) and morphisms \(\{ \varphi _j :{{\mathscr {Y}}}_{c_j} \rightarrow Y \}_{j \in J}\) with \(\pi \circ \varphi _j = \varphi \circ f_j\) for all \(j \in J\).
One directly checks the following:
Lemma 2.7
For any site \(({\mathscr {C}},\tau )\), the class of \(\tau \)-local epimorphisms is stable under pullback. In particular, the collection of \(\tau \)-local epimorphisms defines a coverage \({{\widehat{\tau }}}\) on \({{\widehat{{\mathscr {C}}}}}\).
Note that in the Grothendieck site \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\) every covering family consists of a single morphism. We list some general properties of \(\tau \)-local epimorphisms:
Lemma 2.8
Let \(({\mathscr {C}},\tau )\) be a site.
-
(1)
Consider morphisms \(p \in {{\widehat{{\mathscr {C}}}}}(Y,X)\), \(q \in {{\widehat{{\mathscr {C}}}}}(Z,Y)\). If \(p \circ q\) is a \(\tau \)-local epimorphism, then so is p.
-
(2)
For any covering family \(\{c_i \rightarrow c\}_{i \in I}\), the induced morphism \(\coprod _{i \in I} {{\mathscr {Y}}}_{c_i} \rightarrow {{\mathscr {Y}}}_c\) is a \(\tau \)-local epimorphism.
-
(3)
\(\tau \)-local epimorphisms are stable under colimits: let \({\mathscr {J}}\) be a small category, let \(D', D :{\mathscr {J}}\rightarrow {{\widehat{{\mathscr {C}}}}}\) be diagrams in \({{\widehat{{\mathscr {C}}}}}\), and let \(\pi :D' \rightarrow D\) be a morphism of diagrams such that each component \(\pi _j :D'_j \rightarrow D_j\) is a \(\tau \)-local epimorphism, for any \(j \in {\mathscr {J}}\). Then, the induced morphism \({\text {colim}}\, \pi :{\text {colim}}\, D' \rightarrow {\text {colim}}\, D\) is a \(\tau \)-local epimorphism.
-
(4)
If \(X(c) \ne \emptyset \) for each \(c \in {\mathscr {C}}\), then the projection \(X \times Z \rightarrow Z\) is a \(\tau \)-local epimorphism, for any \(Z \in {{\widehat{{\mathscr {C}}}}}\).
-
(5)
The site \(({\mathscr {C}},\tau )\) is closed if and only if \(\tau \)-local epimorphisms are stable under composition, if and only if \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\) is closed.
Proof
Claims (1) appears as property LE2 in [31, p. 390]. Claim (2) follows straightforwardly from the definition of a \(\tau \)-local epimorphism. Claim (3) can be found as [31, Prop. 16.1.12].
Claim (4) is immediate since by assumption the projection \(X(c) \times Y(c) \rightarrow Y(c)\) is surjective for each \(c \in {\mathscr {C}}\); we can hence use the identity covering of c to obtain the desired lift.
For (5), it readily follows from the closedness of \(({\mathscr {C}},\tau )\) that \(\tau \)-local epimorphisms are stable under composition, and thus also that \(({{\widehat{{\mathscr {C}}}}},{{\widehat{\tau }}})\) is closed. On the other hand, assume that \(\tau \)-local epimorphisms are stable under composition. Consider an object \(c \in {\mathscr {C}}\), a covering family \(\{f_i :c_i \rightarrow c\}_{i \in I}\), and for each \(i \in I\) a covering family \(\{c_{i,k} \rightarrow c_i\}_{k \in K_i}\). By claims (2) and (3), we thus obtain \(\tau \)-local epimorphisms
By assumption, their composition is a \(\tau \)-local epimorphism again, and hence it follows (using that \({{\widehat{{\mathscr {C}}}}}({{\mathscr {Y}}}_c,-)\) preserves colimits) that \(({\mathscr {C}},\tau )\) is closed. Finally, assume that \(({{\widehat{{\mathscr {C}}}}},{{\widehat{\tau }}})\) is closed. Let \(f :Z \rightarrow Y\) and \(g :Y \rightarrow X\) be \(\tau \)-local epimorphisms, and let \(p {:}{=}g \circ f\). By assumption, there exists a \(\tau \)-local epimorphism \(Z' \rightarrow X\) which factors through g; that is, there exists a morphism \(q :Z' \rightarrow Z\) such that \(p \circ q\) is a \(\tau \)-local epimorphism. But then p is a \(\tau \)-local epimorphism by claim (1). \(\square \)
Let \(({\mathscr {C}},\tau )\) be a site, and consider a covering \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\). We can form its Čech nerve, which is the simplicial object in \({{\widehat{{\mathscr {C}}}}}\) whose level-n object reads as
Note that, in general, \(C_{i_0 \ldots i_n} \in {{\widehat{{\mathscr {C}}}}}\) is not representable as soon as \(n \ne 0\). The simplicial structure morphisms are given by projecting out or doubling the i-th factor, respectively. Depending on the context we will view the Čech nerve \({\check{C}}{{\mathcal {U}}}\) either as a simplicial object \({\check{C}}{{\mathcal {U}}}_\bullet \) in \({{\widehat{{\mathscr {C}}}}}\) or as an augmented simplicial object \({\check{C}}{{\mathcal {U}}}_\bullet \rightarrow {{\mathscr {Y}}}_c\) in \({{\widehat{{\mathscr {C}}}}}\). For convenience, we recall the following definitions:
Definition 2.10
Let \(({\mathscr {C}},\tau )\) be a site, and let \(X \in {{\widehat{{\mathscr {C}}}}}\) be a presheaf on \({\mathscr {C}}\). Then, X is called a sheaf on \(({\mathscr {C}},\tau )\) if for every object \(c \in {\mathscr {C}}\) and for every covering family \(\{f_i :c_i \rightarrow c\}_{i \in I} \in \tau (c)\) the diagram

is an equaliser diagram in \({{\mathscr {S}}\text {et} }_\text {L} \). The category \({{\mathscr {S}}\text {h} }({\mathscr {C}},\tau )\) of sheaves on \(({\mathscr {C}},\tau )\) is the full subcategory of \({{\widehat{{\mathscr {C}}}}}\) on the sheaves.
3 Homotopy Sheaves and Descent Along Local Epimorphisms
Let \(({\mathscr {C}},\tau )\) be a small site, and let \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {{\widehat{{\mathscr {C}}}}}\) denote its Yoneda embedding. In this section we show that the homotopy right Kan extension along \({{\mathscr {Y}}}_*\) maps large higher \(\tau \)-sheaves on \({\mathscr {C}}\) to large higher \({{\widehat{\tau }}}\)-sheaves on \({{\widehat{{\mathscr {C}}}}}\). Here, \({{\widehat{\tau }}}\) is the pretopology of \(\tau \)-local epimorphisms on \({{\widehat{{\mathscr {C}}}}}\) (see Definition 2.6 and Lemma 2.7).
3.1 Sheaves of \(\infty \)-Groupoids
Let \({\mathscr {C}}\) be a small category. Let  denote the extra-large category of large simplicial presheaves on \({\mathscr {C}}\). It is enriched, tensored and cotensored over
denote the extra-large category of large simplicial presheaves on \({\mathscr {C}}\). It is enriched, tensored and cotensored over  . Composing the Yoneda embedding with the functor
. Composing the Yoneda embedding with the functor  , we obtain a fully faithful functor \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {\mathscr {H}}_{\infty ,0}\). From now on, we view the category \({\mathscr {H}}_{\infty ,0}\) as endowed with the projective model structure.
, we obtain a fully faithful functor \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {\mathscr {H}}_{\infty ,0}\). From now on, we view the category \({\mathscr {H}}_{\infty ,0}\) as endowed with the projective model structure.
Definition 3.1
A presheaf of \(\infty \)-groupoids on \({\mathscr {C}}\) is a fibrant object in \({\mathscr {H}}_{\infty ,0}\).
Proposition 3.2
\({\mathscr {H}}_{\infty ,0}\) is a left proper, tractable, model  -category. If \({\mathscr {C}}\) has finite products, then \({\mathscr {H}}_{\infty ,0}\) is additionally a symmetric monoidal model category.
-category. If \({\mathscr {C}}\) has finite products, then \({\mathscr {H}}_{\infty ,0}\) is additionally a symmetric monoidal model category.
Proof
The existence and tractability of the projective model structure follow from [3, Thm. 2.14] (since \({\mathscr {C}}\) is small). \({\mathscr {H}}_{\infty ,0}\) is left proper since its pushouts and weak equivalences are defined objectwise, its cofibrations are (in particular) objectwise cofibrations, and  is left proper. Its simplicial enrichment is a consequence of [3, Prop. 4.50]. If \({\mathscr {C}}\) has finite products, then \({\mathscr {H}}_{\infty ,0}\) is symmetric monoidal by [3, Prop. 4.52], using that the Yoneda embedding preserves limits and that \({\mathscr {H}}_{\infty ,0}\) is a simplicial model category. \(\square \)
is left proper. Its simplicial enrichment is a consequence of [3, Prop. 4.50]. If \({\mathscr {C}}\) has finite products, then \({\mathscr {H}}_{\infty ,0}\) is symmetric monoidal by [3, Prop. 4.52], using that the Yoneda embedding preserves limits and that \({\mathscr {H}}_{\infty ,0}\) is a simplicial model category. \(\square \)
Note that [3, Prop. 4.52] gives a more general criterion for when a projective model structure inherits a symmetric monoidal structure; however, for us the main case of interest will be where \({\mathscr {C}}\) admits finite products.
Projective model categories of simplicial presheaves have an explicit cofibrant replacement functor Q [18]. In order to write it down, it is convenient to introduce the two-sided bar construction; here, we follow [44, Sec. 4.2]:
Definition 3.3
Let \({{\mathscr {M}}}\) be a large cocomplete category tensored over  . Consider a large category \({\mathscr {I}}\) and functors \(H :{\mathscr {I}}\rightarrow {{\mathscr {M}}}\) and
. Consider a large category \({\mathscr {I}}\) and functors \(H :{\mathscr {I}}\rightarrow {{\mathscr {M}}}\) and  .
.
-
(1)
The two-sided simplicial bar construction of (G, H) is the simplicial object

-
(2)
The two-sided bar construction of (F, G) is the realisation of \(B_\bullet (G,{\mathscr {I}},H)\), i.e.

For later reference, we record the following direct consequences of this definition:
Lemma 3.4
In the setting of Definition 3.3, the following statements hold true:
-
(1)
Bar constructions commute: let \({\mathscr {J}}\) be a second large category, and let
 and \(D :{\mathscr {I}}\times {\mathscr {J}}\rightarrow {{\mathscr {M}}}\) be diagrams. Then, there is a canonical natural isomorphism $$\begin{aligned} B \big ( G', {\mathscr {J}}, B(G, {\mathscr {I}}, D) \big ) \cong B \big ( G, {\mathscr {I}}, B(G', {\mathscr {J}}, D) \big )\,. \end{aligned}$$
and \(D :{\mathscr {I}}\times {\mathscr {J}}\rightarrow {{\mathscr {M}}}\) be diagrams. Then, there is a canonical natural isomorphism $$\begin{aligned} B \big ( G', {\mathscr {J}}, B(G, {\mathscr {I}}, D) \big ) \cong B \big ( G, {\mathscr {I}}, B(G', {\mathscr {J}}, D) \big )\,. \end{aligned}$$ -
(2)
Bar constructions are pointwise: if
 is the category of large simplicial presheaves on a large category \({\mathscr {C}}\) and \(c \in {\mathscr {C}}\) is any object, then evaluation at c commutes with bar constructions: there is a natural isomorphism $$\begin{aligned} B(G,{\mathscr {I}},H)(c) \cong B \big ( G, {\mathscr {I}}, H(c) \big )\,. \end{aligned}$$
is the category of large simplicial presheaves on a large category \({\mathscr {C}}\) and \(c \in {\mathscr {C}}\) is any object, then evaluation at c commutes with bar constructions: there is a natural isomorphism $$\begin{aligned} B(G,{\mathscr {I}},H)(c) \cong B \big ( G, {\mathscr {I}}, H(c) \big )\,. \end{aligned}$$ -
(3)
In the above setting, let additionally
 . Then there is a natural morphism
. Then there is a natural morphism 
where \({\text {diag}}\) denotes the functor taking the diagonal of a bisimplicial set. This morphism is a weak equivalence of simplicial sets.
-
(4)
If \({{\mathscr {M}}}\) is a large simplicial model category with cofibrant replacement functor \(Q^{{\mathscr {M}}}\), the bar construction is a model for the homotopy colimit, i.e.
$$\begin{aligned} \underset{j \in {\mathscr {J}}}{{\text {hocolim}}}^{{\mathscr {M}}}(Dj) \simeq B(*, {\mathscr {J}}, Q^{{\mathscr {M}}}\circ D)\,. \end{aligned}$$In particular, if Dj is already cofibrant in \({{\mathscr {M}}}\) for each \(j \in {\mathscr {J}}\), then we may compute the homotopy colimit of D as
$$\begin{aligned} \underset{j \in {\mathscr {J}}}{{\text {hocolim}}}^{{\mathscr {M}}}(Dj) \simeq B(*, {\mathscr {J}}, D)\,. \end{aligned}$$
Proof
Claim (1) follows readily from the fact that colimits commute. Claim (2) is a direct consequence of the fact that colimits in presheaf categories are computed pointwise. Finally, Claim (3) is an application of the Bousfield-Kan map (see [22, Sec. 18.7] for details), and Claim (4) is [44, Cor. 5.1.3]. \(\square \)
Remark 3.5
Analogous statements hold true in the Grothendieck universes \(\text {S} \) and \(\text {XL} \) of small and extra-large sets, respectively. \(\triangleleft \)
We now define the cofibrant replacement functor in \({\mathscr {H}}_{\infty ,0}\) which we will be using throughout this article; it was introduced in [18].
Definition 3.6
We let \(Q :{\mathscr {H}}_{\infty ,0} \rightarrow {\mathscr {H}}_{\infty ,0}\) denote the functor whose action on \(F \in {\mathscr {H}}_{\infty ,0}\) is given by
Observe that for X a simplicially constant simplicial presheaf on \({\mathscr {C}}\), we have a canonical isomorphism
Definition 3.8
Let \(({\mathscr {C}},\tau )\) be a small Grothendieck site, and let \({{\check{\tau }}}\) denote the class of morphisms in \({\mathscr {H}}_{\infty ,0}\) consisting of Čech nerves of coverings in \(({\mathscr {C}},\tau )\) (see (2.9)). Since \({\mathscr {C}}\) is small, this is a small set. We let \({\mathscr {H}}_{\infty ,0}^{loc}\) denote the left Bousfield localisation \({\mathscr {H}}_{\infty ,0}^{loc} {:}{=}L_{{\check{\tau }}}{\mathscr {H}}_{\infty ,0}\) of the large category \({\mathscr {H}}_{\infty ,0}\). A sheaf of \(\infty \)-groupoids on \(({\mathscr {C}},\tau )\) is a fibrant object in \({\mathscr {H}}_{\infty ,0}^{loc}\).
The model structure on \({\mathscr {H}}_{\infty ,0}^{loc}\) is also called the local projective model structure on  . Explicitly, an object F in
. Explicitly, an object F in  is fibrant if
is fibrant if
-
(1)
F(c) is a Kan complex for every \(c \in {\mathscr {C}}\), and
-
(2)
for every covering family \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\) in \(({\mathscr {C}},\tau )\), the morphism

is a weak equivalence in
 (compare (2.9)). Here we have used that Q is a left adjoint.
(compare (2.9)). Here we have used that Q is a left adjoint.
Proposition 3.9
\({\mathscr {H}}_{\infty ,0}^{loc}\) is a proper, tractable,  -model category. If \({\mathscr {H}}_{\infty ,0}\) is symmetric monoidal as a model category, then so is \({\mathscr {H}}_{\infty ,0}^{loc}\).
-model category. If \({\mathscr {H}}_{\infty ,0}\) is symmetric monoidal as a model category, then so is \({\mathscr {H}}_{\infty ,0}^{loc}\).
Proof
The first claim follows form [3, Thm. 2.14, Thm 4.56] and the fact that  is a large, proper, tractable model category. The second claim is an application of [3, Thm. 4.58]. \(\square \)
is a large, proper, tractable model category. The second claim is an application of [3, Thm. 4.58]. \(\square \)
Remark 3.10
If \({\mathscr {C}}\) has finite products, then the conditions of [3, Prop. 4.52] are satisfied, so that in this case \({\mathscr {H}}_{\infty ,0}\), and hence also \({\mathscr {H}}_{\infty ,0}^{loc}\), are symmetric monoidal model categories. \(\triangleleft \)
The  -enriched hom in both \({\mathscr {H}}_{\infty ,0}\) and \({\mathscr {H}}_{\infty ,0}^{loc}\) is given by
-enriched hom in both \({\mathscr {H}}_{\infty ,0}\) and \({\mathscr {H}}_{\infty ,0}^{loc}\) is given by

where the argument of the end is given by the internal hom in  . In particular, there is a natural isomorphism \(\underline{{\mathscr {H}}}_{\infty ,0}({{\mathscr {Y}}}_c, F) \cong F(c)\) for any \(c \in {\mathscr {C}}\) and any \(F \in {\mathscr {H}}_{\infty ,0}\).
. In particular, there is a natural isomorphism \(\underline{{\mathscr {H}}}_{\infty ,0}({{\mathscr {Y}}}_c, F) \cong F(c)\) for any \(c \in {\mathscr {C}}\) and any \(F \in {\mathscr {H}}_{\infty ,0}\).
Since \({\mathscr {C}}\) is a small category (hence also large, since \(\text {S} \in \text {L} \)) and \({{\mathscr {S}}\text {et} }_\text {S} \) is a large category, \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\) is a large category. We define the extra-large category

Since  is \(\text {L} \)-tractable, the projective model structure on \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) exists and is itself \(\text {L} \)-tractable [3, Thm. 2.14]. We will always view \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) as endowed with this projective model structure.
is \(\text {L} \)-tractable, the projective model structure on \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) exists and is itself \(\text {L} \)-tractable [3, Thm. 2.14]. We will always view \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) as endowed with this projective model structure.
By Proposition 2.7, if \(({\mathscr {C}},\tau )\) is a small site, then \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\) is a large site. Let \(({{\widehat{\tau }}}){}\check{}\) denote the large set of Čech nerves of coverings in \(({{\widehat{{\mathscr {C}}}}},{{\widehat{\tau }}})\) (this is a large set since \({{\widehat{{\mathscr {C}}}}}\) is large). Since \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) is left proper and \(\text {L} \)-tractable, and \(({{\widehat{\tau }}}){}\check{}\) is \(\text {L} \)-small, we can form the left Bousfield localisation
Both \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) and \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}^{loc}\) are symmetric monoidal since \({{\widehat{{\mathscr {C}}}}}\) has finite products (by Propositions 3.2 and 3.9, respectively).
The Yoneda embedding \({{\mathscr {Y}}}:{\mathscr {C}}\rightarrow {{\widehat{{\mathscr {C}}}}}\) induces a pullback functor \({{\mathscr {Y}}}^* :{{\widehat{{\mathscr {H}}}}}_{\infty ,0} \rightarrow {\mathscr {H}}_{\infty ,0}\). Since both \({\mathscr {C}}\) and \({{\widehat{{\mathscr {C}}}}}\) are large, and since both \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) and \({\mathscr {H}}_{\infty ,0}\) have all large limits and colimits, there is a triple of adjunctions

We can compute the right adjoint as
(Note that here we view \(X \in {{\widehat{{\mathscr {C}}}}}\) as an object in \({\mathscr {H}}_{\infty ,0}\) via the canonical inclusions  .)
.)
We now ask whether one of the functors \({{\mathscr {Y}}}_!\) or \({{\mathscr {Y}}}_*\) maps sheaves of \(\infty \)-groupoids on \(({\mathscr {C}},\tau )\) to sheaves of \(\infty \)-groupoids on \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\), i.e. preserves fibrant objects as a functor \({\mathscr {H}}_{\infty ,0}^{loc} \rightarrow {{\widehat{{\mathscr {H}}}}}_{\infty ,0}^{loc}\). Since this indicates that we are looking for a right Quillen functor, we focus on the right adjoint \({{\mathscr {Y}}}_*\). In general, \({{\mathscr {Y}}}_*\) will not even preserve fibrant objects as a functor \({\mathscr {H}}_{\infty ,0} \rightarrow {{\widehat{{\mathscr {H}}}}}_{\infty ,0}\). However, if \({\tilde{Q}} :{\mathscr {H}}_{\infty ,0} \rightarrow {\mathscr {H}}_{\infty ,0}\) is a functorial cofibrant replacement, then the functor
preserves fibrations and trivial fibrations: \({\mathscr {H}}_{\infty ,0}\) is a model  -category, and so the simplicially enriched hom
-category, and so the simplicially enriched hom

is a right Quillen functor whenever \(A \in \underline{{\mathscr {H}}}_{\infty ,0}\) is cofibrant.
Remark 3.11
The above holds true for any cofibrant replacement functor \({\tilde{Q}}\) in \({\mathscr {H}}_{\infty ,0}\). However, for technical reasons we always use Dugger’s functor Q from (3.7) for cofibrant replacement in the projective model structure of simplicial presheaves in the remainder of this article. We abbreviate \(S_{\infty ,0} {:}{=}S^Q_{\infty ,0}\). \(\triangleleft \)
Let \(F \in {\mathscr {H}}_{\infty ,0}\) and \(X \in {{\widehat{{\mathscr {C}}}}}\). Using that QX is a bar construction we compute

where  and \(B^{{\mathscr {H}}_{\infty ,0}}\) are the cobar and bar constructions in
and \(B^{{\mathscr {H}}_{\infty ,0}}\) are the cobar and bar constructions in  and in \({\mathscr {H}}_{\infty ,0}\), respectively. If F is projectively fibrant, then the last expression is a model for the homotopy limit (see also recalled as Proposition 3.31 below),
and in \({\mathscr {H}}_{\infty ,0}\), respectively. If F is projectively fibrant, then the last expression is a model for the homotopy limit (see also recalled as Proposition 3.31 below),

Now, using the Yoneda Lemma and [44, Ex. 9.2.11] we conclude:
Proposition 3.12
If \(F \in {\mathscr {H}}_{\infty ,0}\) is fibrant, \(S_{\infty ,0} F\) is the homotopy right Kan extension of F along the (opposite of the) Yoneda embedding of \({\mathscr {C}}\), i.e.
Remark 3.13
In view of Sect. 5, we emphasize that \(S_{\infty ,0}\) is a presentation of the \(\infty \)-categorical right Kan extension of presheaves of spaces on \({\mathscr {C}}\) to presheaves of spaces on \({{\widehat{{\mathscr {C}}}}}\). \(\triangleleft \)
In order to show that \(S_{\infty ,0}\) is a right Quillen functor, it remains to show that it is a right adjoint. Since \({{\widehat{{\mathscr {C}}}}}\) is a large category, \({{\widehat{{\mathscr {C}}}}}\)-indexed (co)ends exist in  , the extra-large category of large simplicial sets. Therefore, a left adjoint to \(S_{\infty ,0}\) is given by
, the extra-large category of large simplicial sets. Therefore, a left adjoint to \(S_{\infty ,0}\) is given by
We also set
Lemma 3.14
There is a canonical natural isomorphism
Thus, \(Re_{\infty ,0}\) is also a left adjoint to \(S_{\infty ,0}\).
Proof
Using (3.7), we have the following natural isomorphisms
where the isomorphism is an application of the Yoneda Lemma for \({{\widehat{{\mathscr {C}}}}}\). \(\square \)
Proposition 3.15
The functors \(Re_{\infty ,0}\) and \(S_{\infty ,0}\) give rise to a simplicial Quillen adjunction which sits inside the following non-commutative diagram

Further, there exists a natural isomorphism \(\eta :Re_{\infty ,0} \circ {\widehat{{{\mathscr {Y}}}}} \overset{\cong }{\longrightarrow }Q\).
Proof
We have already shown above that \(Re_{\infty ,0} \dashv S_{\infty ,0}\) and that \(S_{\infty ,0}\) preserves fibration and trivial fibrations. The rest is then a direct application of [18, Prop. 2.3]. In the present case, \(\eta \) as written down there turns out to be an isomorphism as a consequence of the Yoneda Lemma: recall that \(Re_{\infty ,0} = Q \circ {{\mathscr {Y}}}^*\) and that there is a canonical isomorphism
natural in \(X \in {{\widehat{{\mathscr {C}}}}}\). \(\square \)
Proposition 3.16
The functors \(Re_{\infty ,0}\) and \(S_{\infty ,0}\) have the following properties:
-
(1)
The functor \(Re_{\infty ,0} :{{\widehat{{\mathscr {H}}}}}_{\infty ,0} \rightarrow {\mathscr {H}}_\infty \) is homotopical.
-
(2)
Let \({{\widehat{Q}}}:{{\widehat{{\mathscr {H}}}}}_{\infty ,0} \rightarrow {{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) denote the cofibrant replacement functor on \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) defined in analogy with (3.7). For each fibrant object \(F \in {\mathscr {H}}_{\infty ,0}\), there is a zig-zag of weak equivalences
$$\begin{aligned} F \overset{\sim }{\longleftarrow }\ Q F \overset{\sim }{\longrightarrow }Re_{\infty ,0} \circ S_{\infty ,0}(F) \overset{\sim }{\longleftarrow }\ Re_{\infty ,0} \circ {{\widehat{Q}}}\circ S_{\infty ,0} (F) \,, \end{aligned}$$which is natural in F.
Proof
By Lemma 3.14, \(Re_{\infty ,0} \cong Q \circ {{\mathscr {Y}}}^*\). The functor \({{\mathscr {Y}}}^*\) is homotopical since weak equivalences in both \({\mathscr {H}}_{\infty ,0}\) and in \({{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) are defined objectwise. Thus, claim (1) follows since Q is homotopical. As a consequence, the morphism
is a weak equivalence. For \(F \in {\mathscr {H}}_{\infty ,0}\), we find that
and since F is fibrant and \({{\mathscr {Y}}}_c\) is cofibrant, the functor \(\underline{{\mathscr {H}}}_{\infty ,0}(-,F)\) preserves the weak equivalence \(Q{{\mathscr {Y}}}_c \rightarrow {{\mathscr {Y}}}_c\). Hence, there is a natural weak equivalence \(F \overset{\sim }{\longrightarrow }{{\mathscr {Y}}}^* \circ S_{\infty ,0}(F)\). To complete the proof, we apply the homotopical functor Q to this morphism. \(\square \)
We now investigate whether the Quillen adjunction \(Re_{\infty ,0} \dashv S_{\infty ,0}\) between the projective model structures descends to a Quillen adjunction between the local projective model structures. We recall the following standard result:
Proposition 3.17
[22, Prop. 3.1.6, Prop. 3.3.18] Let \({{\mathscr {M}}}\) and \({{\mathscr {N}}}\) be two large simplicial model categories, and let \(F \dashv G\) be a simplicial Quillen adjunction from \({{\mathscr {M}}}\) to \({{\mathscr {N}}}\). Suppose that A, B are large sets of morphisms in \({{\mathscr {M}}}\) and in \({{\mathscr {N}}}\), respectively, such that the left Bousfield localisations \(L_A {{\mathscr {M}}}\) and \(L_B {{\mathscr {N}}}\) exist. If G maps B-local objects to A-local objects, then \(F \dashv G\) descends to a Quillen adjunction between the localised model categories.
Theorem 3.18
([17, Cor. A.3]) Let \({\mathscr {C}}\) be a small category endowed with a coverage \(\tau \), and let \(\pi :Y \rightarrow X\) be a \(\tau \)-local epimorphism in \({{\widehat{{\mathscr {C}}}}}\) with Čech nerve \({\check{C}}\pi \). The augmentation map \(\pi ^{[\bullet ]} :{\check{C}}\pi \rightarrow X\) is a weak equivalence in \({\mathscr {H}}_{\infty ,0}^{loc}\).
The proof of Theorem 3.18 is rather technical; it requires a “wrestling match with the small object argument” ([17] Subsection A.12). We refer the reader to that reference for details.
Remark 3.19
In [17], Theorem 3.18 is proven for the Čech localisation of the injective model structure \({\mathscr {H}}^i\) on \({\mathscr {H}}\). However, it also holds true in \({\mathscr {H}}_{\infty ,0}\) because the injective and projective model structures on \({\mathscr {H}}\) (and \({{\widehat{{\mathscr {H}}}}}\)) have the same weak equivalences, and so do the associated local model structures (see also [11, Prop. 2.6] for details). \(\triangleleft \)
Lemma 3.20
Let \(\pi :Y \rightarrow X\) be a \(\tau \)-local epimorphism in \({{\widehat{{\mathscr {C}}}}}\). Let  denote the simplicial diagram which sends
denote the simplicial diagram which sends  to the simplicially constant presheaf \({\check{C}}\pi _n\). There is a commutative triangle in \({\mathscr {H}}_{\infty ,0}\):
to the simplicially constant presheaf \({\check{C}}\pi _n\). There is a commutative triangle in \({\mathscr {H}}_{\infty ,0}\):

The top morphism is an objectwise weak equivalence, and the diagonal morphisms are weak equivalences in \({\mathscr {H}}_{\infty ,0}^{loc}\).
Proof
The top morphism is induced by the Bousfield-Kan, or last-vertex map. It is an objectwise weak equivalence by Lemma 3.4(3). The right-hand side is a local weak equivalence by Theorem 3.18. Thus, it remains to show that the triangle commutes. We check this explicitly: for each object \(c \in {\mathscr {C}}\), there are canonical natural isomorphisms

where \({\textsf {N}}\) denotes the nerve functor. For  , recall the last-vertex map
, recall the last-vertex map

of small simplicial sets (see, for instance, [14, Lemma 7.3.11, Par. 7.3.14]). We describe this explicitly in our case, i.e. for \(X = {\check{C}}\pi (c)\). An n-simplex in this simplicial set is explicitly given by a sequence of morphisms

of small simplicial sets. We denote these data by \((\alpha , \kappa )\). Consider the map \(\varphi _\alpha :[n] \rightarrow [k_n]\) in  which acts as
which acts as
The top morphism in diagram (3.21) acts by sending the n-simplex \((\alpha , \kappa )\) to the n-simplex of \({\check{C}}\pi (c)\) which is given by the composition

where the first map is the one constructed above from the data \((\alpha , \kappa )\). Explicitly, for a given n-simplex  , the resulting map
, the resulting map
is the projection onto the Y-factors in positions \(\varphi _\alpha (0), \ldots , \varphi _\alpha (n)\). This map commutes with the maps to X. \(\square \)
Proposition 3.22
The functor \(S_{\infty ,0} :{\mathscr {H}}_{\infty ,0}^{loc} \rightarrow {{\widehat{{\mathscr {H}}}}}_{\infty ,0}^{loc}\) preserves local objects.
Proof
Let \(\pi :Y \rightarrow X\) be a \(\tau \)-local epimorphism in \({{\widehat{{\mathscr {C}}}}}\), and let \(F \in {\mathscr {H}}_{\infty ,0}^{loc}\) be fibrant. We need to show that the canonical morphism

is a weak equivalence in  . Substituting the definition of \(S_{\infty ,0}\), this is the same as the canonical map
. Substituting the definition of \(S_{\infty ,0}\), this is the same as the canonical map

Observe that there is a canonical isomorphism

in the homotopy category  (in fact, this can even be modelled as an isomorphism in
(in fact, this can even be modelled as an isomorphism in  in light of Lemma 3.4(1) and Proposition 3.31 below). Since the functor Q is a bar construction (see (3.7)), it commutes with the homotopy colimit (which is also a bar construction) by Lemma 3.4(1). Then, the morphism
in light of Lemma 3.4(1) and Proposition 3.31 below). Since the functor Q is a bar construction (see (3.7)), it commutes with the homotopy colimit (which is also a bar construction) by Lemma 3.4(1). Then, the morphism

is the image of the left-hand diagonal morphism in the commutative triangle (3.21) under the functor \(\underline{{\mathscr {H}}}_{\infty ,0}(Q(-),F)\). Observe that the functor

is homotopical since F is fibrant in \({\mathscr {H}}_{\infty ,0}^{loc}\) and \({\mathscr {H}}_{\infty ,0}^{loc}\) is enriched over  . Combining this with Lemma 3.20, we obtain that the above morphism is a weak equivalence in
. Combining this with Lemma 3.20, we obtain that the above morphism is a weak equivalence in  . \(\square \)
. \(\square \)
Combining Proposition 3.17 and Proposition 3.22, we obtain
Theorem 3.23
The Quillen adjunction \(Re_{\infty ,0}: {{\widehat{{\mathscr {H}}}}}_{\infty ,0} \rightleftarrows {\mathscr {H}}_{\infty ,0}:S_{\infty ,0}\) induces a Quillen adjunction

In Sect. 5 we provide a version of Theorem 3.23 for fully coherent diagrams of spaces in a quasi-categorical language; on the underlying quasi-categories, we will show that \(S_{\infty ,0}\) is fully faithful and we identify its essential image.
3.2 Homotopy Sheaves with Values in Simplicial Model Categories
We now extend the results from Sect. 3.1 to homotopy sheaves on a small site \(({\mathscr {C}}, \tau )\), valued not just in  , but in any large, combinatorial or cellular simplicial model category. We begin by recalling some technology for enriched model categories.
, but in any large, combinatorial or cellular simplicial model category. We begin by recalling some technology for enriched model categories.
Recall the notion of a \({{\mathscr {V}}}\) be a symmetric monoidal model category. A \({{\mathscr {V}}}\)-enriched model category, or model \({{\mathscr {V}}}\)-category \({{\mathscr {M}}}\) (see, for instance, [23, Def. 4.2.18]). We denote the three functors which are part of the enrichment by
We import the following definition (using [44, Thms. 7.6.3, 11.5.1]):
Definition 3.24
Let \({\mathscr {I}}\) be a small category.
-
(1)
The weighted \({\mathscr {I}}\)-colimit functor of \({{\mathscr {M}}}\) is the functor
$$\begin{aligned} (-) \otimes _{\mathscr {I}}(-) :\textrm{Fun}({\mathscr {I}}^{\text {op}}, {{\mathscr {V}}}) \times \textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}}) \longrightarrow {{\mathscr {M}}}\,, \qquad (D, F) \longmapsto \int ^{i \in {\mathscr {I}}} Di \otimes Fi\,. \end{aligned}$$(3.25) -
(2)
The weighted \({\mathscr {I}}\)-limit functor of \({{\mathscr {M}}}\) is the functor
$$\begin{aligned} \{-,-\}^{\mathscr {I}}:\textrm{Fun}({\mathscr {I}}, {{\mathscr {V}}})^{\text {op}}\times \textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}}) \longrightarrow {{\mathscr {M}}}\,, \qquad (D, F) \longmapsto \int _{i \in {\mathscr {I}}} \{Di, Fi\}\,. \end{aligned}$$(3.26)
From now on we consider  with the Kan-Quillen model structure, and thus \({{\mathscr {M}}}\) a large simplicial model category. The following result is [20, Thms. 3.2, 3.3] (see also [44, Thm. 11.5.1]).
with the Kan-Quillen model structure, and thus \({{\mathscr {M}}}\) a large simplicial model category. The following result is [20, Thms. 3.2, 3.3] (see also [44, Thm. 11.5.1]).
Theorem 3.27
Let \({{\mathscr {M}}}\) be a large simplicial model category and \({\mathscr {I}}\) a large category. Suppose that the projective and injective model structures on \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) both exist.
-
(1)
The weighted \({\mathscr {I}}\)-colimit functor (3.25) is a left Quillen functor of two variables [23, Def. 4.2.1] if its source and target are either endowed with the projective and injective model structures, respectively, or with the injective and projective model structures, respectively.
-
(2)
The weighted \({\mathscr {I}}\)-limit functor (3.26) is a right Quillen functor of two variables if its source and target are either both endowed with the projective model structures, or are both endowed with the injective model structures.
Recall that if \({{\mathscr {M}}}\) is combinatorial (in \(\text {L} \)), then the projective and injective model structures on \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) exist and are again combinatorial (see, for instance, [3, Thms. 2.14, 2.16]). The projective model structure also exists when \({{\mathscr {M}}}\) is cellular, and is itself cellular [22, Prop. 12.1.5].
We also define functors

In the original reference [20] the following observation is the crucial ingredient in the proof of Theorem 3.27:
Proposition 3.28
In the situation of Theorem 3.27(2), with either the projective or injective model structure on both  and \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\), the functors
and \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\), the functors

form a Quillen adjunction of two variables.
Proof
In the projective case the functor

applies the  -enrichment of \({{\mathscr {M}}}\) objectwise. Since pullbacks in functor categories are computed objectwise, it follows from the properties of this enrichment that \(\underline{{{\mathscr {M}}}}^{ptw}_{\mathscr {I}}(-,-)\) satisfies the pullback-product axiom (see [23, Lemma 4.2.2]). One proves the injective case analogously, using the functor \((-) \otimes ^{ptw}_{\mathscr {I}}(-)\) in place of \(\underline{{{\mathscr {M}}}}^{ptw}_{\mathscr {I}}\). \(\square \)
-enrichment of \({{\mathscr {M}}}\) objectwise. Since pullbacks in functor categories are computed objectwise, it follows from the properties of this enrichment that \(\underline{{{\mathscr {M}}}}^{ptw}_{\mathscr {I}}(-,-)\) satisfies the pullback-product axiom (see [23, Lemma 4.2.2]). One proves the injective case analogously, using the functor \((-) \otimes ^{ptw}_{\mathscr {I}}(-)\) in place of \(\underline{{{\mathscr {M}}}}^{ptw}_{\mathscr {I}}\). \(\square \)
As before, we let \(Q :{\mathscr {H}}_{\infty ,0} \rightarrow {\mathscr {H}}_{\infty ,0}\) denote Dugger’s cofibrant replacement functor (see Definition 3.6). Consider the functors
They form an adjoint pair

Proposition 3.30
The adjunction (3.29) is a Quillen adjunction with respect to the projective model structures.
Proof
Let \(X \in {{\widehat{{\mathscr {C}}}}}\), and consider the functor
Here we have used the notation from (3.26). By Theorem 3.27 and [23, Rmk. 4.2.3] this functor is right Quillen, for each \(X \in {{\widehat{{\mathscr {C}}}}}\). Since fibrations and weak equivalences in the projective model structure on \(\textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {M}}})\) are defined objectwise, it follows that the functor \(S_{{\mathscr {M}}}\) preserves projective fibrations and trivial fibrations. \(\square \)
We recall some useful technology for computing homotopy limits from [44] (see, in particular, Chapters 4–6). Let \({{\mathscr {M}}}\) be a large simplicial model category (enriched, tensored and cotensored over  ). Let \({\mathscr {I}}\) be a large category and consider functors
). Let \({\mathscr {I}}\) be a large category and consider functors  and \(F :{\mathscr {I}}\rightarrow {{\mathscr {M}}}\). The (two-sided) cosimplicial cobar construction associated to these data is the cosimplicial object in \({{\mathscr {M}}}\) whose l-th level reads as
and \(F :{\mathscr {I}}\rightarrow {{\mathscr {M}}}\). The (two-sided) cosimplicial cobar construction associated to these data is the cosimplicial object in \({{\mathscr {M}}}\) whose l-th level reads as
where  denotes the nerve of \({\mathscr {I}}\). The (two-sided) cobar construction \(C(G, {\mathscr {I}}, F)\) in \({{\mathscr {M}}}\) is the totalisation
denotes the nerve of \({\mathscr {I}}\). The (two-sided) cobar construction \(C(G, {\mathscr {I}}, F)\) in \({{\mathscr {M}}}\) is the totalisation

formed in \({{\mathscr {M}}}\). If the ambient model category \({{\mathscr {M}}}\) is not clear from context, we will write \(C_{{\mathscr {M}}}\) for the cobar construction in \({{\mathscr {M}}}\).
Proposition 3.31
[44, Cor. 5.1.3] The cobar construction is a model for the homotopy limit: let \({{\mathscr {M}}}\) be a large simplicial model category with fibrant replacement functor \(R^{{\mathscr {M}}}\), and let \(F :{\mathscr {I}}\rightarrow {{\mathscr {M}}}\) a functor as above. Then,
In particular, if \(Fi \in {{\mathscr {M}}}\) is fibrant for each \(i \in {\mathscr {I}}\), then
Lemma 3.32
Let \({{\mathscr {M}}}\) be a large simplicial model category, \({\mathscr {I}}\) a large category and \(F :{\mathscr {I}}\rightarrow {{\mathscr {M}}}\) a functor. Suppose that the projective model structure on \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) exists and that F is projectively fibrant. Then, the cobar construction \(C(*, {\mathscr {I}}, F) \in {{\mathscr {M}}}\) is fibrant.
Proof
Recall the notation from Definition 3.24. By [44, Thm. 6.6.1] there is a canonical natural isomorphism
By Theorem 3.27, the functor  is a right Quillen functor in two variables if we endow
is a right Quillen functor in two variables if we endow  and \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) with their projective model structures. The claim then follows from the fact that the functor
and \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) with their projective model structures. The claim then follows from the fact that the functor  is a projectively cofibrant object in \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) [22, Cor. 14.8.8]. \(\square \)
is a projectively cofibrant object in \(\textrm{Fun}({\mathscr {I}}, {{\mathscr {M}}})\) [22, Cor. 14.8.8]. \(\square \)
Definition 3.33
Suppose \({{\mathscr {M}}}\) is left proper, as well as cellular or combinatorial. Let \(\tau \) be a Grothendieck coverage on \({\mathscr {C}}\), and \({{\widehat{\tau }}}\) the induced Grothendieck coverage of \(\tau \)-local epimorphisms on \({{\widehat{{\mathscr {C}}}}}\).
-
(1)
Let \(S({{\mathscr {M}}}, \tau )\) be the collection of morphisms in \(\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\) of the form
$$\begin{aligned} Q ({\check{C}}{{\mathcal {U}}}\rightarrow {{\mathscr {Y}}}_c) \otimes _{{\mathscr {C}}^{\text {op}}}^{ptw} m\,, \end{aligned}$$where \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\) is a \(\tau \)-covering of \(c \in {\mathscr {C}}\), with associated Čech nerve \({\check{C}}{{\mathcal {U}}}\in {\mathscr {H}}_{\infty ,0}\), and \(m \in {{\mathscr {M}}}\) is a cofibrant object in \({{\mathscr {M}}}\). Define the left Bousfield localisation
$$\begin{aligned} \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})^{loc} {:}{=}L_{S({{\mathscr {M}}}, \tau )} \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\,. \end{aligned}$$ -
(2)
Let \(S({{\mathscr {M}}}, {{\widehat{\tau }}})\) be the collection of morphisms in \(\textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {M}}})\) of the form
$$\begin{aligned} ({\check{C}}\pi \rightarrow {{\widehat{{{\mathscr {Y}}}}}}_X) \otimes _{{\mathscr {C}}^{\text {op}}}^{ptw} m\,, \end{aligned}$$where \(\pi :Y \rightarrow X\) is a \(\tau \)-local epimorphism in \({{\widehat{{\mathscr {C}}}}}\), with associated Čech nerve \({\check{C}}\pi \in {{\widehat{{\mathscr {H}}}}}_{\infty ,0}\), and \(m \in {{\mathscr {M}}}\) is a cofibrant object in \({{\mathscr {M}}}\). Define the left Bousfield localisation
$$\begin{aligned} \textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {M}}})^{loc} {:}{=}L_{S({{\mathscr {M}}}, {{\widehat{\tau }}})} \textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {M}}})\,. \end{aligned}$$
These Bousfield localisations exist by [22, Thm. 4.4.1] and [3, Thm. 4.7]. The following is a generalisation of [3, Thm. 4.56] to the case where the model category \({{\mathscr {M}}}\) is not monoidal:
Proposition 3.34
In the situation of Definition 3.33 the following statements hold true:
-
(1)
An object \(F \in \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\) is \(S({{\mathscr {M}}}, \tau )\)-local if and only if it is projectively fibrant and, for each \(\tau \)-covering \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\), the induced morphism

in \({{\mathscr {M}}}\) is a weak equivalence (where \({\check{C}}_k {{\mathcal {U}}}\) is viewed as a simplicially constant presheaf on \({\mathscr {C}}\)).
-
(2)
An object \({\widehat{G}} \in \textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {M}}})\) is \(S({{\mathscr {M}}}, {{\widehat{\tau }}})\)-local if and only if it is projectively fibrant and, for each \({{\widehat{\tau }}}\)-covering \(\pi :Y \rightarrow X\) in \({{\widehat{{\mathscr {C}}}}}\), the induced morphism

in \({{\mathscr {M}}}\) is a weak equivalence.
Remark 3.35
Suppose that \(({\mathscr {C}}, \tau )\) is such that, for each \(\tau \)-covering \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\), each presheaf \(C_{i_0 \cdots i_k}\) from (2.9) is again representable. In that case, the Čech nerve \({\check{C}}{{\mathcal {U}}}\) is projectively cofibrant (it is then objectwise a coproduct of representables), and so we can omit the cofibrant replacement functor Q from Definition 3.33(1) and Proposition 3.34. Furthermore, the enrichment and the Yoneda Lemma provide a canonical isomorphism
thus reproducing the more familiar form of the homotopy descent condition. \(\triangleleft \)
Proof of Proposition 3.34
We show Claim (1); the proof of Claim (2) is analogous. By definition, an object \(F \in \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\) is \(S({{\mathscr {M}}}, \tau )\)-local if and only if it is projectively fibrant and, for each cofibrant \(m \in {{\mathscr {M}}}\) and each \(\tau \)-covering \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\) in \({\mathscr {C}}\), the morphism
induced by the augmentation \({\check{C}}{{\mathcal {U}}}\rightarrow {{\mathscr {Y}}}_c\) is a weak homotopy equivalence in  (note that the left-hand arguments in both functors above are cofibrant in \(\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\), and so the above simplicially enriched hom spaces indeed compute map** spaces). By adjointness, this morphism is isomorphic to the morphism
(note that the left-hand arguments in both functors above are cofibrant in \(\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\), and so the above simplicially enriched hom spaces indeed compute map** spaces). By adjointness, this morphism is isomorphic to the morphism
Next, we use the isomorphisms in the homotopy category  ,
,

Here we have used that we can commute Q and the homotopy colimit, since both are bar constructions. The claim now follows from the fact that a morphism \(f :a \rightarrow b\) in \({{\mathscr {M}}}\) between fibrant objects is a weak equivalence if and only if, for each cofibrant \(m \in {{\mathscr {M}}}\), the induced morphism
is a weak homotopy equivalence; in other words, we use that the functors \(\underline{{{\mathscr {M}}}}(m, -)\), for \(m \in {{\mathscr {M}}}\) cofibrant, jointly detect weak equivalences between fibrant objects [22, Prop. 9.7.1]. \(\square \)
Definition 3.36
If \(({\mathscr {D}}, \tau _{\mathscr {D}})\) is an \(\text {L} \)-small category with a Grothendieck coverage \(\tau _{\mathscr {D}}\) and \({{\mathscr {M}}}\) a left proper, \(\text {L} \)-small, combinatorial or cellular model category, then we call the fibrant objects of \(L_{S({{\mathscr {M}}}, \tau _{\mathscr {D}})}\textrm{Fun}({\mathscr {D}}^{\text {op}}, {{\mathscr {M}}})\) the \({{\mathscr {M}}}\)-valued (homotopy) sheaves on \({\mathscr {D}}\).
Theorem 3.37
Let \({{\mathscr {M}}}\) be a left proper cellular or combinatorial simplicial model category in the universe \(\text {L} \) and \({\mathscr {C}}\) a small category. Let \(\tau \) be a Grothendieck coverage on \({\mathscr {C}}\), and \({{\widehat{\tau }}}\) the induced Grothendieck coverage of \(\tau \)-local epimorphisms on \({{\widehat{{\mathscr {C}}}}}\). The Quillen adjunction (3.29) descends to a Quillen adjunction

Proof
By Proposition 3.17, it suffices to show that the right adjoint \(S_{{\mathscr {M}}}\) preserves local objects. To that end, let \(F \in \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\) be \(S({\mathscr {C}}, \tau )\)-local, and let \(\pi :Y \rightarrow X\) be a \(\tau \)-local epimorphism in \({{\widehat{{\mathscr {C}}}}}\). By Proposition 3.34 we thus need to show that the canonical morphism

is a weak equivalence in \({{\mathscr {M}}}\). Since \({\check{C}}_k \pi \) is representable in  , the Yoneda Lemma for \({{\widehat{{\mathscr {C}}}}}\) implies that
, the Yoneda Lemma for \({{\widehat{{\mathscr {C}}}}}\) implies that
The problem is thus equivalent to showing that the canonical morphism

is a weak equivalence in \({{\mathscr {M}}}\). Since the functors  jointly detect weak equivalences, where m ranges over all cofibrant objects in \({{\mathscr {M}}}\) (and where \({{\mathscr {M}}}_{fib} \subset {{\mathscr {M}}}\) is the full subcategory on the fibrant objects), it suffices to show that, for each cofibrant \(m \in {{\mathscr {M}}}\), the morphism
jointly detect weak equivalences, where m ranges over all cofibrant objects in \({{\mathscr {M}}}\) (and where \({{\mathscr {M}}}_{fib} \subset {{\mathscr {M}}}\) is the full subcategory on the fibrant objects), it suffices to show that, for each cofibrant \(m \in {{\mathscr {M}}}\), the morphism

is a weak homotopy equivalence. Here we have used that F is projectively fibrant, so that the functor \(\{Q(-), F\}^{{\mathscr {C}}^{\text {op}}}\) takes values in \({{\mathscr {M}}}_{fib}\), and that the homotopy limit of an objectwise fibrant diagram is again a fibrant object. Using the simplicial enrichment and the two-variable Quillen adjunction from Proposition 3.28, the above problem is further equivalent to showing that, for each cofibrant \(m \in {{\mathscr {M}}}\), the morphism

is a weak homotopy equivalence. Note that this morphism is the same as the canonical morphism

in the homotopy descent condition for the simplicial presheaf

By Theorem 3.23 it now suffices to show that the simplicial presheaf

is \(\tau \)-local, for each cofibrant object \(m \in {{\mathscr {M}}}\).
To that end, let \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in I}\) be a \(\tau \)-covering in \({\mathscr {C}}\). We have to check that the canonical morphism

is a weak homotopy equivalence. Again using the two-variable Quillen adjunctions, this is equivalent to checking that

is a weak homotopy equivalence, for each cofibrant \(m \in {{\mathscr {M}}}\). Again since the functors \(\underline{{{\mathscr {M}}}}(m,-)\) jointly detect weak equivalences between fibrant objects in \({{\mathscr {M}}}\), this is the case if and only if

is a weak equivalence in \({{\mathscr {M}}}\). However, that is true by the assumption that F is \(S({{\mathscr {M}}}, \tau )\)-local. \(\square \)
Finally, we record a generalisation of Proposition 3.12:
Proposition 3.38
In the setting of Theorem 3.30, for each projectively fibrant \(F \in \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {M}}})\) and any \(X \in {{\widehat{{\mathscr {C}}}}}\), there is a canonical natural weak equivalence
Proof
We have canonical weak equivalences

In the second-to-last line we have used the enriched cobar construction for the simplicially enriched category \({{\mathscr {M}}}\). The final weak equivalence follows from Proposition 3.31. \(\square \)
3.3 Sheaves of \((\infty ,n)\)-Categories
The specific instances of Theorem 3.37 in which we are interested most arise from choosing the target model category \({{\mathscr {M}}}\) to be a model for \((\infty ,n)\)-categories. Various such model categories exist in the literature, including the model structures for n-fold complete Segal spaces [2, 
Further, the category  is cartesian closed, with internal hom given by
is cartesian closed, with internal hom given by

where  is the Yoneda embedding of
is the Yoneda embedding of  . For each \(n \in {\mathbb {N}}\), there is a monoidal adjunction
. For each \(n \in {\mathbb {N}}\), there is a monoidal adjunction

where \({\textsf {c}}_\bullet \) is the constant-diagram functor, i.e. \(({\textsf {c}}_\bullet X)_{k_0, \ldots , k_{n-1}} = X_{k_1, \ldots , k_{n-1}}\). Therefore, the category  is enriched, tensored, and cotensored over
is enriched, tensored, and cotensored over  for any \(0 \le k \le n\).
for any \(0 \le k \le n\).
Moreover, for each \(k,l \in {\mathbb {N}}\) there is a functor

Iterating this, we have a functor

which satisfies that  and \({\textsf {c}}_\bullet X = \Delta ^0 \boxtimes X\), for each
and \({\textsf {c}}_\bullet X = \Delta ^0 \boxtimes X\), for each  .
.
The category  of large bisimplicial sets carries a Reedy model structure, and it is a well-known fact that this coincides with the injective model structure [22, Thm. 15.8.7]. It is a less well-known fact that an analogous identity of the injective and Reedy model structures holds true for the categories
of large bisimplicial sets carries a Reedy model structure, and it is a well-known fact that this coincides with the injective model structure [22, Thm. 15.8.7]. It is a less well-known fact that an analogous identity of the injective and Reedy model structures holds true for the categories  [7, Prop. 3.15]. Whenever we refer to
[7, Prop. 3.15]. Whenever we refer to  as a model category, we will mean the Reedy (or, equivalently, the injective) model structure. The model category
as a model category, we will mean the Reedy (or, equivalently, the injective) model structure. The model category  is cellular, left proper, combinatorial and cartesian closed, i.e. it is a symmetric monoidal model structure in the sense of [23, Def. 4.2.6] whose monoidal product agrees with the categorical binary product: this follows readily from the fact that
is cellular, left proper, combinatorial and cartesian closed, i.e. it is a symmetric monoidal model structure in the sense of [23, Def. 4.2.6] whose monoidal product agrees with the categorical binary product: this follows readily from the fact that  with the Kan-Quillen model structure is cartesian closed [23, Prop. 4.2.8] and the Reedy model structure on
with the Kan-Quillen model structure is cartesian closed [23, Prop. 4.2.8] and the Reedy model structure on  agrees with the injective model structure.
agrees with the injective model structure.
For the reader’s convenience, we briefly recall the presentation of a model category for n-fold complete Segal spaces, following [25, App. A] (see, in particular, the ‘Lurie-presentation’ in loc. cit.).
For \(k \in {\mathbb {N}}\), \(k \ge 2\), define the k-th spine inclusion

in  . Localising at maps of this type will implement the Segal conditions.
. Localising at maps of this type will implement the Segal conditions.
Let  denote the pushout
denote the pushout

where the top morphism consists of the inclusions of \(\Delta ^1\) into \(\Delta ^3\) as the edge \(0 \rightarrow 2\) and \(1 \rightarrow 3\), respectively. Let \(\kappa \) denote the collapse map
Localising at maps of the type \(\kappa \) will implement the completeness conditions below.
Definition 3.39
Let \(n \in {\mathbb {N}}\). The model category for (large) n-fold complete Segal spaces is obtained by left Bousfield localisation of  at the following morphisms:
at the following morphisms:
-
(1)
(Segal conditions) For each \(k \in {\mathbb {N}}\), \(i \in \{0, \ldots , n-1\}\) and each \(k_0, \ldots , k_{i-2}, k_i, \ldots , k_{n-1} \in {\mathbb {N}}_0\), we localise at the morphism
$$\begin{aligned} \Delta ^{k_0} \boxtimes \cdots \boxtimes \Delta ^{k_{i-2}} \boxtimes \sigma _k \boxtimes \Delta ^{k_i} \boxtimes \cdots \boxtimes \Delta ^{k_{n-1}}\,. \end{aligned}$$ -
(2)
(Completeness) For each \(i \in \{0, \ldots , n-1\}\) and each \(k_0, \ldots , k_{i-2}, k_i, \ldots , k_{n-1} \in {\mathbb {N}}_0\), we localise at the morphism
$$\begin{aligned} \Delta ^{k_0} \boxtimes \cdots \boxtimes \Delta ^{k_{i-2}} \boxtimes \kappa \boxtimes \Delta ^{k_i} \boxtimes \cdots \boxtimes \Delta ^{k_{n-1}}\,. \end{aligned}$$ -
(3)
(Essential constancy) For each \(i \in \{0, \ldots , n-1\}\) and each \(k_0, \ldots , k_{i-2}, k_i, \ldots , k_{n-1} \in {\mathbb {N}}_0\), we localise at the morphism
$$\begin{aligned} \Delta ^{k_0} \boxtimes \cdots \boxtimes \Delta ^{k_{i-2}} \boxtimes \Delta ^0 \boxtimes \Delta ^{k_i} \boxtimes \cdots \boxtimes \Delta ^{k_{n-1}} \longrightarrow \Delta ^{k_0} \boxtimes \cdots \boxtimes \Delta ^{k_{i-2}} \boxtimes \Delta ^0 \boxtimes \Delta ^0 \boxtimes \cdots \boxtimes \Delta ^0\,. \end{aligned}$$
We denote the resulting model category by \(\mathscr {C}\mathscr {S}\mathscr {S}_n\). Fibrant objects in \(\mathscr {C}\mathscr {S}\mathscr {S}_n\) are called n-fold complete Segal spaces, or \((\infty ,n)\)-categories.
Remark 3.40
The model categories \(\mathscr {C}\mathscr {S}\mathscr {S}_n\) exist and are left proper, cellular and simplicial [25, Lemma A.6]. In particular, we can apply Theorem 3.37 to presheaves with values in \(\mathscr {C}\mathscr {S}\mathscr {S}_n\), for each \(n \in {\mathbb {N}}\). \(\triangleleft \)
Lemma 3.41
Let \(n \in {\mathbb {N}}\), let \({\mathscr {I}}\) be a large category, and let \(D :{\mathscr {I}}\rightarrow \mathscr {C}\mathscr {S}\mathscr {S}_n\) be a projectively fibrant diagram, i.e. Di is an n-fold complete Segal space for every \(i \in {\mathscr {J}}\).
-
(1)
The homotopy limit of D can be computed levelwise: for each \(k \in {\mathbb {N}}_0\), there exist canonical natural isomorphisms
$$\begin{aligned} \big ( {\text {holim}}^{\mathscr {C}\mathscr {S}\mathscr {S}_n}_{\mathscr {J}}(D) \big )_k \cong {\text {holim}}^{\mathscr {C}\mathscr {S}\mathscr {S}_{n-1}}_{\mathscr {J}}(D_k)\,, \end{aligned}$$where for \(i \in {\mathscr {J}}\) the object \(D_k i = (Di)_k\) is the k-th simplicial level of
 .
. -
(2)
The homotopy limit of D can be computed objectwise when viewing the diagram as a functor
 . That is, for any
. That is, for any  there is an isomorphism (natural in
there is an isomorphism (natural in  )
) 
Proof
We use the explicit model for homotopy limits in simplicially enriched categories from Proposition 3.31. For the sake of brevity, for \(l \in {\mathbb {N}}_0\), we set

Since D is objectwise fibrant, a model for the homotopy limit of D is given by the two-sided cobar construction \(C(*,{\mathscr {I}},D) \in \mathscr {C}\mathscr {S}\mathscr {S}_n\) [44, Cor. 5.1.3].
For any \(n \in {\mathbb {N}}_0\), there are canonical natural isomorphisms of simplicial sets

The last identity relies on [44, Cor. 5.1.3] (see also Proposition 3.31), together with the following facts: the functor \(D :{\mathscr {I}}\rightarrow \mathscr {C}\mathscr {S}\mathscr {S}_n\) is objectwise fibrant. In particular, for each \(i \in {\mathscr {J}}\), the object  is fibrant in the Reedy model structure (equivalently, the injective model structure), where
is fibrant in the Reedy model structure (equivalently, the injective model structure), where  carries the Reedy (equivalently, injective) model structure. Forgetting the localisations in Definition 3.39 at morphisms which are non-trivial in the first
carries the Reedy (equivalently, injective) model structure. Forgetting the localisations in Definition 3.39 at morphisms which are non-trivial in the first  -factor, we further obtain that \((Di)_m\) is fibrant in \(\mathscr {C}\mathscr {S}\mathscr {S}_{n-1}\), for each \(i \in {\mathscr {I}}\) and
-factor, we further obtain that \((Di)_m\) is fibrant in \(\mathscr {C}\mathscr {S}\mathscr {S}_{n-1}\), for each \(i \in {\mathscr {I}}\) and  . Consequently, the functor
. Consequently, the functor  , \(i \mapsto D_m(i) = (Di)_m\) is also fibrant in the projective model structure on
, \(i \mapsto D_m(i) = (Di)_m\) is also fibrant in the projective model structure on  . Thus, the cobar construction in the second-to-last line indeed models its homotopy limit. Part (2) follows in analogy with part (1), replacing \({{\mathscr {Y}}}^n\) with \({{\mathscr {Y}}}\) (i.e. replacing \(\Delta ^k \boxtimes \Delta ^0 \boxtimes \cdots \boxtimes \Delta ^0\) by \(\Delta ^{k_0} \boxtimes \cdots \boxtimes \Delta ^{k_{n-1}}\)) and using that injectively fibrant diagrams are, in particular, projectively fibrant. \(\square \)
. Thus, the cobar construction in the second-to-last line indeed models its homotopy limit. Part (2) follows in analogy with part (1), replacing \({{\mathscr {Y}}}^n\) with \({{\mathscr {Y}}}\) (i.e. replacing \(\Delta ^k \boxtimes \Delta ^0 \boxtimes \cdots \boxtimes \Delta ^0\) by \(\Delta ^{k_0} \boxtimes \cdots \boxtimes \Delta ^{k_{n-1}}\)) and using that injectively fibrant diagrams are, in particular, projectively fibrant. \(\square \)
Definition 3.42
Let \({\mathscr {C}}\) be a small category.
-
(1)
We write
$$\begin{aligned} {\mathscr {H}}_{\infty ,n} {:}{=}\textrm{Fun}({\mathscr {C}}^{\text {op}}, \mathscr {C}\mathscr {S}\mathscr {S}_n) \end{aligned}$$and view this as endowed with the projective model structure. A fibrant object in \({\mathscr {H}}_{\infty ,n}\) is called a presheaf of \((\infty ,n)\)-categories on \({\mathscr {C}}\).
-
(2)
In the notation of Definition 3.33, we define the left Bousfield localisation
$$\begin{aligned} {\mathscr {H}}_{\infty ,n}^{loc} {:}{=}L_{S(\mathscr {C}\mathscr {S}\mathscr {S}_n,\tau )} {\mathscr {H}}_{\infty ,n}\,. \end{aligned}$$A fibrant object in \({\mathscr {H}}_{\infty ,n}^{loc}\) is called a sheaf of \((\infty ,n)\)-categories on \(({\mathscr {C}},\tau )\).
Proposition 3.43
Let \({\mathscr {C}}\) be a small category. Then \({\mathscr {H}}_{\infty ,n}\) is a left proper, tractable (large) simplicial model category. Further, if \({\mathscr {C}}\) is endowed with a Grothendieck pretopology \(\tau \), then \({\mathscr {H}}_{\infty ,n}^{loc}\) is a \(\mathscr {C}\mathscr {S}\mathscr {S}_n\)-model category, and it is symmetric monoidal if \({\mathscr {H}}_{\infty ,n}\) is so.
Proof
The statement about \({\mathscr {H}}_{\infty ,n}\) is a consequence of [3, Prop. 4.50]. For \({\mathscr {H}}_{\infty ,n}^{loc}\), the claim follows from [3, Prop. 4.47]. The statement about symmetric monoidal structures is an application of [3, Thm. 4.58]. \(\square \)
Analogously to Sects. 3.1, \({\mathscr {H}}_{\infty ,n}\) is symmetric monoidal whenever \({\mathscr {C}}\) has finite products.
Definition 3.44
Let \({\mathscr {C}}\) be a small category. As before, we write \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\).
-
(1)
We write
$$\begin{aligned} {{\widehat{{\mathscr {H}}}}}_{\infty ,n} {:}{=}\textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, \mathscr {C}\mathscr {S}\mathscr {S}_n) \end{aligned}$$for the category \(\textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, \mathscr {C}\mathscr {S}\mathscr {S}_n)\), endowed with the projective model structure. A fibrant object in \({{\widehat{{\mathscr {H}}}}}_{\infty ,n}\) is called a presheaf of \((\infty ,n)\)-categories on \({{\widehat{{\mathscr {C}}}}}\).
-
(2)
In the notation of Definition 3.33, we define the left Bousfield localisation
$$\begin{aligned} {{\widehat{{\mathscr {H}}}}}_{\infty ,n}^{loc} {:}{=}L_{S(\mathscr {C}\mathscr {S}\mathscr {S}_n,{{\widehat{\tau }}})} {{\widehat{{\mathscr {H}}}}}_{\infty ,n}\,. \end{aligned}$$A fibrant object in \({{\widehat{{\mathscr {H}}}}}_{\infty ,n}^{loc}\) is called a sheaf of \((\infty ,n)\)-categories on \(({{\widehat{{\mathscr {C}}}}},{{\widehat{\tau }}})\).
Remark 3.45
Lemma 3.41 implies that an object \({\mathscr {F}}\in \textrm{Fun}({\mathscr {C}}^{\text {op}}, \mathscr {C}\mathscr {S}\mathscr {S}_n)\) is \(S(\mathscr {C}\mathscr {S}\mathscr {S}_n,\tau )\)-local if and only if, for each  the object
the object  is \(\tau \)-local, and analogously for \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\) in place of \(({\mathscr {C}}, \tau )\). \(\triangleleft \)
is \(\tau \)-local, and analogously for \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\) in place of \(({\mathscr {C}}, \tau )\). \(\triangleleft \)
In the notation of (3.29), we further write
We can compute this functor more explicitly as follows: for  , we have canonical isomorphisms
, we have canonical isomorphisms

We have the following direct corollary of Proposition 3.38:
Proposition 3.46
On any fibrant object \({\mathscr {F}}\in {\mathscr {H}}_{\infty ,n}\), the functor \(S_{\infty ,n}\) agrees with the homotopy right Kan extension of \({\mathscr {F}}:{\mathscr {C}}^{\text {op}}\rightarrow \mathscr {C}\mathscr {S}\mathscr {S}_n\) along the Yoneda embedding,
As a direct application of Proposition 3.30, we have:
Proposition 3.47
The functor \(S_{\infty ,n}\) is the right adjoint in a Quillen adjunction

Moreover, Theorem 3.37 implies the following result:
Corollary 3.48
Let \(({\mathscr {C}},\tau )\) be a small site. For any \(n \in {\mathbb {N}}\), the Quillen adjunction \(Re_{\infty ,n} \dashv S_{\infty ,n}\) descends to a Quillen adjunction

Remark 3.49
The descent results in this subsection also imply corresponding results for strict presheaves of 1-categories, i.e. functors
from \({\mathscr {C}}^{\text {op}}\) to the 1-category of large categories. Rezk’s classifying diagram functor \(N_{rel} :{{\mathscr {C}}\text {at} }_\text {L} \rightarrow \mathscr {C}\mathscr {S}\mathscr {S}_1\) from large categories to large complete Segal spaces is a fully faithful embedding of categories which preserves and detects weak equivalences (weak equivalences in \({{\mathscr {C}}\text {at} }_\text {L} \) being equivalences of categories) and which preserves exponentials; this is the content of [41, Thm. 3.7]. Explicitly, if \({\mathscr {D}}^\sim \) denotes the maximal subgroupoid of a category \({\mathscr {D}}\), we have, for each \(n \in {\mathbb {N}}_0\),
Now let \(({\mathscr {C}}, \tau )\) be a site. One checks that, given a presheaf \(F :{\mathscr {C}}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \) and a \(\tau \)-covering family \({{\mathcal {U}}}= \{c_i \rightarrow c\}_{i \in \Lambda }\) such that all \(C_{i_0 \ldots i_n}\) are representable (see (2.9) for the notation), there is an equivalence
where \({{\mathscr {D}}\text {esc} }(F; {{\mathcal {U}}})\) is the usual descent category associated to F and the covering family \({{\mathcal {U}}}\) (see, for instance, [37, Def. 2.5] or [10, Def. 2.9]). It follows that F is a sheaf of categories precisely if \(N_{rel} F\) is fibrant in \({\mathscr {H}}_{\infty ,1}^{loc}\). Given a small presheaf \(X \in {{\widehat{{\mathscr {C}}}}}\), one can check that
in \(\mathscr {C}\mathscr {S}\mathscr {S}_1\), where the homotopy limit is computed in the canonical model structure on \({{\mathscr {C}}\text {at} }_\text {L} \) (see, for instance, [40]). We define a functor
Given a \(\tau \)-local epimorphism \(\pi :Y \rightarrow X\), we thus have a commutative diagram

Since \(N_{rel}\) reflects weak equivalences, it now follows from Corollary 3.48 that \(S_{1,1}F\) satisfies \({{\widehat{\tau }}}\)-descent whenever F satisfies \(\tau \)-descent. \(\triangleleft \)
4 Applications in Geometry and Field Theory
Here we apply the results of Sect. 3 to diffeological vector bundles, gerbes with connection, 2-vector bundles and smooth field theories on background manifolds.
4.1 Strictification of Diffeological Vector Bundles and Descent Along Subductions
Vector bundles form a sheaf of categories on the site of manifolds and surjective submersions. One can show this either by providing an explicit descent construction, or by using a strictification of vector bundles which describes them in terms of their transition functions.
Diffeological spaces form a popular generalisation of manifolds; their category \({{\mathscr {D}}{\textrm{fg}}}\) sits in a sequence of canonical fully faithful inclusion functors

Apart from the first inclusion, these functors each have a left adjoint. Diffeological spaces have been introduced in [24] and are increasingly used to carry out smooth constructions in geometry and topology (see, for instance, [28, 36]). Despite this, there is currently no descent theorem for diffeological vector bundles. That is a large gap in the literature, which we close here: as the main step, we extend the strictification of vector bundles on manifolds to diffeological vector bundles. The desired descent property of diffeological vector bundles then follows readily from Corollary 3.48 and Remark 3.49.
4.1.1 Background on Diffeological Spaces
We start by recalling the category of diffeological spaces, mostly following [5]. As a slight variation to the standard literature, we define diffeological spaces as concrete sheaves on a site which differs from the usual choice, but this is just for technical convenience (cf. Remark 4.7). Throughout this section, we let \({\mathscr {C}}\) be a small category.
Definition 4.1
([5, Def. 17]) A site \(({\mathscr {C}},\tau )\) is called subcanonical if every representable presheaf on \({\mathscr {C}}\) is a sheaf.
Definition 4.2
([5, Def. 18]) A site \(({\mathscr {C}},\tau )\) is concrete if \({\mathscr {C}}\) has a terminal object \(* \in {\mathscr {C}}\), \(({\mathscr {C}},\tau )\) is subcanonical and satisfies the following two additional conditions:
-
(1)
The functor \(\text {Ev} _* = {\mathscr {C}}(*,-) :{\mathscr {C}}\rightarrow {{\mathscr {S}}\text {et} }_\text {S} \) is faithful.
-
(2)
Each covering \(\{f_i :c_i \!\rightarrow \! c\}_{i \in I} \!\in \! \tau (c)\) is jointly surjective: we have \( \bigcup _{i \in I} (f_i)_* \big ( {\mathscr {C}}(*,c_i) \big ) = {\mathscr {C}}(*,c). \)
Definition 4.3
([5, Def. 19, Def. 46]) A presheaf X on a concrete site \(({\mathscr {C}},\tau )\) is called concrete if for every object \(c \in {\mathscr {C}}\) the map
is injective. In this case, we define the subset \(\text {Plot} _X(c) {:}{=}\text {Ev} _*(X(c)) \subset {{\mathscr {S}}\text {et} }_\text {S} \big ( {{\mathscr {Y}}}_c(*), X(*) \big )\) of plots of X over \(c \in {\mathscr {C}}\).
In other words, a concrete presheaf X has an underlying set \(X(*)\), and, for each \(c \in {\mathscr {C}}\), the set X(c) can canonically be described as a subset of the maps of sets \({{\mathscr {Y}}}_c(*) \rightarrow X(*)\).
Definition 4.4
([5, Def. 20]) Let \(({\mathscr {C}},\tau )\) be a concrete site. The category \({{\mathscr {D}}{\textrm{fg}}}({\mathscr {C}},\tau )\) of (small) \(({\mathscr {C}},\tau )\)-spaces is the full subcategory of \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\) whose objects are the concrete small sheaves on \(({\mathscr {C}}, \tau )\). For \(X \in {{\mathscr {D}}{\textrm{fg}}}({\mathscr {C}},\tau )\), the elements of X(c) are called plots of X over c. We refer to \(({{\mathscr {C}}\text {art} },\tau _{dgop})\)-spaces as diffeological spaces, and we abbreviate \({{\mathscr {D}}{\textrm{fg}}}{:}{=}{{\mathscr {D}}{\textrm{fg}}}({{\mathscr {C}}\text {art} },\tau _{dgop})\).
We commit an abuse of notation and denote the underlying set of a diffeological space X also by X; it will be clear from context whether we are referring only to the underlying set, or to the underlying set endowed with the structure of a diffeological space.
Example 4.5
The site \(({{\mathscr {C}}\text {art} },\tau _{dgop})\) from Example 2.4 is concrete: first, note that \({{\mathscr {C}}\text {art} }\) has a terminal object \(* = {\mathbb {R}}^0\). Further, the functor \({{\mathscr {C}}\text {art} }({\mathbb {R}}^0, -) :{{\mathscr {C}}\text {art} }\rightarrow {{\mathscr {S}}\text {et} }_\text {S} \) takes the underlying set of \(c \in {{\mathscr {C}}\text {art} }\); thus, it is faithful. Since smooth maps to a target manifold form a sheaf with respect to open coverings, \(({{\mathscr {C}}\text {art} },\tau _{dgop})\) is subcanonical. Finally, the fact that covering families in \(({{\mathscr {C}}\text {art} },\tau _{dgop})\) are jointly surjective is immediate from the definition of \(\tau _{dgop}\). Analogously, one checks that the site \(({{\mathscr {O}}\text {p} },\tau _{op})\) from Example 2.5 is concrete. \(\triangleleft \)
The relation between Sects. 3 and Sect. 4 relies on the following observation.
Remark 4.6
The category \({{\mathscr {D}}{\textrm{fg}}}({\mathscr {C}},\tau )\), together with the collection of those \(\tau \)-local epimorphisms whose source and target are \(({\mathscr {C}},\tau )\)-spaces, form a site which is contained in the site \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}})\) as a full subcategory. The \(\tau \)-local epimorphisms between \(({\mathscr {C}},\tau )\)-spaces are also called subductions [24]. We denote the site of \(({\mathscr {C}},\tau )\)-spaces with this coverage by \(({{\mathscr {D}}{\textrm{fg}}}({\mathscr {C}},\tau ), \tau _{subd})\). \(\triangleleft \)
Remark 4.7
In [24], diffeological spaces are defined as concrete presheaves on \(({{\mathscr {O}}\text {p} },\tau _{op})\), whereas here we define them on \(({{\mathscr {C}}\text {art} }, \tau _{dgop})\). However, the two categories are equivalent because the canonical inclusion of \(({{\mathscr {C}}\text {art} }, \tau _{dgop})\) into \(({{\mathscr {O}}\text {p} },\tau _{op})\) is an inclusion of a dense subsite. For any manifold M, the presheaf \(\underline{M}\) from Example 2.4 is a diffeological space. \(\triangleleft \)
Proposition 4.8
([5, Section 5.3]) Let \(({\mathscr {C}},\tau )\) be a concrete site. There exists an adjunction

whose right adjoint is a fully faithful inclusion, i.e. \({{\mathscr {D}}{\textrm{fg}}}({\mathscr {C}},\tau ) \subset {{\widehat{{\mathscr {C}}}}}\) is a reflective localisation.
4.1.2 Strictification and Descent of Diffeological Vector Bundles
We now specialise to the case \(({\mathscr {C}},\tau ) = ({{\mathscr {C}}\text {art} }, \tau _{dgop})\) and to \({{\mathscr {D}}{\textrm{fg}}}= {{\mathscr {D}}{\textrm{fg}}}({{\mathscr {C}}\text {art} }, \tau _{dgop})\). We will denote the underlying set \({{\mathscr {Y}}}_c(*)\) of a cartesian space \(c \in {{\mathscr {C}}\text {art} }\) again by c.
Definition 4.9
Let \(X \in {{\mathscr {D}}{\textrm{fg}}}\) be a diffeological space.
-
(1)
A (complex rank-k) vector bundle on X is a pair \((E,\pi )\) of a diffeological space E and a morphism \(\pi :E \rightarrow X\) in \({{\mathscr {D}}{\textrm{fg}}}\) with the structure of a \({\mathbb {C}}\)-vector space on each fibre \(E_{|x} {:}{=}\pi ^{-1}(\{x\})\), for \(x \in X\), satisfying the following condition: for each plot \(\varphi :c \rightarrow X\) there exists an isomorphism of diffeological spaces
$$\begin{aligned} \Phi :c \times {\mathbb {C}}^k \longrightarrow c \underset{X}{\times }\ E \end{aligned}$$such that \(\text {pr} _c \circ \Phi = \text {pr} _c\) and such that for every \(y \in c\) the restriction \(\Phi _{|y} :{\mathbb {C}}^k \rightarrow E_{|\varphi (y)}\) is linear.
-
(2)
Let \((E,\pi )\) and \((E',\pi ')\) be vector bundles on X. A morphism \((E,\pi ) \rightarrow (E', \pi ')\) is a morphism \(\Psi \in {{\mathscr {D}}{\textrm{fg}}}(E,E')\) with \(\pi ' \circ \Psi = \pi \) and such that \(\Psi _{|x} :E_{|x} \rightarrow E'_{|x}\) is a linear map for every \(x \in X\).
This defines a category \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}(X)\) of diffeological vector bundles on X.
Example 4.10
If M is a smooth manifold, which we view as a diffeological space, then the category \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}(X)\) is canonically equivalent to the ordinary category of vector bundles on M. \(\triangleleft \)
Any morphism \(f \in {{\mathscr {D}}{\textrm{fg}}}(X',X)\) gives rise to a pullback functor
where \(\pi '\) is the pullback of \(\pi \) along f.
Definition 4.11
We let \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}:{{\mathscr {D}}{\textrm{fg}}}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \) denote the pseudo-functor resulting from the above assignments (where \({{\mathscr {C}}\text {at} }_\text {L} \) is the 2-category of large categories).
The goal of this subsection is to prove the following theorem:
Theorem 4.12
The pseudo-functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}:{{\mathscr {D}}{\textrm{fg}}}^{\text {op}}\longrightarrow {{\mathscr {C}}\text {at} }_\text {L} \) satisfies descent along subductions of diffeological spaces (see Remark 4.6).
Remark 4.13
We use the following strategy for the proof of Theorem 4.12:
-
(1)
Replace the pseudo-functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\) by a strictification, i.e. find a (strict) functor
$$\begin{aligned} {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} :{{\mathscr {D}}{\textrm{fg}}}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \end{aligned}$$and an equivalence of pseudo-functors between \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) and \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\).
-
(2)
Recall that \(({{\mathscr {D}}{\textrm{fg}}}, \tau _{subd}) \subset ({{\widehat{{{\mathscr {C}}\text {art} }}}}, {{\widehat{\tau }}})\) is a subsite (see Remark 4.6). Show that \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) is in fact a restriction along the inclusion \(\iota :{{\mathscr {D}}{\textrm{fg}}}\hookrightarrow {{\widehat{{{\mathscr {C}}\text {art} }}}}\) of a functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} :{{\widehat{{{\mathscr {C}}\text {art} }}}}{}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \).
-
(3)
Show that the functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} :{{\widehat{{{\mathscr {C}}\text {art} }}}}{}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \) satisfies descent with respect to \({{\widehat{\tau }}}_{dgop}\).
Theorem 4.12 then readily follows from the equivalences in points (2) and (3).
We will achieve the above goals by means of Remark 3.49: we give a strict functor
satisfying the following two properties:
-
The functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} :{{\mathscr {C}}\text {art} }^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \) satisfies \(\tau _{dgop}\)-descent.
-
Consider the functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} {:}{=}S_{1,1}{{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \in \textrm{Fun}({{\widehat{{{\mathscr {C}}\text {art} }}}}{}^{\text {op}}, {{\mathscr {C}}\text {at} }_\text {L} )\). Its restriction to \({{\mathscr {D}}{\textrm{fg}}}\subset {{\widehat{{{\mathscr {C}}\text {art} }}}}\) is a strictification of \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\) (thus yielding point (1) above).
Remark 3.49 then ensures that points (2) and (3) above are satisfied. \(\triangleleft \)
We now carry out the above strategy:
Definition 4.14
We define a strict presheaf \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) of categories on \({{\mathscr {C}}\text {art} }\) as follows: for \(c \in {{\mathscr {C}}\text {art} }\), the category \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} (c)\) has objects (c, n), where \(n \in {\mathbb {N}}_0\), and a morphism \((c,n) \rightarrow (c,m)\) is a smooth function \(\psi :c \rightarrow \textsf {Mat}( m{\times }n, {\mathbb {C}})\) from c to the vector space of complex m-by-n matrices; to make clear that \(\psi \) is defined over c we also write \((c,\psi )\) instead of just \(\psi \). A smooth map \(f :c' \rightarrow c\) acts via
Using the functor \(S_{1,1} :\textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {C}}\text {at} }_\text {L} ) \longrightarrow \textrm{Fun}({{\widehat{{\mathscr {C}}}}}^{\text {op}}, {{\mathscr {C}}\text {at} }_\text {L} )\) from Remark 3.49 we also define the strict functor
Let \({\mathscr {H}}_{\infty ,1}\) denote the model category for presheaves of \(\infty \)-categories on the site \(({{\mathscr {C}}\text {art} }, \tau _{dgop})\) (as in Definition 3.42). As in Remark 3.49, let  denote Rezk’s classifying diagram functor [41, Sec. 3].
denote Rezk’s classifying diagram functor [41, Sec. 3].
Proposition 4.15
Both \(N_{rel} \circ {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) and \(N_{rel} \circ {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) are fibrant objects in \({\mathscr {H}}_{\infty ,1}^{loc}\) and in \({{\widehat{{\mathscr {H}}}}}_{\infty ,1}^{loc}\), respectively. Equivalently (by Remark 3.49), \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) satisfies \(\tau _{dgop}\)-descent, and \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) satisfies \({{\widehat{\tau }}}_{dgop}\)-descent.
Proof
We only need to show that \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \in {\mathscr {H}}_{\infty ,1}^{loc}\) is fibrant. That \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) is fibrant in \({{\widehat{{\mathscr {H}}}}}_{\infty ,1}^{loc}\) will then follow from Corollary 3.48. First, \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) is fibrant in \({\mathscr {H}}_{\infty ,1}\): for each \(c \in {{\mathscr {C}}\text {art} }\), the bisimplicial set \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} (c) = N_{rel}({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} (c))\) is the classification diagram of an ordinary category and hence a complete Segal space by [41, Prop. 6.1]. In order to show that \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) is also fibrant in \({\mathscr {H}}_{\infty ,1}^{loc}\), it suffices to show that the presheaf of categories \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) satisfies descent with respect to \(\tau _{dgop}\), which is standard: for instance, one can see this by using that vector bundles glue along isomorphisms over open coverings of manifolds. Thus, given descent data for \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) with respect to a differentiably good open covering of a cartesian space c, we obtain a vector bundle on c. This vector bundle is, in general, non-trivial, but since \(c \cong {\mathbb {R}}^n\) for some \(n \in {\mathbb {N}}_0\), it is isomorphic to a trivial vector bundle. This provides the essential surjectivity of the descent functor for vector bundles. Its full faithfulness follows since morphisms of trivial vector bundles are the same as smooth matrix-valued functions, which form sheaves of sets with respect to open coverings of manifolds. \(\square \)
For the proof of Theorem 4.12 we are thus left to show that \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} \in \textrm{Fun}({{\widehat{{{\mathscr {C}}\text {art} }}}}{}^{\text {op}}, {{\mathscr {C}}\text {at} }_\text {L} )\) restricts to a strictification of the pseudo-functor \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\) on the full subcategory \({{\mathscr {D}}{\textrm{fg}}}\subset {{\widehat{{{\mathscr {C}}\text {art} }}}}\). To that end, we first identify a more concrete description of the functor \(\iota ^* {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} = \iota ^* S_{1,1} ({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} )\), where \(\iota :{{\mathscr {D}}{\textrm{fg}}}\hookrightarrow {{\widehat{{{\mathscr {C}}\text {art} }}}}\) denotes the canonical inclusion: it is the homotopy right Kan extension of \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_\text {triv} \) along the inclusion \({{\mathscr {C}}\text {art} }\hookrightarrow {{\mathscr {D}}{\textrm{fg}}}\):
Lemma 4.16
We can compute the values of \(\iota ^* {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str} :{{\mathscr {D}}{\textrm{fg}}}^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \) as

Proof
This follows directly from Remark 3.49. \(\square \)
Remark 4.17
In this proof we first show that each diffeological vector bundle is determined by its strictified transition data (i.e. matrix-valued functions), and then use that the latter satisfy descent, using Remark 3.49. Alternatively, we could have shown first an analogue of Lemma 4.16 for \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\) and then compared \(\iota ^* {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{{\mathscr {D}}{\textrm{fg}}}\) and \({{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) on \({{\mathscr {C}}\text {art} }\subset {{\mathscr {D}}{\textrm{fg}}}\) only. However, the proof of the first step is not significantly less complicated than the proof of Theorem 4.18 below. Additionally, from the route chosen here it becomes evident how one can assign a total space to any vector bundle on any diffeological space from its transition data, as well as that \(N_{rel}{{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }_{str}\) is a classifying object in \({\mathscr {H}}_{\infty ,1}\) for vector bundles. \(\triangleleft \)
We obtain the following strictification theorem for diffeological vector bundles:
Theorem 4.18
There is an objectwise equivalence of (non-strict) presheaves of categories on \({{\mathscr {D}}{\textrm{fg}}}\)
Proof
The proof Theorem 4.18 consists of several individual steps, which we present in detail in Appendix A: first, we fix an arbitrary diffeological space X and restrict our attention to the evaluation of (4.19) at X, i.e. to the functor
Using Lemma 4.16 we define the functor \({\mathcal {A}}_{|X}\) on objects and (Definition A.4) and show in Proposition A.5 that it indeed produces diffeological vector bundles on X. Next, we define \({\mathcal {A}}_{|X}\) on morphisms (Definition A.7) and show that, for each \(X \in {{\mathscr {D}}{\textrm{fg}}}\), it is fully faithful (Proposition A.8) and essentially surjective A.9. Only then do we let \(X \in {{\mathscr {D}}{\textrm{fg}}}\) vary and complete the proof by showing that the functors \({\mathcal {A}}_{|X}\) we constructed for each \(X \in {{\mathscr {D}}{\textrm{fg}}}\) assemble into a morphism of pseudo-functors \({{\mathscr {C}}\text {art} }^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }_\text {L} \). Since we have already shown that this morphism of pseudo-functors is objectwise an equivalence of categories, we obtain the desired equivalence result. \(\square \)
This completes the proof of Theorem 4.12.
4.2 Descent for the \((\infty ,2)\)-Sheaf of Gerbes with Connection
An important example of higher geometric structures consists of (higher) gerbes with connection. The simplicial presheaf of n-gerbes with connection on \({{\mathscr {C}}\text {art} }\) is obtained by applying the Dold-Kan correspondence to the chain complex

with the sheaf \(\text {U} (1)\) of smooth \(\text {U} (1)\)-valued functions in degree zero. The resulting simplicial presheaf is denoted \(\text {B} ^{n+1}_\nabla \text {U} (1)\). It satisfies descent with respect to \(\tau _{dgop}\), and thus \(S_{\infty ,0}(\text {B} _\nabla ^{n+1}\text {U} (1)) \in {{\widehat{{\mathscr {H}}}}}_{\infty ,0}\) is a fibrant object. It classifies n-gerbes on objects of \({{\widehat{{\mathscr {C}}}}}\).
However, this only captures invertible morphisms of n-gerbes with connection. At least for \(n=1\) there also exists a theory of interesting non-invertible morphisms, due to Waldorf [50]. There, Waldorf showed that the morphisms between two fixed gerbes on a manifold satisfy descent along surjective submersions. This was later improved upon by Nikolaus-Schweigert in [39]; they proved that the presheaf of 2-categories which assigns to a manifold its gerbes and their 1- and 2-morphisms satisfies descent along surjective submersions of manifolds. Descent properties for gerbes and their non-invertible morphisms on more general spaces are so far unknown.
However, given our results in Sect. 3, we can establish such results: consider the following strict presheaf \({{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla \) of strict 2-categories on \({{\mathscr {C}}\text {art} }\): for \(c \in {{\mathscr {C}}\text {art} }\), an object of \({{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla (c)\) is a 2-form \(\rho \in \Omega ^2(c;{{\mathfrak {u}}}(1))\). A 1-morphism \(\rho _0 \rightarrow \rho _1\) consists of a 1-form \(A \in \Omega ^1(c;{{\mathfrak {u}}}(k))\), for some \(k \in {\mathbb {N}}_0\). Composition of 1-morphisms is given by \(A' \circ A = A' \otimes \mathbb {1}+ \mathbb {1}\otimes A\), with unit matrices \(\mathbb {1}\) of the respective dimensions of A and \(A'\). Given a pair \(A \in \Omega ^2(c;{{\mathfrak {u}}}(k))\), \(A' \in \Omega ^2(c;{{\mathfrak {u}}}(k'))\) of 1-morphisms \(\rho _0 \rightarrow \rho _1\), a 2-morphism \(A \rightarrow A'\) consists of a smooth, matrix-valued function \(\psi :c \rightarrow \textsf {Mat}(k {\times } k';{\mathbb {C}})\). Vertical composition of 2-morphisms is given by pointwise matrix multiplication. Note that a 1-morphism \(A \in \Omega ^1(c;{{\mathfrak {u}}}(k))\) is invertible precisely if \(k=1\) and a 2-morphism is invertible precisely if it takes values in \({\textsf {GL}}(k;{\mathbb {C}})\). Then, \({{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla \) satisfies descent with respect to \(\tau _{dgop}\) [39, 50].
Remark 4.20
\({{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla (c)\) as defined above is the most relaxed definition of a 2-category of gerbes with connection on c. One can restrict attention to parallel 2-morphisms, i.e. satisfying \(\text {d} \psi + (A-A')\psi = 0\), and independently to 1-morphisms satisfying either \(\text {tr} (\text {d} A + \frac{1}{2} [A,A]) = \rho _1 - \rho _0\) (as in [50]) or the fake curvature condition \(\text {d} A + \frac{1}{2} [A,A] = \rho _1 - \rho _0\). These choices produce various 2-categories of gerbes with connection on c with different properties; our arguments below apply to each of these cases. \(\triangleleft \)
Applying the \((\infty ,2)\)-categorical nerve from [38, Thm. B] objectwise at each \(c \in {{\mathscr {C}}\text {art} }\) produces a fibrant presheaf \(N_{2,rel} {{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla \in {\mathscr {H}}_{\infty ,2}\). It follows from the descent property of \({{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla \) that \(N_{2,rel} {{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla \) is even fibrant in \({\mathscr {H}}_{\infty ,2}^{loc}\), i.e. satisfies descent with respect to \(\tau _{dgop}\). By Corollary 3.48, the homotopy right Kan extension \(S_{\infty ,2}(N_{2,rel} {{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla ) \in {{\widehat{{\mathscr {H}}}}}_{\infty ,2}^{loc}\) is again fibrant and classifies gerbes with connection and their not necessarily invertible 1- and 2-morphisms on generic objects in \({{\widehat{{\mathscr {C}}}}}\). We thus obtain:
Theorem 4.21
Gerbes with connection and their generic (not necessarily invertible or parallel) 2-morphisms form a sheaf of \((\infty ,2)\)-categories on the site \(({{\widehat{{\mathscr {C}}}}}, {{\widehat{\tau }}}_{dgop})\).
In particular, restricting to objects \(X \in {{\widehat{{\mathscr {C}}}}}\) of the form \(X = \underline{M}\) for some manifold M, we directly obtain the result of [39] that gerbes with connection form a sheaf of 2-categories on the site of manifolds and surjective submersions.
Remark 4.22
To conclude this subsection, we remark that since \(N_{2,rel} {{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla (c)\) is a (2, 2)-category, i.e. it is truncated, for each \(c \in {{\mathscr {C}}\text {art} }\), and since truncatedness is stable under limits, \(S_{\infty ,2}(N_{2,rel} {{\mathscr {G}}\text {rb} }_\text {triv} ^\nabla )\) should be a sheaf of (2, 2)-categories as well (see, for instance, [42, Sec. 11] for truncations of \((\infty ,n)\)-categories). \(\triangleleft \)
4.3 Descent and Coherence for Smooth Functorial Field Theories
We now apply our findings to smooth functorial field theories (FFTs), a family-version of topological quantum field theories (TQFTs).
4.3.1 Background on Presentations of Topological Quantum Field Theories
We briefly recall some well-known background on TQFTs, highlighting only those technical details which are relevant to this paper. TQFTs were introduced in [1, 47]; for some modern introductions, we refer the reader to [30, 45]. The formulation of d-dimensional TQFTs rests on the d-dimensional cobordism category \(\textsf {Bord}_d\). Its objects are \((d{-}1)\)-dimensional closed, oriented manifolds. Its morphisms are diffeomorphism classes of d-dimensional oriented cobordisms between these. Composition is given by gluing bordisms along the mutual boundary. The category \(\textsf {Bord}_d\) is symmetric monoidal under disjoint union of manifolds. If \({\textsf {T}}\) is a symmetric monoidal category, a d-dimensional \({\textsf {T}}\)-valued TQFT is a symmetric monoidal functor \({\textsf {Z}}:\textsf {Bord}_d \rightarrow {\textsf {T}}\).
If Y is an object in \(\textsf {Bord}_d\), then any orientation-preserving diffeomorphism \(f :Y \rightarrow Y\) induces a morphism \(C_f :Y \rightarrow Y\) in \(\textsf {Bord}_d\). Isotopic diffeomorphisms induce the same morphism. Via the TQFT functor \({\textsf {Z}}\), the object \({\textsf {Z}}(Y) \in {\textsf {T}}\) thus carries an action of the map** class group of Y. Let \(c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1}\) denote the groupoid of closed oriented \((d{-}1)\)-manifolds and their orientation-preserving diffeomorphisms. We let \(c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1}/{\sim }\) denote the groupoid with the same objects, but with morphisms given by isotopy classes of diffeomorphisms. Observe that there are functors \(c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1} \longrightarrow c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1}/{\sim } \longrightarrow \textsf {Bord}_d\). If \(Y_0 \in c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1}\) and \(\text {MCG} (Y_0)\) is its map** class group, let \(Y_0 {/\hspace{-0.1cm}/}\text {MCG} (Y_0)\) denote the associated action groupoid. The inclusion \(Y_0 {/\hspace{-0.1cm}/}\text {MCG} (Y_0) \hookrightarrow c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1} /{\sim }\) is an equivalence onto a connected component, and hence the inclusion

is an equivalence. Consequently, we can recover the values of any TQFT \({\textsf {Z}}\) on all of \(c{{\mathscr {M}}{\text {fd}}}^{or}_{d-1}\) from its restrictions to \(Y_0 {/\hspace{-0.1cm}/}\text {MCG} (Y_0)\), where \(Y_0\) ranges over all diffeomorphism classes of closed, oriented \((d{-}1)\)-manifolds. Further, considering a generating set of bordisms between the chosen representatives \(Y_0\), we can then recover the full TQFT up to natural isomorphism from its values on the \(Y_0\), the respective map** class group actions and the generating bordisms.
4.3.2 Diffeomorphism Actions in Smooth Functorial Field Theories
The picture changes when we pass to smooth FFTs. These differ from TQFTs in several ways: most importantly, we would like to decorate the manifolds underlying objects and morphisms in \(\textsf {Bord}_d\) with additional geometric structure, and we would like to keep track of how the value of a field theory varies when we vary this additional geometric structure. In the most common and relevant case the additional structure consists of a smooth map to a fixed background manifold M. We restrict our attention to this case here. Smooth FFTs were introduced by Stolz and Teichner in [49]. For background, we refer the reader there; the specific formalism employed in this paper was developed in [13].
Remark 4.23
One can set up smooth FFTs with geometric structures in a fully general way: the additional data is modelled by a section of a (higher) sheaf on a site of families of d-manifolds and embeddings; we refer the reader to [21, 33] for the full framework. \(\triangleleft \)
In this setup, the bordism category \(\textsf {Bord}_d\) is replaced by a presheaf of symmetric monoidal categories \({\mathscr {B}}\text {ord} ^M_d :{{\mathscr {C}}\text {art} }^{\text {op}}\rightarrow {{\mathscr {C}}\text {at} }^\otimes \); this assigns to \(c \in {{\mathscr {C}}\text {art} }\) the symmetric monoidal category \({\mathscr {B}}\text {ord} ^M_d(c)\), whose objects are essentially pairs of a closed, oriented d-manifold Y and a smooth map \(f :c \times Y \rightarrow M\). Its morphisms \((Y_0,f_0) \rightarrow (Y_1,f_1)\) can be described as bordisms \(\Sigma :Y_0 \rightarrow Y_1\), together with a smooth map \(\sigma :c \times \Sigma \rightarrow M\) which restricts to \(f_0\) and \(f_1\) on the respective incoming and outgoing boundaries of the bordism (for the full details of this model for \({\mathscr {B}}\text {ord} _d^M\), see [Example 4.24
Consider a 2-dimensional smooth FFT on M with values in the higher sheaf of vector bundles, \({\mathscr {Z}}:{\mathscr {B}}\text {ord} _1^M \rightarrow {{\mathscr {V}}\hspace{-0.02cm}{\mathscr {B}}\hspace{-0.02cm}\text {un} }\). Fix \(Y = {\mathbb {S}}^1\). The collection of all objects \(({\mathbb {S}}^1,f)\) in \({\mathscr {B}}\text {ord} _d^M\) forms the smooth free loop space LM of M, which carries a canonical smooth \(\text {Diff} _+({\mathbb {S}}^1)\)-action. The FFT \({\mathscr {Z}}\) contains the data of a smooth, \(\text {Diff} _+({\mathbb {S}}^1)\)-equivariant vector bundle on LM. An explicit construction of an FFT of this type is presented in [13]. \(\triangleleft \) In general, FFTs can take values in higher categories; therefore, we study fully coherent equivariant structures (or homotopy fixed points) on sections of higher sheaves under diffeomorphism actions. If we aim to reconstruct the values of a smooth FFT on any closed \((d{-}1)\)-manifold Y with smooth map \(f :Y \rightarrow M\), we need to work with the smooth \(\text {Diff} _+(Y)\)-actions rather than map** class group actions. This motivates the following consideration: we restrict our attention to the diffeomorphism class [Y] of a closed, oriented \((d{-}1)\)-manifold Y. Let \({{\mathscr {M}}{\text {fd}}}^{\textsf {or}}\) denote the groupoid of oriented manifolds and orientation-preserving diffeomorphisms, and let \({{\mathscr {M}}}_Y\) be the connected component of Y in \({{\mathscr {M}}{\text {fd}}}^{\textsf {or}}\). For \(X,X' \in {{\mathscr {M}}{\text {fd}}}^{\textsf {or}}\), we let \(\text {D} (X,X')\) denote the presheaf on \({{\mathscr {C}}\text {art} }\) consisting of diffeomorphisms from X to \(X'\) (this is even a diffeological space). Concretely, an element of \(D(X,X')(c)\) is a smooth map \(\varphi ^\dashv :c \times X \rightarrow X'\) which is a diffeomorphism at each \(x \in c\) and such that the map of pointwise inverses is also smooth. We equivalently write this as a morphism \(\varphi :{{\mathscr {Y}}}_c \rightarrow \text {D} (X,X')\). This establishes both \({{\mathscr {M}}{\text {fd}}}^{\textsf {or}}\) and \({{\mathscr {M}}}_Y\) as categories enriched in \({\widehat{{{\mathscr {C}}\text {art} }}}\); the enriched map** objects are \(\underline{{{\mathscr {M}}}}^{{\widehat{{{\mathscr {C}}\text {art} }}}}_Y(Y_0,Y_1) = \text {D} (Y_0,Y_1)\). We also use the shorthand notation \(\text {D} (Y) {:}{=}\text {D} (Y,Y)\). One could even consider \({{\mathscr {M}}{\text {fd}}}\) and \({{\mathscr {M}}{\text {fd}}}^{\textsf {or}}\) as enriched in \({{\mathscr {D}}{\textrm{fg}}}\); the results in this section still go through because they only rely on the (pre)sheaf aspects of the diffeological spaces involved. \(\triangleleft \) Consider \({\widehat{{{\mathscr {C}}\text {art} }}}\)-enriched functors \(P :{{\mathscr {M}}}_Y^{\text {op}}\longrightarrow {\widehat{{{\mathscr {C}}\text {art} }}}\) and \(G :{{\mathscr {M}}}_Y \longrightarrow {\widehat{{{\mathscr {C}}\text {art} }}}\), as well as the functors \(G^n\), with \(G^n(X) {:}{=}(G(X))^n\). Setting \(G^0(X) {:}{=}*\) gives rise to an augmented simplicial object where In the context of smooth field theories on a manifold M, the relevant choice of P is \(M^{(-)}\), which assigns to \(Y' \in {{\mathscr {M}}}_Y\) the map** presheaf \(M^{Y'}\). Given two diffeomorphic manifolds \(Y_0 \cong Y_1\) in \({{\mathscr {M}}}_Y\), there is a canonical morphism of presheaves which sends a map \(\varphi ^\dashv :c \times Y_0 \rightarrow Y_1\) to the composition This makes \(M^{(-)}\) into an enriched functor. \(\triangleleft \) This setup allows us to form, for each \(n \in {\mathbb {N}}_0\), the enriched two-sided simplicial bar construction [44, Section 9.1], which produces a simplicial object We now consider the case of \(G = \text {D} (Y,-) :{{\mathscr {M}}}_Y \rightarrow {{\mathscr {D}}{\textrm{fg}}}\). Define morphisms \(\Phi _n\) as the composition where \(\Delta \) denotes the diagonal morphism, and where \(\text {Ev} :P(Y_0) \times \text {D} (Y,Y_0) \rightarrow P(Y)\) is defined via the tensor adjunction. The morphism \(\delta \) acts as Let \({\textsf {B}}\text {D} (Y) \subset {{\mathscr {M}}}_Y\) denote the full \({{\widehat{{{\mathscr {C}}\text {art} }}}}\)-enriched subcategory on the object Y. We call the action groupoid of the \(\text {D} (Y)\)-action via \(\text {Ev} \) on \(P(Y) \in {\widehat{{{\mathscr {C}}\text {art} }}}\). We further set For every \(n \in {\mathbb {N}}_0\), the morphism is an augmentation of the simplicial object \(B_\bullet \big ( \text {D} (Y,-)^{n+1}, {{\mathscr {M}}}_Y^{\text {op}}, P \big )\) in \({\widehat{{{\mathscr {C}}\text {art} }}}\). This follows directly from the compatibility of \(\text {Ev} \) with compositions. \(\square \) We further define morphisms \(\Psi _k :B_k (\text {D} (Y,-), {{\mathscr {M}}}_Y^{\text {op}}, P) \longrightarrow (P {/\hspace{-0.1cm}/}{{\mathscr {M}}}_Y)_k\), which arise from the augmentation \(\text {D} (Y,-)^\bullet \rightarrow \text {D} (Y,-)^0 = *\) . Let \(k \in {\mathbb {N}}_0\). The morphism is an augmentation of the simplicial object \(B_k \big ( \text {D} (Y,-)^{\bullet +1}, {{\mathscr {M}}}_Y^{\text {op}}, P \big )\) in \({\widehat{{{\mathscr {C}}\text {art} }}}\). The morphism \(\Psi _k\) is a \({{\widehat{\tau }}}_{dgop}\)-local epimorphism, and the simplicial object \(B_k (\text {D} (Y,-)^{\bullet +1}, {{\mathscr {M}}}_Y^{\text {op}}, P)\) is isomorphic to the Čech nerve of \(\Psi _k\). Part (1) is immediate from the construction of \(\Psi _k\). For part (2), we only need to observe that \(\Psi _k\) is a coproduct of projections onto a factor in a product and apply Lemma 2.8. \(\square \) For \(k,l \in {\mathbb {N}}_0\), we introduce the short-hand notation We obtain a bisimplicial object in \({{\widehat{{{\mathscr {C}}\text {art} }}}}\) which is augmented in each direction, and where the vertical simplicial objects are the Čech nerves of the subductions \(\Psi _k\). Explicitly, diagram (4.30) reads as The morphisms \(\Phi _\bullet \) and \(\Psi _\bullet \) have the following properties: Each \(\Phi _n\) induces a weak equivalence in \({\mathscr {H}}_{\infty ,0}\): Each \(\Psi _k\) induces a weak equivalence in \({\mathscr {H}}_{\infty ,0}^{loc}\): Ad (1): We claim that the augmented simplicial object in \({\mathscr {H}}_{\infty ,0}\) admits extra degeneracies. To see this, we define morphisms in \({{\mathscr {C}}\text {art} }\) where the image lies in the summand labelled by \(Y \in {{\mathscr {M}}}_Y\). For \(k \in {\mathbb {N}}_0\), we set where the image lies in the component of the coproduct labelled by \((Y_0, \ldots , Y_k, Y)\). These morphisms yield the desired extra degeneracies. Ad (2): This follows from Proposition 4.28 together with Theorem 3.18. \(\square \) With the above notation, the following statements hold true: We have a weak equivalence in \({\mathscr {H}}_{\infty ,0}\): We have a weak equivalence in \({\mathscr {H}}_{\infty ,0}^{loc}\): By Proposition 4.31, the morphism \(\Phi :\text {Coh} (Y,P) \rightarrow {\textsf {c}}_\bullet (P(Y) {/\hspace{-0.1cm}/}\text {D} (Y))\) is a levelwise weak equivalence of simplicial objects in \({\mathscr {H}}_{\infty ,0}\). Since the functor For claim (2), we observe that we have a commutative diagram The top morphism is a local weak equivalence by Proposition 4.31, and the vertical morphisms are projective weak equivalences by Proposition 3.4. It follows that the bottom morphism is a local weak equivalence. \(\square \) Let \(n \in {\mathbb {N}}_0\), and let \({\mathscr {F}}\in {\mathscr {H}}_{\infty ,n}\) be a presheaf of \((\infty ,n)\)-categories on \({{\mathscr {C}}\text {art} }\). We define \((\infty ,n)\)-categories where we make use of the simplicial enrichment of \(\mathscr {C}\mathscr {S}\mathscr {S}_n\). We call \({\mathscr {F}}(P)^{\text {D} (Y)}\) the \((\infty ,n)\)-category of equivariant sections of \({\mathscr {F}}\) over \(P(Y) \in {{\widehat{{{\mathscr {C}}\text {art} }}}}\). We define \((\infty ,n)\)-categories and we call \({\mathscr {F}}(P)^{coh}\) the \((\infty ,n)\)-category of coherent sections of \({\mathscr {F}}\) over P. Note that by Proposition 3.31\({\mathscr {F}}(P)^{\text {D} (Y)}\) and \({\mathscr {F}}(P)^{coh}\) are models for the homotopy limits By Lemma 3.32 these are indeed both \((\infty ,n)\)-categories, i.e. fibrant objects in \(\mathscr {C}\mathscr {S}\mathscr {S}_n\). The first homotopy limit describes the \((\infty ,n)\)-category of homotopy fixed points of the smooth action of \(\text {D} (Y)\) on sections of \({\mathscr {F}}\) over P(Y). In particular, the homotopy fixed point data depends smoothly on the diffeomorphisms in \(\text {D} (Y)\). The second homotopy limit can be described as follows: for each manifold \(Y_0 \in {{\mathscr {M}}}_Y\), we can form the \((\infty ,n)\)-category of sections of \({\mathscr {F}}\) over \(P(Y_0)\); it is given by \(S_{\infty ,n}({\mathscr {F}})(P(Y_0))\). Given another manifold \(Y_1 \in {{\mathscr {M}}}_Y\), there is a small presheaf (even a diffeological space) \(\text {D} (Y_0,Y_1)\) of diffeomorphisms from \(Y_0\) to \(Y_1\). We can pull back sections of \({\mathscr {F}}\) over \(P(Y_1)\) along any such diffeomorphism, and the resulting section over \(P(Y_0)\) should depend smoothly on the diffeomorphism. The homotopy limit \({\mathscr {F}}^{coh}\) can be understood as the \((\infty ,n)\)-category of families of sections of \({\mathscr {F}}(Y_0)\) over \(P(Y_0)\), for all \(Y_0 \in {{\mathscr {M}}}_Y\); these sections further are homotopy coherent with respect to all diffeomorphisms \(Y_0 \rightarrow Y_1\), and their homotopy coherence data depends smoothly on these diffeomorphisms. After this preparation, we give two different proofs (in Theorems 4.34 and 4.35) that the \((\infty ,n)\)-categories of equivariant sections and coherent sections are equivalent. The first proof relies on the fact that the inclusion \({\textsf {B}}\text {D} (Y) \hookrightarrow {{\mathscr {M}}}_Y\) of groupoid objects in \({\widehat{{{\mathscr {C}}\text {art} }}}\) is an equivalence, whereas the second proof relies on the descent results from Sect. 3. Both of these proofs have different advantages: the first is more slick and less involved. However, the choice of an inverse equivalence to the inclusion \({\textsf {B}}\text {D} (Y) \hookrightarrow {{\mathscr {M}}}_Y\) is by no means canonical, thus making the equivalences obtained in this proof less helpful in practice. In the second proof, the inverse equivalence is obtained as the inverse of a pullback along a \({{\widehat{\tau }}}_{dgop}\)-local epimorphism. That is, it is given precisely by descent. In many important cases, descent functors are available, so that the second perspective is more helpful for practical purposes. Let \({\mathscr {F}}\in {\mathscr {H}}_{\infty ,n}\) projectively fibrant. There are (weakly) inverse weak equivalences We view the truncations to simplicial levels zero and one of \(P(Y) {/\hspace{-0.1cm}/}\text {D} (Y)\) and of \(P {/\hspace{-0.1cm}/}{{\mathscr {M}}}_Y = B(*,{{\mathscr {M}}}_Y^{\text {op}}, P)\) as strict presheaves of groupoids on \({{\mathscr {C}}\text {art} }\). Let us denote these by \(Gr(P(Y) {/\hspace{-0.1cm}/}\text {D} (Y))\) and \(Gr(B(*,{{\mathscr {M}}}_Y^{\text {op}}, P))\), respectively. Observe that and that there is a canonical inclusion Any choice of a family of diffeomorphisms \(\{ f_{Y_0} :Y_0 \rightarrow Y \}_{Y_0 \in {{\mathscr {M}}}_Y}\) determines a morphism for which there exist 2-isomorphisms (i.e. natural isomorphisms, coherent over \({{\mathscr {C}}\text {art} }\)) \(p \circ \iota = 1\) and \(\eta :\iota \circ p \rightarrow 1\) of presheaves of groupoids over \({{\mathscr {C}}\text {art} }\). In particular, \(N \eta \) determines a simplicial homotopy between the identity and \(N(p \circ \iota )\) in \({\mathscr {H}}_{\infty ,0}\). This, in turn, shows that both \(\iota \) and p are homotopy equivalences, weakly inverse to each other. Consequently, we obtain a pair of projective weak equivalences The weak equivalences in the claim are \((Q\iota )^*\) and \((Qp)^*\). \(\square \) For any \(n \in {\mathbb {N}}_0\) and for any fibrant \({\mathscr {F}}\in {\mathscr {H}}_{\infty ,n}^{loc}\) there is a canonical zig-zag of weak equivalences between fibrant objects in \(\mathscr {C}\mathscr {S}\mathscr {S}_n\), The second and third weak equivalences are direct consequences of Proposition 4.32. The first and last weak equivalences follow by a direct computation: we have canonical isomorphisms Using the Bousfield-Kan map in the first argument of the functor tensor product now induces a canonical weak equivalence to this object from the object This completes the proof. \(\square \) That \((Q {\text {diag}}(\Psi ))^*\) is a weak equivalence relies on the descent results in Sect. 3; these entered in the proof of Proposition 4.31 and hence also Proposition 4.32. In the case where \({\mathscr {F}}\) is the sheaf of diffeological vector bundles from Definition 4.9 the insights from Theorem 4.35 were used in [13] in order to obtain a coherent vector bundle on P, where \(Y = {\mathbb {S}}^1\) and \(P = M^{(-)}\) for some manifold M, from the equivariant structure of the transgression line bundle of a bundle gerbe with connection. Moreover, this procedure was also applied to bundles over certain spaces of paths in M, and the coherent vector bundles thus obtained were subsequently assembled into a smooth open-closed FFT on M. In this sense, that smooth FFT was built from its values on generating objects by means of the equivalence of equivariant and coherent sections of a sheaf of higher categories as explored here. There is also great interest in extended field theories, which are formulated in the language of n-fold complete Segal spaces [15, 35]. It is with this in mind that we prove Theorems 4.34 and 4.35 in the setting of \((\infty ,n)\)-categories. \(\triangleleft \) In this section we point out potential applications of Corollary 3.48 to the theory of categorified vector bundles. The gerbes of Sect. 4.2 can be considered as a model for rank-one 2-vector bundles. The theory for 2-vector bundles of higher rank, and more generally for higher categorifications of vector bundles, is currently only little understood (see below for references). Thus, this section does not contain formal results, but outlines how the results of Sect. 3.3 will be applicable to the theory of higher vector bundles. This will be similar to the ideas in Sects. 4.1 and 4.2. We start by briefly mentioning several models for categorified vector bundles: In [39, Sec. 4.3] the authors consider 2-categorical presheaves of Kapranov-Voevodsky 2-vector bundles on the category of manifolds. They apply the Grothendieck plus-construction to sheafify these higher presheaves and obtain a 2-categorical sheaf which assigns to each manifold a 2-category of 2-vector bundles, modelled on Kapranov-Voevodsky 2-vector spaces (as defined in [32]). A similar 2-category was considered in [4]. In [29] the authors defined a presheaf of 2-categories on the site of manifolds with surjective submersions as coverings which assigns to each manifold a 2-categoryFootnote 4 built from bimodule bundles over bundles of super-algebras. The authors then sheafify this presheaf of 2-categories and propose the resulting sheaf of 2-categories as a model for 2-vector bundles on the site of manifolds and surjective submersions. Extending this, one can consider presheaves of \((\infty ,n)\)-categories on a small category \({\mathscr {C}}\) which assign to each object higher Morita categories of \({\mathbb {E}}_n\)-bimodules; for \({\mathscr {C}}= {{\mathscr {C}}\text {art} }\) or \({\mathscr {C}}= {{\mathscr {M}}{\text {fd}}}\), these could, for instance, be A-B-bimodules for the \({\mathbb {E}}_\infty \)-algebras \(A = {\mathbb {C}}\) and B the algebra of smooth functions on the underlying manifold (or derived versions thereof). Sheafifying these higher presheaves on \({{\mathscr {C}}\text {art} }\) with respect to differentiably good open coverings would give viable candidates for generalisations of higher vector bundles. In each of these cases, one is presented with a sheaf of \((\infty ,n)\)-categories in the sense of Sect. 3.3. Then, Corollary 3.48 applies, and we obtain that each such sheaf of \((\infty ,n)\)-categories of higher vector bundles on \(({{\mathscr {C}}\text {art} }, \tau _{dgop})\) extends to a sheaf of \((\infty ,n)\)-categories on \(({{\widehat{{{\mathscr {C}}\text {art} }}}}, {{\widehat{\tau }}})\). The resulting extended higher sheaves are good candidates for a description of categorified vector bundles on generalised smooth spaces and \({{\widehat{\tau }}}_{dgop}\)-coverings, such as manifolds and surjective submersions, or diffeological spaces and subductions.Remark 4.25

 is the simplex category
is the simplex category  with an initial object \([-1]\) adjoined to it.
with an initial object \([-1]\) adjoined to it.Example 4.26

 . Explicitly,
. Explicitly,


Lemma 4.27
Proof
Proposition 4.28
Proof
Corollary 4.29


Proposition 4.31
Proof

Proposition 4.32
Proof
 is homotopical (it is left Quillen and all objects in
is homotopical (it is left Quillen and all objects in  are cofibrant), \({\text {diag}}(\Phi )\) is a weak equivalence in \({\mathscr {H}}_{\infty ,0}\). This implies (1), since Q is homotopical.
are cofibrant), \({\text {diag}}(\Phi )\) is a weak equivalence in \({\mathscr {H}}_{\infty ,0}\). This implies (1), since Q is homotopical.
Definition 4.33



Theorem 4.34

Proof

Theorem 4.35

Proof

Remark 4.36
Remark 4.37
4.4 Remarks on Descent for Sheaves of 2-Vector Bundles
5 The Image of Right Kan Extension on Sheaves of Spaces
We now classify those presheaves of \(\infty \)-groupoids on \({{\widehat{{\mathscr {C}}}}}\) which are extensions of sheaves of \(\infty \)-groupoids on \(({\mathscr {C}},\tau )\). We achieve this by passing to \(\infty \)-categorical language using quasi-categories (the model for \((\infty ,1)\)-categories used in [14, 34]), rather than working with model-categorical presentations, and prove an enhancement of Theorem 3.23 to an equivalence of quasi-categories of homotopy-coherent sheaves of \(\infty \)-groupoids.
5.1 On a Quasi-categorical Site
Let \({\textsf {C}}\) be a quasi-category, and let \(({\textsf {C}}, \tau )\) be a small quasi-categorical Grothendieck site (as defined in [34, Def. 6.2.2.1], where they are called ‘\(\infty \)-sites’) with underlying quasi-category \({\textsf {C}}\). We let  be the quasi-category of presheaves of small spaces on \({\textsf {C}}\). Let
be the quasi-category of presheaves of small spaces on \({\textsf {C}}\). Let  denote the quasi-category of presheaves of large spaces on \({\textsf {C}}\), and let \({\textsf {Sh}}({\textsf {C}},\tau ) \subset {\textsf {PSh}}({\textsf {C}})\) denote the quasi-category of sheaves on \({\textsf {C}}\) with respect to \(\tau \). This induces the standard reflective localisation
denote the quasi-category of presheaves of large spaces on \({\textsf {C}}\), and let \({\textsf {Sh}}({\textsf {C}},\tau ) \subset {\textsf {PSh}}({\textsf {C}})\) denote the quasi-category of sheaves on \({\textsf {C}}\) with respect to \(\tau \). This induces the standard reflective localisation

where \(\text {L} \) is the sheafification functor.
Remark 5.1
In this section all quasi-categories denoted \({\textsf {PSh}}\) and \({\textsf {Sh}}\) are categories of functors taking values in \({\textsf {S}}_\text {L} \), i.e. the quasi-category of large spaces, unless otherwise indicated. \(\triangleleft \)
In this set-up, a morphism \(f :Y \rightarrow X\) in \({\widehat{{\textsf {C}}}_\infty }\) is a \(\tau \)-local epimorphism whenever its sheafification \({{\textsf {L}}}f :{{\textsf {L}}}Y \rightarrow {{\textsf {L}}}X\) is an effective epimorphism in \({\textsf {Sh}}({\textsf {C}},\tau )\) [34, Lemma 6.2.2.8]. Since effective epimorphisms are stable under pullback and \({{\textsf {L}}}\) is left exact, \(\tau \)-local epimorphisms induce a coverage---and hence a Grothendieck topology---on the homotopy category \(\text {h} {\widehat{{\textsf {C}}}_\infty }\). Since a Grothendieck topology on \(\text {h} {\widehat{{\textsf {C}}}_\infty }\) is the same as a Grothendieck topology on \({\widehat{{\textsf {C}}}_\infty }\) [34, Rmk. 6.2.2.3], we obtain a new quasi-categorical Grothendieck site \(({\widehat{{\textsf {C}}}_\infty }, {{\widehat{\tau }}})\), whose topology is generated by the \(\tau \)-local epimorphisms in \({\widehat{{\textsf {C}}}_\infty }\). The corresponding quasi-category \({\textsf {Sh}}({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}})\) of sheaves on \({\widehat{{\textsf {C}}}_\infty }\) is the localisation of \({\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) at the morphisms
where \(f :Y \rightarrow X\) is any \(\tau \)-local epimorphism, \({{\widehat{{{\mathscr {Y}}}}}}\) is the Yoneda embedding of \({\widehat{{\textsf {C}}}_\infty }\), and \({\check{C}}{{\widehat{{{\mathscr {Y}}}}}}_f\) is the Čech nerve of \({{\widehat{{{\mathscr {Y}}}}}}_f :{{\widehat{{{\mathscr {Y}}}}}}_Y \rightarrow {{\widehat{{{\mathscr {Y}}}}}}_X\). We thus obtain another reflective localisation

whose left adjoint \({\widehat{{{\textsf {L}}}}}\) is left exact. Note that since the Yoneda embedding preserves limits and \({\widehat{{\textsf {C}}}_\infty }\) is complete, there is a canonical equivalence \({{\widehat{{{\mathscr {Y}}}}}}_{{\check{C}}f} \simeq {\check{C}}{{\widehat{{{\mathscr {Y}}}}}}_f\). This directly leads to:
Lemma 5.2
A presheaf \({\mathcal {G}}\in {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) is \({{\widehat{\tau }}}\)-local, i.e. it lies in the full sub-quasi-category \({\textsf {Sh}}({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}}) \subset {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\), if and only if  is an equivalence, for every \(\tau \)-local epimorphism \(f :Y \rightarrow X\).
is an equivalence, for every \(\tau \)-local epimorphism \(f :Y \rightarrow X\).
Let \({\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty }) = \underline{\text {Hom} }_!({\widehat{{\textsf {C}}}_\infty }^{\text {op}}, {\textsf {S}}_\text {L} )\) denote the full sub-quasi-category of \({\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) on those functors which preserve small limits (equivalently the small-colimit-preserving functors \({\widehat{{\textsf {C}}}_\infty }\rightarrow {\textsf {S}}_\text {L} ^{\text {op}}\)). We also define a quasi-category \({\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}})\) as the pullback of quasi-categories

That is, \({\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}}) \subset {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) is the full sub-quasi-category on those \({{\widehat{\tau }}}\)-sheaves whose underlying functor \({\widehat{{\textsf {C}}}_\infty }^{\text {op}}\rightarrow {\textsf {S}}_\text {L} \) turns small colimits in \({\widehat{{\textsf {C}}}_\infty }\) into limits in \({\textsf {S}}_\text {L} \). The functor \({{\mathscr {Y}}}:{\textsf {C}}\rightarrow {\widehat{{\textsf {C}}}_\infty }\) induces a functor \({\textsf {C}}^{\text {op}}\rightarrow {\widehat{{\textsf {C}}}_\infty }^{\text {op}}\), and by a slight abuse of notation we again denote this functor by \({{\mathscr {Y}}}\). As before, we leave the inclusion \({\textsf {S}}_\text {S} \subset {\textsf {S}}_\text {L} \) of the quasi-category of small spaces into that of large spaces implicit. Observe that the left and right Kan extensions \({{\mathscr {Y}}}_!, {{\mathscr {Y}}}_*\) yield functors \({\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty }) \rightarrow {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\).
Lemma 5.3
Let \({\textsf {C}}\) be a small quasi-category.
-
(1)
For any \(A \in {\widehat{{\textsf {C}}}_\infty }\subset {\textsf {PSh}}({\textsf {C}})\) and \({\mathcal {G}}\in {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) there is a natural equivalence
$$\begin{aligned} {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })({{\mathscr {Y}}}_*A, {\mathcal {G}}) \simeq {\mathcal {G}}(A)\,. \end{aligned}$$Equivalently, the restriction \({{\mathscr {Y}}}_{*|{\widehat{{\textsf {C}}}_\infty }}\) agrees with \({{\widehat{{{\mathscr {Y}}}}}}\) as functors \({\widehat{{\textsf {C}}}_\infty }\rightarrow {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\).
-
(2)
For any \(A \in {\widehat{{\textsf {C}}}_\infty }\subset {\textsf {PSh}}({\textsf {C}})\) and \({\mathcal {G}}\in {\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty })\) there is a natural equivalence
$$\begin{aligned} {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })({{\mathscr {Y}}}_!A, {\mathcal {G}}) \simeq {\mathcal {G}}(A)\,. \end{aligned}$$
Proof
Using the equivalence \(X \simeq {\text {colim}}_{c \in {\textsf {C}}_{/X}} {{\mathscr {Y}}}_c\), for \(X \in {\widehat{{\textsf {C}}}_\infty }\), we obtain
proving the first equivalence. To see the second equivalence, we use that
In the second-to-last step we have used that \({\mathcal {G}}\) turns colimits in \({\widehat{{\textsf {C}}}_\infty }\) into limits in \({\textsf {S}}_\text {L} \). \(\square \)
Lemma 5.4
Let \(D :{\mathscr {J}}\rightarrow {\widehat{{\textsf {C}}}_\infty }\) be any small diagram. There is a canonical equivalence
Proof
This follows by a repeated application of the Yoneda Lemma and the fact that colimits in presheaf categories are computed objectwise. In particular, we have
which yields the desired equivalence. \(\square \)
We then have the following quasi-categorical enhancement of Theorem 3.23. This fully unveils the importance of the topology induced on \({\widehat{{\textsf {C}}}_\infty }\) by the \(\tau \)-local epimorphisms.
Theorem 5.5
Let \({\textsf {C}}\) be a small quasi-category, and let \({{\mathscr {Y}}}_* :{\textsf {PSh}}({\textsf {C}}) \rightarrow {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) denote the right Kan extension along \({{\mathscr {Y}}}:{\textsf {C}}^{\text {op}}\rightarrow {\widehat{{\textsf {C}}}_\infty }^{\text {op}}\).
-
(1)
The adjunction \({{\mathscr {Y}}}^* \dashv {{\mathscr {Y}}}_*\) induces an equivalence

-
(2)
More generally, let \(\tau \) be a Grothendieck topology on \({\textsf {C}}\). The adjunction \({{\mathscr {Y}}}^* \dashv {{\mathscr {Y}}}_*\) restricts to an equivalence

Proof
Claim (1) is an explicit incidence of a well-known theorem: there is a canonical equivalence \(\underline{\text {Hom} }({\textsf {C}}, {\textsf {D}}) \simeq \underline{\text {Hom} }_!({\widehat{{\textsf {C}}}_\infty },{\textsf {D}})\) between the quasi-categories of functors from \({\textsf {C}}\) to any \(\text {S} \)-cocomplete quasi-category \({\textsf {D}}\) and (small-)colimit-preserving functors \({\widehat{{\textsf {C}}}_\infty }\rightarrow {\textsf {D}}\). For \({\textsf {D}}= {\textsf {S}}_\text {L} ^{\text {op}}\), this equivalence is established by \({{\mathscr {Y}}}_*\). In particular, \({{\mathscr {Y}}}_*\) is fully faithful even as a functor \({\textsf {PSh}}({\textsf {C}}) \rightarrow {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\). The adjunction \({{\mathscr {Y}}}^*: {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty }) \rightleftarrows {\textsf {PSh}}({\textsf {C}}): {{\mathscr {Y}}}_*\) restricts to an adjunction \({{\mathscr {Y}}}^*: {\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty }) \rightleftarrows {\textsf {PSh}}({\textsf {C}}): {{\mathscr {Y}}}_*\), whose right adjoint \({{\mathscr {Y}}}_*\) is an equivalence. Thus, the left adjoint \({{\mathscr {Y}}}^*\) is an equivalence as well [14, Prop. 6.1.6].
We now prove (2): first, we show that \({{\mathscr {Y}}}_*\) maps \({\textsf {Sh}}({\textsf {C}},\tau )\) to \({\textsf {Sh}}({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}})\), i.e. that it maps \(\tau \)-sheaves on \({\textsf {C}}\) to \({{\widehat{\tau }}}\)-sheaves on \({\widehat{{\textsf {C}}}_\infty }\). Let \(F \in {\textsf {Sh}}({\textsf {C}},\tau )\), and let \(f :Y \rightarrow X\) be a \(\tau \)-local epimorphism in \({\widehat{{\textsf {C}}}_\infty }\). We need to prove that the morphism
is an equivalence. By Lemma 5.3(1), Lemma 5.4, and because \({{\mathscr {Y}}}_*\) is fully faithful, we have equivalences
Using that F is a \(\tau \)-sheaf and that \({{\textsf {L}}}\) is a left exact left adjoint, we then compute
Thus, \({{\mathscr {Y}}}_*F\) is a \({{\widehat{\tau }}}\)-sheaf whenever F is a \(\tau \)-sheaf. In particular, \({{\mathscr {Y}}}_*\) restricts to a fully faithful functor
Finally, we claim that the functor \({{\mathscr {Y}}}^* :{\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty }) \rightarrow {\textsf {PSh}}({\textsf {C}})\) restricts to a functor \({{\mathscr {Y}}}^* :{\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}}) \rightarrow {\textsf {Sh}}({\textsf {C}},\tau )\); by part (1), this restriction is automatically fully faithful. To that end, let \({\mathcal {G}}\in {\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty }, {{\widehat{\tau }}})\). We have to show that \({{\mathscr {Y}}}^*{\mathcal {G}}\in {\textsf {PSh}}({\textsf {C}})\) is \(\tau \)-local, i.e. that the presheaf \({{\mathscr {Y}}}^*{\mathcal {G}}\) is a \(\tau \)-sheaf. That is the case precisely if
is an equivalence for every \(\tau \)-covering \(g :Y \rightarrow {{\mathscr {Y}}}_c\). (Note that if g is a \(\tau \)-covering, then \({{\textsf {L}}}(|{\check{C}}g| \rightarrow {{\mathscr {Y}}}_c)\) is an equivalence, i.e. g is a \(\tau \)-local epimorphism.) On the right-hand side, we have canonical equivalences

The first equivalence is simply the adjunction \({{\mathscr {Y}}}_! \dashv {{\mathscr {Y}}}^*\), the second equivalence is Lemma 5.3(2), which applies since \({\mathcal {G}}\) turns colimits into limits. This property also provides the third equivalence. The final equivalence arises from Lemma 5.2, as \({\mathcal {G}}\) is a \({{\widehat{\tau }}}\)-sheaf.
We have thus shown that \({{\mathscr {Y}}}^*\) and \({{\mathscr {Y}}}_*\) restrict to functors between \({\textsf {Sh}}({\textsf {C}},\tau )\) and \({\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}})\). Since \({\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}}) \subset {\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty })\) and \({\textsf {Sh}}({\textsf {C}},\tau ) \subset {\textsf {PSh}}({\textsf {C}})\) are full subcategories, the natural equivalences \({{\mathscr {Y}}}^* {{\mathscr {Y}}}_* \rightarrow 1\) and \(1 \rightarrow {{\mathscr {Y}}}_* {{\mathscr {Y}}}^*\) from part (1) establish that these restrictions of \({{\mathscr {Y}}}^*\) and \({{\mathscr {Y}}}_*\) furnish an equivalence as claimed. \(\square \)
Corollary 5.6
If \(\tau _0\) is the trivial topology on \({\textsf {C}}\) (whose coverings are generated solely by the identity morphisms), then \({\textsf {Sh}}_!({\widehat{{\textsf {C}}}_\infty },{{\widehat{\tau }}}_0) \simeq {\textsf {Sh}}({\textsf {C}}, \tau _0) \simeq {\textsf {PSh}}({\textsf {C}}) \simeq {\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty })\).
Proof
This follows from Theorem 5.5(1) since pullbacks of equivalences in a quasi-category are again equivalences. \(\square \)
Remark 5.7
In particular, if \({\mathcal {G}}\in {\textsf {PSh}}({\widehat{{\textsf {C}}}_\infty })\) is colimit-preserving, then it satisfies \({{\widehat{\tau }}}_0\)-descent. One can also see this directly: the \({{\widehat{\tau }}}_0\)-local epimorphisms are exactly the effective epimorphisms in \({\widehat{{\textsf {C}}}_\infty }\), i.e. those morphisms \(p :Y \rightarrow X\) whose induced morphism \(|{\check{C}}p| \rightarrow X\) is an equivalence in \({\widehat{{\textsf {C}}}_\infty }\). Thus, for \({\mathcal {G}}\in {\textsf {PSh}}_!({\textsf {C}})\), we have that  is an equivalence, and hence that \({\mathcal {G}}\) satisfies \({{\widehat{\tau }}}_0\)-descent. \(\triangleleft \)
is an equivalence, and hence that \({\mathcal {G}}\) satisfies \({{\widehat{\tau }}}_0\)-descent. \(\triangleleft \)
We summarise various characterisations of the sheaves in the image of \({{\mathscr {Y}}}_*\): Let \(\underline{\text {Hom} }_{! W_\tau }({\widehat{{\textsf {C}}}_\infty }^{\text {op}}, {\textsf {S}}_\text {L} ) \subset {\textsf {PSh}}_!({\widehat{{\textsf {C}}}_\infty })\) denote the full sub-quasi-category on those limit-preserving functors \({\widehat{{\textsf {C}}}_\infty }^{\text {op}}\rightarrow {\textsf {S}}_\text {L} \) (equivalently colimit-preserving functors \({\widehat{{\textsf {C}}}_\infty }\rightarrow {\textsf {S}}_\text {L} ^{\text {op}}\)) which send all morphisms in \(W_\tau \) to equivalences.
Theorem 5.8
There are equivalences of quasi-categories

Proof
The first equivalence is Theorem 5.5. The second equivalence follows from [34, Cor. 4.4.5.16] and [34, Cor. 5.1.6.11] (note that \({{\widehat{{{\mathscr {Y}}}}}}:{\textsf {Sh}}({\textsf {C}}, \tau ) \rightarrow {\textsf {PSh}}_!({\textsf {Sh}}({\textsf {C}},\tau ))\), with the codomain restricted to colimit-preserving presheaves, is colimit-preserving).Footnote 5 The third is an application of [14, Thm. 7.7.9] (with the class of cofibrations given by all morphisms in \({\widehat{{\textsf {C}}}_\infty }\) and the weak equivalences given by \(W_\tau \)). \(\square \)
5.2 On a 1-Site
For many geometric applications it is more convenient to work not with \(\infty \)-presheaves on a quasi-category, but only with \({{\mathscr {S}}\text {et} }_\text {L} \)-valued presheaves on an ordinary category. For instance, many geometric problems are set on manifolds or diffeological spaces (such as in Sects. 4.1 and 4.3), and it is often more efficient (though less general) to treat these as particular presheaves of sets. Thus, in this section we prove a version of Theorem 5.2 where \({\mathscr {C}}\) is an ordinary (1-)category and we replace \({\widehat{{\textsf {C}}}_\infty }\) by the ordinary category \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\) of \({{\mathscr {S}}\text {et} }_\text {S} \)-valued presheaves on \({\mathscr {C}}\). The quasi-category of \({\textsf {S}}_\text {S} \)-valued presheaves on \({\mathscr {C}}\) is  .
.
We let \({{\widehat{{\mathscr {C}}}}}= \textrm{Fun}({\mathscr {C}}^{\text {op}}, {{\mathscr {S}}\text {et} }_\text {S} )\) denote the category of ordinary, small presheaves on \({\mathscr {C}}\). Let \({\textsf {N}}{\mathscr {C}}\) denote the quasi-category given by the nerve of \({\mathscr {C}}\). The Yoneda embedding of \({\textsf {N}}{\mathscr {C}}\) factorises as

where \({{\mathscr {Y}}}^0\) is the 1-categorical Yoneda embedding of \({\mathscr {C}}\) and  is the quasi-category of small presheaves of spaces on \({\textsf {N}}{\mathscr {C}}\). Note that \({{\widehat{{\mathscr {C}}}}}\hookrightarrow \widehat{{\textsf {N}}{\mathscr {C}}}_\infty \) is a reflective localisation with localisation functor \(\pi _0\). As before, we write
is the quasi-category of small presheaves of spaces on \({\textsf {N}}{\mathscr {C}}\). Note that \({{\widehat{{\mathscr {C}}}}}\hookrightarrow \widehat{{\textsf {N}}{\mathscr {C}}}_\infty \) is a reflective localisation with localisation functor \(\pi _0\). As before, we write  .
.
Lemma 5.10
Let \(F \in {\textsf {PSh}}({\textsf {N}}{\mathscr {C}})\). There is a natural equivalence \({{\mathscr {Y}}}^0_* F \simeq \iota ^* {{\mathscr {Y}}}_* F\) of objects in \({\textsf {PSh}}({\textsf {N}}{{\widehat{{\mathscr {C}}}}})\).
Proof
This is a direct application of [16, Lemma 3.13] (noting that \({\textsf {N}}{{\widehat{{\mathscr {C}}}}}\) is large and the target \({\textsf {S}}_\text {L} \) is \(\text {L} \)-cocomplete). \(\square \)
Applying the functor \(\iota _*\), we obtain a natural equivalence \(\iota _* {{\mathscr {Y}}}^0_* F \simeq \iota _* \iota ^* {{\mathscr {Y}}}_* F\).
Lemma 5.11
For \({\mathcal {G}}\in {\textsf {PSh}}_!(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty )\), there is an equivalence \(\iota _* \iota ^*{\mathcal {G}}\simeq {\mathcal {G}}\).
Proof
By Theorem 5.5, there exists \(F \in {\textsf {PSh}}({\textsf {N}}{\mathscr {C}})\) and an equivalence \({{\mathscr {Y}}}_*F \simeq {\mathcal {G}}\). We have equivalences
The second equivalence is Lemma 5.10 and the second-to-last equivalence is the factorisation (5.9). \(\square \)
In particular, we have that \(\iota _* \iota ^* {{\mathscr {Y}}}_*F \simeq {{\mathscr {Y}}}_*F\), for each \(F \in \textrm{Fun}({\textsf {N}}{\mathscr {C}}^{\text {op}}, {\textsf {S}}_\text {L} )\), by Theorem 5.5. Combining this with Lemma 5.10, we thus obtain that the canonical morphism
is an equivalence, for each \(F \in {\textsf {PSh}}({\textsf {N}}{\mathscr {C}})\).
Theorem 5.12
Let \({{\textsf {X}}}\) denote the full sub-quasi-category of \({\textsf {PSh}}({\textsf {N}}{{\widehat{{\mathscr {C}}}}})\) on those presheaves F where \(\iota _* F \in {\textsf {PSh}}_!(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty )\). The functor \({{\mathscr {Y}}}^0_* :{\textsf {PSh}}({\textsf {N}}{\mathscr {C}}) \rightarrow {{\textsf {X}}}\) is an equivalence with inverse \(({{\mathscr {Y}}}^0)^*\).
Proof
Combining the observation preceding Theorem 5.12 with Theorem 5.5(1) shows that \({{\mathscr {Y}}}^0_*\) takes values in \({{\textsf {X}}}\). Since \({{\mathscr {Y}}}^0\) is fully faithful, so is \({{\mathscr {Y}}}^0_*\); it remains to check that \({{\mathscr {Y}}}^0_*\) is essentially surjective. To that end, let \(G \in {{\textsf {X}}}\). By Theorem 5.5(1) and the definition of \({{\textsf {X}}}\) there exists an \(F \in {\textsf {PSh}}({\textsf {N}}{\mathscr {C}})\) and an equivalence \(\iota _*G = {{\mathscr {Y}}}_*F\). Lemma 5.10 implies that
The first equivalence is (the inverse of) the counit of the adjunction \(\iota ^* \dashv \iota _*\); this is an equivalence since \(\iota \)---and therefore \(\iota _*\)---is fully faithful. \(\square \)
Corollary 5.13
The functor \(\iota _* :{{\textsf {X}}}\rightarrow {\textsf {PSh}}_!(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty )\) is an equivalence with inverse \(\iota ^*\). That is, presheaves in \({\textsf {PSh}}_!(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty )\) are fully determined by their restriction to \({\textsf {N}}{{\widehat{{\mathscr {C}}}}}\).
This merely reflects the fact that \(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty \) is generated under small colimits by the image of the inclusion \({\textsf {N}}{{\widehat{{\mathscr {C}}}}}\hookrightarrow \widehat{{\textsf {N}}{\mathscr {C}}}_\infty \).
Theorem 5.14
Let \({{\textsf {X}}}_\tau \subset {\textsf {PSh}}({\textsf {N}}{{\widehat{{\mathscr {C}}}}})\) be the full sub-quasi-category on those presheaves X where \(\iota _*X \in {\textsf {Sh}}_!(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty ,{{\widehat{\tau }}})\). There is a canonical equivalence \({\textsf {Sh}}({\mathscr {C}},\tau ) \simeq {{\textsf {X}}}_\tau \).
Proof
Consider the diagram

By definition of \({{\textsf {X}}}\) and \({{\textsf {X}}}_\tau \) and the pasting law for pullbacks, both squares in this diagram are pullback squares. We also consider the diagram

It suffices to show that the outer square in this diagram is a pullback. Theorem 5.12 states that the right-hand square in this diagram is a pullback square of quasi-categories. Additionally, Theorem 5.5 implies that the left and centre vertical morphisms are equivalences of quasi-categories, so that the left-hand square is a pullback as well. The claim now follows by the pasting law for pullbacks. \(\square \)
This provides a very general perspective on the statement that open coverings and surjective submersions define the same quasi-categories of sheaves on the category \({{\mathscr {M}}{\text {fd}}}\) of manifolds:
Corollary 5.15
Consider the case \({\mathscr {C}}= {{\mathscr {M}}{\text {fd}}}\). Let \(\tau _{dgop}\) be the topology on \({{\mathscr {M}}{\text {fd}}}\) induced by differentiably good open coverings, \(\tau _{op}\) the topology induced by open coverings and \(\tau _{ssub, \sqcup }\) the topology induced by surjective submersions of manifolds and open coverings by disjoint open subsets (i.e. by connected components). The canonical functors

are equivalences.
Proof
It is clear that second inclusion exists. For the first inclusion, we need to check that, for each \(F \in {\textsf {Sh}}({\textsf {N}}{{\mathscr {M}}{\text {fd}}}, \tau _{ssub, \sqcup })\), we also have that \(F \in {\textsf {Sh}}({\textsf {N}}{{\mathscr {M}}{\text {fd}}}, \tau _{op})\). Note that for \(F :{\textsf {N}}{{\mathscr {M}}{\text {fd}}}^{\text {op}}\rightarrow {\textsf {S}}_\text {L} \) to satisfy descent with respect to coverings by disjoint open subsets means precisely that F sends coproducts in \({{\mathscr {M}}{\text {fd}}}\) to products in \({\textsf {S}}_\text {L} \). Let \({{\mathcal {U}}}= \{U_i \hookrightarrow M\}_{i \in I}\) be an open covering of a manifold M. Consider the surjective submersion
Its Čech nerve, taken in \({{\mathscr {M}}{\text {fd}}}\), reads as
Note that the canonical map \({{\mathscr {Y}}}^0_M \sqcup {{\mathscr {Y}}}^0_N \longrightarrow {{\mathscr {Y}}}^0_{M \sqcup N}\) is not an isomorphism in \({\widehat{{{\mathscr {M}}{\text {fd}}}}}\), since manifolds are allowed to be non-connected. However, for \(F :{{\mathscr {M}}{\text {fd}}}^{\text {op}}\rightarrow {\textsf {S}}_\text {L} \) sending coproducts in \({{\mathscr {M}}{\text {fd}}}\) to products, the canonical morphism
is an equivalence, for each \(k \in {\mathbb {N}}_0\). The left-hand side are the terms in the descent condition for F with respect to the open covering \({{\mathcal {U}}}\), whereas the right-hand side are the terms in the descent condition for F with respect to the surjective submersion \(\coprod _{i \in I} U_i \rightarrow M\). Since we assumed F to satisfy descent with respect to surjective submersions, the latter descent condition is satisfied. By the above observation, it thus follows that \(F \in {\textsf {Sh}}({\textsf {N}}{{\mathscr {M}}{\text {fd}}}, \tau _{op})\).
We are left to check that the inclusions in the claim are in fact essentially surjective. For the first inclusion, we claim that \({{\widehat{\tau }}}_{ssub, \sqcup } \subset {{\widehat{\tau }}}_{op}\). Indeed, let \(\pi :Y \rightarrow X\) be a \(\tau _{ssub, \sqcup }\)-local epimorphism in \({\widehat{{{\mathscr {M}}{\text {fd}}}}}\). Therefore, given any morphism \(f :{{\mathscr {Y}}}^0_M \rightarrow X\) from a representable presheaf, there exists either an open cover by disjoint subsets of M and lifts of f to Y over the patches, or a surjective submersion \(p :N \rightarrow M\) together with a commutative square commutative square

in \({\widehat{{{\mathscr {M}}{\text {fd}}}}}\). In the first case, there is nothing to prove, since we have already lifted f through an open covering of M. In the second case, let \({{\mathcal {U}}}= \{U_i \rightarrow M\}_{i \in I}\) be an open covering of M such that p admits a section \(s_i :U_i \rightarrow N\) over each patch \(U_i\). This gives, for each \(i \in I\), a commutative diagram

Thus, we have that \(\pi \in {{\widehat{\tau }}}_{op}\). An analogous argument shows that \({{\widehat{\tau }}}_{op} \subset {{\widehat{\tau }}}_{dgop}\). We thus have canonical inclusions

Recalling the definition of \({{\textsf {X}}}_\tau \subset {\textsf {PSh}}({\textsf {N}}{\mathscr {C}})\) as the preimage under \(\iota _*\) of \({\textsf {Sh}}_!(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty , {{\widehat{\tau }}}) \subset {\textsf {PSh}}(\widehat{{\textsf {N}}{\mathscr {C}}}_\infty )\), we obtain inclusions

By Theorem 5.14 this is equivalently a chain of inclusions

This completes the proof. \(\square \)


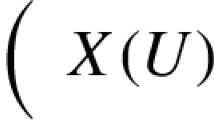


 , and
, and .
.


 and
and  is the category of large simplicial presheaves on a large category
is the category of large simplicial presheaves on a large category  . Then there is a natural morphism
. Then there is a natural morphism 

 (compare (
(compare (

 .
. . That is, for any
. That is, for any  there is an isomorphism (natural in
there is an isomorphism (natural in  )
) 

















