Reliable multiplex semi-local random walk based on influential nodes to improve link prediction in complex networks

Abstract

In recent years, the exponential growth of online social networks as complex networks has presented challenges in expanding networks and forging new connections. Link prediction emerges as a crucial technique to anticipate future relationships among users, leveraging the current network state to address this challenge effectively. While link prediction models on monoplex networks have a well-established history, the exploration of similar tasks on multilayer networks has garnered considerable attention. Extracting topological and multimodal features for weighting links can improve link prediction in weighted complex networks. Meanwhile, establishing reliable and trustworthy paths between users is a useful way to create metrics that convert unweighted to weighted similarity. The local random walk is a widely used technique for predicting links in weighted monoplex networks. The aim of this paper is to develop a semi-local random walk over reliable paths to improve link prediction on a multilayer social network as a complex network, which is denoted as Reliable Multiplex semi-Local Random Walk (RMLRW). RMLRW leverages the semi-local random walk technique over reliable paths, integrating intra-layer and inter-layer information from multiplex features to conduct a trustworthy biased random walk for predicting new links within a target layer of multilayer networks. In order to make RMLRW scalable, we develop a semi-local random walk-based network embedding to represent the network in a lower-dimensional space while preserving its original characteristics. Extensive experimental studies on several real-world multilayer networks demonstrate the performance assurance of RMLRW compared to equivalent methods. Specifically, RMLRW improves the average f-measure of the link prediction by 3.2% and 2.5% compared to SEM-Path and MLRW, respectively.

1 Introduction

The exponential growth of the number of users in social networks has led to the formation of complex connections that can be visualized by large graphs (Daud et al. 2020; Divakaran and Mohan 2020). Nodes in these networks represent user roles, while links indicate user relationships. Analyzing online social networks through the lens of complex networks poses a significant challenge for researchers across various sciences (Divakaran and Mohan 2020; Yasami and Safaei 2018). These challenges forecast future behaviors and interactions for social networks. For example, predicting a potential friendship between two individuals (Haghani and Keyvanpour 2019; Lü and Zhou 2010). In general, some connections with fake users and bots may develop over time. Meanwhile, some connections may disappear from the network due to various reasons. Link prediction can estimate the strength of links to identify spurious links or missing links (Gao et al. 2021), but this may lead to more efficient solutions when combined with reliability paths. Reliability paths intends to develop unweighted to weighted similarity metrics.

Link prediction based on influential nodes is a technique used in complex network analysis to predict future links between nodes in a network, with a particular focus on the influence of certain nodes that play crucial roles in sha** network dynamics (Curado et al. 2023). The identification problem of influential nodes is a widely studied subject in the field of complex network analysis. The goal of this problem is to assign a quantitative importance to network nodes based on the estimation of a ranking score (Curado et al. 2023). By leveraging the influence of key nodes, an influential node identification approach can improve the accuracy of link prediction models and provide valuable insights into the dynamics of complex networks.

In this paper, we introduce Reliable Multiplex semi-Local Random Walk (RMLRW) for link prediction in MLN. In order to enable MLN to employ both intralayer and interlayer information for link prediction, RMLRW develops local random walk based on the concept of extended neighborhood. Here, a new jump probability is proposed for local random walk based on extended neighborhood as well as reliable paths. We calculate the weights of interlayer and intralayer links based on several topological criteria. Also, we integrate a community random walk-based network embedding into RMLRW to be efficient in dealing with large-scale social networks. In addition, we consider using influential nodes to improve link prediction in RMLRW.

Our main contributions to the development of local random walks are summarized as follows: (1) We develop local random walk based on semi-local metrics to improve link prediction in MLN; (2) Correlation between layers is computed based on link weights by combining a number of intralayer and interlayer similarity metrics; (3) By identifying the influential nodes, we improve the local random walk technique so that the walker moves to stronger nodes at each step; (4) Reliable paths between users are used to construct a biased local random walk policy; (5) We present a community random walk-based network embedding to use a compact representation of the network when predicting links.

The organization of the outline is as follows: Section 2 surveys related work on link prediction. Section 3 discusses some fundamental concepts related to the link prediction problem and methodology. Section 4 presents the proposed strategy. Section 5 describes the data set and analyzes the results of the simulations. Finally, the conclusion along with future directions in Section 6 ends the paper.

2 Related works

Social networks are growing dynamically. This makes link prediction challenging because these techniques suffer from the complexity of large-scale social networks (Daud et al. 2020). On the other hand, machine learning technologies are constantly evolving and the development of new link prediction methods is constantly needed. In the following, some of the latest link prediction techniques are reviewed.

For MLN, Nasiri et al. (2021) presented a biased local random walk-based link prediction method, known as the Multiplex Local Random Walk (MLRW). The degree is used as the intralayer similarity in MLRW. Three distinct approaches have been investigated as inter-layer similarity: link-overlap, layer activity, and degree-degree correlation.

Battiston et al. (2016) investigated the biased local random walk on MLN. The authors analyzed the parameters of this technique, such as the entropy rate and occupation probability distribution. In addition, the influence of the MLN structure on the steady-state behavior of walkers as well as the correlations between layers and the overlap of links are discussed in this study.

Samei and Jalili (2019) used the combination of some topological criteria such as Adamic Adar and common neighbors to estimate intralayer similarity. The correlation between layers is measured through Pearson correlation coefficient and link-overlap. Here, interlayer connectivity is combined with intralayer similarity to detect spurious links in MLN.

Luo et al. (2021) proposed a Multiple-Attribute Decision-Making (MADM) method to address link prediction in MLN. In this approach, some information from various layers is used to extract attributes and then forecast potential links in the target layer. MADM is equipped with a layer similarity metric that uses cosine similarity to weight each layer.

Link prediction for multilayer ego-networks was approached as a classification problem by Rezaeipanah et al. (2020). The authors use classification techniques to extract many features from the network architecture and model it as a data set. Three different feature types are retrieved as SEM-Paths in this case: ego-paths, structural, and meta-paths.

Yang et al. (2022) introduced a similarity measure based on reliable paths for link prediction in MLN. The authors extract several topological attributes from different layers and then consider a combination of them as link weights. Here, reliable paths between users based on link weights are used to calculate similarity. The similarity measure introduced in this study includes an extended version of the FriendLink metric, where reliable paths are considered. This paper also uses the idea of reliable paths to develop a similarity metric based on local random walks.

Gao and Rezaeipanah (2022) introduced an extended version of the Katz metric for MLN. The authors used a wide range of intralayer and interlayer topological attributes to calculate link weights and map the network to a weighted network. Here, reliable paths are used to influence the strength of each edge in the path. The authors calculated the similarity between users with high precision by develo** the Katz based on reliable paths.

Weighted Common Neighbors (WCN), an extended version of the common neighbors metric (** factor for link prediction to reduce the impact of long paths on information flow, as well as the concept of ranking layers based on density.

3 Background

This section contains some basic information about MPN as well as MLN. Also, some fundamental concepts related to the link prediction problem, similarity metrics, local random walk and reliable paths are described. Table 1 summarizes the most important notations and definitions used in this paper.

Table 1 Description of all notations and definitions

3.1 Link prediction in monoplex networks

The purpose of link prediction is to forecast the probability of establishing an edge between two nodes/users in the future (Khayatnezhad et al. 2023; Shahidinejad and Abawajy 2024). The assumption of doing link prediction between two nodes is that there is currently no connection between them.

By using $G=(V,E)$, we can express the MPN as a single-layer network. In general, the set of nodes in this case is $V=\left\{{v}_{i}|i=\text{1,2},\dots ,N\right\}$, while the set of links is $E=\left\{{e}_{j}|j=\text{1,2},\dots ,M\right\}$; $N$ and $M$ represent the numbers of nodes and links, respectively. Furthermore, the link between ${v}_{i}$ and ${v}_{j}$ is specified as ${e}_{i,j}$. The adjacency matrix $A$ can be used to represent the $G$ in binary form. Here, the link status from ${v}_{i}$ to ${v}_{j}$ nodes is displayed as ${a}_{i,j}\in A$.

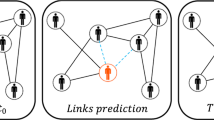
To describe link prediction in MPN, we consider two consecutive sub-graphs of the network with $G[{t}_{\tau }]$ and $G[{t}_{\tau +1}]$ respectively. Here, $\tau$ refers to a time in the network. The aim of this problem is to predict links given the information $G[{t}_{\tau }]$, where these links may appear in $G[{t}_{\tau +1}]$. Hence, $G[{t}_{\tau }]$ is considered as the training network and $G[{t}_{\tau +1}]$ is considered as the test network. Validation of predictions can be done by considering the subgraph $G\left[{t}_{\tau +1}\right]-G[{t}_{\tau }]$ of the network. In fact, this subgraph represents the set of actual links created after a timeslot. Figure 1 illustrates the link prediction architecture for MPN.

Fig. 1

Link prediction architecture for MPN. Link prediction for red node is done based on $G[{t}_{\tau }]$. Predicted links are highlighted in yellow. Green color represents the actual links created (as correctly predicted links) in $G[{t}_{\tau +1}]$, while links in red represent incorrect predictions

3.2 Link prediction in multilayer networks

Network modeling, based on MLN, is the concept of analyzing users through several social network platforms (Nasiri et al. 2021). MPN typically contains all links of the same type, which can lead to the misrepresentation of some events (Fındık and Özkaynak 2021). Meanwhile, MLN can provide more detailed information about links between users because individuals on each layer have distinct communication structures.

Let MLNs be formulated as $G=({G}^{1},{G}^{2},\dots ,{G}^{K})$, where ${G}^{\alpha }=\left({V}^{\alpha },{E}^{\alpha }\right)$ denotes a layer of $G$. Since not all users are the same in all social networks, $G$ only contains the same users in all layers. Hence, $G=(V,{E}^{1},{E}^{2},\dots ,{E}^{K})$ can be used to formally express MLN, where ${N}^{1}={N}^{2}=\dots ={N}^{K}$ and ${V}^{1}={V}^{2}=\dots ={V}^{K}$. Here, $K$ is the total number of layers, and ${N}^{\alpha }$ is the number of nodes in ${G}^{\alpha }$. The adjacency matrix for layer ${G}^{\alpha }$ is represented by ${A}^{\alpha }$, where the neighborhood status of ${v}_{i}$ and ${v}_{j}$ in ${G}^{\alpha }$ is indicated by ${\alpha }_{i,j}^{\alpha }\in {A}^{\alpha }$.

At MLN, link prediction entails forecasting at a target layer by taking into account all available layer’s information. Figure 2 illustrates the link prediction architecture for MLN. In general, MLNs have different types of links. For example, consider the link between ${v}_{i}$ and ${v}_{j}$ in Fig. 2. Here, there is a link between ${v}_{i}$ and ${v}_{j}$ in ${G}^{\beta }$, while this link does not exist in ${G}^{\alpha }$. Also, there is a link between ${v}_{j}$ and ${v}_{k}$ in ${G}^{\alpha }$, while this link does not exist in ${G}^{\beta }$. Moreover, there is a link between ${v}_{i}$ and ${v}_{k}$ in both ${G}^{\alpha }$ and ${G}^{\beta }$. Therefore, MLN architecture with two layers can contain three different types of links.

Fig. 2

Link prediction architecture for MLN (two-layer network). Here, link prediction for ${v}_{i}$ in layer ${G}^{\alpha }$ is done considering both layers ${G}^{\alpha }$ and ${G}^{\beta }$. Two links are predicted based on $G[{t}_{\tau }]$, one of which appeared in $G[{t}_{\tau +1}]$

3.3 Similarity metrics

Typically, all link prediction techniques are learning-based or similarity-based (Divakaran and Mohan 2020). Learning-based techniques include extracting some features from the network graph and transforming the link prediction into a classification problem (Haghani and Keyvanpour 2019; Fındık and Özkaynak 2021). In contrast, similarity-based techniques use a similarity metric to compute the likeness between nodes and estimate the probability of links between them (Li and Wang 2021). The similarity between nodes is often considered as the weight of links in the link prediction problem. Let each metric compute the similarity for each pair of nodes ${v}_{i}\in {\varepsilon }^{TS}$ and ${v}_{j}\in {\varepsilon }^{TR}$.

3.3.1 Intralayer Similarity Metrics

Typically, link prediction-based techniques use a similarity metric for the forecast task (Duan et al. 2022; Yin et al. 2017). The following is an introduction to some of the most well-known intralayer similarity measures in MPN.

Common neighbors (Lorrain and White 1971): This metric measures how many nodes in the network are shared by two specific nodes. Equation (1) defines this metric.

$${CN}_{i,j}=\left|\Gamma (i)\cap \Gamma (j)\right|$$

(1)

where $\Gamma (i)$ is set of neighbors of ${v}_{i}$. Moreover, the notation $\left|*\right|$ denotes the number of members in a set.

Adamic-Adar (Adamic and Adar 2003): This metric correlates with common neighbors and confers greater influence on nodes with fewer neighbors. The Adamic-Ader metric is defined by Eq. (2).

$${AA}_{i,j}=\sum_{z\in \Gamma (i)\cap \Gamma (j)}\frac{1}{\mathit{log}{k}_{z}}$$

(2)

where ${k}_{z}$ denotes the degree of node $z$.

Jaccard (1901): This metric is developed based on the measurement of similarity and diversity between collections. The ratio of the number of common neighbors to the total number of neighbors is used to calculate the similarity score in this metric. The Jaccard metric is defined by Eq. (3).

$${JA}_{i,j}=\frac{\left|\Gamma (i)\cap \Gamma (j)\right|}{\left|\Gamma (i)\cup \Gamma (j)\right|}$$

(3)

Katz (1953): This metric, known as global similarity, determines how similar two nodes are throughout all pathways of varying lengths. Equation (4) defines this metric.

$${KT}_{i,j}=\sum_{l=2}^{\infty }{\beta }^{l}.\left|{paths}_{i,j}^{<l>}\right|$$

(4)

where the number of pathways with length $l$ between ${v}_{i}$ and ${v}_{j}$ is indicated by the symbol $\left|{paths}_{i,j}^{<l>}\right|$, and $\beta$ is a dam** coefficient to lower the similarity value on long paths.

FriendLink (Papadimitriou et al. 2012): With the exception of only taking pathways with a maximum length of $L$ into account when calculating similarity, this metric is comparable to Katz metric. Equation (5) defines this metric.

$${FL}_{i,j}=\sum_{l=2}^{L}\frac{1}{l-1}.\frac{\left|{paths}_{i,j}^{<l>}\right|}{\prod_{k=2}^{l}(N-k)}$$

(5)

where $L$ is the longest path length taken into account when measuring similarity, and $N$ is the number of nodes.

Common interest (Sarhangnia et al. 2022): Let keywords used by each user in posts/tweets be available. This metric shows the number of keywords used by each pair of users. This metric denotes the common behavior and interests between users, which is formulated by Eq. (6).

$${CI}_{i,j}=\left|\psi (i)\cap \psi (j)\right|$$

(6)

where $\psi (i)$ and $\psi (j)$ denote the set of keywords used by ${v}_{i}$ and ${v}_{j}$, respectively.

Local random walk (Liu and Lü 2010): By taking into account the degree of nodes, this metric can determine the similarity between ${v}_{i}$ and ${v}_{j}$ in step $\tau$ without sacrificing generality. Equation (7) defines this metric.

$${LRW}_{i,j}= \frac{{k}_{i}}{2M} . {\pi }_{i,j}\left(\tau \right)+ \frac{{k}_{j}}{2M} .{\pi }_{j,i}\left(\tau \right)$$

(7)

where $M$ denotes the total number of links in the network and ${\pi }_{i,j}$ is the probability of reaching from ${v}_{i}$ to ${v}_{j}$.

Reputation-optimism (Rezaeipanah et al. 2020): The reputation index indicates the popularity of a node in the social network. Specifically, more users follow a user with a high reputation. The reputation index in a directed network is calculated based on Eq. (8). On the other hand, the optimism index indicates a positive sign towards other users. In particular, a user with high optimism can follow other users. The optimism index in a directed network is calculated based on Eq. (9).

$${RI}_{i}=\frac{{d}_{in}^{+}\left(i\right)-{d}_{in}^{-}(i)}{{d}_{in}^{+}\left(i\right)+{d}_{in}^{-}(i)}$$

(8)

$${OI}_{j}=\frac{{d}_{out}^{+}\left(j\right)-{d}_{out}^{-}(j)}{{d}_{out}^{+}\left(j\right)+{d}_{out}^{-}(j)}$$

(9)

where ${d}_{out}^{+}\left(j\right)$ and ${d}_{out}^{-}\left(j\right)$ are the numbers of positive and negative output links from ${v}_{j}$, respectively. Also, ${d}_{in}^{+}(i)$ and ${d}_{in}^{-}(i)$ are the numbers of positive and negative input links to ${v}_{i}$, respectively. Here, a positive sign for a link in both input and output directions indicates two-way communication. Meanwhile, the negative sign in both input and output directions indicates no link between two nodes. Besides, the negative sign in one direction and the positive sign in the other direction express one-way communication.

Reputation-optimism metric combines both indexes to compute the similarity between ${v}_{i}$ and ${v}_{j}$. This metric in directed networks is defined by Eq. (10).

$${RO}_{i,j}={OI}_{i}+\frac{2{RI}_{i}.{OI}_{j}}{{RI}_{i}+{OI}_{j}}$$

(10)

3.3.2 Interlayer Similarity Metrics

In general, MLN contain more information than MPN (Lü et al. 2015). The following is an introduction to some of the most well-known interlayer similarity measures in MLN.

Meta-paths (Luo et al. 2024): Let $i\stackrel{\alpha }{\to }z\stackrel{\beta }{\to }j$ represent the two-length meta-path connecting ${v}_{i}$ and ${v}_{j}$ through ${v}_{z}$. Here, ${e}_{i,z}$ and ${e}_{z,j}$ are at ${G}^{\alpha }$ and ${G}^{\beta }$, respectively. An example of the meta-paths metric is shown in Fig. 3. Additionally, Eq. (11) formulates this metric for pathways of length 2.

$${MP}_{i,j}=\sum_{(i\to z\to j)\in {Paths}_{i,j}^{2}}\left\{\begin{array}{cc}1& {e}_{i,z}\in {G}^{\alpha } and {e}_{z,j}\in {G}^{\beta }\\ 1& {e}_{i,z}\in {G}^{\beta } and {e}_{z,j}\in {G}^{\alpha }\\ 0& otherwise\end{array}\right.$$

(11)

where all pathways of length two between ${v}_{i}$ and ${v}_{j}$ are indicated by ${Paths}_{i,j}^{2}$.

Fig. 3

An example of the meta-paths metric

Common meta-paths (Sarhangnia et al. 2022): Let $i\stackrel{\alpha }{\to }z\stackrel{\alpha ,\beta }{\to }j$ represent the two-length common meta-path connecting ${v}_{i}$ and ${v}_{j}$ through ${v}_{z}$. Here, ${e}_{z,j}$ is in both ${G}^{\alpha }$ and ${G}^{\beta }$. In fact, in this metric at least one of the links must exist in both layers. Similarly, $i\stackrel{\beta }{\to }z\stackrel{\alpha ,\beta }{\to }j$, $i\stackrel{\alpha ,\beta }{\to }z\stackrel{\alpha }{\to }j$ and $i\stackrel{\alpha ,\beta }{\to }z\stackrel{\alpha }{\to }j$ are also other common meta-paths with length 2. The common meta-paths metric can also be configured based on paths with length 3. In Fig. 4, ${v}_{i}$ is a common meta-path with length 3, where $i\to z\to h$ exists in both ${G}^{\alpha }$ and ${G}^{\beta }$ layers, and $h\to j$ exists in ${G}^{\beta }$ layer. Additionally, Eq. (12) formulates this metric for pathways of length 2.

Fig. 4

An example of meta-paths-based clustering metric

$${CMP}_{i,j}=\sum_{(i\to z\to j)\in {Paths}_{i,j}^{2}}\left\{\begin{array}{cc}1& {e}_{i,z}\in {G}^{\alpha } and {{e}_{i,z},e}_{z,j}\in {G}^{\beta }\\ 1& {e}_{i,z}\in {G}^{\beta } and {{e}_{i,z},e}_{z,j}\in {G}^{\alpha }\\ 0& otherwise\end{array}\right.$$

(12)

Meta-paths-based clustering (Rezaeipanah et al. 2020): A meta-path of length two in this metric is denoted as $i\stackrel{\alpha }{\to }C\stackrel{\beta }{\to }j$, where $C$ represents the collection of nodes within a cluster. Hence, in this metric, ${v}_{i}$ and ${v}_{j}$ can be connected by a group of nodes. Additionally, Eq. (13) formulates this metric for pathways of length 2.

$${MPC}_{i,j}=\sum_{\left(i\to z\to j\right)\in CB\_{Paths}_{i,j}^{2}}\left\{\begin{array}{cc}1& {e}_{i,z}\in {G}^{\alpha } and {e}_{z,j}\in {G}^{\beta }\\ 1& {e}_{i,z}\in {G}^{\beta } and {e}_{z,j}\in {G}^{\alpha }\\ 0& otherwise\end{array}\right.$$

(13)

where $CB\_{Paths}_{i,j}^{2}$ represents all 2-length clustering-based pathways between ${v}_{i}$ and ${v}_{j}$.

Degree-degree correlation (Arruda et al. 2016; Zhao et al. 2014): Based on the correlation of nodes in various levels, this metric displays how similar they are to one another. Let the degree of ${v}_{i}$ in ${G}^{\alpha }$ be denoted by ${k}_{i}^{\alpha }$. Furthermore, let ${k}_{i}^{M}$ be the degree of ${v}_{i}$ in all layers and let ${k}_{i}^{C}$ be the number of same neighbors of ${v}_{i}$ in all layers. According to this, ${k}_{i}^{M}={k}_{i}^{\alpha }+{k}_{i}^{\beta }-{k}_{i}^{C}$. Equation (14) defines this metric.

$${DDC}_{i,j}=\frac{{ASN}_{i,j}}{{DDC}_{\alpha ,\beta }}$$

(14)

where ${DDC}_{\alpha ,\beta }$ indicates the degree-degree correlation in ${G}^{\alpha }$ and ${G}^{\beta }$, and ${ASN}_{i,j}$ indicates the average similarity value of the neighbors between ${v}_{i}$ and ${v}_{j}$.

$${ASN}_{i,j}=\frac{{k}_{i}^{C}+{k}_{j}^{C}}{{k}_{i}^{M}+{k}_{j}^{M}}$$

(15)

$${DDC}_{\alpha ,\beta }=\left[\sum_{i\in {G}^{\alpha }}\sum_{i\in {G}^{\beta }}\left({k}_{i}^{\alpha }{k}_{i}^{\beta }P({k}_{i}^{\alpha },{k}_{i}^{\beta })-\left(\sum_{i\in {G}^{\alpha }}P({k}_{i}^{\alpha },{k}_{i}^{\beta })\right)\left(\sum_{i\in {G}^{\beta }}P({k}_{i}^{\alpha },{k}_{i}^{\beta })\right)\right)\right]/\left[\sum_{i\in {G}^{\alpha }}P({k}_{i}^{\alpha },{k}_{i}^{\beta })\sum_{i\in {G}^{\beta }}{({k}_{i}^{\beta })}^{2}-{\left(\sum_{i\in {G}^{\alpha }}P({k}_{i}^{\alpha },{k}_{i}^{\beta })\sum_{i\in {G}^{\beta }}{k}_{i}^{\beta }\right)}^{2}\right]$$

(16)

where $P({k}_{i}^{\alpha },{k}_{i}^{\beta })$ represents the likelihood that ${v}_{i}$ will have degrees of ${k}_{i}^{\alpha }$ in ${G}^{\alpha }$ and ${k}_{i}^{\beta }$ in ${G}^{\beta }$.

3.4 Local random walk in monoplex networks

A random walk is a process that occurs over time and each step in it is done randomly. The selection of each step in this technique can include various distributions such as normal and uniform (Nasiri et al. 2021; Wu et al. 2022). The local random walk has wide applications such as centrality analysis, community detection, recommendation systems, and link prediction in online social networks and complex networks (Daud et al. 2020; Guo et al. 2016). Liu and Lü were the first to introduce this technique (Liu and Lü 2010). In a local random walk, the walker starts moving from ${v}_{i}$ and goes to the neighboring ${v}_{j}$ in every step $\tau$. All walker steps are defined by $\pi \left(\tau \right), \forall (\tau =\text{0,1},\text{2,3},\dots )$ where ${\pi }_{ij}\left(\tau \right)$ is formulated by Eq. (17).

$${\pi }_{ij}=\left\{\begin{array}{cc}1& if (i=j)\\ 0& otherwise\end{array}\right.$$

(17)

Basically, there are two various types of local random walk: pure and biased (** from ${v}_{i}$ to ${v}_{j}$ is calculated. Each jump by the walker leads to the creation of a new matrix $\pi (\tau +1)$, according to Eq. (19).

$${P}_{i,j}=\frac{{a}_{i,j}}{{k}_{i}}$$

(18)

$$\pi \left(\tau +1\right)={P}^{T}\pi \left(\tau \right)$$

(19)

where ${a}_{i,j}$ denotes the adjacency matrix element for $(i,j)$ and ${k}_{i}$ denotes the degree of ${v}_{i}$.

In a biased local random walk, the probability of neighboring nodes is unequal, and the walker tends to choose the nearest node with high topological properties. A biased walker is a suitable navigation strategy for discovering unknown networks by adjusting biased parameters such as degree and strength (Nasiri et al. 2021; ** from the present ${v}_{i}$ to a neighboring ${v}_{j}$.

$${P}_{i,j}=\frac{{w}_{j}.{a}_{i,j}}{{\sum }_{j\in \Gamma (j)}{w}_{j}.{a}_{i,j}}$$

(20)

where ${w}_{j}$ indicates the weight of ${v}_{j}$ according to its topological characteristics and $\Gamma (j)$ represents the set of neighbors for ${v}_{j}$. Here, the walker's steps from one node to another are biased based on the weight.

3.5 Local random walk-in multilayer networks

Assume that the walker is at ${v}_{i}$ of ${G}^{\alpha }$. In the meantime, there are only four possibilities for local random walks in MLN: ${P}_{i,i}^{\alpha }$ represents the probability of staying in the current ${v}_{i}$ from the identical ${G}^{\alpha }$; ${P}_{i,j}^{\alpha }$ represents the probability of jum** from the current ${v}_{i}$ to the neighboring ${v}_{j}$ in the identical ${G}^{\alpha }$; ${P}_{i,i}^{\alpha ,\beta }$ represents the probability of jum** from the current ${v}_{i}$ in ${G}^{\alpha }$ to its counterpartying node in ${G}^{\beta }$, and ${P}_{i,j}^{\alpha ,\beta }$ represents the chance of jum** from the current ${v}_{i}$ in layer ${G}^{\alpha }$ to the neighboring ${v}_{j}$ in ${G}^{\beta }$ (Luo et al. 2024). An overview of the local random walk-in MLN is shown in Fig. 5.

Fig. 5

An overview of local random walk in MLN

Let ${\mu }_{i,j}^{\alpha }$ represent the cost of lea** through ${v}_{i}$ from ${G}^{\alpha }$ to ${v}_{j}$, and let ${\lambda }_{i}^{\alpha ,\beta }$ represent the cost of jum** through ${v}_{i}$ from ${G}^{\alpha }$ to ${G}^{\beta }$. This means that Eqs. (21) and (22), respectively.

$${s}_{i,\alpha }^{intra}={\sum }_{j\in \Gamma (j)}{\mu }_{i,j}^{\alpha }$$

(21)

$${s}_{i,\alpha }^{inter}={\sum }_{\beta \in G}{\lambda }_{i}^{\alpha ,\beta }$$

(22)

Classical Local Random Walk (CLRW) is one version of the local random walk for MLN (Childs et al. 2002). This approach selects the next node based on a probability, similar to the biased local random walk in MPN. Here, the inverse of the nodes' degree is considered as its selection probability. CLRW is extended by considering interlayer links as intralayer links for MLN. In CLRW, ${P}_{i,j}^{\alpha ,\beta }$ is equal to ‘0’, while ${P}_{i,i}^{\alpha ,\alpha }$, ${P}_{i,i}^{\alpha ,\beta }$ and ${P}_{i,j}^{\alpha ,\alpha }$ are formulated by Eqs. (23), (24) and (25), respectively.

$${P}_{i,i}^{\alpha ,\alpha }=\frac{{\lambda }_{i}^{\alpha ,\alpha }}{{s}_{i,\alpha }^{intra}+{s}_{i,\alpha }^{inter}}$$

(23)

$${P}_{i,i}^{\alpha ,\beta }=\frac{{\lambda }_{i}^{\alpha ,\beta }}{{s}_{i,\alpha }^{intra}+{s}_{i,\alpha }^{inter}}$$

(24)

$${P}_{i,j}^{\alpha ,\alpha }=\frac{{\mu }_{i,j}^{\alpha }}{{s}_{i,\alpha }^{intra}+{s}_{i,\alpha }^{inter}}$$

(25)

Diffusive Local Random Walk (DLRW) is another version of the local random walk for MLN (Vamoş et al. 2003). The probability of jum** between each pair of nodes in DLRW is estimated by the strength in the source node. Typically, the strength in the source node is measured by $\underset{i, \alpha }{\text{max}}\{{s}_{i,\alpha }^{intra}+{s}_{i,\alpha }^{inter}\}$. According to this, ${P}_{i,j}^{\alpha ,\beta }$ is equal to ‘0’, while ${P}_{i,i}^{\alpha ,\alpha }$, ${P}_{i,i}^{\alpha ,\beta }$ and ${P}_{i,j}^{\alpha ,\alpha }$ are formulated by Eqs. (26), (27) and (28), respectively.

$${P}_{i,i}^{\alpha ,\alpha }=\frac{{s}_{i,\alpha }^{max}+{\lambda }_{i}^{\alpha ,\alpha }-{s}_{i,\alpha }^{intra}-{s}_{i,\alpha }^{inter}}{{s}_{i,\alpha }^{max}}$$

(26)

$${P}_{i,i}^{\alpha ,\beta }=\frac{{\lambda }_{i}^{\alpha ,\beta }}{{s}_{i,\alpha }^{max}}$$

(27)

$${P}_{i,j}^{\alpha ,\alpha }=\frac{{\mu }_{i,j}^{\alpha }}{{s}_{i,\alpha }^{max}}$$

(28)

where ${s}_{i,\alpha }^{max}$ denotes the maximum strength of ${v}_{i}$.

Physical Local Random Walk (PLRW) is another version of the local random walk for MLN (Burioni and Cassi 2005). PLRW is similar to CLRW, but it has the possibility of interlayer jump. In PLRW, ${P}_{i,i}^{\alpha ,\alpha }$ and ${P}_{i,i}^{\alpha ,\beta }$ are equal to ‘0’, while ${P}_{i,j}^{\alpha ,\alpha }$ and ${P}_{i,j}^{\alpha ,\beta }$ are defined by Eqs. (29) and (30), respectively.

$${P}_{i,j}^{\alpha ,\alpha }=\frac{{\mu }_{i,j}^{\alpha }}{{s}_{i,\alpha }^{intra}}.\frac{{\lambda }_{i}^{\alpha ,\alpha }}{{s}_{i,\alpha }^{inter}}$$

(29)

$${P}_{i,j}^{\alpha ,\beta }=\frac{{\mu }_{i,j}^{\beta }}{{s}_{i,\beta }^{intra}}.\frac{{\lambda }_{i}^{\alpha ,\beta }}{{s}_{i,\alpha }^{inter}}$$

(30)

Maximal Entropy Local Random Walk (MELRW) is another version of the local random walk for MLN (Burda et al. 2009). MELRW uses network architecture information and in that walker seeks to select a node that maximizes entropy in the entire walk. MELRW uses a supra-adjacency matrix considering the largest eigenvalue ${\delta }_{max}$ with eigenvector $\psi$ to calculate the probability of jum** in MLN. In MELRW, ${P}_{i,j}^{\alpha ,\beta }$ is equal to ‘0’, while ${P}_{i,i}^{\alpha ,\alpha }$, ${P}_{i,i}^{\alpha ,\beta }$ and ${P}_{i,j}^{\alpha ,\alpha }$ are formulated by Eqs. (31), (32) and (33), respectively.

$${P}_{i,i}^{\alpha ,\alpha }=\frac{{\lambda }_{i}^{\alpha ,\alpha }}{{\delta }_{max}}$$

(31)

$${P}_{i,i}^{\alpha ,\beta }=\frac{{\lambda }_{i}^{\alpha ,\beta }}{{\delta }_{max}}.\frac{{\psi }_{\left(\beta -1\right)N+i}}{{\psi }_{\left(\alpha -1\right)N+i}}$$

(32)

$${P}_{i,j}^{\alpha ,\alpha }=\frac{{\mu }_{i,j}^{\alpha }}{{\delta }_{max}}.\frac{{\psi }_{\left(\alpha -1\right)N+i}}{{\psi }_{\left(\alpha -1\right)N+i}}$$

(33)

Lévy flight Local Random Walk (LLRW) is another version of the local random walk for MLN (Yang et al. 2013). LLRW uses the nearest-neighbor navigation mechanism to estimate jump probabilities, where it is possible to jump between two non-connected nodes. In LLRW, ${P}_{i,i}^{\alpha ,\alpha }$ and ${P}_{i,j}^{\alpha ,\beta }$ are equal to ‘0’, while ${P}_{i,i}^{\alpha ,\beta }$ and ${P}_{i,j}^{\alpha ,\alpha }$ are defined by Eqs. (34) and (35), respectively.

$${P}_{i,i}^{\alpha ,\beta }=\frac{{\lambda }_{i}^{\alpha ,\beta }}{{s}_{i,\alpha }^{intra}+{s}_{i,\alpha }^{inter}}$$

(34)

$${P}_{i,j}^{\alpha ,\alpha }=\frac{{\mu }_{i,j}^{\alpha }}{{s}_{i,\alpha }^{intra}+{s}_{i,\alpha }^{inter}}$$

(35)

3.6 Reliable paths

Any single similarity metric or a combination of them can be considered the weight of the network links and convert unweighted into weighted graphs. The weight of a link measures its strength and significance in relation to other linkages in the network (Yang et al. 2022; Sarhangnia et al. 2022). Most of the time, the weight of the links can highlight the safety of each link of the path. In Zhao et al. (2015), the extension of the unweighted network to the weighted network offers a dependable path. In this work, the authors define a reliable path by Eq. (36).

$${RR}_{i,j}=\prod_{(x,y)\in {Path}_{i,j}}{w}_{x,y}$$

(36)

where ${Path}_{i,j}$ is a path between ${v}_{i}$ and ${v}_{j}$ in the network and ${w}_{x,y}$ is the link weight between nodes ${v}_{x}$ and ${v}_{y}$. Here, the reliability for a path is estimated by multiplying the weights of its links.

By taking into account the significance of each link, reliable paths can determine the similarity between nodes. Hence, this technique can estimate the similarity value more accurately. For example, Yang et al. (2022) presented an extended version of the Katz metric considering reliable paths. This similarity metric is based on Eq. (37) in which reliable weighted paths are used instead of the number of paths. Meanwhile, Zhang and Abolfathi (2022) presented an extended version of the FriendLink metric considering reliable paths, which is shown in Eq. (38).

$${RR}_{i,j}^{KT}= \sum_{l=2}^{L}{\beta }^{l}.\left[\sum_{P \in {Paths}_{i,j}^{<l>}}\prod_{\left(x,y\right) \in P}{w}_{x,y}\right]$$

(37)

$${RR}_{i,j}^{FL}= \sum_{l=2}^{L}\frac{1}{l-1}.\frac{\sum_{P \in {Paths}_{i,j}^{<l>}}\prod_{\left(x,y\right) \in P}{w}_{x,y}}{\prod_{k=2}^{l}(N-k)}$$

(38)

Figure 6 illustrates an example of similarity calculation by KT and FL compared to ${RR}_{i,j}^{KT}$ and ${RR}_{i,j}^{FL}$. Figure 6(a) is an unweighted graph used to calculate the similarity by ${KT}_{i,j}$ and ${FL}_{i,j}$. Also, Fig. 6(b) is the same graph with weighted links used to calculate similarity by ${RR}_{i,j}^{KT}$ and ${RR}_{i,j}^{FL}$. In this example, $N$ is set to 6, $L$ is set to 3, and $\beta$ is set to 0.1. According to this configuration, Eqs. (39) and (40) calculate the similarity value for ${KT}_{i,j}$ and ${FL}_{i,j}$, respectively. Besides, the similarity value for ${RR}_{i,j}^{KT}$ and ${RR}_{i,j}^{FL}$ is shown by Eqs. (41) and (42), respectively.

Fig. 6

A synthetic graph with 6 nodes and 8 links, (a) unweighted graph and (b) weighted graph

$${KT}_{i,j}=\left[{0.1}^{2}\times 1\right]+\left[{0.1}^{3}\times 3\right]=0.013$$

(39)

$${FL}_{i,j}=[\frac{1}{1}\times \frac{1}{4}]+[\frac{1}{2}\times \frac{3}{12}]=0.375$$

(40)

$${RR}_{i,j}^{KT}=\left[{0.1}^{2}\times \left(0.5\times 0.7\right)\right]+[{0.1}^{3}\times (\left(0.3\times 0.6\times 0.3\right)+\left(0.3\times 0.9\times 0.6\right)+\left(0.5\times 0.4\times 0.6\right))]=0.0038$$

(41)

$${RR}_{i,j}^{FL}=\left[\frac{1}{1}\times \frac{\left(0.5\times 0.7\right)}{4}\right]+ [\frac{1}{2}\times \frac{(0.3\times 0.6\times 0.3)+(0.3\times 0.9\times 0.6)+(0.5\times 0.4\times 0.6)}{12}]=0.1015$$

(42)

Specifically, the Katz and FriendLink metrics only use the number of paths of various lengths to compute similarity, which is available through the adjacency matrix. Without loss of generality, using the adjacency matrix ${A}^{2}$ provides the number of length-2 paths per element. For ${A}^{3}$ this can provide the number of paths of length-3 and so on. For example, ${a}_{i,j}\in {A}^{3}$ denotes the number of paths with length equal to 3 between ${v}_{i}$ and ${v}_{j}$. However, using reliable paths requires discovering paths between two nodes with different lengths. Therefore, the metrics developed based on reliable paths are only suitable for small-scale networks.

Common algorithms like Rubin (1978) can generally perform path discovery, but their link prediction complexity is high. Luo et al. (2024) proposed a distributed technique for finite-length path discovery to be able to use reliable paths in similarity estimation in large-scale networks. This technique can add trust to nodes by creating dynamic neighborhood tables.

3.7 Influential nodes

In the realm of complex networks, understanding the influence and significance of nodes holds paramount importance. A central challenge lies in identifying and characterizing influential nodes within these networks, which play pivotal roles in sha** their structure, dynamics, and functionalities (Zhao et al. 2023c). These influential nodes, often referred to as hubs or seeds, possess a disproportionate impact on information flow, resource allocation, and network resilience. The study of influential nodes in complex networks has garnered substantial attention due to its implications across various domains, including social networks, biological networks, transportation networks, and information networks (Curado et al. 2023).

Influential nodes can be identified based on centrality metrics. Several centrality metrics are instrumental in quantifying the importance and influence of nodes within complex networks (Curado et al. 2023). Degree centrality, measuring the number of connections a node possesses, offers insights into its immediate influence within the network. Betweenness centrality evaluates the extent to which a node serves as a bridge facilitating communication between other nodes, thereby capturing its critical role in network connectivity. Eigenvector centrality accounts for both the quantity and quality of a node's connections, considering not only the number of connections but also their importance, thus reflecting the node's overall influence within the network.

The importance of influential nodes extends beyond MPN networks, including MLN networks (Curado et al. 2023). In MPN networks, influential nodes exert considerable influence over the overall network dynamics, often serving as key connectors or opinion leaders. In contrast, MLN networks introduce additional complexity by integrating multiple layers of interactions or relationships among nodes. In such networks, influential nodes may exert influence and control over diverse aspects of network functionality across different layers, leveraging their interconnectedness to amplify their impact. Understanding the role of influential nodes in both MPN and MLN networks is crucial for unraveling the complexities of real-world systems and devising effective strategies for network analysis, optimization, and intervention.

We only describe a semi-local centrality metric from some representative methods, given the long-standing study of the problem of identifying the influential node in MPN. We developed Local Structural Centrality (LSC), a semi-local metric, based on topological connections between neighbors (Gao et al. 2014). While maintaining a constant level, the LSC algorithm takes into account both the number of neighbors and the number of nearest neighbors. Furthermore, LSC ensures that topological links are established among neighboring elements throughout the ranking process. The influence of node ${v}_{i}$ based on LSC is calculated by Eq. (43).

$${LSC}_{MPN}\left({v}_{i}\right)=\sum_{j\in \Gamma (i)}\left(\alpha .{k}_{j}+(1-\alpha )\sum_{w\in \Gamma (j)}{C}_{w}\right)$$

(43)

where ${C}_{w}$ is the local clustering coefficient for node $w$, and $\alpha$ is a tunable balance parameter.

As shown in Eq. (44), the influence of node ${v}_{i}$ in MLNs can be measured based on the average LSC over all layers.

$${LSC}_{MLN}\left({v}_{i}\right)=\sum_{\alpha =1}^{K}{LSC}_{MPN}\left({v}_{i},{G}^{\alpha }\right)$$

(44)

where $K$ is the number of layers in MLN, and ${LSC}_{MPN}\left({v}_{i},{G}^{\alpha }\right)$ is the LSC metric value for node ${v}_{i}$ in layer ${G}^{\alpha }$.

Considering the reputation-optimism metric, the influence of node ${v}_{i}$ compared to node ${v}_{j}$ is calculated by Eq. (45).

$${LSC}_{i,j}=LSC\left({v}_{i}\right)+\frac{2LSC\left({v}_{i}\right).LSC\left({v}_{j}\right)}{LSC\left({v}_{i}\right)+LSC\left({v}_{j}\right)}$$

(45)

4 Proposed strategy

This section describes the details of RMLRW for link prediction in complex networks. Figure 7 provides an overview of the link prediction process in RMLRW.

Fig. 7

Overview of the link prediction process in RMLRW

It is common to use both intralayer and interlayer communication in MLN to address the link prediction problem. An intralayer connection is a pair of nodes in a given layer, whereas an interlayer connection chains a node in two different layers. MPN often applies link prediction techniques based on intralayer similarity metrics, disregarding the valuable information from other layers. However, link prediction is computationally expensive because of feature learning for large-scale MLNs. Network embedding provides a compressed representation of the network by representing it in a reduced dimensional representation space with the same features. It can reduce the computational complexity of the link prediction process for large-scale networks as much as possible and improve performance. For network embedding, we first extract communities using the Louvain algorithm (Blondel et al. 2008). Community detection in Louvain is done by maximizing modularity. As shown in Eq. (46), modularity is a measure to assess the ratio of links within a community to the links that connect other communities.

$$\text{Q}=\frac{1}{2M}\sum_{{v}_{i}, {v}_{j}\in \text{V}}\left[{a}_{i,j}-\frac{{k}_{i}.{k}_{j}}{2M}\right]\delta ({c}_{i},{c}_{j})$$

(46)

where ${c}_{i}$ is the node associated with ${v}_{i}$, and $\delta$ is a delta function to identify identical communities.

We construct a personalized random walk to analyze the neighborhood structure of a node. ${\mathcal{W}}_{i}$ represents a personalized random walk originating from node ${v}_{i}$. We select a node from the nodes that belong to the identical community as the $k$-th node of ${\mathcal{W}}_{i}$. Let ${\mathcal{W}}_{i}^{1},{\mathcal{W}}_{i}^{2},\dots ,{\mathcal{W}}_{i}^{k}$ be a random walk starting from node ${v}_{i}$, where ${\mathcal{W}}_{i}^{k+1}$ is a node selected from among nodes that are neighbors to the $k$-th node in a community. This process continues until it reaches a preset length for the route. If a node along the route does not have any additional neighboring nodes, we cease extending the route. According to this process, several custom routes are created for each node to consider structural information in the network embedding. These routes include nodes with a neighborhood structure that belong to a community. Therefore, the community random walk policy can encourage the walker to make two-hop or multi-hop jumps at each step. This process leads to the development of local random walk to semi-local random walk by considering the concept of extended neighborhood.

After extracting the neighborhood structure with the community random walk policy, the node representation vector is learned with the Skip-gram technique (Lin and Cohen 2010). This technique can discover a map** function $f:V\to {\mathbb{R}}^{d}$, where $d$ is the representation size of each network node. In general, The Skip-gram technique determines the optimal representation vector for a node by analyzing the structural information within its vicinity. This technique is a linguistic strategy that maximizes the conditional chance of words co-occurring within a specified window $w$, as demonstrated in Eq. (47).

$$\begin{array}{c}\text{Pr}\left(w|f\left({v}_{i}\right)\right)=\underset{f}{\text{max}}\prod_{j=i-w;j\ne i}^{i+w}\text{Pr}\left({v}_{j}|f\left({v}_{i}\right)\right),\\ w=\left\{{v}_{i-w},\dots ,{v}_{i+w}\right\}\backslash {v}_{i}\end{array}$$

(47)

For each node in the network, this process is applied to all customized routes. Here, a window $w$ is created to slide on a path. Also, we consider the assumption of independence of conditional probabilities. Accordingly, the probability distribution approximation is determined by the Softmax function, as defined in Eq. (48).

$$\text{Pr}\left({v}_{j}|f\left({v}_{i}\right)\right)=\frac{1}{\left(1+{e}^{-f\left({v}_{i}\right).f\left({v}_{j}\right)}\right)}$$

(48)

By applying the Skip-gram technique, the embedded network is extracted and link prediction is applied to it by RMLRW. It can reduce the computational complexity of the link prediction process for large-scale networks as much as possible and improve the performance.

In MPN, the local random walk is one of the most popular methods for link prediction. In order to solve the link prediction, we want to carry out a comparable operation on MLN using the local random walk. We employ PLRW to further refine the local random walk-in MLN. Overall, it's critical to give links in MLN the proper weight. To compute intralayer and interlayer weights, we make use of topological and multimodal information. By using the common links between the layers, the link-overlap index (Nasiri et al. 2021) can determine the correlation between them. We apply the contribution of each layer of MLN to the similarity estimation through this index when predicting links. Furthermore, establishing trustworthy paths between users is a useful method for creating local similarity metrics that are weighted to unweighted. To overcome the link prediction problem, we designed a reliable path on MLN that is a local random walk. For this purpose, we developed RMLRW in this study, which performs local random walk with reliable paths in MLN. Meanwhile, to improve the local random walk, we apply the rank of the nodes in the similarity measure so that the walker chooses the next node by considering its effect on the current node. According to the above-mentioned issues, RMLRW uses Eq. (49) to estimate the similarity between ${v}_{i}$ and ${v}_{j}$.

$${RMLRW}_{i,j}=\frac{{k}_{i}^{T}.\prod_{\tau }{\pi }_{u,v}(\tau )}{2{M}^{T}}+\frac{{k}_{j}^{T}.\prod_{\tau }{\pi }_{u,v}(\tau )}{2{M}^{T}}$$

(49)

where $T$ is the target layer, $v$ is the node the walker chose in $\tau$, $u$ is the node the walker chose as the current node in $\tau -1$, ${k}_{i}^{T}$ is the degree of ${v}_{i}$ in ${G}^{T}$, ${M}^{T}$ is the number of edges in ${G}^{T}$, and ${\pi }_{u,v}(\tau )$ is the probability that the walker will choose nodes $v$ over $u$.

The dependability of the path between ${v}_{i}$ and ${v}_{j}$ can be ensured by multiplying all of the probability of the nodes that the walker chose. In this case, ${\pi }_{i}\left(0\right)$ is taken to be equal to 1, and ${\pi }_{u,v}(\tau )$ is computed using Eq. (50).

$$\begin{array}{cc}{\pi }_{u,v}\left(\tau \right)={P}^{T}{\pi }_{u,v}\left(\tau -1\right),& \forall \tau >0\end{array}$$

(50)

RMLRW is configured using PLRW, therefore defining intralayer and interlayer jump probabilities is crucial. As defined in Eqs. (51) and (52), it is necessary to specify ${P}_{u,v}^{T,T}$ and ${P}_{u,v}^{T,F}$ in RMLRW, where $F$ might be any layer of the MLN other than the target layer.

$${P}_{u,v}^{T,T}=\frac{{\mu }_{u,v}^{T}}{{\sum }_{z\in \Gamma (u)}{\mu }_{u,z}^{T}}.\frac{{\lambda }_{u}^{T,T}}{{\sum }_{F\in G}{\lambda }_{u}^{T,F}}$$

(51)

$$\begin{array}{cc}{P}_{u,v}^{T,F}={LO}^{T,F}.\left[\frac{{\mu }_{u,v}^{F}}{{\sum }_{z\in \Gamma (u)}{\mu }_{u,z}^{F}}.\frac{{\lambda }_{u}^{T,F}}{{\sum }_{F\in G}{\lambda }_{u}^{T,F}}\right],& \forall F\in G\end{array}$$

(52)

where ${\mu }_{u,v}^{T}$ is the intralayer weight of nodes $u$ and $v$ based on ${G}^{T}$, ${\lambda }_{u}^{T,F}$ is the weight between layers ${G}^{T}$ and ${G}^{F}$ of nodes $u$ and $v$, and ${LO}^{T,F}$ is the link-overlap between ${G}^{T}$ and ${G}^{F}$:

$${\mu }_{u,v}^{T}={\xi }_{1}.{CN}_{u,v}^{T}+{\xi }_{2}.{AA}_{u,v}^{T}+{\xi }_{3}.{JA}_{u,v}^{T}+{\xi }_{4}.{KT}_{u,v}^{T}+{\xi }_{5}.{FL}_{u,v}^{T}+{\xi }_{6}.{CI}_{u,v}^{T}+{\xi }_{7}.{LRW}_{u,v}^{T}+{\xi }_{8}.{RO}_{u,v}^{T}+{\xi }_{9}.{LSC}_{u,v}^{T}$$

(53)

$${\lambda }_{u}^{T,F}=\frac{1}{{k}_{u}^{F}}.\sum_{z\in {\Gamma }_{u}^{F}}\left[{\zeta }_{1}.{MP}_{u,z}^{T,F}+{\zeta }_{2}.{CMP}_{u,z}^{T,F}+{\zeta }_{3}.{MPC}_{u,z}^{T,F}+{\zeta }_{4}.{DDC}_{u,z}^{T,F}+{\zeta }_{5}.{LSC}_{u,z}^{T,F}\right]$$

(54)

$${LO}^{T,F}=\frac{{\sum }_{i>j}{A}^{T}{A}^{F}}{min\left\{{\sum }_{i>j}{A}^{T},{\sum }_{i>j}{A}^{F}\right\}}$$

(55)

where ${k}_{u}^{F}$ indicates degree of $u$ in ${G}^{F}$, and ${\Gamma }_{u}^{F}$ indicates the set of neighbors of $u$ in ${G}^{F}$. Furthermore, the influence coefficient for similarity metrics used to calculate intralayer similarity is denoted by ${\xi }_{*}$, and the influence coefficient for similarity metrics used to calculate interlayer similarity is denoted by ${\zeta }_{*}$. In this case, it is assumed that $\sum_{k}{\xi }_{k}=1$ and $\sum_{k}{\zeta }_{k}=1$.

5 Evaluation

This section is related to the evaluation of RMLRW as the proposed strategy compared to classical and state-of-the-art algorithms for link prediction. We evaluate the proposed strategy using real-world data sets from both MPN and MLN networks. All tests were performed by an ASUS laptop equipped with Intel Core i7-1355U up to 4.00 GHz processor, and 32 GB (2 × 16 GB) DDR4 of memory. Additionally, we employ the MALTAB R2023a simulator to put the proposed strategy and other techniques used in the comparisons into practice. We conduct all comparisons under identical parameters and conditions. Additionally, we report all experiment results as the average of 20 trials.

To assess RMLRW in MPN, we employ traditional similarity metrics such as Katz (1953), FriendLink (Papadimitriou et al. 2012), and local random walk (Liu and Lü 2010). Additionally, SEM-Path is a state-of-the-art technique for comparing with RMLRW in MPN (Rezaeipanah et al. 2020). In the meantime, RMLRW is assessed on MLN by contrasting it with three equivalent and state-of-the-art techniques: MADM (Luo et al. 2021), WCN (Nasiri et al. 2022), and MLRW (Nasiri et al. 2021). Comparisons are based on some standard evaluation metrics including f-measure, precision, and recall.

6 Evaluation criteria

For a network, link prediction is performed through two subgraphs ${\varepsilon }^{TR}$ and ${\varepsilon }^{TS}$, where these represent the training and test sets, respectively. Here, for each node of ${\varepsilon }^{TR}$ a set of nodes from ${\varepsilon }^{TS}$ is selected as connection recommendations. The number of recommendations can be adjusted using the $TopK$ parameter.

In this study, we assess link prediction methods using the internal and external double cross-validation technique (Zhou et al. 2007; Papadimitriou et al. 2012). This technique divides the data set $D$ into 10 subsets. Evaluation in external cross-validation is performed for each subset as ${\varepsilon }^{TS}$ set in turn, while the remaining 9 subsets are considered as ${\varepsilon }^{TR}$ set for internal cross-validation. Finally, the performance of each link prediction approach is reported based on the average on external 10-fold cross-validation.

Let ${\varepsilon }^{TR}=(V,{E}_{Train})$ and ${\varepsilon }^{TS}=(V,{E}_{Test})$ be two subgraphs of $G$ for training and testing, respectively. For the link prediction problem, $E=\left\{{E}_{Train}\cup {E}_{Test}\right\}$ is a set of edges, where ${E}_{Train}$ contains the set of edges for training and ${E}_{Test}$ contains the set of edges for testing. However, there is no training process in the link prediction problem. Indeed, a link prediction method seeks to recommend available links from ${\varepsilon }^{TS}$ that are likely to be observed in ${\varepsilon }^{TR}$. In general, any node that has at least one edge in ${\varepsilon }^{TS}$ is considered for the link prediction task.

This study uses f-measure, precision, and recall as evaluation criteria. These metrics provide a quantitative way to measure the accuracy and effectiveness of predictions, allowing researchers and practitioners to understand how well a model is performing. In the context of link prediction, precision measures the accuracy of the predicted links. It tells us how many of the predicted links are actually relevant and correct. Additionally, recall measures the model's ability to identify all relevant links. It reveals the number of successfully predicted actual links. Finally, f-measure is the harmonic mean of recall and precision (Zhou et al. 2007). F-measure is particularly useful when there is an imbalance between positive and negative instances in the data. Online social networks often exhibit complex structures, and link prediction algorithms aim to identify potential connections between nodes. These metrics help in making informed decisions about the suitability of a particular link prediction model for a given social network application. Equations (56–58) formulates precision, recall and f-measure criteria for link prediction.

$$Precision=\frac{1}{\left|{\varepsilon }^{TS}\right|}\sum_{j\in {\varepsilon }^{TS}}\frac{{RN}_{j}}{TopK}$$

(56)

$$Recall=\frac{1}{\left|{\varepsilon }^{TS}\right|}\sum_{j\in {\varepsilon }^{TS}}\frac{{RN}_{j}}{{AN}_{j}}$$

(57)

$$F\_measure=\frac{2\times Precision\times Recall}{Precision+Recall}$$

(58)

where ${RN}_{j}$ and ${AN}_{j}$ are the number of relevant nodes and actual relevant nodes for the target node ${v}_{j}\in {\varepsilon }^{TS}$, respectively.

6.1 Data set

The Twitter-Foursquare dataset is used as a network based on MLN for evaluation work. Two layers comprise this network: Foursquare and Twitter. Foursquare is a location-based online social network, whereas Twitter is a microblogging social network (Rezaeipanah et al. 2020). We consider both layers of the Twitter-Foursquare data set separately as the target layer to evaluate the methods on MPN (e.g., Twitter network and Foursquare network). In this regard, the Twitter-Foursquare data set is considered as MLN based on the Twitter target layer, while the simulation on the Foursquare-Twitter data set is based on the Foursquare target layer. In addition, we consider each network separately and use it to predict connectivity in MPN.

In addition to this Twitter-Foursquare data set, we use the Higgs Friendships-Higgs Retweet (Higgs-FSRT) data set in our simulations to verify the performance of the proposed strategy. This data set was created by De Domenico et al. (2013) based on FriendShips (FS) and ReTweet (RT) networks. Higgs-FSRT focuses on the processes of Twitter propagation during and after the discovery of a new particle with the properties of the Higgs boson. More details of these data sets are given in Table 2.

Table 2 Statistical information of the used data set

6.2 Benchmark approaches

Evaluations with MPN as well as MLN are performed. The details of the approaches for comparison in the MPN are as follows:

• Katz (1953): a classical similarity metric introduced by Katz (1953).

• FriendLink (Papadimitriou et al. 2012): a classical similarity metric presented by Papadimitriou et al. (2012).

• Local Random Walk (LRW) (Liu and Lü 2010): a classical similarity metric presented by Liu and Lü (2010).

• Structural, Ego-Paths and Meta-Paths features (SEM-Path) (Rezaeipanah et al. 2020): a state-of-the-art algorithm presented by Rezaeipanah et al. (2020).

Also, the details of the approaches for comparison in the MLN are as follows:

• Multiple-Attribute Decision-Making (MADM) (Luo et al. 2021): a state-of-the-art algorithm presented by Luo et al. (2021).

• Weighted Common Neighbors (WCN) (Nasiri et al. 2022): a state-of-the-art approach presented by Nasiri et al. (2022).

• Multiplex Local Random Walk (MLRW) (Nasiri et al. 2021): a state-of-the-art approach presented by Nasiri et al. (2021).

7 Results and discussion

In the link prediction process for RMLRW, $\beta$ and $L$ are two influential parameters. In particular, Luo et al. (2024) have validated $\beta =0.05$ and $L=3$. To confirm the optimal values for these parameters, a numerical experiment is presented in Tables 3 and 4, where the optimal values for $\beta$ and $L$ are bolded. In these tables, symbols @P, @R, and @F refer to precision, recall, and f-measure, respectively. As shown, in most comparisons, RMLRW with $\beta =0.03$ and $L=4$ performs optimal for link prediction. Taking into account the f-measure average result, the superiority of the proposed strategy over other settings for MPN and MLN related data sets is 2.41% and 15.13%, respectively. These results were obtained by applying the Twitter-Foursquare data set.

Table 3 Evaluation of RMLRW with different values for parameter $\beta$ on Twitter-Foursquare data set

Table 4 Evaluation of RMLRW with different values for parameter $L$ on Twitter-Foursquare data set

Other influential parameters in the proposed strategy are ${\xi }_{k}$ and ${\zeta }_{k}$. Here, ${\xi }_{1}$ – ${\xi }_{9}$ and ${\zeta }_{1}$ – ${\zeta }_{5}$ denote the impact coefficient of the metrics used to calculate intralayer and interlayer similarity, respectively. In this paper, the values of these parameters are searched for the optimal state by a hill climbing algorithm. The objective function in the hill climbing algorithm is configured based on f-measure. Table 5 shows the set values for these parameters by the hill climbing algorithm. These experiments have been performed on both MPN and MLN networks in Twitter-Foursquare data set. Each row is dedicated to the results of one network, while the last row presents the average results for all networks.

Table 5 Adjusted values for parameters ${\xi }_{1}$ – ${\xi }_{9}$ and ${\zeta }_{1}$ – ${\zeta }_{5}$ by hill climbing algorithm considering the Twitter-Foursquare data set

The results of this experiment show that among the intralayer similarity metrics, the FriendLink metric with ${\xi }_{5}=0.264$ has the most impact on the accuracy of predictions. In addition, the Katz metric with ${\xi }_{4}=0.256$ has a great impact on the performance of RMLRW for link prediction. After these metrics, local random walk and reputation-optimism are among the most effective metrics for calculating intralayer similarities. Meanwhile, Jaccard and Adamic-Adar have the least impact on the link prediction accuracy obtained by RMLRW with ${\xi }_{3}=0.007$ and ${\xi }_{2}=0.014$, respectively. In fact, removing these metrics does not have a significant impact on the intralayer similarity calculation for RMLRW. On the other hand, the most important interlayer similarity metric with ${\xi }_{3}=0.314$ belongs to meta-path-based clustering. Also, the effectiveness of degree–degree correlation and common meta-paths metrics is also high in calculating interlayer similarity.

In the continuation of the evaluations, some benchmark approaches including Katz (1953), FriendLink (Papadimitriou et al. 2012), LRW (Liu and Lü 2010) and SEM-Path (Rezaeipanah et al. 2020) are used to compare with RMLRW in MPN. Meanwhile, MADM (Luo et al. 2021), WCN (Nasiri et al. 2022) and MLRW (Nasiri et al. 2021) methods are considered to evaluate the proposed strategy in MLN. The comparative findings of RMLRW and other Twitter network-based approaches are shown in Fig. 8. In Fig. 9, this comparison is also presented for the Foursquare network. The results of the defined evaluation criteria for all methods are analyzed based on a minimum $TopK$ of 1 and a maximum of 30.

Fig. 8

Evaluation findings of the Twitter network with different values for $TopK$

Fig. 9

Evaluation findings of the Foursquare network with different values for $TopK$

When considering Twitter as the target network in Fig. 8, RMLRW achieves the best results. RMLRW with $TopK=8$ has achieved an f-measure of 0.6184 in the best scenario. This outcome with $TopK=7$ is given for the Foursquare network in Fig. 9 through an f-measure of 0.6802. On Twitter, RMLRW performs 7.84%, 10.93%, and 4.11% better than traditional similarity metrics like Katz, FriendLink, and LRW. Furthermore, RMLRW yielded a 3.57% greater improvement than SEM-Path. The proposed strategy outperforms Katz, FriendLink, LRW, and SEM-Path in Foursquare by 7.16%,6.87%,2.97%, and 1.22%, respectively. Meanwhile, Figs. 10 and 11 shown the outcomes of comparing RMLRW with MADM, WCN, and MLRW on MLN, such as Foursquare-Twitter and Twitter-Foursquare. Based on the average results, RMLRW was able to perform better than MADM and WCN in all comparisons.

Fig. 10

Evaluation findings of the Twitter-Foursquare network with different values for $TopK$

Fig. 11

Evaluation findings of the Foursquare-Twitter network with different values for $TopK$

The findings of the comparisons in both MPN and MLN networks have been compiled. Table 6 is related to the evaluation of RMLRW compared to Katz, FriendLink, LRW and SEM-Path on MPN. Also, Table 7 shows the evaluation results for RMLRW compared to MADM, WCN and MLRW on MLN. The average of all examined $TopKs$ is used to report these results. In these tables, the results are presented based on precision, recall and f-measure in each network. Also, the last rows of the tables are related to the average results for each method. As depicted, RMLRW performs better in both MPN and MLN networks compared to other algorithms. In the tables, the optimal results for each method are highlighted in bold.

Table 6 Summary of results for RMLRW compared to approaches based on MPN

Table 7 Summary of results for RMLRW compared to approaches based on MLN

8 Conclusion

In online social networks, strategies based on link prediction problems seek to forecast the probability of connection between two users/nodes in the future. These strategies can be used as friend suggestions or to infer social interactions in complex networks. There are various applications of link prediction strategies on MPN with cross, heterogeneous, weighted and dynamic characteristics. However, with the advancement of complex network modeling and the significant growth of social networks, link prediction analysis on MLN has become difficult. In this paper, we designed a new algorithm based on multiplex semi-local random walk-through reliable paths, namely RMLRW, for link prediction in MLN. RMLRW uses topological and multimodal features to weight links and discover reliable paths between nodes. Here, a new similarity metric generalizes the similarity value from unweighted to weighted graphs to create reliable paths. Also, RMLRW takes advantage of interlayer and intralayer information for biasing the random walk. In addition, we applied the influential node identification policy to formulate the similarity metric in RMLRW. The results obtained from the simulations show the superiority of RMLRW compared to the equivalent approaches on both MPN and MLN networks. Meanwhile, our observations prove that the use of the bias function provides a higher link prediction precision than the effectiveness of the local random walk.

Although RMLRW has decent performance, but the high computational complexity to discover reliable paths is one of its limitations. In the past decade, several models have been proposed to identify paths between nodes in online social networks, and we will consider the development of RMLRW based on these models as a future work. Our future work primarily focuses on develo** the proposed strategy for applications like community detection, intrusion analysis, anomaly detection, and recommendation systems.

Anchor link prediction and link prediction for multi-layer networks share some similarities. Both involve predicting the likelihood of links between entities. They can both utilize network-based features such as node centrality, similarity measures, and structural properties of the network to make predictions. Also, machine learning and statistical modeling techniques often tackle both tasks. In general, while both tasks involve predicting connections between entities, anchor link prediction specifically deals with linking entities across distinct networks using shared anchors, whereas link prediction for multi-layer networks focuses on predicting links within or between layers of a single network with multiple types of relationships. We suggest that anchor link prediction should be considered as a future work to improve the data sparsity problem in link prediction.