SpringerLink
Log in

Dynamic Response of Tunnel Structures in Inhomogeneous Medium Under SH Wave: Shear Modulus in Quadratic Functional Form

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

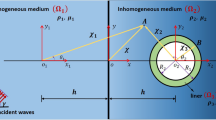
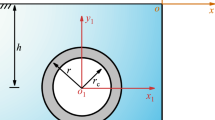
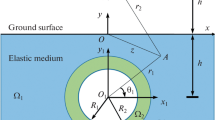
The task of this work is to study the scattering of SH waves by homogeneous tunnel structures in an unbounded inhomogeneous medium. The shear modulus is assumed to be a function of coordinates (x,y). A two-dimensional scattering model is established. Selecting different inhomogeneous parameters, the medium has different properties, expressed as a rigid variation. The stress concentration phenomenon of the structure is analyzed for material design. Based on the complex function theory, the expressions of wave field in the tunnel are derived. The stress concentration phenomenon on the tunnel is discussed with numerical examples. The distribution of dynamic stress concentration factor on the inner and outer boundaries is analyzed under different influencing factors. Finally, it is found that the distribution of dynamic stress concentration factor is significantly affected by the inhomogeneous parameters and reference wave numbers of the medium.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Availability of Data and Material

All data generated or analyzed to support the findings of this study are included within the article.

References

  1. Pao YH, Mao CC. Diffraction of elastic waves and dynamic stress concentration. New York: Crane and Russak; 1973.

    Book  Google Scholar 

  2. Popov A, Kovalchuk V. Parametric representation of wave propagation in nonuniform media (both in transmission and stop bands). Math Meth Appl Sci. 2013;36(11):1350–62.

    Article  MATH  Google Scholar 

  3. Urena M, Benito JJ, Urena F, Salete E, Gavete L. Application of generalised finite differences method to reflection and transmission problems in seismic SH waves propagation. Math Meth Appl Sci. 2017;41(6):2328–39.

    MathSciNet  MATH  Google Scholar 

  4. Sing H, Das A, Mistri KC, Chattopadhyay A. Green’s function approach to study the propagation of SH-wave in piezoelectric layer influenced by a point source. Math Meth Appl Sci. 2017;40(13):4771–84.

    MathSciNet  MATH  Google Scholar 

  5. Han X, Liu GR. Effects of SH waves in a functionally graded plate. Mech Res Commun. 2002;29(5):327–38.

    Article  MATH  Google Scholar 

  6. Martin PA. Scattering by a cavity in an exponentially graded half-space. J Appl Mech Trans ASME. 2009;76(3):540–5.

    Article  Google Scholar 

  7. Liu QJ, Zhao MJ, Zhang C. Antiplane scattering of SH waves by a circular cavity in an exponentially graded half space. Int J Eng Sci. 2014;78:61–72.

    Article  MathSciNet  MATH  Google Scholar 

  8. Ghafarollahi A, Shodja HM. Scattering of SH-waves by an elliptic cavity/crack beneath the interface between functionally graded and homogeneous half-spaces via multipole expansion method. J Sound Vib. 2018;435:372–89.

    Article  Google Scholar 

  9. Zhang LL, Fang XQ, Liu JX. The multiple scattering of non-homogeneous shear waves from two cavities in functionally graded materials. Philos Mag. 2010;90(24):3375–87.

    Article  Google Scholar 

  10. Golub MV, Fomenko SI, Bui TQ. Transmission and band gaps of elastic SH waves in functionally graded periodic laminates. Int J Solids Struct. 2012;49(2):344–54.

    Article  Google Scholar 

  11. Hei BP, Yang ZL, Sun BT, Wang Y. Modelling and analysis of the dynamic behavior of inhomogeneous continuum containing a circular inclusion. Appl Math Model. 2015;39(23–24):7364–74.

    Article  MathSciNet  MATH  Google Scholar 

  12. Hei BP, Yang ZL, Sun BT, Liu DK. Dynamic stress analysis around a circular cavity in two-dimensional inhomogeneous medium with density variation. J Mech. 2016;32(5):519–26.

    Article  Google Scholar 

  13. Kundu S, Manna S, Gupta S. Propagation of SH-wave in an initially stressed orthotropic medium sandwiched by a homogeneous and an inhomogeneous semi-infinite media. Math Method Appl Sci. 2015;38(9):1926–36.

    Article  MathSciNet  MATH  Google Scholar 

  14. Jiang GXX, Yang ZL, Sun C, Sun BT, Yang Y. Dynamic analysis of anisotropic half space containing an elliptical inclusion under SH waves. Math Meth Appl Sci. 2020;43(11):6888–902.

    Article  MathSciNet  MATH  Google Scholar 

  15. Bednarik M, Cervenka M, Lotton P, Simon L. Analytical solutions for elastic SH-waves propagating through an isotropic inhomogeneous layer. Compos Struct. 2019;220:875–87.

    Article  Google Scholar 

  16. Daros CH. Green’s function for SH-waves in inhomogeneous anisotropic elastic solid with power-function velocity variation. Wave Motion. 2013;50(2):101–10.

    Article  MathSciNet  MATH  Google Scholar 

  17. Singh BM, Rokne J. Propagation of SH waves in layered functionally gradient piezoelectric–piezomagnetic structures. Philos Mag. 2013;93(14):1690–700.

    Article  Google Scholar 

  18. Negi A, Singh AK, Yadav RP. Analysis on dynamic interfacial crack impacted by SH-wave in bi-material poroelastic strip. Compos Struct. 2020;233: 111639.

    Article  Google Scholar 

  19. Manolis GD, Dineva PS, Rangelov TV. Dynamic fracture analysis of a smoothly inhomogeneous plane containing defects by BEM. Eng Ana Bound Elem. 2012;36(5):727–37.

    Article  MathSciNet  MATH  Google Scholar 

  20. Gamer U. Dynamic stress concentration in an elastic half space with a semi-circular cavity excited by SH waves. Int J Solids Struct. 1977;13(7):675–81.

    Article  MATH  Google Scholar 

  21. Tao M, Zhao R, Du K. Dynamic stress concentration and failure characteristics around elliptical cavity subjected to impact loading. Int J Solids Struct. 2020;191:401–17.

    Article  Google Scholar 

  22. Meade KP, Keer LM. Dynamic response of an embedded rectangular foundation to antiplane shear waves. Int J Solids Struct. 1982;18(3):249–61.

    Article  MATH  Google Scholar 

  23. Kara HF, Aydogdu M. Dynamic response of a functionally graded tube embedded in an elastic medium due to SH-Waves. Compos Struct. 2018;206:22–32.

    Article  Google Scholar 

  24. Jang P, Paek U, Jong K, Yun D, Kim C, Ri S. Dynamic analysis of SH wave by a three-layer inclusion near interface in bi-material half space. AIP Adv. 2020;10(5): 055107.

    Article  Google Scholar 

  25. Sheikhhassani R, Dravinski M. Dynamic stress concentration for multiple multilayered inclusions embedded in an elastic half-space subjected to SH-waves. Wave Motion. 2016;62:20–40.

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu DK, Gai BZ, Tao GY. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion. 1982;4(3):293–304.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (No. 12002143) and Research Team Project of Heilongjiang Natural Science Foundation (No.TD2020A001) and the program for Innovative Research Team in China Earthquake Administration.

Author information

Authors and Affiliations

  1. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150001, China

    Zailin Yang, **lai Bian & Yong Yang

  2. School of Resource Engineering, Longyan University, Longyan, 364012, China

    Huanan Xu

  3. Key Laboratory of Advanced Material of Ship and Mechanics, Ministry of Industry and Information Technology, Harbin Engineering University, Harbin, 150001, China

    Zailin Yang & Yong Yang

Authors
  1. Zailin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. **lai Bian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huanan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

ZY and YY conceived the idea. JB and HX carried out formula derivation and example analysis. All authors contributed to the writing and revision.

Corresponding authors

Correspondence to Huanan Xu or Yong Yang.

Ethics declarations

Conflict of interest

No conflict of interest exists in the submission of this manuscript, and the manuscript is approved by all authors for publication.

Appendices

Appendix

Stress Fields in an Unbounded Inhomogeneous Medium

Incident waves in an unbounded medium

$$ \begin{gathered} \tau_{rz}^{{\text{i}}} = \frac{1}{2}\mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{ - i\alpha } + \overline{\zeta } {\text{e}}^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta } } \right)} \right] \hfill \\ \left[ {\left( {\beta \overline{z} + \eta } \right)\left( {ik_{T} {\text{e}}^{ - i\alpha } - 1} \right){\text{e}}^{i\theta } + \left( {\beta z + \eta } \right)\left( {ik_{T} {\text{e}}^{i\alpha } - 1} \right){\text{e}}^{ - i\theta } } \right] \hfill \\ \end{gathered} $$
(A1)
$$ \begin{gathered} \tau_{\theta z}^{{\text{i}}} = \frac{1}{2}i\mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta e^{ - i\alpha } + \overline{\zeta } e^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta } } \right)} \right] \hfill \\ \left[ {\left( {\beta \overline{z} + \eta } \right)\left( {ik_{T} {\text{e}}^{ - i\alpha } - 1} \right){\text{e}}^{i\theta } - \left( {\beta z + \eta } \right)\left( {ik_{T} {\text{e}}^{i\alpha } - 1} \right){\text{e}}^{ - i\theta } } \right] \hfill \\ \end{gathered} $$
(A2)

Scattering waves generated by the outer boundary

$$ \begin{gathered} \tau_{rz}^{{\text{s}}} = \frac{1}{2}\mu_{0} \beta \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta } } \right)} \right] \hfill \\ \sum\limits_{n = - \infty }^{n = + \infty } {A_{n} } \left[ {\left( {k_{T} H_{n - 1}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n - 1} - H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n} } \right)} \right.\left( {\beta \overline{z} + \eta } \right){\text{e}}^{i\theta } \hfill \\ \left. { - \left( {H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n} + k_{T} H_{n + 1}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n + 1} } \right)\left( {\beta z + \eta } \right){\text{e}}^{ - i\theta } } \right] \hfill \\ \end{gathered} $$
(A3)
$$ \begin{aligned} & \tau_{\theta z}^{{\text{s}}} = \frac{1}{2}i\mu_{0} \beta \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta } } \right)} \right] \\ & \sum\limits_{n = - \infty }^{n = + \infty } {A_{n} } \left[ {\left( {k_{T} H_{n - 1}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n - 1} - H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n} } \right)} \right.\left( {\beta \overline{z} + \eta } \right){\text{e}}^{i\theta } \\ &\qquad \left. {{ + }\left( {H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n} + k_{T} H_{n + 1}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n + 1} } \right)\left( {\beta z + \eta } \right){\text{e}}^{ - i\theta } } \right] \end{aligned} $$
(A4)

Refracted waves generated by the outer boundary

$$\begin{aligned} & \tau_{rz}^{{\text{f}}} = \frac{1}{2}\mu_{2} k_{2} \sum\limits_{n = - \infty }^{\infty }\\ & {B_{n} \left[ {H_{n - 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n - 1} {\text{e}}^{i\theta } - H_{n + 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n + 1} {\text{e}}^{ - i\theta } } \right]}\end{aligned} $$
(A5)
$$\begin{aligned} & \tau_{\theta z}^{{\text{f}}} = \frac{1}{2}i\mu_{2} k_{2} \sum\limits_{n = - \infty }^{\infty }\\ & {B_{n} \left[ {H_{n - 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n - 1} {\text{e}}^{i\theta } + H_{n + 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n + 1} {\text{e}}^{ - i\theta } } \right]}\end{aligned} $$
(A6)

Scattering waves generated by the inner boundary

$$\begin{aligned} \tau_{rz}^{{{\text{s}}R_{{1}} }} & = \frac{1}{2}\mu_{2} k_{2} \sum\limits_{n = - \infty }^{\infty } C_{n} \left[ H_{n - 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta }\right.\\ &\quad \left. - H_{n + 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{n + 1} {\text{e}}^{ - i\theta } \right]\end{aligned} $$
(A7)
$$\begin{aligned} \tau_{\theta z}^{{{\text{s}}R_{{1}} }} & = \frac{1}{2}i\mu_{2} k_{2} \sum\limits_{n = - \infty }^{\infty } C_{n} \left[ H_{n - 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta }\right.\\ & \quad \left. + H_{n + 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{n + 1} {\text{e}}^{ - i\theta } \right]\end{aligned} $$
(A8)

Wave Fields (Sect. 5.1) in Boundary Conditions

$$ E_{n}^{11} = - \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right]H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n} $$
(A9)
$$ E_{n}^{12} = H_{n}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n} $$
(A10)
$$ E_{n}^{13} = H_{n}^{(1)} \left( {k_{2} \left| {z_{1} } \right|} \right)\left( {\frac{{z_{1} }}{{\left| {z_{1} } \right|}}} \right)^{n} $$
(A11)
$$ \begin{aligned} & E_{n}^{21} = - \mu_{0} \beta \exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right]\\ & \left[ {\left( {k_{T} H_{n - 1}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n - 1} - H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n} } \right)} \right. \\ & \left. \left( {\beta \overline{z} + \eta } \right){\text{e}}^{i\theta } - \left( H_{n}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n}\right.\right. \\ & \left.\left. + k_{T} H_{n + 1}^{(1)} \left( {k_{T} \left| \zeta \right|} \right)\left( {\frac{\zeta }{\left| \zeta \right|}} \right)^{n + 1} \right)\left( {\beta z + \eta } \right){\text{e}}^{ - i\theta } \right] \end{aligned} $$
(A12)
$$\begin{aligned} & E_{n}^{22} = \mu_{2} k_{2} \left[ H_{n - 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n - 1} {\text{e}}^{i\theta }\right.\\ & \left. - H_{n + 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{{n{ + }1}} {\text{e}}^{ - i\theta } \right]\end{aligned} $$
(A13)
$$\begin{aligned} & E_{n}^{23} = \mu_{2} k_{2} \left[ H_{n - 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta }\right.\\ & \left. - H_{n + 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{{n{ + }1}} {\text{e}}^{ - i\theta } \right]\end{aligned} $$
(A14)
$$ E_{n}^{32} = H_{n - 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{n - 1} {\text{e}}^{i\theta } - H_{n + 1}^{(2)} \left( {k_{2} \left| z \right|} \right)\left( {\frac{z}{\left| z \right|}} \right)^{{n{ + }1}} {\text{e}}^{ - i\theta } $$
(A15)
$$ E_{n}^{33} = H_{n - 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{n - 1} {\text{e}}^{i\theta } - H_{n + 1}^{(1)} \left( {k_{2} \left| {z_{{1}} } \right|} \right)\left( {\frac{{z_{{1}} }}{{\left| {z_{{1}} } \right|}}} \right)^{{n{ + }1}} {\text{e}}^{ - i\theta } $$
(A16)
$$ E^{1} = \varphi_{0} \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{ - i\alpha } + \overline{\zeta }{\text{e}}^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] $$
(A17)
$$ \begin{gathered} E^{2} = \mu_{0} \varphi_{0} \beta \exp \left[ {\frac{{ik_{T} }}{2}\left( {\zeta {\text{e}}^{ - i\alpha } + \overline{\zeta }{\text{e}}^{i\alpha } } \right)} \right]\exp \left[ { - \frac{1}{2}\left( {\zeta + \overline{\zeta }} \right)} \right] \hfill \\ \left[ {\left( {\beta \overline{z} + \eta } \right)\left( {ik_{T} {\text{e}}^{ - i\alpha } - 1} \right){\text{e}}^{i\theta } + \left( {\beta z + \eta } \right)\left( {ik_{T} {\text{e}}^{i\alpha } - 1} \right){\text{e}}^{ - i\theta } } \right] \hfill \\ \end{gathered} $$
(A18)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Z., Bian, J., Xu, H. et al. Dynamic Response of Tunnel Structures in Inhomogeneous Medium Under SH Wave: Shear Modulus in Quadratic Functional Form. Acta Mech. Solida Sin. 36, 457–468 (2023). https://doi.org/10.1007/s10338-023-00395-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-023-00395-y

Keywords

Search

Navigation