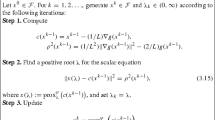Abstract
This paper studies several solution paths of sparse quadratic minimization problems as a function of the weighing parameter of the bi-objective of estimation loss versus solution sparsity. Three such paths are considered: the “\(\ell _0\)-path” where the discontinuous \(\ell _0\)-function provides the exact sparsity count; the “\(\ell _1\)-path” where the \(\ell _1\)-function provides a convex surrogate of sparsity count; and the “capped \(\ell _1\)-path” where the nonconvex nondifferentiable capped \(\ell _1\)-function aims to enhance the \(\ell _1\)-approximation. Serving different purposes, each of these three formulations is different from each other, both analytically and computationally. Our results deepen the understanding of (old and new) properties of the associated paths, highlight the pros, cons, and tradeoffs of these sparse optimization models, and provide numerical evidence to support the practical superiority of the capped \(\ell _1\)-path. Our study of the capped \(\ell _1\)-path is interesting in its own right as the path pertains to computable directionally stationary (= strongly locally minimizing in this context, as opposed to globally optimal) solutions of a parametric nonconvex nondifferentiable optimization problem. Motivated by classical parametric quadratic programming theory and reinforced by modern statistical learning studies, both casting an exponential perspective in fully describing such solution paths, we also aim to address the question of whether some of them can be fully traced in strongly polynomial time in the problem dimensions. A major conclusion of this paper is that a path of directional stationary solutions of the capped \(\ell _1\)-regularized problem offers interesting theoretical properties and practical compromise between the \(\ell _0\)-path and the \(\ell _1\)-path. Indeed, while the \(\ell _0\)-path is computationally prohibitive and greatly handicapped by the repeated solution of mixed-integer nonlinear programs, the quality of \(\ell _1\)-path, in terms of the two criteria—loss and sparsity—in the estimation objective, is inferior to the capped \(\ell _1\)-path; the latter can be obtained efficiently by a combination of a parametric pivoting-like scheme supplemented by an algorithm that takes advantage of the Z-matrix structure of the loss function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study and compare different approaches for sparse quadratic minimization [31] with a Stieltjes matrix [4] and bounded variables. In particular, given vectors \(q\in \mathbb {R}^n\), \(\ell \in \mathbb {R}_-^n\), \(u \in \mathbb {R}_+^n\), \(p \in \mathbb {R}_{++}^n\) a Stieltjes (i.e., a symmetric M-)matrix \(Q \in \mathbb {R}^{n \times n}\) and a regularization parameter \(\gamma \in \mathbb {R}_+\), we consider:
-
The \(\ell _0\)-problem
$$\begin{aligned} f_0(\gamma ) \, \triangleq \, \displaystyle { \mathop {{\textbf {minimum}}}\limits _{\ell \, \le x \, \le \, u} } \ \underbrace{q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx}_{\text {denoted}\,q(x)} + \gamma \, \displaystyle { \sum _{i=1}^n } \ p_i \, | \, x_i \, |_0, \end{aligned}$$(1)where the univariate \(\ell _0\)-function \(| \, t \, |_0 \triangleq \left\{ \begin{array}{ll} 1 &{} \text{ if } t \ne 0 \\ 0 &{} \text{ if } t = 0 \end{array} \right. \) for \(t \in \mathbb {R}\) is the indicator function of sparsity.
-
For an additional scalar \(\delta > 0\), the \(\ell _1\)-problem
$$\begin{aligned} f_1(\gamma ) \, \triangleq \, \displaystyle { \mathop {{\textbf {minimum}}}\limits _{\ell \, \le x \, \le \, u} } \ q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx + \gamma \, \displaystyle { \sum _{i=1}^n } \ p_i \, \frac{| \, x_i \, |}{\delta }; \end{aligned}$$(2)see also (8).
-
For \(\delta > 0\) as above, the (nonconvex) capped \(\ell _1\)-problem
$$\begin{aligned} f_{\textrm{cap}}(\gamma ) \, \triangleq \, \displaystyle { \mathop {{\textbf {minimum}}}\limits _{\ell \, \le x \, \le \, u} } \ q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx + \gamma \, \displaystyle { \sum _{i=1}^n } \ p_i \, \min \left( \, \displaystyle { \frac{| \, x_i \, |}{\delta } }, \, 1 \, \right) . \end{aligned}$$(3)In general, an M-matrix is a real square matrix with nonpositive off-diagonal elements (i.e., a Z-matrix) and whose principal minors are all positive; there are many equivalent characterizations of this class of matrices; see [9, 18].
Problem (1) is the exact formulation of the sparsity optimization problem of practical interest; (2) is a popular convexification of this discrete problem; and (3) attempts to enhance the sparsity of the solution of the convex approximation. There has been an extensive literature in solving problems (1)–(3) for a given value of the parameter \(\gamma \). In contrast, the parametric versions of the three problems constitute the focus of this paper. In other words, we focus on computing \(f_0(\gamma )\), \(f_1(\gamma )\) or \(f_{\textrm{cap}}(\gamma )\) for all values of \(\gamma \ge 0\) (i.e., the complete paths and not just at discrete values) and their corresponding “solutions”; for the nonconvex nondifferentiable problem (3), the analysis and computation of a (strongly) locally minimizing solution path will be a highlight of our study. In contrast to widely-used grid search, studying the entire paths for \(\ell _0\)-type problems is a relatively unexplored topic in the mathematical programming literature, and we present a study on this in the current paper.
1.1 Motivation
Problems (1)–(3) arise in sparse inference problems with Gaussian Markov random fields (GMRFs). Specifically, we consider a special class of GMRF models know as Besag models [11], which are widely used in the literature [12, 13, 28, 33, 37, 42] to model spatio-temporal processes including image restoration and computer vision, disease map**, and evolution of financial instruments. Given an undirected graph \(\mathcal {G}=(V,E)\) with vertex set V and edge set E, where edges encode adjacency relationships, consider a multivariate random variable \(X\in \mathbb {R}^{| V |}\) indexed by the vertices of \(\mathcal {G}\) with probability distribution
Such probability distribution encodes the prior belief that adjacent variables have similar values. The values of X cannot be observed directly, but rather some noisy observations y of X are available, where \(y_i=X_i+\varepsilon _i\), with \(\varepsilon _i\sim \mathcal {N}(0,\sigma _i^2)\). Figure 1 depicts a sample GMRF commonly used to model spatial processes, where edges correspond to horizontal and vertical adjacency.
In this case, the maximum a posteriori estimate of the true values of X can be found by solving the optimization problem
Instead of problem (4) (which can be solved in closed form), we consider the situation where the random variable is also assumed to be sparse [6]. For example, few pixels in an image may be salient from the background, few geographic locations may be affected by an epidemic, or the underlying value of a financial instrument may change sparingly over time. Moreover, models such as (4) with sparsity have also been proposed to estimate precision matrices of time-varying Gaussian processes [24]. In all cases, the sparsity prior can be included in model (4) with the inclusion of the \(\ell _0\) term \(\gamma \, \sum _{i=1}^n \, p_i \, | \, x_i \, |_0\), or an approximation such as the \(\ell _1\) or capped \(\ell _1\), resulting in an optimization problem with a Stieltjes matrix of the form (1)–(3). Since the true sparsity of the underlying statistical process is rarely known a priori, one is interested in solving (1)–(3) for all values of \(\gamma \), and then using either cross-validation or information criteria [2, 39] to select the best alternative.
1.2 Summary of contributions and outline of paper
While the parametric version of problem (2) has been studied in the literature [23, 40], there is a paucity of research concerning the parametric problems (1) and (3). This is not surprising, due to the nonconvex structure of the optimization problems. A major contribution of the present work is to fill this gap and to highlight the benefits brought by the Z-property of the matrix Q. These contributions are of two kinds: analytical and computational. From an analytical perspective, we show in particular that in the special case where the variable x is nonnegatively constrained, the functions \(f_0\), \(f_1\) and \(f_{\textrm{cap}}\) can be described compactly using at most \(n+1\) concave functions. In contrast, if Q is not Stieltjes and x is free, the description of these value functions may require an exponential number of simpler functions.
From a computational perspective, for each fixed \(\delta >0\), we propose an algorithm to compute a possibly discontinuous solution path of strongly locally optimal objective values of the capped \(\ell _1\)-problem:
There are several major contributions of this study from a mathematical programming perspective that deserve to be highlighted: (a) this study addresses a stationary solution path of a parameter-dependent capped \(\ell _1\) regularized quadratic optimization problem, which in this case, coincides with a path of (strongly) locally optimal solutions; (b) interesting properties of this stationary (= locmin) solution path are revealed in the study, in particular, its discontinuity and the fast restoration of a stationary solution at a discontinuous point; and (c) an extensive set of computational results provide strong evidence to support the benefits of this nonconvex nonsmooth regularizer in practical sparse optimization. Taken together, the analytical and computational results provide evidence demonstrating the benefits of the capped \(\ell _1\)-regularizer in the class of parametric sparse optimization problems studied in this paper.
At this point, it would be useful to mention that while there are other approximations of the \(\ell _0\)-function such as the minimax concave penalty mcp function [45], and the smoothly clipped absolute deviation scad function [25], we have chosen the capped \(\ell _1\)-regularizer because it is a piecewise linear function, resulting in the parametric problem (3) being of the parametric linear-quadratic, albeit nonconvex, kind whose (stationary) solution path can be traced out in finite time. In general, a multivariate piecewise linear-quadratic function differs from a piecewise quadratic function in that each “piece” of the former function is a polyhedron whereas no such polyhedrality is required for the latter [21, Sect. 4.4.2]. In the present context, the piecewise property is due to the univariate regularizer of the \(\ell _0\)-function and is thus much simpler. Nevertheless, with the former mcp and scad regularizers, the computational task of tracing the entire solution path as defined by the same \(\gamma \)-parameterization as in (3) cannot be accomplished exactly or in finite time, because the regularizers lead to parameterization of a quadratic term, resulting in a parameterized problem whose solution path is piecewise smooth with complicated changed points that cannot be computed exactly during the tracing process. A method that circumvents the parameterization of the quadratic term for the mcp regularizer is described in [45].
The rest of the paper is organized as follows. In Sect. 2 we present some relevant background for the paper. In Sect. 3 we review known results concerning the parametric versions of problems (1)–(3), and in Sect. 4 we prove the new analytical results. In Sects. 5 and 6 we discuss the computation of the local minimum path given by \(f_\textrm{locmin}(\gamma )\); in Sect. 7 we specialize the methods to the nonnegative case \(x\ge 0\); and in Sect. 8 we illustrate the performance of the proposed method via numerical experiments.
Notation: We follow the standard notation of submatrices and subvectors indexed by subsets of \([ n ] \triangleq \{ 1, \cdots , n \}\); for instance, if \(\alpha \) and \(\beta \) are two such index sets, then \(Q_{\alpha \beta }\) is the submatrix of Q with rows and columns indexed by elements in \(\alpha \) and \(\beta \), respectively. If \(\alpha \) (\(\beta \)) is the full set [n], then we write \(Q_{\bullet \beta }\) (\(Q_{\alpha \bullet }\), respectively) for \(Q_{\alpha \beta }\). Similar definition applies to a subvector \(q_{\alpha }\) of q. For two vectors x and y of the same dimension, \(\min (x,y)\) is the vector of componentwise minima of x and y.
2 Some details of the problem setting
The basic problem with exact sparsity is (1), where the following blanket assumption is made unless otherwise specified:
-
\(0< \min ( \, -\ell _i,u_i \, ) \le \max ( -\ell _i,u_i \, ) < \infty \) for all \(i \in [ n ]\).
The results in this paper can easily be generalized to the case where some or all of the bounds \(\ell _i\) and \(u_i\) are \(\pm \infty \), respectively (as in many machine learning applications that are unconstrained problems), and also to the case where some bounds are equal to zero (so that the corresponding variables are sign-restricted). In order to avoid some inessential discussion, we focus on the above conditions on the bounds, although we will devote Sects. 4 and 7 to address the case where \(\ell _i = 0\) for all \(i \in [ n ]\).
Due to the disjunctive (thus discontinuous) nature of the \(\ell _0\)-function, there are many proposals to approximate the \(\ell _0\)-function by continuous functions; most prominent among these in the statistics literature is the family of folded concave functions [1, 26, 34]. In turn, simplest in this family are the weighted \(\ell _1\) and capped \(\ell _1\)-functions; the latter functions employ a (sufficiently small) scalar \(\delta > 0\) satisfying the condition
We restrict \(\delta \) to satisfy this condition for the sake of simplifying some discussion. These regularizers lead to the approximated problems (2) and (3). Parameter \(\gamma \) is a weight between the quadratic loss function and the variable sparsity, the scalar \(\delta \) controls the approximation of the \(\ell _0\)-function by the convex absolute-value function, or the truncation of the latter. Subsequently, we devote Sect. 7 to the nonnegatively constrained capped \(\ell _1\)-problem:
where the nonnegativity restriction enables a strongly polynomial complexity of the parametric method for tracing a (directional stationary) solution path of the problem.
Problem (2) is equivalent, via an obvious re-definition of the tuplet \(( q,Q,\ell ,u )\), to the problem
where the weights associated with the absolute-value term are all equal. Such a transformation is not possible for the nonconvex problems (1) and (3).
For fixed \(( \gamma ,\delta ) > 0\), the 3 problems (1), (2), and (3) are quite different structurally:
-
(1) is a discontinuous minimization problem that can be formulated as either a mixed-integer program [6, 22, 41] or a quadratic program with linear complementarity constraints [7, 27];
-
(2) is a convex, bounded-variable, piecewise linear-quadratic program [20] that is solvable by a strongly polynomially bounded algorithm [29], which we refer as the GHP Algorithm, where GHP refers to the last names of the authors of the latter reference.
-
as a special coupled nonconvex nondifferentiable optimization problem [21], (3) is a piecewise linear-quadratic program [20], whose local minimizers are computable by the same GHP Algorithm.
When specialized to (3), the GHP Algorithm consists of outer loops each composed of inner iterations. Initialized with the index set \(S = [ n ]\), each outer loop computes a “directional stationary” solution (see Sect. 5 for a formal definition) of a fixed-sign version of the problem where variables indexed by a current set S are constrained to be nonnegative while those not in S are nonpositive. Each inner loop (which is not needed for the \(\ell _1\)-problem (2)) accomplishes this task by breaking up the pointwise minimum function and solves a sequence of convex quadratic programs. By exploiting the Z-structure of the matrix Q, both loops have a monotonic property that results in a strongly polynomial complexity of the overall algorithm for computing a directional stationary solution (= strong local minimum) of (3) (and an optimal solution in the case of (2) due to its convexity). A noteworthy remark about the GHP Algorithm as presented in [29] is that it is initialized with the full index set [n]; most importantly, if an “almost dstat” solution is available, as is in the problem of tracing a solution path to be introduced next, then one would want to modify the algorithm to take advantage of the available candidate solution. Details of the motivation and description of the “modified GHP Algorithm” are presented in Sect. 6.
2.1 Solution paths
Unlike the case of a fixed \(\gamma > 0\), there is to date a lack of a systematic study of a solution path of either problem (1) or (3) for all positive values of \(\gamma \). In contrast, the earliest study of the parametric “LASSO path”, i.e., the problem (2) with a general symmetric positive (semi)definite matrix Q appears to be the paper [23] followed by [40]. The LARS algorithm therein is like a classical parametric quadratic programming algorithm in the optimization literature [14] although the LASSO structure is explicitly exploited. Its complexity is in general exponential in the number of variables due to the possible exponential number of breakpoints of the solution path [35].
A parametric study of the exact \(\ell _0\)-problem (1) with equal weights (\(p_i=1\) for all \(i\in [n]\)) can be found in [38], where the piecewise affine property of the path is established; the description of this path involves in general the solution of a linear number of fixed-cardinality variable selection problems. Similar ideas of enumerating all \(n+1\) cardinalities are commonly used in the literature [10, 19]. However, there is a scarcity of efficient techniques for the case of unequal weights. Methods for multiobjective optimization, often designed in the context of mixed-integer linear optimization, often call for solving a large sequence of mixed-integer programs [15, 16]. Naturally, such methods may perform poorly if a large number of calls to a mixed-integer optimization solver are necessary, particularly in the context of mixed-integer nonlinear optimization, since each problem is comparatively more difficult than for the linear case.
A parametric study of \(\ell _p\)-regularized “critical path” (\(0< p < 1\)) connecting the origin to a given “local minimizer” of the problem is done in [44]. The construction of such a “piecewise smooth” function involves following a smooth path between breakpoints by solving a system of parametric nonlinear equations and a heuristic scheme to switch between two breakpoints. In general, a nonlinear regularizer such as the \(\ell _p\)-function will lead to nonlinear equations and following the solution path of such equations can be accomplished at best only approximately; this is in contrast to following a piecewise affine path induced by the \(\ell _1\)- and capped \(\ell _1\)-regularizers. Note that the \(\ell _p\)-regularized problem is strongly NP-hard for fixed value of the regularization parameter [17], thus tracing the exact parametric path is certainly difficult.
Unlike the parametric \(\ell _0\)- and \(\ell _1\)-paths, as we have mentioned before, there is to date no study of the solution path of the capped \(\ell _1\)-regularized problem. As it turns out, a careful study of the latter path has significant practical benefits from a computational optimization perspective and also from a statistical point of view; this manifestation of the capped \(\ell _1\)-path is supported by the numerical results in Sect. 8.
We first summarize the theoretical results of our study, whose detailed proofs will be the subject of subsequent sections where the un-defined terms will be clarified.
-
The optimal objective value function \(f_0(\gamma )\) of the exact \(\ell _0\)-problem is concave, nondecreasing, and piecewise affine with possibly exponentially many pieces of linearity; the evaluation of \(f_0(\gamma )\) for each fixed \(\gamma > 0\) requires solving a mixed-integer quadratic program. While it is known that when the weights \(p_i\) are all equal, the optimal objective value:
$$\begin{aligned} f_0^=(\gamma ) \, \triangleq \, \displaystyle { \mathop {{\textbf {minimum}}}\limits _{\ell \, \le x \, \le \, u} } \ q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx + \gamma \, \displaystyle { \sum _{i=1}^n } \ | \, x_i \, |_0 \end{aligned}$$has no more than \(n+1\) pieces of linearity [38], subsequently, in Sect. 4 we give an example to show that the more general path \(f_0(\gamma )\) can indeed have an exponential number of affine pieces if Q is not an M-matrix. Such an example seems to be new in the literature. Nonetheless, we show that, if Q is an M-matrix and \(\ell _i=0\) for \(i\in [n]\), then \(f_0(\gamma )\) (with unequal weights) has at most \(n+1\) affine pieces.
-
The optimal objective value function \(f_1(\gamma )\) of the \(\ell _1\)-problem is concave, nondecreasing, once continuously differentiable, and piecewise linear-quadratic composed of finitely many quadratic functions over an exponential number of non-overlap** intervals. The evaluation of \(f_1(\gamma )\) for each fixed \(\gamma > 0\) can be accomplished by a strongly polynomially bounded algorithm. The reference [35] contains a class of \(\ell _1\)-regularized problems where the number of smooth pieces of the solution path is exponential; yet Q in these problems cannot be a Z-matrix. While it remains an open question to date whether the number of such pieces of the solution path is an exponential or polynomial function of n when Q is a Stieltjes matrix, there are cases [29, Sect. 6] where this number is linear in n.
-
For each fixed \(\delta > 0\), the optimal objective value function \(f_{\textrm{cap}}(\gamma )\) of the (nonconvex) capped \(\ell _1\)-problem is concave, nondecreasing, and piecewise linear-quadratic with possibly exponentially many quadratic pieces; the evaluation of \(f_{\textrm{cap}}(\gamma )\) for each fixed \(\gamma > 0\) can be accomplished by solving an exponential number of convex quadratic programs. However, if Q is an M-matrix and \(\ell _i=0\) for \(i\in [n]\), a similar polynomiality property on the number of smooth pieces of the \(\ell _0\) and \(\ell _1\)-solution path can be proved for the capped \(\ell _1\)-problem. To be specific, in this case, \(f_{\textrm{cap}}(\gamma )\) has at most \(\text{ O }\left( n^2\right) \) quadratic pieces, based on a very loose count.
-
Since the capped \(\ell _1\)-regularizer is nonconvex, we may be interested in a local minimum path whose computation may be significantly less demanding than the computation of the global minimum path \(f_{\textrm{cap}}(\gamma )\). To this end, we propose a finite algorithm to compute a path of locally optimal objective values of (5) via its directional stationary points. This algorithm has a strongly polynomial complexity when the lower bounds \(\ell _i = 0\) for all \(i \in [ n ]\). Computationally, this solution path of local minima has many benefits over the previous paths of global minima that we will demonstrate via numerical computations.
3 Paths of global minimum objectives: enhanced known results
The results presented in the section are either known or easy consequences of more general results. We include them for the sake of completeness and also for comparative purposes among themselves and with the results in subsequent sections. Throughout this section, the Z-property of the matrix Q is not always needed, but positive definiteness of Q is still in place. The first result concerns the path of the \(\ell _0\)-problem.
Proposition 1
Let \(Q \in \mathbb {R}^{n \times n}\) be symmetric positive definite. The function \(f_0: [ 0,\infty ) \rightarrow \mathbb {R}\) is concave, nondecreasing, and piecewise affine with possibly exponentially many pieces of linearity. The function \(f_0^=\) with all the \(p_i\)’s equal has no more than \(n+1\) pieces of linearity.
Proof
The concavity of \(f_0\) requires no proof since the objective function in (1) is a linear function in \(\gamma \) for fixed x. The nondecreasing property of \(f_0\) is fairly obvious too. The proof of the piecewise property consists of three steps:
-
Step 1: We claim that
$$\begin{aligned} f_0(\gamma ) = \displaystyle { \mathop {{\textbf {minimum}}}\limits _{S \, \subseteq \, [ \, n \, ]} } \ v(S) + \gamma \, \displaystyle { \sum _{i \in S} } \, p_i \quad \text{ where } \left\{ \begin{array}{lll} v(S) \, \triangleq &{} \displaystyle { \mathop {{\textbf {minimum}}}\limits _{\ell \, \le \, x \, \le \, u} } &{} q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx \\ &{} \textbf{subject to} &{} x_i \, = \, 0, \quad \forall \, i \, \not \in \, S. \end{array} \right. \nonumber \\ \end{aligned}$$(9)Indeed, if \(\bar{x} \in \displaystyle { \mathop {{\textbf {argmin}}}\limits _{\ell \, \le x \, \le \, u} } \ q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx + \gamma \, \displaystyle { \sum _{i=1}^n } \ p_i \, | \, x_i \, |_0\), then
$$\begin{aligned} f_0(\gamma ) \, = \, v( \text{ supp }(\bar{x}) ) + \gamma \, \displaystyle { \sum _{i \in \text{ supp }(\bar{x})} } \ p_i \, \ge \, \displaystyle { \mathop {{\textbf {minimum}}}\limits _{S \, \subseteq \, [ \, n \, ]} } \ v(S) + \gamma \, \displaystyle { \sum _{i \in S} } \, p_i, \end{aligned}$$where \(\text{ supp }(\bar{x}) \triangleq \{ i \mid \bar{x}_i \ne 0 \}\) is the “support” of the vector \(\bar{x}\). To prove the reverse inequality, let \(S_{\min }\) be a minimizing index set of the right-hand subset-minimization problem. If \(\widehat{x}\) is the unique minimizer of \(v(S_{\min })\), then
$$\begin{aligned} v(S_{\min }) + \gamma \, \displaystyle { \sum _{i \in S_{\min }} } \, p_i \, \ge \, q^{\top }\widehat{x} + {\textstyle {\frac{1}{2}}}\, \widehat{x}^{\, \top }Q \widehat{x} + \gamma \, \displaystyle { \sum _{i=1}^n } \ p_i \, | \, \widehat{x}_i \, |_0 \, \ge \, f_0(\gamma ), \end{aligned}$$where the inequality holds because some components \(\widehat{x}_i\) for \(i \in S_{\min }\) may equal to zero in addition to those not in \(S_{\min }\). Hence (9) holds.
-
Step 2: For each \(S \subseteq [ \, n \, ]\), \(\gamma \mapsto v(S) + \gamma \, \sum _{i \in S} \, p_i \) is an affine function in \(\gamma \) with slope \( \sum _{i \in S} \, p_i \) and intercept v(S). Thus \(f_0(\gamma )\) is the pointwise minimum of finitely many affine functions, and hence is itself concave and piecewise affine.
-
Step 3: When all the \(p_i\)’s are equal to one, then \(\sum _{i \in S} \, p_i = \text{ card }(S)\), where “card” denotes the “cardinality of”. Hence, we have the following simplified expression:
$$\begin{aligned} f_0^=(\gamma ) \, = \, \displaystyle { \mathop {{\textbf {minimum}}}\limits _{0 \, \le \, k \, \le n} } \, ( \, v_k + \gamma \, k \, ), \quad \text{ where } \quad \left\{ \begin{array}{lll} v_k \, \triangleq &{} \displaystyle { \mathop {{\textbf {minimum}}}\limits _{S \, \subseteq \, [ \, n \, ]} } &{} v(S) \\ &{} \textbf{subject to} &{} \text{ card }(S) \, = \, k. \end{array} \right. \end{aligned}$$
This is enough to establish that \(f_0^=(\gamma )\) is a piecewise affine function in \(\gamma \) with at most \(n+1\) pieces of linearity. \(\square \)
The next two results concern the \(\ell _1\)-regularized path.
Proposition 2
Let \(Q \in \mathbb {R}^{n \times n}\) be symmetric positive definite. The function \(f_1: [ 0,\infty ) \rightarrow \mathbb {R}\) is concave, nondecreasing, once continuously differentiable, and piecewise linear-quadratic; the latter means that there exists a finite partition:
of the interval \([ \, 0,\infty \, )\) such that on each subinterval \([ \, \gamma _k,\gamma _{k+1} \, ]\) for \(k = 0, 1, \cdots , K\), \(f_1(\gamma )\) is a quadratic function in \(\gamma \). Moreover, \(f_1^{\, \prime }(\gamma ) = \, \frac{1}{\delta } \, \sum _{i=1}^n \, p_i \, | \, \bar{x}_i^1(\gamma ) \, |\) is a piecewise affine function in \(\gamma \), where \(\bar{x}^1(\gamma )\) is the unique minimizer of the value function \(f_1(\gamma )\).
Proof
For the piecewise property, it suffices to note that with the signed decomposition of the variable \(x = x^+ - x^-\), where \(x^{\, \pm } \ge 0\), we have
where the right-hand minimization is a standard convex quadratic program in the variables \(x^{\pm }\). As such, the claimed piecewise property of \(f_1(\gamma )\) follows from known results for parametric convex quadratic programming. The once continuous differentiability of \(f_1(\gamma )\) is due to the uniqueness and continuity of the optimal solution to the value function \(f_1(\gamma )\). The derivative formula for \(f_1^{\, \prime }(\gamma )\) is an immediate consequence of the well-known Danskin Theorem of parameter-dependent optimization problems. \(\square \)
Proposition 3
[29, Theorem 18] If Q is a Stieltjes matrix, the nonnegatively constrained path:
has a linear number (at most \(2n + 1\)) of quadratic pieces on \([ \, 0,\infty \, )\). \(\square \)
The final result in this section concerns the capped \(\ell _1\)-solution path.
Proposition 4
Let \(Q \in \mathbb {R}^{n \times n}\) be symmetric positive definite. The function \(f_{\textrm{cap}}: [ \, 0,\infty \, ) \rightarrow \mathbb {R}\) is concave, nondecreasing, and piecewise linear-quadratic.
Proof
Similarly to the proof of Proposition 1, we first show that
where
Indeed, let \(\bar{x} \in \mathop {{\textbf {argmin}}}\limits _{\ell \, \le \, x \, \le \, u} \ q^{\top }x + {\textstyle {\frac{1}{2}}}\, x^{\top }Qx + \gamma \, \left[ \, { \sum _{i=1}^n } \, p_i \, \min \left( \, \frac{| \, x_i \, |}{\delta } , \, 1 \, \right) \, \right] \) and \(S_{\textrm{cap}} \, \triangleq \, \left\{ \, i \, \mid \, | \, \bar{x}_i \, | \, \le \, \delta \, \right\} \). Then for any \(x \in [ \, \ell ,u \, ]\) satisfying \(| \, x_i \, | \le \delta \) for all \(i \in S_{\textrm{cap}}\), we have
Since x is an arbitrary feasible solution to the minimization problem of \(\widehat{v}_{S_{\textrm{cap}}}(\gamma )\), it follows that \(\bar{x}\) is an optimal solution to the latter minimization problem. Hence, we deduce
The reverse inequality can be proved in the same way as that in Proposition 1. Thus (11) holds. Since each value function \(\widehat{v}_S(\gamma )\) is concave and piecewise linear-quadratic and since \(f_{\textrm{cap}}(\gamma )\) is the pointwise minimum of these value functions, it follows that \(f_{\textrm{cap}}(\gamma )\) is piecewise quadratic; i.e., there exist finitely many quadratic functions \(\{ g_i(\gamma ) \}_{i=1}^I\) for some positive integer I such that \(f_{\textrm{cap}}(\gamma ) \in \{ \, g_i(\gamma ) \, \}_{i=1}^I\) for all \(\gamma \in [ 0,\infty )\). Finally, the piecewise linear-quadratic property of \(f_{\textrm{cap}}(\gamma )\) follows from the fact that every univariate piecewise quadatic function on the (nonnegative) real line must be piecewise linear-quadratic. In turn this fact can be proved as follows. Any two quadratic functions cross at most at 2 points; thus I such quadratic functions have at most \(\left( \begin{array}{c} I \\ 2 \end{array} \right) \) cross points. Arranging these breakpoints in a nondecreasing order yields a desired partition (10) of the interval \([ \, 0,\infty )\) into finitely many intervals within each of which \(f_{\textrm{cap}}(\gamma )\) is a quadratic function. \(\square \)
4 Paths of global minimum objectives: new results
In general, singly parametric optimization problems may contain an exponential number of breakpoints. This is indeed the case for general lasso regression, as demonstrated in [35]. However, as stated in Proposition 3, the solution path of the \(\ell _1\)-regularized problem has a linear number of breakpoints if Q is a Stieltjes matrix and the variables are restricted to be nonnegative. In this section we show that analogous results hold as well for the \(\ell _0\)- and capped \(\ell _1\)-problem. Moreover, as we discuss in Sect. 7, the solution path of local minimizers of the capped \(\ell _1\)-problem also has a linear number of smooth pieces under similar assumptions.
First, to show that the solution path of the \(\ell _0\)-problem with unequal weights is non-trivial, we give a class of problems below for which the path \(f_0(\gamma )\) has an exponential number of breakpoints; thus such a path is quite different from the one with equal weights.
Example 5
Let \(Q \triangleq c \, \mathbb {I} + q \, q^{\top }\) where \(c > 0\), \(\mathbb {I}\) is the identity matrix, \(q_i\) is such that \(q_i^2 = 2^{\, i}\), and \(p_i = q_i^2\) for all \(i = 1, \cdots , n\). We make a preliminary remark about the choice of the pair (q, p): namely, for every pair of subsets \(S \ne S^{\, \prime }\) of [n],
Let each \(u_i = -\ell _i\) be such that \(\ell _S \le -[ \, Q_{SS} \, ]^{-1}q_S \le u_S\) for all subsets S of [n]. With these bounds, using the well-known Sherman-Morrison formula [30], we have
where v(S) is defined in (9). Hence,
The univariate convex function \(t ( > 0) \mapsto \displaystyle { \frac{c}{2 \, t} } + \gamma \, t\) attains its unique minimum at \(t = \sqrt{\displaystyle { \frac{c}{2 \, \gamma } }}\) with the minimum value equal to \(\sqrt{\, 2 \, \gamma \,c}\). When \(\gamma \) is such that \(\sqrt{\displaystyle { \frac{c}{2 \, \gamma } }} = c + \Vert \, q_{S_{\gamma }} \, \Vert _2^2\), or equivalently, when \(\gamma = \displaystyle { \frac{c}{2 \, ( \, c + \Vert \, q_{S_{\gamma }} \, \Vert _2^2 \, )^2} }\) for some subset \(S_{\gamma }\) of [n], then \(S_{\gamma }\) is the unique minimizing subset S in \(f_0(\gamma )\). Thus
The important point in this derivation of \(f_0(\gamma )\) is that as \(\gamma \) ranges over the nonnegative real line, the family \(\{ \, S_{\gamma } \}\) will range over all \(2^n\) subsets S of [n], producing \(2^n\) breakpoints of the path \(f_0(\gamma )\). \(\square \)
Now consider the optimization problem with nonnegative variables
where Q is a Stieltjes matrix. The key to showing the linear number of pieces of \(f_0^+\) is a support monotonicity property of the solutions to (12) that is asserted in the first part of the next result. Roughly speaking, this property says that the supports of the solutions corresponding to each piece are nested; in other words, if a variable “becomes positive", it never becomes zero again as \(\gamma \downarrow 0\).
Proposition 6
Let \(0 \le \gamma _1 < \gamma _2\) and \(p\in \mathbb {R}^n_{++}\). Let \(x^k\) be an optimal solution of (12) corresponding to value \(\gamma _k\), \(k=1,2\). Then \(\text {supp}(x^2)\subseteq \text {supp}(x^1)\). Thus \(f_0^+(\gamma )\) has at most \(n+1\) affine pieces.
Proof
Write \([n] = S^{\, c} \cup S^+\) where
Define \(\tilde{\ell } \triangleq \min \{ x^1,x^2 \}\). Then for \(k=1,2\),
where the equality holds since the optimal solutions \(x^k\) for (12) are still feasible. With the change of variables \(y= x-\tilde{\ell }\), the right-hand optimization problem can be rewritten as
where \(C_k\) is a certain constant, \(\tilde{q} \triangleq q + Q \tilde{\ell }\) and \({\tilde{u}} \triangleq u - \tilde{\ell }\). Note that the optimal solutions \(y^k = x^k - \tilde{\ell }\) satisfy the complementary condition \(y^1_iy^2_i=0\) for all \(i\in [n]\). Thus, \(|y^1_i+y_i^2|_0 = |y^1_i|_0 + |y^2_i|_0\). Moreover, since Q is a Z-matrix and \(y^1\) and \(y^2\) are both nonnegative, we have \((y^1)^{\top }Qy^2 = { \sum _{i\ne j} } \, Q_{ij}y^1_iy^2_j \le 0\). Furthermore, the minimum value \(g(y^k;\gamma _k)\) is nonpositive, since the zero vector is feasible. Hence,
Consequently, \((\gamma _1-\gamma _2) \, { \sum _{i\in S^c} } \, p_i|y^2_i|_0 = 0\), i.e. \(x_i^2=y_i^2=0\) for all \(i \in S^{\, c}\). Hence, \(\text {supp}(x(\gamma ))\) is nested for any optimal solution \(x(\gamma )\) to (12). Applying this nested property to the representation (9) yields a piecewise affine representation of \(f_0^+(\gamma )\) over a partition (10) of the interval \([ \, 0,\infty \, )\) (with \(K \le n\)) and a corresponding family \(\{ S_k \}_{k=0}^K\) of index subsets of [n] such that \(\text {supp}(x(\gamma )) = S_k\) for all \(\gamma \in ( \, \gamma _k,\gamma _{k+1} \, )\) for \(k = 0, 1, \cdots , K\); i.e.,
which is an affine function over the kth interval. \(\square \)
Next consider the capped \(\ell _1\)-problem with nonnegative variables
where Q is a Stieltjes matrix. With the alternative definition \({\textrm{supp}}_{\textrm{cap}}(x)\triangleq \{ i: x_i>\delta \}\) and two modified index subsets \(S_<\) and \(S_>\), the proof of the next result is similar to that of the previous proposition. For clarity, we provide the complete proof, which employs an important property [29, Proposition 14] of an optimal solution of (13); namely no component of such a solution is equal to \(\delta \).
Proposition 7
Let \(0\le \gamma _1<\gamma _2\) and \(p\in \mathbb {R}^n_{++}\). Let \(x^k\) be an optimal solution of (13) corresponding to value \(\gamma _k\), \(k=1,2\). Then \({\textrm{supp}}_{\textrm{cap}} (x^2)\subseteq {\textrm{supp}}_{\textrm{cap}} (x^1)\). Thus, \(f_{\textrm{cap}}^{+}(\gamma )\) has at most \(2n^2 + 3n + 1\) pieces.
Proof
Without loss of generality, assume \(\delta =1\). Write \([n] = S_< \cup S_>\) where
Define \(\tilde{\ell } \triangleq \min \{ x^1,x^2 \}\). Since no component of an optimal solution of (13) is equal to 1, it follows that \(\tilde{\ell }_i < 1\) for all \(i \in S_<\). For \(k=1,2\), we have
With the change of variables \(y = x-\tilde{\ell }\), the right-hand optimization problem can be rewritten as
where \(C_k,k=1,2\) is a certain constant, \(\tilde{q} \triangleq q + Q \tilde{\ell }\) and \({\tilde{u}} \triangleq u - \tilde{\ell }\). The optimal solution \(y^k=x^k-\tilde{\ell }\) satisfies the complementary condition \(y^1_iy^2_i=0\) for all \(i \in [n]\). Hence, we deduce that for \(i \in S_<\), \(\min \left\{ y_i^1+y_i^2,1-\tilde{\ell }_i\right\} = \min \left\{ y_i^1,1-\tilde{\ell }_i\right\} + \min \left\{ y_i^2,1-\tilde{\ell }_i\right\} \). As before, we have \((y^1)^\top Qy^2 \le 0\) and \(g(y^k;\gamma _k) \le 0\). Together, these yield \((\gamma _1-\gamma _2) { \sum _{i\in S_<} } \, p_i \, \min \left\{ y_i^2,1-\tilde{\ell }_i\right\} =0\); thus \(y_i^2=0 \) for all \(i\in S_<\). Since for \(i\in S_<\), \(\tilde{\ell }_i < 1\), we deduce that \(x^2_i = y^2_i+\tilde{\ell }_i < 1\) and the first assertion of the proposition follows.
Similar to the proof of Proposition 1, we deduce the existence of a partition (10) of the interval \([ \, 0,\infty \, )\) with \(K \le n\) and a corresponding family \(\{ S_k \}_{k=0}^K\) of index subsets of [n] such that
With the change of variables \(x_i^{\, \prime } \triangleq x_i - 1\) for \(i \in S_k\), we can apply Proposition 3 to deduce that the minimum value function within the square bracket has at most \(2n + 1\) quadratic pieces; since there are at most \(n + 1\) such value functions, the second conclusion in the proposition follows. \(\square \)
We next present a special case of the paths \(f_0(\gamma )\) and \(f_1(\gamma )\) for which the number of breakpoints is linear in the number of variables. This is accomplished by demonstrating that this case reduces to that of a nonnegatively constrained path to which Propositions 1 and 3, respectively, are applicable. Specifically, consider the following problems
and
where \(q \in \mathbb {R}^n_-\), \(r \in \mathbb {R}^m\), \(M \triangleq \left[ \begin{array}{cc} Q &{} R \\ R^{\top } &{} P \end{array} \right] \) is a Stieltjes matrix, \(p \in \mathbb {R}_{++}^n\) and \(p^{\, \prime } \in \mathbb {R}^m_{++}\) are positive vectors. The special feature of these problems is that the variables are of two kinds: the sign-unrestricted variable x and the nonnegative variable y. The vector q (associated with the sign-unrestricted variable x) is nonpositive, while the vector r associated with the nonnegative variable y is not signed.
Proposition 8
Let M be a Stieltjes matrix and \(q \le 0\). For any pair \(( \gamma ,\delta )\) with \(\gamma \ge 0\) and \(\delta > 0\), if \(( \bar{x},\bar{y} )\) is an optimal solution of either (15) or (16), then \(\bar{x} \ge 0\).
Proof
Let \(\alpha \triangleq \{ \, i \mid \, \bar{x}_i \, < \, 0 \, \}\) and \(\beta \triangleq \, [ \, n \, ] \, \setminus \, \alpha \). By the optimality of \(\bar{x}\), we have
Suppose \({\bar{x}}\) is optimal for (16). Since Q is an M-matrix, \([ \, Q_{\alpha \alpha } \, ]^{-1}\) is nonnegative, it follows that
which is a contradiction because the left-hand side is negative if \(\alpha \ne \emptyset \). An identical argument holds if \({\bar{x}}\) is optimal for (15). \(\square \)
Remark 9
Consider problem (1) with the additional assumption that \(q\le 0\). In the motivational discussion of Sect. 1.1, this case corresponds to settings where the data vector y is known to be nonnegative. From Propositions 6 and 8, we find that in such cases \(f_0(\gamma )\) has at most \(n+1\) affine pieces. Moreover, in [4], it is shown that such problems can be solved in strongly polynomial time for fixed \(\gamma \). Taken together, it means that problem (1) with \(q \le 0\) and Stieltjes matrix Q is a rare example of \(\ell _0\)-problem with unequal weights whose entire solution path can be computed in strongly polynomial time. Nonetheless, we point out that a simple application of the aforementioned ideas would result in a prohibitive complexity of approximately \(\mathcal {O}(n^7)\) to compute the solution path.
5 The (Strong) local-minimum path \(f_\textrm{locmin}(\gamma )\)
Starting in this section, we study the path of local minima of the capped \(\ell _1\)-problem (3). As mentioned before, this study of the “solution” path of a parameter dependent nonconvex nondifferentiable optimization problem is a novel contribution of our work. In particular, in this section, we show that every non-constant local-minimum path of (3) is discontinuous provided that \(\delta \) is small enough.
The starting point of the study is a known fact [20] that, for a given pair \((\gamma ,\delta ) > 0\), every directional stationary point of the piecewise linear-quadratic program (3), which we repeat for ease for reference:
is a strong local minimizer. Moreover, there are only finitely many of these minimizers. In turn, such a directional stationary (abbreviated as dstat) solution is, by definition, a feasible vector \(\bar{x}\) in \([ \, \ell , u \, ] \, \triangleq \, \left\{ \, x \, \in \, \mathbb {R}^n \, \mid \, \ell \, \le \, x \, \le \, u \, \right\} \) satisfying \(\theta _{\gamma }^{\, \prime }(\bar{x};x - \bar{x}) \ge 0\) for all \(x \in [ \, \ell ,u \, ]\), where \(\theta _{\gamma }^{\, \prime }(\bar{x};v)\) is the directional derivative of the objective function \(\theta _{\gamma }(x)\) at \(\bar{x}\) along the direction v:
where for a nonzero scalar t, \(\text{ sign }(t) \triangleq \left\{ \begin{array}{cl} 1 &{} \text{ if } t > 0 \\ -1 &{} \text{ if } t < 0; \end{array} \right. \) and
Such a vector has the following characterization [29, Proposition 1]. We recall the sign setting of the lower and upper bound vectors \(\ell < 0\) and \(u > 0\), respectively.
Proposition 10
Let Q be symmetric positive definite. For every \(\gamma > 0\), a feasible vector \(\bar{x} \in [ \, \ell ,u \, ]\) is a dstat solution of (17) if and only if the following conditions (a)–(f) hold:
-
(a)
\(| \, \bar{x}_i \, | \ne \delta \) for all \(i = 1, \cdots , n\);
-
(b)
\(( \, q + Q\bar{x} \, )_i + \gamma \, \displaystyle { \frac{p_i}{\delta } } \, \text{ sign }( \bar{x}_i) \, = \, 0\) for all i such that \(i \in {{\mathcal {A}}}_<^{\, \delta }(\bar{x})\);
-
(c)
\(( \, q + Q\bar{x} \, )_i \, = \, 0\) for all i such that \(\delta < | \, \bar{x}_i \, |\) and \(\ell _i< \bar{x}_i < u_i\);
-
(d)
\(| \, ( \, q + Q\bar{x} \, )_i \, | \, \le \, \gamma \, \displaystyle { \frac{p_i}{\delta } }\) for all i such that \(\bar{x}_i = 0\);
-
(e)
\(( \, q + Q\bar{x} \, )_i \, \ge \, 0\) for all i such that \(\bar{x}_i = \ell _i\).
-
(f)
\(( \, q + Q\bar{x} \, )_i \, \le \, 0\) for all i such that \(\bar{x}_i = u_i\). \(\square \)
An immediate consequence of the above characterization is the following special property for \(\gamma > 0\) sufficiently large.
Corollary 11
Let Q be symmetric positive definite. For every \(\delta \) satisfying (6), there exists \(\overline{\gamma } > 0\) such that for every \(\gamma \ge \overline{\gamma }\), if \(\bar{x}\) is a dstat solution of (17), then for every \(i = 1, \cdots , n\), either \(\bar{x}_i = 0\) or \(| \bar{x}_i | > \delta \).
Proof
The set of dstat points must be bounded independently of the parameter \(\gamma \). Hence, conditions (a) and (b) in Proposition 10 yield that there does not exist a component i such that \(0 < | \, \bar{x}_i \, | \le \delta \), provided that \(\gamma > 0\) is sufficiently large. \(\square \)
With the above results, we can establish that with an additional, very mild stipulation on the scalar \(\delta > 0\), there is at most one continuous path of dstat solutions of the problem (17) for \(\gamma \ge 0\).
Proposition 12
Let Q be symmetric positive definite. Let \(\bar{x}^0 \triangleq {{{\textbf {argmin}}}_{x \, \in \, [ \, \ell ,u \, ]} } \, q(x)\) and \(S_0 \triangleq \left\{ i \mid \bar{x}^0_i = 0 \right\} \). Let also
Let \(\{ \bar{x}(\gamma ) \}_{\gamma \ge 0 }\) be a path of dstat solutions of the problem (17). If this path is continuous, then \(\bar{x}(\gamma ) = \bar{x}^0\) for all \(\gamma \ge 0\). Thus, for all \(\delta > 0\) sufficiently small, any non-constant locmin path of (3) must be discontinuous.
Proof
Note that \(\bar{x}(0) = \bar{x}^0\). Consider an arbitrary component i. Suppose \(\bar{x}^0_i = 0\). Then we must have \(| \, \bar{x}_i(\gamma ) \, | < \delta \) for all \(\gamma \ge 0\). Otherwise, we have \(| \, \bar{x}_i(\gamma ) \, |> \delta > 0 = \bar{x}_i(0)\) for some \(\gamma > 0\). Thus by continuity of the path \(\bar{x}( \bullet )\), there exists \(\gamma ^{\, \prime } \in ( \, 0,\gamma )\) such that \(| \, \bar{x}_i(\gamma ^{\, \prime }) \, | = \delta \), which contradicts the stationarity property (a) in Proposition 10. Suppose instead \(| \, \bar{x}^0_i \, | > \delta \). Then we must have \(| \, \bar{x}_i(\gamma ) \, | > \delta \) for all \(\gamma \ge 0\) by the same continuity argument. Therefore, it follows that the path \(\bar{x}( \bullet )\) has the property that \(| \, \bar{x}_i(\gamma ) \, | < \delta \) for all \(\gamma \ge 0\) and all \(i \in S_0\) while \(| \, \bar{x}_i(\gamma ) \, | > \delta \) for all \(\gamma \ge 0\) and all \(i \not \in S_0\). Thus for every \(\gamma \ge 0\), \(\bar{x}(\gamma )\) is a dstat solution of the restricted problem:
that contains the nonconvex bound constraint: \(| \, x_i \, | \, \ge \, \delta \) for \(i \not \in S_0\). Nevertheless, since \(\bar{x}(\gamma )\) satisfy these nonconvex bound constraints strictly, the objective function of (18) is convex, and \(\bar{x}(\gamma )\) is a dstat solution of this problem, it follows that \(\bar{x}(\gamma )\) is a global minimizer of (18). To show that \(\bar{x}(\gamma )\) is a constant, we claim that \(\bar{x}(\gamma ) = \bar{x}^0\) for all \(\gamma \ge 0\). Indeed, if \(\bar{x}(\gamma ) \ne \bar{x}^0\), then
This contradiction establishes the constancy of the path \(\{ \bar{x}(\gamma ) \}_{\gamma \ge 0}\) provided that it is continuous. The remaining statements of the proposition require no proof. \(\square \)
The discontinuity of a path of strong local minima of the capped \(\ell _1\)-regularized problem (17) makes the task of tracing this path not easy. The numerical tracing of such a path starts by letting \(\gamma \) be sufficiently large so that \(x = 0\) is a dstat solution of (17). In general, the tracing procedure is divided into two parts: continuous tracing by parametric pivoting via condensed matrix operations, and dstat recovery at a discontinuous point by a modification of the GHP algorithm [29] sketched in Sect. 2 that was designed for a fixed \(\gamma \). Details are presented in the next section.
6 Computing a (discontinuous) locmin path of (17)
Conditions (b)–(f) in Proposition 10 suggest the classification of the components of a vector x to facilitate the verification of its directional stationarity. Specifically, let \(\left( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \right) \) be a tuple of index sets partitioning \(\{ 1, \cdots , n \}\), based on which we set \(x_i = 0\) for all \(i \in \alpha _0\), \(x_i = \ell _i\) for all \(i \in \alpha _{\ell }\), and \(x_i = u_i\) for all \(i \in \alpha _u\); we then solve for the variables \(( x_{\alpha _<}^{\pm }, x_{\alpha _>}^{\pm } )\) from the equations in conditions (b) and (c); obtaining
Also define the remaining components:
We have the following result that requires no proof.
Corollary 13
Let Q be symmetric positive definite, \(( \gamma ,\delta ) {>} 0\), and \(\big (\, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \big )\) be a tuple of index sets partitioning \(\{ 1, \cdots , n \}\). With \(\left( \, x_{\alpha _<}^{\pm }(\gamma ), x_{\alpha _>}^{\pm }(\gamma ) \right) \) given by (19), the vector \(\bar{x}(\gamma ) \, \triangleq \, \left( \, 0_{\alpha _0}, \, x_{\alpha _<}^{\pm }(\gamma ), \, x_{\alpha _>}^{\pm }(\gamma ), \, \ell _{\alpha _{\ell }}, \, u_{\alpha _u} \,\right) \) is a dstat solution of (3) if
-
\(0 \,< \, x_{\alpha _<^+}(\gamma ) \,< \, \delta \, \textbf{1}_{\alpha _<^+}\);
-
\(u_{\alpha _>^+} \,> \, x_{\alpha _>^+}(\gamma ) \,> \, \delta \, \textbf{1}_{\alpha _>^+}\);
-
\(0 \,> \, x_{\alpha _<^-}(\gamma ) \, > \, -\delta \, \textbf{1}_{\alpha _<^-}\);
-
\(\ell _{\alpha _>^-} \,< \, x_{\alpha _>^-}(\gamma ) \, < \, -\delta \, \textbf{1}_{\alpha _>^-}\);
-
\(0 \, \le \, \bar{q}_{\alpha _0} + \gamma \, \bar{p}_{\alpha _0} \, \le \, \gamma \, \displaystyle { \frac{2 \, p_{\alpha _0}}{\delta } }\);
-
\(\bar{q}_{\alpha _{\ell }} + \gamma \, \bar{p}_{\alpha _{\ell }} \, \ge \, 0\); and \(\bar{q}_{\alpha _u} + \gamma \, \bar{p}_{\alpha _u} \, \le \, 0\). \(\square \)
6.1 Continuous tracing
Suppose that a dstat solution \(\bar{x}(\gamma _0)\) is available at a given value \(\gamma _0\). Associated with this solution is the index tuple \(\left( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \right) \) defined by the solution \(\bar{x}(\gamma _0)\):
As in parametric linear programming, we determine the smallest and largest value of \(\gamma \) (denoted by \(\underline{\gamma }\) and \(\overline{\gamma }\), respectively) so that the associated vector \(\bar{x}(\gamma )\) corresponding to this tuple of index sets \(\left( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \right) \) remains a dstat solution for all values of \(\gamma \) such that \(\underline{\gamma }<\gamma <\overline{\gamma }\). We accomplish this by some standard ratio tests to maintain the conditions in Corollary 13 [remark: the min/max over an empty set is taken to be \(\pm \infty \), respectively]:

Depending on whether we want to trace the path to the left or right of the interval \(\left[ \, \underline{\gamma },\overline{\gamma } \, \right] \), we determine the maximum/minimum ratio in the two end points of this interval, respectively, and update the index tuple \(\left( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \right) \) accordingly. This is essentially parametric pivoting implemented via matrix operations as in the revised simplex method. Since we started the tracing procedure from very large values of \(\gamma \), we devote our subsequent discussion to always moving beyond the left endpoint of the interval.
Decreasing \(\gamma \) beyond its current value. At the value \(\underline{\gamma }\), we make the following transfer of a maximizing index \(i_{\max }\) depending on which case \(i_{\max }\) corresponds to:
-
Case 1\(_{\downarrow }\) through 4\(_{\downarrow }\): the absolute value of the variable \(x_{i_{\max }}\) has reached the critical value \(\delta \), which invalidates the dstat property of the current vector at \(\underline{\gamma }\). In this case, we can in principle apply the GHP Algorithm to recover a dstat solution at \(\underline{\gamma }\). Nevertheless, since we already have on hand an “almost dstat” solution, i.e., one that satisfies the conditions in Corollary 13 at \(\underline{\gamma }\) but has a component with absolute value equal to \(\delta \), we will subsequently propose a modification of the GHP Algorithm that takes advantage of this availability. After the restoration, we let \(\gamma _0 \leftarrow \underline{\gamma }\) and repeat the above procedure to continue the decrease of \(\gamma \) beyond the current \(\underline{\gamma }\).
-
Case 5\(_{\downarrow }\) and 6\(_{\downarrow }\): the variable \(x_{i_{\max }}\) has reached the value zero; transfer the index \(i_{\max }\) from \(\alpha _<^{\pm }\), respectively, to \(\alpha _0\) and repeat the above procedure to continue the decrease of \(\gamma \);
-
Case 7\(_{\downarrow }\): the variable \(x_{i_{\max }}\) has reached the upper bound \(u_{i_{\max }}\); transfer the index \(i_{\max }\) from \(\alpha _>^+\) to \(\alpha _u\) and repeat the above procedure to continue the decrease of \(\gamma \).
-
Case 8\(_{\downarrow }\): the variable \(x_{i_{\max }}\) has reached the lower bound \(\ell _{i_{\max }}\); transfer the index \(i_{\max }\) from \(\alpha _>^-\) to \(\alpha _{\ell }\) and repeat the above procedure to continue the decrease of \(\gamma \);
-
Case 9\(_{\downarrow }\): the variable \(x_{i_{\max }}\) is becoming positive; transfer \(i_{\max }\) from \(\alpha _0\) to \(\alpha _<^+\) and repeat the above procedure to continue the decrease of \(\gamma \);
-
Case 10\(_{\downarrow }\): the variable \(x_{i_{\max }}\) is becoming negative; transfer \(i_{\max }\) from \(\alpha _0\) to \(\alpha _<^-\) and repeat the above procedure to continue the decrease of \(\gamma \);
-
Case 11\(_{\downarrow }\): the variable \(x_{i_{\max }}\) is decreasing below its upper bound; transfer \(i_{\max }\) from \(\alpha _u\) to \(\alpha _>^+\) and repeat the above procedure to continue the decrease of \(\gamma \);
-
Case 12\(_{\downarrow }\): the variable \(x_{i_{\max }}\) is increasing above its lower bound; transfer \(i_{\max }\) from \(\alpha _{\ell }\) to \(\alpha _>^-\) and repeat the above procedure to continue the decrease of \(\gamma \);
Notice that if one of the first four cases occurs, there is a discontinuity of the path of dstat points at the value \(\underline{\gamma }\); in all other cases, the path of dstat points will remain continuous beyond \(\underline{\gamma }\) until the next discontinuity occurs.
Monotonicity of objective values. On the closed interval \(\left[ \, \underline{\gamma },\overline{\gamma } \, \right] \), the function \(\bar{x}(\gamma )\) defined in Corollary 13 with the tuple of index sets \(\left( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \right) \) given by (20) is linear in \(\gamma \); moreover, for every \(\gamma \) in the open interval, none of the components of \(\bar{x}(\gamma )\) satisfies \(| \bar{x}_i(\gamma ) | = \delta \); thus \(\bar{x}(\gamma )\) is a dstat (thus strongly locally optimal), but not necessarily globally optimal solution of the problem (17). Nevertheless, \(\bar{x}(\gamma )\) has a restricted optimality property as asserted in the proof of the following result, based on which it follows that the objective value \(\theta _{\gamma }(x(\gamma ))\) of (17) along this line segment of the dstat path has certain monotonicity properties.
Proposition 14
Let Q be symmetric positive definite. On the interval \({{\mathcal {I}}} \triangleq \left[ \, \underline{\gamma },\overline{\gamma } \, \right] \), the following statements hold:
-
\(\theta _{\gamma }(\bar{x}(\gamma )) \, \triangleq \, q^{\top }\bar{x}(\gamma ) + {\textstyle {\frac{1}{2}}}\, \bar{x}(\gamma )^{\top }Q\bar{x}(\gamma ) + \gamma \, { \sum _{i=1}^n } \ p_i \, \min \left( \, { \frac{| \, \bar{x}_i(\gamma ) \, |}{\delta } }, \, 1 \, \right) \) is nondecreasing in \(\gamma \);
-
\({ \sum _{i=1}^n } \ p_i \, \min \left( \, \displaystyle { \frac{| \, \bar{x}_i(\gamma ) \, |}{\delta } }, \, 1 \, \right) \) is nonincreasing in \(\gamma \);
-
\(q(\bar{x}(\gamma )) \, = q^{\top } \bar{x}(\gamma ) + {\textstyle {\frac{1}{2}}}\, \bar{x}(\gamma )^{\top }Q \bar{x}(\gamma )\) is nondecreasing in \(\gamma \);
Suppose that the path \(\{ \bar{x}(\gamma ) \mid \gamma \in {{\mathcal {I}}} \}\) has the property that \(| \, \bar{x}_i(\gamma ) \, | < \delta \Rightarrow \bar{x}_i(\gamma ) = 0\) for all \(i = 1, \cdots , n\), then the following two additional statements hold:
-
the combined \(\ell _0\)-objective \(q^{\top }\bar{x}(\gamma ) + {\textstyle {\frac{1}{2}}}\, \bar{x}(\gamma )^{\top }Q\bar{x}(\gamma ) + \gamma \, { \sum _{i=1}^n } \ p_i \, | \, \bar{x}_i(\gamma ) \, |_0\) is nondecreasing in \(\gamma \);
-
the \(\ell _0\)-regularizer \({ \sum _{i=1}^n } \ p_i \, | \, \bar{x}_i(\gamma ) \, |_0\) is nonincreasing in \(\gamma \).
Proof
The proof is based on a restricted optimality property of the path \(\{ \bar{x}(\gamma ) \}\) for \(\gamma \in {{\mathcal {I}}}\); namely, for all such \(\gamma \), \(\bar{x}(\gamma )\) is the unique optimal solution of the program:
whose objective on the feasible set, denoted \(S(\gamma _0)\), is equal to the sum of the convex function \(\widehat{\theta }_{\gamma }(x)\) plus a constant:
This stated (restricted) optimality of \(\bar{x}(\gamma )\) follows from the dstat conditions in Corollary 13 for \(\gamma \) in the open interval, and by continuity of the conditions at the two end points of \({{\mathcal {I}}}\); the uniqueness of \(\bar{x}(\gamma )\) is due to the strict convexity of \(\widehat{\theta }_{\gamma }(x)\). Moreover, the restricted optimal objective value \(f_\textrm{rcap}^{\, 0}(\gamma ) \, \triangleq \, {{\textbf {minimum}}}_{x \in S(\gamma _0)} \ \theta _{\gamma }(x)\) is concave, nondecreasing, and continuously differentiable on the interval \(\left( \, \underline{\gamma },\overline{\gamma } \, \right) \). Hence, \(\theta _{\gamma }(\bar{x}(\gamma ))\) is nondecreasing in \(\gamma \); moreover, \(( \, f_\textrm{rcap}^{\, 0} \, )^{\prime }(\gamma ) = \, { \sum _{i=1}^n } \ p_i \, \min \left( \, \displaystyle { \frac{| \, \bar{x}_i(\gamma ) \, |}{\delta } }, \, 1 \, \right) \) is nonincreasing, by the concavity of \(f_\textrm{rcap}^{\, 0}(\gamma )\). To show that \(q(\bar{x}(\gamma )) \triangleq q^{\top }\bar{x}(\gamma ) + {\textstyle {\frac{1}{2}}}\, \bar{x}(\gamma )^{\top }Q\bar{x}(\gamma )\) is nondecreasing in \(\gamma \), it suffices to observe that for \(\gamma > \gamma ^{\, \prime }\) in the interval \({{\mathcal {I}}}\), we have
where the first inequality holds by the optimality of \(\bar{x}(\gamma ^{\, \prime })\) for \(\theta _{\gamma ^{\, \prime }}\) on \(S(\gamma _0)\) and the second inequality holds by the nonincreasing property of capped \(\ell _1\)-term; the above inequality easily implies the desired nondecreasing property of \(q(\bar{x}(\gamma ))\) in \(\gamma \in {{\mathcal {I}}}\), since \(\gamma \) is nonnegative. Finally, under the additional assumption of the path \(\{ \bar{x}(\gamma ) \}\), it follows that \(\min \left( \, \displaystyle { \frac{| \, \bar{x}_i(\gamma ) \, |}{\delta } }, \, 1 \, \right) = | \, \bar{x}_i(\gamma ) \, |_0\); thus the last two statements of the proposition are obvious. \(\square \)
Remark 15
The monotonicity properties in Proposition 14 are reminiscent of the same properties in the penalization theory of nonlinear programs; see e.g. [8, part 2, Lemma 9.2.1]. Nevertheless, there is a major difference; namely, each \(\bar{x}(\gamma )\) is at best a dstat solution of (17), whereas such a classical result in nonlinear programming pertains to a global minimizer of the penalized problem. Nevertheless, the proof of the proposition relies on the global optimality of \(\bar{x}(\gamma )\) of \(\theta _{\gamma }\) on the restricted constraint set \(S(\gamma _0)\) for \(\gamma \) in the interval \({{\mathcal {I}}}\). \(\square \)
If at \(\underline{\gamma }\), none of the components of \(| \, \bar{x}_i(\underline{\gamma }) \, |\) are equal to \(\delta \) (these are Cases 5 through 12), then \(\bar{x}(\underline{\gamma })\) remains a dstat (thus strongy locally optimal) solution of the problem (17) at \(\underline{\gamma }\). If however some component \(| \, \bar{x}_i(\underline{\gamma }) \, | = \delta \), then a restoration of d-stationarity at \(\underline{\gamma }\) is needed.
6.2 Recovery of a dstat solution
As mentioned before, we have on hand a value \(\underline{\gamma }\) and an associated vector \(\bar{x} = \bar{x}(\underline{\gamma })\) that satisfies the following six conditions obtained by taking the limit \(\gamma \downarrow \underline{\gamma }\) in the conditions in Corollary 13:
- (D1):
-
\(( \, q + Q\bar{x} \, )_i + \underline{\gamma } \text{ sign }(\bar{x}_i) \, \displaystyle { \frac{p_i}{\delta } } \, = \, 0\) for all i such that \(0< | \, \bar{x}_i \, | < \delta \);
- (D2):
-
\(| \, ( \, q + Q\bar{x} \, )_i \, | \, \le \, \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } }\) for all i such that \(\bar{x}_i = 0\);
- (D3):
-
\(( \, q + Q\bar{x} \, )_i \, = \, 0\) for all i such that i such that \(\delta < | \, \bar{x}_i \, |\) and \(\ell _i< \bar{x}_i < u_i\);
- (D4):
-
\(( \, q + Q\bar{x} \, )_i \, \ge \, 0\) for all i such that \(\bar{x} = \ell _i\);
- (D5):
-
\(( \, q + Q\bar{x} \, )_i \, \le \, 0\) for all i such that \(\bar{x} = u_i\);
- (D6\(_1\)):
-
\(( \, q + Q\bar{x} \, )_i + \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, = \, 0\) for all i such that \(\bar{x}_i = \delta \) and \(i \in \alpha ^+_<\) (Cases 1\(_{\downarrow }\));
- (D6\(_2\)):
-
\(( \, q + Q\bar{x} \, )_i \, = \, 0\) for all i such that \(\bar{x}_i = \delta \) and \(i \in \alpha ^+_>\) (Cases 2\(_{\downarrow }\));
- (D6\(_3\)):
-
\(( \, q + Q\bar{x} \, )_i - \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, = \, 0\) for all i such that \(\bar{x}_i = -\delta \) and \(i \in \alpha ^-_<\) (Cases 3\(_{\downarrow }\));
- (D6\(_4\)):
-
\(( \, q + Q\bar{x} \, )_i \, = \, 0\) for all i such that \(\bar{x}_i = -\delta \) and \(i \in \alpha ^-_>\) (Cases 4\(_{\downarrow }\)).
A distinguished feature of this vector is that \({{\mathcal {A}}}_=^{\, \delta }(\bar{x}) \triangleq \{ i \mid | \, \bar{x}_i \, | = \delta \} \ne \emptyset \); thus \(\bar{x}\) is not a dstat point of (17) at \(\underline{\gamma }\). Here the goal is to recover such a point by modifying the GHP algorithm so that it can start at \(\bar{x}\), after which the path of dstat solutions can be continued, albeit with a discontinuity at \(\underline{\gamma }\). When Q has the Z-property, the restoration of d-stationarity can be accomplished with strongly polynomial complexity. The idea of the modified algorithm is quite similar to the original version and involves successively solving convex quadratic programs with bounded variables.
The modification of the GHP algorithm to start at \(\bar{x}\) achieves several goals: (a) the almost dstationarity of the vector \(\bar{x}\) is expected to expedite the recovery of dstationarity; (b) running the original GHP Algorithm from scratch could yield a much inferior dstat path in terms of the two criteria defining the overall objective; for one thing, the monotonic decreasing property of the objective values (as \(\gamma \downarrow \)) would be jeopardized at a discontinuous point; (c) in contrast, the modified GHP Algorithm decreases the objective values, as demonstrated in Lemma 18; and (d) embedded in the overall path-tracing procedure, the modified GHP Algorithm plays an important role in the strongly polynomial complexity of the procedure specialized to the nonnegatively constrained capped \(\ell _1\)-regularized problem; see Theorem 21 in Sect. 7. The first two advantages will be demonstrated numerically via experimentations in the last section.
In general, given a pair of complementary index subsets of \(S^{\pm }\) of \(\{ 1, \cdots , n \}\) with the decomposition \(S^{\pm } \, = \, S^{\pm }_< \, \cup \, S^{\pm }_>\), where \(S^{\pm }_<\) and \(S^{\pm }_>\) are disjoint (specifically, \(S^+_< \cap S^+_> = \emptyset \) and \(S^-_< \cap S^-_> = \emptyset \)), consider the sign-restricted bounded-variable quadratic program:
and let \(x^{\textrm{opt}}(S^{\pm })\) be its unique optimal solution. Problem (21) for various index sets is the workhorse of the modified GHP algorithm presented below; the modification allows the initialization at the non-dstat solution \(\bar{x} = \bar{x}(\underline{\gamma })\) mentioned above. We first establish the following result that gives some important properties of the solution \(x^{\textrm{opt}}(S^{\pm })\).
Proposition 16
Let Q be symmetric positive definite. The following three statements (a), (b), and (c) hold for the solution \(x^{\textrm{opt}}(S^{\pm })\) for any pair of subsets \(S^{\, \pm } \subseteq \{ 1, \cdots , n \}\) with the decomposition \(S^{\pm } \, = \, S^{\pm }_< \, \cup \, S^{\pm }_>\) into two disjoint subsets:
-
(a)
\(x^{\textrm{opt}}(S^{\, \pm })\) is the unique feasible vector \(\widehat{x}\) to (21) satisfying
-
\(( \, q + Q \widehat{x} \, )_i + \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^+_< \\ 0 &{} \text{ if } i \in S^+_> \end{array} \right\} \, = \, 0\) if \(i \in S^+\) and \(0< \widehat{x}_i < u_i\);
-
\(( \, q + Q \widehat{x} \, )_i + \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^+_< \\ 0 &{} \text{ if } i \in S^+_> \end{array} \right\} \, \le \, 0\) if \(i \in S^+\) and \(\widehat{x}_i = u_i\);
-
\(( \, q + Q \widehat{x} \, )_i + \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^+_< \\ 0 &{} \text{ if } i \in S^+_> \end{array} \right\} \, \ge \, 0\) if \(i \in S^+\) and \(\widehat{x}_i = 0\);
-
\(( \, q + Q \widehat{x} \, )_i - \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^-_< \\ 0 &{} \text{ if } i \in S^-_> \end{array} \right\} \, = \, 0\) if \(i \in S^-\) and \(\ell _i< \widehat{x}_i < 0\);
-
\(( \, q + Q \widehat{x} \, )_i - \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^-_<\\ 0 &{} \text{ if } i \in S^-_> \end{array} \right\} \, \le \, 0\) if \(i \in S^-\) and \(\widehat{x}_i = 0\);
-
\(( \, q + Q \widehat{x} \, )_i - \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^-_<\\ 0 &{} \text{ if } i \in S^-_> \end{array} \right\} \, \ge \, 0\) if \(i \in S^-\) and \(\widehat{x}_i = \ell _i\);
-
(b)
if the following six index sets associated with \(\widehat{x} = x^{\textrm{opt}}(S^{\pm })\) are empty:
$$\begin{aligned} \begin{array}{l} \left\{ \, i \, \in \, S^+_< \,: \, \widehat{x}_i \, \ge \, \delta \, \right\} , \quad \left\{ \, i \, \in \, S^-_< \,: \, \widehat{x}_i \, \le \, -\delta \, \right\} \\ \left\{ \, i \, \in \, S^+_> \,: \, \widehat{x}_i \, \le \, \delta \, \right\} , \quad \left\{ \, i \, \in \, S^-_> \,: \, \widehat{x}_i \, \ge \, -\delta \, \right\} \\ \left\{ \, i \, \in \, S^+_< \,: \, \widehat{x}_i \, = \, 0 \text{ and } ( \, q + Q\widehat{x} \, )_i - \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, > \, 0 \, \right\} \\ \left\{ \, i \, \in \, S^-_< \,: \, \widehat{x}_i \, = \, 0 \text{ and } ( \, q + Q\widehat{x} \, )_i + \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, < \, 0 \, \right\} , \end{array} \end{aligned}$$(22)then \(x^{\textrm{opt}}(S^{\pm })\) is a dstat point of (17) at \(\underline{\gamma }\);
-
(c)
if Q is additionally a Z-matrix, then \(x^{\textrm{opt}}(S^{\pm })\) is the componentwise least vector of the set:
$$\begin{aligned} Z(S^{\pm }) \, \triangleq \, \left\{ \, \begin{array}{ll} \bullet &{} 0 \le x_{S^+} \le u_{S^+} \text{ and } \ell _{S^-} \le x_{S^-} \le 0 \\ \bullet &{} i \in S^+ \text{ and } x_i< u_i \text{ implies } \left( \, q + Qx \, \right) _i + \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^+_< \\ 0 &{} \text{ if } i \in S^+_> \end{array} \right\} \, \ge \, 0 \\ \bullet &{} i \in S^- \text{ and } x_i< 0 \text{ implies } \left( \, q + Qx \, \right) _i - \underline{\gamma } \, \left\{ \begin{array}{ll} \displaystyle { \frac{p_i}{\delta } } &{} \text{ if } i \in S^-_< \\ 0 &{} \text{ if } i \in S^-_> \end{array} \right\} \, \ge \, 0 \end{array} \right\} ; \end{aligned}$$
Proof
Statement (a) provides the optimality conditions of \(x^{\textrm{opt}}(S^{\pm })\) as a minimizer of the convex program (21). To prove statement (b), first observe that if the six sets in (22) are all empty, then no component \(| \, x^{\textrm{opt}}_i(S^{\pm }) \, |\) is equal to \(\delta \). Next, comparing the conditions (b)–(e) in Proposition 10 with the optimality conditions of (21) and taking into account the emptiness of the sets in (22), we may deduce statement (b) readily. Finally, statement (c) follows from [36, Theorem 3.1]. \(\square \)
The non-dstat vector \(\bar{x} = \bar{x}(\underline{\gamma })\) on hand has the property that the two sets
are both empty (cf. the last two sets in (22)); this follows from the property (D2) of \(\bar{x}\). Using \(\bar{x}\) we define a tuple of index sets \(( S^{\pm }_<, S^{\pm }_> )\) such that three (to be specified below) of the six index sets in (22) associated with the optimal solution \(x^{\textrm{opt}}(S^{\pm })\) are empty. The goal of the algorithm is to adjust these index sets so that all six of them are empty, at which point, a dstat solution of (17) at \(\underline{\gamma }\) is recovered. There are two versions of the algorithm, which we term the nonincreasing versus nondecrasing version, respectively, depending on whether the candidate solution in the algorithm is (componentwise) nonincreasing or nondecreasing; this monotonicity of the iterates is due to the least-element characterization of the optimal solution of (21); see part (c) in Proposition 16.
The nonincreasing version of GHP: Let
In this definition, the left-hand set in line 1 (labelled L1L), the right-hand set in line 2 (labelled L2R), and the set in line 4 (labelled L4) of (22), all associated with \(\bar{x}\), are empty; so is the set in line 3; during the algorithm, the former three sets will remain empty while the latter one may become nonempty.
The nondecreasing version of GHP: Let
In this definition, the right-hand set in line 1 (L1R), the left-hand set in line 2 (L2L), and the set in line 3 (labelled L3) of (22), all associated with \(\bar{x}\), are empty; so is the set in line 4; during the algorithm, the former three sets will remain empty while the latter one may become nonempty.
Upon examining the optimality conditions of the problem (21), it is not difficult to see that for the above pairs \(( S^{\pm }_<, S^{\pm }_> )\), \(\bar{x}\) may not be equal to \(x^{\textrm{opt}}(S^{\pm })\). The following lemma provides sufficient conditions for these two vectors to equal.
Lemma 17
The following two statements hold for the pairs \(( S^{\pm }_<, S^{\pm }_> )\) defined in (23) and (24).
-
If (\({\textbf{A}}_\textrm{ninc}\)) \(\{ \, i \, \mid \, | \, \bar{x}_i \, | \, = \, \delta \, \} \, \subseteq \alpha ^+_> \cup \alpha ^-_<\), then \(\bar{x} = x^{\textrm{opt}}(S^{\pm })\) for the pair \(( S^{\pm }_<, S^{\pm }_> )\) defined in (23).
-
If (\({\textbf{A}}_{\textrm{ndec}}\)) \(\{ \, i \, \mid \, | \, \bar{x}_i \, | \, = \, \delta \, \} \, \subseteq \alpha ^+_< \cup \alpha ^-_>\), then \(\bar{x} = x^{\textrm{opt}}(S^{\pm })\) for the pair \(( S^{\pm }_<, S^{\pm }_> )\) defined in (24).
Proof
It suffices to compare the optimality conditions of the program (21) in Proposition 16 and the conditions (D1)–(D5) and (D6\(_1\))–(D6\(_4\)) satisfied by \(\bar{x}\), and to notice that these two sets of conditions coincide under the stated assumption in the respective assertions. \(\square \)
To understand the assumptions in the above lemma, we recall that in a well-known simplex-type parametric pivoting scheme, which is the basis of the continuous tracing routine, it is common to assume a nondegeneracy assumption that stipulates the uniqueness of the maximizing index. Under this uniqueness assumption, the set \(\{ \, i \, \mid \, | \, \bar{x}_i \, | \, = \, \delta \, \}\) is a singleton, say \(\{ i_{\max } \}\). In this case, one of the two mutually exclusive inclusions (\({\textbf{A}}_\textrm{ninc}\)) and (\({\textbf{A}}_{\textrm{ndec}}\)) in Lemma 17 must be satisfied. Depending on which inclusion is satisfied, we can define the pairs \(( S^{\pm }_<, S^{\pm }_> )\) accordingly so that the lemma is applicable. In general, this lemma relaxes the uniqueness requirement by postulating that all the maximizing indices of \(\underline{\gamma }\) are one of two types: either all in \(\alpha ^+_> \cup \alpha ^-_<\) leading to the nonincreasing definition (23); or all in \(\alpha ^+_< \cup \alpha ^-_>\) leading to the nondecreasing definition (24).
The key argument for us to show that the GHP restoration will obtain a dstat solution of (17) at the discontinuous \(\underline{\gamma }\) in linearly many steps is to inductively prove that L1R, L2L, L3 (resp. L1L, L2R, L4) will remain empty throughout the nondecreasing (resp. nonincreasing) version of GHP. The induction step of this is proved in Lemma 18, whereas the base case, i.e., the initial step, follows from Lemma 17. In particular, in order to satisfy the conditions in Lemma 17 when \(\underline{\gamma }\) corresponds to Cases \(1_{\downarrow }\) and \(4_{\downarrow }\) (resp. Cases \(2_{\downarrow }\) and \(3_{\downarrow }\)), we should apply the nondecreasing (resp. nonincreasing) version of modified GHP Algorithm. For simplicity, the discussion below focuses on the nondecreasing version of the algorithm. All of the analysis on this version hold symmetrically for its nonincreasing counterpart, which involves an analogous update of the pair \(( S^{\pm }_<, S^{\pm }_> )\) in the general iteration. It is also worth noting that the nondecreasing version is more appropriate to obtain a favorable strongly polynomial complexity of the overall path-following scheme for the special case of the parametric capped \(\ell _1\)-problem with nonnegative bounds, see Sect. 7. In stating the algorithm below, we assume that A\(_{\text {ndec}}\) for the vector \(\bar{x}=\bar{x}(\underline{\gamma })\) is in place.

In the lemma below, we show several things under the Z-property of Q: (a) a componentwise monotonicity of the iterates produced by the algorithm; (b) the persistent emptiness of the three sets L1R, L2L, and L3 in (22); and (c) a monotonicity property of the objective function \(\theta _{\gamma }\). In turn, the least-element characterization of the optimal solution \(x^{\textrm{opt}}(S^{\pm })\) of each problem (21) is crucial for the demonstration. The former two properties are central to the proof of linear (in n) number of iterations of Algorithm II\(_{\textrm{ndec}}\); the monotonicity property of \(\theta _{\gamma }\) is interesting in its own right and extends Proposition 14 to a discontinuous point on a dstat path.
Lemma 18
Let Q be a Stieltes matrix. Let \(\left( \, S^{\pm }_<, S^{\pm }_> \, \right) \) and \(\left( \, S^{\pm }_<, S^{\pm }_> \, \right) _{\textrm{new}}\) be two tuples of index sets entering and exiting a general iteration of Algorithm II\(_{\textrm{ndec}}\), respectively; let \(\bar{x} \triangleq x^{\textrm{opt}}(S^{\pm })\) and \(\bar{x}_{\textrm{new}} \triangleq x^{\textrm{opt}}(S^{\pm }_{\textrm{new}})\) be the corresponding optimal solution of (21). If
-
(a\(_{\textrm{ndec}}\)) the sets L1R, L2L, and L3 in (22) associated with \(\bar{x}\) are empty, and
-
(b\(_{\textrm{ndec}}\)) \(\bar{x}_i > \delta \) for all \(i \in S^+_>\) and \(\bar{x}_i > -\delta \) for all \(i \in S^-_<\) (this is implied by (a)),
-
then the following five statements hold:
-
\(\bullet \) \(\bar{x}_{\textrm{new}} \ge \bar{x}\);
-
\(\bullet \) strict inequality in \(\bar{x}_{\textrm{new}} \ge \bar{x}\) holds for a component i for which \(| \, \bar{x}_i \, | = \delta \);
-
\(\bullet \) \(( \bar{x}_{\textrm{new}} )_i > \delta \) for all \(i \in ( S^+_> )_{\textrm{new}}\) and \(( \bar{x}_{\textrm{new}} )_i > -\delta \) for all \(i \in ( S^-_< )_{\textrm{new}}\),
-
\(\bullet \) the sets L1R, L2L, and L3 in (22) associated with \(\bar{x}_{\textrm{new}}\) remain empty; and
-
\(\bullet \) \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}}) \le \theta _{\underline{\gamma }}(\bar{x})\); moreover, strict inequality holds if \(\bar{x}\) has at least one component i for which \(| \, \bar{x}_i \, | = \delta \) (such as when \(\bar{x}\) is the non-dstat point that initializes the algorithm).
Proof
To show \(\bar{x}_{\textrm{new}} \ge \bar{x}\), it suffices to show that \(\bar{x}_{\textrm{new}}\) belongs to the set
because \(\bar{x}\) is the least element of \(Z(S^{\pm })\), by part (c) of Proposition 16. The first bulleted conditions are clear. For the second bulleted condition, let \(i \in S^+\) and \(( \bar{x}_{\textrm{new}} )_i < u_i\). Since \(S^+ = S^+_< \cup S^+_>\), there are the following two cases:
-
\(i \in S^+_<\): there are two subcases: (a) \(i \in ( S^+_< )_{\textrm{new}}\), or (b) \(i \in (S^+_> )_{\textrm{new}}\); in both subcases, since \(( \bar{x}_{\textrm{new}} )_i < u_i\), we have \(\left( \, q + Q\bar{x}_{\textrm{new}} \, \right) _i + \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \ge 0\); thus the second bulleted condition for \(\bar{x}_{\textrm{new}}\) to be in the set \(Z(S^{\pm })\) holds in this case;
-
\(i \in S^+_>\): then \(i \in ( S^+_> )_{\textrm{new}}\); again since \(( \bar{x}_{\textrm{new}} )_i < u_i\), we have \(\left( \, q + Q\bar{x}_{\textrm{new}} \, \right) _i \ge 0\); thus \(\bar{x}_{\textrm{new}}\) satisfies the second bulleted condition in the set \(Z(S^{\pm })\).
This completes the proof of the second bulleted condition for \(\bar{x}_{\textrm{new}}\). For the third bulleted condition, let \(i \in S^-\) and \(( \bar{x}_{\textrm{new}} )_i < 0\). Similarly, there are the following cases:
-
\(i \in S^-_<\): there are two subcases: (a) \(i \in ( S^+_< )_{\textrm{new}}\), or (b) \(i \in (S^-_< )_{\textrm{new}}\); subcase (a) is ruled out because \(( \bar{x}_{\textrm{new}} )_i < 0\); in subcase (b) we have \(\left( \, q + Q\bar{x}_{\textrm{new}} \, \right) _i - \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \ge 0\); thus \(\bar{x}_{\textrm{new}}\) satisfies the third bulleted condition in the set \(Z(S^{\pm })\);
-
\(i \in S^-_>\): there are two subcases: (a) \(i \in ( S^-_< )_{\textrm{new}}\), or (b) \(i \in (S^-_> )_{\textrm{new}}\); in both subcases, since \(( \bar{x}_{\textrm{new}} )_i < 0\), we have \(\left( \, q + Q\bar{x}_{\textrm{new}} \, \right) _i \ge 0\); thus \(\bar{x}_{\textrm{new}}\) satisfies the third bulleted condition in the set \(Z(S^{\pm })\).
In summary, we have verified, case by case, that \(\bar{x}_{\textrm{new}}\) satisfies all the defining conditions of \(Z(S^{\pm })\); the desired nondecreasing conclusion \(\bar{x}_{\textrm{new}} \ge \bar{x}\) follows. To prove the second assertion of the lemma, suppose by contradiction that i is such that \(( \bar{x}_{\textrm{new}} )_i = \bar{x}_i\) and \(| \, \bar{x}_i \, | = \delta \). Consider first \(\bar{x}_i > 0\). Then \(i \in S^+_<\) by assumption (b\(_{\textrm{ndec}}\)). Hence, \(i \in ( S^+_> )_{\textrm{new}}\) and by optimality of \(\bar{x} = x^{\textrm{opt}}(S^{\pm })\) and \(\bar{x}_{\textrm{new}} = x^{\textrm{opt}}(S^{\pm }_{\textrm{new}})\), it follows that
where the first equality holds by the first optimality property of \(\bar{x}\) for such an index \(i \in S^+_<\) (see Proposition 16); the strict inequality holds because \(( \bar{x}_{\textrm{new}} )_i = \bar{x}_i\), \(\bar{x}_{\textrm{new}} \ge \bar{x}\), and Q has nonpositive off-diagonal entries; and the last equality holds by the same optimality property of \(\bar{x}_{\textrm{new}}\) because \(i \in ( S^+_> )_{\textrm{new}}\). This contradiction completes the proof of the case where \(\bar{x}_i = \delta \). The other case is when \(\bar{x}_i = -\delta \). Then \(i \in S^-_>\) by the same assumption (b). Hence, \(i \in ( S^-_< )_{\textrm{new}}\), and for similar reasons,
This contradiction establishes the second assertion of the lemma. The third assertion follows from assumption (b), the fact that \(\bar{x}_{\textrm{new}} \ge \bar{x}\), when a componentwise strict inequality holds, and the definition of \(( S^+_> )_{\textrm{new}}\) and \(( S^-_< )_{\textrm{new}}\). This also shows that the two sets L1R and L2L at \(\bar{x}_{\textrm{new}}\) are empty. Finally, consider the set L3 at \(\bar{x}_{\textrm{new}}\). Suppose there is an index \(i \in ( S^+_< )_{\textrm{new}}\) such that \(( \bar{x}_{\textrm{new}} )_i = 0\) and \(( \, q + Q\bar{x}_{\textrm{new}} \, )_i - \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, > \, 0\). There are two cases: (a) \(i \in S^+_<\) or (b) \(i \in S^-_<\); \(\bar{x}_i = 0\) and \(( \, q + Q\bar{x} \, )_i + \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, < \, 0\). In the former case, we have \(0 = ( \bar{x}_{\textrm{new}} )_i \ge \bar{x}_i\); hence \(\bar{x}_i = 0\). Since \(\bar{x} \le \bar{x}_{\textrm{new}}\) and Q has non-positive off-diagonal entries, we deduce \(( \, q + Q\bar{x} \, )_i - \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, \ge \, ( \, q + Q\bar{x}_{\textrm{new}} \, )_i - \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, > \, 0\). Thus i belongs to the set L3 at \(\bar{x}\), which is a contradiction. A similar contradiction can be obtained in the other case. Therefore, the set L3 at \(\bar{x}_{\textrm{new}}\) is empty.
To prove the last assertion of the lemma, we compare the updated QP at the pair \(\left( \, S^{\pm }_<, S^{\pm }_> \, \right) _{\textrm{new}}\):
versus (21), which is the QP at the pair \(\left( \, S^{\pm }_<, S^{\pm }_> \, \right) \). Notice that \(\bar{x}\) remains feasible to (25). Hence
we relate these objective values to the original ones \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}})\) and \(\theta _{\underline{\gamma }}(\bar{x})\) with the full capped \(\ell _1\)-regularizer as follows. For an arbitrary vector x, we have
where the last inequality holds at equality for \(x={\bar{x}}\). Hence,
For \(i \in ( S^{\, +}_> )_{\textrm{new}}\), we have \(( \bar{x}_{\textrm{new}} )_i > \delta \) by the third assertion and \(\bar{x}_i \ge \delta \) by the definition of \(( S^{\, +}_> )_{\textrm{new}}\). Hence for such an i,
For \(i \in ( S^{\, -}_> )_{\textrm{new}}\), we have \(\bar{x}_i \le ( \bar{x}_{\textrm{new}} )_i \le 0\), yielding \(| \, \bar{x}_i \, | \ge | \, ( \bar{x}_{\textrm{new}} )_i \, |\). Hence for such an i, we have
also. Consequently, \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}}) \le \theta _{\underline{\gamma }}(\bar{x})\) as desired. Lastly, if \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}}) = \theta _{\underline{\gamma }}(\bar{x})\), then \(\bar{x}\) is also an optimal solution of the strictly convex program (25); hence \(\bar{x}_{\textrm{new}} = \bar{x}\) by the uniqueness of the optimal solution of this program. Thus there is no component i for which \(| \, \bar{x}_i \, | = \delta \). This completes the proof of all assertions of the lemma. \(\square \)
Remark I: The nondecreasing property \(\bar{x}_{\textrm{new}} \ge \bar{x}\) of the iterates is the reason for terming Algorithm II\(_{\textrm{ndec}}\); this property also accounts for the nonincreasing property \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}}) \le \theta _{\underline{\gamma }}(\bar{x})\) of the objective function \(\theta _{\underline{\gamma }}\). This conflict is somewhat regrettable and we caution the reader not to be confused by it.
Remark II: Under the parallel assumptions:
-
(a\(_{\textrm{ninc}}\)) the sets L1R, L2R, and L4 in (22) associated with \(\bar{x}\) are empty, and
-
(b\(_{\textrm{ninc}}\)) \(\bar{x}_i < \delta \) for all \(i \in S^+_>\) and \(\bar{x}_i < -\delta \) for all \(i \in S^-_<\),
conclusions similar to those of Lemma 18 hold for the alternative Algorithm II\(_\textrm{ninc}\) whose description we have omitted; in particular, we have \(\bar{x}_{\textrm{new}} \le \bar{x}\); while \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}}) \le \theta _{\underline{\gamma }}(\bar{x})\) continues to hold. \(\square \)
Based on Lemma 18, we can establish the linear-step termination of Algorithm II\(_{\textrm{ndec}}\) for computing a dstat solution of (17) at \(\underline{\gamma }\) under the Z- property of Q.
Theorem 19
Let Q be a Stieltjes matrix. In no more than 3n iterations, Algorithm II\(_{\textrm{ndec}}\) will compute a dstat solution \(\bar{x}^{\, \mathrm end}\) of (17) at \(\underline{\gamma }\). Moreover, \(\theta _{\underline{\gamma }}(\bar{x}^{\, \mathrm end}) < \theta _{\underline{\gamma }}(\bar{x}^{\, \mathrm beg})\) where \(\bar{x}^{\, \mathrm beg}\) (with at least one component i for which \(| \ \bar{x}^{\, \mathrm beg}_i \, | = \delta \)) and \(\bar{x}^{\, \mathrm end}\) (with no component i such that \(| \ \bar{x}^{\, \mathrm end}_i \, | = \delta \)) are the beginning and ending iterates of the algorithm, respectively.
Proof
Associated with a given iterate \(\bar{x}\) during the algorithm, the followings describe all possible transitions of an index i among the tuple of index sets \(( S^{\pm }_<, S^{\pm }_> )\)
-
\(i \in S^-_> \, \rightarrow \, ( S^-_< )_{\textrm{new}}\) if \(\bar{x}_i \ge - \delta \); otherwise i stays in \(S^-_<\);
-
\(i \in S^-_< \, \rightarrow \, ( S^+_< )_{\textrm{new}}\) if \(\bar{x}_i = 0\) and \(( \, q + Q\bar{x} \, )_i + \underline{\gamma } \, \displaystyle { \frac{p_i}{\delta } } \, < \, 0\); otherwise i stays in \(S^-_<\);
-
\(i \in S^+_< \, \rightarrow \, ( S^+_> )_{\textrm{new}}\) if \(\bar{x}_i \ge \delta \); otherwise i stays in \(S^+_<\);
-
\(i \in S^+_>\) stays in same set.
Several observations can be drawn from the above transitions at each iteration: (a) if no transition occurs, then the current \(\bar{x}\) must be a desired dstat solution as claimed; (b) no index will return to the same set once it leaves the set; (c) once an index reaches the set \(S^+_>\), it stays there till the end of the algorithm. Indeed, for (a), it suffices to check that the sets L1L, L2R, and L4 are empty; this holds because there is no transition. Combining all these facts, we may conclude that one of the following two situations must happen: either all indices stay in the same sets without transition to another set during a particular iteration, or there is at least one transition at every iteration. Since there are n variables, and it takes at most 3 (not necessarily consecutive) transitions to reach the absorbing set \(S^+_>\), the 3n-step termination of the algorithm with a desired dstat solution follows readily. Throughout the algorithm, the objective values \(\theta _{\underline{\gamma }}(\bar{x}_{\textrm{new}}) \le \theta _{\underline{\gamma }}(\bar{x})\) with strict inequality holding if \(\bar{x} = \bar{x}^{\, \mathrm beg}\), by Lemma 18. Consequently, we deduce that \(\theta _{\underline{\gamma }}(\bar{x}^{\, \mathrm end}) < \theta _{\underline{\gamma }}(\bar{x}^{\, \mathrm beg})\). \(\square \)
6.3 The overall scheme and its finite termination
We can now summarize the algorithm to trace a dstat (thus strongly locally minimum) solution path of the capped \(\ell _1\)-regularized problem (17). While it is possible to initiate the algorithm with \(\gamma > 0\) sufficiently large so that \(x = 0\) is a global minimum of (17) for all such \(\gamma \), we employ a simplified initialization with an easily identified \(\gamma \) so that \(x = 0\) is guaranteed to be a dstat solution only. Even with the former initialization, the globally minimizing property of the dstat solution is no longer guaranteed as soon as the algorithm moves past the first critical value \(\underline{\gamma }\) of the parameter.

Similar to a well-known simplex-type pivoting method, the parametric scheme terminates in a finite number of iterations provided that there are no degenerate pivots. We state this sufficient condition below in terms of the uniqueness of the maximizing index \(i_{\max }\) of \(\underline{\gamma }\) in the ratio tests at each iteration. Were it not for the discontinuity of the path that necessitated the restoration of directional stationarity, the proof of this result would follow from standard arguments. The additional argument takes care of the latter possibility.
Theorem 20
Let Q be Stieltjes matrix. Suppose the maximizing index \(i_{\max }\) of \(\underline{\gamma }\) in the ratio tests at each iteration of the parametric scheme is unique. Then Algorithm III will trace a (discontinuous) path of dstat solutions of the capped \(\ell _1\)-regularized problem (17) for all values of \(\gamma \ge 0\) in a finite number of iterations.
Proof
Associated with each dstat point \(\bar{x}(\gamma )\) on the path is a tuple \(\tau \triangleq ( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \alpha _{\ell }, \, \alpha _u \, )\) of index sets partitioning \(\{ 1, \cdots , n \}\) and satisfying the conditions in Corollary 13. Between any two discontinuous breakpoints of this path, say \(\gamma _{\, \mathrm L} < \gamma _{\, \mathrm R}\), the \(\theta _{\gamma }\)-values are nonincreasing (from right to left) (Proposition 14), and at the left discontinuous breakpoint \(\gamma _\textrm{L}\), the \(\theta _{\gamma }\)-value strictly decreases (Theorem 19). Now suppose that a left end-point \(\underline{\gamma }\) leads to the vector \(\bar{x}(\underline{\gamma })\) that ceases to be dstat, then after the recovery scheme, there is a restored dstat solution \(\bar{x}^\textrm{new}\) and an alternate tuple of index sets, denoted \(\tau _{\textrm{new}}\), at the same \(\underline{\gamma }\); moreover \(\theta _{\underline{\gamma }}(\bar{x}^\textrm{new}) < \theta _{\underline{\gamma }}(\bar{x}(\underline{\gamma }))\). We claim that this alternate tuple cannot be the same as those tuples encountered before. Otherwise, say \(\tau _{\textrm{new}} = \tau _\textrm{pre}\) corresponding to a value \(\gamma _\textrm{pre} > \underline{\gamma }\). Applying Corollary 13 to this common tuple yields a linear function \(\widehat{x}(\gamma )\) consisting of dstat points for all \(\gamma \in \left[ \, \underline{\gamma }, \gamma _\textrm{pre} \, \right] \) with \(\bar{x}^\textrm{new} = \widehat{x}(\gamma _\textrm{pre}) = \bar{x}(\gamma _\textrm{pre})\). Moreover, the ratio test starting at the right end-point \(\gamma _\textrm{pre}\) will reach the left end-point \(\underline{\gamma }\) along a dstat line segment joining \(\bar{x}(\gamma _\textrm{pre})\) and \(\bar{x}_{\textrm{new}}\), skip** the non-dstat point \(\bar{x}(\underline{\gamma })\). This is a contradiction. Therefore, throughout the parametric steps, including the recovery of directional stationarity at a discontinuous breakpoint, no index tuple of the kind \(\tau \) can repeat. Since there are only finitely many such tuples of index sets, finite termination of the overall scheme follows readily. \(\square \)
A caveat in the successful tracing of the complete dstat path of the parametric capped \(\ell _1\)-problem via Algorithm III is noteworthy. Namely, it assumes the uniqueness of the maximizing index \(i_{\max }\), or more generally, the validity of either A\(_\textrm{ninc}\) or A\(_{\textrm{ndec}}\), when the maximum ratio \(\underline{\gamma }\) yields a discontinuity of the solution path (with the vector \(| \bar{x}(\underline{\gamma }) |\) having a component equal to the critical value \(\delta \)). In general, the uniqueness of such a maximizing index in ratio tests can presumably be ensured by a degeneracy resolution scheme (e.g., a perturbation technique) as done in the finiteness proof of the simplex method and its parametric extension; in essence such a scheme is in the background of Theorem 20. Whether it is possible to modify the algorithm without relying on such a scheme requires further work that will lengthen this already lengthy paper. Nevertheless, this assumption turns out not needed in the special case discussed in the next section.
7 The nonnegatively constrained cappled \(\ell _1\)-problem
In this section, we consider the following special case of the problem (17) where \(\ell = 0\) and Q is a Stieltjes matrix:
In this case, among the index tuple \(\left( \, \alpha _0, \, \alpha _<^{\pm }, \, \alpha _>^{\pm }, \, \alpha _{\ell }, \, \alpha _u \, \right) \) defined by the dstat solution \(\bar{x}(\gamma _0)\) according to (20), for some \(\gamma _0 > 0\), the following two are empty: \(\alpha ^-_< = \alpha ^-_> = \emptyset \) and \(\alpha _{\ell }\) coincides with \(\alpha _0\). Moreover, we have
So the twelve ratios in \(\underline{\gamma }\) reduce to three: Case 1\(_{\downarrow }\), 7\(_{\downarrow }\), and 9\(_{\downarrow }\), respectively,
The following summarizes the one-way transitions of an index among the remaining four index sets \(\left( \, \alpha _0, \alpha _<^+, \alpha _>^+, \alpha _u \, \right) \) during the continuous tracing phase of Algorithm III:
There are two important consequences of the above one-way transitions: (a) if the maximum ratio \(\underline{\gamma }\) is not such that \(\bar{x}_i(\underline{\gamma }) = \delta \) for some i, then once an index reaches the index set \(\alpha _u\), it will stay there; (b) if a discontinuity is reached by the maximum ratio \(\underline{\gamma }\), then any maximizing index \(i_{\max }\) (possibly nonunique) can only come from \(\alpha _<^+\); in other words, the condition A\(_{\textrm{ndec}}\) is satisfied. Thus, if case (b) occurs, then Algorithm II\(_{\textrm{ndec}}\) can be used to restore dstationarity and its linear termination as asserted by Theorem 19 is ensured.
We can now complete a refined analysis of the overall Algorithm III for computing a dstat solution path of the problem (26). For this purpose, we need to examine the change of the index sets during the operation of Algorithm II\(_{\textrm{ndec}}\). Let \(( \alpha _0, \alpha ^+_<, \alpha ^+_>, \alpha _u )_{\textrm{beg}}\) denote the tuple of index sets of the dstat solution that leads to \(\underline{\gamma }\) which triggers the application of the latter Algorithm; this tuple yields the initial pair \(( S^+_<, S^+_> )_{\textrm{beg}}\) defined in (24); specifically,
At a general iteration of Algorithm II\(_{\textrm{ndec}}\) defined by the pair \(( S_<^+,S_>^+ )\), the subproblem (21) is:
whose optimal solution we denote \(x^{\textrm{opt}}\). The update of the pair \(( S^+_<, S^+_> )\) is as follows:
Thus, the set \(S^+_<\) is monotonically decreasing and its complement \(S^+_>\) is monotonically increasing; it follows that at the termination of Algorithm II\(_{\textrm{ndec}}\), a new tuple \(( \alpha _0, \alpha ^+_<, \alpha ^+_>, \alpha _u )_\textrm{end}\) that corresponds to a restored dstat point at \(\underline{\gamma }\) is obtained such that \((\alpha _0 \cup \alpha ^+_<)_\textrm{end}\) is a proper subset of \((\alpha _0 \cup \alpha ^+_<)_{\textrm{beg}}\). We recall that the parametric Algorithm III is initiated with \(\alpha _0 = [ n ]\); since \(\alpha _0 \cup \alpha ^+_<\) is monotonically nonincreasing throughout, it follows that in a linear number (in n) of iterations, the entire Algorithm III will terminate with a complete dstat path. We formally state this conclusion in the theorem below; other than noting that no nondegeneracy assumption is needed, there is no need for a proof.
Theorem 21
Let Q be Stieltjes matrix. Specialized to the problem (26), Algorithm III (without the nondegeneracy assumption) will trace a (discontinuous) path of dstat solutions for all values of \(\gamma \ge 0\) in \(\text{ O }(n)\) iterations. In particular, such a path has \(\text{ O }(n)\) number of breakpoints, some of which are discontinuous points of the path. \(\square \)
The nonnegatively constrained problem (26) is not as special as it seems. In what follows, we show that a dstat solution of the capped \(\ell _1\)-version of the structured problem (16):
must be nonnegative, provided that \(q \le 0\). With dstat solutions as the target (thus applicable to global minimizers too), the result below extends Proposition 8 that pertains to the global minimizers of the \(\ell _0\) and \(\ell _1\) problems (15) and (16) to the capped \(\ell _1\)-problem.
Proposition 22
Let \(\left[ \begin{array}{cc} Q &{} R \\ R^{\top } &{} P \end{array} \right] \) be a Stieltjes matrix and \(q \le 0\). If \(( \bar{x},\bar{y} )\) is a dstat solution of (28), then \(\bar{x} \ge 0\). Conversely, if \(( \bar{x}^{\, \prime },\bar{y}^{\, \prime } )\) is a dstat point of the same objective on the subset \([ 0,u ] \times [ 0,v ]\), then \(( \bar{x}^{\, \prime },\bar{y}^{\, \prime } )\) is a dstat solution of (28).
Proof
For the first assertion, it suffices to note that by Proposition 10, if i is such that \(\bar{x}_i < 0\), then \(( \, q + Q\bar{x} + R\bar{y} \, )_i \ge 0\). With this property, the same proof as that of Proposition 8 can be applied to deduce that \(\bar{x} \ge 0\). Conversely, by examining the conditions in the proposition, it suffices to show that if i is such that \(\bar{x}^{\, \prime }_i = 0\), then \(| \, q + Q\bar{x}^{\, \prime } + R\bar{y}^{\, \prime } \, |_i \le \, \gamma \, \displaystyle { \frac{p_i}{\delta } }\). By the dstationarity of the pair \(( \bar{x}^{\, \prime },\bar{y}^{\, \prime } )\) on \([ 0,u ] \times [ 0,v ]\), we have for such an index i,
Since \({\bar{x}}^{\, \prime }_i = 0\), we readily deduce \(| \, q + Q\bar{x}^{\, \prime } + R\bar{y}^{\, \prime } \, |_i \, = \, -( \, q + Q\bar{x}^{\, \prime } + R\bar{y}^{\, \prime } \, ) _i \, \le \, \gamma \, \displaystyle { \frac{p_i}{\delta } }\), where the equality is because (i) q and R are both nonpositive, and (ii) Q has nonpositive off-diagonal entries. \(\square \)
8 Numerical experiments
In this section, we compare the numerical performance of the three solution paths:
-
The exact \(\ell _0\)-path: this is computed by solving (independently) a sequence of mixed-integer nonlinear programs determined by the weighted sum method, see [3, 16]. Some details of the mixed-integer formulation used to solve (29) (for a fixed value of \(\gamma \)) is given in Sect. 8.2. We use the CPLEX solver to solve each mixed-integer program.
-
The \(\ell _1\)-path: this is computed by a MATLAB R2017b implementation of the parametric procedure in [29] when specialized to (2).
-
The capped \(\ell _1\)-locmin path: this is computed by Algorithm III coded in MATLAB R2017b.
All the numerical experiments are conducted on a Mac OS X personal computer with 2.3 GHz Intel Core i7 and 8 GB RAM. The reported times are in seconds on this computer.
8.1 The \(\ell _1\)- and capped \(\ell _1\)-paths on synthetic problems
To gain some preliminary experience with the relative performance of Algorithm III, we first carry out a set of experiments on some synthetic \(\ell _1\)- and capped \(\ell _1\)-problems with randomly generated data and two dimensions: \(n = 500\) and 5,000. We did not include the \(\ell _0\)-path in this set of experiments because these dimensions are too large for this exact sparsity path (more details below). Since our next goal is to compare all three paths on the GMRF problems whose matrix Q is very sparse, we generate Q in the synthetic problems as a sparse symmetric M-matrix in the following way. With an overall density of 2/n among the off-diagonal elements, which is the same as a tridiagonal matrix, these entries are random numbers uniformly sampled in the interval \([-1,0]\). With these off-diagonal elements generated, we add sufficiently large diagonal terms to keep Q positive definite. Additionally, we randomly generate iid \(q_i\sim \text {Uniform}([-10,10])\) and \(p_i\sim \text {Uniform}([0,1])\) for all \(i \in [n]\). The experiments consist of unconstrained and constrained problems; for the latter, we set \(-\ell _i = u_i = \max \{\frac{11}{10}\delta ,\frac{1}{2}|(-Q^{-1}q)_i|\}\) for all \(i\in [n]\) and test several values of \(\delta \in \{ 10, 1, 10^{-1}, 10^{-4} \}\). The results are summarized in Table 1, where “Bpts.” and “Dis. Bpts.” stand for the total numbers of break points and discontinuous break points (i.e., number of GHP restorations). All the statistics are averaged over 10 runs.
From Table 1 we can observe that when \(\delta =10\), hence relatively large, the behavior of capped \(\ell _1\)-path is similar to the \(\ell _1\)-path in terms of computational time and number of break points; moreover, there is no need for dstat restoration in the computation of the capped \(\ell _1\)-path; thus these two paths are comparable. On the other hand, for the other values of \(\delta \), the computation of the capped \(\ell _1\)-path requires more time, and such paths possess more pieces and discontinuous break points. This is consistent with our previous analysis in Proposition 12, when \(\delta \) is small, e.g., \(\delta =10^{-4}\), the only continuous dstat path is a constant one which is \(\bar{x}(\gamma )=\bar{x}^0\) for all \(\gamma \ge 0\), where \(\bar{x}^0\) is the unique optimal solution at \(\gamma =0\) which is in general totally dense. Thus when we start with \(\bar{x}(\gamma )=0\) for \(\gamma \ge \displaystyle { \max _{i\in [n]} } \, \left| \frac{\delta q_i}{p_i} \right| \) and pivot towards \(\bar{x}^0\), the computed capped \(\ell _1\)-path is discontinuous with more discontinuous points when \(\delta \) is smaller, requiring substantially more computational times (in one case, more than 10 times than the computed \(\ell _1\)-path) depending on the instances with the most time taken still within 2 min on our personal computer (when \(n = 5,000\) and \(\delta = 10^{-4}\)). However, for the unconstrained cases, the capped \(\ell _1\)-paths with small \(\delta \) (e.g., \(10^{-4}\)) always achieve better q(x) values than the \(\ell _1\)-path and the capped \(\ell _1\)-paths with larger \(\delta \) when the solutions from these paths have the same sparsity. For the constrained cases, this phenomenon remains valid when we compare a capped \(\ell _1\)-path with its \(\ell _1\) counterpart under the same \(\delta \). To demonstrate this, in Figs. 2 and 3 we plot q(x) as function of sparsity \(\Vert x\Vert _0\) for the paths considered when they are computed from representative instances in both unconstrained and constrained scenarios.
These figures confirm that the increased computational times of the capped \(\ell _1\)-path result in higher-quality solutions per the computed q(x)-values. In the next section, we show more advantages of capped \(\ell _1\)-path in the context of the GMRF model.
Note that in our experiments the constrained paths generally take less time to trace than the unconstrained paths. This is reasonable in that the two major computing expenses, namely solving linear systems for (19) and discontinuity restorations by GHP algorithms, are significantly reduced in the constrained cases due to the presence of sets \(\alpha _u,\alpha _\ell \) which indicate the elements in the solutions that are equal to upper and lower bounds. Finally, note that the times reported correspond to computing local minimizers for all values of \(\gamma \), and can be interpreted as solving \(\mathcal {O}(n)\) fixed parameter problems for judiciously chosen values of the parameter. The time complexity per fixed-parameter problem is thus between 1 and 10 milliseconds for the case \(n=5000\), which is competitive if not better than existing heuristics in the literature [43]. Moreover, for context, in [32] the authors evaluate the solution at 100 discrete values of \(\gamma \) in a problem with \(n=17,000\) in 3 s; while the times reported here a larger by an order of magnitude, we compute the complete path instead of a discrete approximation, and runtimes of minutes are perfectly acceptable in most situations.
8.2 Results on the GMRF problem
We consider a two-dimensional graphical model as depicted in Fig. 1: given a grid size \(p\in \mathbb {Z}_+\) (with \(n=p^2\)), a “spike size" parameter \(s \in \mathbb {Z}_+\), a “spike number" parameter \(h\in \mathbb {Z}_+\) and a noise parameter \(\sigma \), we generate the true values of the stochastic process \(X\in \mathbb {R}^{p\times p}\) as follows. Construct the precision matrix \(\Theta \in \mathbb {R}^{(s\times s)\times (s\times s)}\) such that \(\Theta _{ij,ij}=4\) for all \(i,j\in [s]\), \(\Theta _{ij,(i+1)j}=\Theta _{(i+1)j,ij}=-1\) for \(i\in [s-1]\) and \(j\in [s]\), \(\Theta _{ij,i(j+1)}=\Theta _{i(j+1),ij}=-1\) for \(i\in [s]\) and \(j\in [s-1]\), and \(\Theta _{ij,k\ell }=0\) otherwise. We use the notation \(X_{[i,j],[k,\ell ]}\) to denote the submatrix of X from rows i to j (inclusive) and columns k to \(\ell \) (inclusive). Initially, X is fully sparse, this is, \(X=0\). Then we iteratively repeat h times the following process.
-
Randomly select indexes \(i\in [p+1-s]\) and \(j\in [p+1-s]\), corresponding to the initial row and column of a spike.
-
Sample a Gaussian shock \(w\in \mathbb {R}^{s\times s}\) such that \(w\sim \mathcal {N}(0,\Theta ^{-1})\).
-
Add shock w to X, this is, \(X_{[i,i+s],[j,j+s]}=X_{[i,i+s],[j,j+s]}+w\).
The resulting X is thus mostly sparse, but each non-zero \(s\times s\) spike is according to a two-dimensional GMRF. Finally, we sample noisy observations from X, given by \(y_{ij}=X_{ij}+\varepsilon _{ij}\), where \(\varepsilon _{ij} \sim \mathcal {N}(0,\sigma ^2)\) are independent and identically distributed. The values \(y_{ij}\) are the inputs of the \(\ell _0\)-optimization problem of interest, given by
The mixed-integer formulation for solving the above problem for a given value of \(\gamma \) is based on the following convexification from [5]. The resulting relaxation is stronger than the perspective relaxation, commonly used in mixed-integer programming [10, 43].
Proposition 23
Let set
Then the closure of the convex hull of X is given by
An application of Proposition 23 to problem (29) yields the mixed-integer second-order conic formulation:
We compare the three paths on problems with \(p = 10\) (thus 100 variables in total, in this setting we use \(h=s=3\)), where the \(\ell _1\)- and capped \(\ell _1\)-paths are obtained from problem (29) with the \(\ell _0\)-regularizer substituted by the \(\ell _1\)- and capped \(\ell _1\)-regularizer. In addition, the \(\ell _1\)- and capped \(\ell _1\)-paths are also tested with \(p = 100\) (thus 10,000 variables in total, in this setting we use \(h=s=10\)). The numerical tracing of the \(\ell _0\)-path is handicapped by the challenge of solving nonlinear mixed-integer programs by the CPLEX solver; on problems with 100 variables, the computation already takes 800 s. Thus, the computation of the exact \(\ell _0\)-path on the larger-sized problems is expected to be prohibitively impractical and thus omitted. The experiments aim to evaluate the different methods both from an optimization standpoint (computational time and objective values) and a statistical standpoint (how well can the methods recover the underlying “true" signal?). Moreover, we are most interested in: (i) confirming the improved quality of the capped \(\ell _1\)-dstat path as a surrogate for the \(\ell _0\)-path from an optimization point of view, and (ii) showing the advantage of the capped \(\ell _1\)-path over the \(\ell _1\)-path when applied to hyper-parameter selection for the GMRF maximum a posteriori inference, namely problem (29) with the appropriate regularizer. Through these experiments, we can confirm the effectiveness of the capped \(\ell _1\)-dstat path as a practical compromise between the \(\ell _0\)-path and the \(\ell _1\)-path, remedying the slow computational speed of the former for large-scale problems and improving the solution quality over the latter without sacrificing solution speed.
Optimization standpoint. Each plot in Fig. 4 shows, for each x corresponding to a breakpoint in the solution path of a given method, the value of the quadratic term q(x) as a function of the sparsity \(\Vert x\Vert _0\), where each plot corresponds to a single instance. In the small instances, the solution path of the exact \(\ell _0\)-problem always produces the best solutions, as expected. Moreover, the solution path of the \(\ell _1\)-approximation is consistently the worst, and the solution paths of the capped \(\ell _1\)-problems gradually increase in quality as \(\delta \) decreases (despite the increasing non-convexity of the optimization problem). In particular, for \(\delta \in \{10^{-4},10^{-3}\}\), the capped \(\ell _1\)-paths are almost indistinguishable from the \(\ell _0\)-path, showing that Algorithm III is effective at consistently finding high-quality local (if not global) minimizers of the associated optimization problems. In the large instances, while it is not possible to compare with the exact \(\ell _0\)-path, we still observe that the path of the capped \(\ell _1\)-method delivers substantially better solutions than the \(\ell _1\)-path. In both small and large instances, the improvements achieved by the capped \(\ell _1\)-formulation over the \(\ell _1\)-formulation are particularly pronounced in low signal-to-noise regimes.
Table 2 presents the computational times (in seconds) required to compute the solution paths. We only report the capped \(\ell _1\)-results for \(\delta =10^{-4}\) (averaged over 5 instances) since this is a preferred choice according to our previous experience. It is worth mentioning that similar to what is reported in Table 1, capped \(\ell _1\)-paths under \(\delta =10^{-4}\) generally require more time to compute than the capped \(\ell _1\)-paths under larger \(\delta \) values, e.g., \(\delta =10\). All methods require more time as the noise (\(\sigma \)) increases: for the \(\ell _1\)- and capped \(\ell _1\)-problems, computational times increase at most by a factor of three, whereas for the \(\ell _0\)-problem, computational times increase by two orders of magnitude.
We observe that in small instances, the exact \(\ell _0\)-path can be computed in approximately one minute in high signal-to-noise regimes, and under one hour in low signal-to-noise regimes. Note that, for \(n=100\), computing the solution path requires solving approximately 160 nonlinear mixed-integer optimization problems. Thus, while each problem is solved relatively fast (from under one second to 15 s, depending on the noise), the lack of an integrated parametric scheme results in large computational times. For reference, computing the exact solution path in instances with \(n=225,\sigma =1\) requires more than one day, and thus handling instances with \(n=10,000\) exactly seems beyond the capabilities of current solvers.
Computing the local capped \(\ell _1\)-path is up to 10 times more expensive than the \(\ell _1\)-path, but four orders-of-magnitude faster than the \(\ell _0\)-method in instances with \(n=100\). Indeed, solution paths are computed in under one second for \(n=100\), and in under 10 min for \(n=10,000\); these are acceptable times in an experimental matlab implementation. Thus, since the capped \(\ell _1\)-method also delivers near-optimal solutions, we conclude that it is a much more practical choice than the \(\ell _0\)-path in large instances without compromising quality. The pure \(\ell _1\)-path can be computed very quickly, in under one minute even in large instances although, as noted previously, the fast computation comes at the expense of lesser solution quality.
Statistical standpoint. In inference problems with the GMRF model, finding (near-) optimal solutions of (29) is of secondary importance, and the main goal is to recover the underlying signal X. In particular, letting \(x^*(\gamma )\) denote a computed solution of the three paths for a given value of \(\gamma \), we evaluate how good \(x^*(\gamma )\) estimates X using two metrics:
Each plot in Fig. 5 shows, for each computed solution corresponding to a breakpoint in the solution path of a given method, the value of the signal recovery as a function of the support recovery. Again, each plot corresponds to a particular random instance. Note that by computing the solution path, each method produces multiple estimates of the true signal X, one for each value of the parameter \(\gamma \) (in particular, at the breakpoints of the respective paths). Moreover, while some such solutions may yield poor estimates of X (corresponding to situations where \(\gamma \) is mispecified), others may perform well with respect to the above two metrics; in such cases, a procedure like cross-validation on the training data may be able to identify the best candidates. In addition to these plots, we also report the best support and signal recovery results achieved by different paths (all averaged over 5 instances), see the columns labelled “Supp. Rec.” and “Sig. Rec.” in Table 3.
From the plots in Fig. 5, we can see that the \(\ell _1\)- and capped \(\ell _1\)-solution curves are similar from a statistical standpoint in the small noise regimes: both methods are able to produce solutions that perform well in terms of signal and support recovery, that could be presumably identified via cross-validation. However, as \(\sigma \) increases, the solutions produced by each method perform differently from a statistical point of view.
-
For the capped \(\ell _1\)-method, if the parameter \(\gamma \) is chosen so that the support of the solutions coincides approximately with the true support, then the resulting estimators perform well in terms of signal recovery as well. As \(\gamma \) differs from this critical value, the resulting estimators are worse in terms of both signal and support recovery.
-
For the pure \(\ell _1\)-method, if the parameter \(\gamma \) is chosen so that the support of the solutions coincides approximately with the true support, then the resulting estimators are poor in terms of signal recovery. Similarly, values of \(\gamma \) that result in good signal recovery often correspond to solutions with poor support recovery. Thus, it is unclear which value of \(\gamma \) results in the better performance.
The aforementioned results suggest that the path of local minimizers of the capped \(\ell _1\)-formulation is more attractive from a statistical perspective. Indeed, cross-validation may be able to identify solutions that simultaneously achieve good signal and support recovery, whereas the pure \(\ell _1\)-solution path does not produce any such solutions. Note that such nice statistical property of the capped \(\ell _1\)-paths is also possessed by the \(\ell _0\)-paths, see the plots in Fig. (5a, c, e) which provide additional supporting evidence in favor of capped \(\ell _1\)-path. Finally, we also observe that in general there are several solutions obtained from the capped \(\ell _1\)-path that dominate all \(\ell _1\)-solutions in terms of signal recovery, suggesting that the capped \(\ell _1\)-method is preferable when signal recovery is the main criterion.
Additional comments. Referred to as modified GHP initializations, our specific initialization strategy for GHP restorations via the initial index pairs (23) and (24) is crucial both theoretically and empirically, by taking advantage of the “almost” dstationarity of a candidate solution. From the theoretical perspective, this initialization provides us with key conditions so that the conclusions in the fourth bullet of Lemma 18 and Proposition 22 hold. On the other hand, the specialized initialization is also crucial for us to maintain all the nice properties of the computed capped \(\ell _1\)-dstat path which we have mentioned earlier. As a comparison, we test Algorithm III with the following initializations in the dstat restoration, which we call naïve GHP initializations:
Note that by [29] these initializations also restore dstat solutions of the capped \(\ell _1\)-problem at a discontinuous break point. To demonstrate how the naïve initializations could potentially sabotage the judicious selection of the parameter \(\gamma \) in the presence of a secondary objective, we summarize the behavior of the capped \(\ell _1\)-dstat paths obtained by different GHP initialization strategies, when being tested on the GMRF problem with \(n=100,\sigma =0.4\), in Fig. 6. More specifically, Fig. 6a contains the curves of support recovery and sparsity as functions of \(\text {log}(\gamma )\) (details see the legend therein), whereas Fig. 6b presents the Pareto curves of signal versus support recovery. As shown in Fig. 6a, the path with the modified GHP initializations attains a dstat point \(x^*\) achieving the minimum support recovery of 5 at around \(\gamma _*\approx 10^{-4}\). In contrast, when \(\gamma \) is in the range of \(10^{-3.5}\) and \(10^{-4.5}\), the results of the modified GHP initializations are significantly better than those of the naïve GHP whose best support recovery is in the mid-50’s, which is 10 times more than the best result from the modified GHP. The superiority of the modified GHP occurs as early as the first few dstat restorations. More precisely, when \(\gamma \) is near the right end of the curves in Fig. 6b, the solution of the naïve GHP path changes from being totally sparse to relatively dense; thus the overall sparsity of this path has been elevated to a relatively high level even in the early phase. The consequence of this is that at \(\gamma _*\) the naïve GHP path assigns another dstat solution that is far worse than \(x^*\) in both measures considered in Fig. 6b. This explains why the resulting path from the naïve GHP initialization does not possess the nice statistical properties as compared to the modified GHP initialization, as shown in Fig. 6b.
Conclusion. This paper has studied and compared several solution paths of sparse quadratic minimization problems with Stieltjes matrices. Old properties of two such paths (\(\ell _0\) and \(\ell _1\)) are reviewed and supplemented with new results along with the previously un-examined capped \(\ell _1\)-path. Numerical experiments on some synthetic problems and the applied GMRF model demonstrate that the latter discontinuous path yields superior practical performance on realistically sized problems that are too large for the \(\ell _0\)-path and for which the \(\ell _1\)-path is much less desirable. The numerical computation of the entire capped \(\ell _1\)-path is accomplished by a rigorous algorithm that involves continuous tracing and dstat recovery. Resonating the previous study [29], the present work has again demonstrated the key role the Z-structure of the quadratic form plays in the favorable computational complexity of the developed parametric algorithm.
References
Ahn, M., Pang, J.S., **n, J.: Difference-of-convex learning: directional stationarity, optimality, and sparsity. SIAM J. Optim. 27(3), 1637–1665 (2017)
Akaike, H.: Information theory and an extension of the maximum likelihood principle. Proceeding of IEEE International Symposium on Information Theory 267–281 (1973)
Aneja, Y.P., Nair, K.P.K.: Bicriteria transportation problem. Manag. Sci. 25, 73–78 (1979)
Atamtürk, A., Gómez, A.: Strong formulations for quadratic optimzation with M-matrices and indicator variables. Math. Program. Series B 170, 141–176 (2018)
Atamtürk, A., Gómez, A.: Rank-one convexifications for sparse regression. ar**v:1901.10334 (2019)
Atamtürk, A., Gómez, A., Han, S.: Sparse and smooth signal estimation: convexification of L0 formulations. J. Mach. Learn. Res. 22, 1–43 (2021)
Bai, L., Mitchell, J.E., Pang, J.S.: On convex quadratic programs with linear complementarity constraints. Comput. Optim. Appl. 54, 517–544 (2013)
Bazaraa, M.S., Sherali, H.D., Shetty, C.M.: Nonlinear Programming: Theory and Algorithms. Wiley and Sons, Hoboken (1993)
Berman, A., Plemmons, R.J.: Nonnegative Matrices in the Mathematical Sciences. Classics in Applied Mathematics, vol. 9. SIAM Publications, Philadelphia (1994)
Bertsimas, D., Pauphilet, J., Van Parys, B.: Sparse regression: scalable algorithms and empirical performance. Stat. Sci. 35, 555–578 (2020)
Besag, J.: Spatial interaction and the statistical analysis of lattice systems. J. Royal Stat. Soc.: Series B (Methodol.) 36, 192–225 (1974)
Besag, J., York, J., Mollié, A.: Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 43, 1–20 (1991)
Besag, J., Kooperberg, C.: On conditional and intrinsic autoregressions. Biometrika 82, 33–746 (1995)
Best, M.J.: An algorithm for the solution of the parametric quadratic programming problem. In: Fischer, H., Riedml̈ler, B., Schäffler, S. (eds). Applied Mathematics and Parallel Computing. pp. 57–76 (Physica-Verlag 1996)
Boland, N.L., Charkhgard, H., Savelsbergh, M.W.P.: A criterion space search algorithm for biobjective mixed-integer programming: the triangle search method. INFORMS J. Comput. 27, 597–618 (2015)
Boland, N.L., Charkhgard, H., Savelsbergh, M.W.P.: Criterion space search algorithms for biobjective integer programming: the balanced box Method. INFORMS J. Comput. 27, 735–754 (2015)
Chen, X., Ge, D., Wang, Z., Ye, Y.: Complexity of unconstrained \( L_2-L_p \) minimization. Math. Program. 143(1), 371–383 (2014)
Cottle, R.W., Pang, J.S., Stone, R.E.: The Linear Complementarity Problem. Classics in Applied Mathematics, Volume 60. SIAM, Philadelphia (2009). [Originally published by Academic Press, Boston (1992).]
Cozad, A., Sahinidis, N., Miller, D.: Learning surrogate models for simulation-based optimization. AIChE J. 60, 2211–2227 (2014)
Cui, Y., Chang, T.H., Hong, M., Pang, J.S.: A study of piecewise linear-quadratic programs. J. Optim. Theory Appl. 186, 523–553 (2020)
Cui, Y., Pang, J.S.: Modern Nonconvex Nondifferentiable Optimization. SIAM Publications, forthcoming (November 2021)
Dong, H., Chen, K., Linderoth, J.: Regularization vs. relaxation: a conic optimization perspective of statistical variable selection. ar**v:1510.06083 (2015)
Efron, B., Hastie, T., Johnstone, I., Tibshirani, R.J.: Least angle regression. Ann. Stat. 32(2), 407–499 (2004)
Fattahi, S., Gómez, A.: Scalable inference of sparsely-changing Markov random fields with strong statistical guarantees. ar**v:2102.03585v1 (2021)
Fan, J., Li, R.: Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96(456), 1348–1360 (2001)
Fan, J., Xue, L., Zou, H.: Strong oracle optimality of folded concave penalized estimation. Ann. Stat. 42(3), 819–849 (2014)
Feng, M., Mitchell, J.E., Pang, J.S., Wächter, A., Shen, X.: Complementarity formulations of \(\ell _0\)-norm optimization problems. Pac. J. Optim. 14(2), 273–305 (2018)
Geman, S., Graffigne, C.: Markov random field image models and their applications to computer vision. Proc. Int. Congr. Math. 1, 1496–1517 (1986)
Gomez, A., He, Z., Pang, J.S.: Linear-step solvability of some folded concave and singly-parametric sparse optimization problems. Math. Program. Series B (2022). https://doi.org/10.1007/s10107-021-01766-4
Hager, W.W.: Updating the inverse of a matrix. SIAM Rev. 31(2), 221–239 (1989)
Hastie, T., Tibshirani, R.J., Wainwright, M.: Statistical Learning with Sparsity: the Lasso and Generalizations. CRC Press. Monographs on Statistics and Applied Probability 143 (2015)
Hazimeh, H., Mazumder, R.: Fast best subset selection: coordinate descent and local combinatorial optimization algorithms. Oper. Res. 68(5), 1517–1537 (2020)
Hochbaum, D.: An efficient algorithm for image segmentation, Markov random fields and related problems. J. ACM (JACM) 48, 686–701 (2001)
Le Thi, H.A., Pham Dinh, T., Vo, X.T.: DC approximation approaches for sparse optimization. Eur. J. Oper. Res. 244(1), 26–46 (2015)
Mairal, J., Yu, B.: Complexity analysis of the Lasso regularization path. Proceedings of the 29th International Conference on Machine Learning Edinburgh Scotland U.K. June 26–July 1, (2012) http://icml.cc/2012/papers/202.pdf
Pang, J.S.: On a class of least-element linear complementarity problems. Math. Program. 16, 111–126 (1979)
Saquib, S.S., Bouman, C., Sauer, K.: ML parameter estimation for Markov random fields with applications to Bayesian tomography. IEEE Trans. Image Process. 7, 1029–1044 (1998)
Soussen, C., Idier, J., Duan, J., Brie, D.: Homotopy based algorithms for \(\ell _0\)-regularized least-squares. IEEE Trans. Signal Process. 63(13), 3301–3316 (2015)
Schwarz, G.: Estimating the dimension of a model. Ann. Stat. 6(2), 461–464 (1978)
Tibshirani, R.J.: The lasso problem and uniqueness. Electron. J. Stat. 7, 1456–1490 (2013)
Wei, L., Gómez, A., Küçükyavuz, S.: On the convexification of constrained quadratic optimization problems with indicator variables. ar**v preprint ar**v:2002.09142 (2020)
Wu, H., Noé, F.: Maximum a posteriori estimation for Markov chains based on Gaussian Markov random fields. Procedia Comput. Sci. 1, 1665–1673 (2010)
**e, W., Deng, X.: Scalable algorithms for the sparse ridge regression. SIAM J. Optim. 30(4), 3359–3386 (2020)
Yukawa, M., Amari, S.I.: \(\ell _p\)-regularized least squares (\(0 < p < 1\)) and critical path. IEEE Trans. Inf. Theory 62(1), 488–502 (2015)
Zhang, C.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38(2), 894–942 (2010)
Acknowledgements
The authors are grateful to two referees for their constructive comments that have helped to clarify and improve the presentation of the paper.
Funding
Open access funding provided by SCELC, Statewide California Electronic Library Consortium
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work of Gomez was based on research support by the National Science Foundation under grant CIF-2006762. The work of Pang was based on research supported by the U.S. Air Force Office of Scientific Research under grant FA9550-18-1-0382.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
He, Z., Han, S., Gómez, A. et al. Comparing solution paths of sparse quadratic minimization with a Stieltjes matrix. Math. Program. 204, 517–566 (2024). https://doi.org/10.1007/s10107-023-01966-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-023-01966-0