Effect of unsteady flow dynamics on the impact of monodisperse and bidisperse granular flow

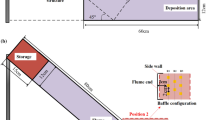
Abstract

Protective barriers provide crucial resistance against the impact of granular flows. However, the adoption of characterized flow depth and velocity values in impact force estimation remains unclear and requires further investigation, especially with consideration of unsteady flow dynamics. Previous practices suggest that the bulk flow velocity with the assumption of uniform distribution should be used in impact force estimation, while we observe the lower part of the flow consistently exhibits lower velocities than the upper part, because granular shear behavior is enhanced within the boundary layer, which strongly affects the flow velocity. As a result, using a bulk velocity in debris impact force estimation may result in that a larger dynamic pressure coefficient must be used in hydrodynamic model. We made a quantitative assessment. For rapid granular flows, the use of a bulk velocity to calculate the dynamic force component could result in underestimation of approximately 10–30%. Therefore, based on the numerical results, it is suggested that the average velocity of the upper 50% of the flow body can be adopted in impact force estimation. If the front flow depth is used to calculate the dynamic impact force component, the results may be approximately 50% lower than the true value, which indicates that the dynamic force on a barrier is likely not controlled by the granular flow front and that a maximum flow depth may be more appropriate if a hydrodynamic model is adopted. In addition, it seems that the strategy we proposed can be used for both of monodisperse and bidisperse granular flow when boulder impact is excluded.

Appendix. DEM contact model and input parameters

The DEM is a promising tool because it directly deals with each individual particle (Bi et al. 2018; Cagnoli and Piersanti 2015; Goodwin and Choi 2021; Ng et al. 2019; Wang et al. 2019). In this study, a non-linear contact model, named Hertz-Mindlin (no slip) model, is adopted to calculate the particle contact force including both the normal and tangential component. And a mature software EDEM is used to run simulations (DEM solutions 2020).

The normal force (${F}_{n}$) between two contact objects is given as

$$\begin{array}{c}{F}_{n}={E}^{*}\sqrt{{R}^{*}}{\lambda }_{n}^\frac{3}{2}\end{array}$$

(8)

where ${E}^{*}$, ${R}^{*}$, and ${\lambda }_{n}$ are respectively the equivalent Young’s modulus, equivalent radius, and normal contact overlap. ${E}^{*}$ and ${R}^{*}$ are formulated as follows:

$$\begin{array}{c}\frac{1}{{E}^{*}}=\frac{\left(1-{\nu }_{i}^{2}\right)}{{E}_{i}}+\frac{\left(1-{\nu }_{j}^{2}\right)}{{E}_{j}}\end{array}$$

(9)

$$\begin{array}{c}\frac{1}{{R}^{*}}=\frac{1}{{R}_{i}}+\frac{1}{{R}_{j}}\end{array}$$

(10)

where subscripts i and j, respectively, represent two contact objects (e.g., particle–particle or particle–wall), and $E$, $\nu$, and $R$ are the Young’s modulus, Poisson’s ratio, and radius, respectively.

The tangential force (${F}_{t}$) is calculated as

$$\begin{array}{c}{F}_{t}=-{S}_{t}{\lambda }_{t}\end{array}$$

(11)

where ${S}_{t}$ is the tangential stiffness, ${\lambda }_{t}$ denotes the tangential overlap, and ${S}_{t}$ is a function of the equivalent shear modulus (${G}^{*}$):

$$\begin{array}{c}{S}_{t}=8{G}^{*}\sqrt{{R}^{*}{\lambda }_{n}}\end{array}$$

(12)

$$\begin{array}{c}\frac{1}{{G}^{*}}=\frac{\left(1-{\nu }_{i}^{2}\right)}{{G}_{i}}+\frac{\left(1-{\nu }_{j}^{2}\right)}{{G}_{j}}\end{array}$$

(13)

A dam** component is respectively applied to the normal and tangential directions:

$$\begin{array}{c}{F}_{n}^{d}=-\sqrt{\frac{10}{3}} \cdot \gamma \cdot \sqrt{{S}_{n}{m}^{*}}{v}_{n}^{\underset{rel}{\to }}\end{array}$$

(14)

$$\begin{array}{c}{F}_{t}^{d}=-\sqrt{\frac{10}{3}} \cdot \gamma \cdot \sqrt{{S}_{t}{m}^{*}}{v}_{t}^{\underset{rel}{\to }}\end{array}$$

(15)

where ${m}^{*}$ is the equivalent mass given in Eq. (16), $\gamma$ and ${S}_{n}$ are given in Eqs. (17) and (18), respectively, and ${v}_{n}^{\mathrm{rel}}$ and ${v}_{t}^{\mathrm{rel}}$ are the normal and tangential components of the relative velocity, respectively.

$$\begin{array}{c}{m}^{*}={\left(\frac{1}{{m}_{i}}+\frac{1}{{m}_{j}}\right)}^{-1}\end{array}$$

(16)

$$\begin{array}{c}\gamma =\frac{-\mathit{ln}\;e}{\sqrt{{ln}^{2}e+{\pi }^{2}}}\end{array}$$

(17)

$$\begin{array}{c}{S}_{n}=2\cdot {E}^{*}\sqrt{{R}^{*}{\delta }_{n}}\end{array}$$

(18)

where ${m}_{i}$ and ${m}_{j}$ are the mass of the interacting elements and e is the restitution coefficient.

The magnitude of ${F}_{t}$ is limited by ${\mu }_{s}{F}_{n}$, where ${\mu }_{s}$ is the Coulomb’s friction coefficient of the particles. A torque is also applied to the contact surfaces to account for the effect of rolling friction:

$$\begin{array}{c}{M}_{r}={-\mu }_{r}{F}_{n}{d}_{i}{\widehat{\omega }}_{i}\end{array}$$

(19)

where ${\mu }_{r}$ is the coefficient of rolling friction, ${d}_{i}$ is the distance between the contact point and center of mass, and ${\widehat{\omega }}_{i}$ is the unit angular velocity vector of particle i at the contact point.

Detailed calibration process could be accessed in Supplementary Material S1. And DEM input parameters are presented in Table 4.