Motion and force control with a linear force error filter for the manipulator of an underwater vehicle-manipulator system

Abstract

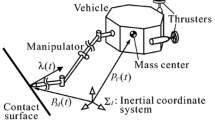
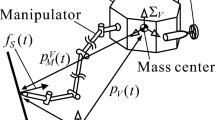
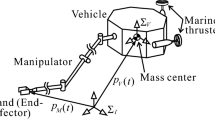
This paper deals with a motion and force control scheme for underwater robots, each of which is equipped with a manipulator. Several motion and force controllers for this type of underwater robot have been developed. Most of them were designed under the assumption that the control capability of each robot body is the same as that of each manipulator. However, it has been pointed out in the literature that for a real underwater robot, its robot body control is more challenging than its manipulator control, because the robot body has much larger inertia, and many more inaccurate position sensors and actuators than the manipulator. Therefore, even if an advanced control law with good performance is implemented in the vehicle controller of each control system, its original control performance may not be achieved. In this paper, we develop a motion and force controller for the manipulator under the condition that the robot body is independently controlled by a motion controller with poor performance. Its features are (1) to be designed in consideration of the dynamics of the robot body including its actuators (i.e., marine thrusters), (2) to ensure the stability properties in the presence of bounded disturbances, and (3) to include a linear force error filter, which can facilitate the stability analysis in comparison with existing nonlinear force error filters. Furthermore, the theoretical results were supported by those obtained in numerical simulations.

Appendices

Appendix 1: Derivation of (24)

Differentiating (3) with respect to time, and then using (5), we have

$$\begin{aligned} n_{C}(t)^{\mathrm {T}}\dot{p}_M(t)=0. \end{aligned}$$

(70)

Applying the relation $R(\phi _{V})R(\phi _{V})^{\mathrm {T}} =I_{3}$ to (70), then multiplying both its sides by $1/\Vert n_{C}(t)\Vert$, and then using the fourth equation of (21), we obtain

$$\begin{aligned} a_{CM}(t)^{\mathrm {T}} R(\phi _{V})^{\mathrm {T}}\dot{p}_{M}(t)=0. \end{aligned}$$

(71)

It should be noted that $n_{C}(t)$ is a nonzero vector. Substituting the equation

$$\begin{aligned} \dot{p}_{M}(t)=\dot{p}_{V}(t)+S(\omega _{V})R(\phi _{V})p_{M}^{V}(t)+R(\phi _{V}) \dot{p}_{M}^{V}(t), \end{aligned}$$

(72)

into (71), then using the relations $R(\phi _{V})^{\mathrm {T}} R(\phi _{V})=I_{3}$ and $R(\phi _{V})S(\bar{a})\bar{b}=S(R(\phi _{V})\bar{a})R(\phi _{V})\bar{b}$ for any vectors $\bar{a},\;\bar{b}\in R^{3}$, and then utilizing the first equation of (25), we can derive (24). It should be noted that (72) is an original form of (11).

Appendix 2: Derivation of third inequality of (26)

Differentiating the fourth equation of (21) with respect to time, and then using the sixth and seventh inequalities of (22), we can write the norm of $\dot{a}_{CM}(t)$ as

$$\begin{aligned} \Vert \dot{a}_{CM}(t)\Vert \le 2c_{C1} c_{R1}\Vert \dot{n}_{C}(t)\Vert +c_{R2}\Vert \dot{u}(t)\Vert , \end{aligned}$$

(73)

where $c_{C1}=\max \{ 1/ \Vert n_{C}(t)\Vert \}$. It should be noted that $c_{C1}$ is a bounded positive constant, because $n_{C}(t)$ is a nonzero vector. Utilizing (4) and (5), we obtain the inequality $\Vert \dot{n}_{C}(t)\Vert \le c_{C2}\Vert \dot{p}_{M}(t)\Vert$, where $c_{C2}$ is a positive constant. Applying this inequality to (73), then substituting (11) into it, and then using the first, second and sixth inequalities of (22), and the inequalities $\Vert \dot{x}_{V}(t)\Vert \le \Vert \dot{u}(t)\Vert$ and $\Vert \dot{q}(t)\Vert \le \Vert \dot{u}(t)\Vert$, we can derive the third inequality of (26).

Appendix 3: Derivations of (30) and (32)

For simplicity, we use the expression $e^{\bar{x}}$ instead of the expression $\exp (\bar{x})$ for any scalar $\bar{x}$ in this appendix. In the derivation of (30), we utilize the inequalities

$$\begin{aligned} \left. \begin{array}{l} \Vert M_{V}(\phi )\Vert \le \bar{c}_{1},\;\Vert \dot{M}_{V}(\cdot )\Vert \le \bar{c}_{2} \Vert \dot{u}(t) \Vert \\ \Vert M_{VM}(\phi )\Vert \le \bar{c}_{3},\;\Vert \dot{M}_{VM}(\cdot )\Vert \le \bar{c}_{4}\Vert \dot{u}(t)\Vert \\ \Vert n_{V}(\cdot )\Vert \le \bar{c}_{5}+\bar{c}_{6}\Vert \dot{u}(t)\Vert +\bar{c}_{7} \Vert \dot{u}(t)\Vert ^2\\ \Vert T(\phi _{V})\Vert \le \bar{c}_{8},\;\Vert \dot{T}(\cdot )\Vert \le \bar{c}_{9}\Vert \dot{u}(t)\Vert \\ \Vert D(v)\Vert \le \bar{c}_{10}\Vert v(t)\Vert ,\;\Vert M_{M}(\phi )\Vert \le \bar{c}_{11}\\ \Vert \dot{M}_{M}(\cdot )\Vert \le \bar{c}_{12}\Vert \dot{u}(t)\Vert ,\;\Vert M_{V}(\phi )\Vert ^{-1}\Vert \le \bar{c}_{13}\\ \Vert n_{M}(\cdot )\Vert \le \bar{c}_{14}+\bar{c}_{15}\Vert \dot{u}(t)\Vert +\bar{c}_{16}\Vert \dot{u}(t)\Vert ^2 \end{array} \right\} , \end{aligned}$$

(74)

where $\bar{c} _{1}$ to $\bar{c}_{16}$ are positive constants.

Using the third equation of (17), we can write the norm of the solution of $z_{VF}(t)$ as

$$\begin{aligned} \Vert z_{VF}(t)\Vert \le e^{-\rho t} \int _{0}^{t} e^{\rho \bar{\tau }}\Vert \bar{z}_{VF}(\bar{\tau })\Vert d\bar{\tau }, \end{aligned}$$

(75)

where $\bar{z}_{VF}(\bar{\tau })\in R^{6}$ is given by

$$\begin{aligned} \bar{z}_{VF}(t)& =\rho [ \rho M_{V}(\phi )+\dot{M}_{V}(\cdot ) ] \dot{x}_{V}(t)\\ & \quad+\rho [\rho M_{VM}(\phi )+\dot{M}_{VM}(\cdot ) ] \dot{q}(t) -\rho n_{V}(\cdot )\\ & \quad -[ \dot{T}(\cdot )-T(\phi _{V})C_{1}D(v) ] C_{3}D(v)v(t) \\& \quad -T(\phi _{V})C_{2}C_{3}D(v)\tau _{V}(t)+\rho a_{CV}(t)\lambda (t).\end{aligned}$$

Using the first inequality of (26), the first to eighth inequalities of (74), and the inequalities $\Vert \dot{x}_{V}(t)\Vert \le \Vert \dot{u}(t)\Vert$ and $\Vert \dot{q}(t)\Vert$ $\le \Vert \dot{u}(t)\Vert$, we can rewrite (75) as

$$\begin{aligned} &\Vert z_{VF}(t)\Vert \le \bar{c}_{VF1} \int _{0}^{t} e^{-\rho (t-\bar{\tau })}\{ \rho +\rho \Vert \dot{u}(\bar{\tau })\Vert ^{2}\\ & \quad+(1+\rho )\rho \Vert \dot{u}(\bar{\tau })\Vert +\Vert \dot{u}(\bar{\tau })\Vert \Vert v(\bar{\tau })\Vert ^{2}\\ &\quad +\Vert v(\bar{\tau })\Vert ^{3}+\Vert v(\bar{\tau })\Vert \Vert \tau _{V}(\bar{\tau })\Vert +\rho |\lambda (\bar{\tau })|\} d\bar{\tau } , \end{aligned}$$

(76)

where $\bar{c}_{VF1}\in R^{+}$ is given by

$$\begin{aligned} \bar{c}_{VF1}&=\max \{ \bar{c}_{5},\,\bar{c}_{6},\,\bar{c}_{1}+\bar{c}_{3},\,\bar{c}_{2}+\bar{c}_4 +\bar{c}_{7},\Vert C_{3}\Vert \bar{c}_{9}\bar{c}_{10},\\ & \quad \Vert C_{1}\Vert \Vert C_{3}\Vert \bar{c}_{8} \bar{c}_{10}^{2},\,\Vert C_{2}C_{3}\Vert \bar{c}_{8}\bar{c}_{10},\,c_{AC1}\}. \end{aligned}$$

Comparing the solution of the first-order filter (31) with (76), we have

$$\begin{aligned} \Vert z_{VF}(t)\Vert \le \bar{c}_{VF1}z_{PF}(t). \end{aligned}$$

(77)

Using the first equation of (16), we can write the norm of $z_{C}(t)$ as

$$\begin{aligned}& \Vert z_{C}(t)\Vert \le \Vert n_{V}(\cdot )\Vert +\rho \Vert M_{V}(\phi )\Vert \Vert \dot{x}_{V}(t)\Vert +\Vert z_{VF}(t)\Vert \\ &\quad +\rho \Vert M_{VM}(\phi )\Vert \Vert \dot{q}(t)\Vert +|\lambda (t)|\Vert a_{CV}(t)\Vert . \end{aligned}$$

(78)

Using the first inequality of (26), the first, third and fifth inequalities of (74), and the inequalities $\Vert \dot{x}_{V}(t)\Vert \le \Vert \dot{u}(t)\Vert$ and $\Vert \dot{q}(t)\Vert \le \Vert \dot{u}(t)\Vert$, we can rewrite (78) as

$$\begin{aligned} & \Vert z_{C}(t)\Vert \le \bar{c}_{5}+[\bar{c}_{6}+(\bar{c}_{1}+\bar{c}_{3})\rho ]\Vert \dot{u}(t)\Vert +\bar{c}_{7}\Vert \dot{u}(t)\Vert ^{2}\\ & \quad +\Vert z_{VF}(t)\Vert +c_{AC1} |\lambda (t)|.\end{aligned}$$

(79)

Utilizing the second equation of (19), we can write the norm of the solution of $z_{Q}(t)$ as

$$\begin{aligned} \Vert z_{Q}(t)\Vert \le \Vert n_{M}(\cdot )\Vert +\Vert M_{VM}(\phi )\Vert \Vert M_{V}(\phi )^{-1}\Vert \Vert z_{C}(t)\Vert . \end{aligned}$$

(80)

Using the third, eleventh and twelfth inequalities of (74), we can rewrite (80) as

$$\begin{aligned} & \Vert z_{Q}(t)\Vert \le \bar{c}_{14}+\bar{c}_{15}\Vert \dot{u}(t)\Vert +\bar{c}_{16} \Vert \dot{u}(t)\Vert ^{2}\\ & \quad +\bar{c}_{3} \bar{c}_{13}\Vert z_{C}(t)\Vert .\end{aligned}$$

(81)

Utilizing the second equation of (21), we can write the norm of $z_{P}(t)$ as

$$\begin{aligned}& \Vert z_{P}(t)\Vert \le \Vert J_{M}^{V}(q)^{-1} \Vert [\Vert z_{Q}(t)\Vert \\ & \quad +\Vert M_{Q}(\phi )\Vert \Vert J_{M}^{V}(q)^{-1}\Vert \Vert \dot{J}_{M}^{\,V}(\cdot )\Vert \Vert \dot{q}(t)\Vert ]. \end{aligned}$$

(82)

Utilizing (23), the first equation of (19), the third inequality of (22), the third, ninth and eleventh inequalities of (74), and the inequality $\Vert \dot{q}(t)\Vert \le \Vert \dot{u}(t)\Vert$, we can rewrite (82) as

$$\begin{aligned} \Vert z_{P}(t)\Vert \le c_{J6} \Vert z_{Q}(t)\Vert +c_{J3}c_{J6}^{2}(\bar{c}_{11} +\bar{c}_{3}^{2}\bar{c}_{13})\Vert \dot{u}(t)\Vert ^2. \end{aligned}$$

(83)

Applying (77), (79) and (81), to (83), we can derive (30).

In view of the condition that the disturbances $d_{V}(t)$ and $d_{M}(t)$ are bounded, we obtain the inequalities

$$\begin{aligned} \Vert d_{V}(t)\Vert \le c_{D1},\;\Vert d_{M}(t)\Vert \le c_{D2}, \end{aligned}$$

(84)

where $c_{D1}$ and $c_{D2}$ are positive constants. Using the first equation of (17), we can write the norm of the solution of $w_{VF1}(t)$ as

$$\begin{aligned} \Vert w_{VF1}(t)\Vert \le \Vert w_{VF10}\Vert . \end{aligned}$$

(85)

Similarly, utilizing the second equation of (17), and then applying the first inequality of (84) to it, we can write the norm of the solution of $w_{VF2}(t)$ as

$$\begin{aligned} \Vert w_{VF2}(t)\Vert \le c_{D1} (1-e^{-\rho t}) \le c_{D1}. \end{aligned}$$

(86)

Using the third equation of (21), we can write the norm of $w_{P}(t)$ as

$$\begin{aligned} \Vert w_{P}(t)\Vert \le \Vert J_{M}^{V}(q)^{-1}\Vert \Vert w_{Q}(t)\Vert . \end{aligned}$$

(87)

Substituting the third equation of (19) and the second equation of (16) into (87), and then using (23), (85), (86), the third and eleventh inequality of (74), and the first and second inequalities of (84), we can derive (32).

Appendix 4: Derivation of (48)

The motion error $e_{P}(t)$ with respect to $\varSigma _{I}$ is parallel to the tangent plane $g_{C}(p_{M})=0$, because the positions $p_{M}(t)$ and $p_{MRC}(t)$ are points on the plane. Therefore, the following relation holds:

$$\begin{aligned} n_{C}(t)^{\mathrm {T}}e_{P}(t)=0. \end{aligned}$$

(88)

Applying the relation $R(\phi _{V})R(\phi _{V})^{\mathrm {T}}=I_{3}$ to (88), then multiplying both its sides by $1/\Vert n_{C}(t)\Vert$, and then using the fourth equation of (21), we obtain

$$\begin{aligned} a_{CM}(t)^{\mathrm {T}}R(\phi _{V})^{\mathrm {T}}e_{P}(t)=0. \end{aligned}$$

(89)

Using (47), and then multiplying both its sides by $\alpha _{M}$, we have

$$\begin{aligned} \alpha _{M} a_{CM}(t)^{\mathrm {T}}e_{P}^{V}(t)=0. \end{aligned}$$

(90)

Subtracting each side of (42) from the corresponding side of (24), and then utilizing the second equation of (45), we obtain

$$\begin{aligned} a_{CM}(t)^{\mathrm {T}} [\dot{e}_{P}^{V}(t)+S(\omega _{V}^{V})e_{P}^{V}(t)]=0. \end{aligned}$$

(91)

Finally, adding (90) to (91), and then using the first equation of (45), we can derive (48).

Appendix 5: Derivation of (54)

Using (53), and then applying the first and second inequalities of (28) to it, we can write the norm of $f_{P1}(t)$ as

$$\begin{aligned} \Vert f_{P1}(t)\Vert & \le \Vert z_{P}(t)\Vert +c_{M1} [ \alpha _{M}\Vert \dot{e}_{P}^{V}(t)\Vert \\ & \quad +\Vert S(\omega _{V}^{V})\Vert \Vert \dot{e}_{P}^{V}(t)\Vert +\Vert S(\dot{\omega }_{V}^{V})\Vert \Vert e_{P}^{V}(t)\Vert +\Vert \dot{e}_{F}(t)\Vert ]\\ & \quad +(c_{M2}/2)\Vert \dot{u}(t)\Vert \Vert e_{H}(t)\Vert +\Vert e_{P}^{V}(t)\Vert . \end{aligned}$$

(92)

Applying the inequality $\Vert S(\bar{x})\Vert \le 6\Vert \bar{x}\Vert$ [$\bar{x}\in R^{3}$] (derived from the skew-symmetric property) to (92), and then using the second and fourth inequalities of (27), we obtain

$$\begin{aligned} \Vert f_{P1}(t)\Vert & \le \Vert z_{P}(t)\Vert +\{ 1+6c_{M1} [c_{\varOmega 5} \Vert \dot{u}(t)\Vert ^2\\ & \quad +c_{\varOmega 6}\Vert \ddot{\phi }_{V}(t)\Vert ]\} \Vert e_{P}^{V}(t)\Vert +[ c_{M1}\alpha _{M}\\ & \quad +6c_{M1}c_{\varOmega 2}\Vert \dot{u}(t)\Vert ] \Vert \dot{e}_{P}^{V}(t)\Vert +c_{M1}\Vert \dot{e}_{F}(t)\Vert \\ & \quad +(c_{M2}/2)\Vert \dot{u}(t)\Vert \Vert e_{H}(t)\Vert . \end{aligned}$$

(93)

Using (52), and then applying the second inequality of (22), the second equation of (26), and the first inequality of (34) to it, we can write the norm of $\tau _{M}(t)$ as

$$\begin{aligned} \Vert \tau _{M}(t)\Vert & \le c_{J2}c_{\varLambda R1}+c_{J2}\alpha _{M}\Vert e_{H} (t)\Vert +c_{J2}\alpha _{F} | e_{\varLambda }(t) | \\ & \quad +c_{J2}\Vert f_{P1}(t)\Vert .\end{aligned}$$

(94)

Applying (93) to (94), and then defining the positive constants $\bar{c}_{T1}$ to $\bar{c}_{T3}$ as

$$\begin{aligned} \left. \begin{array}{l} \bar{c}_{T1}=\max \{ 1,\,6c_{M1}c_{\varOmega 5},\,6c_{M1}c_{\varOmega 6}\}\\ \bar{c}_{T2}=\max \{ 1,\,6c_{\varOmega 2}\},\;\bar{c}_{T3}=\max \{ 1,\,c_{M2}/2\} \end{array} \right\} , \end{aligned}$$

(95)

we can derive (54).

Appendix 6: Derivation of (55)

Differentiating (44) with respect to time, then multiplying both its sides by $M_{P}(\phi )$, and then using the first and second equations of (45), we have

$$\begin{aligned}M_{P}(\phi )\dot{e}_{H}(t) & =M_{P}(\phi )\ddot{p}_{M}^{V}(t)-M_{P}(\phi )\ddot{p}_{MR}^{V}(t)\\ & \quad +M_{P}(\phi )\{ [ \alpha _{M}I_{3}+S(\omega _{V}^{V}) ] \dot{e}_{P}^{V}(t) +S(\dot{\omega }_{V}^{V})e_{P}^{V}(t)\\ & \quad +\dot{e}_{F}(t)\} . \end{aligned}$$

(96)

Substituting (20) into (96), and then using (53) and (57), we obtain

$$\begin{aligned} M_{P}(\phi )\dot{e}_{H}(t)& =J_{M}^{V}(q)^{-\mathrm {T}}\tau _{M}(t)-f_{P1}(t) +a_{CM}(t)\lambda (t)\\ & \quad -f_{P2}(t)-(1/2)\dot{M}_{P}(\cdot )e_{H}(t)-e_{P}^{V}(t). \end{aligned}$$

(97)

Substituting (52) into (97), and then using (50), we can derive (55).

Appendix 7: Proof of Theorem 1

We choose the positive definite function

$$\begin{aligned} V_{1}(t)&=(1/2) [ e_H (t)^{\mathrm {T}}M_{P}(\phi )e_{H}(t) +e_{P}^{V}(t)^{\mathrm {T}}e_{P}^{V}(t)\\ & \quad +e_{F}(t)^{\mathrm {T}}e_{F}(t) ]. \end{aligned}$$

(98)

Differentiating (98) with respect to time, and then substituting the error models (49), (56) and (58) into it, we have

$$\begin{aligned} \dot{V}_{1}(t) &=-\alpha _{M}e_{H}(t)^{\mathrm {T}}e_{H}(t) -\alpha _{M}e_{P}^{V}(t)^{\mathrm {T}}e_{P}^{V}(t)\\ & \quad -\beta _{F}e_{F}(t)^{\mathrm {T}}e_{F}(t) -e_{P}^{V}(t)^{\mathrm {T}} S(\omega _{V}^{V})e_{P}^{V}(t)\\& \quad +(1+\alpha _{F}) [ e_{H}(t)-e_{F}(t) ]^{\mathrm {T}}a_{CM}(t) e_{\varLambda }(t)\\ & \quad +e_{P}^{V}(t)^{\mathrm {T}} [ e_{M}(t)+e_{F}(t)-e_{H}(t) ]. \end{aligned}$$

(99)

Substituting (44) into (99), then applying (48) and the skew-symmetric property $e_{P}^{V}(t)^{\mathrm {T}}S(\omega _{V}^{V})e_{P}^{V}(t)=0$ to it, and then defining $W(t)\in R$ as

$$\begin{aligned} W(t)& =\alpha _{M}e_{H}(t)^{\mathrm {T}}e_{H}(t) +\alpha _{M}e_{P}^{V}(t)^{\mathrm {T}}e_{P}^{V}(t)\\ & \quad +\beta _{F}e_{F} (t)^{\mathrm {T}}e_{F}(t), \end{aligned}$$

(100)

we obtain

$$\begin{aligned} \dot{V}_{1}(t)=-W(t)\le 0. \end{aligned}$$

(101)

It follows from (98) and (101) that the signals $V_{1}(t)$, $e_{H}(t)$, $e_{P}^{V}(t)$ and $e_{F}(t)$ are bounded. Using their bounded properties, the inequalities in the properties P1 to P6 and P9, and the assumptions A2, A3 and A9, we can prove that the other closed-loop signals are bounded.

The signals $e_{H}(t)$, $e_{P}^{V}(t)$ and $e_{F}(t)$ are uniformly continuous, because their time derivatives $\dot{e}_{H}(t)$, $\dot{e}_{P}^{V}(t)$ and $\dot{e}_{F}(t)$ are bounded. This means that the signal W(t) is uniformly continuous. It follows from (98), (101) and the uniform continuity of W(t) that $\lim _{t\rightarrow \infty }W(t)=0$ (e.g., Lemma A.6 of [47]). It should be noted that instead of Lemma A.6 of [47], we can use LaSalle-Yoshizawa Theorem A.8 of [48]. In this case, instead of the uniform continuity of W(t) , it is required that the error models (49), (56) and (58) are locally Lipschitz. It follows from the zero convergence of W(t) that the error signals $e_{P}^{V}(t)$, $e_{H}(t)$ and $e_{F}(t)$ are asymptotical stable. Furthermore, using (47) and the sixth inequality of (22), and then applying the asymptotic stability of $e_{P}^{V}(t)$, we can prove that $e_{P}(t)$ is asymptotical stable.

Integrating $\dot{e}_{F}(t)$ from 0 to t with respect to time, and then taking its limit, we have

$$\begin{aligned} \lim _{t\rightarrow \infty }\int _{0}^{t}\dot{e}_{F}(\bar{\tau }) d\bar{\tau } & =\lim _{t\rightarrow \infty }\{ e_{F}(t)-e_{F}(0)\}\\ &=-e_F (0).\end{aligned}$$

(102)

In the derivation of (102), we use the asymptotic stability of $e_{F}(t)$. The Eq. (102) means that the limit of the integration of $\dot{e}_{F}(t)$ exists and is finite. Furthermore, the boundedness of $\ddot{e}_{F}(t)$ implies that $\dot{e}_{F}(t)$ is uniformly continuous. Therefore, the conditions of Barbalat Lemma (e.g., Lemma A.6 of [48]) are satisfied, and hence $\dot{e}_{F}(t)$ is asymptotically stable. Solving (49) for the term $a_{CM}(t)e_{\varLambda }(t)$, and then applying the asymptotic stabilities of $e_{P}^{V}(t)$, $e_{F}(t)$ and $\dot{e}_{F}(t)$ to it, we obtain

$$\begin{aligned} \lim _{t\rightarrow \infty }\{ a_{CM}(t)e_{\varLambda } (t)\} &= [ 1/(1+\alpha _F)]\\ & \quad\times \lim _{t\rightarrow \infty }\{ -\dot{e}_{F}(t)-\beta _{F}e_{F}(t) +e_{P}^{V}(t)\} =0. \end{aligned}$$

(103)

Moreover, it follows from (103) and the second equation of (26) that $e_{\varLambda }(t)$ is asymptotically stable. The proof is complete.

Appendix 8: Proof of Theorem 2

We choose the positive definite function

$$\begin{aligned}&V_{2}(t)=V_{21}(t)+V_{22}(t), \end{aligned}$$

(104)

$$\begin{aligned}&\left. \begin{array}{l} V_{21}(t)=(1/2) [ e_{H}(t)^{\mathrm {T}}M_{P}(\phi )e_{H}(t) +e_{P}^{V}(t)^{\mathrm {T}} e_{P}^{V}(t) ] \\ V_{22}(t)=(1/2)e_F (t)^{\mathrm {T}}e_{F}(t) \end{array} \right\} . \end{aligned}$$

(105)

Differentiating (104) with respect to time, and then substituting the error models (49), (55) and (56) into it, we have

$$\begin{aligned} \dot{V}_{2}(t)=\dot{V}_{1}(t)-e_{H}(t)^{\mathrm {T}}f_{P2}(t), \end{aligned}$$

(106)

where $\dot{V}_{1}(t)$ is given by (99). Moreover, substituting (44) into (106), then applying (48) and the skew-symmetric property $e_{P}^{V}(t)^{\mathrm {T}}S(\omega _{V}^{V})e_{P}^{V}(t)=0$ to it, and then defining $Y_{1}(t)\in R$ as

$$\begin{aligned} Y_{1}(t)=-(\alpha _{M}/2)e_{H}(t)^{\mathrm {T}}e_{H}(t) -e_{H}(t)^{\mathrm {T}}f_{P2}(t), \end{aligned}$$

(107)

we obtain

$$\begin{aligned} \dot{V}_{2}(t)&=-(\alpha _{M}/2)e_{H}(t)^{\mathrm {T}}e_{H}(t) -\alpha _{M}e_{P}^{V}(t)^{\mathrm {T}}e_{P}^{V}(t)\\ & \quad -\beta _{F}e_{F}(t)^{\mathrm {T}}e_{F}(t)+Y_{1}(t). \end{aligned}$$

(108)

We can rewrite (107) as

$$\begin{aligned} Y_{1}(t)\le \bar{c}_{17}/\alpha _{M}, \end{aligned}$$

(109)

where $\bar{c}_{17}$ is a positive constant. In the derivation of (109), we use (32), (57), the first inequality of (28), the sixth inequality of (41), and the inequality $\bar{a}\bar{b}\le \bar{c}\bar{a}^{2}+\bar{b}^{2}/(4\bar{c})$ [$\bar{a},\,\bar{b}\in R$; $\bar{c}\in R^{+}$]. Applying (29) and (109) to (108), then defining $\bar{c}_{18}$ and $\alpha$ as

$$\begin{aligned} \bar{c}_{18}=\min \{ 1/c_{M5},\,2\},\;\alpha =\min \{\alpha _{M},\,\beta _{F}\}, \end{aligned}$$

respectively, and then using (104), we have

$$\begin{aligned} \dot{V}_{2}(t)\le -\bar{c}_{18}\alpha V_{2}(t)+\bar{c}_{17}/\alpha . \end{aligned}$$

(110)

Moreover, applying Lemma 3.2.4 of [49] to (110), we obtain

$$\begin{aligned} V_{2}(t)\le \exp (-\bar{c}_{18}\alpha t) V_{2}(0)+\bar{c}_{17}/(\bar{c}_{18} \alpha ^{2}). \end{aligned}$$

(111)

In a way similar to the proof of Theorem 1, except that the “bounded” disturbance term $f_{P2}(t)$ exists, we can prove that the closed-loop signals are bounded.

In a way similar to the aforementioned analysis of $\dot{V}_{2}(t)$, we can obtain the time derivative

$$\begin{aligned}& \dot{V}_{21}(t)\le -\bar{c}_{19}\alpha _{M}V_{21}(t) +(1+\alpha _{F})\Vert e_{F}\Vert _{\infty }\Vert e_{\varLambda }\Vert _{\infty }\\ & \quad +Y_{1}(t)+Y_{2}(t), \end{aligned}$$

(112)

where $\bar{c}_{19}=\min \{ 1/c_{M5},\,1\}$, and $Y_{2}(t)\in R$ is given by

$$\begin{aligned} Y_{2}(t)=-(\alpha _{M}/2) e_{P}^{V}(t)^{\mathrm {T}}e_{P}^{V}(t) -e_{P}^{V}(t)^{\mathrm {T}}e_{F}(t). \end{aligned}$$

(113)

In a way similar to the derivation of (109), we can rewrite (113) as

$$\begin{aligned} Y_{2}(t)\le \Vert e_{F}\Vert _{\infty }^{2}/(2\alpha _{M}). \end{aligned}$$

(114)

Applying (109) and (114) to (112), and then applying Lemma 3.2.4 of [49] to it, we have

$$\begin{aligned}& V_{21}(t)\le \exp (-\bar{c}_{19}\alpha _{M}t) V_{21}(0)\\ & \quad+(1+\alpha _{F})\Vert e_{F}\Vert _{\infty } \Vert e_{\varLambda }\Vert _{\infty }/(\bar{c}_{19}\alpha _{M})\\ & \quad +[ \bar{c}_{17}+(\Vert e_{F}\Vert _{\infty }^{2}/2)] /(\bar{c}_{19}\alpha _{M}^{2}). \end{aligned}$$

(115)

We can derive (59) and (61) from (115), and furthermore, using (47), (59), and the sixth inequality of (22), we obtain (60). Similarly, we can derive the time derivative

$$\begin{aligned}& V_{22}(t)\le \exp (-\beta _{F}t) V_{22}(0)\\ & \quad +[ \Vert e_{\varLambda }\Vert _{\infty }^{2}(1+\alpha _{F})^{2} +\Vert e_{P}^{V}\Vert _{\infty }^{2}] /\beta _{F}^{2}. \end{aligned}$$

(116)

We can derive (62) from (116), and furthermore, using (49) and the second equation of (26), we obtain (63). The proof is complete.