SpringerLink
Log in

Higher-order buckling analysis of FG porous cylindrical micro-shells integrated with GPLs-RC patches in hygrothermal environment immersed on Kerr foundation

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

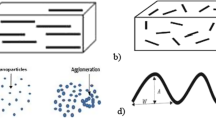
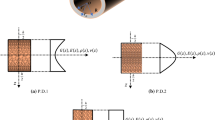
This study investigates the buckling behavior of functionally graded (FG) porous micro-shell covered with nanocomposite facesheets; graphene nanoplatelets (GPLs) are hired to reinforce and strengthen the faces. This micro-shell is under a hygrothermal environment and rested on Kerr foundations which consist of two rows of springs and one shear layer. Due to considering the size effect for this microstructure, modified couple stress theory is implemented in the strain energy. Reddy’s theory in the Cartesian coordinate system is applied to analyze shear stress distribution through z-direction. In the end, the Navier’s solution method is employed to solve equations analytically for simply supported edges. Moreover, the validity of the outcomes is confirmed by comparing them with a previous published study. After validation, the key findings of the research are examined; it highlights the influences of GPLs of facesheets and porous distribution on the stiffness of the structure, and the impact of Kerr foundation on the result is the most significant outcomes. The main implications show that the symmetric porosity distribution and FG V-A GPLs distribution make this engineering structure become stiffer which consequently leads to an increase in critical buckling load.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Amir, S., Arshid, E., Maraghi, Z.K.: Free vibration analysis of magneto-rheological smart annular three-layered plates subjected to magnetic field in viscoelastic medium. Smart Struct. Syst. 25(5), 581–592 (2020). https://doi.org/10.12989/sss.2020.25.5.581

    Article  Google Scholar 

  2. Liu, Y., Guan, J., **ao, Z., Sun, Z., Ma, H.: Chromium doped barium titanyl oxalate nano-sandwich particles: a facile synthesis and structure enhanced electrorheological properties. Mater. Chem. Phys. 122(1), 73–78 (2010). https://doi.org/10.1016/j.matchemphys.2010.02.077

    Article  Google Scholar 

  3. Yanase, K., Moriyama, S., Ju, J.W.: Effects of CNT waviness on the effective elastic responses of CNT-reinforced polymer composites. Acta Mech. 224(7), 1351–1364 (2013). https://doi.org/10.1007/s00707-013-0808-3

    Article  Google Scholar 

  4. Shahgholian, D., Safarpour, M., Rahimi, A.R., Alibeigloo, A.: Buckling analyses of functionally graded graphene-reinforced porous cylindrical shell using the Rayleigh-Ritz method. Acta Mech. 231(5), 1887–1902 (2020). https://doi.org/10.1007/s00707-020-02616-8

    Article  MathSciNet  Google Scholar 

  5. Iijima, S.: Helical microtubules of graphitic carbon. Nature 354(6348), 56 (1991)

    Article  Google Scholar 

  6. Novoselov, K.S., et al.: Electric field effect in atomically thin carbon films. Science 306(5696), 666–669 (2004). https://doi.org/10.1126/science.1102896

    Article  Google Scholar 

  7. Wang, P.N., Hsieh, T.H., Chiang, C.L., Shen, M.Y.: Synergetic effects of mechanical properties on graphene nanoplatelet and multiwalled carbon nanotube hybrids reinforced epoxy/carbon fiber composites. J. Nanomater. 2015, 1–9 (2015). https://doi.org/10.1155/2015/838032

    Article  Google Scholar 

  8. Arshid, E., Momeni Nia, M.J., Ghorbani, M.A., Civalek, Ö., Kumar, A.: On the poroelastic vibrations of lightweight FGSP doubly-curved shells integrated with GNPs-reinforced composite coatings in thermal atmospheres. Appl. Math. Model. 124, 122–141 (2023). https://doi.org/10.1016/j.apm.2023.07.036

    Article  MathSciNet  Google Scholar 

  9. Arshid, E., Ghorbani, M.A., Momeni Nia, M.J., Civalek, Ö., Kumar, A.: Thermo-elastic buckling behaviors of advanced fluid-infiltrated porous shells integrated with GPLs-reinforced nanocomposite patches. Mech. Adv. Mater. Struct. (2023). https://doi.org/10.1080/15376494.2023.2251015

    Article  Google Scholar 

  10. Mousavi, S.B., Amir, S., Jafari, A., Arshid, E.: Analytical solution for analyzing initial curvature effect on vibrational behavior of PM beams integrated with FGP layers based on trigonometric theories. Adv. Nano Res. 10(3), 235–251 (2021). https://doi.org/10.12989/anr.2021.10.3.235

    Article  Google Scholar 

  11. Arshid, E., Amir, S., Loghman, A.: Thermoelastic vibration characteristics of asymmetric annular porous reinforced with nano-fillers microplates embedded in an elastic medium: CNTs Vs GNPs. Arch. Civ. Mech. Eng. 23(2), 100 (2023). https://doi.org/10.1007/s43452-023-00624-8

    Article  Google Scholar 

  12. Afshari, H., Adab, N.: Size-dependent buckling and vibration analyses of GNP reinforced microplates based on the quasi-3D sinusoidal shear deformation theory. Mech. Based Des. Struct. Mach. (2020). https://doi.org/10.1080/15397734.2020.1713158

    Article  Google Scholar 

  13. Nguyen, D.D.: Nonlinear thermo- electro-mechanical dynamic response of shear deformable piezoelectric sigmoid functionally graded sandwich circular cylindrical shells on elastic foundations. J. Sandw. Struct. Mater. 20(3), 351–378 (2018). https://doi.org/10.1177/1099636216653266

    Article  Google Scholar 

  14. Zenkour, A.M., Hafed, Z.S.: Bending response of functionally graded piezoelectric plates using a two variable shear deformation theory. Adv. Aircr. Spacecr. Sci. 7(2), 115–134 (2020). https://doi.org/10.12989/aas.2020.7.2.115

    Article  Google Scholar 

  15. Sobhy, M.: Buckling and vibration of FG graphene platelets/aluminum sandwich curved nanobeams considering the thickness stretching effect and exposed to a magnetic field. Results Phys. 16, 102865 (2020). https://doi.org/10.1016/j.rinp.2019.102865

    Article  Google Scholar 

  16. Habibi, M., Hashemabadi, D., Safarpour, H.: Vibration analysis of a high-speed rotating GPLRC nanostructure coupled with a piezoelectric actuator. Eur. Phys. J. Plus 134(6), 1–23 (2019). https://doi.org/10.1140/epjp/i2019-12742-7

    Article  Google Scholar 

  17. Wang, Y., Feng, C., Zhao, Z., Yang, J.: Eigenvalue buckling of functionally graded cylindrical shells reinforced with graphene platelets (GPL). Compos. Struct. 202, 38–46 (2018). https://doi.org/10.1016/j.compstruct.2017.10.005

    Article  Google Scholar 

  18. Habibi, M., Mohammadi, A., Safarpour, H., Shavalipour, A., Ghadiri, M.: Wave propagation analysis of the laminated cylindrical nanoshell coupled with a piezoelectric actuator. Mech. Based Des. Struct. Mach. 49, 640–658 (2019). https://doi.org/10.1080/15397734.2019.1697932

    Article  Google Scholar 

  19. Fu, Y., Wang, J., Mao, Y.: Nonlinear analysis of buckling, free vibration and dynamic stability for the piezoelectric functionally graded beams in thermal environment. Appl. Math. Model. 36(9), 4324–4340 (2012). https://doi.org/10.1016/j.apm.2011.11.059

    Article  MathSciNet  Google Scholar 

  20. Roque, C.M.C., Ferreira, A.J.M., Jorge, R.M.N.: Free vibration analysis of composite and sandwich plates by a trigonometric layerwise deformation theory and radial basis functions. J. Sandw. Struct. Mater. 8(6), 497–515 (2006). https://doi.org/10.1177/1099636206065873

    Article  Google Scholar 

  21. Mokhtar, Y., Heireche, H., Bousahla, A.A., Houari, M.S.A., Tounsi, A., Mahmoud, S.R.: A novel shear deformation theory for buckling analysis of single layer graphene sheet based on nonlocal elasticity theory. Smart Struct. Syst. 21(4), 397–405 (2018). https://doi.org/10.12989/sss.2018.21.4.397

    Article  Google Scholar 

  22. Alhaifi, K., Khorshidvand, A.R., Al-Masoudy, M.M., Arshid, E., Madani, S.H.: A shooting method for buckling and post-buckling analyses of FGSP circular plates considering various patterns of Pores’ placement. Struct. Eng. Mech. 85(3), 419–432 (2023). https://doi.org/10.12989/sem.2023.85.3.419

    Article  Google Scholar 

  23. Kargar, J., Ghorbanpour Arani, A., Arshid, E., Irani Rahaghi, M.: Vibration analysis of spherical sandwich panels with MR fluids core and magneto-electro-elastic face sheets resting on orthotropic viscoelastic foundation. Struct. Eng. Mech. 78(5), 572 (2021). https://doi.org/10.12989/SEM.2021.78.5.557

    Article  Google Scholar 

  24. Arshid, E., Khorshidvand, A.R.: Free vibration analysis of saturated porous FG circular plates integrated with piezoelectric actuators via differential quadrature method. Thin-Walled Struct. 125(January), 220–233 (2018). https://doi.org/10.1016/j.tws.2018.01.007

    Article  Google Scholar 

  25. Zhu, P., Lei, Z.X., Liew, K.M.: Static and free vibration analyses of carbon nanotube-reinforced composite plates using finite element method with first order shear deformation plate theory. Compos. Struct. 94(4), 1450–1460 (2012). https://doi.org/10.1016/j.compstruct.2011.11.010

    Article  Google Scholar 

  26. Kheirikhah, M.M., Khalili, S.M.R., Malekzadeh Fard, K.: Analytical solution for bending analysis of soft-core composite sandwich plates using improved high-order theory. Struct. Eng. Mech. 44(1), 15–34 (2012). https://doi.org/10.12989/sem.2012.44.1.015

    Article  Google Scholar 

  27. Arshid, H., Khorasani, M., Soleimani-Javid, Z., Dimitri, R., Tornabene, F.: Quasi-3D hyperbolic shear deformation theory for the free vibration study of honeycomb microplates with graphene nanoplatelets-reinforced epoxy skins. Molecules 25(21), 5085 (2020). https://doi.org/10.3390/molecules25215085

    Article  Google Scholar 

  28. Alhaifi, K., Arshid, E., Khorshidvand, A.R.: Large deflection analysis of functionally graded saturated porous rectangular plates on nonlinear elastic foundation via GDQM. Steel Compos. Struct. 39(6), 795–809 (2021). https://doi.org/10.12989/scs.2021.39.6.795

    Article  Google Scholar 

  29. Ghorbanpour Arani, A., BabaAkbar-Zarei, H., Pourmousa, P., Eskandari, M.: Investigation of free vibration response of smart sandwich micro-beam on Winkler-Pasternak substrate exposed to multi physical fields. Microsyst. Technol. 24(7), 3045–3060 (2018). https://doi.org/10.1007/s00542-017-3681-5

    Article  Google Scholar 

  30. Thai, H., Kim, S.: Composites : part B a size-dependent functionally graded Reddy plate model based on a modified couple stress theory. Compos. Part B 45(1), 1636–1645 (2013). https://doi.org/10.1016/j.compositesb.2012.09.065

    Article  Google Scholar 

  31. Shafiei, N., Kazemi, M.: Nonlinear buckling of functionally graded nano-/micro-scaled porous beams. Compos. Struct. 178, 483–492 (2017). https://doi.org/10.1016/J.COMPSTRUCT.2017.07.045

    Article  Google Scholar 

  32. Şimşek, M., Aydın, M.: Size-dependent forced vibration of an imperfect functionally graded (FG) microplate with porosities subjected to a moving load using the modified couple stress theory. Compos. Struct. 160, 408–421 (2017). https://doi.org/10.1016/J.COMPSTRUCT.2016.10.034

    Article  Google Scholar 

  33. Zhang, X., Ye, W., Sahmani, S., Safaei, B.: Quasi-3D nonlinear primary resonance of randomly oriented CNT-reinforced micro/nano-beams incorporating nonlocal and couple stress tensors. Acta Mech. 234(8), 3259–3285 (2023). https://doi.org/10.1007/s00707-023-03554-x

    Article  MathSciNet  Google Scholar 

  34. Ansari, R., Gholami, R., Sahmani, S.: Free vibration analysis of size-dependent functionally graded microbeams based on the strain gradient Timoshenko beam theory. Compos. Struct. 94(1), 221–228 (2011). https://doi.org/10.1016/j.compstruct.2011.06.024

    Article  Google Scholar 

  35. Arshid, E., Amir, S., Loghman, A.: Static and dynamic analyses of FG-GNPs reinforced porous nanocomposite annular micro-plates based on MSGT. Int. J. Mech. Sci. 180, 105656 (2020). https://doi.org/10.1016/j.ijmecsci.2020.105656

    Article  Google Scholar 

  36. Khorasani, M., Soleimani-Javid, Z., Arshid, E., Lampani, L., Civalek, Ö.: Thermo-elastic buckling of honeycomb micro plates integrated with FG-GNPs reinforced Epoxy skins with stretching effect. Compos. Struct. 258, 1–28 (2021). https://doi.org/10.1016/j.compstruct.2020.113430

    Article  Google Scholar 

  37. Arefi, M., Mohammad-Rezaei Bidgoli, E., Rabczuk, T.: Thermo-mechanical buckling behavior of FG GNP reinforced micro plate based on MSGT. Thin-Walled Struct. 142, 444–459 (2019). https://doi.org/10.1016/j.tws.2019.04.054

    Article  Google Scholar 

  38. Kitipornchai, S., Chen, D., Yang, J.: Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 116, 656–665 (2017). https://doi.org/10.1016/j.matdes.2016.12.061

    Article  Google Scholar 

  39. Eslami, M.R.: Buckling analysis of a porous circular plate with piezoelectric sensor–actuator layers under uniform radial compression. Acta Mech. 225(1), 179–193 (2013). https://doi.org/10.1007/s00707-013-0959-2

    Article  MathSciNet  Google Scholar 

  40. Arshid, E., Amir, S., Loghman, A.: On the vibrations of FG GNPs-RPN annular plates with piezoelectric/metallic coatings on Kerr elastic substrate considering size dependency and surface stress effects. Acta Mech. 234(9), 4035–4076 (2023). https://doi.org/10.1007/s00707-023-03593-4

    Article  MathSciNet  Google Scholar 

  41. Yiqi, M., Yiming, F.: Nonlinear dynamic response and active vibration control for piezoelectric functionally graded plate. J. Sound Vib. 329(11), 2015–2028 (2010). https://doi.org/10.1016/j.jsv.2010.01.005

    Article  Google Scholar 

  42. Ghorbanpour Arani, A., Khani, M., Khoddami Maraghi, Z.: Dynamic analysis of a rectangular porous plate resting on an elastic foundation using high-order shear deformation theory. J. Vibr. Control 24(16), 3698–3713 (2017). https://doi.org/10.1177/1077546317709388

    Article  MathSciNet  Google Scholar 

  43. Yesilce, Y., Catal, H.H.: Solution of free vibration equations of semi-rigid connected Reddy–Bickford beams resting on elastic soil using the differential transform method. Arch. Appl. Mech. 81(2), 199–213 (2011). https://doi.org/10.1007/s00419-010-0405-z

    Article  Google Scholar 

  44. Khoddami Maraghi, Z., Amir, S., Arshid, E.: On the natural frequencies of smart circular plates with magnetorheological fluid core embedded between magnetostrictive patches on Kerr elastic substance. Mech. Based Des. Struct. Mach. (2022). https://doi.org/10.1080/15397734.2022.2156885

    Article  Google Scholar 

  45. Cong, P.H., Chien, T.M., Khoa, N.D., Duc, N.D.: Nonlinear thermomechanical buckling and post-buckling response of porous FGM plates using Reddy’s HSDT. Aerosp. Sci. Technol. 77, 419–428 (2018). https://doi.org/10.1016/j.ast.2018.03.020

    Article  Google Scholar 

  46. Mustapha, K.B., Hawwa, M.A.: Eigenanalyses of functionally graded micro-scale beams entrapped in an axially-directed magnetic field with elastic restraints. Int. J. Struct. Stab. Dyn. 16(6), 1–38 (2016). https://doi.org/10.1142/S0219455415500224

    Article  MathSciNet  Google Scholar 

  47. Zhang, W., Ma, H., Wang, Y.: Stability and vibration of nanocomposite microbeams reinforced by graphene oxides using an MCST-based improved shear deformable computational framework. Acta Mech. (2022). https://doi.org/10.1007/s00707-022-03467-1

    Article  Google Scholar 

  48. Khorasani, M., Soleimani-Javid, Z., Arshid, E., Amir, S., Civalek, Ö.: Vibration analysis of graphene nanoplatelets’ reinforced composite plates integrated by piezo-electromagnetic patches on the piezo-electromagnetic media. Waves Random Complex Media (2021). https://doi.org/10.1080/17455030.2021.1956017

    Article  Google Scholar 

  49. Akgöz, B., Civalek, Ö.: A microstructure-dependent sinusoidal plate model based on the strain gradient elasticity theory. Acta Mech. 226(7), 2277–2294 (2015). https://doi.org/10.1007/s00707-015-1308-4

    Article  MathSciNet  Google Scholar 

  50. Li, Q., Wu, D., Gao, W., Tin-Loi, F., Liu, Z., Cheng, J.: Static bending and free vibration of organic solar cell resting on Winkler-Pasternak elastic foundation through the modified strain gradient theory. Eur. J. Mech. A/Solids 78, 103852 (2019). https://doi.org/10.1016/j.euromechsol.2019.103852

    Article  MathSciNet  Google Scholar 

  51. Arshid, E., Soleimani-Javid, Z., Amir, S., Duc, N.D.: Higher-order hygro-magneto-electro-thermomechanical analysis of FG-GNPs-reinforced composite cylindrical shells embedded in PEM layers. Aerosp. Sci. Technol. 126, 107573 (2022). https://doi.org/10.1016/j.ast.2022.107573

    Article  Google Scholar 

  52. Lim, C.W., Kitipornchai, S., Wang, C.M., Yuen, R.K.K.: Buckling of vertical cylindrical shells under combined end pressure and body force. J. Eng. Mech. 129(8), 876–884 (2004)

    Article  Google Scholar 

  53. Toan Thang, P., Nguyen-Thoi, T., Lee, J.: Mechanical stability of metal foam cylindrical shells with various porosity distributions. Mech. Adv. Mater. Struct. 27(4), 295–303 (2020). https://doi.org/10.1080/15376494.2018.1472338

    Article  Google Scholar 

  54. Soleimani-Javid, Z., Arshid, E., Amir, S., Bodaghi, M.: On the higher-order thermal vibrations of FG saturated porous cylindrical micro-shells integrated with nanocomposite skins in viscoelastic medium. Def. Technol. 18(8), 1416–1434 (2022). https://doi.org/10.1016/j.dt.2021.07.007

    Article  Google Scholar 

Download references

Acknowledgements

This research has been jointly supported by The China’s Liaoning Province “**ng Liao Talents Plan” Youth Top-notch Talent Funding Project under Grant No. XLYC2007146 and Science and Technology Research Plan of China Railway 19th Bureau Co. Ltd under Grant No.2021-B03.

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. School of Architecture and Art, Zhejiang Business Technology Institute, Ningbo, 315012, Zhejiang, People’s Republic of China

    Yi-Fan Ying

  2. The Third Engineering Co., Ltd., China Railway 19th Bureau Group, Shenyang, 110136, Liaoning, People’s Republic of China

    Li-Cai Zhao

  3. Department of Civil and Construction Engineering, National Taiwan University of Science and Technology, No.43, Sec.4, Keelung Road, Taipei City, Taiwan

    Yi-Fan Ying & Li-Cai Zhao

  4. Department of Nuclear and Renewable Energy, Ural Federal University Named After the First President of Russia, Boris Yeltsin, 19 Mira Street, Yekaterinburg, 620002, Russia

    Abhinav Kumar

Authors
  1. Yi-Fan Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li-Cai Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abhinav Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li-Cai Zhao.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

Κijk that are presented in Eq. (22) are defined as follows:

$${\kappa }_{\mathrm{xxx}}=\frac{{\partial }^{2}}{\partial {x}^{2}}u,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\kappa }_{xx\alpha }=\frac{{\partial }^{2}}{\partial {x}^{2}}v,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\kappa }_{zz\alpha }=\frac{{\partial }^{2}}{\partial {z}^{2}}v,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\kappa }_{\mathrm{xxz}}=\frac{{\partial }^{2}}{\partial {x}^{2}}w,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\kappa }_{xz\alpha }={\kappa }_{zx\alpha }=\frac{{\partial }^{2}}{\partial z\partial x}v,$$
$${\kappa }_{\mathrm{zxx}}={\kappa }_{\mathrm{xzx}}=\frac{{\partial }^{2}}{\partial x\partial z}u,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}{\kappa }_{\mathrm{zzz}}=\frac{{\partial }^{2}}{\partial {z}^{2}}w\text{\hspace{0.17em}},\text{\hspace{0.17em}\hspace{0.17em}}{\kappa }_{\mathrm{zzx}}=\frac{{\partial }^{2}}{\partial {z}^{2}}u,\text{\hspace{0.17em}\hspace{0.17em}}{\kappa }_{\mathrm{xzz}}={\kappa }_{\mathrm{zxz}}=\frac{{\partial }^{2}}{\partial z\partial x}w,$$
$${\kappa }_{x\theta \theta }={\kappa }_{\alpha x\alpha }=\left(\frac{{\partial }^{2}}{\partial x\partial \alpha }v+\frac{\partial }{\partial x}w\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{\alpha xx}={\kappa }_{x\alpha x}=\left(\frac{{\partial }^{2}}{\partial x\partial \alpha }u\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{\alpha \alpha x}=\left(\frac{{\partial }^{2}}{\partial {\alpha }^{2}}u{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}+\frac{\partial }{\partial z}u\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{x\alpha z}={\kappa }_{\alpha xz}=\left(\frac{{\partial }^{2}}{\partial x\partial \alpha }w-\frac{\partial }{\partial x}v\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{\alpha \alpha z}=\left(\frac{{\partial }^{2}}{\partial {\alpha }^{2}}w-2\frac{\partial }{\partial \alpha }v+R\left(1+\frac{z}{R}\right)\frac{\partial }{\partial z}w-w\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-2},$$
$${\kappa }_{z\alpha \alpha }={\kappa }_{\alpha z\alpha }=\left(\frac{{\partial }^{2}}{\partial z\partial \alpha }v-\frac{\partial }{\partial \alpha }v{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}+\frac{\partial }{\partial z}w-w{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{z\alpha z}={\kappa }_{\alpha zz}=\left(\frac{{\partial }^{2}}{\partial z\partial \alpha }w-\frac{\partial }{\partial \alpha }w{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}-\frac{\partial }{\partial z}v+v{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{\alpha zx}=\left(\frac{{\partial }^{2}}{\partial z\partial \alpha }u-\frac{\partial }{\partial \alpha }u{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{z\alpha x}=\left(\frac{{\partial }^{2}}{\partial z\partial \alpha }u-\frac{\partial }{\partial \alpha }u{\left(R\left(1+\frac{z}{R}\right)\right)}^{-1}\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-1},$$
$${\kappa }_{\alpha \alpha \alpha }=\left(\frac{{\partial }^{2}}{\partial {\alpha }^{2}}v+2\frac{\partial }{\partial \alpha }w+R\left(1+\frac{z}{R}\right)\frac{\partial }{\partial z}v-v\right){\left(R\left(1+\frac{z}{R}\right)\right)}^{-2},$$

Appendix B

$$\delta u:\frac{1}{4}\frac{{K}_{15}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }-\frac{1}{4}\frac{{K}_{1}}{R}\frac{{\partial }^{4}}{\partial {x}^{3}\partial \alpha }{\varphi }_{\alpha }-\frac{1}{2}\frac{{K}_{16}}{{R}^{2}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{1}{4}\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}{\varphi }_{x}-\frac{1}{4}\frac{{K}_{0}}{R}\frac{{\partial }^{4}}{\partial {x}^{3}\partial \alpha }v+\frac{1}{4}\frac{{K}_{0}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}u+\frac{1}{4}\frac{{K}_{15}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}-\frac{1}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\alpha }^{3}}{\varphi }_{\alpha }+\frac{1}{4}\frac{{K}_{1}}{{R}^{4}}\frac{{\partial }^{4}}{\partial {\alpha }^{4}}{\varphi }_{x}-\frac{1}{4}\frac{{K}_{0}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\alpha }^{3}}v+\frac{1}{4}\frac{{K}_{0}}{{R}^{4}}\frac{{\partial }^{4}}{\partial {\alpha }^{4}}u+\frac{1}{4}\frac{{K}_{6}}{{R}^{3}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}-\frac{3}{2}\frac{{K}_{7}}{{R}^{3}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{3}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }-\frac{{K}_{0}}{{R}^{3}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{3}{4}\frac{{K}_{0}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \alpha }v+\frac{5}{4}\frac{{K}_{6}}{{R}^{2}}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }-\frac{3}{4}\frac{{K}_{2}}{{R}^{4}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w-{C}_{110}\frac{{\partial }^{2}}{\partial {x}^{2}}u-{C}_{111}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{x}+{C}_{112}\frac{{\partial }^{3}}{\partial {x}^{3}}w-\frac{{C}_{120}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }v-\frac{{C}_{121}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }+\frac{{C}_{122}}{{R}^{2}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w-\frac{{C}_{120}}{R}\frac{\partial }{\partial x}w-\frac{{C}_{660}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }v-\frac{{C}_{661}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }+2\frac{{C}_{662}}{{R}^{2}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w-\frac{{C}_{660}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}u-\frac{{C}_{661}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}=0$$
$$\delta v:-\frac{1}{4}\frac{{K}_{15}}{{R}^{2}}{\varphi }_{\alpha }+\frac{{K}_{16}}{{R}^{3}}\frac{\partial }{\partial \theta }w-\frac{{K}_{6}}{{R}^{3}}{\varphi }_{\alpha }+\frac{{K}_{7}}{{R}^{4}}\frac{\partial }{\partial \theta }w+\frac{{K}_{1}}{{R}^{4}}{\varphi }_{\alpha }-\frac{{K}_{2}}{{R}^{5}}\frac{\partial }{\partial \theta }w-\frac{{K}_{0}}{{R}^{4}}\frac{\partial }{\partial \theta }w+\frac{{K}_{0}v}{{R}^{4}}-\frac{{K}_{15}}{R}\frac{{\partial }^{2}}{\partial x\partial \theta }{\varphi }_{x}+\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\theta }^{2}}{\varphi }_{\alpha }+\frac{{K}_{0}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\theta }^{2}}v+2\frac{{K}_{7}}{{R}^{2}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \theta }w-\frac{1}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\theta }^{3}}{\varphi }_{x}-\frac{{K}_{6}}{R}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }-\frac{7}{4}\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }-\frac{7}{4}\frac{{K}_{0}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {x}^{2}}{v}_{0}+2\frac{{K}_{0}}{{R}^{2}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \theta }w+\frac{{K}_{2}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \theta }w-\frac{{K}_{6}}{{R}^{2}}\frac{{\partial }^{2}}{\partial x\partial \theta }{\varphi }_{x}+\frac{3}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \theta }{\varphi }_{x}+\frac{3}{4}\frac{{K}_{0}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \theta }u-\frac{1}{4}\frac{{K}_{6}}{{R}^{3}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}{\varphi }_{\alpha }-\frac{{K}_{1}}{{R}^{4}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}{\varphi }_{\alpha }-\frac{{K}_{0}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\theta }^{3}}u+\frac{{K}_{2}}{{R}^{5}}\frac{{\partial }^{3}}{\partial {\theta }^{3}}w+\frac{{K}_{7}}{{R}^{4}}\frac{{\partial }^{3}}{\partial {\theta }^{3}}w+\frac{{K}_{0}}{{R}^{4}}\frac{{\partial }^{3}}{\partial {\theta }^{3}}w-\frac{{K}_{0}}{{R}^{4}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}v+\frac{{K}_{16}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \theta }w-\frac{{C}_{120}}{R}\frac{{\partial }^{2}}{\partial x\partial \theta }u-\frac{{C}_{121}}{R}\frac{{\partial }^{2}}{\partial x\partial \theta }{\varphi }_{x}+\frac{{C}_{122}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \theta }w-\frac{{C}_{220}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}v-\frac{{C}_{221}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\theta }^{2}}{\varphi }_{\alpha }+\frac{{C}_{222}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {\theta }^{3}}w-\frac{{C}_{220}}{{R}^{2}}\frac{\partial }{\partial \theta }w-{C}_{660}\frac{{\partial }^{2}}{\partial {x}^{2}}v-{C}_{661}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }+2\frac{{C}_{662}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \theta }w-\frac{{C}_{660}}{R}\frac{{\partial }^{2}}{\partial x\partial \theta }u-\frac{{C}_{661}}{R}\frac{{\partial }^{2}}{\partial x\partial \theta }{\varphi }_{x}=0$$
$$\begin{aligned} & \delta w:\frac{1}{4}\Bigg(\frac{{K}_{12}}{{R}^{2}}\frac{\partial }{\partial x}{\varphi }_{x}+\left(\frac{{K}_{12}}{{R}^{3}}-\frac{{K}_{15}}{{R}^{2}}\right)\frac{\partial }{\partial \alpha }{\varphi }_{\alpha }+\left(\frac{{K}_{2}}{{R}^{5}}-\frac{{K}_{16}}{{R}^{3}}\right)\frac{\partial }{\partial \alpha }v-\frac{{K}_{6}}{{R}^{3}}\frac{\partial }{\partial \alpha }{\varphi }_{\alpha }+\left(\frac{{K}_{5}}{{R}^{5}}-\frac{{K}_{18}}{{R}^{3}}\right)\frac{\partial }{\partial \alpha }{\varphi }_{\alpha}\\ & \qquad +\left(-\frac{{K}_{19}}{{R}^{3}}+\frac{{K}_{1}}{{R}^{4}}\right)\frac{\partial }{\partial \alpha }{\varphi }_{\alpha }-\left(-\frac{{K}_{10}}{{R}^{4}}-\frac{{K}_{23}}{R}+\frac{{K}_{9}}{{R}^{4}}\right)\frac{\partial }{\partial \alpha }{\varphi }_{\alpha }-\frac{{K}_{7}}{{R}^{4}}\frac{\partial }{\partial \alpha }v+\frac{{K}_{15}}{R}\frac{\partial }{\partial x}{\varphi }_{x}+\frac{{K}_{0}}{{R}^{4}}\frac{\partial }{\partial \alpha }v\\ & \qquad +\left(\frac{{K}_{21}}{{R}^{2}}+\frac{{K}_{27}}{{R}^{2}}\right)\frac{\partial }{\partial \alpha }{\varphi }_{\alpha }+\left(\frac{{K}_{26}}{R}+\frac{{K}_{27}}{R}+\frac{{K}_{6}}{{R}^{2}}{K}_{23}\right)\frac{\partial }{\partial x}{\varphi }_{x}+\left({K}_{0}+{C}_{115}\right)\frac{{\partial }^{4}}{\partial {x}^{4}}w+\left(-{K}_{24}-2\frac{{K}_{7}}{{R}^{2}}\right)\frac{{\partial }^{2}}{\partial {x}^{2}}w\\ & \qquad +\left(-{K}_{6}+{K}_{12}\right)\frac{{\partial }^{3}}{\partial {x}^{3}}{\varphi }_{x}+\left(5\frac{{K}_{10}}{{R}^{3}}-3\frac{{K}_{12}}{{R}^{2}}-3\frac{{K}_{6}}{{R}^{2}}+4\frac{{K}_{1}}{{R}^{3}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}{\varphi }_{x}+\left(-\frac{{K}_{24}}{{R}^{2}}-\frac{{K}_{14}}{{R}^{4}}\right)\frac{{\partial }^{2}}{\partial {\alpha }^{2}}w\\ & \qquad +\left(6\frac{{K}_{7}}{{R}^{3}}-5\frac{{K}_{2}}{{R}^{4}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}+\left(-3\frac{{K}_{5}}{{R}^{3}}-2\frac{{K}_{18}}{R}-11\frac{{K}_{9}}{{R}^{2}}-\frac{{C}_{124}}{R}-2\frac{{C}_{664}}{R}-3\frac{{K}_{6}}{R}\right)\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }{\varphi }_{\alpha }\\ & \qquad -\left(5\frac{{K}_{5}}{{R}^{4}}+5\frac{{K}_{12}}{R}+8\frac{{K}_{18}}{{R}^{2}}+6\frac{{K}_{9}}{{R}^{3}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}{\varphi }_{x}+\left(2\frac{{K}_{16}}{{R}^{3}}+2\frac{{K}_{20}}{{R}^{4}}+2\frac{{K}_{7}}{{R}^{4}}\right)\frac{{\partial }^{2}}{\partial {\alpha }^{2}}w+14\frac{{K}_{7}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}w\\ & \qquad +\left(-\frac{{K}_{14}}{{R}^{2}}-2\frac{{K}_{16}}{R}-\frac{{K}_{0}}{{R}^{2}}-2\frac{{K}_{28}}{R}\right)\frac{{\partial }^{2}}{\partial {x}^{2}}w+\left(2\frac{{K}_{11}}{{R}^{5}}-2\frac{{K}_{28}}{{R}^{3}}\right)\frac{{\partial }^{2}}{\partial {\alpha }^{2}}w\\ & \qquad +\left(-7\frac{{K}_{0}}{{R}^{2}}-3\frac{{K}_{2}}{{R}^{3}}-2\frac{{K}_{16}}{R}-11\frac{{K}_{7}}{{R}^{2}}\right)\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }v+\left(-\frac{{K}_{5}}{{R}^{5}}-\frac{{K}_{10}}{{R}^{4}}-\frac{{K}_{6}}{{R}^{3}}-\frac{{K}_{1}}{{R}^{4}}-\frac{{K}_{9}}{{R}^{4}}-\frac{{K}_{12}}{{R}^{3}}\right)\frac{{\partial }^{3}}{\partial {\alpha }^{3}}{\varphi }_{\alpha }\\ & \qquad +\left(-\frac{{K}_{2}}{{R}^{5}}-\frac{{K}_{7}}{{R}^{4}}-\frac{{K}_{0}}{{R}^{4}}\right)\frac{{\partial }^{3}}{\partial {\alpha }^{3}}v+\left(2\frac{{K}_{16}}{{R}^{2}}+4\frac{{K}_{0}}{{R}^{3}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}u+\left(2\frac{{K}_{11}}{{R}^{5}}+2\frac{{K}_{7}}{{R}^{4}}+\frac{{K}_{4}}{{R}^{6}}+\frac{{K}_{0}}{{R}^{4}}\right)\frac{{\partial }^{4}}{\partial {\alpha }^{4}}w\\ & \qquad +\left(-\frac{{K}_{0}}{{R}^{4}}-2\frac{{K}_{2}}{{R}^{5}}-\frac{{K}_{4}}{{R}^{6}}\right)\frac{{\partial }^{2}}{\partial {\alpha }^{2}}w+\left(\frac{{K}_{14}}{{R}^{4}}+2\frac{{K}_{2}}{{R}^{5}}+\frac{{C}_{225}}{{R}^{4}}\right)\frac{{\partial }^{4}}{\partial {\alpha }^{4}}w\\ & \qquad +\left(8\frac{{K}_{11}}{{R}^{3}}+6\frac{{K}_{2}}{{R}^{3}}+8\frac{{K}_{14}}{{R}^{2}}+6\frac{{K}_{0}}{{R}^{2}}+8\frac{{K}_{4}}{{R}^{4}}\right)\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}w\\ & \qquad +\left(-8\frac{{K}_{10}}{{R}^{2}}-7\frac{{K}_{1}}{{R}^{2}}\right)\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }{\varphi }_{\alpha }+\left(-{C}_{5511}+2{C}_{559}-{C}_{550}-2\frac{{C}_{122}}{R}-{H}_{2}+{N}_{x}^{HT}\right)\frac{{\partial }^{2}}{\partial {x}^{2}}w\\ & \qquad -{C}_{112}\frac{{\partial }^{3}}{\partial {x}^{3}}u-{C}_{114}\frac{{\partial }^{3}}{\partial {x}^{3}}{\psi }_{x}-\frac{{C}_{224}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}{\varphi }_{\alpha }+\left(-\frac{{C}_{440}}{{R}^{2}}+2\frac{{C}_{449}}{{R}^{2}}-\frac{{C}_{4411}}{{R}^{2}}-2\frac{{C}_{222}}{{R}^{3}}\right)\frac{{\partial }^{2}}{\partial {\alpha }^{2}}w\\ & \qquad +\left(-2\frac{{C}_{664}}{{R}^{2}}-\frac{{C}_{124}}{{R}^{2}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}{\varphi }_{x}+\left(-2\frac{{C}_{662}}{{R}^{2}}-\frac{{C}_{122}}{{R}^{2}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}u+\left(-\frac{{C}_{122}}{R}-\frac{{C}_{222}}{{R}^{3}}-2\frac{{C}_{662}}{R}\right)\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }v\\ & \qquad +\left(2\frac{{C}_{125}}{{R}^{2}}+4\frac{{C}_{665}}{{R}^{2}}\right)\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}w+\left({C}_{5510}-{C}_{556}+\frac{{C}_{121}}{R}\right)\frac{\partial }{\partial x}{\varphi }_{x}+\left(\frac{{C}_{221}}{{R}^{2}}-\frac{{C}_{446}}{R}+\frac{{C}_{4410}}{R}\right)\frac{\partial }{\partial \alpha }{\varphi }_{\alpha }\\ & \qquad +\frac{{C}_{120}}{R}\frac{\partial }{\partial x}u+\frac{{C}_{220}}{{R}^{2}}\frac{\partial }{\partial \alpha }v-\frac{1}{{R}^{2}}({H}_{2}+{N}_{\alpha }^{HT})\frac{{\partial }^{2}w}{\partial {\alpha }^{2}}+\left({H}_{1}+\frac{{C}_{220}}{{R}^{2}}\right)w=0\end{aligned}$$
$$\delta {\varphi }_{x}:-2\frac{{K}_{3}}{{R}^{4}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}-2\frac{{K}_{1}}{{R}^{4}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}u-\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w-\frac{{K}_{6}}{{R}^{2}}\frac{{\partial }^{2}}{\partial x\partial \alpha }v-2\frac{{K}_{13}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}+\left(\frac{3}{4}\frac{{K}_{3}}{{R}^{3}}-\frac{7}{4}\frac{{K}_{8}}{{R}^{2}}\right)\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }-\frac{1}{2}\frac{{K}_{18}}{{R}^{2}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{9}{2}\frac{{K}_{8}}{{R}^{3}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}-\frac{1}{4}\frac{{K}_{3}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\alpha }^{3}}{\varphi }_{\alpha }-\frac{1}{4}\frac{{K}_{1}}{R}\frac{{\partial }^{4}}{\partial {x}^{3}\partial \alpha }v+\frac{1}{4}\frac{{K}_{3}}{{R}^{4}}\frac{{\partial }^{4}}{\partial {\alpha }^{4}}{\varphi }_{x}-\frac{1}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\alpha }^{3}}v+\frac{5}{4}\frac{{K}_{13}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }+\frac{3}{4}\frac{{K}_{12}}{{R}^{2}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w-\frac{5}{4}\frac{{K}_{10}}{{R}^{3}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w-\frac{3}{2}\frac{{K}_{9}}{{R}^{3}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{1}{4}\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}u+\frac{3}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \alpha }v-\frac{1}{4}\frac{{K}_{3}}{R}\frac{{\partial }^{4}}{\partial {x}^{3}\partial \alpha }{\varphi }_{\alpha }+\frac{9}{4}\frac{{K}_{6}}{{R}^{3}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}u+\frac{1}{4}\frac{{K}_{15}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}u-\frac{1}{4}\frac{{K}_{15}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }v+\frac{1}{4}\frac{{K}_{3}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}{\varphi }_{x}+\frac{1}{2}\frac{{K}_{17}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}+\frac{1}{4}\frac{{K}_{1}}{{R}^{4}}\frac{{\partial }^{4}}{\partial {\alpha }^{4}}u+\frac{3}{4}\frac{{K}_{6}}{{R}^{2}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{5}{4}\frac{{K}_{5}}{{R}^{4}}\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\frac{1}{4}{K}_{6}\frac{{\partial }^{3}}{\partial {x}^{3}}w-\frac{1}{4}{K}_{13}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{x}+\frac{1}{4}{K}_{12}\frac{{\partial }^{3}}{\partial {x}^{3}}w+\frac{1}{4}({K}_{22}+\frac{{K}_{13}}{{R}^{2}}+2\frac{{K}_{25}}{R}){\varphi }_{x}-\frac{1}{4}\left(\frac{{K}_{27}}{R}+\frac{{K}_{12}}{{R}^{2}}+\frac{{K}_{6}}{{R}^{2}}+{K}_{23}+\frac{{K}_{15}}{R}+\frac{{K}_{26}}{R}\right)\frac{\partial }{\partial x}w+\left(-{C}_{111}-\frac{{C}_{661}}{{R}^{2}}\right)\frac{{\partial }^{2}}{\partial {x}^{2}}u-{C}_{113}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{x}+{C}_{114}\frac{{\partial }^{3}}{\partial {x}^{3}}w+\left(-\frac{{C}_{123}}{R}-\frac{{C}_{663}}{R}\right)\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{\alpha }+\left(\frac{{C}_{124}}{{R}^{2}}+2\frac{{C}_{664}}{{R}^{2}}\right)\frac{{\partial }^{3}}{\partial x\partial {\alpha }^{2}}w+\left(-\frac{{C}_{121}}{R}+{C}_{556}-{C}_{5510}\right)\frac{\partial }{\partial x}w+{C}_{558}{\varphi }_{x}+\left(-\frac{{C}_{661}}{R}-\frac{{C}_{121}}{R}\right)\frac{{\partial }^{2}}{\partial x\partial \alpha }v-\frac{{C}_{663}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{x}=0$$
$$\delta {\varphi }_{\alpha }:\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad$$
$$\frac{1}{4}\Bigg({K}_{22}{\varphi }_{\alpha }-\frac{{K}_{15}}{{R}^{2}}v-\frac{{K}_{27}}{{R}^{2}}\frac{\partial }{\partial \alpha }w-\frac{{K}_{6}}{{R}^{3}}v+\frac{{K}_{19}}{{R}^{3}}\frac{\partial }{\partial \alpha }w+\frac{{K}_{1}}{{R}^{4}}v+\frac{{K}_{17}}{R}{\varphi }_{\alpha }+\frac{{K}_{10}}{{R}^{4}}\frac{\partial }{\partial \alpha }w+\frac{{K}_{13}}{{R}^{2}}{\varphi }_{\alpha }-\frac{{K}_{21}}{{R}^{2}}\frac{\partial }{\partial \alpha }w-\frac{{K}_{8}}{{R}^{3}}{\varphi }_{\alpha }+\frac{{K}_{3}}{{R}^{4}}{\varphi }_{\alpha }-\frac{{K}_{1}}{{R}^{4}}\frac{\partial }{\partial \alpha }w-\frac{{K}_{12}}{{R}^{3}}\frac{\partial }{\partial \alpha }w+\frac{{K}_{9}}{{R}^{4}}\frac{\partial }{\partial \alpha }w+\frac{{K}_{6}}{{R}^{3}}\frac{\partial }{\partial \alpha }w+\frac{{K}_{18}}{{R}^{3}}\frac{\partial }{\partial \alpha }w-\frac{{K}_{5}}{{R}^{5}}\frac{\partial }{\partial \alpha }w \Bigg)-{K}_{15}\frac{{\partial }^{2}}{\partial {x}^{2}}v+\frac{1}{4}{K}_{1}\frac{{\partial }^{4}}{\partial {x}^{4}}v-\frac{1}{2}{K}_{17}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }-2{K}_{13}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }+\frac{1}{4}{K}_{3}\frac{{\partial }^{4}}{\partial {x}^{4}}{\varphi }_{\alpha }+\frac{1}{4}\frac{{K}_{15}}{{R}^{2}}\frac{\partial }{\partial \alpha }w-\frac{1}{2}\frac{{K}_{17}{\varphi }_{\alpha }}{{R}^{2}}-\frac{1}{4}\frac{{K}_{23}}{R}\frac{\partial }{\partial \alpha }w+\frac{1}{4}\frac{{K}_{25}{\varphi }_{\alpha }}{R}+\frac{1}{4}\frac{{K}_{3}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}{\varphi }_{\alpha }+\frac{3}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \alpha }u+\frac{5}{2}\frac{{K}_{8}}{R}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }+\frac{3}{4}\frac{{K}_{12}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{5}{4}\frac{{K}_{6}}{R}\frac{{\partial }^{2}}{\partial {x}^{2}}v-\frac{1}{4}\frac{{K}_{3}}{R}\frac{{\partial }^{4}}{\partial {x}^{3}\partial \alpha }{\varphi }_{x}+\frac{1}{4}\frac{{K}_{9}}{{R}^{4}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w+\frac{9}{4}\frac{{K}_{9}}{{R}^{2}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{7}{4}\frac{{K}_{8}}{{R}^{2}}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{x}+\frac{5}{4}\frac{{K}_{13}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{x}+\frac{1}{4}\frac{{K}_{15}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }u-\frac{1}{4}\frac{{K}_{1}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\alpha }^{3}}u-\frac{3}{4}\frac{{K}_{6}}{{R}^{2}}\frac{{\partial }^{2}}{\partial x\partial \alpha }u+\frac{1}{4}\frac{{K}_{6}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w+\frac{1}{2}\frac{{K}_{18}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{3}{2}\frac{{K}_{3}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }+\frac{7}{4}\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w+\frac{1}{4}\frac{{K}_{1}}{{R}^{4}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w+\frac{1}{4}\frac{{K}_{5}}{{R}^{5}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w+\frac{3}{4}\frac{{K}_{5}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{1}{4}\frac{{K}_{6}}{{R}^{3}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}v-\frac{1}{4}\frac{{K}_{3}}{{R}^{4}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{\alpha }-\frac{1}{4}\frac{{K}_{1}}{{R}^{4}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}v+2\frac{{K}_{10}}{{R}^{2}}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w+\frac{1}{4}\frac{{K}_{12}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w-\frac{3}{2}\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {x}^{2}}v+\frac{1}{4}\frac{{K}_{10}}{{R}^{4}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w-\frac{1}{4}\frac{{K}_{3}}{{R}^{3}}\frac{{\partial }^{4}}{\partial x\partial {\alpha }^{3}}{\varphi }_{x}-\frac{1}{4}\frac{{K}_{1}}{R}\frac{{\partial }^{4}}{\partial {x}^{3}\partial \alpha }{u}_{0}-\frac{1}{4}\frac{{K}_{13}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{\alpha }+\frac{1}{4}\frac{{K}_{1}}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{2}\partial {\alpha }^{2}}v+\frac{3}{4}\frac{{K}_{6}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{1}{2}\frac{{K}_{8}}{{R}^{3}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{\alpha }+\frac{3}{4}\frac{{K}_{3}}{{R}^{3}}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{x}-\frac{{C}_{121}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }u-\frac{{C}_{123}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{x}+\frac{{C}_{124}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{{C}_{221}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}v-\frac{{C}_{223}}{{R}^{2}}\frac{{\partial }^{2}}{\partial {\alpha }^{2}}{\varphi }_{\alpha }+\frac{{C}_{224}}{{R}^{3}}\frac{{\partial }^{3}}{\partial {\alpha }^{3}}w-\frac{{C}_{221}}{{R}^{2}}\frac{\partial }{\partial \alpha }w-{C}_{661}\frac{{\partial }^{2}}{\partial {x}^{2}}v-{C}_{663}\frac{{\partial }^{2}}{\partial {x}^{2}}{\varphi }_{\alpha }+2\frac{{C}_{664}}{R}\frac{{\partial }^{3}}{\partial {x}^{2}\partial \alpha }w-\frac{{C}_{661}}{R}\frac{{\partial }^{2}}{\partial x\partial \theta \alpha }u-\frac{{C}_{663}}{R}\frac{{\partial }^{2}}{\partial x\partial \alpha }{\varphi }_{x}+\frac{{C}_{446}}{R}\frac{\partial }{\partial \alpha }w+{C}_{448}{\varphi }_{\alpha }-\frac{{C}_{4410}}{R}\frac{\partial }{\partial \alpha }w=0$$

in which the used coefficients are:

$$j=\frac{{h}_{c}}{2}+{h}_{f},\frac{{h}_{c}}{2},-\frac{{h}_{c}}{2},\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}i=\frac{{h}_{c}}{2},-\frac{{h}_{c}}{2},-\frac{{h}_{c}}{2}-{h}_{f}$$
$${C}_{b}={\int }_{i}^{j}{Q}_{11}\left(z\right)(\text{\hspace{0.17em}}1,f(z),g(z),f{(z)}^{2},f(z)g(z),g{(z)}^{2}){\text{d}}z,\text{\hspace{0.17em}}\text{\hspace{0.17em}\hspace{0.17em}}b=110...115$$
$${C}_{b}={\int }_{i}^{j}{Q}_{12}\left(z\right)(\text{\hspace{0.17em}}1,f(z),g(z),f{(z)}^{2},f(z)g(z),g{(z)}^{2}){\text{d}}z,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}b=120...125$$
$${C}_{b}={\int }_{i}^{j}{Q}_{22}\left(z\right)(\text{\hspace{0.17em}}1,f(z),g(z),f{(z)}^{2},f(z)g(z),g{(z)}^{2}){\text{d}}z,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}b=220...225$$
$${C}_{b}={\int }_{i}^{j}{Q}_{44}\left(z\right)(\text{\hspace{0.17em}}1,f(z),g(z),f{(z)}^{2},f(z)g(z),g{(z)}^{2},{f}{\prime}(z),f(z){f}{\prime}(z),{{f}{\prime}}{\prime}(z),{g}{\prime}(z)\text{\hspace{0.17em}}){\text{d}}z,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}b=440...449$$
$${C}_{b}={\int }_{i}^{j}{Q}_{44}\left(z\right)({f}{\prime}(z){g}{\prime}(z),{g}{{\prime\prime} }(z),f(z){g}{\prime}(z),{f}{\prime}(z)g(z),g(z){g}{\prime}(z))\mathrm{d}z,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}b=4411...44415$$
$${C}_{550},{C}_{556},{C}_{558},{C}_{559},{C}_{5510},{C}_{5511}=\text{\hspace{0.17em}}{\int }_{i}^{j}{Q}_{55}\left(z\right)(\text{\hspace{0.17em}}1,{f}{\mathrm{{\prime}}}(z),{{f}{\mathrm{{\prime}}}}{\mathrm{{\prime}}}(z),{g}{\mathrm{{\prime}}}(z),{f}{\mathrm{{\prime}}}(z){g}{\mathrm{{\prime}}}(z),{g}{{\prime\prime} }(z)){\text{d}}z,$$
$${C}_{660},{C}_{661},{C}_{662},{C}_{663},{C}_{664},{C}_{665}={\int }_{i}^{j}{Q}_{66}\left(z\right)(\text{\hspace{0.17em}}1,f(z),g(z),f{(z)}^{2},f(z)g(z),g{(z)}^{2}){\text{d}}z,$$
$${K}_{b}={\int }_{i}^{j}{{l}_{m}}^{2}\mu (z)(\text{\hspace{0.17em}}1,f(z),g(z),f{(z)}^{2},g{(z)}^{2},f(z)g(z),{f}{\prime}(z),{g}{\prime}(z),f(z){f}{\prime}(z),$$
$${g}{\prime}\left(z\right)f\left(z\right),g\left(z\right){f}{\prime}\left(z\right),{g}{\prime}\left(z\right)g\left(z\right),{f}{\prime}\left(z\right){g}{\prime}\left(z\right),{f}{\prime}{(}^{z},{g}{\prime}{(}^{z},{f}{{\prime\prime} }\left(z\right),{g}{{\prime\prime} }\left(z\right),$$
$$f\left(z\right){f}{{\prime\prime} }\left(z\right),{g}{{\prime\prime} }\left(z\right)f\left(z\right),g\left(z\right){f}{{\prime\prime} }\left(z\right),{g}{{\prime\prime} }\left(z\right)g\left(z\right)\text{\hspace{0.17em}},{g}{{\prime\prime} }\left(z\right){f}{\prime}\left(z\right),{f}{{\prime\prime} }{(}^{z},{f}{{\prime\prime} }\left(z\right){g}{{\prime\prime} }\left(z\right),$$
$${g}{{\prime\prime} }{(}^{z},{f}{{\prime\prime} }(z){f}{\prime}(z),\text{\hspace{0.17em}}{g}{{\prime\prime} }(z){f}{\prime}(z),{g}{{\prime\prime} }(z){f}{\prime}(z),\text{\hspace{0.17em}}{g}{{\prime\prime} }(z){g}{\prime}(z)){\text{d}}z,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}b=0...28$$

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ying, YF., Zhao, LC. & Kumar, A. Higher-order buckling analysis of FG porous cylindrical micro-shells integrated with GPLs-RC patches in hygrothermal environment immersed on Kerr foundation. Acta Mech 235, 1785–1802 (2024). https://doi.org/10.1007/s00707-023-03809-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03809-7

Search

Navigation