Big Data Nanoindentation and Analytics Reveal the Multi-Staged, Progressively-Homogenized, Depth-Dependent Upscaling of Rocks’ Properties

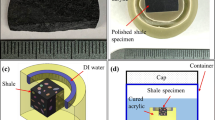
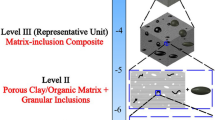
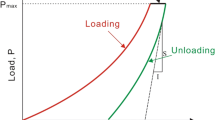
Abstract

This paper presents a newly observed phenomenon of upscaling of rocks’ properties using big data nanoindentation and analytics involving Gaussian mixture modeling (GMM), leading to characterizing the cross-scale mechanical properties of four shales and one sandstone. A large number (i.e., ~ 500) of statistical indentation measurements to depths of 6–8 μm were performed on each rock, resulting in continuous depth-dependent hardness and Young’s modulus data from unknown phases, which were then segmented at various depths to extract an array of discretized subdatasets. Two-dimensional GMM of each subdataset yields the number, fraction, and properties of mechanically distinct phases, and re-assembly of these results leads to clearly discernible property-depth curves. Such improved data analytics consisting of data segmentation, GMM deconvolution, and re-assembly enables the transformation of a massive number of chaotic curves from unknown phases into a few discernible lines corresponding to identified phases, from which the mechanical properties of individual phases are accurately determined at relatively small depths. With increasing depth, initially unique mechanical properties of individual phases undergo multistage merging at the intermediate mesoscale and progressively homogenize into a unified value at large depths or macroscale (e.g., >  ~ 5 μm), which is regarded as the bulk rock’s properties. More importantly, such depth-dependent transition and progressive merging and homogenization actually manifest the micromechanics of nanoindentation on a heterogeneous composite, including the indentation surround effect and rock’s microstructure (e.g., sizes and spacings of different solid particles and their properties). Compared to different micromechanical upscaling models, this newly developed big data indentation technique and pertinent data analytics enable more accurate, multi-parameter, and cross-scale characterization of highly heterogeneous materials and explicitly uncover the multi-staged, progressively-homogenized, depth-dependent upscaling of elasticity from individual constituents at the nanoscale to merged virtual interface phases at the mesoscale and to bulk material at the macroscale.

Appendices

Appendix A: Criteria for Results Filtering

For the purpose of clarification in the following discussion, use of different subscripts is explained here: (1) μ_{m, n, r} denotes the mean values of H and E of the mth phase in the nth solution derived from the model with r phases, where m = 1, 2, …, k, n = 1, 2, …, 1000, and r = 1, 2, …, N; (2) the same notation rule is applied to other parameters, except that logL_{n, r} represents the logarithmic likelihood value of the nth solution of the model with r phases. Not all the 8000 fitted solutions were desired with the consideration of both the statistical perspective and the rationality in mechanical testing, so only those solutions that would satisfy all the following criteria (1)–(4) were selected for further analysis:

• 1. The successful application of statistical nanoindentation is based on an important premise that the mechanical properties of individual phases of the studied composites have sufficient contrast that can be captured by nanoindentation testing at small scales. It means that a rational solution should not display severe overlaps between the adjacent distributions of two or more different phases. For any two distributions (i.e., corresponding to Phase A and Phase B) in a solution with r > 1, the pairwise overlap between Phase A and B can be defined as ω_ab = ω_a|b + ω_b|a, where ω_a|b given below is the misclassification probability that the random variable x originates from Phase B but is mistakenly assigned to Phase A, and vice versa (Maitra and Melnykov 2010):

  $$\omega_{{\text{a|b}}} = \Pr \left[ {\pi_{{\text{b, n, r }}} g({\mathbf{x}} \, ; \, {\varvec{\mu}}_{{\text{b, n, r}}} \, , \, {{\varvec{\Sigma}}}_{{\text{b, n, r}}} ) < \pi_{{\text{a, n, r }}} g({\mathbf{x}} \, ; \, {\varvec{\mu}}_{{\text{a, n, r}}} \, , \, {{\varvec{\Sigma}}}_{{\text{a, n, r}}} )|{\mathbf{x}}\sim g({\varvec{\mu}}_{{\text{b, n, r}}} \, , \, {{\varvec{\Sigma}}}_{{\text{b, n, r}}} )} \right].$$

  (10)

  In this study, the pairwise overlaps of all phases were calculated using the R package MixSim (Melnykov et al. 2012), and the maximum pairwise overlap was limited to 0.5, i.e. the solution that had two phases with over 50% chance of misclassification was excluded from subsequent analysis.

• 2. According to the data published in the literature (Zhang et al. 2013; Abedi et al. 2016; Akono and Kabir 2016; Sun et al. 2018), a positive correlation is usually observed between the hardness and Young’s modulus measured by nanoindentation. Therefore, the covariance term of each unrestricted variance–covariance matrix should be positive. Likewise, for any two distributions (e.g., Phase A and Phase B when r > 1) in a solution, their mean values μ = (μ_H, μ_E) were required to satisfy that both μ_E_{a, n, r} ≥ μ_E_{b, n, r} and μ_H_{a, n, r} ≥ μ_H_{b, n, r} held true.

• 3. For any two different solutions (e.g., Solutions C and D) having the same k (i.e., using the same model to fit the data but with different initializing parameters), they should have enough contrast in their estimates of parameters to be considered “unique”. In this work, the maximum difference calculated as follows was required to be greater than 5% if Solution C was not a duplicate of Solution D (presumably μ_H_{m+1, n, r} ≥ μ_H_{m, n, r} and μ_E_{m+1, n, r} ≥ μ_E_{m, n, r}):

  $$\max \left\{ \begin{gathered} \max \left( {\left| {\frac{{\pi_{{\text{1, c, r}}} - \pi_{{\text{1, d, r}}} }}{{\min \;(\pi_{{\text{1, c, r}}} , \, \pi_{{\text{1, d, r}}} )}}} \right| \, , \ldots , \, \left| {\frac{{\pi_{{\text{k, c, r}}} - \pi_{{\text{k, d, r}}} }}{{\min \;(\pi_{{\text{k, c, r}}} , \, \pi_{{\text{k, d, r}}} )}}} \right|} \right) \\ \, \max \left( {\left| {\frac{{\mu \_H_{{\text{1, c, r}}} - \mu \_H_{{\text{1, d, r}}} }}{{\min \;(\mu \_H_{{\text{1, c, r}}} , \, \mu \_H_{{\text{1, d, r}}} )}}} \right| \, , \ldots , \, \left| {\frac{{\mu \_H_{{\text{k, c, r}}} - \mu \_H_{{\text{k, d, r}}} }}{{\min \;(\mu \_H_{{\text{k, c, r}}} , \, \mu \_H_{{\text{k, d, r}}} )}}} \right|} \right) \, \\ \max \left( {\left| {\frac{{\mu \_E_{{\text{1, c, r}}} - \mu \_E_{{\text{1, d, r}}} }}{{\min \;(\mu \_E_{{\text{1, c, r}}} , \, \mu \_E_{{\text{1, d, r}}} )}}} \right| \, , \ldots , \, \left| {\frac{{\mu \_E_{{\text{k, c, r}}} - \mu \_E_{{\text{k, d, r}}} }}{{\min \;(\mu \_E_{{\text{k, c, r}}} , \, \mu \_E_{{\text{k, d, r}}} )}}} \right|} \right) \\ \end{gathered} \right\} \ge 0.05.$$

  (11)

  For any two solutions (e.g., Solutions E and F) having different k, the solution derived from a more complicated model (i.e., model with more parameters) should provide a higher logarithmic likelihood, i.e., logL_{e, r} < logL_{f, r+1}.

• 4. For Gaussian mixtures with unrestricted covariance matrices, it is almost inevitable to have some spurious solutions (Seo and Kim 2012). Generally, a spurious solution has one or more phases which overfit a small localized random pattern in the data rather than any other underlying group structure, resulting in a solution with a high likelihood but very small generalized variance and mixing proportion of the overfitted phase (McLachlan and Peel 2000; Kim and Seo 2014). In addition, prior studies on composites have shown that their mechanical properties can only be significantly enhanced when the amount of additive or filling phase reaches above ~ 5 wt.% (Maiti and Subbarao 1991; Koerner et al. 2004; Sreekanth et al. 2009). Thus, the final constraint specified a critical concentration of 5% to identify and eliminate the spurious solutions, i.e. the fraction of each phase for a qualified solution should be at least 5% (i.e., π_{m, n, r} ≥ 0.05).

Appendix B: Upscaling Models for Calculation of Bulk Rock Properties

In geophysics, the Voigt and Reuss models are widely used to estimate the theoretical maximum and minimum elastic moduli of the dry rock frame, respectively, based on the known constituents and their volumetric fractions (Sone and Zoback 2013a, b). The Voigt upper bound is determined by assuming that the strain is uniform throughout the bulk rock, while the Reuss lower bound is obtained by assuming an iso-stress situation. For a heterogeneous rock with k phases, the two bounds are then calculated by:

$$E_{{{\text{Voigt}}}} = \sum\limits_{{r{ = 1}}}^{k} {f_{{\text{r}}} E_{{\text{r}}} } ,$$

(12)

$$\frac{1}{{E_{{{\text{Reuss}}}} }} = \sum\limits_{{r{ = 1}}}^{k} {\frac{{f_{{\text{r}}} }}{{E_{{\text{r}}} }}} ,$$

(13)

where k is the number of mechanically distinct phases; E_r the Young’s modulus of the rth identified phase with a volumetric fraction of f_r. Then the effective Young’s modulus of the bulk rock is often estimated by taking the average of the upper and lower bounds, known as the Voigt-Reuss-Hill (VRH) average:

$$E_{{{\text{VRH}}}} = \frac{{E_{{{\text{Voigt}}}} + E_{{{\text{Reuss}}}} }}{2}.$$

(14)

However, the stress and strain are generally nonuniform in rocks. Similar to the aforementioned bounding methods, the Mori–Tanaka (MT) model uses the average local stress and strain fields in the matrix-inclusion structure of a composite to predict the homogenized moduli, K_hom and G_hom, of the composites (Mori and Tanaka 1973; Benveniste 1987), which can be determined by (da Silva et al. 2013; Huang et al. 2014):

$$K_{\hom } = \left( {\sum\limits_{{r{ = 1}}}^{k} {\frac{{f_{{\text{r}}} K_{{\text{r}}} }}{{3K_{{\text{r}}} + 4G_{1} }}} } \right)\left( {\sum\limits_{{r{ = 1}}}^{k} {\frac{{f_{{\text{r}}} }}{{3K_{{\text{r}}} + 4G_{1} }}} } \right)^{ - 1} ,$$

(15)

$$G_{\hom } = \frac{{\sum\nolimits_{{r{ = 1}}}^{k} {f_{{\text{r}}} G_{{\text{r}}} \left[ {G_{1} \left( {9K_{1} + 8G_{1} } \right) + 6G_{{\text{r}}} \left( {K_{1} + 2G_{1} } \right)} \right]^{ \, - 1} } }}{{\sum\nolimits_{{r{ = 1}}}^{k} {f_{{\text{r}}} \left[ {G_{1} \left( {9K_{1} + 8G_{1} } \right) + 6G_{{\text{r}}} \left( {K_{1} + 2G_{1} } \right)} \right]^{ \, - 1} } }},$$

(16)

$$E_{\hom } = \frac{{9K_{\hom } G_{\hom } }}{{3K_{\hom } + G_{\hom } }},$$

(17)

where K₁ and G₁ particularly denote the bulk and shear moduli of the matrix in the composite. The bulk modulus K_r and shear modulus G_r of the r^th phase can be calculated by its Young’s modulus E_r and Poisson’s ratio ν_r, which is assumed to be 0.2 for all phases:

$$K = \frac{E}{3(1 - 2\nu )},$$

(18)

$$G = \frac{E}{2(1 + \nu )}.$$

(19)

The third model used in this study is the self-consistent (SC) approximation that estimates the effective moduli of a composite by not only using the volumetric fractions and properties of individual phases, but also including their geometric information, such as sphere, needle, and disk (Budiansky 1965; Wu 1966; O’Connell and Budiansky 1974, 1977). The self-consistent (SC) effective moduli $K_{{{\text{SC}}}}^{*}$ (i.e., bulk modulus) and $G_{{{\text{SC}}}}^{*}$ (i.e., shear modulus) of the bulk composite can be approximated by (Berryman 1980, 1995):

$$\sum\limits_{{r{ = 1}}}^{k} {f_{{\text{r}}} (K_{{\text{r}}} - K_{{{\text{SC}}}}^{*} )P^{{*{\text{r}}}} } = 0,$$

(20)

$$\sum\limits_{{r{ = 1}}}^{k} {f_{{\text{r}}} (G_{{\text{r}}} - G_{{{\text{SC}}}}^{*} )Q^{{*{\text{r}}}} } = 0,$$

(21)

where P^*r and Q^*r are geometric factors of the r^th phase (refer to Table 4 in Berryman 1995). Eqs. (20) and (21) are coupled and thus need to be solved simultaneously by iterations, and the self-consistent effective Young’s modulus can then be calculated by Eq. (17) with the converged solutions of $K_{{{\text{SC}}}}^{*}$ and $G_{{{\text{SC}}}}^{*}$.