IHHO: an improved Harris Hawks optimization algorithm for solving engineering problems

Abstract

Harris Hawks optimization (HHO) algorithm was a powerful metaheuristic algorithm for solving complex problems. However, HHO could easily fall within the local minimum. In this paper, we proposed an improved Harris Hawks optimization (IHHO) algorithm for solving different engineering tasks. The proposed algorithm focused on random location-based habitats during the exploration phase and on strategies 1, 3, and 4 during the exploitation phase. The proposed modified Harris hawks in the wild would change their perch strategy and chasing pattern according to updates in both the exploration and exploitation phases. To avoid being stuck in a local solution, random values were generated using logarithms and exponentials to explore new regions more quickly and locations. To evaluate the performance of the proposed algorithm, IHHO was compared to other five recent algorithms [grey wolf optimization, BAT algorithm, teaching–learning-based optimization, moth-flame optimization, and whale optimization algorithm] as well as three other modifications of HHO (BHHO, LogHHO, and MHHO). These optimizers had been applied to different benchmarks, namely standard benchmarks, CEC2017, CEC2019, CEC2020, and other 52 standard benchmark functions. Moreover, six classical real-world engineering problems were tested against the IHHO to prove the efficiency of the proposed algorithm. The numerical results showed the superiority of the proposed algorithm IHHO against other algorithms, which was proved visually using different convergence curves. Friedman's mean rank statistical test was also inducted to calculate the rank of IHHO against other algorithms. The results of the Friedman test indicated that the proposed algorithm was ranked first as compared to the other algorithms as well as three other modifications of HHO.

1 Introduction

Optimization solved nonlinear, complex, real-time issues. The metaheuristic algorithm became an intrinsic feature of all optimization processes [1]. Metaheuristics had been grown as a solution for real-world optimization problems in the last two decades. A method of optimization was defining the system's objective function, variables, limits, system properties, and optimal solution [2]. Trajectory-based and population-based approaches were two types of metaheuristic optimization. These two groups exhibit a wide range of probable answers employed in each iterative stage [3].

Randomness marked stochastic search and optimization algorithms. Two types of stochastic algorithms were heuristic and metaheuristic [4]. Heuristics are problem-dependent, and numerous heuristics can be created [5]. A metaheuristic method, on the other hand, makes few assumptions about the problem and can combine various heuristics and generate candidate solutions [6]. Metaheuristics solve intractable optimization problems. Since the initial metaheuristic was proposed, several new algorithms have now been created [7].

Metaheuristic optimization algorithms' computational efficiency is dependent on striking the right balance between exploration and exploitation [8]. Combining the terms Meta and Heuristic produces the term "metaheuristics" [9]. Metaheuristic algorithms are often characterized as just a master strategy that guides and modifies other heuristics to get answers beyond those typically generated in the pursuit of local optimality [10]. Optimizing metaheuristic algorithms has become such an active area of research and one of the most well-known high-level procedures for generating, selecting, or locating heuristics that optimize solutions as well as provide a better objective function for a real-world optimization problem [11] [12].

Every metaheuristic technique must achieve a reasonable balance between exploration and utilization of the search space for optimal performance [13]. Metaheuristics have gained appeal over exact methods for addressing optimization issues due to the ease and resilience of the answers they give in a variety of sectors, such as engineering, business, transportation, as well as the social sciences [14] [15]. A metaheuristic is an algorithm meant to tackle a wide variety of difficult optimization problems without requiring extensive problem-specific adaptation. The prefix "meta" indicates that these heuristics are "higher level" than problem-specific heuristics. Metaheuristics are often used to solve unsolvable situations [16].

For mathematical optimization problems with more than one objective for which no single solution exists, multiobjective optimization is used [17]. Stochastic optimization methods, such as metaheuristics, use mechanisms inspired by nature to solve optimization problems [18]. Metaheuristic algorithms are very good optimization techniques that have been utilized to solve a wide variety of optimization issues. Metaheuristics can be viewed as a global algorithmic framework utilized to solve multiple optimization problems with minimal modification [19], 20.

Metaheuristics outperform simple heuristics. Metaheuristic algorithms use randomization and local search. In most situations, complexity analysis, performance assessment, and metaheuristic parameter adjustment were ignored when metaheuristics were used to address optimization problems [21], 22. Single-solution metaheuristics focus on a single starting solution, whereas population-based metaheuristics focus on a large number of possible solutions [18]. It is generally more effective to use the standard metaheuristics when dealing with typical research challenges [23].

Genetic algorithms [24], evolutionary methods [25], and cultural algorithms [26] are a few of the most well-known types of algorithms. Particular to this topic is the metaheuristics for optimizing the foraging of particles as well as those for bees, insects, and bacteria [27]. The basic flow diagram for population-based metaheuristic optimization is shown in Fig. 1.

Fig. 1

Schematic flow diagram for population-based metaheuristic optimization methods

Structural control issues that require a fast convergence of the best solution sometimes benefit from metaheuristic methods. These heuristic techniques are called "metaheuristics" since they are based on a real-world phenomenon [28]. High-level problem-solving techniques can be applied regardless of the nature of the challenge. Metaheuristic procedures have an advantage over traditional methods since they can establish a unique starting point, convexity, continuity, and differentiability [29]. As illustrated in Fig. 2, metaheuristic algorithms can be categorized into a variety of subclasses based on the theory they are derived from [30]. Evolutionary, physical, and bio-inspired algorithms-based metaheuristics are the three main kinds of metaheuristics. The first technique is based on evolution, while the second technique is based on physical phenomena. On the other hand, swarm intelligence-based metaheuristics mimic social species' collective activity[31]. Single-solution algorithms may trap local optima, preventing us from finding global optimum, because they generate just one solution for a particular problem [32]. Population-based algorithms can escape local optima [33]. These algorithms are classed by their theoretical roots. Adaptive algorithms take their cues from natural selection, mutation, and recombination in nature[29]. These algorithms pick the best candidate based on population survival [34].

Fig. 2

Formalization of metaheuristic methods

One of the popular swarm-based metaheuristic optimization algorithms is called the Harris Hawks optimization (HHO) algorithm [14]. HHO is inspired by the feeding method that Harris Hawks use to search for and attack the prey. This algorithm has powerful exploration and exploitation capabilities that make it a suitable choice for solving complex problems [35]. However, HHO can sometimes fail to balance between local exploitation and global exploration. Therefore, improvements in both the exploration and exploitation phases are necessary to find additional ideal locations.

In this paper, an improved HHO (IHHO) that improves upon HHO by fixing its flaws was presented. We have compared our proposed algorithm to the original HHO and to other modifications of HHO algorithm implementations, namely BHHO [36], MHHO [37], and logHHO [38]. Also, we have compared IHHO to other recent algorithms, namely grey wolf optimization (GWO) [39], BAT algorithm [40], teaching–learning-based optimization (TLBO)[41], moth-flame optimization (MFO) [42], and whale optimization algorithm (WOA)[43]. GWO has simpler principles and fewer parameters. However, it suffers from poor convergence speed and limited solution accuracy [44]. BAT algorithm has rapid convergence but suffers from poor exploration [19]. Although the TLBO operation has no required parameters, the algorithm's drawbacks include its time-consuming iterations [41]. MFO has few configuration parameters, but early convergence is its biggest downside [42]. WOA exhibits slow convergence as a drawback, while it boasts the advantage of straightforward operation [43]. Mainly, this paper contributed in the following ways:

• Enhancing exploration ability by using the advantages of logarithms and exponentials.

• Enhancing exploitation ability by using the concept of traveling distance rate.

• Testing and comparing IHHO with other modifications of HHO and other algorithms like GWO, BAT, TLBO, WOA, and MFO on 23 standard test functions, CEC2017, CEC2019, and CEC2020.

• Testing and comparing IHHO with other modifications of HHO and other algorithms like GWO, BAT, TLBO, WOA, and MFO on six classical real-world engineering problems.

• Testing and comparing IHHO with other modifications of HHO and other algorithms like GWO, BAT, TLBO, WOA, and MFO on standard benchmark functions consists of 14 variable-dimension unimodal, 5 fixed-dimension unimodal, 20 multimodal fixed-dimension, and 13 multimodal fixed-dimension benchmark functions.

• Using Friedman mean rank statistical test to calculate the rank of IHHO against other algorithms.

The remainder of this study is structured as follows. The second section provides a literature review regarding HHO and its modifications. In Sect. 3, the mathematical concept and computing techniques of the HHO algorithm are explained. In Sect. 4, the concepts behind our proposed IHHO are provided. In Sect. 5, the simulation results of IHHO as compared to other algorithms on several benchmarks are discussed. Finally, Sect. 6 includes the conclusion of the work and future works.

2 Related work

Harris hawks are one of nature's most intelligent birds. These birds know how to lead a group and work together to find a certain rabbit. Various forms of assault and evasion take place during this stage [45]. A Harris hawk hunts with support from family members in the same stable [46]. This desert predator can follow, surround, and flush its prey [47]. This hawk's chase habits may differ based on its environment and prey. A Harris hawk switches activity and works with other predators to confuse prey [48]. HHO is based on Harris hawks' cooperative hunting and esca**. Multiple Harris hawks strike from different angles to converge on an esca** rabbit and use varied hunting strategies [49].

Harris Hawks optimization (HHO) is based on hawk hunting. With fewer modification parameters and a significant optimization effect, it's competitive with similar methods [50]. Many academics prefer HHO's global search efficiency as a population-based metaheuristic algorithm [51]. HHO keeps a flock of hawks. The literature shows that HHO has solved challenging optimization problems in several fields [52].

According to Alabool et al., 2021, Fig. 3 shows that HHO's adaptability has been enhanced, and/or additional algorithms have been merged to increase the quality of optimization solutions. There were 49 different HHO variants studied in this review, including six different modifications, 26 distinct hybridizations, one multiobjective version 2, a binarization variant, and 7 chaotic variants [14]. This form of HHO demonstrates HHO's capacity to develop answers to a wide range of optimization issues.

Fig. 3

HHO and HHO editions

2.1 Modifications of HHO

According to Ridha et al. [36], the exploration and exploitation stages of the boosted mutation-based Harris Hawks optimization (BHHO) algorithm are built using two adaptive approaches. Random steps inspired by the flower pollination algorithm (FPA) with levy flight (LF) ideal notion are employed in the first adaptive approach. Also, the second adaptive technique examines an ideal mutation vector using differential evolution (DE) influenced by the 2-Opt method. A wide range of meteorological conditions has been used to test the proposed BHHO algorithm's performance [53]. The new version has a lot more sturdiness. An increase in diversification is the starting point of its search patterns, but it quickly moves on to exploitation. Average absolute error levels for the proposed BHHO approach were no better than those for other methods [54].

According to Gupta et al. [56], differential fast dives and opposition-based learning are all part of typical HHO. As a result of these techniques, HHO's search efficiency is increased and problems like stagnation at poor options and premature convergence are resolved. modified HHO (mHHO) was the reworked HHO. Standard HHO can't achieve the balance between these two operators that are needed to improve exploration and extraction quality [55]. In issue F7, the mHHO solution surpasses traditional HHO and obtains its optimal value. mHHO can't get to the optima in F9, but it's more accurate than regular HHO in terms of searching [56].

According to Yousri et al. [58], using a new technique dubbed the modified Harris Hawks optimizer, the switching matrix can be reconfigured in such a way as to maximize array generated power, according to the findings in the research [57]. Different stages of the investigation apply the basic Harris Hawk's optimizer for the same problem. To top it all off, the enhanced Harris Hawks optimizer generates the optimal solar array arrangement in less than a single second [58].

According to Devarapalli et al. [59], the HHO algorithm was put out as a potential solution. Dam** devices were evaluated with HHO, GWO, and MFO algorithms under various loads. To find the best control parameters, 500 iterations were used for each method to undertake a variety of system analyses. Eigenvalue analysis and system performance characteristics under perturbation were compared among the various optimization methodologies. According to a detailed comparison, the logarithmic function of the modified HHO resulted in superior system operating conditions [38].

According to Hussain et al. [52], long-term memory HHO (LMHHO) could be better investigated. When the search isn't halted at a predetermined level, the new method produces superior results. It was important for LMHHO to maintain a balance between exploration and extraction during its extensive search [59]. On numerical optimization challenges with low- and high-dimensional landscapes, LMHHO proved its search efficiency by outperforming the original and numerous established and recently released competitors [60]. Figure 4 presents summary of the modifications to HHO.

Fig. 4

Specifics of some HHO editions

2.2 Hybridization of HHO

Fan et al., 2020, claimed that HHO tends to be stuck in limited variety, local optimums, and imbalanced exploitation abilities. As a way to increase the performance of HHO, a new quasi-reflected Harris Hawk’s algorithm (QRHHO) was presented, which incorporated the HHO method and the QRBL together. After introducing the QRBL mechanism to promote population diversity, QRBL was added to each population update to raise the convergence rate. The QRBL mechanism is primarily used in the starting phase and each population update phase of the proposed technique. The experimental results revealed that the QRHHO algorithm performs better than the standard HHO, two versions of HHO, and six other swarm-based intelligent algorithms [70] proposed a chaotic multiverse Harris Hawks optimization (CMVHHO), a modified form of multiverse optimizer (MVO) based on chaos theory and HHO. The suggested method uses chaotic maps to get the optimal MVO parameters. Local searches help MVO maximize search space. The original MVO was modified using HHO. Chaos maps were used to determine appropriate MVO settings, while HHO increased the MVO's searchability. The recommended strategy for global optimal solutions showed great convergence and statistical analysis. The proposed CMVHHO solved four engineering problems better than the current methods. When compared to PSO and GA, CMVHHO consumed more CPU time, although it is still faster than using the simple MVO algorithm [69].

Menesy et al., 2019, proposed chaotic HHO (CHHO) to precisely estimate the operational parameters of the proton exchange membrane fuel cell (PEMFC), which models and duplicates its electrical performance. By preventing HHO from being stuck in local optima, the CHHO was intended to improve on the normal HHO's search capabilities while still maintaining its functionality. CHHO outperformed current metaheuristic optimization techniques. In all case scenarios, the CHHO predicted the optimal PEMFC stack characteristics precisely [70].

It is clear from the discussion above that there is a lot of literature in this field. The Harris Hawks optimization (HHO) method is a sophisticated metaheuristic algorithm for addressing complicated problems [11]. However, HHO can easily fall within the local minimum. Because of the adjustments to each phase, the other modifications of HHO make it impossible to achieve a healthy balance between exploration and exploitation [39]. Improved Harris Hawks optimization (IHHO) algorithm is capable of handling various engineering jobs and is capable of reaching a good equilibrium between exploitation and exploration as a result of phase-by-phase adjustments [59].

3 Harris Hawk’s optimization (HHO)

The Harris Hawk Optimizer, proposed by Heidari et al., is an optimization technique inspired by the natural world Harris Hawks [47]. HHO is an innovative swarm-based optimizer that is both quick and effective. It possesses several exploratory and exploitative methods that are deceptively straightforward yet very efficient, and it has a dynamic structure for addressing continuous problems [71]. This method is a population-based metaheuristic that mathematically mimics natural events. In addition, the coordinated manner in which Harris's Hawks pursue their prey and surprise it served as inspiration for this algorithm's design [72]. The victim is startled because multiple hawks are attempting to attack it from different directions at the same time [73]. Since HHO is an inhabitant’s optimization technique that does not use gradients, it can be used for any optimization issue as long as it is formulated correctly. Figure 5 depicts all of the phases of HHO, each of which will be discussed within the next subsections.

Fig. 5

Explains the HHO's major stages

3.1 Exploration phase

During this stage of the HHO, Harris' hawks perch at random in various areas and wait to locate a victim characterized by two tactics that take into account the fact that the hawks would wait at various places to identify the prey. Following is a mathematical model Eq. (1). of the search strategies utilized for the investigation of the search space:

$$X\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {X_{{{\text{rand}}}} \left( t \right) - r_{1} \left| {X_{{{\text{rand}}}} \left( t \right) - 2r_{2} X\left( t \right)} \right|} \hfill & {q \ge 0.5} \hfill \\ {\left( {X_{{{\text{rabbit}}}} \left( t \right) - X_{m} \left( t \right)} \right) - r_{3} \left( {{\text{LB}} + r_{4} \left( {{\text{BU}} - {\text{LB}}} \right)} \right)q} \hfill & {q < 0.5} \hfill \\ \end{array} } \right.$$

(1)

Here $X (t + 1)$ seems to be the coordinates of hawks within the next iteration,${X}_{rabbit}(t)$ is the location for rabbit, $X(t)$ is just the current position vector for hawks, and ${r}_{1}$, ${r}_{2}$, ${r}_{3}$, ${r}_{4}$, and $q$ are randomized values within (0,1) updated in each iteration. ${\text{LB}}$ and ${\text{UB}}$ display variable upper and lower boundaries, ${X}_{{\text{rand}}}(t)$ is chosen at the random hawk, and ${X}_{m}$ is the population's average position. Equation (2) gives the average hawk posture.

$${X}_{m }\left(t\right)= \frac{1}{N} \sum_{i=1}^{N}{X}_{i}(t)$$

(2)

where $N$ is the count of Hawks and ${X}_{i}(t)$ is its position at iteration $t$.

3.2 The transformation from exploration to exploitation

Exploration and exploitation are two different stages of the HHO algorithm. It is possible to model the energy required to make this shift using Eq. (3):

$$E = 2{E}_{0}\left(1 - \frac{t}{T}\right)$$

(3)

$E$ represents the prey's fleeing energy, $T$ is just the maximum number of rounds, and ${E}_{0}$ randomly fluctuates within the interval (−1, 1) which is modeled using Eq. (4).

$${E}_{0} = 2 * {\text{rand}}-1$$

(4)

3.3 Exploitation phase

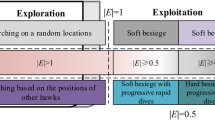
The hawks use the surprise pounce to strike the rabbit in their transition from the exploring stage to the exploitation phase. Additionally, the rabbit makes a desperate bid to flee this perilous scenario. The hawks are required to use a variety of chasing techniques. Harris' hawks use a variety of evasive tactics to get their prey. The attacking stage can be described using four well-considered techniques.

The $r$ represents the probability of the rabbit evading the hawks. When it is greater than or equal to 0.5, the rabbit is unable to evade the hawks who employ either a soft besiege or a hard besiege. When the rabbit's health is less than 0.5, hard besieges with progressive rapid dives or soft besieges with progressive rapid dives are the techniques employed by the hawks.

3.3.1 Soft besiege

When $r$ and $|E| \ge 0.5$, the rabbit can elude the hawks because it has a great deal of endurance. As a result, the Harris hawks gently encircle the rabbit before performing the surprise pounce. This behavior is modeled by using Eq. (5) and Eq. (6):

$$X \left(t + 1\right)= \Delta X\left(t\right)-E\left|{JX}_{{\text{rabbit}}}\left(t\right)- X\left(t\right)\right|$$

(5)

where $J = 2*(1-{r}_{5})$

$$\Delta X\left(t\right)= {X}_{{\text{rabbit}}}\left(t\right)- X\left(t\right)$$

(6)

$\Delta X(t)$ specifies the difference between the rabbit's position vector as well as its current position in iteration $t$. The r 5 parameter is a random number between 0 and 1, and $J$ reflects the rabbit's randomized leap strength as it flees.

3.3.2 Hard besiege

When $r \ge 0.5$ and $|E| < 0.5$, the rabbit can evade the hawks, but he has quite a bit of energy. To pull off the final surprise pounce, the Harris hawks barely have time to encircle their prey. This behavior is modeled by using Eq. (7):

$$\Delta X\left(t\right)= {X}_{{\text{rabbit}}}\left(t\right)- E\left|\Delta X\left({\text{t}}\right)\right|$$

(7)

Figure 6 shows a simple illustration of this process with one hawk.

Fig. 6

Vectors for a hard-besieged situation

3.3.3 Soft besiege with progressive rapid dives

When $r < 0.5$ and$|E| \ge 0.5$, the rabbit is still alive, but it has lost its capacity to run away. This flying mimics the rabbit’s zigzag motion and the erratic dives made by hawks around a fleeing rabbit. Using the Levy flight, this behavior is modeled by using Eq. (8):

$$Y = {X}_{{\text{rabbit}}}\left(t\right) -E\left|{JX}_{{\text{rabbit}}}\left(t\right)- X\left(t\right)\right|$$

(8)

Then, they compare the likely outcome of such a movement to the prior dive to determine whether or not it was a good dive. They will dive according to the following rule by Eq. (9):

$$Z = Y + S \times {\text{LF}} \left(D\right)$$

(9)

where $D$ denotes the problem dimension, $S$ denotes a random vector of size $1\times D$, and $LF$ denotes the levy flight function, which is computed using Eq. (10):

$${\text{LF}} \left(x\right)= 0.01 \times \frac{\mathrm{u }\times\upsigma }{{\left|{\text{v}}\right|}^{\frac{1}{\upbeta }}}, \sigma = {\left(\frac{\Gamma \left(1 +\upbeta \right)\times {\text{sin}}\left(\frac{\mathrm{\pi \beta }}{2}\right)}{\Gamma \left(\frac{1+\upbeta }{2}\right)\times\upbeta \times {2}^{\frac{\upbeta -1}{2}}}\right)}^{\frac{1}{\upbeta }}$$

(10)

where $u$, $v$ are random values within (0,1), and $\upbeta$ is a constant set to 1.5 by default.

Thus, Eq. (11) can be used to determine the ultimate approach for updating the positions of hawks throughout the gentle besiege phase:

$$X\left(t + 1\right)= \left\{\begin{array}{c}Y \; if \; F \left({\text{Y}}\right)< F \left({\text{X}}\left({\text{t}}\right)\right)\\ Z \; if \; F \left({\text{Z}}\right)< F \left({\text{X}}\left({\text{t}}\right)\right)\end{array}\right.$$

(11)

Figure 7 shows an example of this process applied to a single hawk.

Fig. 7

An illustration of general vectors in the scenario of a hard besiege with progressive quick dives

3.3.4 Hard besiege with progressive rapid dives

When $r$ and $|E| < 0.5$, the rabbit has exhausted its reserves of energy and is unable to flee. Hawks make an effort to decrease the distance between their usual locations. This behavior is modeled by using Eq. (12):

$$X\left(t + 1\right)= \left\{\begin{array}{c}Y \; if \; F \left({\text{Y}}\right)< F \left({\text{X}}\left({\text{t}}\right)\right)\\ Z \; if \; F \left({\text{Z}}\right)< F \left({\text{X}}\left({\text{t}}\right)\right)\end{array}\right.$$

(12)

where $Y$ and $Z$ are calculated according to new principles in Eq. (13) and Eq. (14). Figure 8 shows a simple illustration of this phase in action.

$$Y = {X}_{{\text{rabbit}}}\left(t\right) -E\left|{JX}_{{\text{rabbit}}}\left(t\right)- {X}_{m}\left(t\right)\right|$$

(13)

$$Z = Y + S \times LF \left(D\right)$$

(14)

where ${X}_{m}\left(t\right)$ is found by solving Eq. (2).

Fig. 8

An illustration of general vectors in the scenario of a hard besiege with progressive quick dives in 2D and 3D space [47]

Algorithm 1 presents the details of how the traditional HHO works.

Algorithm 1

Pseudo-code of HHO algorithm

The accompanying flowchart is in Fig. 9 which outlines the operation of HHO.

Fig. 9

HHO flowchart

4 Proposed modification of HHO

Even though the original HHO has a special weight compared to other common approaches, while working on the local exploitation of feasible solutions, it may not reach an optimal set of scales between locally accurate exploitation and worldwide exploratory search because some of the used strategies are simple and can quickly converge, which might lead it to skip several of the optimal regions. Therefore, improvements in both the exploration and exploitation phases are necessary to find additional ideal locations and optimize the exploitation approach. Therefore, the following can serve as updates to the exploration phase (perching based on random locations) and exploitation strategies 1, 3, and 4:

4.1 Updating exploration phase (perching based on random locations):

To find prey, Harris' hawks use one of two methods during the exploration phase: perching at random in various areas and waiting for the right moment. When solving for the first line of Eq. (1) in the standard HHO, the hawks typically use the prey's location and that of any other household members. Setting each phase of the global search to be completely random is unlikely to happen. Consequently, it still might be unable to achieve a perfect balance between very specific local searches and broad, exploratory ones. In conventional HHO, the first line of Eq. (1) is dependent on the range of values for the variable from 0 to 1. There are two ways to find a hawk's prey: either immediately or after a lengthy search.

To avoid becoming stuck in a rut and settling for suboptimal solutions, we exploit the features of logarithms and exponentials to generate random values in previously unexplored regions [74]. It can be seen that the exponential function of the current iteration concerning the upper bound of the iteration problem helps to increase the exploration rate in the early stages of the iteration. To avoid being stuck in a local solution, we generated random values using logarithms and exponentials to explore new regions more quickly and locations we had not yet reached.

$$X\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {X_{m} \left( t \right)*0.5 - \left( {\left( {X_{{{\text{rand}}}} \left( t \right) + r_{1} *X\left( t \right)} \right) + \left( {X_{{{\text{rand}}}} \left( t \right) + r_{1} *X\left( t \right)} \right)} \right)} \hfill & {q \ge 0.5} \hfill \\ {\left( {X_{{{\text{rabbit}}}} \left( t \right) - X_{m} \left( t \right)} \right) - r_{3} \left( {LB + r_{4} \left( {UB - LB} \right)} \right)} \hfill & {q < 0.5} \hfill \\ \end{array} } \right.$$

(15)

$${r}_{1} = 1-log\left(1+{e}^{ub}\right)$$

(16)

Here $X (t + 1)$ seems to be the coordinates of hawks within the next iteration, ${X}_{rabbit}\left(t\right)$ is the location for rabbit, $X(t)$ is just the current position vector for hawks, ${r}_{3}$, ${r}_{4}$, and $q$ are randomized values within (0,1) updated in each iteration, $LB,$ and $UB$ display variable upper and lower boundaries, ${X}_{rand}\left(t\right)$ is chosen at the random hawk, and ${X}_{m}\left(t\right)$ is the population's average position.

4.2 Updating exploitation (strategy 1):

At this stage, the Harris hawks have barely cornered their victim before they pounce. The prey may be wary, but this stage ignores the rabbit's unnatural jumps to freedom that can occur. Since this stage contains local drops that cause local falls, we modified it by providing the probability of random jumps of prey that might occur, allowing us to quickly reach an optimal solution. The following equation Eq. 17 is an updated version of Eq. 7:

$$X\left(t + 1\right) =0.01*E*{X}_{{\text{rabbit}}}\left(t\right)-0.1*\left|{J}_{1}* {X}_{{\text{rabbit}}}\left(t\right)-{X}_{m}\left(t\right)\right|$$

(17)

where ${J}_{1}= (2*rand-1)$

${X}_{m}$ is the population's average position. The rand parameter is a random number between 0 and 1, and $J$ reflects the rabbit's randomized leap strength as it flees.

4.3 Updating exploitation (strategy 3):

To swiftly increase the diversity of options for the existing population, Strategy 3 is replaced by steps inspired by the average distance traveled [75], which helps to (1) discover new solutions, (2) prevent slip** into the local solution as a result of the larger diversity of results, and (3) reach the ideal solution in a faster way as a result of the faster increase in the existing population. It can be expressed by the following equation Eq. 18:

$${G}_{1}=i*\left(1-\frac{{t}^\frac{1}{i}}{{T}^\frac{1}{i}}\right)$$

(18)

where $i$ is a constant that dictates the exploitation accuracy as iterations go. That is, when $i$ is higher, exploitation and local search occur faster and with more precision. The following equations Eq. (19), Eq. (20) is an updated version of Eq. 8 and Eq. 9:

$$\text{Y }= \frac{{{\text{X}}}_{{\text{rabbit}}}\left({\text{t}}\right)}{{\text{i}}} - {\text{rand}}*{\text{E}}\left|{{{\text{G}}}_{1}*{\text{JX}}}_{rabbit}\left({\text{t}}\right)-\text{ X}\left({\text{t}}\right)\right|$$

(19)

$$Z = {X}_{{\text{rabbit}}}\left(t\right)- {\text{rand}}*E\left|{G}_{1}*J{X}_{{\text{rabbit}}}\left(t\right)- X\left(t\right)\right| -1.5*\frac{{G}_{2}}{{\text{Levy}}({\text{dim}})}$$

(20)

where ${G}_{2}$ considers $i$ in Eq. 18 to be a constant set to 6.

$$X(t + 1) = \left\{\begin{array}{c}Y \; if \; F (Y) < F (X(t))\\ Z \; if \; F (Z) < F (X(t))\end{array}\right.$$

(21)

4.4 Updating exploitation (strategy 4)

Hawks make an effort to shorten the distance between their typical roosting and feeding grounds. To swiftly enhance the diversity of possibilities for the current population, Strategy 4 is replaced with steps inspired by the average distance traveled [61]. Because there is a greater variety of results, it is easier to (1) discover new solutions and (3) locate the optimum answer faster because the present population is growing at a faster rate. The modeling of this behavior utilizes the Eq. (20):

$$X\left(t + 1\right)= \left\{\begin{array}{c}Y \; if \; F \left({\text{Y}}\right)< F \left({\text{X}}\left({\text{t}}\right)\right)\\ Z \; if \; F \left({\text{Z}}\right)< F \left({\text{X}}\left({\text{t}}\right)\right)\end{array}\right.$$

(22)

where $Y$ and $Z$ are calculated according to new principles in Eq. (23) and Eq. (24)

$$Y = \frac{{X}_{{\text{rabbit}}}\left(t\right)}{i} - {\text{rand}}*E\left|{{G}_{1}*JX}_{{\text{rabbit}}}\left(t\right)- Xm\left(t\right)\right|$$

(23)

$$Z = {X}_{{\text{rabbit}}}\left(t\right)- {\text{rand}}*E\left|{G}_{1}*J{X}_{{\text{rabbit}}}\left(t\right)- Xm\left(t\right)\right| -1.5*\frac{{G}_{2}}{{\text{Levy}}({\text{dim}})}$$

(24)

Algorithm 2 gives explains the details of Improved HHO (IHHO).

Algorithm 2

Pseudo-code of modified HHO algorithm (IHHO)

The accompanying flowchart is in Fig. 10 which outlines the operation of IHHO.

Fig. 10

IHHO flowchart

5 Experimental results and analysis

This section presents the experimental results of applying IHHO on various benchmarks and testing its performance against other algorithms. To ensure that all algorithms are given a fair chance, all algorithms have been applied for 30 separate runs and 500 iterations. All algorithms have the same population size of 30. The parameters of the different algorithms are given in Table 1.

Table 1 Parameter Setting

The Friedman mean rank statistical test was used. Friedman recommended using a rank-based statistic to overcome the implicit assumption of normalcy in the analysis of variance[76]. The independence of several experiments leading to ranks is evaluated using Friedman's test. In practical use, the hypothesis testing can be obtained using an asymptotic analytical approximation valid for big N or large k, or from published tables containing accurate values for small k and N[77]. This assertion applies to both approximate tests of significance for comparing all (^k₂) = k(k − 1)/2 pairs of treatments and tests for comparing k − 1 treatments with a single control. The utility of asymptotic tests is dependent on their ability to approximate the exact sample distribution of the discrete rank sum difference statistic [78].

The precise null distribution improves significance testing in the comparison of Friedman rank sums and serves as a foundation for assessing theoretical approximations of the genuine distribution. For both many-one and all-pairs comparisons, the simple normal approximation matches the precise results the best among the large-sample approximation techniques [78]. For major occurrences farther into the distribution's tail, there may be a big discrepancy between the approximation p-values that are exact and normal. These kinds of events specifically happen when there are a lot of groups (k) and few blocks (n). Application of the normal approximation raises the likelihood of a Type-II error in a multiple testing setting with "large k and small n," leading to mistaken acceptance of the null hypothesis of "no difference."[79]

5.1 CEC 2005 benchmark functions

The proposed algorithm IHHO is examined by utilizing a well-studied collection of various benchmark functions taken from the IEEE CEC 2005 competition [80]. Unimodal (UM), High-dimensional multimodal (MM), and fixed-dimension multimodal are the three basic types of benchmark landscapes that are represented in this set. These are the UM operations (F1–F7), the MM Procedures (F8–F13), and functions of several dimensions that are fixed (F14–F23). Tables 2, 3, 4 demonstrate the mathematical formalism and features of Unimodal, High-dimensional multimodal, and fixed-dimension multimodal problems, respectively.

Table 2 Description of unimodal benchmark functions of CEC2005

Table 3 Description of High-dimensional multimodal benchmark functions of CEC2005

Table 4 Description of fixed-dimension multimodal benchmark functions of CEC2005

5.1.1 IHHO vs HHO

The proposed IHHO has shown to be effective not just for lower-dimensional problems, but also for higher-dimensional jobs, and these benchmarks have been used in earlier studies to highlight the effect of dimension on the quality of solutions. In this experiment, original HHO and IHHO are utilized to solve the 30-dimensional, scaled versions of the UM, MM, and fixed-dimension multimodal F1-F23 multimodal test cases. For each metric, we record and compare the average AVG, STD, minimum, and maximum of the achieved results. The outcomes of IHHO against HHO to F1-F23 issues are shown in Table 5.

Table 5 Comparison of results of IHHO and HHO on standard benchmark functions

As compared to HHO, IHHO achieves vastly improved results attesting to the optimizer's higher performance. Convergence curves shown in Fig. 11 allow us to visually compare the convergence rates of IHHO and HHO algorithms. These diagrams depict typical objective values achieved by algorithms at various stages of their iterative process. Convergence plots depict iterations on the horizontal axis and objective function values on the vertical axis. The graphs make it clear that the suggested IHHO has a faster convergence rate than the original HHO method.

Fig. 11

Convergence curves for IHHO vs HHO on standard benchmark functions

5.1.2 IHHO vs other algorithms

In this part, we compare the proposed IHHO to various optimization algorithms, namely GWO [39], BAT [40], MFO [42], TLBO [41], and WOA [43]. The outcomes are compared along the 30th dimension and from F14 to F23 with a fixed dimension. Table 6 shows the obtained experimental results for scalable problems. The table shows the average and standard deviation of the objective function. Figure 12 also presents the findings about the convergence of the various techniques.

Table 6 Comparison of results between IHHO and other algorithms on standard benchmark functions

Fig. 12

Convergence curves for IHHO vs other algorithms on standard benchmark functions

As evidence of the proposed optimizer's superior performance, IHHO generates significantly better outcomes than competing methods. In particular, the theoretical best can be attained by IHHO for F1–F4. The purpose of unimodal benchmark problems is to evaluate a system's potential for exploitation. Using F1-F7 as experimental tests showed that the suggested algorithm is quite good at local searches.

It is clear from these tables and curves that the IHHO has solved the majority of the difficulties to their satisfaction. The IHHO's reliability is demonstrated by the low standard value observed for the vast majority of the problems. Because of this, the suggested IHHO has been proven to have higher accuracy in finding the global optimum by extensive experimental and statistical research.

It is possible to visually compare the convergence rates of IHHO vs other algorithms by inspecting the curves depicted in Fig. 12. The diagrams show the usual objective values attained by algorithms at different iterations. The convergence plot displays the value of the goal function on the vertical axis and the number of iterations on the horizontal axis. The figures demonstrate that the proposed IHHO has a higher rate of convergence than other recent algorithms.

The purpose of multimodal functions is to assess a system's exploratory prowess; IHHO achieves the best mean values (except F19) as well as the best standard deviations (except F17, F20, and F23). The results of the F8-F23 test demonstrate that IHHO has superb exploration ability. As seen from Table 6, the total rank is 1, making the IHHO algorithm the best of all algorithms.

In conclusion, the IHHO algorithm is more efficient than the other examined algorithms for unimodal functions; this is because the random walk method effectively increases the algorithm's capacity to jump out of the local optimum.

5.1.3 IHHO vs other modifications of HHO

In this part, the proposed IHHO to other modifications of HHO was compared, namely BHHO[36], MHHO[37], and LogHHO[38]. The outcomes are compared along the 30th dimension and from F14 to F23 with a fixed dimension. Experimental results addressing scalability issues are presented in Table 7. A summary of the objective function's mean and standard deviation is displayed below. Results on the convergence of the various methods are also shown in Fig. 13.

Table 7 Comparison of results of IHHO vs other modifications of HHO on standard benchmark functions

Fig. 13

Convergence curves for IHHO vs HHO modifications on standard benchmark functions

When compared to other modifications made to HHO, the mean values achieved by IHHO are superior. For all functions except F20, IHHO has the highest average values in accordance with BHHO, especially for (F1, F2, F3, F4). When compared to MHHO and LogHHO, the average values for IHHO are higher in every respect (F1–F4 and F20–F23). Except for F5 and F15, the median values achieved by IHHO are the highest. The results of the F8-F23 tests confirm IHHO's exceptional global capability. Table 7 shows that overall the IHHO algorithm ranks first, making it the best of its kind.

Since the random walk method effectively increases the algorithm's ability to jump from the local optimum, it can be concluded that the IHHO algorithm is more efficient than other modification algorithms analyzed for unimodal functions.

5.2 CEC 2017 benchmark functions

One of the most challenging evaluation tools is called CEC2017 [82], and it consists of thirty test jobs in a variety of formats as shown in Table 8, namely single-modal (F1), multimodal (F3–F9), hybrid (F10–F19), or combination (F20–F30). In this investigation, we set the dimensions to 10.

Table 8 Description of CEC 2017

5.2.1 IHHO vs HHO

The HHO approach is not very useful for solving difficult issues such as CEC 2017, but it does exceptionally well on routine, low-dimensional projects. In agreement with the first HHO, the newly proposed IHHO has proven to be effective in finding solutions to challenging challenges.

In Table 9, IHHO to HHO after putting it through its paces on the CEC2017 test functions (except F2, which is unstable) was compared. This was done to determine which of the two was superior.

Table 9 Comparison of results of IHHO and HHO on CEC2017

As can be seen in Table 9, the suggested algorithm IHHO fared well in all functions with the original HHO. According to the tests, IHHO outperforms the original HHO algorithm in every used metric. Generally speaking, IHHO achieves the greatest median values, except for F8, F21, and F24. IHHO algorithm outperforms other analyzed modification methods for unimodal functions due to its increased capacity to escape the local optimum using the random walk approach.

Visually contrasting the convergence of the original HHO algorithm is done by examining the curves in Fig. 14. Typical objective values reached by algorithms throughout multiple iterations are depicted in these figures. On the vertical axis of the convergence plot is the value of the objective function, and on the horizontal axis is the number of iterations. As can be seen in the figures, the suggested IHHO has a faster speed of convergence than that of the original HHO.

Fig. 14

Convergence curves for IHHO vs HHO on CEC2017

5.2.2 IHHO vs other algorithms

Here, we evaluate the proposed IHHO in comparison to other popular optimization methods, namely the BAT algorithm [40], MFO [42], TLBO [41], and WOA [43]. Experimental results addressing scalability issues are presented in Table 10, which presents a summary of the objective function's mean and standard deviation. Results on the convergence of the various methods are also shown in Fig. 15.

Table 10 Comparison of results between IHHO and other algorithms on CEC2017

Fig. 15

Convergence curves for IHHO vs other algorithms on CEC2017

The average values attained by using IHHO are higher than those obtained using other recent algorithms. According to the TLBO and BAT algorithms, IHHO typically has the greatest average values across the board for all frequencies. IHHO has higher average values than the WOA algorithm does across the board, but especially for (F1, F3, F9, F12, F14, F19, F30). In every case, the average values for IHHO are greater than those for the MFO method, particularly for (F1 to F10, F19, F26, F30). Except for F18 and F27, IHHO consistently produces the highest average results. Table 10 shows that the performance of the proposed IHHO algorithm outperforms the performance of the original HHO method as well as all other algorithms and the rank for all equations is 1.

The IHHO technique outperforms other analyzed modification methods for unimodal functions due to its increased capacity to escape the local optimum using the random walk approach. Because the random walk approach effectively boosts the algorithm's capacity to jump out of the local optimum, the IHHO algorithm outperforms the other algorithms studied for unimodal functions.

5.2.3 IHHO vs other modifications of HHO

Here, the proposed IHHO to other HHO variants such as BHHO [54], MHHO[37], and LogHHO [38]. Table 11 displays experimental results that address scalability concerns in terms of the mean and standard deviation of the objective function evaluated. Figure 16 also displays the convergence results for the different approaches.

Table 11 Comparison of results of IHHO vs other modifications of HHO on CEC2017

Fig. 16

Convergence curves for IHHO vs HHO modifications on CEC2017

Using CEC2017 functions, we compared the suggested change IHHO to other modifications of the original HHO and found that IHHO provided much better performance. The IHHO algorithm is superior to the other examined variations for functions because of random walk technique significantly improves the algorithm's ability to escape the local optimum. Table 11 shows that the performance of the IHHO algorithm outperforms the performance of the original HHO method as well as all other HHO modification algorithms and the rank for all equations is 1.

Figure 16 shows typical objective values attained by algorithms over the course of numerous iterations, allowing for a visual comparison of the convergence rates. A convergence plot displays the value of the goal function along the vertical axis and the number of repetitions along the horizontal axis. The results clearly show that the proposed IHHO has a higher rate of convergence compared to the baseline HHO method and various modifications.

5.3 CEC 2019 benchmark functions

The benchmark test functions from the IEEE Congress on Evolutionary Computation serve as the basis for IHHO's evaluation (CEC-C06, 2019 Competition) [83]. Functions for 2019 Benchmark Tests in the CEC-C06 Standard As a secondary measure, IHHO is applied to 10 state-of-the-art CEC benchmark test functions.

Unlike CEC01-CEC03, CEC04-CEC10 undergoes both translation and rotation. There is, however, scalability across the board for the test procedures. Although CEC04–CEC10 have the same dimensions as a 10-dimensional constrained optimization problem in the [-100, 100] border range, CEC01–CEC03 have different dimensions, as indicated in Table 12.

Table 12 The description of CEC2019

5.3.1 IHHO vs HHO

In Table 13, a comparison of the results of IHHO vs HHO after putting it through its paces on the CEC2019 test functions is presented. This was done so that we could determine which one was superior. CEC01-CEC03 has varied dimensions, however, CEC04-CEC10 had a 10-dimensional constrained optimization problem within the [–100, 100] border range.

Table 13 Comparison of results of IHHO and HHO on CEC2019

According to Table 13, the performance of IHHO is superior to that of the original HHO, with the exception of CEC02. IHHO outperforms other analyzed approaches for modifying functions due to its higher capacity to escape the local optimum utilizing the random walk approach. This is the primary reason for IHHO's superior performance.

Viewing the curves in Fig. 17 allows for a comparison of the convergence periods of IHHO and the original HHO method to be carried out visually. The figures present an illustration of the typical objective values that are attained by algorithms after going through some iterations. It is clear from looking at the figures that the proposed IHHO method converges at a point more quickly than the conventional HHO approach does.

Fig. 17

Convergence curves for IHHO vs HHO on CEC2019

5.3.2 IHHO vs other algorithms

Our comparison of IHHO to other algorithms, namely GWO [39], BAT [40], MFO [42], TLBO [41], and WOA [43], can be found in Table 14 after putting it through the paces on the test functions for the CEC2019 examination. This was done so that we could decide which algorithm was the better one. For CEC04-CEC10, a 10-dimensional optimal solution is restricted within the [− 100, 100] border range. Since CEC01-CEC03 has different dimensions evaluated this function 30 times.

Table 14 Comparison of results between IHHO and other algorithms on CEC2019

According to Table 14, the performance of the IHHO algorithm is better than that of all other algorithms, with the exception of the CEC02 method. IHHO outperforms BAT by a significant margin when the two are compared to each other. When compared to MFO, IHHO performs better, except for CEC06. IHHO outperforms TLBO since the latter is unable to solve CEC2019 functions ranging from CEC04 to CEC10 which the former can solve. IHHO performs better than GWO and WOA in all functions with the exception of CEC02. IHHO has an overall rank of 1.

A visual comparison of the convergence periods of the IHHO method can be carried out using the convergence curves shown in Fig. 18. This allows for the comparison to be carried out visually. The figures offer a visual representation of the usual objective values that can be achieved by algorithms after they have been subjected to a certain number of iterations. When looking at the figures, it is obvious that the proposed IHHO converges at a point more quickly than the other used algorithms.

Fig. 18

Convergence curves for IHHO vs other algorithms on CEC2019

5.3.3 IHHO vs other modifications of HHO

In this paper, the proposed IHHO to other HHO variants, namely BHHO [54], MHHO [37], and LogHHO, was compared[38]. The objective function's mean and standard deviation are shown in Table 15. The results of the various approaches' convergence are also shown in Fig. 19.

Table 15 Comparison of results of IHHO vs other modifications of HHO on CEC2019

Fig. 19

Convergence curves for IHHO vs HHO modifications on CEC2019

According to Table 15, the performance of the HHO algorithm is better than that of all other modifications of HHO, with the exception of the CEC02 method. When compared to BHHO, IHHO performs better, with the exception of CEC06. IHHO performs better than MHHO and LogHHO in all functions with the exception of CEC02. IHHO has an overall rank of 1.

A visual comparison of the convergence periods of the IHHO method can be carried out using the convergence curves shown in Fig. 19. When looking at the figures, it is obvious that the proposed IHHO approach converges more quickly than the other algorithms that are traditionally used.

5.4 CEC2020 benchmark functions

Algorithms for optimizing a single-objective problem serve as the building blocks from which more complex methods, such as multiobjective, niching, and constrained optimization, are constructed. Therefore, it is crucial to work on improving single-objective optimization methods, as this can have repercussions in other areas [84]. Trials with single-objective benchmark functions are essential to the iterative refinement of these algorithms. New and more difficult algorithms are required as computing power increases. As a result, the CEC'20 Special Session has been designed in real parameter optimization to foster this symbiotic relationship between Methods and issues, which is what drives development [85].

F1–F10 has the same dimensions as a 10-dimensional constrained optimization problem in the [− 100, 100] border range as indicated in Table 16.

Table 16 The description of CEC2020

5.4.1 HHO vs IHHO

In Table 17, after putting IHHO through its paces on the CEC2020 test functions, the results are compared to those obtained using HHO. We did this to establish which option is best. Functions F1–F10 all fall into a 10-dimensional restricted optimization problem with a boundary range of [-100, 100].

Table 17 Comparison of results of IHHO and HHO on CEC2020

As can be seen in Table 17, the proposed algorithm IHHO performed similarly to the original HHO across the board. The results show that IHHO is superior to the classic HHO algorithm across the board. For unimodal functions, the IHHO algorithm excels above other studied modification methods due to its greater capacity to escape the local optimum using the random walk approach.

Figure 20 is a visual comparison of the curves used in the initial HHO method and its subsequent iterations. These examples illustrate the typical objective values that algorithms can achieve after some rounds. Convergence plots typically have the goal function's value on the vertical axis and the number of iterations on the horizontal. Convergence times for the proposed IHHO and the baseline HHO both improve, as shown graphically.

Fig. 20

Convergence curves for IHHO vs HHO on CEC2020

5.4.2 IHHO vs other algorithms

In this section, the proposed IHHO to some established competitors, such as the BAT algorithm [30], MFO [32], TLBO [31], and WOA [33] was compared. Table 18 summarizes the mean and standard deviation of the goal function and contains experimental results that address scalability concerns. Convergence results for several different approaches are also displayed in Fig. 21.

Table 18 Comparison of results between IHHO and other algorithms on CEC2020

Fig. 21

Convergence curves for IHHO vs other algorithms on CEC2020

When compared to other modern algorithms, IHHO often yields greater average results. IHHO has the highest average values across the board for all functions, as compared to WOA, MFO, TLBO, and BAT algorithms. On average, IHHO always has the best outcomes. According to Table 18, the proposed IHHO algorithm has superior performance compared to the original HHO method, as well as to all other methods and the rank for all equations of 1.

For unimodal functions, IHHO performs better than other analyzed modification approaches due to its superior ability to break out of the local optimum via a random walk. The IHHO algorithm outperforms its competitors for unimodal functions because the random walk strategy improves the algorithm's ability to escape the local optimum.

5.4.3 IHHO vs other modifications of HHO

The proposed IHHO to other HHO variants such as BHHO [40], MHHO[27], and LogHHO [28] were compared. The experimental outcomes that meet scalability concerns in terms of the mean and standard deviation of the objective function are shown in Table 19. Similarly, the convergence results for each method are shown in Fig. 22.

Table 19 Comparison of results of IHHO vs other modifications of HHO on CEC2017

Fig. 22

Convergence curves for IHHO vs HHO modifications on CEC2020

Using CEC2020 functions, we discovered that the proposed IHHO significantly improved performance over other changes of the original HHO. To get away from the local optimum, IHHO uses a random walk technique that gives it a significant advantage over the other variants tested for the function. According to Table 19, the modified HHO algorithm has superior performance compared to the original HHO method, as well as all other HHO modification algorithms and the rank for all equations of 1.

In contrast to the original HHO approach and its variants, the suggested IHHO is shown to converge faster.

5.5 Standard benchmark functions

An optimization algorithm has to be able to sift through the Search space, identify attractive regions, and then capitalize on those regions to get a global optimum [82]. For an algorithm to converge on the global optimum, it has to strike a balance between exploring new territory and capitalizing on what has already been discovered. In this part, IHHO's efficiency, reliability, and stability were assessed.

The 52 benchmark functions used to assess IHHO’s efficacy fall into four categories: (i) 14 unimodal variable-dimension benchmark functions; (ii) 5 unimodal fixed-dimension benchmark functions; (iii) 20 multimodal fixed-dimension benchmark functions; and (iv) 13 multimodal variable-dimension benchmark functions. Tables 20, 21, 22 and 23 list the names of all these methods and their associated attributes.

Table 20 A characterization of benchmark functions with variable dimensions and unimodality

Table 21 A characterization of benchmark functions with fixed dimensions and unimodality

Table 22 An explanation of benchmark functions for multimodal that are fixed in dimension

Table 23 An explanation of benchmark functions for multimodal that are variable in dimension

A table's global minimum is denoted by the column labeled"${f}_{min}$," while the column labeled "Dim" displays the number of variables (design variables) for the functions. Additionally, the variable-dimension unimodal benchmark functions are described in Table 20; the fixed-dimension unimodal benchmark functions are shown in Table 21; the multimodal benchmark functions are described in Table 22; and the variable-dimension multimodal benchmark functions are presented in Table 23.

5.5.1 IHHO vs HHO

In Table 24, a comparison between HHO and IHHO is shown after putting it through its paces on the benchmark functions. This was done so that the best option could be determined. These functions thirty times for a total of five hundred iterations were evaluated.

Table 24 Comparison of results of IHHO and HHO on 52 benchmark functions

According to unimodal variable-dimension benchmark functions, the results shown in Table 25 indicate that the performance of HHO is better than that of the original HHO, with the exception of F6 HHO and IHHO achieving the fitness function. The fitness function is attained via HHO and IHHO. Since IHHO uses a random walk strategy to break out of the local optimum, it outperforms the other approaches examined for modifying functions. Because of this, IHHO outperforms the alternatives. That is much to credit for IHHO's improved efficiency. Besides F5, F9, F11, and F14, IHHO satisfies the fitness function in all other functions.

Table 25 Comparison of results between IHHO and other algorithms on 52 benchmark functions

Looking at the curves in Fig. 23, one can quickly and easily compare the convergence times of the original HHO technique with the original HHO.

Fig. 23

Unimodal variable-dimension curves

Data from Table 24 show that IHHO outperforms the original HHO when compared to unimodal fixed-dimension benchmark functions. IHHO excels at changing functions because it utilizes a random walk method to escape the local optimum. This is why IHHO performs better than its competitors. Having that as a factor has greatly contributed to IHHO's increased productivity.

Convergence periods for the original HHO method and the original HHO may be easily compared from the curves in Fig. 24.

Fig. 24

Convergence curves for IHHO vs HHO on unimodal fixed-dimension curves

Table 24 reveals that when compared to multimodal fixed-dimension benchmark functions, IHHO performs better than the original HHO. Because it employs a random walk strategy to break out of the local optimum, IHHO is particularly effective at resha** functions. The averages at which the HHO fitness was achieved, IHHO achieved as well, and the commentators that the original HHO could not achieve the required physical fitness, the modification achieved. Because of this, IHHO outperforms its rivals. The presence of such a component is a major reason for IHHO's improved output.

The curves in Fig. 25 allow for a direct comparison of the convergence times of the IHHO technique with the original HHO.

Fig. 25

Convergence curves for IHHO vs HHO on multimodal fixed-dimension curves

Table 24 reveals that when compared to multimodal fixed-dimension benchmark functions, IHHO performs better than the original HHO. IHHO is so powerful at function transformation because it uses a random walk method to escape the local optimum. Even while some critics claimed that the original HHO couldn't provide the desired level of physical fitness, IHHO did so on average at or above that level. As a result, IHHO is more successful than its competitors. Having this component present is crucial to the increased efficiency of IHHO.

The curves in Fig. 26 allow for a direct comparison of the convergence times of the original HHO technique with the IHHO.

Fig. 26

Convergence curves for IHHO vs HHO on multimodal fixed-dimension curves

5.5.2 IHHO vs other algorithms

Table 25 contains our comparison of IHHO to various algorithms, namely GWO [39], BAT [40], MFO [42], TLBO [41], and WAO [43] after giving it a thorough workout on the test features to prepare for the engineering problems. This was done so that could make a decision regarding which of the possibilities was preferable. We have performed this evaluation a total of 30 times, making the total number of cycles 500.

According to Table 25, the performance of the IHHO algorithm is better than that of all unimodal variable-dimension benchmark functions, with the exception of the F6: IHHO, HHO, and MFO achieve the required fitness. IHHO, HHO, TLBO, and WAO achieve the requirement fitness for F8. IHHO outperforms BAT by a significant margin when the two are compared to one another. Because of this, IHHO outperforms its rivals. The presence of such a component is a major reason for IHHO's improved output. IHHO achieved an overall rank of 1.

A visual comparison of the convergence periods of the IHHO method and other algorithms can be carried out using the convergence curves shown in Fig. 27.

Fig. 27

Convergence curves for IHHO vs other algorithms on unimodal variable-dimension functions

Table 25 shows that, except for F2, the IHHO method outperforms all of the unimodal fixed-dimension benchmark functions. When comparing IHHO to TLBO, IHHO is the superior option. In particular, the benchmark functions F1, F2, and F4 with a single variable dimension are intractable to TLBO. As a result, IHHO is more successful than its competitors. Having this component present is crucial to the increased efficiency of IHHO. IHHO ranked first among its competitors.

The convergence curves depicted in Fig. 28. can be used to visually examine the differences between the IHHO technique and other algorithms concerning the time required for them to reach convergence.

Fig. 28

Convergence curves for IHHO vs other algorithms on Unimodal fixed-dimension functions

Table 25 reveals that when compared to multimodal fixed-dimension benchmark functions, IHHO performs better than the original HHO. Because it employs a random walk strategy to break out of the local optimum, IHHO is particularly effective at resha** functions. The averages at which the HHO fitness was achieved, IHHO achieved as well, and the commentators that the original HHO could not achieve the required physical fitness, the modification achieved. In particular, some benchmark functions with a single variable dimension are intractable to TLBO. IHHO has a rank of 1 for these types of functions.

The curves in Fig. 29 allow for a direct comparison of the convergence times of the IHHO technique with other algorithms.

Fig. 29

Convergence curves for IHHO vs other algorithms on multimodal fixed-dimension functions

Table 25 shows that IHHO outperforms all of the multimodal variable-dimension benchmark functions except F2 and F12. When comparing IHHO to TLBO, IHHO is the superior option. As a result, IHHO is more successful than its competitors. Having this component present is crucial to the increased efficiency of IHHO.

The convergence curves depicted in Fig. 30 can be used to visually examine the differences between the IHHO technique and other algorithms concerning the time required for them to reach convergence.

Fig. 30

Convergence curves for IHHO vs other algorithms on multimodal variable-dimension functions

5.5.3 IHHO vs other modifications of HHO

As such, the proposed IHHO to existing HHO variations, namely BHHO[26], MHHO [27], and LogHHO [28], was compared. To give all algorithms a fair opportunity, we've decided to set the swarm size at 30, and the stop** condition at 500 iterations. The experimental findings in Table 26 address the issue of scalability. The objective function's mean and standard deviation are shown in the table below. The convergence outcomes of the various methods are shown in Figs. 31, 32, 33, and 34.

Table 26 Comparison of results of IHHO vs other modifications of HHO on 52 benchmark functions

Fig. 31

Convergence curves for IHHO vs HHO modifications on unimodal variable-dimension functions

Fig. 32

Convergence curves for IHHO vs HHO modifications on unimodal fixed-dimension functions

Fig. 33

Convergence curves for IHHO vs HHO modifications on multimodal fixed-dimension functions

Fig. 34

Convergence curves for IHHO vs HHO modifications on multimodal variable-dimension functions

According to Table 26, the performance of the IHHO algorithm is better than that of all other modifications of HHO, except the F11 and F13 methods. When compared to MHHO and LogHHO, IHHO performs better for all unimodal variable-dimension benchmark functions. As a result, IHHO is more successful than its competitors. Having this component present is crucial to the increased efficiency of IHHO. A visual comparison of the convergence periods of the IHHO method can be carried out using the Convergence curves shown in Fig. 31.

According to Table 26, the performance of the IHHO algorithm is better than or equal to the required fitness of all other modifications of HHO, with the exception of the F1 method. As a result, IHHO is more successful than its competitors. Having this component present is crucial to the increased efficiency of IHHO. Utilizing the convergence curves that are depicted in Fig. 32, one can carry out a visual comparison of the convergence periods of different HHO modifications.

Table 26 reveals that when compared to multimodal fixed-dimension benchmark functions, IHHO performs better than the original HHO and other HHO modifications or achieves the required fitness. Because it employs a random walk strategy to break out of the local optimum, IHHO is particularly effective at resha** functions. Because of this, IHHO outperforms its rivals. The presence of such a component is a major reason for IHHO's improved output. The curves in Fig. 33 allow for a direct comparison of the convergence times of the IHHO technique with different HHO modifications.

According to Table 26, the performance of the HHO algorithm is better than that of all other modifications of HHO, with the exception of the F12 method. When compared to MHHO and LogHHO, IHHO performs better for all unimodal variable-dimension benchmark functions. As a result, IHHO is more successful than its competitors. Having this component present is crucial to the increased efficiency of IHHO.

A visual comparison of the convergence periods of the HHO method can be carried out using the Convergence curves shown in Fig. 34.

5.6 Engineering problems

5.6.1 Tension/compression spring design

Designing coil springs with the ideal tension and compression is a classic engineering optimization challenge [88]. Figure 35 shows the tension/compression spring design problem (TCSD). Assuming a constant tension/compression load, the goal is to minimize the volume V of the coil spring. There are three potential configurations for this issue:

• the number of usable coils in a spring $P= {x}_{1} \epsilon [\mathrm{2,15}]$

• the size of the winding in centimeters $D= {x}_{2} \epsilon [\mathrm{0.25,1.3}]$

• the size of the wire's diameter $d= {x}_{3} \epsilon [\mathrm{0.005,2}]$

Fig. 35

Tension/compression spring design problem

The TCSD problem may be expressed mathematically as follows: [89]

$${\text{min}}f\left(x\right)=\left({x}_{3}+2\right){x}_{2}{x}_{1}^{2}$$

(25)

Subject to:

$$\begin{gathered} q_{1} \left( x \right) = 1 - \frac{{x_{2}^{3} x_{3} }}{{71785x_{1}^{4} }} \le 0 \hfill \\ q_{2} \left( x \right) = \frac{{4x_{2}^{2} - x_{1} x_{2} }}{{12566\left( {x_{2} x_{1}^{3} - x_{1}^{4} } \right)}} + \frac{1}{{5108x_{1}^{2} }} - 1 \le 0 \hfill \\ q_{3} \left( x \right) = 1 - \frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }} \le 0 \hfill \\ q_{4} \left( x \right) = \frac{{x_{2} + x_{1} }}{1.5} - 1 \le 0 \hfill \\ \end{gathered}$$

(26)

5.6.2 Pressure vessel design

Figure 36 shows a pressure vessel created to reduce the entire cost of the pressure vessel's materials, form, and welding [73, 90]. The thickness of the shell (${T}_{s}={x}_{1}$), the depth of the head (${T}_{h}={x}_{2}$), the inner radius ($R={x}_{3}$), and the height of a cylindrical section ($L={x}_{4}$) are the four design parameters. Here is how the pressure vessel problem is formulated:

Fig. 36

Pressure vessel design problem

$${f}_{\left(x\right)}=0.0624{x}_{1}{x}_{3}{x}_{4}+1.7781{x}_{2}{x}_{3}^{3}+3.1661 {x}_{1}^{2}{x}_{4} +19.84 {x}_{1}^{3}{x}_{3}$$

(27)

Subject to:

$$\begin{aligned}{g_1}\left( x \right) = \, & 0.0193{x_{3}} - {x_1} \le 0\\{g_2}\left( x \right) = \, & 0.00954{x_3} - {x_2} \le 0\\{g_3}\left( x \right) = \, & 1296000 - \Pi x_{3}^{2}{x_{4}} - \frac{4}{3}\Pi x{_3^{3}} \le 0\\{g_4}\left( x \right) =\, & {x_{4}} - 240 \end{aligned}$$

(28)

where

$${x}_{1} \epsilon \left[\mathrm{0.0625,6.187}\right], {x}_{2} \epsilon \left[\mathrm{0.0625,6.187}\right], {x}_{3} \epsilon \left[10, 200\right], {x}_{4} \epsilon [10, 200]$$

5.6.3 Welded beam design

The welded beam design (WBD) issue takes into account several design factors such as design for minimal cost while subjected to shear stress limits (τ), beams' end deflection ($\updelta$), bending stress in the beam (θ), buckling load on the bar (${P}_{c}$), and side constraints [91]. According to Fig. 37 WDB took into account four design factors in order to build a welded beam using the fewest possible resources. These parameters are $h(x)$, $i({x}_{2}$), $t({x}_{3}$), and $b({x}_{4}$). This is a mathematical representation of the WDB issue:

$${\text{Min}}\;f\left( x \right) = 1.10471x_{1}^{2} x_{2} + \, 0.0{4811}x_{3} x_{4} \left( {14.0 - { }x_{2} } \right)$$

(29)

Fig. 37

Welded beam design problem

Subject to:

$$\begin{gathered} g_{1} \left( x \right) = {\uptau }\left( {\text{x}} \right) - 13000 \le 0 \hfill \\ g_{2} \left( x \right) = \delta \left( {\text{x}} \right) - 30000 \le 0 \hfill \\ g_{3} \left( x \right) = x_{1} - x_{4} \le 0 \hfill \\ g_{4} \left( x \right) = 0.1047x_{1}^{2} + 0.04811x_{3} x_{4} \left( {14.0 + x_{2} } \right) - 5 \le 0 \hfill \\ g_{5} \left( x \right) = 0.125 - x_{1} \le 0 \hfill \\ x_{6} \left( x \right) = {\updelta }\left( {\text{x}} \right) - 0.25 \le 0 \hfill \\ g_{7} \left( x \right) = 6000 - { }P_{c} \left( x \right) \le 0 \hfill \\ \end{gathered}$$

(30)

where

$$\uptau \left({\text{x}}\right)= \sqrt{{({\uptau }^{\prime})}_{2}+2{\uptau }^{\prime} {\uptau }^{{\prime}{\prime}} \frac{{x}^{2}}{2R}+{({\uptau }^{{\prime}{\prime}})}^{2}}$$

$${\uptau }{{^{\prime}}}= \frac{6000}{\sqrt{2}{x}_{1}{x}_{2}},$$

$${\uptau }{{^{\prime}}{^{\prime}}}= \frac{MR}{J}$$

$$M=6000 \left(14+ \frac{{x}_{2}}{4}\right)$$

$$R= \sqrt{\frac{{x}_{2}^{2}}{4}+ {(\frac{{x}_{1}+{x}_{3}}{2})}^{2}}$$

$$J=2\left\{\sqrt{2}\right.{x}_{1}{x}_{2}[\frac{{x}_{2}^{2}}{12}+ {(\frac{{x}_{1}+{x}_{3}}{2})}^{2}$$

$${\gamma}\left({\text{x}}\right)= \frac{504000}{{x}_{4}{x}_{3}^{2}}$$

$$\updelta \left({\text{x}}\right)= \frac{2.1952}{{x}_{4}{x}_{3}^{3}}$$

$$Pc\left(x\right)=64746.022(1- 0.0282346{X}_{3}){X}_{3}{X}_{4}^{3}$$

5.6.4 Gear train design problem

The challenge of designing gears with the optimal ratio comprises five different design variables, a nonlinear objective function, and five different nonlinear limitations [92]. The goal of this exercise is to find the gear ratio for the gear train depicted in Fig. 38 with the lowest possible cost [93]. To specify the gear ratio, we say:

$$Gear ratio= \frac{{\eta }_{{\varvec{B}}}{\eta }_{{\varvec{D}}}}{{\eta }_{{\varvec{F}}}{\eta }_{{\varvec{A}}}}$$

(31)

$${\text{Min}}\;f\left( x \right) = \left( {\frac{1}{6.931} - \frac{{x_{3} x_{2} }}{{x_{1} x_{4} }}} \right)^{2}$$

(32)

Fig. 38

Gear train design problem

Subject to:

$$12 \le {x}_{i} \le 60 \quad where i=1,\dots .,4$$

5.6.5 Three-bar truss design

Ray and Saini [94] were the first to identify the optimization difficulty inherent in the design of a three-bar truss. As seen in Fig. 39, three bars are preferred in light of this. The goal is to reduce the total bar weight by placing them in this orientation [77]. This issue contains three constrained functions and two design parameters (${x}_{1}$, ${x}_{2}$). A mathematical formulation of the issue is as follows:

$${\text{Min}}\;f\left( x \right) = \left( {2\sqrt 2 x_{1} + { }x_{2} } \right)x{ }L$$

(33)

$$\begin{gathered} g_{1} = \frac{{\sqrt 2 x_{1} + x_{2} }}{{\sqrt 2 x_{1}^{2} + 2 x_{1} x_{2} }}P - \sigma \le 0 \hfill \\ g_{2} = \frac{{ x_{2} }}{{\sqrt 2 x_{1}^{2} + 2 x_{1} x_{2} }}P - \sigma \le 0 \hfill \\ g_{3} = \frac{1}{{x_{1} + \sqrt 2 x_{2} }}P - \sigma \le 0 \hfill \\ \end{gathered}$$

(34)

Fig. 39

Three-bar truss design problem

where:${x}_{1}\ge 0, {x}_{2}\le 1, \text{the} \, \text{constant} \, \text{are} \, L=100 cm, P=2KN/{cm}^{2}$

And $\sigma = 2KN/{\text{cm}}^{2}$ [1, 2, 6].

5.6.6 speed reducer problem

As shown in Fig. 40, there are countless applications for gear reducers because of their versatility and importance in the mechanical transmission of a wide variety of processes [95]. The reducer has several issues that make it less than ideal for use in modern applications, including its heft, high transmission ratio, and low mechanical efficiency [96]. Good power, big transmission ratio, compact size, high mechanical efficiency, and long service life are all requirements for an energy-efficient current reducer [75]. The following constraints are obtained:

Fig. 40

Speed reducer problem [97]

$$\mathrm{Min }f\left(x\right)=\frac{{m}_{n1}{z}_{1}\left(1+{i}_{1}\right)+{m}_{n2}{z}_{3}\left(1+{i}_{2}\right)}{2cos\beta }$$

(35)

Subject to:

$$\begin{gathered} g_{1} = 3.098~x~10^{{ - 6}} x_{1}^{3} x_{3}^{2} x_{5} - \cos ^{3} x_{6} ~ \ge 0 \hfill \\ g_{2} = 1.017~x~10^{{ - 4}} x_{2}^{3} x_{4}^{3} - x_{5}^{2} \cos ^{3} x_{6} /x_{3}^{2} ~ \ge 0 \hfill \\ g_{3} = 9.939~x~10^{{ - 5}} .\left( {1 + x_{5} /x_{3} } \right)x_{1}^{3} x_{3}^{2} - \cos ^{3} x_{6} ~ \ge 0 \hfill \\ g_{4} = 1.076~x~10^{{ - 4}} .\left( {31.5 + x_{5} /x_{3} } \right)x_{2}^{3} x_{4}^{2} - x_{5}^{2} \cos ^{2} x_{6} /x_{3}^{2} ~ \ge 0 \hfill \\ g_{5} = x_{2} x_{4} \left( {31.5 + \frac{{x_{5} }}{{x_{3} }}} \right) - \frac{{x_{5} }}{{x_{3} }}.\left[ {2\left( {x_{1} + 50} \right).\cos x_{6} + x_{1} x_{5} } \right] \ge 0 \hfill \\ \end{gathered}$$

(36)

5.6.7 Results

In that part, we will test IHHO with the previous six engineering problems as in Table 27. The problems are tension/compression spring design [98], pressure vessel design [99], welded beam design [100], speed reducer problem [101], gear train design problem [68], and three-bar truss design [103].

Table 27 Description of engineering problems

5.6.7.1 IHHO vs HHO

The comparison of IHHO against HHO is presented in Table 28. This was done so that we could decide which of the two options was the better one. However, F2, F3, and F5 have a four-dimensional restricted optimization problem inside the given range for each equation. Because F1, F4, and F6 have different dimensions, this function 30 times for a total of 500 iterations was evaluated.

Table 28 Comparison of results of IHHO and HHO on six engineering problems

The results shown in Table 28 indicate that the performance of IHHO is better than that of the original HHO, except for F5 and F6. IHHO outperforms other analyzed methods for changing functions because of its greater capacity to escape the local optimum utilizing the random walk methodology. This gives IHHO a performance advantage over HHO. The higher performance of IHHO can largely be attributed to this factor.

A visual comparison of the convergence times of the IHHO method and the original HHO can be carried out by looking at the curves in Fig. 41, which shows the results of the comparison.

Fig. 41

Convergence curves for IHHO vs HHO on six engineering problems

5.6.7.2 IHHO vs other algorithms

Table 29 contains our comparison of IHHO to various algorithms, namely BAT [40], MFO [42], TLBO [41], and WOA [43]. This was done so that could make a decision regarding which of the possibilities was preferable. This evaluation a total of 30 times, making the total number of cycles 500 was performed.

Table 29 Comparison of results between IHHO and other algorithms on six engineering problems

According to Table 29, the performance of the HHO algorithm is better than that of other algorithms on all engineering problems, with the exception of the F5 and F6 methods. IHHO outperforms BAT by a significant margin when the two are compared to one another. When compared to MAT, IHHO performs better, with the exception of F6. IHHO outperforms TLBO since the former cannot solve all engineering problems. IHHO performs better than WOA in all functions with the exception of F2.

A visual comparison of the convergence periods of the IHHO method can be carried out using the Convergence curves shown in Fig. 42.

Fig. 42

Convergence curves for IHHO vs other algorithms on six engineering problems

5.6.7.3 IHHO vs other modifications of HHO

Here, the proposed IHHO with other HHO variants such as MHHO [37] and LogHHO [38] was evaluated. We have set the swarm size at 30, and the halting criterion at 500 iterations, to ensure that all algorithms get a fair shot. Table 30 displays experimental results regarding the mean and standard deviation of the objective functions. Figure 43 also displays the convergence results for the different approaches.

Table 30 Comparison of results of IHHO vs other modifications of HHO on six engineering problems

Fig. 43

Convergence curves for IHHO vs HHO modifications on six engineering problems

According to Table 30, the performance of the IHHO algorithm is better than that of all other modifications of HHO, with the exception of the F5, and F6 methods. When compared to MHHO and LogHHO, IHHO performs better, except for the F5, and F6 methods.

A visual comparison of the convergence periods of the IHHO method can be carried out using the convergence curves shown in Fig. 43.

In CEC 2017, BHHO outperformed other variants of HHO; however, in CEC 2020 and CEC 2019, it was unable to progress and break free from the local solution. While LogHHO performed admirably in CEC 2019, it was unable to break free from the local solution in CEC 2017 and CEC 2020. While MHHO performed well in CEC 2020, it was unsuccessful in CEC 2017 and CEC 2019. But in most benchmark equations (CEC2017, CEC2019, etc.), the improved modification (IHHO) outperformed all other changes that were applied to it.

The suggested approach, IHHO, outperforms other algorithms (GWO, BAT, WOA, TLBO, and MFO), as demonstrated by the numerical results. This is visually demonstrated by various convergence curves, but IHHO was able to overcome these and obtain the global solution in the majority of benchmarks. An analysis of the mean Friedman rank statistical test is used to compare the IHHO rank with other algorithms. The recommended method beats out GWO, BAT, WOA, TLBO, MFO, and three variants of HHO (BHHO, LogHHO, and MHHO), according to Friedman tests.

6 Conclusion and future work

Metaheuristic optimization algorithms are now commonly used to solve different engineering problems. Despite the available algorithms, new algorithms with extended abilities are continuously proposed to overcome the problems of the existing algorithms. This paper proposes an Improved algorithm based on the well-known Harris Hawks optimization algorithm. The algorithm proposed in this study emphasizes the utilization of random location-based habitats during the exploration phase and the implementation of strategies 1, 3, and 4 during the exploitation phase. The improved algorithm is capable of achieving a good balance between exploration and exploitation due to the modifications of each phase. Our suggested algorithm IHHO is benchmarked against not only the original HHO, but also against state-of-the-art algorithms, namely grey wolf optimization, BAT algorithm, teaching–learning-based optimization, moth-flame optimization, and whale optimization algorithm. IHHO is also compared with other modifications of HHO, namely BHHO, MHHO, and logHHO. Different benchmark functions with varying difficulties CEC2017, CEC2019, CEC2020, and 52 benchmark functions were used. We have also applied these algorithms to six classical real-world engineering problems.

Compared to other variations of HHO, BHHO performed well in CEC 2017 but failed to advance and escape the local solution in CEC 2020 and CEC 2019. LogHHO did well in CEC 2019 but was not able to get ahead and out of the local solution in CEC 2017, and CEC 2020 MHHO did well in CEC 2020, however, it failed in CEC 2017 and CEC 2019. However, the enhanced modification (IHHO) demonstrated exceptional performance in the majority of benchmark equations (CEC2017, CEC2019, etc.), surpassing all other modifications implemented on it.

The numerical results show the superiority of the proposed algorithm IHHO over other algorithms (GWO, BAT, WOA, TLBO, and MFO), which is visually proven using different convergence curves but IHHO was able to overcome them and achieve the global solution in most benchmarks. The IHHO rank is compared to other algorithms using a statistical test of the mean Friedman rank. Friedman tests showed that the suggested algorithm outperforms GWO, BAT, WOA, TLBO, MFO, and three HHO variations (BHHO, LogHHO, and MHHO).

As with every proposed algorithm, IHHO has some limitations. First, IHHO has solved the problem of sensitivity to parameters in the original HHO. The results of the discussed problems are promising. However, this may be ineffective in other problems. Second, convergence time increases with complexity, which opens a window for future research directions to solve this issue. Finally, as this area of research is continuously improving, new algorithms with better performance may be developed.

In future work, we plan to further improve the proposed algorithm. Problem–based adaptive parameters can be used. The binary version of the algorithm can also be developed for classification tasks.