Effective forecasting of stock market price by using extreme learning machine optimized by PSO-based group oriented crow search algorithm

Abstract

Stock index price forecasting is the influential indicator for investors and financial investigators by which decision making capability to achieve maximum benefit with minimum risk can be improved. So, a robust engine with capability to administer useful information is desired to achieve the success. The forecasting effectiveness of stock market is improved in this paper by integrating a modified crow search algorithm (CSA) and extreme learning machine (ELM). The effectiveness of proposed modified CSA entitled as Particle Swarm Optimization (PSO)-based Group oriented CSA (PGCSA) to outperform other existing algorithms is observed by solving 12 benchmark problems. PGCSA algorithm is used to achieve relevant weights and biases of ELM to improve the effectiveness of conventional ELM. The impact of hybrid PGCSA ELM model to predict next day closing price of seven different stock indices is observed by using performance measures, technical indicators and hypothesis test (paired t-test). The seven stock indices are considered by incorporating data during COVID-19 outbreak. This model is tested by comparing with existing techniques proposed in published works. The simulation results provide that PGCSA ELM model can be considered as a suitable tool to predict next day closing price.

1 Introduction

Stock market (SM) provides a path for companies to make profit by allowing businesses traded publically which enhance the financial capital for expansion by selling shares of the company in public market. The objective of investment in SM is to raise revenue through purchasing and holding a portfolio of stocks, mutual funds, bonds and other instruments. In last few decades, the investors and traders experience huge risk to invest in stock portfolios because of its inconsistency and variations. The inconsistency in SM occurs due to the factors such as economic condition, political activities and trader’s prediction. From the fluctuating market, traders always try to make transactions over a small time frame to achieve frequent profit. The key of stock traders to get maximum profits with less risk is conceivable by establishing an accurate trading decision making tool with respect to time. The future price is predicted with better accuracy by concerning the patterns of historical data (price and volume) [1].

So, the prediction of closing price of highly dynamic and nonlinear SM is very indispensable. Auto Regressive Integrated Moving Average (ARIMA) model is used to interpret the time series data and to forecast the future in that series [2]. But, this conventional technique is not adequate enough to forecast the SM price whose movements are influenced by some macro-economic factors [3, 4]. Singh et al. [5] have proposed a hybrid wavelet denoise-ARIMA model to improve the prediction accuracy of stock market price. The close prediction of SM helps investors to draw better benefits from SM. In this work, optimized ELM model is developed to capture the hidden structural changes in volatility processes of portfolio returns.

Some researchers have proposed decision making tools based on artificial intelligence (AI) and deep learning techniques to enhance the accuracy of the SM forecasting. Bustos et al. [6] have contributed a brief survey of different methods implemented to predict stock market price. Artificial neural network (ANN)-based model is preferred to forecast SM [7,8,9,10], because of its benefits such as organic learning, nonlinear data processing, fault tolerance and self-overhaul. Feedforward neural network (FFNN) is a simple form of ANN, which has very less computational time to solve simple problems with less complexity [11]. The effectiveness of deep feedforward neural network to forecast stock indices price is analysed by a comparative analysis with ANN [12]. Multilayer perceptron (MLP) is a persuasive ANN to be used for regression and is efficient enough to predict SM price [13]. Back propagation neural network (BPNN) is also implemented to solve SM index forecasting problem [14, 15]. Convolutional neural network (CNN) is a fully connected MLP, which facilitates less computational complexity without defeating the substance of the data. The improvement analysis of CNN to predict intraday price forecasting is studied in [16, 17]. From last few decades, different forms of ANN are accepted in the field of SM forecasting. All of these forms of ANN are gradient-based algorithms with certain constraints such as high computational time to train and probability to get trapped in local optima of the problem. The dilemma of ANN is overwhelmed by support vector machines (SVM) to predict time series data [18]. A comparative analysis between SVM and Adaptive Neuro Fuzzy Inference System (ANFIS) in terms of finger-vein identification is portrayed and the SVM is concluded as a superior technique over ANFIS with less computational time and robust classifier [19]. Further, the efficacy of SVM to forecast stock market price is improved by integrating piecewise linear representation with weighted SVM and optimized SVM techniques in [20] and [21] respectively. Long short-term memory (LSTM) is validated over ANN and SVM to predict stock index [22]. Huang et al. [23] have proposed a Single-hidden Layer Feed forward Neural Network (SLFNN) entitled as ELM. It is required to regulate the number of neurons & activation function of ELM as the input weights & hidden layer biases are fixed during the employment. These properties of ELM enhance the notoriety to contribute better generalization performance with immensely rapid learning. Cheng et al. [24] have beautifully conferred the supremacy of ELM over SVM to predict petroleum reservoir permeability. Huang et al. [25] have implemented ELM for regression and classification in various fields. From previous decade, ELM is considerably demonstrated the superiority over traditional techniques in the field of SM forecasting [26, 27].

Some researchers are considered the optimization techniques to boost the efficiency of existing machine learning techniques to predict SM with superior accuracy. Genetic algorithm (GA)-based fuzzy [28], SVM [29], ANN [30], multi-chanel CNN [31] and Probabilistic Weight Support Vector Machine (PWSVM) [32] are flourishingly implemented to forecast SM price, return and trend with improved accuracy. Hegazy et al. [33] have applied particle swarm optimization (PSO) optimized ANN and Least Square Support Vector Machine (LS-SVM), respectively, to predict SM. Computationally Efficient Functional Link Artificial Neural Network (CEFLANN) optimized by Differential Evolution (DE) algorithm is implemented with better performance to predict SM [34]. The accuracy of stock index forecasting is enhanced by Artificial Fish Swarm Algorithm (AFSA)-based Radial Basis Functional Neural Network (RBFNN) and Grey Wolf optimization-based Elman neural network proposed by Shen et al. [35] and Chander [36] respectively. SM price forecasting problem is solved with improved accuracy by implementing chaotic Firefly Algorithm (FA)-based Support Vector Regression (SVR) [37] and Discrete PSO (DPSO)-based Fully Complex-valued Radial Basis Functional Neural Network (FCRBFNN) [38]. Hybrid Artificial Bee Colony-Differential Evolution (ABC-DE) is applied to optimize weights of Feed Forward Neural Network (FFNN) to predict foreign exchange rate [39].

The conventional techniques may not efficient enough to solve high dimension multimodal objective function. Because of the flexibility and gradient free mechanism, metaheuristic techniques are mostly preferred methods to deal with high dimension, nonlinear, complex and multimodal problems. Evolutionary based, physics based, swarm based and nature inspired algorithms are the most well-known categories of metaheuristic algorithms [40]. Genetic Algorithm (GA) [41], Differential Evolution (DE) [42], Gravitational Search Algorithm (GSA) [43], Particle Swarm Optimization (PSO) [44], Artificial Bee Colony (ABC) [45], Grasshopper Optimisation Algorithm (GOA) [46] and Symbiotic Organism Search (SOS) [47] etc. are the most desirable optimization techniques under these categories mentioned above. CSA is a recent metaheuristic algorithm proposed by Askarzadeh [48]. This algorithm is derived by the social behaviour of quick witted and clever organism of ecosystem. By doing a team work, crows perform incredible sample of brilliance and gain good results. The techniques used by crows to memorizing and recognizing faces are unique. The sluggish convergence rate and chance of got stuck in local optima are the considerations which motivate researchers to overcome the dilemma. Chaotic maps are implemented in CSA to overcome this dilemma and the improvement is realized favourably by solving engineering and constrained problems [49, 50]. The ‘flight length’ of CSA is made adaptive iteratively and applied in economic load dispatch problem [51]. The hybridization of CSA with Rough Searching Scheme (RSS) and Sine Cosine Algorithm (SCA) algorithms are endorsed to enhance the proficiency of individual algorithms [52, 53].

From the survey, ELM technique is established as an adequate and admirable technique to predict time series data. The weights and biases of ELM are an influential aspect to enhance the performance. In this paper, a strive approach is introduced to enhance the potential of CSA entitled as PGCSA. CSA and PGCSA algorithms are used to optimize the weights and biases of ELM for forecasting different SMs price. PGCSA ELM is concluded as a superior technique by contributing a fine comparative analysis with some published paper MLP, GARCH-DAN2 and BNNMAS techniques [10, 54].

Contributions of the article are as follows:

• i. Optimized ELM (with optimized weights and biases) is proposed to forecast price of seven distinct stock markets.

• ii. Two phases (with and without awareness probability) of CSA is altered to enhance the searching capability of CSA algorithm entitled as PGCSA.

• iii. PGCSA and CSA algorithms are substantiated over some recently published papers by resolving benchmark equations and hypothetically tested by using Wilcoxon signed-rank test.

• iv. Comparative analysis of PGCSA-ELM with CSA-ELM and ELM (randomly fixed weights and biases). The proposed model predicted closing price is tested by using some technical indicators such as MSE, MAE, MAPE, MAAPE, CoV, CORR and Theil’s U of SM forecasting.

• v. The accuracy of predicted closing price is tested hypothetically by using paired t-test and by using financial indicators such as sharpe ratio, and modified sharpe ratio.

2 Methodology and data

2.1 Extreme learning machine (ELM)

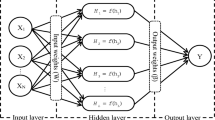
Huang et al. [23] have introduced a SLFNN entitled as ELM. Input, hidden and output layers are the basic segments of ELM. The hidden layer neurons are not to be optimized during training period. These neurons are distributed arbitrarily and never refurbished. Inputs are linked to hidden layers with randomly fixed weights (w_i) and the biases (b_j). In this work, CSA and PGCSA algorithms are administrated to search convenient weights and biases of the ELM. The structure of ELM is illustrated in Fig. 1. ELM has immense convergence which is thousand time faster than BPNN [25]. Non-gradient-based ELM has not only better generalized performance over gradient-based techniques but also avoid the local minima, erroneous learning rate and over fitting. The output function of ELM with L hidden nodes for a training set $\mathbf{R}=\left\{\left({\mathbf{X}}_{\mathbf{i}},{\mathbf{t}}_{\mathbf{i}}\right)\right\},\mathbf{i}=1,2,...,\mathbf{n}$ is illustrated in Eq. (1).

$$f\left(R\right)=\sum_{j=1}^{L}{\beta }_{j}H\left(X\right)={t}_{j}$$

(1)

where, β = β₁, β₂,..., β_L is the weight matrix between hidden and output layer and t = t₁, t₂,..., t_j is the target matrix of training data. The output of hidden layer is estimated by Eq. (2).

Fig. 1

Structure of ELM

$$H=\left[\begin{array}{c}\begin{array}{ccc}G\left({w}_{1},{b}_{1},{X}_{1}\right)& \cdots & G\left({w}_{L},{b}_{L},{X}_{1}\right)\\ G\left({w}_{1},{b}_{1},{X}_{2}\right)& \cdots & G\left({w}_{L},{b}_{L},{X}_{2}\right)\end{array}\\ \begin{array}{ccc}\vdots & \vdots & \vdots \\ G\left({w}_{1},{b}_{1},{X}_{n}\right)& \cdots & G\left({w}_{L},{b}_{L},{X}_{n}\right)\end{array}\end{array}\right]$$

(2)

$$\beta ={\left[\begin{array}{c}{\beta }_{1}\\ {\beta }_{2}\\ \begin{array}{c}\vdots \\ {\beta }_{L}\end{array}\end{array}\right]=\left({H}^{T}H\right)}^{-1}{H}^{T}$$

“G” is the activation function in terms of weight, bias and inputs. Sigmoidal, Gaussian, Hard limit and Fourier series functions are adopted as activation functions. In this work, sigmoidal function is adopted as activation function as illustrated in Eq. (3).

$$G\left({w}_{i}, {b}_{i}, {X}_{i}\right)=\frac{1}{1+{e}^{-\left(wx+b\right)}}$$

(3)

The desired output of the ELM is determined by using Eq. (4).

$${T}_{test}=H\beta $$

(4)

The ELM is trained by considering intraday open, high & low prices of stock indices as inputs and closing price as target. The closing price of stock market is predicted by conceding open, high & low prices. The weight matrix (w_ij) and bias (b_j) are optimized by CSA and PGCSA algorithms to enhance the forecasting capability of ELM. The performance of the forecasting capability of ELM is graded by the performance measure such as MSE (Mean Squared Error).

2.2 Crow search algorithm (CSA)

CSA algorithm is derived from the social behavior of crows [48]. Crows are opted as the ultimate brilliant bird. Compared to their physical structure they have tremendous brain. Crows conceal their overabundance food in undoubted location and when it is essential they recoup it. Crows acquire food by doing a great team work always. Hiding foods for the next season is not that much easy for a crow because some opponent crows can also come after to follow the food. At that moment, the crow endeavors to mislead by changing the direction in the territory. Here the crows can be taken as path finders or searches whereas the territory can be taken as search area. Every location of the territory is considered as optimum point and the fitness value is the quality of the nourishment source. Crows steal the hiding nourishment of other birds by observing and following them and at the same time the crows take some supplemental prevention like changing the concealing places to stay away from becoming an upcoming easy target. By considering these clever action CSA algorithm has developed. The ideas of CSA are check listed as given below:

• i. Crows reside like a group.

• ii. Crows remember the location of their concealing places of food.

• iii. Crows observe and follow one another to rustle food.

Like other optimization techniques initialization of CSA is quite similar. In initialization phase, the flock of crows is initialized randomly by conceding designed variables (D) and number of crows (NC) by satisfying the constraints as characterized in Eq. (5). Each row of the matrix represents one crow in the flock and each column represents one design variable of the problem. Each crow denotes a feasible solution of the problem.

$$\mathrm{Crows}=\left[\begin{array}{c}\begin{array}{ccc}{X}_{1}^{1}& \begin{array}{cc}{X}_{2}^{1}& \cdots \end{array}& {X}_{D}^{1}\\ {X}_{1}^{2}& \begin{array}{cc}{X}_{2}^{2}& \cdots \end{array}& {X}_{D}^{2}\end{array}\\ \begin{array}{ccc} \vdots & \begin{array}{cc}\vdots & \vdots \end{array}& \vdots \\ {X}_{1}^{{N}_{C}}& \begin{array}{cc}{X}_{2}^{{N}_{C}}& \cdots \end{array}& {X}_{D}^{{N}_{C}}\end{array}\end{array}\right]$$

(5)

X represents the design variable of a crow. In the first iteration, assume that they have concealed their foods in the initial position because crows have less experience in the beginning. The memory (M) of each crow is initialized as described in Eq. (6).

$$\mathrm{Memory}=\left[\begin{array}{c}\begin{array}{ccc}{M}_{1}^{1}& \begin{array}{cc}{M}_{2}^{1}& \cdots \end{array}& {M}_{D}^{1}\\ {M}_{1}^{2}& \begin{array}{cc}{M}_{2}^{2}& \cdots \end{array}& {M}_{D}^{2}\end{array}\\ \begin{array}{ccc} \vdots & \begin{array}{cc}\vdots & \vdots \end{array}& \vdots \\ {M}_{1}^{{N}_{C}}& \begin{array}{cc}{M}_{2}^{{N}_{C}}& \cdots \end{array}& {M}_{D}^{{N}_{C}}\end{array}\end{array}\right]$$

(6)

The memory matrix represents the best feasible solutions of crows obtained so far. M is the element of memory matrix which represents the design variable of a memory of crow. The fitness value can be calculated by putting the value of designed variables (D) in the objective function. The crows update their position with the help of other crow. The ith crow finds their food by following and observing another jth crow. The jth crow tries to fool the ith crow by changing the location of the food on the territory by knowing the intention of opponent crow. The updated position of the crow is characterized in Eq. (7).

$${X}_{new}^{i}=\left\{\begin{array}{c}{X}_{old}^{i}+r\times {fl}^{i}\times \left({M}^{j}-{X}_{old}^{i}\right) \quad {r}_{1}\ge AP\\ LB+\left(UB-LB\right)\times rand \quad \quad Otherwise\end{array}\right.$$

(7)

where, ‘r’ and ‘r₁’ are two random numbers within the range from 0 to 1. ‘AP’ is the awareness probability of crow. Small value of AP enhances the intensification and the high value of AP enhances the diversification. The memory of crow is updated with fitter crow position as depicted in Eq. (8).

$$ M_{{new}}^{i} = \left\{ \begin{gathered} X_{{new}}^{i} \quad \quad f\left( {X_{{new}}^{i} } \right) \ge f\left( {M_{{old}}^{i} } \right) \hfill \\ M_{{old}}^{i} \quad \quad Otherwise \hfill \\ \end{gathered} \right. $$

(8)

2.3 Proposed PSO-based group oriented CSA (PGCSA)

CSA is categorized into two phases (phase-1 and phase-2) by concerning the awareness probability (AP). In phase-1 (without awareness probability), if the jth crow (X_j) is unaware that i^th crow (X_i) is following it, i.e. r₁ ≥ AP, then the ith crow (X_i) is supposed to follow the food hiding place of j^th crow (M_j) as characterized in (7). If the functional value of X_i is better than the functional value of M_j, then the crow with better functional value will follow the worst one. This may downturn the convergence rate of the algorithm to achieve the optimal solution. In this work, the entire flock of crows is subdivided into small groups. The fittest crow of the corresponding group is considered as leader and the rest of the crows of that group (followers) are updated by following the leader crow as characterized in (9).

$$ X_{{new}}^{i} = X_{{old}}^{i} + r \times fl^{i} \times \left( {X_{L}^{k} - X_{{old}}^{i} } \right),If \quad r_{1} \ge AP $$

(9)

k = 1, 2, 3,..., ng. Where, ‘ng’ is the number of groups. Crows are distributed among the groups by conceding their weight (W) as characterized in Eq. (10) [55].

$${W}^{i}=\mathrm{exp}\left(-D\frac{f\left({X}^{i}\right)-f\left({X}^{Best}\right)}{\sum_{i=1}^{{N}_{c}}f\left({X}^{i}\right)-f\left({X}^{Best}\right)}\right)$$

(10)

Weight (W) is evaluated in such a manner that W of better functional value is higher. W of the best crow is one and for other crows are in between 0 to 1. The crows with highest W are chosen as group leaders. The followers are distributed among the groups by conceding the weight of the crows. The numbers of crows in one group are evaluated by using Eqs. (11) and (12).

$${\alpha }^{i}=\frac{{W}_{i}^{G}}{{\sum }_{i=1}^{ng}{W}_{i}^{G}}$$

(11)

$${N}_{{G}_{i}}=round\left({\alpha }^{i}\times {N}_{f}\right)$$

(12)

where, W_i^G, ${N}_{{G}_{i}}$, and N_f are weight of the group leader, numbers of group members, and numbers of followers respectively. By this approach, the local search space is enhanced and explored. In phase-2 (with awareness probability), if X_j is aware that X_i is following it, i.e. r₁ < AP, then the ith crow (X_i) is replaced by a random position as characterized in (7). X_i may have better functional value than the random position of crow.

Algorithm 1. Pseudo code of PGCSA algorithm.

In the later stage of iteration, there is a higher probability that fittest X_i may be replaced by random position. In this work, the second stage of Eq. (7) is modified by conceding the velocity as depicted in (13).

$${X}_{new}^{i}={X}_{old}^{i}+{v}^{i}$$

(13)

where, ${v}^{i}$ is the velocity of ith particle evaluated in the same fashion as in PSO [44]. Velocity (v) is updated by conceding the memory (M) and best crow as depicted in (14).

$${v}_{new}^{i}=w\times {v}_{old}^{i}+rand\times {c}_{1}\times \left({M}^{i}-{X}^{i}\right)+rand\times {c}_{2}\times \left({X}^{Best}-{X}^{i}\right)$$

(14)

$$Weight w=0.9-\left[0.5\frac{it}{itermax}\right]$$

where, c₁ and c₂ are the participation factors of M and X_Best respectively. M is memory of crows. This approach is used to enhance the exploitation. The movement of crows is illustrated in Fig. 2. The flow chart of proposed PGCSA algorithm is depicted in Fig. 3. The algorithm is briefly elaborated through pseudo code in algorithm 1. The main benefits of this proposed PGCSA algorithm are as follows:

Fig. 2

Crow position updating a if r₁ ≥ AP and b if r₁ < AP

Fig. 3

Flow chat of PGCSA algorithm

• i. In first phase (without awareness probability), the subdivided groups of crows throughout the search space will help to explore local optima. So, it enhances the exploration capability of the algorithm.

• ii. In second phase (with awareness probability), the velocity concept of PSO algorithm enhances the exploitation capability by contributing a direction towards optimal point. This approach helps to avoid the solution trapped into local optima.

• iii. PGCSA algorithm enhances the balance between exploration and exploitation capability of the technique. The capability to solve high dimensional problem is enhanced with these two approaches.

2.4 Research data

In this work, the time series historical price of period from 1st January 2004 to 10th May 2020 of seven stock indices such as Dow Jones Industrial Average (DJI), Hang Seng Index (HSI), Nasdaq Composite (IXIC), Euronext-100 (N 100), Nifty 50 (NSEI), Russell 2000 (RUT) and DAX performance index (GDAXI) are considered for SM forecasting collected from (https://www.investing.com). Daily high, low and open prices of these indices are treated as inputs of ELM to predict the closing price of next day. The normalized data of open, low, high and closing prices are determined by employing Eq. (15).

$$S=\frac{x-{x}_{min}}{{x}_{max}-{x}_{min}}$$

(15)

The training and testing data are considered in ratio of 7:3, respectively. The actual closing price is determined by de-normalizing the output of ELM as formulated in (16).

$$X=S*\left({x}_{max}-{x}_{min}\right)+{x}_{min}$$

(16)

where, S, ${x}_{max}$ and ${x}_{min}$ are the normalized data, maximum value and minimum value, respectively.

2.5 Performance measures

Performance measure is a measurement which numerically quantifies the closeness of predicted data to actual data. Mean squared error (MSE), Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE) are used as error measurements which indicate error measured from the origin and accuracy in percentage respectfully. Minimum MSE, MAE and MAPE values indicate better predicted data. MSE, MAE and MAPE are the performance measures expressed in Eqs. (17)–(19), respectively.

$$ {\text{MSE}} = \frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left( {s_{i} - \widehat{{s_{i} }}} \right)^{2} } $$

(17)

$$ {\text{MAE}} = \frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left| {s_{i} - \widehat{{s_{i} }}} \right|} $$

(18)

$$ {\text{MAPE}} = \frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left| {\frac{{s_{i} - \widehat{{s_{i} }}}}{{\widehat{{s_{i} }}}}} \right|} \times 100 $$

(19)

where, N_test is the numbers of data to be tested. ${s}_{i}$ and $\widehat{{s}_{i}}$ are the actual and predicted closing prices, respectively. In this work, MSE is used as functional value to be minimized by optimizing the weights and biases of ELM model. The performance measures used for this purpose are shown in Eqs. (20)–(23).

$$ {\text{Mean}}\;{\text{Arctangent}}\;{\text{Absolute}}\;{\text{Percentage}}\;{\text{Error}}\left( {{\text{MAAPE}}} \right) = \frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left( {AAPE_{i} } \right)} $$

(20)

where, ${AAPE}_{i}=\mathrm{arctan}\left(\left|\frac{{S}_{i}-\widehat{{S}_{i}}}{{S}_{i}}\right|\right)$

$$Coefficient of Variation (CoV)=\frac{Standard Deviation}{Mean}\times 100$$

(21)

$$\mathrm{Corelations }(\mathrm{CORR})=\frac{\sum_{i=1}^{{N}_{test}}\left({S}_{i}-mean\left({S}_{i}\right)\right)\left(\widehat{{S}_{i}}-mean\left(\widehat{{S}_{i}}\right)\right)}{\sqrt{\sum_{i=1}^{{N}_{test}}{\left({S}_{i}-mean\left({S}_{i}\right)\right)}^{2}\sum_{i=1}^{{N}_{test}}{\left(\widehat{{S}_{i}}-mean\left(\widehat{{S}_{i}}\right)\right)}^{2}}}$$

(22)

$$ {\text{Theil's}}\;{\text{U}} = \frac{{\sqrt {\frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left( {S_{i} - \widehat{{S_{i} }}} \right)^{2} } } }}{{\sqrt {\frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left( {S_{i} } \right)^{2} } } + \sqrt {\frac{1}{{N_{{test}} }}\sum\nolimits_{{i = 1}}^{{N_{{test}} }} {\left( {\widehat{{S_{i} }}} \right)^{2} } } }} $$

(23)

CoV is useful performance measures to interpret a difference between two predicted data sets. The CoV demonstrates the variability of data in a sample in relation to the mean of the population. In this work, CoV is used to measure the volatility and risk in compare to return. MAAPE is a scale-independent and interpretability performance measure to estimate forecast accuracy. It achieves extra balanced penalty of errors over MAPE [56]. CORR is a statistical measure which determines the relative movements of actual and predicted closing price. The range of correlation coefficient is between -1 to 1. The positive correlation coefficient near to 1 ($CORR\ngtr 1)$ provides a strong linear relationship between actual and predicted closing price. Theil’s U is used as a statistical measure to determine the forecasting accuracy. The smaller value of Theil’s U indicates more accuracy of forecast.

2.6 Hypothesis testing (paired t-test)

In this work, paired t-test is used to hypothetically test the accuracy of predicted closing price. Paired t-test requires two samples of observations such as predicted price ($\widehat{{S}_{i}}$) and actual price (${S}_{i}$) with n samples. The t-test performs to state the acceptance of null (H₀) and alternative (H₁) hypotheses. The null and alternative hypotheses adopted for this work are:

H₀—The mean difference is equal to zero (${\mu }_{{S}_{i}}={\mu }_{\widehat{{S}_{i}}}$).

H₁—The mean difference is not equal to zero (${\mu }_{{S}_{i}}\ne {\mu }_{\widehat{{S}_{i}}}$).

The paired t-test is mathematically described in Eqs. (24)–(27).

$$dif={S}_{i}-\widehat{{S}_{i}}$$

(24)

$$\overline{dif }=\frac{\sum dif}{n}$$

(25)

$$SD=\sqrt{\frac{\sum {\left(dif-\overline{dif }\right)}^{2}}{n-1}}$$

(26)

$$ t{\text{ - value}} = \sqrt n \frac{{\overline{{dif}} }}{{SD}} $$

(27)

where, dif, $\overline{dif }$, and SD are the difference, mean of difference, and sample standard deviation, respectively. In this work, the acceptance/failure of acceptance of null hypothesis is decided by conceding the significance level of 5% (0.05).

2.7 Sharpe ratio (SR) and modified sharpe ratio (MSR)

An investor requires nimble investment to achieve good return with less risk. For the purpose to help investors to understand the return of an investment compared to its risk, sharpe ratio is an useful financial tool. The mathematical expression of SR is defined in Eq. (28).

$$SR=\frac{{R}_{P}-{R}_{F}}{{\sigma }_{p}}$$

(28)

where, R_P, R_F and ${\sigma }_{p}$ are the portfolio return, risk free rate and standard deviation of portfolio return, respectively. Modified Sharpe ratio (MSR) is a modified tool of SR, which encourages that any abnormalities (abnormal distributed assets) are precluded from its calculation. Modified Sharpe Ratio (MSR) is used for a statistical analysis by concerning Modified Value at Risk (MVaR). MVaR measures the level of risk within a portfolio with non-normal distribution return of a specific time [57]. MSR and MVaR are determined as illustrated in Eq. (29) and (30).

$$MSR=\frac{{R}_{P}-{R}_{F}}{MVaR}$$

(29)

$$MVaR=W\left[\mu -\left\{{Z}_{c}+\frac{1}{6}\left({Z}_{c}^{2}-1\right)S+\frac{1}{24}\left({Z}_{c}^{3}-3{Z}_{c}\right)K-\frac{1}{36}(2{Z}_{c}^{3}-5{Z}_{c}){S}^{2}\right\}\sigma \right]$$

(30)

where, Z_c = Critical value for probability. S = Skewness. K = Excess kurtosis. μ = Rate of drift of asset value. W = Amount at risk or portfolio.

3 Result and discussion

3.1 Validation of proposed algorithm through benchmark test functions

The novelty of CSA is favorably demonstrated in various engineering applications. This algorithm has certain kind of scarcity to solve complex problems. CSA largely depends on random position of crows and randomly selected crow. The position of a crow may be updated by conceding unfit and worst crow which is not acceptable. The sluggish convergence rate and probability to trap into local optima may be caused by this dilemma. The competence of CSA algorithm is enhanced by modifying the mathematical expression of the algorithm. The proposed PGCSA algorithm is demonstrated in this work in contrast with DE [42], PSO [44], Teaching Learning-Based Optimization (TLBO) [58], Salp Swarm Algorithm (SSA) [59] and CSA [48] algorithms. The competence of PGCSA algorithm to pluck optimum point, convergence rate and evading from local optima is portrayed by an admirable comparative analysis among recently proposed algorithms. The comparative analysis is observed by solving 9 benchmark functions without constraint and 3 benchmark functions with constraints. All the algorithms are executed individually for individual benchmark equations with same population and termination criteria.

For all algorithms, population size and maximum iterations are chosen as 20 and 1000, respectively. The solutions of each benchmark equations are evaluated by executing each algorithm for 50 times. The best solution among 50 runs is considered as the solution of the corresponding algorithms. The benchmark functions adopted for this work are categorized as unimodal separable/non-separable (US/UN) and multimodal separable/non separable (MS/MN). The constraint and unconstraint benchmark equations are tabulated in Tables 1 and 2 respectively. The different categories of functions are adopted to contribute a fine validation of proposed algorithm in different environments. The Best value (BV), Average value (Avg) and Standard Deviation (SD) of the solution are opted as performance parameters. The comparative analysis is graded by conceding these parameters. All the adopted benchmark functions are minimization problems. The solutions of benchmark problems without constraints are portrayed in Table 3 and the solutions of benchmark problems with constraints are portrayed in Table 4. The convergence plots of each algorithm of benchmark problems without constraints are illustrated in Fig. 4 and the convergence of benchmark problems with constraints are portrayed in Fig. 5. From Figs. 4, 5 and Tables 3, 4, the proficiency of proposed PGCSA algorithm along with faster convergence and capability to escape from local optima are validated over CSA, SSA, TLBO, PSO and DE algorithms. From Tables 3 and 4, the performance parameters contributed by PGCSA of almost all benchmark functions are favorably less. The convergence rate of PGCSA algorithm is also validated from Figs. 4 and 5 for first 100 iterations.

Table 1 Benchmark Equations (Unconstraint)

Table 2 Benchmark Equations (Constraint)

Table 3 Performance parameters of different algorithms of benchmark equations without constraints

Table 4 Performance parameters of different algorithms of benchmark equations with constraints

Fig. 4

Convergence plot of PGCSA, CSA, SSA, TLBO, PSO and DE on the benchmark functions without constraint

Fig. 5

Convergence plot of PGCSA, CSA, SSA, TLBO, PSO and DE on the benchmark functions with constraint

The better standard deviation and mean values of an algorithm demonstrate that the average performance and stability of proposed PGCSA algorithm is better over other considered algorithms. In addition to mean and standard deviation, a pairwise hypothesis test is conducted by using Wilcoxon signed-rank test. Null hypothesis (H₀) and alternative hypothesis (H₁) are considered to interpret the superiority of PGCSA algorithm.

$$ \left\{ \begin{gathered} H_{0} :{\text{Mean}}\;{\text{difference}}\;{\text{is}}\;{\text{zero}} \hfill \\ H_{1} :{\text{Mean}}\;{\text{difference}}\;{\text{is}}\;{\text{not}}\;{\text{zero}} \hfill \\ \end{gathered} \right. $$

The main concerns to reject or accept the null hypothesis are p-value and significance level (α = 0.05). A p-value larger than significance level fails to reject null hypothesis, while a p-value smaller than significance level reject the null hypothesis. The p-values have been determined and portrayed in Table 5. From Table 5, all p-values are less than 0.05 which indicates the evidence to reject null hypothesis with a significance level of 95%.The rank sum values have been calculated between PGCSA and other algorithms which are shown in Table 6. R + is the sum of positive ranks which indicates the PGCSA algorithm outperformed the other algorithm and R − is the sum of negative ranks which indicates the failure of PGCSA algorithm to outperform the other algorithm. From Table 6, the sum of positive ranks for all benchmark functions is higher than the sum of negative ranks which substantiates that the PGCSA outperforms other algorithms in each comparison.

Table 5 p-Values obtained from the Wilcoxon signed rank test

Table 6 Rank sum values obtained from the Wilcoxon signed rank test

3.2 Simulation experiments for validation of proposed technique of stock market forecasting

In previous section, the evidence to validate the efficacy of proposed PGCSA is achieved by outperforming other existing techniques. In this section, the proposed PGCSA-ELM technique is executed in stock market index price forecasting for analysing the effectiveness of proposed technique with some existing techniques. IXIC stock index is considered for the comparative analysis with existing techniques such as multilayer perceptron (MLP), hybrid GARCH-MLP, dynamic architecture for artificial neural networks (DAN2), GARCH-DAN2 [10]. GDAXI index is considered to achieve a performance comparison of proposed technique with existing techniques such as GA-NN, GRNN, RBE and BNNMAS proposed by Hafezi et al. [54]. The two indices are considered with exactly same data as considered in [10, 54]. The performance measures (MAE, MSE, and MAPE) of different techniques for IXIC stock index forecasting testing period are tabulated in Table 7. The PGCSA-ELM, CSA-ELM and ELM predicted IXIC index testing data are portrayed in Fig. 6a and MAE values of prediction is portrayed in Fig. 6b. The performance indices and predicted quarterly GDAXI index are portrayed in Table 8 and Fig. 7a. The MAE values of predicted closing price by different models are portrayed in Fig. 7b. From this analysis, the effectiveness of PGCSA ELM techniques is substantiated with minimum performance measures. The testing results of GDAXI index predicted by different models are portrayed in appendix. The superiority of proposed PGCSA ELM model over CSA ELM and ELM models predicted can be concluded from this analysis.

Table 7 Comparison of performance measures of testing period of IXIC index

Fig. 6

a Next day predicted and actual closing price of IXIC index, b MAE values

Table 8 Comparison of performance measures of testing period of GDAXI index

Fig. 7

a Next quarter predicted and actual closing price of GDAXI index, b MAE values

3.3 Simulation experiments of stock market forecasting

For each stock index, CSA and PGCSA algorithm are executed individually with 100 populations to optimize ELM with ten neurons for 1000 iterations. The prime objective of optimization technique is to minimize Mean Squared Error (MSE). The competence of ELM model is influenced by the numbers of neurons of hidden layer. Initially, the ELM model is executed by varying the neurons of hidden layer. MSE, MAE and MAPE of ELM predicted closing price of IXIC are tabulated in Table 9 with different neurons. From Table 9, the CSA-ELM model with ten neurons is realized with better performance parameters. So, the ELM with ten hidden neurons is executed for all indices to predict closing price. The activation function of ELM is also a decisive factor by which the performance is influenced. The selection of relevant activation function for this work is done by a comparative analysis. The activation functions considered for the comparative analysis are sigmoid, hyperbolic tangent (tanh), softsign and rectified linear unit (ReLU) activation functions. The performance measures of forecasted closing price of IXIC with different activation functions are portrayed in Table 10. From Table 10, sigmoid activation function is concluded as a better activation function with better overall performance.

Table 9 Statistical analysis of ELM models with different neurons for IXIC market

Table 10 Statistical analysis of ELM models with different activation functions for IXIC market

The performance parameters (MSE, MAE and MAPE) of stock indices with PGCSA-ELM, CSA-ELM and ELM models are tabulated in Table 11. PGCSA-ELM, CSA-ELM and ELM models predicted closing price with respect to actual closing price, absolute error, and MAE are portrayed in Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28. The testing results of different models are illustrated by splitting into four parts to portray a clear comparative analysis. The comparative analysis is portrayed to validate proposed PGCSA ELM over CSA ELM and CSA ELM over ELM in these figures. The zoomed part of predicted closing price is illustrated to contribute a fair comparative analysis. Figures 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 represent the performance of prediction to substantiate PGCSA ELM over CSA ELM and ELM model in terms of prediction of closing price. From Table 11 and Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, PGCSA-ELM model to predict SM closing price is favourably affirmed as a superior model in comparison with CSA-ELM, and ELM models.

Table 11 MSE, MAE and MAPE values of PGCSA-ELM, CSA-ELM and ELM models for various markets

Fig. 8

PGCSA ELM and CSA ELM models predicted next day closing price of DJI

Fig. 9

CSA ELM and ELM models predicted next day closing price of DJI

Fig. 10

absolute error and MAE values of predicted DJI closing price

Fig. 11

PGCSA ELM and CSA ELM models predicted next day closing price of HSI

Fig. 12

CSA ELM and ELM models predicted next day closing price of HSI

Fig. 13

absolute error and MAE values of predicted HSI closing price

Fig. 14

PGCSA ELM and CSA ELM models predicted next day closing price of IXIC

Fig. 15

CSA ELM and ELM models predicted next day closing price of IXIC

Fig. 16

Absolute error and MAE values of predicted IXIC closing price

Fig. 17

PGCSA ELM and CSA ELM models predicted next day closing price of N100

Fig. 18

CSA ELM and ELM models predicted next day closing price of N100

Fig. 19

Absolute error and MAE values of predicted N100 closing price

Fig. 20

PGCSA ELM and CSA ELM models predicted next day closing price of NSEI

Fig. 21

CSA ELM and ELM models predicted next day closing price of NSEI

Fig. 22

Absolute error and MAE values of predicted NSEI closing price

Fig. 23

PGCSA ELM and CSA ELM models predicted next day closing price of RUT

Fig. 24

CSA ELM and ELM models predicted next day closing price of RUT

Fig. 25

Absolute error and MAE values of predicted NSEI closing price

Fig. 26

PGCSA ELM and CSA ELM models predicted next day closing price of GDAXI

Fig. 27

CSA ELM and ELM models predicted next day closing price of GDAXI

Fig. 28

Absolute error and MAE values of predicted GDAXI closing price

Further, the comparison between actual closing price and predicted closing price in terms of statistical measures (MAAPE, CoV, CORR and Theil’s U) is portrayed in Table 12. The PGCSA-ELM predicted model is substantiated with better performance measures in comparison to CSA-ELM and ELM models. From Table 12, PGCSA-ELM predicted closing price is substantiated as better forecast over CSA-ELM predicted closing price.

Table 12 Comparison of performance measures

The computational time of ELM, CSA-ELM and PGCSA-ELM models evaluated during the training period is portrayed in Table 13. The weights and biases of ELM are evaluated by optimization techniques during training period and the evaluated parameters are fixed to test the prediction ability. So, the computational time is evaluated during training period. The increased computational complexity of the metaheuristic-based ELM models are observed to possess a higher computational time. However, the computational time can be compensated with a significant improvement in prediction performance.

Table 13 Computational time of different models in seconds

The evidence to substantiate the integration of proposed PGCSA algorithm and optimized ELM has been depicted by simulation results as portrayed in previous sections. Seven different stock market indices are considered for the analysis. The improvement (in percentage) of performances in terms of measures of PGCSA ELM over CSA ELM and ELM methods is portrayed in Table 14.

Table 14 Improvement of performance measures of PGCSA ELM in percentage

3.3.1 Verification of SM price prediction by Paired t-test

The accuracy of prediction of closing price of SM is hypothetically tested by employing paired t-test. This test substantiates the proposed algorithm to contribute mean difference between predicted closing price and actual closing price. The statistical measure (paired t-test) requires two samples of observations of n numbers population. In this work, actual closing price (S_i) and predicted closing price ($\widehat{{S}_{i}}$) are considered as two samples for paired t-test. The paired t-test results are tabulated in Table 15. The significance level of 5% (0.05) is adopted to accept the paired t-test. From Table 15, it is clearly realized |t| <|t_critical| and ρ > 0.05 for all seven markets. The absolute value of t-value contributed by proposed algorithm is less as compared with CSA-ELM and ELM models.

Table 15 The paired t-test result

3.3.2 Verification of SM price prediction by sharpe ratio and modified sharpe ratio

In previous section, the predicted data administered by proposed method is hypothetically tested by paired t-test. In this section, the predicted closing price is tested through financial indicators such as annual return (AR), Sharpe ratio (SR) and modified sharpe ratio (MSR). AR is the yearly profit in percentage as defined in Eq. (31).

$$AR=\left({\left(\frac{Return}{capital}\right)}^\frac{1}{nt}-1\right)*100$$

(31)

where, ‘nt’ is the number of trading days of a year. The AR, SR and MSR of actual & predicted closing price of stock markets have been portrayed in Table 16. These financial indicators of PGCSA-ELM predicted closing price are higher in comparison with CSA-ELM and ELM predicted closing price.

Table 16 Comparison of financial indicators

From Table 16, PGCSA-ELM predicted closing price is more sensitivity to non-normal distribution of return and financial indicators. PGCSA-ELM predicted price is close to the indicators of actual closing price of an index which means, the proposed model predicts price close enough to the actual trading cost.

4 Conclusion

Accurate forecasting of the stock markets price is the subject of extreme concern, especially in recent years. This study proposed a novel approach based on PGCSA and ELM for forecasting stock market closing price precisely. The proposed technique is also substantiated by including the data of seven indices during COVID-19 outbreak.

First, PGCSA algorithm is mainly based upon the awareness probability of a crow. Without awareness probability, the flock of crows are splited into different groups to explore the search space. The crows with awareness probability are updated with velocity by concerning each group’s best crow. The proficiency of proposed PGCSA algorithm to solve 9 benchmark equations without constraints and 3 benchmark equations with constraints is substantiated over CSA, SSA, TLBO, PSO and DE algorithms. The effectiveness of proposed algorithm to resolve benchmark equations are acknowledged by conceding best value, mean and standard deviation as performance parameters. In addition to that, Wilcoxon test is considered for the hypothetical validation of the proposed approach.

Moreover, the CSA and proposed PGCSA algorithms are enforced individually to optimize the weight and bias of ELM to forecast next day closing price of seven different stock indices. MSE, MAE and MAPE are considered as statistical weighs to contribute a fair comparative analysis to demonstrate the supremacy of PGCSA-ELM over CSA-ELM and ELM predicted models. Further, MAAPE, CoV, CORR and Theil’s U are used as statistical measures to substantiate PGCSA-ELM over CSA-ELM and ELM forecasting models with maximum CORR and minimum MAAPE, CoV & Theil’s U. From this work, it is corroborated that PGCSA-ELM forecasting model outperforms CSA-ELM and ELM forecasting models to predict next day closing price.

Finally, the mean difference between actual and forecasted closing price is hypothetically substantiated by adopting paired sample t-test. The risk adjusted basis relevant measures like AR, SR, MSR of actual and predicted closing price is also considered to achieve good return with less risk.

Appendix

See Table

Table 17 Comparative analysis of GDAXI predicted value

17.