The existence and stability of spikes in the one-dimensional Keller–Segel model with logistic growth

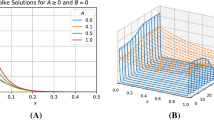
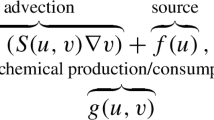Abstract

It is well known that Keller–Segel models serve as a paradigm to describe the self aggregation phenomenon, which exists in a variety of biological processes such as wound healing, tumor growth, etc. In this paper, we study the existence of monotone decreasing spiky steady state and its linear stability property in the Keller–Segel model with logistic growth over one-dimensional bounded domain subject to homogeneous Neumann boundary conditions. Under the assumption that chemo-attractive coefficient is asymptotically large, we construct the single boundary spike and next show this non-constant steady state is locally linear stable via Lyapunov–Schmidt reduction method. As a consequence, the multi-symmetric spikes are obtained by reflection and periodic extension. In particular, we present the formal analysis to illustrate our rigorous theoretical results.

Appendices

Appendix A: Formal expansion of single boundary spikes

In Appendix A, we shall employ the matched asymptotic analysis to reconstruct the non-constant steady state (1.4), which can support our rigorous argument.

We firstly multiply the both hand side of the u-equation by $\frac{1}{\chi }$ in (1.3) to obtain

$$\begin{aligned} \left\{ \begin{array}{ll} 0=\frac{1}{\chi }u_{xx}- (uv_x)_x+\frac{\mu }{\chi }u({{\bar{u}}}-u),&{}x\in (0,L),\\ 0=v_{xx}-v+u,&{}x\in (0,L). \end{array} \right. \end{aligned}$$

(1.1)

Our aim is to look for a localized pattern with the centre being 0. Recall $\epsilon :=\sqrt{1/\chi }$, then in the inner region, we introduce

$$\begin{aligned} U(y):=u(x),\quad V(y):=v(x)\text {~with~} y:=\frac{x }{\epsilon }. \end{aligned}$$

(1.2)

Upon substituting (1.2) into (1.1), one has

$$\begin{aligned} \left\{ \begin{array}{ll} 0=U_{yy}-\epsilon ^{-2} (U V_y)_y+\epsilon ^2\mu U({{\bar{u}}}-U),&{}y\in (0,\frac{L}{\epsilon }),\\ 0=\epsilon ^{-2} V_{yy}-V+U,&{}y\in (0,\frac{L}{\epsilon }). \end{array} \right. \end{aligned}$$

(1.3)

We expand

$$\begin{aligned} U(y)=U_0+\epsilon ^{2}U_1+\ldots , \quad V(y)= V_0+\epsilon ^{2} V_1\cdots \end{aligned}$$

(1.4)

and substitute it into (1.3). To the leading order, we see that $V_{0yy}=0$. Since we would like to find the uniformly bounded solution in $(0,\infty )$, one takes $V_0=V_{00}$, where $V_{00}$ is an undetermined constant. Moreover, we collect the following hierarchy from (1.3) and (1.4):

$$\begin{aligned} \left\{ \begin{array}{ll} U_{0yy}-(U_0 V_{1y})_y=0, &{}y\in (0,\infty ),\\ V_{1yy}-V_{00}+U_0=0, &{}y\in (0,\infty ), \end{array} \right. \end{aligned}$$

(1.5)

and

$$\begin{aligned} \left\{ \begin{array}{ll} U_{1yy}-(U_1V_{1y})_y-(U_0V_{2y})_y=-\mu U_0({{\bar{u}}}-U_0),&{}y\in (0,\infty ),\\ V_{2yy}=V_1-U_1,&{}y\in (0,\infty ). \end{array} \right. \end{aligned}$$

Noting $U\ll 1$ in the outer region, one has $U_0\rightarrow 0$ as $\vert y\vert \rightarrow 0$. Thus, we infer from the first equation of (1.5) that $U_0(y)=U_{00} e^{ V_1(y)}$, where $U_{00}$ is an unknown constant. Now in the outer region, we can replace U in sense of distribution by

$$\begin{aligned} U\rightarrow \epsilon U_{00}\int _0^\infty e^{V_1}d\rho \delta _0(x). \end{aligned}$$

As such we find the outer problem for v is

$$\begin{aligned} \left\{ \begin{array}{ll} v_{yy}-v=-\epsilon U_{00}C\delta _0(x), &{}x\in (0,L),\\ v_{y}(0)=v_{y}(L)=0, \end{array} \right. \end{aligned}$$

where $C:=\int _0^\infty e^{V_1}d\rho$ and we impose that C is a finite integral. To express v in the outer region, we introduce the following one-dimensional Neumann Green’s function $G(x;\xi )$:

$$\begin{aligned} \left\{ \begin{array}{ll} G_{xx}-G=-\delta (x-\xi ), &{}x\in (0,L),\\ G_x(0;\xi )=G_x(L;\xi )=0, \end{array} \right. \end{aligned}$$

where G has the following explicit form:

$$\begin{aligned} G(x;\xi )=\left\{ \begin{array}{ll} \frac{\cosh (L-\xi )}{\sinh L}\cosh x,&{}x\in (0,\xi ),\\ \frac{\cosh \xi }{\sinh L}\cosh (L-x), &{}x\in (\xi ,L). \end{array} \right. \end{aligned}$$

Hence, we find v satisfies $v\sim \epsilon U_{00}CG(x;0)$. It follows that as $x\rightarrow 0$ and $\epsilon \rightarrow 0^+$, $v\rightarrow 0$. Recall in the inner expansion, $V=V_{00}+\epsilon ^2 V_1+\cdots ,$ then we conclude from the matching that $V_{00}=0.$

We next solve (1.5) to find the inner solution. Upon substituting $U_0=U_{00}e^{V_1}$ and $V_{00}=0$ into the second equation, we establish the following core problem:

$$\begin{aligned} \left\{ \begin{array}{ll} V_{1yy}+U_{00} e^{V_1}=0, ~y\in (0,\infty ),\\ V_{1y}(0)=0. \end{array} \right. \end{aligned}$$

(1.6)

Solving equation (1.6) gives rise to

$$\begin{aligned} V_1(y)=\log \Bigg (\frac{a}{2 U_{00} \cosh ^2(\frac{\sqrt{a}}{2} y)}\Bigg ), \end{aligned}$$

where a is a free parameter. Since $V_{1y}=-\sqrt{a}\tanh \big (\frac{\sqrt{a}}{2} y\big )$, one has from the relationship between $V_{1}$ and $U_{0}$ that

$$\begin{aligned} U_0 =\frac{a}{2}\textrm{sech}^{2}\Big (\frac{\sqrt{a}}{2} y\Big ). \end{aligned}$$

(1.7)

To determine the constants, we next apply the integral constraint $\int _{0}^L u({{\bar{u}}}-u)dx=0$ thanks to the Neumann boundary condition. Noting $U\sim U_0$, we can arrive at

$$\begin{aligned}\int ^\infty _{0}U_0({{\bar{u}}}-U_0)dy=0.\end{aligned}$$

By using $U_0(y)=U_{00} e^{V_1}$, one has $\int _{0}^{\infty }(e^{V_1}-U_{00} e^{2 V_1})dy=0$, which then yields that

$$\begin{aligned} \int _{0}^{\infty }\Bigg ({{\bar{u}}}\textrm{sech}^{2}\Bigg (\frac{\sqrt{a}}{2} y\Bigg ) -\frac{a}{2}\textrm{sech}^{4}\Bigg (\frac{\sqrt{a}}{2} y\Bigg )\Bigg )dy=0. \end{aligned}$$

(1.8)

Let $z=\frac{\sqrt{a}}{2} y$, then we solve (1.8) to get $a\sim 3{{\bar{u}}}.$ Therefore, we have from (1.7) that for $y\in (0,\infty ),$

$$\begin{aligned} U_0=\frac{a}{2}\textrm{sech}^{2}\Big (\frac{\sqrt{a}}{2} y\Big ) \end{aligned}$$

with $a\sim 3{{\bar{u}}}.$ Now, we have obtained the inner solution.

Focusing on the outer region, one has $u\sim 0$ and $v_{xx}-v\sim 0$ with $v_{0y}(L)=0$. By solving it, we get

$$\begin{aligned}v\sim C_v \cosh (x-L),~~x\in (0,L),\end{aligned}$$

where $C_v$ is an unknown constant to be determined. We next use the matching condition to determine constant $C_v$. From the inner solution, one finds

$$\begin{aligned} \frac{d V}{dy}=-\epsilon ^{2}\sqrt{a}\tanh \Bigg (\frac{\sqrt{a}}{2}y\Bigg ), \end{aligned}$$

which yields

$$\begin{aligned} \frac{d V}{dy}\rightarrow -\epsilon ^{2}\sqrt{a}\text {~~as~~} y\rightarrow +\infty . \end{aligned}$$

(1.9)

On the other hand, from the outer solution, we conclude for $0<x<L,$

$$\begin{aligned}\frac{dv}{dy}=\frac{dv}{dx}\epsilon \sim \epsilon C_v \sinh (x-L).\end{aligned}$$

It follows that

$$\begin{aligned} \frac{dv}{dy}\rightarrow -C_v \epsilon \sinh L~~\text {as}~~x\rightarrow 0. \end{aligned}$$

(1.10)

After matching (1.9) and (1.10), one can get $C_{\nu }=\epsilon \sqrt{a}/\sinh L.$

In summary, the single boundary spike $(u^-,v^-)$ can be asymptotically written as

$$\begin{aligned} u^{-}\sim \frac{a}{2}\textrm{sech}^2\bigg (\frac{\sqrt{a}}{2}\cdot \frac{x}{\epsilon }\Bigg ),~\text {~for}~~x\in (0,L), \end{aligned}$$

and

$$\begin{aligned} v^{-}\sim \epsilon \frac{\sqrt{a}}{\sinh L} \cosh (x-L),\text {~~for~~}x\in (0,L), \end{aligned}$$

where $a\sim 3{{\bar{u}}}$. Next, we use the Van Dyke’s matching principle $v_\text {unif}=v_\text {inner}+v_\text {outer}-v_\text {overlap}$ to find the composite expansion of v, which is

$$\begin{aligned}v^-\sim \epsilon ^2\log \Big (\frac{1}{4}\textrm{sech}^2\Big (\frac{\sqrt{a}}{2}\frac{x}{\epsilon }\Big )\Big )+\epsilon \frac{\sqrt{a}}{\sinh L} \cosh (x-L)+\sqrt{a}\epsilon x.\end{aligned}$$

These results agree with those stated in Theorem 1.1.

Appendix B: Formal analysis of the eigenvalue problem

This section is devoted to the study of linearized eigenvalue problem (4.1) via the matched asymptotic analysis. Similarly, in the inner region, we introduce the following rescaled functions:

$$\begin{aligned}\Phi (y):=\phi (x),~~\Psi (y):=\psi (x)\text {~with~} y=\frac{x}{\epsilon }.\end{aligned}$$

By using it together with (1.2), one can rewrite (4.1) as

$$\begin{aligned} \left\{ \begin{array}{ll} \epsilon ^2\lambda \Phi =\Phi _{yy}-\epsilon ^{-2} (U \Psi _y+\Phi V_{y})_y+\epsilon ^2\mu ({{\bar{u}}}-2U)\Phi ,&{}y\in (0,\frac{L}{\epsilon }),\\ \lambda \Psi =\epsilon ^{-2}\Psi _{yy}-\Psi +\Phi , &{}y\in (0,\frac{L}{\epsilon }),\\ \Phi _y(0)=\Psi _y(0)=\Phi _y(\frac{L}{\epsilon })=\Psi _y(\frac{L}{\epsilon })=0. \end{array} \right. \end{aligned}$$

(2.1)

Similarly as above, we expand

$$\begin{aligned} \lambda =\lambda _0+\cdots ,~~\Phi (y)= \Phi _0(y)+\epsilon ^{2}\Phi _1(y)+\cdots \text {~~and~~} \Psi = \Psi _0(y)+\epsilon ^{2}\Psi _1(y)+\cdots \end{aligned}$$

and substitute them together with (1.4) into (2.1). Then one can find $\Psi _{0y}=0$, and thereby $\Psi _0(y):=\Psi _{00}$ with $\Psi _{00}$ being a constant. Moreover, with the help of matching condition between the inner and the outer solution, we obtain $\Psi _{00}=0.$

We further collect the following leading order system:

$$\begin{aligned} \left\{ \begin{array}{ll} 0=\Phi _{0yy}-(U_0\Psi _{1y}+\Phi _0 V_{1y})_y,&{}y\in (0,\infty ),\\ 0=\Psi _{1yy}+\Phi _0,&{}y\in (0,\infty ),\\ \Phi _{0y}(0)=\Psi _{1y}(0)=0,~~\Phi _0(\infty )=0. \end{array} \right. \end{aligned}$$

(2.2)

The first equation in (2.2) implies that $\Big (\frac{\Phi _0}{U_0}\Big )_y=\Psi _{1y}$, hence $\Phi _0=U_0\Psi _1+CU_0$ thanks to the boundary conditions, where C is some constant to be determined later on. Therefore, (2.2) yields that

$$\begin{aligned} \left\{ \begin{array}{ll} \Psi _{1yy}+U_0\Psi _1+CU_0=0,&{}y\in (0,\infty ),\\ \Psi _{1y}(0)=0. \end{array} \right. \end{aligned}$$

(2.3)

Since $U_0= \frac{a}{2}\textrm{sech}^{2}\Big (\frac{\sqrt{a}}{2}y\Big )$ and $a\sim 3{{\bar{u}}}$, we further solve (2.3) to get the eigenfunctions are unique up to a constant multiplier of the following

$$\begin{aligned} \Psi _1(y)=&\,\frac{1}{\sqrt{a}}y\tanh \Big (\frac{\sqrt{a}}{2} y\Big ),\nonumber \\ \Phi _0(y)=&\Bigg (1-\frac{\sqrt{a}}{2}y\tanh \Bigg (\frac{\sqrt{a}}{2}y\Bigg )\Bigg )\textrm{sech}^{2}\Bigg (\frac{\sqrt{a}}{2}y\Bigg ),~~a\sim 3{{\bar{u}}}. \end{aligned}$$

(2.4)

Next, we proceed to show the corresponding leading eigenvalue $\lambda _0<0$, which tells us that steady state (1.4) is linearly stable.

Proof

We integrate the $\phi$-equation in (4.1) over (0, L) to get

$$\begin{aligned} \lambda \int _{0}^L\phi (x) dx=\mu \int _0^L ({{\bar{u}}}-2u)\phi (x) dx. \end{aligned}$$

(2.5)

Upon substituting (2.4) into (2.5), one has the left hand side and right hand side satisfy

$$\begin{aligned} \lambda \int _0^L\phi (x) dx\sim \epsilon \lambda _0 \int _{0}^\infty \Phi _0(y) dy \end{aligned}$$

(2.6)

and

$$\begin{aligned} \int _0^L \mu ({{\bar{u}}}-2u)\phi (x) dx\sim \epsilon \int _{0}^\infty \mu ({{\bar{u}}}-2 U_0) \Phi _0(y) dy, \end{aligned}$$

(2.7)

respectively. By straightforward calculation, we obtain

$$\begin{aligned} \int _0^\infty \Phi _0 dy=-\frac{1}{\sqrt{a}}, \end{aligned}$$

(2.8)

and

$$\begin{aligned} \int _0^\infty U_0 \Phi _0 dy=-\frac{1}{2}\sqrt{a}. \end{aligned}$$

(2.9)

Combining (2.8) and (2.9), we have from (2.5), (2.6) and (2.1) that $\lambda _0\sim -2\mu {{\bar{u}}}.$ This gives us (1.4) is linearly stable with respect to the even eigenfunction (2.4), then formally verifies Theorem 1.2. $\square$