Quorum-sensing induced transitions between bistable steady-states for a cell-bulk ODE-PDE model with lux intracellular kinetics

Abstract

Intercellular signaling and communication are used by bacteria to regulate a variety of behaviors. In a type of cell-cell communication known as quorum sensing (QS), which is mediated by a diffusible signaling molecule called an autoinducer, bacteria can undergo sudden changes in their behavior at a colony-wide level when the density of cells exceeds a critical threshold. In mathematical models of QS behavior, these changes can include the switch-like emergence of intracellular oscillations through a Hopf bifurcation, or sudden transitions between bistable steady-states as a result of a saddle-node bifurcation of equilibria. As an example of this latter type of QS transition, we formulate and analyze a cell-bulk ODE-PDE model in a 2-D spatial domain that incorporates the prototypical LuxI/LuxR QS system for a collection of stationary bacterial cells, as modeled by small circular disks of a common radius with a cell membrane that is permeable only to the autoinducer. By using the method of matched asymptotic expansions, it is shown that the steady-state solutions for the cell-bulk model exhibit a saddle-node bifurcation structure. The linear stability of these branches of equilibria are determined from the analysis of a nonlinear matrix eigenvalue problem, called the globally coupled eigenvalue problem. The key role on QS behavior of a bulk degradation of the autoinducer field, which arises from either a Robin boundary condition on the domain boundary or from a constant bulk decay, is highlighted. With bulk degradation, it is shown analytically that the effect of coupling identical bacterial cells to the bulk autoinducer diffusion field is to create an effective bifurcation parameter that depends on the population of the colony, the bulk diffusivity, the membrane permeabilities, and the cell radius. QS transitions occur when this effective parameter passes through a saddle-node bifurcation point of the Lux ODE kinetics for an isolated cell. In the limit of a large but finite bulk diffusivity, it is shown that the cell-bulk system is well-approximated by a simpler ODE-DAE system. This reduced system, which is used to study the effect of cell location on QS behavior, is easily implemented for a large number of cells. Predictions from the asymptotic theory for QS transitions between bistable states are favorably compared with full numerical solutions of the cell-bulk ODE-PDE system.

Appendices

Appendices

Non-Dimensionalization

We non-dimensionalize the cell-bulk model (1.1) and (1.2) and the Lux ODE system of Melke et al. (2010). Our dimensional model assumes units of concentration for the extracellular autoinducer and intracellular chemical species whereas the dimensional model in Gou and Ward (2016) uses both mass and concentration units. At the end of this appendix, we give the units for all of the quantities. In Table 1 we list the parameter values for parameter set P1 in Melke et al. (2010), along with their dimensionless counterparts given in (A.3).

Table 1 List of parameter values from the parameter set P1 in Melke et al. (2010) along with the rescaled dimensionless parameters defined in (A.3)

We begin by non-dimensionalizing the Lux ODE kinetics for an isolated cell. In dimensional quantities and without bulk coupling, the system given in Melke et al. (2010) is

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}v_1}{\mathrm {d}T}&= c_1 + \frac{k_{1A}v_4}{k_{DA} + v_4} - k_{2A}v_1 - k_5 v_1 v_2 + k_6 v_3\,, \qquad \\ \frac{\mathrm {d}v_3}{\mathrm {d}T}&= k_5 v_1 v_2 - k_6 v_3 - 2k_3 v_3^2 + 2k_4 v_4\,, \\ \frac{\mathrm {d}v_2}{\mathrm {d}T}&= c_2 + \frac{k_{1R}v_4}{k_{DR} + v_4} - k_{2R}v_2 - k_5 v_1 v_2 + k_6 v_3\,, \qquad \\ \frac{\mathrm {d}v_4}{\mathrm {d}T}&= k_3 v_3^2 - k_4 v_4\,. \end{aligned} \end{aligned}$$

(A.1)

In our non-dimensionalization we eliminate as many parameters as possible, while ensuring that the ODE dynamics reaches its steady-state on an ${\mathcal {O}}(1)$ timescale. To this end, and with $\mathbf {v}\equiv (v_1,\ldots ,v_4)^T$, we introduce the non-dimensional variables $\mathbf {u}$ and t as

$$\begin{aligned} \mathbf {v} \equiv v_c\mathbf {u}\,, \qquad t \equiv k_R T \,, \qquad \text{ where } \qquad v_c\equiv \sqrt{\frac{c_{2}}{k_5}}\,, \quad k_R\equiv \sqrt{k_5 c_{2}}\,. \end{aligned}$$

(A.2)

This choice eliminates $\kappa _5$ and $c_2$. New dimensionless ODE parameters are then defined as

$$\begin{aligned} \begin{aligned} \kappa _{1A}&\equiv \frac{k_{1A}}{c_{2}}\,, \quad \kappa _{DA}\equiv k_{DA}\sqrt{\frac{k_5}{c_{2}}}\,, \quad \kappa _{2A}\equiv \frac{k_{2A}}{\sqrt{k_5c_{2}}}\,, \\ \kappa _{1R}&\equiv \frac{k_{1R}}{c_{2}} \,, \quad \kappa _{DR} \equiv k_{DR}\sqrt{\frac{k_5}{c_{2}}}\,, \\ \kappa _{2R}&\equiv \frac{k_{2R}}{\sqrt{k_5c_{2}}}\,, \quad k_3\equiv \frac{k_3}{k_5}\,, \quad \kappa _4\equiv \frac{k_4}{\sqrt{k_5c_{2}}}\,, \quad \kappa _5\equiv \frac{k_6}{\sqrt{k_5c_{2}}}\,, \quad c\equiv \frac{c_{1}}{c_{2}}\,. \end{aligned} \end{aligned}$$

(A.3)

By using (A.2) and (A.3) in (A.1), we obtain the dimensionless system for the reaction kinetics in (1.5).

The full ODE-PDE system is made dimensionless in a slightly different way than in Gou and Ward (2016). In (1.1) and (1.2) both ${\mathcal {U}}$ and $\mathbf {v}_j$ have units of concentration ($\text {moles}/\text {length}^2$), while in Gou and Ward (2016), $\mathbf {v}_j$ is measured in total amount ($\text {moles}$). With this in mind, we define the dimensionless quantities $\mathbf {x}$ and $U(\mathbf {x},t)$ by $\mathbf {x}\equiv {\mathbf {X}/L}$ and $U\equiv {{\mathcal {U}}/v_c}$. Upon substituting this into (1.1), we readily obtain (1.3) after defining the dimensionless bulk constants D, $\gamma$, and $\kappa$ and the dimensionless cell permeabilities $d_{1j}$ and $d_{2j}$ as

$$\begin{aligned} D\equiv \frac{D_B}{k_R L^2}\,, \quad \gamma \equiv \frac{\gamma _B}{k_R}\,, \quad \kappa \equiv \frac{\kappa _B}{k_R}\,, \quad p_{1j}\equiv L k_R\frac{d_{1j}}{\varepsilon }\,, \quad p_{2j}\equiv L k_R\frac{d_{2j}}{\varepsilon }\,.\nonumber \\ \end{aligned}$$

(A.4)

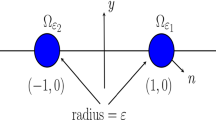
The requirement for the $\varepsilon$-dependent scaling in the permeabilities is so that there is an ${{\mathcal {O}}}(1)$ effect of the coupling of the cells to the bulk. Moreover, if $\mathbf {X}\in \Omega _L$, where $\Omega _L$ has a characteristic length scale of L, then $\mathbf {x}\in \Omega _1\equiv \Omega$. The dimensionless kinetics in (1.4) follows from the definitions in (A.2) and (A.4).

Denoting $\left[ x\right]$ to be the units of x, the units of the Lux and bulk parameters are as follows:

(A.5)

Green’s functions for the unit disk

To implement our steady-state and linear stability theory for the unit disk, two different Green’s functions are required. The Neumann Green’s function, satisfying, (3.5) is needed in §3 for the steady-state analysis with no bulk loss, and in § 5 to analyze the large $D={{\mathcal {O}}}(\nu ^{-1})$ limiting regime. In the GCEP analysis in §3.2 for the $D={{\mathcal {O}}}(1)$ regime, the eigenvalue-dependent Green’s function $G_{\lambda }$ satisfying (3.17) is required. Setting $\lambda =0$ in (3.17) yields the reduced-wave Green’s function in (3.11), which is required in § 3 for the steady-state analysis with bulk degradation.

In the unit disk, the Neumann Green’s function and its regular part are (see equation (4.3) of Kolokolnikov et al. (2005)):

$$\begin{aligned} G_N(\mathbf {x};\mathbf {x}_i)= & {} -\frac{1}{2\pi }\log |\mathbf {x}-\mathbf {x}_i| - \frac{1}{4\pi }\log \left( |\mathbf {x}|^2|\mathbf {x}_i|^2 + 1 - 2 \mathbf {x} \cdot \mathbf {x}_i\right) \nonumber \\&+ \frac{ (|\mathbf {x}|^2 + |\mathbf {x}_i|^2 )}{4\pi } - \frac{3}{8\pi } , \end{aligned}$$

(B.1a)

$$\begin{aligned} R_{Ni}= & {} -\frac{1}{2\pi }\log \left( 1 - |\mathbf {x}_i|^2\right) + \frac{|\mathbf {x}_i|^2}{2\pi } - \frac{3}{8\pi } \,. \end{aligned}$$

(B.1b)

Next, by extending the analysis in Appendix A.1 of Chen and Ward (2011) to allow for a Robin boundary condition, the Green’s function $G_\lambda$ and its regular part $R_\lambda$, satisfying (3.17), are calculated for the unit disk as

$$\begin{aligned} G_\lambda (\mathbf {x};\mathbf {x}_i)&= \frac{1}{2\pi } K_0(\theta _\lambda |\mathbf {x}-\mathbf {x}_i|)\nonumber \\&\quad - \frac{1}{2\pi } \sum \limits _{n=0}^\infty \sigma _n\left( \frac{\theta _\lambda K_n^{\prime }(\theta _\lambda ) + \frac{\kappa }{D} K_n(\theta _\lambda )}{\theta _\lambda I_n^{\prime }(\theta _\lambda ) +\frac{\kappa }{D} I_n(\theta _\lambda )}\right) I_n(\theta _\lambda |\mathbf {x}_i|) I_n(\theta _\lambda |\mathbf {x}|) \cos \left[ n(\phi -\phi _i)\right] \,, \end{aligned}$$

(B.2a)

$$\begin{aligned} R_{\lambda i}&= \frac{1}{2\pi }\left( \ln 2 - \gamma _e -\log \theta _\lambda \right) - \frac{1}{2\pi }\sum \limits _{n=0}^\infty \sigma _n\left( \frac{\theta _\lambda K_n^{\prime }(\theta _\lambda ) + \frac{\kappa }{D} K_n(\theta _\lambda )}{\theta _\lambda I_n^{\prime }(\theta _\lambda ) + \frac{\kappa }{D} I_n(\theta _\lambda )}\right) \left[ I_n(\theta _\lambda |\mathbf {x}_i|)\right] ^2\,, \end{aligned}$$

(B.2b)

where $\mathbf {x}=|\mathbf {x}|(\cos \phi ,\sin \phi )^T$ and $\mathbf {x}_i=|\mathbf {x}_i|(\cos \phi _i,\sin \phi _i)^T$. Here $\sigma _0 \equiv 1$, $\sigma _n \equiv 2$ for $n\ge 2$, and $\gamma _e=0.57721\ldots$ is the Euler-Mascheroni constant. The functions $K_n$ and $I_n$ are the $n^{\text {th}}$-order modified Bessel functions of the first and second kind, respectively. Here, $\theta _\lambda \equiv \sqrt{(\gamma + \lambda )/D}$, where the principle branch of the square root is taken when the argument is complex. Setting $\lambda =0$ in (B.2) yields the result for the reduced-wave Green’s function and its regular part in (3.11).

When the centers $\mathbf {x}_k$, for $k=1,\ldots ,m$, of the cells are equally-spaced on a ring concentric within the unit disk, the Green’s matrices ${{\mathcal {G}}}_N$, ${{\mathcal {G}}}$, and ${{\mathcal {G}}}_{\lambda }$ as needed in the steady-state and linear stability analysis in § 3 are cyclic and symmetric matrices. As such, their matrix spectrum is available analytically.

For an $m\times m$ cyclic matrix ${\mathcal {A}}$, with possibly complex-valued matrix entries, its complex-valued eigenvectors $\tilde{\mathbf {v}}_j$ and eigenvalues $\alpha _j$ are $\alpha _j = \sum \nolimits _{k=1}^m {\mathcal {A}}_{1k} \omega _j^{k-1}$ and $\tilde{\mathbf {v}}_j = \left( 1,\omega _j, ..., \omega _j^{m-1}\right) ^T$, for $j = 1,\ldots , m$. Here $\omega _j \equiv \exp {\left( \frac{2\pi i(j-1)}{m}\right) }$ and ${{\mathcal {A}}}_{1k}$, for $k=1,\ldots ,m$, are the elements of the first row of ${{\mathcal {A}}}$. Since ${{\mathcal {A}}}$ is also a symmetric matrix, we have ${{\mathcal {A}}}_{1,j}={{\mathcal {A}}}_{1,m+2-j}$, for $j=2,\ldots ,\lceil m/2\rceil$, where the ceiling function $\lceil x \rceil$ is defined as the smallest integer not less than x. Consequently, $\alpha _j=\alpha _{m+2-j}$, for $j=2,\ldots ,\lceil m/2\rceil$, so that there are $m-1$ eigenvalues with a multiplicity of two when m is odd, and $m-2$ such eigenvalues when m is even. As a result, it follows that $\frac{1}{2}\left[ \tilde{\mathbf {v}}_j+\tilde{\mathbf {v}}_{m+2-j}\right]$ and $\frac{1}{2i}\left[ \tilde{\mathbf {v}}_j-\tilde{\mathbf {v}}_{m+2-j}\right]$ are two independent real-valued eigenvectors of ${{\mathcal {A}}}$, corresponding to the eigenvalues of multiplicity two. In this way, the matrix spectrum of a cyclic and symmetric matrix ${{\mathcal {A}}}$, with the normalized eigenvectors $\mathbf {v}_j^T\mathbf {v}_j=1$, is

$$\begin{aligned} \begin{aligned} \alpha _j&= \sum \limits _{k=1}^m {\mathcal {A}}_{1k} \cos \left( \theta _j (k-1)\right) \,, \quad j=1,\ldots ,m\,; \qquad \\ \theta _j&\equiv \frac{2\pi (j-1)}{m}\,; \qquad \mathbf {v}_1=\frac{1}{\sqrt{m}}\mathbf {e} \,, \\ \mathbf {v}_j&= \sqrt{\frac{2}{m}} \left( 1, \cos \left( \theta _j \right) , \ldots ,\cos \left( \theta _j (m-1) \right) \right) ^{T} \,, \quad \\ \mathbf {v}_{m+2-j}&= \sqrt{\frac{2}{m}} \left( 0, \sin \left( \theta _j \right) , \ldots , \sin \left( \theta _j (m-1) \right) \right) ^{T} \,, \end{aligned} \end{aligned}$$

(B.3)

for $j = 2,\ldots , \lceil m/2\rceil$, where $\theta _j\equiv {2\pi (j-1)/m}$. When m is even, there is an additional normalized eigenvector of multiplicity one given by $\mathbf {v}_{{m/2}+1}=m^{-1/2}(1,-1,1,\ldots ,-1)^T$.