Mean–Variance Portfolio Selection Under Volterra Heston Model

Abstract

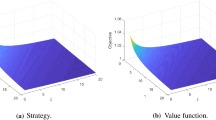
Motivated by empirical evidence for rough volatility models, this paper investigates continuous-time mean–variance (MV) portfolio selection under the Volterra Heston model. Due to the non-Markovian and non-semimartingale nature of the model, classic stochastic optimal control frameworks are not directly applicable to the associated optimization problem. By constructing an auxiliary stochastic process, we obtain the optimal investment strategy, which depends on the solution to a Riccati–Volterra equation. The MV efficient frontier is shown to maintain a quadratic curve. Numerical studies show that both roughness and volatility of volatility materially affect the optimal strategy.

Appendices

Appendix A: Solutions of Riccati–Volterra Equations

To demonstrate the existence and uniqueness of the solution to a Riccati–Volterra equation, we first rephrase the following result from a recent monograph [35] with more general assumptions. The underlying idea of the proof is the Picard iteration.

Theorem A.1

Suppose kernel $K(\cdot )$ is bounded or is the fractional kernel with $\alpha \in (0, 1)$. Let $c_0, c_1, c_2$ be constant. Then there exists $\delta >0$ such that

$$\begin{aligned} f(t) = \int ^t_0 K(t-s) \Big [ c_0 + c_1 f(s) + c_2 f^2(s) \Big ] ds \end{aligned}$$

(A.1)

has a unique continuous solution f on $[0, \delta ]$.

Proof

Note that quadratic function is locally Lipschitz; then according to Theorem 3.1.2 and Theorem 3.1.4 in [35], the claim holds. $\square$

However, $\delta$ in Theorem A.1 is not explicit. Tighter results exist if more assumptions are imposed.

We investigate g(a, t) in (2.8) first. Based on [36, Theorem A.5], we have

Lemma A.1

Suppose Assumption 2.1 holds and $\kappa ^2 - 2a\sigma ^2 > 0$. Then (2.8) has a unique global continuous solution. Moreover,

$$\begin{aligned} 0< g(a, t) \le r_2(t) < w_*, \quad \forall \; t > 0, \end{aligned}$$

(A.2)

where $w_* \triangleq \frac{\kappa - \sqrt{\kappa ^2 - 2a \sigma ^2}}{\sigma ^2}$ and $r_2(t) \triangleq Q^{-1}_2 \Big ( \int ^t_0 K(s) ds \Big )$; that is, the inverse function of $Q_2$, given by

$$\begin{aligned} Q_2(w) = \int ^w_0 \frac{du}{a - \kappa u + \frac{\sigma ^2}{2} u^2}. \end{aligned}$$

(A.3)

Proof

To apply the result in [36, Theorem A.5], we define

$$\begin{aligned} H(w) = a - \kappa w + \frac{\sigma ^2}{2} w^2. \end{aligned}$$

Then H(w) satisfies Assumption A.1 in [36] with $w_{max} \triangleq \frac{\kappa }{\sigma ^2}$ and $w_*$ defined above. The claim follows from [36, Theorem A.5(c)] with $a(t) \equiv 0$ in their theorem. $\square$

For the specific fractional kernel $K(t) = \frac{t^{\alpha -1}}{\varGamma (\alpha )}$, [7, Theorem 3.2] obtains the following tighter results and the proof is based on the scaling limits of the Hawkes processes.

Lemma A.2

If $K(t) = \frac{t^{\alpha -1}}{\varGamma (\alpha )}$, $\alpha \in (1/2, 1)$, then g(a, t) in (2.8) satisfies

$$\begin{aligned} g(a, t) \le \frac{c}{\sigma ^2} \Big [ \kappa + \frac{t^{-\alpha }}{\varGamma (1-\alpha )} + \sigma \sqrt{ a_0(t) - a} \Big ], \end{aligned}$$

(A.4)

with $a_0(t) = \frac{1}{2\sigma ^2} \Big [ \kappa + \frac{t^{-\alpha }}{\varGamma (1-\alpha )} \Big ]^2$ and a constant $c>0$. In other words, if $a < a_0(T)$, then Assumption 2.3 is satisfied.

Next, we study $\psi (\cdot )$ in (4.7). (4.7) has a unique continuous solution on some interval $[0, \delta ]$ if the conditions in Theorem A.1 are satisfied. Without Theorem A.1, we also have the following result.

Lemma A.3

Suppose Assumption 2.1 holds.

• (1) If $1 - 2\rho ^2 > 0$, then (4.7) has a unique global continuous solution $\psi \in L^2_{loc}({\mathbb {R}}_+, {\mathbb {R}})$ and $\psi < 0$ for $t>0$.

• (2) If $1 - 2\rho ^2 = 0$, then (4.7) is linear and has a unique continuous solution on [0, T].

• (3) If $1 - 2\rho ^2 < 0$, further assume $\lambda >0$ and $\lambda ^2 + 2(1-2\rho ^2)\theta ^2\sigma ^2 >0$. Then (4.7) has a unique global continuous solution. Moreover,

  $$\begin{aligned} \frac{{\bar{w}}_*}{1-2\rho ^2}< \frac{{\bar{r}}_2(t)}{1-2\rho ^2} \le \psi (t) < 0, \quad \forall \; t > 0, \end{aligned}$$

  (A.5)

  with ${\bar{w}}_* = \frac{\lambda - \sqrt{\lambda ^2 + 2(1-2\rho ^2)\theta ^2\sigma ^2}}{ \sigma ^2}$ and ${\bar{r}}_2(t) \triangleq {\bar{Q}}^{-1}_2 \Big ( \int ^t_0 K(s) ds \Big )$, where

  $$\begin{aligned} {\bar{Q}}_2(w) = \int ^w_0 \frac{du}{ \frac{\sigma ^2}{2} u^2 - \lambda u - (1-2\rho ^2)\theta ^2}. \end{aligned}$$

  (A.6)

Proof

The claim in (1) follows from [8, Theorem 7.1]. The continuity follows from the uniqueness of the global solution and [21, Theorem 12.1.1]. The claim in (2) is classic and can be found in [35, Theorem 1.2.3]. For (3), we consider ${\tilde{\psi }} = (1 - 2 \rho ^2) \psi$. Then ${\tilde{\psi }}$ satisfies

$$\begin{aligned} {\tilde{\psi }} = K * \Big ( \frac{\sigma ^2}{2} {\tilde{\psi }}^2 - \lambda {\tilde{\psi }} - (1 - 2\rho ^2) \theta ^2 \Big ). \end{aligned}$$

(A.7)

Define

$$\begin{aligned} H(w) = \frac{\sigma ^2}{2} w^2 - \lambda w - (1 - 2\rho ^2) \theta ^2. \end{aligned}$$

(A.8)

Then ${\bar{w}}_*$ is the unique root of $H(w) = 0$ on $(-\infty , {\bar{w}}_{max}]$ with ${\bar{w}}_{max} = \frac{\lambda }{\sigma ^2}$. H(w) satisfies Assumption A.1 in [36]. Therefore, [36, Theorem A.5 (c)] with $a(t) \equiv 0$ implies (A.7) has a unique global continuous solution and

$$\begin{aligned} 0< {\tilde{\psi }}(t) \le {\bar{r}}_2(t) < {\bar{w}}_*, \quad \forall \; t > 0. \end{aligned}$$

(A.9)

Note ${\tilde{\psi }} = (1 - 2 \rho ^2) \psi$. This gives the result desired. $\square$

Appendix B: Positivity of Integrals with Forward Variance

Lemma B.1

Suppose Assumption 2.1 holds. The forward variance $\xi _t(s)$ in (4.3) satisfies $\int ^T_t \xi _t(s) ds > 0$, ${\mathbb {P}}$-${\mathrm{a.s.}}$, for every $t \in [0, T)$.

Proof

As $\int ^T_t \xi _t(s) ds = \mathbb {{\tilde{E}}}[\int ^T_t V_s ds| {{\mathcal {F}}}_t]$ and $V_s$ is non-negative by Theorem 2.2, it is sufficient to show that $\int ^T_t V_s ds > 0$, ${\mathbb {P}}$-${\mathrm{a.s.}}$.

Given $t \in [0, T)$, for $\omega \in \varOmega$ such that $V_s(\omega )$ is continuous in s, we suppose $\int ^T_t V_s(\omega ) ds = 0$. By the continuity of $V_s(\omega )$, $V_s(\omega ) = 0$ for $s \in [t, T]$. Using the argument given in [8, Theorem 3.5, Equation (3.8)], for $0< h < T - t$, we have

$$\begin{aligned} V_{t + h}(\omega )&= V_0 + \int _{0}^{t} K(t+h -s)\left( \kappa \phi - \lambda V_s (\omega ) \right) d s \nonumber \\&\quad + \int _{0}^{t} K(t+h-s) \sigma \sqrt{V_{s} (\omega )} d {\tilde{B}}_{s} (\omega ) \nonumber \\&\quad + \int _{t}^{t+h} K(t+h -s)\left( \kappa \phi - \lambda V_{s} (\omega ) \right) d s \nonumber \\&\quad + \int _{t}^{t+h} K(t+h-s) \sigma \sqrt{V_{s} (\omega ) } d {\tilde{B}}_{s} (\omega ) \nonumber \\&\ge \int _{t}^{t+h} K(t+h -s)\left( \kappa \phi - \lambda V_{s} (\omega ) \right) d s \nonumber \\&\quad + \int _{t}^{t+h} K(t+h-s) \sigma \sqrt{V_{s} (\omega ) } d {\tilde{B}}_{s}(\omega ). \end{aligned}$$

(B.1)

As $V_s (\omega ) = 0,\, s \in [t, t+h]$, then

$$\begin{aligned} V_{t + h} (\omega ) \ge \kappa \phi \int _{t}^{t+h} K(t+h - s) ds > 0. \end{aligned}$$

(B.2)

This contradiction implies that $\int ^T_t V_s ds > 0$, ${\mathbb {P}}$-${\mathrm{a.s.}}$, and the claim follows. $\square$