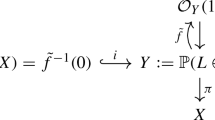Root stacks and periodic decompositions

Abstract

For an effective Cartier divisor D on a scheme X we may form an ${n}^{\text {th}}$ root stack. Its derived category is known to have a semiorthogonal decomposition with components given by D and X. We show that this decomposition is $2n$-periodic. For $n=2$ this gives a purely triangulated proof of the existence of a known spherical functor, namely the pushforward along the embedding of D. For $n > 2$ we find a higher spherical functor in the sense of recent work of Dyckerhoff et al. (N-spherical functors and categorification of Euler’s continuants. ar**v:2306.13350, 2023). We use a realization of the root stack construction as a variation of GIT, which may be of independent interest.

1 Introduction

For an effective Cartier divisor D on a scheme X it is known that the derived pushforward functor from $\text {D}^b{(D)}$ to $\text {D}^b{(X)}$ is spherical. In this paper we explain how this spherical functor arises from a geometric 4-periodic semiorthogonal decomposition of $\text {D}^b{\big (\root \of {X/D}\big )}$, where $\root \of {X/D}$ is the square root stack for the divisor D. We furthermore exhibit a higher spherical functor, namely a $2 n$-spherical functor, in this setting by giving an analogous $2n$-periodic semiorthogonal decomposition of $\text {D}^b{\big (\root n \of {X/D}\big )}$ for $n\ge 2$. Along the way we improve on existing semiorthogonal decomposition results, in particular by working with the bounded coherent derived category, without smoothness assumptions.

1.1 Spherical functors and periodic decompositions

In the original formulation by Anno and Logvinenko [3] a spherical functor is a DG functor $F:\textrm{A} \rightarrow \textrm{B}$ between pretriangulated DG categories with left and right adjoints L and R, such that the cones of the $L\dashv F$ adjunction counit and unit induce autoequivalences of the homotopy categories of $\textrm{A}$ and $\textrm{B}$ respectively. In Halpern-Leistner and Shipman [18] proved that if F is spherical then the category $\textrm{T}$ glued from $\textrm{A}$ and $\textrm{B}$ via F, see [20], admits a 4-periodic semiorthogonal decomposition, see Definition 4.2.

$$\begin{aligned}&\textrm{T} = \langle \textrm{A}, \textrm{B} \rangle = \langle \textrm{B}, \textrm{C} \rangle = \langle \textrm{C}, \textrm{D} \rangle = \langle \textrm{D}, \textrm{A} \rangle \end{aligned}$$

(1.A)

Moreover, given a 4-periodic semiorthogonal decomposition (1.A), the gluing functor $\iota _{\textrm{A}}^R\iota _{\textrm{B}}$ is spherical. These results suggest that one might consider an analogue of a spherical functor for triangulated categories without choosing a DG enhancement.

Similar ideas appeared in the work of Kapranov and Schechtman who in [22] noted that, given a 4-periodic semiorthogonal decomposition (1.A) of a triangulated category $\textrm{T}$ in a suitably-enhanced¹ setting, the functor $\iota _{\textrm{A}}^R\iota _{\textrm{B}}$ is ‘spherical’ in the sense that the cones of adjunction unit and counit are well-defined and are autoequivalences. Indeed, the functorial exact triangles for decompositions $\langle \textrm{B}, \textrm{C} \rangle$ and $\langle \textrm{D}, \textrm{A} \rangle$ respectively imply that the $\iota _{\textrm{B}}^L{\iota _{\textrm{A}}}\dashv \iota _{\textrm{A}}^R {\iota _{\textrm{B}}}$ adjunction unit and counit fit into functorial exact triangles as follows.

$$\begin{aligned} \iota _{\textrm{A}}^R{\iota _{\textrm{C}}}\iota _{\textrm{C}}^R{\iota _{\textrm{A}}} \rightarrow \text {Id}_{\textrm{A}} \rightarrow \iota _{\textrm{A}}^R{\iota _{\textrm{B}}}\iota _{\textrm{B}}^L{\iota _{\textrm{A}}}\rightarrow \end{aligned}$$

(1.B)

$$\begin{aligned} \iota _{\textrm{B}}^L{\iota _{\textrm{A}}}\iota _{\textrm{A}}^R{\iota _{\textrm{B}}} \rightarrow \text {Id}_{\textrm{B}} \rightarrow \iota _{\textrm{B}}^L{\iota _{\textrm{D}}} \iota _{\textrm{D}}^L{\iota _{\textrm{B}}} \rightarrow \end{aligned}$$

(1.C)

The functorial cones of the unit and counit are compositions of mutation functors $\iota _{\textrm{A}}^R{\iota _{\textrm{C}}}$, $\iota _{\textrm{C}}^R{\iota _{\textrm{A}}}$, $\iota _{\textrm{B}}^L{\iota _{\textrm{D}}}$ and $\iota _{\textrm{D}}^L{\iota _{\textrm{B}}}$, hence they are equivalences by [9]. By analogy with this, given a triangulated category $\textrm{T}$ with a 4-periodic semiorthogonal decomposition as in (1.A), we shall say that the gluing functor $\iota _{\textrm{A}}^R\iota _{\textrm{B}}$ is triangle-spherical.

The first example of a geometric 4-periodic decomposition appeared in [5]. There the appropriate quotient of the derived category of the fiber product of two varieties $X^+$ and $X^-$ related by a flop was proved to have a 4-periodic semiorthogonal decomposition with components $\text {D}^b{(}X^{\pm })$ and $\text {D}^b{(}\mathcal {A}_{f^{\pm }})$ for abelian null categories $\mathcal {A}_{f^{\pm }} \subset \text {Coh}(X^{\pm })$.

1.2 Divisors and spherical functors

A basic example of a spherical functor is $i_{D*} :\text {D}^b{(}D)\rightarrow \text {D}^b{(}X)$ for a scheme X and the inclusion ${i_D} :D\rightarrow X$ of a Cartier divisor. This spherical functor appeared in the original paper of  Anno [4] defining spherical functors and later in the work of  Addington [1], though both statements were without proofs. Note that, in [4] a DG enhancement was not present while in [1] the author considered Fourier-Mukai kernels instead of functors between derived categories. In the case when both D and X are smooth, Bondal and  Orlov [8] proved that the cone of the $i_D^* \dashv i_{D*}$ adjunction unit is an autoequivalence of $\text {D}^b{(}X)$. Under the same assumptions, but allowing D and X to be stacks, Kuznetsov in [23, Proposition 3.4] proved the sphericity of $i_{D*}$, compare [21, Lemma 2.8].

Without the smoothness assumption the first named author and Bondal in [5, Theorem 3.1] proved that, for unbounded derived categories of quasi-coherent sheaves, $i_{D*} :\textrm{D}_{\text {QCoh}}(D) \rightarrow \textrm{D}_{\text {QCoh}}(X)$ and its left adjoint form a spherical couple, i.e. the adjunction unit and counit fit into functorial exact triangles as follows.

$$\begin{aligned} \big (\!- \otimes \,\mathcal {O}_X(-D)\big ) \rightarrow \text {Id} \rightarrow i_{D*}i_D^*\rightarrow \end{aligned}$$

(1.D)

$$\begin{aligned} i_D^*i_{D*} \rightarrow \text {Id} \rightarrow \big (\! - \otimes \,\mathcal {O}_D(-D)[2]\big ) \rightarrow \end{aligned}$$

(1.E)

Note that a spherical couple, unlike a spherical functor, requires an adjoint on only one side. More precisely, it is a 2-categorical adjunction in the bicategory ${\textbf {FM}}$ whose objects are quasi-compact, quasi-separated schemes over a field while $\text {Hom}_{{\textbf {FM}}}(X,Y)$ is the category $\textrm{D}_{\text {QCoh}}(X \times Y)$. As the latter is triangulated, once a lifting of the adjunction (co)unit to a 2-morphism in ${\textbf {FM}}$ is fixed, one can consider the cone and check if it is an equivalence.

1.3 Root stacks and higher spherical functors

In this paper we consider the root stacks $\root n \of {X/D}$ for $n\ge 2$. Informally speaking, the root stack construction takes a scheme X and modifies it along an effective Cartier divisor D to get a stack with stabilizer groups $\mu _n$ along D. As explained in Sect. 2.4, the stacky weighted projective line $\mathbb {P}(1,n)$ is an instance of this construction, which becomes important and natural when passing from the setting of schemes to that of stacks.

We prove that $\text {D}^b{\big (\root \of {X/D}\big )}$ admits a 4-periodic semiorthogonal decomposition with components equivalent to $\text {D}^b{(}D)$ and $\text {D}^b{(}X)$, with gluing functor $i_{D*}$ so that in particular $i_{D*}$ is triangle-spherical, see below. More generally, we prove that $\text {D}^b{\big (\root n \of {X/D}\big )}$ admits a $2n$-periodic semiorthogonal decomposition with $n-1$ components equivalent to $\text {D}^b{(}D)$ and one component equivalent to $\text {D}^b{(}X)$. Such decompositions, without the periodicity statement, have previously been obtained by Ishii and Ueda for smooth D and X [19, Theorem 1.6], as well as by Bergh, Lunts and Schnürer for perfect complexes [7, Theorem 4.7]. The $2n$-periodicity of a semiorthogonal decomposition for a root stack has previously been discussed by Bondal [10], speaking on joint work with Logvinenko.

In recent work, Dyckerhoff et al. [15] define N-spherical functors of stable infinity categories. In particular, their 4-spherical functors are analogues of spherical functors for DG categories. They prove that a semiorthogonal decomposition of a stable infinity category is N-periodic if and only if the gluing functor is N-spherical. Hence, one can think of the $2n$-periodicity of the semiorthogonal decomposition of $\text {D}^b{\big (\root \of {X/D}\big )}$ as $2n$-sphericity of the gluing functor.

1.4 Variation of GIT

To construct the $2n$-periodic decomposition we express the passage from X to the root stack $\root n \of {X/D}$ as a wall crossing in geometric invariant theory (GIT), also known as a ‘variation of GIT’. There exists a general framework, see [18], for associating spherical functors to balanced wall crossings in GIT. The wall crossing in our case is not balanced, but for $n=2$ a spherical functor still arises from it, as we shall see from the viewpoint of periodic decompositions.

Previous work including [6, 17] has shown that stacks naturally arise when studying schemes and their derived categories. The present paper further illustrates this theme.

1.5 Results

For an effective Cartier divisor D on a scheme X we write $\root n \of {X/D}$ for the associated ${n}^{\text {th}}$ root stack. This may be described in a number of ways, which we explain in detail in Sect. 2. The most useful description for us is by a variation of GIT for a $\mathbb {G}_m$-action on a scheme $\mathcal {X}$ defined as follows.

Proposition 1.1

(Proposition 2.9) Write $\mathcal {X}$ for the subscheme $\{y z^n= s\}$ of the total space of $\mathcal {O}_X(D) \oplus \mathcal {O}_X$ with fiber coordinates (y, z) and s the canonical section of $\mathcal {O}_X(D)$. Let $\mathbb {G}_m$ act fiberwise with weights $(-n,1)$. Then the GIT quotients are as follows.

$$\begin{aligned}{}[\mathcal {X}^+/\mathbb {G}_m] \simeq \root n \of {X/D},\qquad [\mathcal {X}^-/\mathbb {G}_m] \simeq X. \end{aligned}$$

Base changing the root stack construction to the divisor D itself, we obtain a square

where $\root n \of {\mathcal {O}_D(D)}$ is the root stack of the given line bundle on D, see Definition 2.3.

Theorem 1.2

[Theorem 3.7] We have semiorthogonal decompositions as follows.

$$\begin{aligned}&\text {D}^b{\big (\root n \of {X/D}\big )}\\&\quad = \big \langle \text {D}^b{(}X),\,\text {D}^b{(}D),\,\text {D}^b{(}D)\otimes \mathcal {O}\langle 1 \rangle ,\,\ldots ,\,\text {D}^b{(}D) \otimes \mathcal {O}\langle n-2 \rangle \big \rangle \\&\quad = \big \langle \text {D}^b{(}D),\,\text {D}^b{(}X)\otimes \mathcal {O}\langle 1 \rangle ,\,\text {D}^b{(}D)\otimes \mathcal {O}\langle 1 \rangle ,\,\ldots ,\,\text {D}^b{(}D) \otimes \mathcal {O}\langle n-2 \rangle \big \rangle \\&\quad = \dots \\&\quad = \big \langle \text {D}^b{(}D),\,\text {D}^b{(}D)\otimes \mathcal {O}\langle 1 \rangle ,\,\ldots ,\,\text {D}^b{(}D) \otimes \mathcal {O}\langle n-2 \rangle ,\,\text {D}^b{(}X) \otimes \mathcal {O}\langle n-1 \rangle \big \rangle \end{aligned}$$

Here the bundle $\mathcal {O}\langle 1 \rangle$ on $\root n \of {X/D}$ is induced by $\mathbb {G}_m$-weight 1, and the embeddings of $\text {D}^b{(X)}$ and $\text {D}^b{(D)}$ are respectively $p^*$ and $i_* q^*$.

The last decomposition, twisted by $\mathcal {O}\langle 1-n\rangle$, has been previously obtained but in the smooth setting [19, Theorem 1.6] or for perfect complexes [7, Theorem 4.7].

Remark 1.3

The similarity of these decompositions with the Orlov decomposition for a blowup provides part of the justification for thinking of $\root n \of {X/D}$ as a stacky ‘blowup in codimension one’.

Our main theorem is then the following.

Theorem 1.4

(Theorem 4.3) Take a full subcategory

$$\begin{aligned} \mathcal {D} = \big \langle \text {D}^b{(}D),\,\text {D}^b{(}D) \otimes \mathcal {O}\langle 1\rangle ,\,\ldots ,\,\text {D}^b{(}D) \otimes \mathcal {O}\langle n-2 \rangle \big \rangle \subset \text {D}^b{\big (\root n \of {X/D}\big )}. \end{aligned}$$

Then the semiorthogonal decomposition

$$\begin{aligned} \text {D}^b{\big (\root n \of {X/D}\big )} = \langle \text {D}^b{(}X), \mathcal {D} \rangle \end{aligned}$$

is $2n$-periodic, in the sense that its ${2n}^{\text {th}}$ right dual decomposition is the original decomposition, see Definition 4.2.

In particular, for $n=2$ we get a 4-periodic decomposition as in (1.A)

$$\begin{aligned} \begin{aligned} \text {D}^b{\big (\root \of {X/D}\big )}&= \big \langle \text {D}^b{(}X) ,\,\text {D}^b{(}D) \big \rangle \\&= \big \langle \text {D}^b{(}D) ,\,\text {D}^b{(}X)\otimes \mathcal {O}\langle 1 \rangle \big \rangle \\&= \big \langle \text {D}^b{(}X) \otimes \mathcal {O}\langle 1 \rangle ,\,\text {D}^b{(}D) \otimes \mathcal {O}\langle 1 \rangle \big \rangle \\&= \big \langle \text {D}^b{(}D)\otimes \mathcal {O}\langle 1 \rangle ,\,\text {D}^b{(}X)\big \rangle . \end{aligned} \end{aligned}$$

(1.F)

We calculate the gluing functors for the above decompositions in Proposition 4.4. In particular, we have the following.

Corollary 1.5

(Corollary 4.6) The functor $i_{D*}:\text {D}^b{(D)} \rightarrow \text {D}^b{(X)}$ is triangle-spherical.

1.6 Notation

We write $\root n \of {X/D}$ for the ${n}^{\text {th}}$ root stack associated to a scheme X with an effective Cartier divisor D. For a noetherian scheme or stack X we denote by $\text {D}^b{(}X)$ the bounded derived category of coherent sheaves on X. For the quotient stack of a scheme $\mathcal {X}$ with an action of G we write $[\mathcal {X}/G]$ or simply $\mathcal {X}/G$.

2 Root stacks as variation of GIT

We give definitions and a number of descriptions of the root stack.

2.1 Root stacks

Take an algebraically closed field k of characteristic zero and a reduced separated noetherian k-scheme X, with an effective Cartier divisor D given on an open cover by $\{U_i,f_i\}$. We denote by s the canonical section of $\mathcal {O}_X(D)$.

Recall that the quotient stack $[\mathbb {A}^1_k/\mathbb {G}_m]$ represents the functor which to a scheme B assigns the groupoid of generalized Cartier divisors $(L,\, \rho :L \rightarrow \mathcal {O}_B)$ on B with isomorphisms preserving the morphisms to the structure sheaf, see for instance [25, Proposition 10.3.7]. Let $\delta :X\rightarrow [\mathbb {A}^1_k/\mathbb {G}_m]$ be the morphism given by

$$\begin{aligned} \big (\mathcal {O}_X(-D),\,s(-D) :\mathcal {O}_X(-D) \rightarrow \mathcal {O}_X\big ). \end{aligned}$$

Definition 2.1

[2, 12] The ${n}^{\text {th}}$ root stack $\root n \of {X/D}$ for $n\ge 1$ is given by the following fiber product, where $e_n$ is induced by taking the ${n}^{\text {th}}$ power.

Notation 2.2

Write  $\root \of {X/D}$ for the $n=2$ case, namely the square root stack.

For a scheme B, objects of the groupoid $\root n \of {X/D}(B)$ are morphisms $f :B \rightarrow X$ and sections $t:\mathcal {O}_B \rightarrow \mathcal {L}$ of invertible sheaves on B together with an isomorphism $\mathcal {L}^{\otimes n} \xrightarrow {\sim } f^*\mathcal {O}_X(D)$ which identifies $t^{\otimes n}$ with $f^*(s)$. Morphisms are isomorphisms of invertible sheaves $\mathcal {L} \xrightarrow {\sim } \mathcal {L}'$ commuting with all the additional data.

Recall that any invertible sheaf gives a $\mathbb {G}_m$-torsor and any $\mathbb {G}_m$-torsor can be obtained in this way. Hence, the stack $B\mathbb {G}_m$ represents the functor which to a scheme B assigns the groupoid of invertible sheaves on B. Given $\mathcal {M} \in \text {Pic}(X)$ let $\mu :X\rightarrow B\mathbb {G}_m$ be the morphism given by $\mathcal {M}$.

Definition 2.3

[2] The ${n}^{\text {th}}$ root stack of a line bundle $\root n \of {\mathcal {M}}$ for $n\ge 1$ is given by the following fiber product, where $e_n$ is induced by taking the ${n}^{\text {th}}$ power.

For a base scheme B, an object of the groupoid $\root n \of {\mathcal {M}}(B)$ is a morphism $f:B\rightarrow X$ and an invertible sheaf $\mathcal {L}$ on B together with an isomorphism $\mathcal {L}^{\otimes n} \xrightarrow {\sim } f^*\mathcal {M}$. Morphisms are isomorphisms of invertible sheaves $\mathcal {L} \xrightarrow {\sim } \mathcal {L}'$ commuting with the additional data.

2.2 Quotient description of root stacks

The stack $\root n \of {X/D}$ can be also viewed as a quotient stack, following [2]. Write $\mathcal {T}$ for the total space of $\mathcal {O}_X(D)$ and $\mathcal {T}^\circ$ for the total space of the associated $\mathbb {G}_m$-bundle, namely $\mathcal {T}$ with the zero section removed. On $\mathcal {T}^\circ \times \mathbb {A}^1_k$ consider the $\mathbb {G}_m$-action as follows.

$$ \lambda \cdot (u,z) = (\lambda ^{-n}u, \lambda z) $$

Note that the morphism $\mathcal {T}^\circ \times \mathbb {A}^1_k \rightarrow \mathcal {T}$, $(u,z) \mapsto u z^n$ is $\mathbb {G}_m$-invariant for the trivial $\mathbb {G}_m$-action on $\mathcal {T}$, hence it gives a morphism $[\mathcal {T}^\circ \times \mathbb {A}^1_k/\mathbb {G}_m] \rightarrow \mathcal {T}$.

Proposition 2.4

[2, Appendix B.2] Consider the canonical section s of $\mathcal {O}_X(D)$ as a subscheme of the total space $\mathcal {T}$, and let $\mathcal {V}\subset \mathcal {T}^\circ \times \mathbb {A}^1_k$ be its inverse image. Then

$$\begin{aligned}{}[\mathcal {V}/\mathbb {G}_m] \simeq \root n \of {X/D}. \end{aligned}$$

Proof

Let $u_i$ be a local coordinate on $\mathcal {T}^\circ$, z a coordinate on $\mathbb {A}^1_k$, and $\{U_i,f_i\}$ a representative of D. Then $\mathcal {V}$ is glued from $\mathcal {V}_i = \{u_i z^n= f_i\}\subset \mathcal {T}^\circ |_{U_i} \times \mathbb {A}^1_k$. Let $p :\mathcal {V}\rightarrow X$ be the canonical projection.

Note that z is a section of the trivial line bundle $\mathcal {O}_{\mathcal {V}}\langle -1 \rangle$ with $\mathbb {G}_m$-weight $-1$. Functions $u_i$ glue to an isomorphism $y:\mathcal {O}_{\mathcal {V}}\langle - n\rangle \xrightarrow {\sim } \mathcal {N}$, for a line bundle $\mathcal {N}$ with trivial $\mathbb {G}_m$-action. The composition $\mathcal {O}_{\mathcal {V}} \!\xrightarrow {z^{\otimes n}}\! \mathcal {O}_{\mathcal {V}}\langle -n\rangle \!\!\xrightarrow {y} \!\!\mathcal {N}$ is, by the definition of $\mathcal {V}$, the pullback $p^*(s)$ of the canonical section s of $\mathcal {O}_X(D)$. Hence, $\mathcal {N} \simeq p^*\mathcal {O}_X(D)$ and z defines a section of a line bundle on $\mathcal {V}$ whose ${n}^{\text {th}}$ power is identified by the isomorphism $y$ with $p^*(s)$.

To define a morphism $[\mathcal {V}/\mathbb {G}_m]\rightarrow \root n \of {X/D}$ consider a scheme B and a morphism $B \rightarrow [\mathcal {V}/\mathbb {G}_m]$, i.e. take $\pi$ a principal $\mathbb {G}_m$-bundle and h a $\mathbb {G}_m$-equivariant morphism fitting into a commutative diagram as follows.

Note that f exists as $p \circ h$ is $\mathbb {G}_m$-invariant and $\pi$ is the categorical quotient. Pullback of z along h yields a morphism $h^*(z) :\mathcal {O}_C \rightarrow h^*\mathcal {O}_{\mathcal {V}}\langle -1 \rangle$ of $\mathbb {G}_m$-linearized line bundles on C. As $\pi ^*:\text {Pic}(B) \xrightarrow {\sim }\text {Pic}_{\mathbb {G}_m}(C)$ is an isomorphism, see [11, Proposition 3.3.1], there exists a morphism $t:\mathcal {O}_B \rightarrow \mathcal {L}$ in $\text {Pic}(B)$ which pulls back to $h^*(z)$ along $\pi$. Similarly, there exists an isomorphism $\widetilde{y}:\mathcal {L}^{\otimes n} \rightarrow f^*\mathcal {O}_X(D)$ which pulls back to $h^*(y) :h^*\mathcal {O}_{\mathcal {V}}\langle -n\rangle \rightarrow h^*p^* \mathcal {O}_X(D)$. Then $\widetilde{y} \circ t^{\otimes n}$ is the pullback via f of the canonical section s of $\mathcal {O}_X(D)$. Indeed, applying the isomorphism $\pi ^*$, one gets $\pi ^*(\widetilde{y} \circ t^{\otimes n}) = h^*(y\circ z^{\otimes n}) =h^*p^*(s) = \pi ^*f^*(s)$.

In the opposite direction, let $f:B \rightarrow X$ be a morphism of schemes, $t :\mathcal {O}_B \rightarrow \mathcal {L}$ a morphism of invertible sheaves and $a :\mathcal {L}^{\otimes n} \xrightarrow {\sim } f^*\mathcal {O}_X(D)$ an isomorphism such that $a \circ t^{\otimes n} = f^*(s)$. Let $\pi :C\rightarrow B$ be the $\mathbb {G}_m$-torsor associated with $\mathcal {L}^{-1}$. Consider $\widetilde{h} :C\rightarrow \text {Tot}(\mathcal {O}_X(D) \oplus \mathcal {O}_X)$ given by an element of $\text {Hom}(\mathcal {O}_C, \pi ^*f^*(\mathcal {O}_X(D) \oplus \mathcal {O}_X))$ with components

$$\begin{aligned} a\otimes (\mathcal {L}^{-1})^{\otimes n}&\in \,\text {Hom}(\mathcal {O}_B, (\mathcal {L}^{-1})^{\otimes n} \otimes f^* \mathcal {O}_X(D)) \\&\subset \bigoplus _{k\in \mathbb {Z}} \text {Hom}(\mathcal {O}_B, \mathcal {L}^{\otimes k} \otimes f^* \mathcal {O}_X(D)) \\&\simeq \text {Hom}(\mathcal {O}_B, \pi _* \mathcal {O}_C \otimes f^*\mathcal {O}_X(D)) \\&\simeq \text {Hom}(\mathcal {O}_C, \pi ^*f^*\mathcal {O}_X(D)), \end{aligned}$$

and

$$\begin{aligned} t&\in \, \text {Hom}(\mathcal {O}_B, \mathcal {L}) \\&\subset \bigoplus _{k\in \mathbb {Z}}\text {Hom}(\mathcal {O}_B, \mathcal {L}^{\otimes k}) \\&\simeq \text {Hom}(\mathcal {O}_B, \pi _* \mathcal {O}_C) \\&\simeq \text {Hom}(\mathcal {O}_C, \mathcal {O}_C). \end{aligned}$$

The morphism $\widetilde{h}$ induces a $\mathbb {G}_m$-equivariant morphism $h:C\rightarrow \mathcal {V}$. Indeed, in local coordinates $(b,u) \in B \times \mathbb {G}_m$, the morphism $\widetilde{h}$ is given by $(b,u)\mapsto (f(b), u^{-n}a(b), u t(b))$. Hence, h corresponds to $B \rightarrow [\mathcal {V}/\mathbb {G}_m]$.

It is straightforward to check that the above constructions yield mutually inverse maps $[\mathcal {V}/\mathbb {G}_m]\leftrightarrow \root n \of {X/D}$. $\square$

Remark 2.5

The proof of Proposition 2.4 implies that $\mathcal {O}_{\mathcal {V}}\langle -n\rangle$ is isomorphic to the pullback of $\mathcal {O}_X(D)$.

To view $\root n \of {\mathcal {M}}$ as a global quotient stack, we have the following, by a similar argument to Proposition 2.4.

Proposition 2.6

Consider the $\mathbb {G}_m$-bundle $\mathcal {M}^\circ$ associated to $\mathcal {M}$ with the $\mathbb {G}_m$-action $\lambda \cdot u = \lambda ^{-n} u$. Then

$$\begin{aligned}{}[\mathcal {M}^\circ /\mathbb {G}_m] \simeq \root n \of {\mathcal {M}}. \end{aligned}$$

Proof

Let $p:\mathcal {M}^\circ \rightarrow X$ be the canonical projection. From the definition of $\mathcal {M}^\circ$ it follows that there exists an isomorphism $y :\mathcal {O}_{\mathcal {M}^\circ }\langle -n\rangle \xrightarrow {\sim } p^*\mathcal {M}$.

To define a morphism $[\mathcal {M}^\circ /\mathbb {G}_m] \rightarrow \root n \of {\mathcal {M}}$ consider a scheme B and a morphism $B \rightarrow [\mathcal {M}^\circ /\mathbb {G}_m]$, i.e. take $\pi$ a principal $\mathbb {G}_m$-bundle and h a $\mathbb {G}_m$-equivariant morphism fitting into a commutative diagram as follows.

Note that f exists as $p \circ h$ is $\mathbb {G}_m$-invariant and $\pi$ is the categorical quotient. Then $h^*(\mathcal {O}_{\mathcal {M}^\circ }\langle -1 \rangle )$ is a $\mathbb {G}_m$-linearized line bundle on C, and further there is an isomorphism $h^*(y) :h^*(\mathcal {O}_{\mathcal {M}^\circ }\langle - 1 \rangle )^{\otimes n}\xrightarrow {\sim } h^*p^*\mathcal {M}$. It follows that there exists $\mathcal {L}\in \text {Pic}(B)$ with an isomorphism $\widetilde{y} :\mathcal {L}^{\otimes n} \xrightarrow {\sim } f^*(\mathcal {M})$. Indeed, $\mathcal {L}$ and $\widetilde{y}$ are the preimages under the isomorphism $\pi ^*:\text {Pic}(B) \xrightarrow {\sim }\text {Pic}_{\mathbb {G}_m}(C)$, see [11, Proposition 3.3.1], of $h^* (\mathcal {O}_{\mathcal {M}^\circ }\langle - 1 \rangle )$ and $h^*(y) :h^*(\mathcal {O}_{\mathcal {M}^\circ }\langle -1 \rangle )^{\otimes n} \rightarrow h^*p^*(\mathcal {M}) \simeq \pi ^*f^*(\mathcal {M})$.

In the opposite direction, let $f:B \rightarrow X$ be a morphism of schemes, $\mathcal {L}\in \text {Pic}(B)$ and $a :\mathcal {L}^{\otimes n} \xrightarrow {\sim } f^*\mathcal {M}$. Let $\pi :C\rightarrow B$ be the $\mathbb {G}_m$-torsor associated with $\mathcal {L}$. Consider $\widetilde{h} :C\rightarrow \text {Tot}(\mathcal {M})$ given by the following element of $\text {Hom}(\mathcal {O}_C, \pi ^*f^*\mathcal {M})$.

$$\begin{aligned} a\otimes (\mathcal {L}^{-1})^{\otimes n}&\in \,\text {Hom}(\mathcal {O}_B, (\mathcal {L}^{-1})^{\otimes n} \otimes f^* \mathcal {M}) \\&\subset \bigoplus _{k\in \mathbb {Z}} \text {Hom}(\mathcal {O}_B, \mathcal {L}^{\otimes k} \otimes f^* \mathcal {M}) \\&\simeq \text {Hom}(\mathcal {O}_B, \pi _* \mathcal {O}_C \otimes f^*\mathcal {M}) \\&\simeq \text {Hom}(\mathcal {O}_C, \pi ^*f^*\mathcal {M}) \end{aligned}$$

The morphism $\widetilde{h}$ induces a $\mathbb {G}_m$-equivariant morphism $h:C\rightarrow \mathcal {M}^\circ$. Indeed, in local coordinates $(b,u) \in B \times \mathbb {G}_m$, the morphism $\widetilde{h}$ is given by $(b,u)\mapsto (f(b), u^{-n}a(b))$. Hence, h corresponds to $B \rightarrow [\mathcal {M}^\circ /\mathbb {G}_m]$.

It is straightforward to check that the above constructions yield mutually inverse maps $[\mathcal {M}^\circ /\mathbb {G}_m]\leftrightarrow \root n \of {\mathcal {M}}$. $\square$

Remark 2.7

The proof of Proposition 2.6 implies that $\mathcal {O}_{\mathcal {M}^\circ }\langle -n\rangle$ is isomorphic to the pullback of $\mathcal {M}$.

2.3 GIT description of the root stack $\root n \of {X/D}$

For a scheme $\mathcal {X}$ with a $\mathbb {G}_m$-action, we denote the fixed locus by Z. Then

$$ S^+= \big \{x\in \mathcal {X}\,|\, \lim _{\lambda \rightarrow 0 } \lambda \cdot x \in Z\big \} \qquad \text {and} \qquad S^-= \big \{x\in \mathcal {X}\,|\, \lim _{\lambda \rightarrow 0} \lambda ^{-1}\cdot x \in Z\big \} $$

are the unstable loci. Write $\mathcal {X}^\pm = \mathcal {X} -S^\pm$ for the semistable loci. Note that here we allow finite stabilizers in these loci, so that the GIT quotients $[\mathcal {X}^\pm /\mathbb {G}_m]$ may be Deligne–Mumford stacks, not necessarily schemes.

To construct the root stack as a GIT quotient, we make the following definition. This construction previously appeared, in a certain dimension 2 example for $n=2$, in work of the second named author and Kuwagaki [14, Proposition 5, second case].

Definition 2.8

Let $\mathcal {T}_n$ be the total space of the rank 2 vector bundle $\mathcal {O}_X(D) \oplus \mathcal {O}_X$ with fiber coordinates (y, z), and a fiberwise $\mathbb {G}_m$-action with weights $(-n,1)$. Let $\mathcal {X}_n$ be the hypersurface given by

$$\begin{aligned} \mathcal {X}_n= \{y z^n= s\} \subset \mathcal {T}_n\end{aligned}$$

where s is the canonical section of $\mathcal {O}_X(D)$.

The equation $y z^n= s$ is valued in $\mathcal {O}_X(D)$ and is $\mathbb {G}_m$-invariant by construction. We explicitly describe $\mathcal {X}_n$ using the representative $\{U_i, f_i\}$ of D. Classically, we can view the invertible sheaf $\mathcal {O}_X(D)$ as an ideal sheaf in the sheaf $\mathcal {K}_X$ of total fractions. Namely, take $\mathcal {O}_X(D)$ to be the sub-$\mathcal {O}_X$-module of $\mathcal {K}_X$ generated by $f_i^{-1}$ on $U_i$ [16, Chapter II.6]. Then multiplication with $f_i$ is an isomorphism $\zeta _i :\mathcal {O}_{U_i}(D) \rightarrow \mathcal {O}_{U_i}$. The invertible sheaf $\mathcal {O}_X(D)$ has a canonical section $s = 1\in \Gamma (X, \mathcal {O}_X(D))$. Note that $s|_{U_i}$ corresponds under $\zeta _i$ to the regular function $f_i \in \Gamma (U_i, \mathcal {O}_X)$. The trivializations $\zeta _i$ allow us to consider fiber coordinates $(y_i, z_i)$ on $\mathcal {T}_n|_{U_i}$. The scheme $\mathcal {X}_n$ is then glued from $\{y_iz_i^n= f_i\}\subset \mathcal {T}_n|_{U_i}$.

Noting that the $\mathbb {G}_m$-action on $\mathcal {T}_n$ restricts to $\mathcal {X}_n$, we now describe the GIT quotients for $\mathcal {X}_n$.

Proposition 2.9

Consider $\mathcal {X}_n$ from Definition 2.8 with its $\mathbb {G}_m$-action. The associated GIT quotients are as follows.

$(+)$:

We have $[\mathcal {X}_n^+/\mathbb {G}_m] \simeq \root n \of {X/D}$. The unstable locus $S^+=\{y =0\}$ is isomorphic to the total space of $\mathcal {O}_D$ with fiberwise $\mathbb {G}_m$-action of weight 1.

$(-)$:

We have $[\mathcal {X}_n^-/\mathbb {G}_m] \simeq X$. The unstable locus $S^-=\{z =0\}$ is isomorphic to the total space of $\mathcal {O}_D(D)$ with fiberwise $\mathbb {G}_m$-action of weight $-n$.

The fixed locus $Z = \{ y, z = 0 \}$ is isomorphic to D.

Proof

We first describe the unstable loci for $\mathcal {X}_n$, which are given by restricting the unstable loci for $\mathcal {T}_n$. Since the $\mathbb {G}_m$-action on $\mathcal {T}_n$ is fiberwise, the unstable loci for a given linearization can be computed for the action of $\mathbb {G}_m$ on $\mathbb {A}^2_k$ with weights $(-n,1)$ and coordinates (y, z). The fixed locus of this action is (0, 0), with unstable loci $\{y = 0\}$ and $\{z =0\}$. For $\mathcal {T}_n$ therefore the fixed locus Z is the zero section, and the unstable loci over the open set $U_i$ are $S^+= \{y_i = 0\}$ and $S^- =\{z_i =0\}$, so the description of the unstable loci follows. The rest of the $(+)$ side follows from an isomorphism of $\mathcal {X}_n^+$ and $\mathcal {V}$ as $\mathbb {G}_m$-schemes, see Proposition 2.4. For the $(-)$ side, note that $\mathcal {X}^-_n$ is a $\mathbb {G}_m$-torsor over X. Indeed, $\mathbb {G}_m$ acts freely on the total space of the $\mathbb {G}_m$-bundle associated to $\mathcal {O}_X$ and the coordinate $y_i$ along the fiber of $\mathcal {O}_X(D)$ is uniquely determined by a point of X and the value of $z_i$ in the fiber over it. It follows that X is the geometric quotient of $\mathcal {X}_n^-$ by $\mathbb {G}_m$, hence a categorical one [24, Proposition 0.1]. As $[\mathcal {X}_n^-/\mathbb {G}_m]$ is the categorical quotient too, the required isomorphism follows from the uniqueness of the quotient. $\square$

Remark 2.10

Combining the above proposition and the proof of Proposition 2.4 gives that $\mathcal {O}_{\mathcal {X}_n^+/\mathbb {G}_m}\langle -n\rangle \simeq \mathcal {O}_{\root n \of {X/D}}\langle -n\rangle$ is isomorphic to the pullback of $\mathcal {O}_X(D)$.

2.4 Toric example

For concreteness, we give the following.

Example 2.11

Let $X = \mathbb {P}^1$ with coordinates $(x_0:x_1)$, and let D be the point (1 : 0) so that $\mathcal {O}_X(D) \simeq \mathcal {O}_X(1)$. Then $\root n \of {X/D}$ is isomorphic to the stacky weighted projective line $\mathbb {P}(1,n)$. To see this, note first that X may be viewed as

$$\begin{aligned}{}[\mathbb {A}^2_k/\mathbb {G}_m] -\{x_0,x_1=0\} \end{aligned}$$

where coordinates and $\mathbb {G}_m$-weights are as follows.

Then $\mathcal {X}_n$ with its $\mathbb {G}_m$-action may be presented as

$$\begin{aligned} \{ x_1 = yz^n\} \subset [\mathbb {A}^4_k/\mathbb {G}_m^2] -\{x_0,x_1=0\} \end{aligned}$$

with weights

and $\mathcal {X}_n^+$ is given by removing $\{y=0\}$. Changing basis in the torus $\mathbb {G}_m^2$ corresponds to row operations, so we may take weights as follows.

Now setting $y=1$ using the $\mathbb {G}_m$ factor corresponding to the first row, we deduce that $[\mathcal {X}_n^+/\mathbb {G}_m] \simeq \{x_1 = z^n\} \subset [\mathbb {A}^3_k/\mathbb {G}_m] -\{x_0,x_1=0\}$ with weights below.

This is isomorphic to $[\mathbb {A}^2_k/\mathbb {G}_m] -\{y_0,y_1=0\}$ with weights as follows, giving the claim.

3 Derived category of the root stack

We first explain general theory, before applying to our setting.

3.1 Derived category of GIT quotients

Take $\mathbb {G}_m$ acting on a scheme $\mathcal {X}$ with fixed locus Z and unstable loci $S^\pm$ as in Sect. 2.3. Recall that $\mathcal {X}^\pm = \mathcal {X} -S^\pm$, and let $i_\pm :\mathcal {X}^\pm \rightarrow \mathcal {X}$ be the inclusions. Write $\pi _{\pm }:S^{\pm } \rightarrow Z$ for the maps which send x to

$$\begin{aligned} \lim _{\lambda \rightarrow 0}\lambda \cdot x \qquad \text {and} \qquad \lim _{\lambda \rightarrow 0}\lambda ^{-1}\cdot x \end{aligned}$$

respectively.

Proposition 3.1

[17, Lemma 2.9, Theorem 2.10] Assume

(A):

$\pi _{\pm } :S^{\pm } \rightarrow Z$ are locally trivial bundles of affine spaces, and

(R):

the inclusions $S^{\pm }\rightarrow \mathcal {X}$ are regular embeddings.

Under assumption (R) the derived restriction along the closed immersions $Z\rightarrow S^{\pm }$ of the relative cotangent complex $L^\bullet _{S^{\pm }|\mathcal {X}}$ is $\det \mathcal {N}^\vee _{S^{\pm }|\mathcal {X}}|_Z[1]$. We make the following further assumption.

(L):

$\det \mathcal {N}_{S^{\pm }|\mathcal {X}}^{\mp 1}|_Z$ has positive $\mathbb {G}_m$-weight $\eta _\pm$.

Then the derived restriction functor $i_\pm ^*$ gives an equivalence of

$$\begin{aligned} \mathcal {C}_{[\omega , \omega +\eta _{\pm })}= \big \{ E \in \text {D}^b{(}\mathcal {X}/\mathbb {G}_m) \,\big |\, \mathcal {H}^\bullet ( i_Z^* E) \text { have weights in }[\omega , \omega +\eta _{\pm }) \big \} \end{aligned}$$

(3.A)

and $\text {D}^b{(}\mathcal {X}^{\pm }/\mathbb {G}_m)$ where $i_Z$ is the closed immersion $Z \rightarrow \mathcal {X}$.

Proof

By [17, Theorem 2.10] the conditions (A) and (L) imply an equivalence of $\text {D}^b{(}\mathcal {X}^{\pm }/\mathbb {G}_m)$ with a subcategory $\mathcal {G}_\omega$ of $\text {D}^b{(}\mathcal {X}/\mathbb {G}_m)$ given by

$$\begin{aligned} \mathcal {G}_\omega = \left\{ E \in \text {D}^b{(}\mathcal {X}/\mathbb {G}_m) \,\Bigg |\,\begin{array}{l} \mathcal {H}^\bullet ( k_\pm ^* j_\pm ^* E) \text { have weights }\ge \omega \\ \mathcal {H}^\bullet ( k_\pm ^* j_\pm ^! E) \text { have weights }< \omega \end{array}\right\} \end{aligned}$$

where we notate morphisms as follows.

Then the argument in the proof of [17, Lemma 2.9] shows that if (R) holds the category $\mathcal {G}_\omega$ can be described as $\mathcal {C}_{[\omega , \omega +\eta _{\pm })}$ in (3.A). $\square$

Remark 3.2

The positive integer $\eta _{\pm }$ is known as the window width. It is calculated in our setting in Proposition 3.6 below.

Under the assumptions (A), (R) and (L) the references [6, 17] furthermore give semiorthogonal decompositions of $\mathcal {C}_{[0,\eta _\pm +l)}$ for a positive integer l. For simplicity of notation, we give the $(-)$ side, as this is the one we will use, and write $\eta =\eta _-$.

Proposition 3.3

[17, Amplification 2.11] The full subcategories

$$\begin{aligned} \mathcal {C}_{[0,\eta )}, \mathcal {C}_{[1,\eta +1)}, \ldots , \mathcal {C}_{[l,\eta +l)} \subset \mathcal {C}_{[0,\eta +l)} \end{aligned}$$

can be completed to semiorthogonal decompositions

$$\begin{aligned} \mathcal {C}_{[0,\eta +l)}&= \langle \mathcal {C}_{[0,\eta )}, \mathcal {A}_0, \ldots , \mathcal {A}_{l-1}\rangle \\&= \langle \mathcal {A}_0, \mathcal {C}_{[1,\eta +1)}, \mathcal {A}_1, \ldots , \mathcal {A}_{l-1} \rangle \\&= \ldots \\&= \langle \mathcal {A}_0, \mathcal {A}_1, \ldots , \mathcal {A}_{l-1}, \mathcal {C}_{[l,\eta +l)}\rangle , \end{aligned}$$

where

$$\begin{aligned} \mathcal {A}_w= & {} \big \{ E \in \text {D}^b{(}\mathcal {X}/\mathbb {G}_m) \,\big |\, \mathcal {H}^\bullet (i_Z^* E) \text { have weights in }[w,w+\eta ],\\{} & {} \text { E supported on }S^- \big \}. \end{aligned}$$

Finally, there is an equivalence of $\text {D}^b{(}Z)$ with $\mathcal {A}_w$. For this, set notation

where $\tau$ corresponds to the quotient $\mathbb {G}_m/\mathbb {G}_m\xrightarrow {\sim } 1$. Then we have the following.

Lemma 3.4

[17, Remark 2.13, Corollary 3.28] The functor

$$\begin{aligned} \Phi _{\omega }(-) = j_*\pi _-^*(\tau ^*(-)\otimes \mathcal {O}_{Z/\mathbb {G}_m}\langle \omega \rangle ) \end{aligned}$$

(3.B)

is an equivalence of $\text {D}^b{(}Z)$ with $\mathcal {A}_{\omega } \subset \text {D}^b{(}\mathcal {X}/\mathbb {G}_m)$.

Remark 3.5

For comparison with the original paper [17], note that there the group acts on a scheme denoted X, and $\mathcal {X}$ is the quotient stack, while for us $\mathcal {X}$ is the scheme. We denote the fixed locus by Z as in [17], but we denote the semistable loci by $\mathcal {X}^{\pm }$, in contrast with $X^{ss}$ in [17]. Since we consider a torus action, for a one-parameter subgroup $\lambda$ the ‘blade’ $Y_{\lambda , Z}$ coincides with the stratum $S_{\lambda , Z}$ by [17, Remark 2.1]. We denote the latter by $S^{\pm }$, depending on whether the one-parameter subgroup $\lambda$ is $\mathbb {G}_m$ itself, or is given by inversion. The subcategories denoted here by $\mathcal {G}_{\omega }$ and $\mathcal {C}_{[\omega , \omega + \eta _{\pm })}$ both appear as $\mathcal {G}_{\omega }$ in [17, Definition 2.8] and [17, Lemma 2.9] respectively. The subcategory which we denote by $\mathcal {A}_{\omega }$ is $\textrm{D}^b_{S^-/\mathbb {G}_m}(\mathcal {X}/\mathbb {G}_m)_{\omega }$ from [17, Amplification 3.27]. Indeed, if condition (R) is satisfied then [17, Lemma 2.9] holds, giving the above definition of $\mathcal {A}_\omega$. By [17, Amplifications 3.18 and 3.27] this subcategory $\textrm{D}^b_{S^-/\mathbb {G}_m}(\mathcal {X}/\mathbb {G}_m)_{\omega }$ is equivalent to $\textrm{D}^b(Z/\mathbb {G}_m)_{\omega }$ which appears in [17, Amplification 2.11].

3.2 Derived category of the root stack $\root n \of {X/D}$

We now apply the above theory to the GIT problem $\mathcal {X}_n$ from Definition 2.8. We begin by calculating the window widths $\eta _{\pm }$.

Proposition 3.6

For $\eta _\pm$ the $\mathbb {G}_m$-weight of $\det \mathcal {N}_{S^\pm | \mathcal {X}}^{\mp 1} |_Z$ we have

$$\begin{aligned} \eta _+ = n,\qquad \eta _- = 1. \end{aligned}$$

Proof

Over $U_i$, $S^+ = \{y_i =0\}$ and $S^-= \{z_i =0\}$. Hence, locally, $I_{S^+}/I_{S^+}^2$ is spanned by $y_i$, while $I_{S^-}/I_{S^-}^2$ is spanned by $z_i$. The statement follows as the $\mathbb {G}_m$ action is given by $\lambda \cdot y_i = \lambda ^{-n}y_i$ and $\lambda \cdot z_i = \lambda z_i$. $\square$

Base changing the root stack construction to the divisor D itself, we obtain

where $\root n \of {\mathcal {O}_D(D)}$ is the root stack of the given line bundle on D, see Definition 2.3, compare [19, Section 5]. Indeed, consider $\text {Tot}(\mathcal {O}_D(D) \oplus \mathcal {O}_D)$ with local fiber coordinates $(z_i,y_i)$. Then the pullback of $\mathcal {X}_n^+$ to D is $\mathcal {Y}_n\subset \text {Tot}(\mathcal {O}_D(D) \oplus \mathcal {O}_D)$ given by $\{y_iz_i^n=0, y_i \ne 0\}$. As $y_i$ is non-zero, $\mathcal {Y}_n$ is isomorphic to the total space of the $\mathbb {G}_m$-bundle associated to $\mathcal {O}_D(D)$. The $\mathbb {G}_m$ action on $\mathcal {Y}_n$ is fiberwise with weight $-n$. The isomorphism with $\root n \of {\mathcal {O}_D(D)}$ then follows from Proposition 2.6.

We now obtain decompositions for the root stack.

Theorem 3.7

The category $\text {D}^b{\big (\root n \of {X/D}\big )}$ admits semiorthogonal decompositions

$$\begin{aligned} \begin{aligned}&\big \langle p^*\text {D}^b{(}X),\,i_*q^*\text {D}^b{(}D),\,i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle 1\rangle ,\,\ldots ,\,i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle n-2\rangle \big \rangle \\&\quad = \big \langle i_*q^*\text {D}^b{(}D),\,p^*\text {D}^b{(}X)\otimes \mathcal {O}\langle 1 \rangle ,\,i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle 1\rangle ,\,\ldots ,\,i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle n-2\rangle \big \rangle \\&\quad = \ldots \\&\quad = \big \langle i_*q^*\text {D}^b{(}D),\,i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle 1\rangle ,\,\ldots ,\,i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle n-2\rangle ,\,p^*\text {D}^b{(}X) \otimes \mathcal {O}\langle n-1 \rangle \big \rangle . \end{aligned} \end{aligned}$$

Proof

We check that under the equivalences $\mathcal {A}_\omega \simeq \text {D}^b{(}Z) \simeq \text {D}^b{(}D)$, see Lemma 3.4 and Proposition 2.9, and $i_+^*:\mathcal {C}_{[0,n)} \xrightarrow {\sim }\text {D}^b{\big (\root n \of {X/D}\big )}$, see Propositions 3.1 and 3.6, the required semiorthogonal decompositions are the decompositions given by Proposition 3.3 with $\eta =\eta _-=1$ and $l=n-1$, after noting that $\mathcal {C}_{[0, n)} = \mathcal {C}_{[0, \eta +n-1)}$.

We first check that conditions (A), (R) and (L) of Proposition 3.1 are satisfied. By Proposition 2.9, over $U_i$ we have $S^+=\{y_i = 0\}$, $S^-=\{z_i = 0\}$ and $Z = \{y_i, z_i =0\}$. Furthermore, $S^+ \simeq \text {Tot}(\mathcal {O}_D)$ and $S^- \simeq \text {Tot}(\mathcal {O}_D(D))$ are clearly locally trivial bundles of affine spaces over Z, and the embeddings $S^+ \rightarrow \mathcal {X}$ and $S^- \rightarrow \mathcal {X}$ given by $y_i$ and $z_i$ respectively are regular. Finally, by Proposition 3.6, $\det \mathcal {N}^{\mp 1}_{S^\pm |\mathcal {X}}|_Z$ has positive weights $n$ and 1 respectively.

Embeddings of $\text {D}^b{(}D)$. Recall from Lemma 3.4 the embedding $\Phi _{\omega }$ of $\text {D}^b{(}Z)$ into $\text {D}^b{(}\mathcal {X}/\mathbb {G}_m)$ with $\mathcal {A}_\omega$ as its essential image. We show that under the isomorphism $Z\simeq D$, $i_+^*\circ \Phi _{\omega }(-)\simeq i_*q^*(-) \otimes \mathcal {O}_{\root n \of {X/D}}\langle \omega \rangle$. Let $S^\circ$ be the open subscheme $S^- - Z$ of $S^-$. We have a diagram as follows.

By the description of $\mathcal {X}^+_n$ in Proposition 2.9, the right-hand square is Cartesian, so by flat base change we have

$$\begin{aligned} i_+^*\circ \Phi _{\omega }(-)&\simeq i_+^*j_*\pi _-^*(\tau ^*(-)\otimes \mathcal {O}_{Z/\mathbb {G}_m}\langle \omega \rangle ) \\&\simeq j^\circ _*k^*\pi _-^*(\tau ^*(-)\otimes \mathcal {O}_{Z/\mathbb {G}_m}\langle \omega \rangle ) \\&\simeq j^\circ _*{\pi ^\circ }^*(\tau ^*(-)\otimes \mathcal {O}_{Z/\mathbb {G}_m}\langle \omega \rangle ). \end{aligned}$$

Tensor-pullback distributivity and the projection formula then give that

$$\begin{aligned} i_+^*\circ \Phi _{\omega }(-)&\simeq j^\circ _*({\pi ^\circ }^*\tau ^*(-)\otimes \mathcal {O}_{S^\circ /\mathbb {G}_m}\langle \omega \rangle ) \\&\simeq j^\circ _*\big ({\pi ^\circ }^*\tau ^*(-)\otimes j^{\circ *}\mathcal {O}_{\mathcal {X}^+_n/\mathbb {G}_m}\langle \omega \rangle \big ) \\&\simeq j^\circ _*{\pi ^\circ }^*\tau ^*(-)\otimes \mathcal {O}_{\mathcal {X}^+_n/\mathbb {G}_m}\langle \omega \rangle \\&\simeq j^\circ _* \sigma ^*(-) \otimes \mathcal {O}_{\mathcal {X}^+_n/\mathbb {G}_m}\langle \omega \rangle \end{aligned}$$

where $\sigma = \tau \,\pi ^\circ$ is shown below.

Now for us $S^\circ$ is a $\mathbb {G}_m$-bundle over Z with a $\mathbb {G}_m$-action of weight $-n$. By Proposition 2.9, this is isomorphic to the bundle $\mathcal {O}_D(D)$ over D with $\mathbb {G}_m$-action of weight $-n$ after removing the zero section. In other words we have an isomorphism $S^\circ /\mathbb {G}_m \simeq \root n \of {\mathcal {O}_D(D)}$, see Proposition 2.6. This fits in a commutative diagram as follows.

We thence get the required description of the embeddings of $\text {D}^b{(}D)$, namely

$$\begin{aligned} i_+^*\circ \Phi _\omega (-) \simeq i_*q^*(-)\otimes \mathcal {O}_{\root n \of {X/D}}\langle \omega \rangle . \end{aligned}$$

Embeddings of $\text {D}^b{(}X)$. First, we find an inverse of the equivalence $i_-^* :\mathcal {C}_{[\omega , \omega +1)} \xrightarrow {\sim } \text {D}^b{(}X)$ of Proposition 3.1. Consider a commutative diagram as below, following the argument of [13, Lemma 5.2(1)].

Recall that $\mathcal {T}_n= \text {Tot}(\mathcal {O}_X(D) \oplus \mathcal {O}_X)$. The morphism $\rho$ decomposes into an inclusion of a Cartier divisor $i_{\mathcal {X}}:\mathcal {X}_n/\mathbb {G}_m \rightarrow \mathcal {T}_n/\mathbb {G}_m$ followed by a flat projection $\mathcal {T}_n/\mathbb {G}_m \rightarrow X$. It follows that $\rho ^*$ is a functor $\text {D}^b{(}X) \rightarrow \text {D}^b{(}\mathcal {X}_n/\mathbb {G}_m)$. Indeed, given an object E in $\text {D}^b{(}\mathcal {T}_n/\mathbb {G}_m)$ two of the three terms of the functorial exact triangle (1.D) are objects of $\text {D}^b{(}\mathcal {T}_n/\mathbb {G}_m)$, hence so is the third one $i_{\mathcal {X}*} i_{\mathcal {X}}^* E$. As $i_{\mathcal {X}*}$ has no kernel, we conclude that $i_{\mathcal {X}}^*E \in \text {D}^b{(}\mathcal {X}_n/\mathbb {G}_m)$. Further, $\rho _-$ is an isomorphism, hence $i_-^*\rho ^* \simeq \rho _-^* \simeq \text {Id}_{\text {D}^b{(}X)}$ by the left-hand side of the diagram above. In other words, $\rho ^*$ is an inverse of $i_-^* :\mathcal {C}_{[0,1)} \xrightarrow {\sim } \text {D}^b{(}X)$. It follows that $\rho ^*(-)\otimes \mathcal {O}_{\mathcal {X}_n/\mathbb {G}_m}\langle \omega \rangle$ is an inverse of $i_-^* :\mathcal {C}_{[\omega , \omega +1)} \xrightarrow {\sim } \text {D}^b{(}X)$.

Using Proposition 3.1 again, we thence have a functor $\text {D}^b{(}X) \rightarrow \text {D}^b{\big (\root n \of {X/D}\big )}$ with essential image $i_+^* \mathcal {C}_{[\omega , \omega +1)}$ given by

$$\begin{aligned} i_+^*(\rho ^*(-) \otimes \mathcal {O}_{\mathcal {X}_n/\mathbb {G}_m}\langle \omega \rangle ) \simeq i_+^*\rho ^*(-) \otimes \mathcal {O}_{\root n \of {X/D}}\langle \omega \rangle \simeq p^*(-) \otimes \mathcal {O}_{\root n \of {X/D}}\langle \omega \rangle . \end{aligned}$$

Here the last isomorphism uses the right-hand side of the diagram above, and we find the required description of the embeddings of $\text {D}^b{(}X)$. $\square$

4 Periodic semiorthogonal decompositions

The following is a preparation for the proof of our main theorem.

Proposition 4.1

The autoequivalence

$$\begin{aligned} - \otimes \mathcal {O}_{\root n \of {X/D}} \langle n\rangle \end{aligned}$$

of $\text {D}^b{\big (\root n \of {X/D}\big )}$ preserves the decompositions of Theorem 3.7. Furthermore, it intertwines with autoequivalences

$$\begin{aligned} - \otimes \mathcal {O}_X(-D) \qquad \text {and} \qquad - \otimes \, \mathcal {O}_D(-D) \end{aligned}$$

via the embeddings $p^*$ from $\text {D}^b{(X)}$, and $i_* q^*$ from $\text {D}^b{(D)}$, respectively.

Proof

Note that $\mathcal {O}_{\root n \of {X/D}} \langle n\rangle \simeq p^* \mathcal {O}_X(-D)$ by Remark 2.10. Using tensor-pullback distributivity we have

$$\begin{aligned} \big (- \otimes \mathcal {O}_{\root n \of {X/D}} \langle n\rangle \big ) \,p^*&\simeq (- \otimes p^* \mathcal {O}_X(-D)) \,p^* \\&\simeq p^* (- \otimes \mathcal {O}_X(-D)). \end{aligned}$$

Furthermore using the projection formula and commutativity of square (3.C) gives

$$\begin{aligned} \big (- \otimes \mathcal {O}_{\root n \of {X/D}} \langle n\rangle \big ) \,i_* q^*&\simeq i_* \big (- \otimes \,i^* \mathcal {O}_{\root n \of {X/D}} \langle n\rangle \big ) \,q^* \\&\simeq i_* (- \otimes i^* p^* \mathcal {O}_X(-D)) \,q^* \\&\simeq i_* (- \otimes q^* i_D^* \mathcal {O}_X(-D)) \,q^* \\&\simeq i_* q^*(- \otimes i_D^* \mathcal {O}_X(-D)) \\&\simeq i_* q^*(- \otimes \mathcal {O}_D(-D)). \end{aligned}$$

$\square$

Recall [9] that given a semiorthogonal decomposition

$$\begin{aligned} \mathcal {C}= \big \langle \mathcal {A}, \mathcal {B}\big \rangle \end{aligned}$$

(4.A)

of a triangulated category $\mathcal {C}$ with $\mathcal {A}$ and $\mathcal {B}$ admissible the left and right dual semiorthogonal decompositions, $\big \langle L_{\mathcal {A}}\mathcal {B}, \mathcal {A}\big \rangle$ and $\big \langle \mathcal {B}, R_{\mathcal {B}}\mathcal {A}\big \rangle$ respectively, exist for the left mutation $L_{\mathcal {A}}\mathcal {B}$ of $\mathcal {B}$ over $\mathcal {A}$ and the right mutation $R_{\mathcal {B}}\mathcal {A}$ of $\mathcal {A}$ over $\mathcal {B}$. We say that the semiorthogonal decomposition (4.A) is strongly admissible if the ${N}^{\text {th}}$ left and right dual decompositions exist for any N. Given such a decomposition the Artin braid group on two strands $B_2 \cong \mathbb {Z}$ acts on the set of the decomposition (4.A) and all its left and right duals.

Definition 4.2

[15, Section 4.2] A semiorthogonal decomposition (4.A) of a triangulated category $\mathcal {C}$ is N-periodic if the ${N}^{\text {th}}$ right dual decomposition is again (4.A), i.e. if the decomposition is strongly admissible and the action of $\mathbb {Z}$ factors through $\mathbb {Z}_N$.

Our main theorem now follows rapidly.

Theorem 4.3

Take a full subcategory

$$\begin{aligned} \mathcal {D} = \big \langle i_*q^*\text {D}^b{(}D),\,i_*q^*\text {D}^b{(}D) \otimes \mathcal {O}\langle 1\rangle ,\,\ldots ,\,i_*q^*\text {D}^b{(}D) \otimes \mathcal {O}\langle n-2 \rangle \big \rangle \subset \text {D}^b{\big (\root n \of {X/D}\big )}. \end{aligned}$$

Then the following semiorthogonal decomposition is $2n$-periodic.

$$\begin{aligned} \text {D}^b{\big (\root n \of {X/D}\big )} = \langle p^*\text {D}^b{(}X), \mathcal {D} \rangle \end{aligned}$$

(4.B)

Proof

By Theorem 3.7, the decomposition right dual to $\langle p^*\text {D}^b{(}X), \mathcal {D} \rangle$ is

$$\begin{aligned} \big \langle \mathcal {D},\,p^*\text {D}^b{(}X)\otimes \mathcal {O}_{\root n \of {X/D}}\langle n-1 \rangle \big \rangle \end{aligned}$$

and so the second right dual is

$$\begin{aligned} \big \langle p^*\text {D}^b{(}X)\otimes \mathcal {O}_{\root n \of {X/D}}\langle n-1 \rangle ,\,\mathcal {D} \otimes \mathcal {O}_{\root n \of {X/D}} \langle n-1 \rangle \big \rangle , \end{aligned}$$

i.e. the twist of the original decomposition by $\mathcal {O}_{\root n \of {X/D}} \langle n-1 \rangle$. It follows that the ${2k}^{\text {th}}$ right dual is the twist of the original decomposition by $\mathcal {O}_{\root n \of {X/D}}\langle k(n-1) \rangle$. But then, using Proposition 4.1, the ${2n}^{\text {th}}$ right dual decomposition is the original decomposition, namely $\langle p^*\text {D}^b{(}X), \mathcal {D} \rangle$. $\square$

Finally we describe the gluing functors for the periodic decomposition above.

Proposition 4.4

The gluing functor $\mathcal {D} \rightarrow \text {D}^b{(}X)$ for the decomposition (4.B) after restriction to $i_*q^*\text {D}^b{(}D)\otimes \mathcal {O}\langle k \rangle \subset \mathcal {D}$ is $i_{D*}[1]$ for $k=0$, and zero otherwise.

Proof

Write $\iota _{\mathcal {D}}$ for the embedding $\mathcal {D} \rightarrow \text {D}^b{\big (\root n \of {X/D}\big )}$. Then the gluing functor for (4.B) is $p_* \iota _{\mathcal {D}}[1]$ by [20, Section 2.2]. As

$$\begin{aligned}{} & {} p_*\big (-\otimes \mathcal {O}_{\root n \of {X/D}}\langle k \rangle \big )i_*q^*\simeq p_*i_*\big (q^*(-) \otimes \mathcal {O}_{\root n \of {\mathcal {O}_D(D)}}\langle k \rangle \big )\\{} & {} \quad \simeq i_{D*}q_*\big (q^*(-) \otimes \mathcal {O}_{\root n \of {\mathcal {O}_D(D)}}\langle k \rangle \big ), \end{aligned}$$

the statement follows from

$$ q_*\big (q^*(-)\otimes \mathcal {O}_{\root n \of {\mathcal {O}_D(D)}}\langle k \rangle \big ) = \left\{ \begin{array}{ll}\text {Id} &{} \text {for } k=0\\ 0 &{} \text {for } k=1, \ldots , n-2. \end{array} \right. $$

Local calculations of $\mu _n$-invariants show that $q_*q^* \simeq \text {Id}_{\text {D}^b{(}D)}$. The claimed vanishing for $k =1, \ldots , n-2$ follows from the mutual orthogonality of the essential images of $q^*(-)\otimes \mathcal {O}_{\root n \of {\mathcal {O}_D(D)}}\langle k \rangle$ for $k = 0, \ldots , n-2$ in $\text {D}^b{\big (\root n \of {\mathcal {O}_D(D)}\big )}$, see Remark 2.7 and the proof of [19, Theorem 1.5].

As already discussed in Sect. 1.4, Dyckerhoff et al. [15] consider N-periodic semiorthogonal decompositions of stable infinity categories as well as N-spherical functors of such categories. In particular, a 4-spherical functor is an analogue of a spherical functor of DG categories. In [15, Theorem 4.2.1] the authors prove that a functor is N-spherical if and only if it is the gluing functor for an N-periodic semiorthogonal decomposition. Motivated by their work we give the following.

Definition 4.5

The gluing functor $\iota _{\textrm{A}}^R\iota _{\textrm{B}}$ of an N-periodic semiorthogonal decomposition (4.A) of a triangulated category $\mathcal {C}$ is N-triangle-spherical.

When N is equal to 4, we simply say that the functor is triangle-spherical.

Corollary 4.6

The functor $i_{D*}:\text {D}^b{(D)}\rightarrow \text {D}^b{(X)}$ is triangle-spherical. The unit and the counit for the $i_D^*\dashv i_{D*}$ adjunction fit into functorial exact triangles (1.D) and (1.E).

Proof

Consider the 4-periodic semiorthogonal decomposition (1.F). By definition, the gluing functor $\iota _{\textrm{A}}^R\iota _{\textrm{B}}$ is triangle-spherical, and $\iota _{\textrm{A}}^R\iota _{\textrm{B}} = p_*i_*q^* \simeq i_{D*}$ (see the proof of Proposition 4.4). This gluing functor has left adjoint $\iota _{\textrm{B}}^L\iota _{\textrm{A}} \simeq i_D^*$. By (1.B) and (1.C), the cones of the $i_D^*\dashv i_{D*}$ adjunction unit and counit are compositions of right mutations.

For the pair of semiorthogonal decompositions

$$\begin{aligned} \begin{aligned} \text {D}^b{\big (\root \of {X/D}\big )}&= \big \langle p^*\text {D}^b{(}X) ,\,i_*q^*\text {D}^b{(}D) \big \rangle \\&= \big \langle i_*q^*\text {D}^b{(}D) ,\,p^*\text {D}^b{(}X)\otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle \big \rangle \end{aligned} \end{aligned}$$

(4.C)

the right mutation of $p^*\text {D}^b{(X)}$ is, up to shift, given by $-\otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle :p^*\text {D}^b{(X)} \rightarrow p^*\text {D}^b{(X)} \otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle$. Indeed, the functor is an equivalence of the right and the left orthogonal complements to $i_*q^*\text {D}^b{(D)}$. In order to determine the shift, we evaluate $\iota _{\textrm{C}}^R\iota _{\textrm{A}} \simeq p_*(p^*(-)\otimes \mathcal {O}_{\root \of {X/D}}\langle -1 \rangle )$ at $\mathcal {O}_X$. As $\mathcal {O}_X$ is locally free and the morphism $\mathcal {V}\rightarrow X$ in Proposition 2.4 is affine, $p_*(p^*\mathcal {O}_X \otimes \mathcal {O}_{\root \of {X/D}}\langle -1 \rangle )\in \text {Coh}(X)$. It follows that $-\otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle$ is the mutation functor for (4.C). It is also the mutation for (4.C) twisted by $\mathcal {O}_{\root \of {X/D}}\langle 1 \rangle$. Hence, $-\otimes \mathcal {O}_{\root \of {X/D}}\langle 2 \rangle$ is the composition of mutations between $p^*\text {D}^b{(X)}$ and its fourth left orthogonal complement in $\text {D}^b{\big (\root \of {X/D}\big )}$. By Proposition 4.1, it is the image under $p^*$ of the equivalence $-\otimes \mathcal {O}_X(-D):\text {D}^b{(X)} \rightarrow \text {D}^b{(X)}$. We conclude that $\iota _{\textrm{A}}^R{\iota _{\textrm{C}}}\iota _{\textrm{C}}^R{\iota _{\textrm{A}}} \simeq - \otimes \mathcal {O}_X(-D)$ and (1.D) follows.

Analogously, for the pair of semiorthogonal decompositions

$$\begin{aligned} \begin{aligned} \text {D}^b{\big (\root \of {X/D}\big )}&= \big \langle i_*q^*\text {D}^b{(}D) ,\,p^*\text {D}^b{(}X)\otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle \big \rangle \\&= \big \langle p^*\text {D}^b{(}X) \otimes \mathcal {O}_{\root \of {X/D}} \langle 1 \rangle ,\,i_*q^*\text {D}^b{(}D) \otimes \mathcal {O}_{\root \of {X/D}} \langle 1 \rangle \big \rangle \end{aligned} \end{aligned}$$

(4.D)

the right mutation of $i_*q^*\text {D}^b{(D)}$ is, up to shift, given by $-\otimes \mathcal {O}_{\root \of {X/D}} \langle 1 \rangle$. To determine the shift, we check that $\iota _{\textrm{B}}^R\iota _{\textrm{D}} \simeq q_*i^!(i_*q^*(-)\otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle )$ maps $\mathcal {O}_D$ to an object of $\text {Coh}(D)[-1]$. We conclude that $-\otimes \mathcal {O}_{\root \of {X/D}}\langle 1 \rangle [1]$ is the mutation functor for (4.D). It is also the mutation for (4.D) twisted by $\mathcal {O}_{\root \of {X/D}}\langle 1 \rangle$. Hence, $-\otimes \mathcal {O}_{\root \of {X/D}}\langle 2 \rangle [2]$ is the composition of mutations between $i_*q^*\text {D}^b{(D)}$ and its fourth left orthogonal complement in $\text {D}^b{\big (\root \of {X/D}\big )}$. By Proposition 4.1, it is the image under $i_*q^*$ of the equivalence $-\otimes \mathcal {O}_D(-D)$[2]$:\text {D}^b{(D)} \rightarrow \text {D}^b{(D)}$. We conclude that $\iota _{\textrm{B}}^L{\iota _{\textrm{D}}} \iota _{\textrm{D}}^L{\iota _{\textrm{B}}} \simeq - \otimes \mathcal {O}_D(-D)$[2] and (1.E) follows. $\square$