Sonic-Supersonic Solutions for the Two-Dimensional Steady Full Euler Equations

Abstract

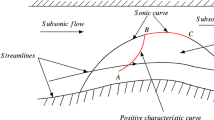
This paper focuses on the structure of classical sonic-supersonic solutions near sonic curves for the two-dimensional full Euler equations in gas dynamics. In order to deal with the parabolic degeneracy near the sonic curve, a novel set of dependent and independent variables are introduced to transform the Euler equations into a new system of governing equations which displays a clear regularity-singularity structure. With the help of technical characteristic decompositions, the existence of a local smooth solution for the new system is first established in a weighted metric space by using the iteration method and then expressed in terms of the original physical variables. This is the first construction of a classical sonic-supersonic solution near a sonic curve for the full Euler equations.

Appendices

Appendices

A The Tricomi Equation

In order to illustrate the methodology of this paper, we take the classical Tricomi equation and propose a similar problem. The Tricomi equation is a second-order partial differential equation of mixed hyperbolic-elliptic type with the form

$$\begin{aligned} yu_{xx}+u_{yy}=0. \end{aligned}$$

(A.1)

Equation (A.1) is hyperbolic in the half plane $y<0$, elliptic in the half plane $y>0$, and degenerates on the line $y=0$. The characteristic equation of (A.1) in $y<0$ is

$$\begin{aligned} dx^2+ydy^2=0, \end{aligned}$$

which gives the explicit expression of characteristic curves,

$$\begin{aligned} x\pm \frac{2}{3}(-y)^{\frac{3}{2}}=C \end{aligned}$$

for any constant C. These two families of characteristics coincide and form cusps perpendicularly to the line $y=0$ (see Figure 2).

The solution of (A.1) is now well-understood, e.g., in [5]. Below we just use our method for a hyperbolic degenerate problem with prescribed data on the degenerate line $y=0$.

Fig. 2

Characteristics of Tricomi equation and region $\overline{D}_{\bar{\delta }}$

1.1 A.1 A Hyperbolic Degenerate Problem

We prescribe the boundary data on $y=0$

$$\begin{aligned} u(x,0)=u_0(x),\quad u_y(x,0)=u_1(x),\ \ x\in [x_1,x_2]. \end{aligned}$$

(A.2)

The rightward characteristics starting from point $(x_1, 0)$ (denoted by $C_r$) and the leftward characteristics starting from point $(x_2, 0)$ (denoted by $C_l$) are, respectively, $x=x_1+\frac{2}{3}(-y)^{\frac{3}{2}}$ and $x=x_2-\frac{2}{3}(-y)^{\frac{3}{2}}$, which intersect at the point $P(\frac{x_2-x_1}{2},-\root 3 \of {\frac{9(x_2-x_1)^2}{16}})$. Let $\bar{\delta }\le \root 3 \of {\frac{9(x_2-x_1)^2}{16}}$ be a positive constant. Denote

$$\begin{aligned} \overline{D}_{\bar{\delta }}=\left\{ (y,x)|\ -\bar{\delta }\le y\le 0,\ x_1+\frac{2}{3}(-y)^{\frac{3}{2}}\le x\le x_2-\frac{2}{3}(-y)^{\frac{3}{2}}\right\} ; \end{aligned}$$

see Figure 2. The basic problem is

Problem A.1

we look for a classical solution for The Tricomi equation (A.1) with the boundary condition (A.2) in the region $\overline{D}_{\bar{\delta }}$ for some constant $\bar{\delta }>0$.

In the context of strictly hyperbolic problems, this is the typical Goursat problem and the solution can be constructed with the standard method of characteristics [30]. However, due to the degeneracy at $y=0$, the characteristic method cannot be applied directly [18]. The method in the present study is “nonlinear" in the sense that it can deal with nonlinear problems. The theorem is stated as follows:

Theorem A.1

Assume $u_0(x)\in C^4([x_1,x_2])$ and $u_1(x)\in C^3([x_1,x_2])$. Then there exists a positive constant $\bar{\delta }\le \root 3 \of {\frac{9(x_2-x_1)^2}{16}}$ such that the boundary problem (A.1) (A.2) has a classical solution in the region $\overline{D}_{\bar{\delta }}$.

Remark A.1

Since the Tricomi equation is a linear equation, it is not difficult to extend the solution in Theorem A.1 to the whole region bounded by $x=x_1+\frac{2}{3}(-y)^{\frac{3}{2}}$, $x=x_2-\frac{2}{3}(-y)^{\frac{3}{2}}$ and $y=0$.

To establish Theorem A.1, we rewrite the second-order equation (A.1) to a hyperbolic system. Let

$$\begin{aligned} \overline{R}=u_y+\sqrt{-y}u_x,\quad \overline{S}=u_y-\sqrt{-y}u_x. \end{aligned}$$

Then, for smooth solutions, equation (A.1) is equivalent to

$$\begin{aligned} \left\{ \begin{array}{l} \overline{R}_y-\sqrt{-y}\overline{R}_x=\frac{\overline{R}-\overline{S}}{4y},\\ \overline{S}_y+\sqrt{-y}\overline{S}_x=\frac{\overline{S}-\overline{R}}{4y},\\ u_y+\sqrt{-y}u_x=\overline{R}. \end{array} \right. \end{aligned}$$

(A.3)

Note that $\overline{R}-\overline{S}=2\sqrt{-y}u_x$ vanishes as the rate $\sqrt{-y}$, which means that the term $(\overline{R}-\overline{S})/y$ in system (A.3) blows up in the order of $(-y)^{-\frac{1}{2}}$ when approaching the line $y=0$. Observing this singularity, we introduce the following transformation:

$$\begin{aligned} t=\sqrt{-y},\quad x=x, \end{aligned}$$

(A.4)

which is an one-to-one map** for $y\le 0$. Denote $\widetilde{R}(x,t)=\overline{R}(x,y)$, $\widetilde{S}(x,t)=\overline{S}(x,y)$ and $\widetilde{u}(x,t)=u(x,y)$. Then system (A.3) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} \widetilde{R}_t+2t^2\widetilde{R}_x=\frac{\widetilde{R}-\widetilde{S}}{2t}, \\ \widetilde{S}_t-2t^2\widetilde{S}_x=\frac{\widetilde{S}-\widetilde{R}}{2t}, \\ \widetilde{u}_t-2t^2\widetilde{u}_x=-2t\widetilde{R}. \end{array} \right. \end{aligned}$$

(A.5)

Corresponding to (A.2), we have the boundary conditions for system (A.5) as follows:

$$\begin{aligned} \begin{array}{l} \quad (\widetilde{R},\widetilde{S},\widetilde{u})(x,0)=(u_1,u_1,u_0)(x),\\ (\widetilde{R}_t,\widetilde{S}_t,\widetilde{u}_t)(x,0)=(u_0',-u_0',0)(x), \end{array}\ \ x\in [x_1,x_2]. \end{aligned}$$

(A.6)

To better understand the singularity, we make the Taylor expansion for $(\widetilde{R},\widetilde{S},\widetilde{u})$ and introduce the following higher order error terms for the variables $(\widetilde{R},\widetilde{S},\widetilde{u})$:

$$\begin{aligned} \left\{ \begin{array}{l} R=\widetilde{R}(x,t)-u_1(x)-u_0'(x)t, \\ S=\widetilde{S}(x,t)-u_1(x)+u_0'(x)t, \\ W=\widetilde{u}(x,t)-u_1(x). \end{array} \right. \end{aligned}$$

(A.7)

Then one has the following system for variables (R, S, W):

$$\begin{aligned} \left\{ \begin{array}{l} R_t+2t^2R_x=\frac{R-S}{2t}-2t^2(u_1'+u_0''t), \\ S_t-2t^2S_x=\frac{S-R}{2t}+2t^2(u_1'-u_0''t), \\ W_t-2t^2W_x=-2t(R+u_1), \end{array} \right. \end{aligned}$$

(A.8)

with the following boundary conditions:

$$\begin{aligned} \begin{array}{l} \quad (R,S,W)(x,0)=(0,0,0),\\ (R_t,S_t,W_t)(x,0)=(0,0,0), \end{array} \ \ x\in [x_1,x_2]. \end{aligned}$$

(A.9)

For system (A.8), the positive characteristic curve from $(x_1,0)$ and negative characteristic curve from $(x_2,0)$ are, respectively, $x=x_1+\frac{2}{3}t^3$ and $x=x_2-\frac{2}{3}t^3$, which intersect at point $(\frac{x_2-x_1}{2}, \root 3 \of {\frac{3(x_2-x_1)}{4}})$. Let $\tilde{\delta }\le \root 3 \of {\frac{3(x_2-x_1)}{4}}$ be a small positive constant. Then we define a region in the plane (x, t)

$$\begin{aligned} \widetilde{D}_{\tilde{\delta }}=\left\{ (x,t)|\ 0\le t\le \tilde{\delta },\ x_1+\frac{2}{3}t^3\le x\le x_2-\frac{2}{3}t^3\right\} . \end{aligned}$$

Hence, Problem A.1 is reformulated to the following new problem in the (x, t) plane, and the corresponding existence theorem holds in parallel.

Problem A.2

we look for a classical solution for system (A.8) with the boundary condition (A.9) in the region $\widetilde{D}_{\tilde{\delta }}$ for some constant $\tilde{\delta }>0$.

Theorem A.2

Assume $u_0(x)\in C^4([x_1,x_2])$ and $u_1(x)\in C^3([x_1,x_2])$, then there exists positive constants $\tilde{\delta }\le \root 3 \of {\frac{3(x_2-x_1)}{4}}$ such that the boundary problem (A.8) (A.9) has a classical solution in the region $\widetilde{D}_{\tilde{\delta }}$.

Since the map $(t,x)\rightarrow (y,x)$ is an one-to-one map** for $y\le 0$, then Theorem A.1 follows directly from Theorem A.2.

To prove Theorem A.2, we need to consider the problem in a refined class of functions due to the fact that the variables (R, S, W) have very small magnitude near the line $t=0$. Let $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$ be a function class which incorporates all continuously differentiable vector functions $\mathbf {F}=(f_1,f_2,f_3)^T: \widetilde{D}_{\tilde{\delta }}\rightarrow \mathbb {R}^3$ satisfying the following properties:

$$\begin{aligned}&\mathrm{(P1)}\ \mathbf {F}(x,0)=\mathbf {F}_t(x,0)=0, \\&\mathrm{(P2)}\ \bigg \Vert \frac{\mathbf {F}(x,t)}{t^2}\bigg \Vert _\infty \le \tilde{M}, \\&\mathrm{(P3)}\ \bigg \Vert \frac{\partial _x\mathbf {F}(x,t)}{t^2}\bigg \Vert _\infty \le \tilde{M}, \\&\mathrm{(P4)}\ \partial _x\mathbf {F}(x,t)\ \mathrm{is\ Lipschitz\ continuous\ with\ respect\ to\ x\ and}\ \bigg \Vert \frac{\partial _{xx}\mathbf {F}(x,t)}{t^2}\bigg \Vert _\infty \le \tilde{M}, \end{aligned}$$

where $\tilde{M}$ is a positive constant and $\Vert \cdot \Vert _\infty$ denotes the supremum norm on the domain $\widetilde{D}_{\tilde{\delta }}$. Denote $\mathcal {W}_{\tilde{\delta }}^{\tilde{M}}$ the function class containing only continuous functions on $\widetilde{D}_{\tilde{\delta }}$ which satisfy the first two conditions $\mathrm{(P1)}$ and $\mathrm{(P2)}$. Obviously, $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$ is a subset of $\mathcal {W}_{\tilde{\delta }}^{\tilde{M}}$ and both $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$ and $\mathcal {W}_{\tilde{\delta }}^{\tilde{M}}$ are subsets of $C^0(\widetilde{D}_{\tilde{\delta }}, \mathbb {R}^3)$. For any elements $\mathbf {F}=(f_1,f_2,f_3)^T, \mathbf {G}=(g_1,g_2,g_3)^T$ in the set $\mathcal {W}_{\tilde{\delta }}^{\tilde{M}}$, we define the weighted metric as follows:

$$\begin{aligned} d(\mathbf {F}, \mathbf {G}):=\bigg \Vert \frac{f_1-g_1}{t^2}\bigg \Vert _\infty + \bigg \Vert \frac{f_2-g_2}{t^2}\bigg \Vert _\infty +\bigg \Vert \frac{f_3-g_3}{t^2}\bigg \Vert _\infty . \end{aligned}$$

(A.10)

One can check that $(\mathcal {W}_{\tilde{\delta }}^{\tilde{M}},d)$ is a complete metric space, while the subset $(\mathcal {S}_{\tilde{\delta }}^{\tilde{M}},d)$ is not closed in the space $(\mathcal {W}_{\tilde{\delta }}^{\tilde{M}},d)$.

1.2 A.2 The Proof of Theorem A.2

We use the fixed point method to prove Theorem A.2 and divide the proof into three steps. In Step 1, we construct an integration iteration map** in the function class $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$. In Step 2, we demonstrate the map** is a contraction for some constants $\tilde{\delta }$ and $\tilde{M}$, which implies that the iteration sequence converge to a vector function in the limit. In Step 3, we show that this limit vector function also belongs to $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$.

Step 1 (The iteration map**). Denote

$$\begin{aligned} \frac{{\mathrm{d}}}{{{\mathrm{d}}}_\pm t}=\partial _t\pm 2t^2\partial _x. \end{aligned}$$

Let vector function $(r,s,w)(x,t)\in \mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$. Then we consider the system

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{\mathrm{d}}}{{{\mathrm{d}}}_+ t}R=\frac{r-s}{2t}-2t^2(u_1'+u_0''t),\\ \frac{{\mathrm{d}}}{{{\mathrm{d}}}_- t}S=\frac{s-r}{2t}+2t^2(u_1'-u_0''t), \\ \frac{{\mathrm{d}}}{{{\mathrm{d}}}_- t}W=-2t(r+u_1). \end{array} \right. \end{aligned}$$

(A.11)

The integral form of (A.11) is

$$\begin{aligned} \left\{ \begin{array}{l} R(\eta ,\xi )=\displaystyle \int _{0}^\xi \bigg (\frac{r(x_+(t),t) -s(x_+(t),t)}{2t}-2t^2(u_1'(x_+(t))+u_0''(x_+(t))t)\bigg )\ {{\mathrm{d}}}t,\\ S(\eta ,\xi )=\displaystyle \int _{0}^\xi \bigg (\frac{s(x_-(t),t) -r(x_-(t),t)}{2t}+2t^2(u_1'(x_-(t))-u_0''(x_-(t))t)\bigg )\ {{\mathrm{d}}}t, \\ W(\eta ,\xi )=-2\displaystyle \int _{0}^\xi t\{r(x_-(t),t)+u_1(x_-(t))\}\ {{\mathrm{d}}}t, \end{array} \right. \end{aligned}$$

(A.12)

where

$$\begin{aligned} x_\pm (t)=\pm \frac{2}{3}t^3+\eta \mp \frac{2}{3}\xi ^3. \end{aligned}$$

Then (A.12) determines an iteration map** $\widetilde{\mathcal {T}}$:

$$\begin{aligned} \widetilde{\mathcal {T}} \left( \begin{array}{l} r \\ s \\ w \end{array} \right) = \left( \begin{array}{l} R \\ S \\ W \end{array} \right) , \end{aligned}$$

(A.13)

and the existence of classical solutions for the boundary problem (A.8) (A.9) is equivalent to the existence of fixed point for the map** $\widetilde{\mathcal {T}}$ in the function class $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$ for some constants $\tilde{\delta }$ and $\tilde{M}$.

Step 2 (Properties of the map**). For the map** $\widetilde{\mathcal {T}}$, we have the following lemma:

Lemma A.1

Let the assumptions in Theorem A.2 hold. Then there exists positive constants $\tilde{\delta }\le \root 3 \of {\frac{3(x_2-x_1)}{4}}, \tilde{M}$ and $0<\tilde{\nu }<1$ depending only on the $C^4$ norm of $u_0$ and $C^3$ norm of $u_1$ such that

• (1) $\widetilde{\mathcal {T}}$ maps $\mathcal {S}^{\tilde{M}}_{\tilde{\delta }}$ into $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$;

• (2) For any vector functions $\mathbf {F}, \widehat{\mathbf {F}}$ in $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$, it holds that

  $$\begin{aligned} d\bigg (\widetilde{\mathcal {T}}(\mathbf {F}),\widetilde{\mathcal {T}} (\widehat{\mathbf {F}})\bigg )\le \tilde{\nu } d(\mathbf {F},\widehat{\mathbf {F}}). \end{aligned}$$

  (A.14)

Proof

Let $\mathbf {F}=(r,s,w)^T$ and $\hat{\mathbf {F}}=(\hat{r},\hat{s}, \hat{w})^T$ be two elements in $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$, where the constants $\tilde{\delta }$ and $\tilde{M}$ will be determined later. Denote $\mathbf {G}=\overline{\mathcal {T}}(\mathbf {F})=(R,S,W)^T$ and $\widehat{\mathbf {G}}=\overline{\mathcal {T}}(\hat{\mathbf {F}}) =(\hat{R},\hat{S},\hat{W})^T$. By the properties of $\mathcal {S}_{\tilde{\delta }}^{\tilde{M}}$, one has

$$\begin{aligned}&|r(x,t)|+|s(x,t)|+|w(x,t)|\le \tilde{M}t^2,\nonumber \\&|r_x(x,t)|+|s_x(x,t)|+|w_x(x,t)|\le \tilde{M}t^2,\nonumber \\&|r_{xx}(x,t)|+|s_{xx}(x,t)|+|w_{xx}(x,t)|\le \tilde{M}t^2. \end{aligned}$$

(A.15)

Denote

$$\begin{aligned} K=1+\Vert u_1\Vert _{C^3([x_1,x_2])}+\root 3 \of {\frac{3(x_2-x_1)}{4}}\Vert u_0\Vert _{C^4([x_1,x_2])}. \end{aligned}$$

It follows that

$$\begin{aligned} |R(\eta ,\xi )|&\le \int _{0}^\xi \bigg (\frac{\tilde{M}}{2}t+2Kt^2\bigg )\ {{\mathrm{d}}}t\le \bigg (\frac{\tilde{M}}{4}+\frac{2K}{3}\tilde{\delta }\bigg )\xi ^2,\\ |S(\eta ,\xi )|&\le \int _{0}^\xi \bigg (\frac{\tilde{M}}{2}t+2Kt^2\bigg )\ {{\mathrm{d}}}t\le \bigg (\frac{\tilde{M}}{4}+\frac{2K}{3}\tilde{\delta }\bigg )\xi ^2, \\ |W(\eta ,\xi )|&\le 2\int _{0}^\xi t(\tilde{M}t^2+K)\ {{\mathrm{d}}}t\le (\tilde{M}\tilde{\delta }^2+K)\xi ^2. \end{aligned}$$

Hence, we have

$$\begin{aligned} \frac{|R(\eta ,\xi )|+|S(\eta ,\xi )|+|W(\eta ,\xi )|}{\xi ^2} \le \bigg (\frac{1}{2}+\tilde{\delta }^2\bigg )\tilde{M} +\bigg (1+\frac{4}{3}\tilde{\delta }\bigg )K. \end{aligned}$$

(A.16)

Noting the fact $\frac{\partial x_\pm }{\partial \eta }=1$, we differentiate system (A.12) with respect to $\eta$ to get

$$\begin{aligned}&\frac{\partial R}{\partial \eta }(\eta ,\xi )\\&\quad =\displaystyle \int _{0}^\xi \bigg (\frac{r_x(x_+(t),t) -s_x(x_+(t),t)}{2t}-2t^2(u_1''(x_+(t))+u_0'''(x_+(t))t)\bigg )\ {{\mathrm{d}}}t,\\&\frac{\partial S}{\partial \eta }(\eta ,\xi )\\&\quad =\displaystyle \int _{0}^\xi \bigg (\frac{s_x(x_-(t),t) -r_x(x_-(t),t)}{2t}+2t^2(u_1''(x_-(t))-u_0'''(x_-(t))t)\bigg )\ {{\mathrm{d}}}t, \\&\frac{\partial W}{\partial \eta }(\eta ,\xi )\\&\quad =-2\displaystyle \int _{0}^\xi t\{r_x(x_-(t),t)+u_1'(x_-(t))\}\ {{\mathrm{d}}}t, \end{aligned}$$

subsequently,

$$\begin{aligned}&\frac{\partial ^2 R}{\partial \eta ^2}(\eta ,\xi )\\&\quad =\displaystyle \int _{0}^\xi \bigg (\frac{r_{xx}(x_+(t),t)-s_{xx}(x_+(t),t)}{2t} -2t^2(u_1'''(x_+(t))+u_0''''(x_+(t))t)\bigg )\ {{\mathrm{d}}}t,\\&\frac{\partial ^2 S}{\partial \eta ^2}(\eta ,\xi )\\&\quad =\displaystyle \int _{0}^\xi \bigg (\frac{s_{xx}(x_-(t),t)-r_{xx}(x_-(t),t)}{2t} +2t^2(u_1'''(x_-(t))-u_0''''(x_-(t))t)\bigg )\ {{\mathrm{d}}}t, \\&\frac{\partial ^2 W}{\partial \eta ^2}(\eta ,\xi )\\&\quad =-2\displaystyle \int _{0}^\xi t\{r_{xx}(x_-(t),t)+u_1''(x_-(t))\}\ {{\mathrm{d}}}t. \end{aligned}$$

Therefore we obtain

$$\begin{aligned} \frac{|R_\eta (\eta ,\xi )|+|S_\eta (\eta ,\xi )|+|W_\eta (\eta ,\xi )|}{\xi ^2}&\le \bigg (\frac{1}{2} +\tilde{\delta }^2\bigg )\tilde{M} +\bigg (1+\frac{4}{3}\tilde{\delta }\bigg )K, \nonumber \\ \frac{|R_{\eta \eta }(\eta ,\xi )|+|S_{\eta \eta }(\eta ,\xi )|+|W_{\eta \eta }(\eta ,\xi )|}{\xi ^2}&\le \bigg (\frac{1}{2}+\tilde{\delta }^2\bigg )\tilde{M} +\bigg (1+\frac{4}{3}\tilde{\delta }\bigg )K. \end{aligned}$$

(A.17)

By choosing $\tilde{M}=10K$ and $\tilde{\delta }=\min \{\frac{1}{2},\root 3 \of {\frac{3(x_2-x_1)}{4}}\}$, we observe

$$\begin{aligned} \bigg (\frac{1}{2}+\tilde{\delta }^2\bigg )\tilde{M} +\bigg (1+\frac{4}{3}\tilde{\delta }\bigg )K\le \frac{11}{12}\tilde{M}<\tilde{M}. \end{aligned}$$

We combine with (A.16) and (A.17) to see that Properties (P2)-(P4) are preserved by the map** $\widetilde{\mathcal {T}}$ for $\tilde{\delta }, \tilde{M}$ chosen above. To determine $\widetilde{\mathcal {T}}(\mathbf {F})\in \mathcal {S}^{\tilde{M}}_{\tilde{\delta }}$, we first find by (A.12) that $R(\eta ,0)=S(\eta , 0)=W(\eta , 0)=0$. Then it suffices to show that $R_\xi (\eta ,0)=S_\xi (\eta , 0)=W_\xi (\eta , 0)=0$. Differentiating system (A.12) with respect to $\xi$ leads to

$$\begin{aligned} \frac{\partial R}{\partial \xi }(\eta ,\xi )&=\frac{r(\eta ,\xi )-s(\eta ,\xi )}{2\xi } -2\xi ^2(u_1'(\eta )+u_0''(\eta )\xi ) \nonumber \\&\quad -2\xi ^2 \displaystyle \int _{0}^\xi \bigg (\frac{r_x(x_+(t),t)-s_x (x_+(t),t)}{2t}\nonumber \\&\quad -2t^2(u_1''(x_+(t))+u_0'''(x_+(t))t)\bigg )\ {\mathrm{d}}t,\nonumber \\ \frac{\partial S}{\partial \xi }(\eta ,\xi )&=\frac{s(\eta ,\xi )-r(\eta ,\xi )}{2\xi } +2\xi ^2(u_1'(\eta )-u_0''(\eta )\xi )\nonumber \\&\quad +2\xi ^2 \displaystyle \int _{0}^\xi \bigg (\frac{s_x(x_-(t),t) -r_x(x_-(t),t)}{2t}\nonumber \\&\quad +2t^2(u_1''(x_-(t))-u_0'''(x_-(t))t)\bigg )\ {\mathrm{d}}t, \nonumber \\ \frac{\partial W}{\partial \xi }(\eta ,\xi )&=-2\xi \{r(\eta ,\xi )+u_1(\eta )\}\nonumber \\&\quad -4\xi ^2\displaystyle \int _{0}^\xi t\{r_x(x_-(t),t)+u_1'(x_-(t))\}\ {\mathrm{d}}t. \end{aligned}$$

(A.18)

It is obvious by (A.15) and (A.18) that $R_\xi (\eta ,0)=S_\xi (\eta , 0)=W_\xi (\eta , 0)=0$, which indicates that $\widetilde{\mathcal {T}}$ do map $\mathcal {S}^{\tilde{M}}_{\tilde{\delta }}$ onto itself.

We now establish (A.14) for $\tilde{\nu }=\frac{3}{4}$. For $(\hat{R},\hat{S},\hat{W})$, it follows that

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d}}{{\mathrm{d}}_+ t}\hat{R}=\frac{\hat{r}-\hat{s}}{2t}-2t^2(u_1'+u_0''t),\\ \frac{\mathrm{d}}{{\mathrm{d}}_- t}\hat{S}=\frac{\hat{s}-\hat{r}}{2t}+2t^2(u_1'-u_0''t), \\ \frac{\mathrm{d}}{{\mathrm{d}}_- t}\hat{W}=-2t(\hat{r}+u_1). \end{array} \right. \end{aligned}$$

(A.19)

Subtracting (A.19) from (A.11) gives

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm{d}}{{\mathrm{d}}_+ t}(R-\hat{R})=\frac{(r-\hat{r})-(s-\hat{s})}{2t},\\ \frac{\mathrm{d}}{{\mathrm{d}}_- t}(S-\hat{S})=\frac{(s-\hat{s})-(r-\hat{r})}{2t}, \\ \frac{\mathrm{d}}{{\mathrm{d}}_- t}(W-\hat{W})=-2t(r-\hat{r}), \end{array} \right. \end{aligned}$$

(A.20)

from which one arrives at

$$\begin{aligned} |R-\hat{R}|&\le \int _{0}^\xi \frac{|r-\hat{r}|+|s-\hat{s}|}{2t}\ {\mathrm{d}}t\le \frac{1}{4}\xi ^2d(\mathbf {F},\hat{\mathbf {F}}),\\ |S-\hat{S}|&\le \int _{0}^\xi \frac{|r-\hat{r}|+|s-\hat{s}|}{2t}\ {\mathrm{d}}t\le \frac{1}{4}\xi ^2d(\mathbf {F},\hat{\mathbf {F}}), \\ |W-\hat{W}|&\le \int _{0}^\xi 2t|r-\hat{r}|\ {\mathrm{d}}t\le \xi ^4d(\mathbf {F},\hat{\mathbf {F}}). \end{aligned}$$

Then we obtain

$$\begin{aligned} d\bigg (\widetilde{\mathcal {T}}(\mathbf {F}),\widetilde{\mathcal {T}} (\widehat{\mathbf {F}})\bigg )&=\bigg \Vert \frac{R-\hat{R}}{\xi ^2}\bigg \Vert _{\infty } +\bigg \Vert \frac{S-\hat{S}}{\xi ^2}\bigg \Vert _{\infty } +\bigg \Vert \frac{W-\hat{W}}{\xi ^2}\bigg \Vert _{\infty } \\&\le \bigg (\frac{1}{2}+\tilde{\delta }^2\bigg )d(\mathbf {F}, \hat{\mathbf {F}}) \le \frac{3}{4}d(\mathbf {F},\hat{\mathbf {F}}), \end{aligned}$$

which means that $\widetilde{\mathcal {T}}$ is a contraction under the metric d. $\quad \square$

Step 3 (Properties of the limit function). Since $(\mathcal {S}^{\tilde{M}}_{\tilde{\delta }},d)$ is not a closed subset in the complete space $(\mathcal {W}^{\tilde{M}}_{\tilde{\delta }},d)$, we need to confirm that the limit vector function of the iteration sequence $\{\mathbf {F}^{(n)}\}$, defined by $\mathbf {F}^{(n)}=\widetilde{\mathcal {T}}\mathbf {F}^{(n-1)}$, is in $\mathcal {S}^{\tilde{M}}_{\tilde{\delta }}$. This follows directly from Arzela- Ascoli Theorem and the following lemma:

Lemma A.2

With the assumptions in Theorem A.2, the iteration sequence $\{\mathbf {F}^{(n)}\}$ has the property that $\{\partial _t \mathbf {F}^{(n)}(x,t)\}$ and $\{\partial _x\mathbf {F}^{(n)}(x,t)\}$ are uniformly Lipschitz continuous on $\widetilde{D}_{\tilde{\delta }}$.

Proof

Let $(r,s,w)^T\in \mathcal {S}^{\tilde{M}}_{\tilde{\delta }}$. Then we obtain by Lemma A.1 that $(R,S,W)^T=\widetilde{\mathcal {T}}(r,s,w)^T$ also in $\mathcal {S}^{\tilde{M}}_{\tilde{\delta }}$. We divide the proof of this lemma into three steps.

We first prove $|R_t|+|S_t|+|W_t|\le 3\tilde{M}t$. It suggests by the first equation of (A.18) that

$$\begin{aligned} \bigg |\frac{\partial R}{\partial \xi }(\eta ,\xi )\bigg |&\le \frac{\tilde{M}}{2}\xi +2K\xi ^2 +2\xi ^2 \displaystyle \int _{0}^\xi \bigg (\frac{\tilde{M}}{2}t+2Kt^2\bigg )\ {\mathrm{d}}t \\&\le \bigg (\frac{1}{2}+\frac{\tilde{\delta }}{5} +\frac{\tilde{\delta }^3}{2}+\frac{\tilde{\delta }^4}{15}\bigg )\tilde{M}\xi \le \frac{7}{10}\tilde{M}\xi . \end{aligned}$$

Similarly, one has $|R_\xi |\le 7\tilde{M}\xi /10$. Moreover, for $|W_\xi |$, we have by the third equation of (A.18)

$$\begin{aligned} \bigg |\frac{\partial W}{\partial \xi }(\eta ,\xi )\bigg |&\le 2\xi \{\tilde{M}\tilde{\delta }^2+K\} +4\xi ^2\displaystyle \int _{0}^\xi t\{\tilde{M}t^2+K\}\ {\mathrm{d}}t\\&\le \bigg (2\tilde{\delta }^2+\frac{1}{5}+2\tilde{\delta }^5+ \frac{\tilde{\delta }^3}{5}\bigg )\tilde{M}\xi \le \frac{9}{10}\tilde{M}\xi . \end{aligned}$$

Thus we get

$$\begin{aligned} \bigg |\frac{\partial R}{\partial \xi }(\eta ,\xi )\bigg |+\bigg |\frac{\partial S}{\partial \xi }(\eta ,\xi )\bigg | +\bigg |\frac{\partial W}{\partial \xi }(\eta ,\xi )\bigg |\le 3\tilde{M}\xi . \end{aligned}$$

(A.21)

We next prove $|R_{tx}|+|S_{tx}|+|W_{tx}|\le 3\tilde{M}t$. Differentiating system (A.18) with respect to $\eta$ yields

$$\begin{aligned} \frac{\partial ^2 R}{\partial \eta \partial \xi }(\eta ,\xi )&=\frac{r_\eta (\eta ,\xi ) -s_\eta (\eta ,\xi )}{2\xi }-2\xi ^2(u_1''(\eta )+u_0'''(\eta )\xi )\\&\quad -2\xi ^2 \displaystyle \int _{0}^\xi \bigg (\frac{r_{xx}(x_+(t),t) -s_{xx}(x_+(t),t)}{2t}\\&\quad -2t^2(u_1'''(x_+(t))+u_0''''(x_+(t))t)\bigg )\ {\mathrm{d}}t, \\ \frac{\partial ^2 S}{\partial \eta \partial \xi }(\eta ,\xi )&=\frac{s_\eta (\eta ,\xi )-r_\eta (\eta ,\xi )}{2\xi }+2\xi ^2(u_1 ''(\eta )-u_0'''(\eta )\xi )\\&\quad +2\xi ^2 \displaystyle \int _{0}^\xi \bigg (\frac{s_{xx}(x_-(t),t) -r_{xx}(x_-(t),t)}{2t}\\&\quad +2t^2(u_1'''(x_-(t))-u_0''''(x_-(t))t)\bigg )\ {\mathrm{d}}t, \\ \frac{\partial ^2 W}{\partial \eta \partial \xi }(\eta ,\xi )&=-2\xi \{r_\eta (\eta ,\xi )+u_1'(\eta )\}\\&\quad -4\xi ^2\displaystyle \int _{0}^\xi t\{r_{xx}(x_-(t),t)+u_1''(x_-(t))\}\ {\mathrm{d}}t, \end{aligned}$$

from which we obtain

$$\begin{aligned} \bigg |\frac{\partial ^2 R}{\partial \eta \partial \xi }(\eta ,\xi )\bigg |+\bigg |\frac{\partial ^2 S}{\partial \eta \partial \xi }(\eta ,\xi )\bigg | +\bigg |\frac{\partial ^2 W}{\partial \eta \partial \xi }(\eta ,\xi )\bigg |\le 3\tilde{M}\xi . \end{aligned}$$

(A.22)

Finally, we show $|R_{tt}|+|S_{tt}|+|W_{tt}|\le 13\tilde{M}$. We differentiate system (A.18) with respect to $\xi$ to achieve

$$\begin{aligned} \frac{\partial ^2 R}{\partial \xi ^2}(\eta ,\xi )&=\frac{r_\xi -s_\xi }{\xi }-\frac{r-s}{\xi ^2} -4\xi (2u_1'(\eta )+3u_0''(\eta )\xi )\\&\quad -4\xi \displaystyle \int _{0}^\xi \bigg (\frac{r_x(x_+(t), t)-s_x(x_+(t),t)}{2t}\\&\quad -2t^2(u_1''(x_+(t)) +u_0'''(x_+(t))t) \bigg )\ {\mathrm{d}}t \\&\quad +4\xi ^4\displaystyle \int _{0}^\xi \bigg (\frac{r_{xx}(x_+ (t),t)-s_{xx}(x_+(t),t)}{2t}\\&\quad -2t^2(u_1'''(x_+(t)) +u_0''''(x_+(t))t)\bigg )\ {\mathrm{d}}t,\\ \frac{\partial ^2 S}{\partial \xi ^2}(\eta ,\xi )&=\frac{s_\xi -r_\xi }{\xi } -\frac{s-r}{\xi ^2} +4\xi (2u_1'-3u_0''\xi ) \\&\quad +4\xi \displaystyle \int _{0}^\xi \bigg (\frac{s_x(x_-(t),t) -r_x(x_-(t),t)}{2t}\\&\quad +2t^2(u_1''(x_-(t))-u_0'''(x_-(t))t)\bigg )\ {\mathrm{d}}t \\&\quad +4\xi ^4 \displaystyle \int _{0}^\xi \bigg (\frac{s_{xx}(x_-(t),t) -r_{xx}(x_-(t),t)}{2t}\\&\quad +2t^2(u_1'''(x_-(t))-u_0''''(x_-(t))t)\bigg )\ {\mathrm{d}}t\\ \frac{\partial ^2 W}{\partial \xi ^2}(\eta ,\xi )=&-4\{r+u_1+\xi r_\xi \} -8\xi \displaystyle \int _{0}^\xi t\{r_x(x_-(t),t)+u_1'(x_-(t))\}\ {\mathrm{d}}t \\&-8\xi ^4\int _{0}^\xi t\{r_{xx}(x_-(t),t)+u_1''(x_-(t))\}\ {\mathrm{d}}t \end{aligned}$$

which together with (A.15) and (A.21) gives

$$\begin{aligned} \bigg |\frac{\partial ^2 R}{\partial \xi ^2}(\eta ,\xi )\bigg |&\le 3\tilde{M}+\tilde{M}+4\xi K+4\xi (1+\xi ^3)\int _{0}^\xi \bigg (\frac{\tilde{M}}{2}t+2Kt^2\bigg )\ {\mathrm{d}}t\le 5\tilde{M}, \\ \bigg |\frac{\partial ^2 S}{\partial \xi ^2}(\eta ,\xi )\bigg |&\le 3\tilde{M}+\tilde{M}+4\xi K+4\xi (1+\xi ^3)\int _{0}^\xi \bigg (\frac{\tilde{M}}{2}t+2Kt^2\bigg )\ {\mathrm{d}}t\le 5\tilde{M}, \\ \bigg |\frac{\partial ^2 S}{\partial \xi ^2}(\eta ,\xi )\bigg |&\le 4(\tilde{M}\xi ^2+K+\tilde{M}\xi ^3)+8\xi (1+\xi ^3)\int _{0}^\xi t(\tilde{M}t^2+K)\ {\mathrm{d}}t\le 3\tilde{M}. \end{aligned}$$

Thus we have

$$\begin{aligned} \bigg |\frac{\partial ^2 R}{\partial \xi ^2}(\eta ,\xi )\bigg |+\bigg |\frac{\partial ^2 S}{\partial \xi ^2}(\eta ,\xi )\bigg | +\bigg |\frac{\partial ^2 W}{\partial \xi ^2}(\eta ,\xi )\bigg |\le 13\tilde{M}. \end{aligned}$$

(A.23)

Combining (A.21)–(A.23) ends the proof of the lemma. $\quad \square$

Hence, the proof of Theorem A.2 is completed.

B The Derivation of Formulations

1.1 B.1 The Derivation of (2.7)

We only derive the third equation of (2.7) since the derivation of the fourth equation is parallel. The first two equations can be derived obviously. Putting the expression of (u, v) in (2.4) into the third equation of (2.2) and using the notation of $\bar{\partial }^+$ in (2.5) yields

$$\begin{aligned} -\frac{\sin \theta }{\cos \omega }\bar{\partial }^+\bigg (\frac{\cos \theta }{\sin \omega }\bigg )+ \frac{\cos \theta }{\cos \omega }\bar{\partial }^+\bigg (\frac{\sin \theta }{\sin \omega }\bigg )+\frac{1}{\gamma p}\bar{\partial }^+p=0. \end{aligned}$$

(B.1)

On the other hand, we have, by the Bernoulli function,

$$\begin{aligned} B=\frac{u^2+v^2}{2}+\frac{c^2}{\gamma -1}&=\bigg (\frac{1}{2\sin ^2\omega } +\frac{1}{\gamma -1}\bigg )c^2\\&=\frac{\gamma (\kappa +\sin ^2\omega )}{2\kappa \sin ^2\omega }\cdot \frac{p}{\rho }, \end{aligned}$$

which, together with the entropy function $S=p\rho ^{-\gamma }$, gives

$$\begin{aligned} \ln p=\frac{\gamma }{\gamma -1}\bigg (\ln B-\frac{1}{\gamma }\ln S-\ln \frac{\gamma (\kappa +\sin ^2\omega )}{2\kappa \sin ^2\omega }\bigg ), \end{aligned}$$

and further provides

$$\begin{aligned} \frac{1}{p}\bar{\partial }^+p=\frac{\gamma }{2\kappa }\bar{\partial }^+\left( \ln B-\frac{1}{\gamma }\ln S\right) +\frac{\gamma \cot \omega }{\kappa +\sin ^2\omega }\bar{\partial }^+\omega . \end{aligned}$$

Inserting the above into (B.1) leads to

$$\begin{aligned}&-\frac{\sin \theta }{\cos \omega } \cdot \frac{-\sin \theta \sin \omega \bar{\partial }^ +\theta -\cos \theta \cos \omega \bar{\partial }^+\omega }{\sin ^2\omega }\\&\quad +\frac{\cos \theta }{\cos \omega } \cdot \frac{\cos \theta \sin \omega \bar{\partial }^ +\theta -\sin \theta \cos \omega \bar{\partial }^+\omega }{\sin ^2\omega } \\&\quad +\frac{1}{2\kappa }\bar{\partial }^+\bigg (\ln B-\frac{1}{\gamma }\ln S\bigg )+\frac{\cot \omega }{\kappa +\sin ^2\omega }\bar{\partial }^+\omega =0. \end{aligned}$$

Doing a simple rearrangement arrives at

$$\begin{aligned} \bar{\partial }^+\theta +\frac{\cos ^2\omega }{\kappa +\sin ^2\omega }\bar{\partial }^+\omega +\frac{\sin (2\omega )}{4\kappa }\bar{\partial }^+\bigg (\ln B-\frac{1}{\gamma }\ln S\bigg )=0, \end{aligned}$$

which is the third equation of (2.7).

1.2 B.2 The Commutator Relation Between $\bar{\partial }^0$ and $\bar{\partial }^+$

By a direct calculation, we obtain from (2.5),

$$\begin{aligned} \bar{\partial }^0\bar{\partial }^+&=(\cos \theta \partial _x+\sin \theta \partial _y) (\cos \alpha \partial _x+\sin \alpha \partial _y)\nonumber \\&=\cos \theta \cos \alpha \partial _{xx}+(\cos \theta \sin \alpha +\sin \theta \cos \alpha )\partial _{xy} +\sin \theta \sin \alpha \partial _{yy} \nonumber \\&\quad -\sin \alpha (\cos \theta \alpha _x+\sin \theta \alpha _y)\partial _x +\cos \alpha (\cos \theta \alpha _x+\sin \theta \alpha _y)\partial _y\nonumber \\&=\cos \theta \cos \alpha \partial _{xx}+(\cos \theta \sin \alpha +\sin \theta \cos \alpha )\partial _{xy} +\sin \theta \sin \alpha \partial _{yy} \nonumber \\&\quad -\sin \alpha \bar{\partial }^0\alpha \partial _x +\cos \alpha \bar{\partial }^0\alpha \partial _y, \end{aligned}$$

(B.2)

and

$$\begin{aligned} \bar{\partial }^+\bar{\partial }^0&=(\cos \alpha \partial _x+\sin \alpha \partial _y) (\cos \theta \partial _x+\sin \theta \partial _y) \nonumber \\&=\cos \theta \cos \alpha \partial _{xx}+(\cos \theta \sin \alpha +\sin \theta \cos \alpha )\partial _{xy} +\sin \theta \sin \alpha \partial _{yy} \nonumber \\&\quad -\sin \theta (\cos \alpha \theta _x+\sin \alpha \theta _y)\partial _x +\cos \theta (\cos \alpha \theta _x+\sin \alpha \theta _y)\partial _y\nonumber \\&= \cos \theta \cos \alpha \partial _{xx}+(\cos \theta \sin \alpha +\sin \theta \cos \alpha )\partial _{xy} +\sin \theta \sin \alpha \partial _{yy} \nonumber \\&\quad -\sin \theta \bar{\partial }^+\theta \partial _x +\cos \theta \bar{\partial }^+\theta \partial _y. \end{aligned}$$

(B.3)

Subtracting (B.3) from (B.2) yields

$$\begin{aligned} \bar{\partial }^0\bar{\partial }^+-\bar{\partial }^+\bar{\partial }^0 =(\sin \theta \bar{\partial }^+\theta -\sin \alpha \bar{\partial }^0\alpha )\partial _x -(\cos \theta \bar{\partial }^+\theta -\cos \alpha \bar{\partial }^0\alpha )\partial _y. \end{aligned}$$

(B.4)

On the other hand, we find from (2.6) and (2.4),

$$\begin{aligned} \partial _x&=\frac{2\sin \alpha \cos \omega \bar{\partial }^0-(\sin \alpha +\sin \beta )\bar{\partial }^+}{\sin (2\omega )} =\frac{\sin \alpha \bar{\partial }^0 -\sin \theta \bar{\partial }^+}{\sin \omega }, \\ \partial _y&=-\frac{2\cos \alpha \cos \omega \bar{\partial }^0-(\cos \alpha +\cos \beta ) \bar{\partial }^+}{\sin (2\omega )} =-\frac{\cos \alpha \bar{\partial }^0 -\cos \theta \bar{\partial }^+}{\sin \omega }. \end{aligned}$$

Inserting the above into (B.4), one has

$$\begin{aligned}&\bar{\partial }^0\bar{\partial }^+-\bar{\partial }^+\bar{\partial }^0 \\&\quad =\frac{(\sin \alpha \sin \theta +\cos \alpha \cos \theta )\bar{\partial }^+\theta -\bar{\partial }^0\alpha }{\sin \omega }\bar{\partial }^0\\&\qquad -\frac{\bar{\partial }^+\theta -(\sin \theta \sin \alpha +\cos \theta \cos \alpha ) \bar{\partial }^0\alpha }{\sin \omega }\bar{\partial }^+\\&\quad = \frac{\cos \omega \bar{\partial }^+\theta -\bar{\partial }^0\alpha }{\sin \omega }\bar{\partial }^0 -\frac{\bar{\partial }^+\theta -\cos \omega \bar{\partial }^0\alpha }{\sin \omega }\bar{\partial }^+, \end{aligned}$$

which leads to the desired result.

1.3 B.3 The Characteristic Decomposition for $\**$

We only derive the first one of (2.19), and the other can be obtained with the same technique. Firstly, we have the following commutator relation between $\bar{\partial }^-$ and $\bar{\partial }^+$:

$$\begin{aligned} \bar{\partial }^-\bar{\partial }^+-\bar{\partial }^+\bar{\partial }^- =\frac{\cos (2\omega )\bar{\partial }^+\beta -\bar{\partial }^-\alpha }{\sin (2\omega )}\bar{\partial }^- -\frac{\bar{\partial }^+\beta -\cos (2\omega )\bar{\partial }^-\alpha }{\sin (2\omega )}\bar{\partial }^+, \end{aligned}$$

which can be derived in a similar way as in Appendix B or see Li and Zheng [27]. Thus we have from (2.17) that

$$\begin{aligned} \bar{\partial }^-\bar{\partial }^+\theta -\bar{\partial }^+\bar{\partial }^-\theta&=\frac{\cos (2\omega )\bar{\partial }^+\beta -\bar{\partial }^-\alpha }{\sin (2\omega )}\bar{\partial }^-\theta -\frac{\bar{\partial }^+\beta -\cos (2\omega )\bar{\partial }^-\alpha }{\sin (2\omega )}\bar{\partial }^+\theta \nonumber \\&=[\cos (2\omega )\bar{\partial }^+\beta -\bar{\partial }^-\alpha ]\bar{\partial }^-\** +[\bar{\partial }^+\beta -\cos (2\omega )\bar{\partial }^-\alpha ]\bar{\partial }^+\** , \end{aligned}$$

(B.5)

and

$$\begin{aligned} \bar{\partial }^+\bar{\partial }^-\** =\bar{\partial }^-\bar{\partial }^+\** -\frac{\cos (2\omega )\bar{\partial }^+\beta -\bar{\partial }^-\alpha }{\sin (2\omega )}\bar{\partial }^-\** +\frac{\bar{\partial }^+\beta -\cos (2\omega )\bar{\partial }^-\alpha }{\sin (2\omega )} \bar{\partial }^+\** . \end{aligned}$$

(B.6)

On the other hand, we find, by using (2.17) again, that

$$\begin{aligned} \bar{\partial }^-\bar{\partial }^+\theta&=-\sin (2\omega )\bar{\partial }^ -\bar{\partial }^+\** -2\cos (2\omega )\bar{\partial }^-\omega \bar{\partial }^+\** ,\\ \bar{\partial }^+\bar{\partial }^-\theta&=\sin (2\omega )\bar{\partial }^ +\bar{\partial }^-\** +2\cos (2\omega )\bar{\partial }^+\omega \bar{\partial }^-\** . \end{aligned}$$

Substituting the above into (B.5) and rearranging the result achieves

$$\begin{aligned}&-\sin (2\omega )(\bar{\partial }^-\bar{\partial }^+\** +\bar{\partial }^ +\bar{\partial }^-\** )\nonumber \\&\quad =\bigg (2\cos (2\omega )\bar{\partial }^+\omega +\cos (2\omega )\bar{\partial }^+\beta -\bar{\partial }^-\alpha \bigg ) \bar{\partial }^-\** \nonumber \\&\qquad +\bigg (2\cos (2\omega )\bar{\partial }^-\omega +\bar{\partial }^+\beta -\cos (2\omega )\bar{\partial }^-\alpha \bigg )\bar{\partial }^+\** . \end{aligned}$$

(B.7)

We put (B.6) into (B.7) to obtain

$$\begin{aligned} \bar{\partial }^-\bar{\partial }^+\**&=-\frac{\cos (2\omega )\bar{\partial }^ +\omega }{\sin (2\omega )}\bar{\partial }^-\** \nonumber \\&\quad -\frac{\cos (2\omega )\bar{\partial }^-\omega +\bar{\partial }^+\beta -\cos (2\omega )\bar{\partial }^-\alpha }{\sin (2\omega )}\bar{\partial }^+\** \nonumber \\&=-\frac{\cos (2\omega )\bar{\partial }^+\omega }{\sin (2\omega )}\bar{\partial }^-\** \nonumber \\&\quad -\frac{\bar{\partial }^+\theta -\bar{\partial }^+\omega -\cos (2\omega ) \bar{\partial }^-\theta }{\sin (2\omega )}\bar{\partial }^+\** \nonumber \\&=-\frac{\cos (2\omega )\bar{\partial }^+\omega }{\sin (2\omega )}\bar{\partial }^-\** \nonumber \\&\quad +\frac{\sin (2\omega )\bar{\partial }^+\** +\bar{\partial }^+\omega +\sin (2\omega )\cos (2\omega )\bar{\partial }^-\** }{\sin (2\omega )}\bar{\partial }^+\** . \end{aligned}$$

(B.8)

Moreover, thanks to (2.15) and (2.17), one arrives at

$$\begin{aligned} \bar{\partial }^+\omega =\frac{2\sin \omega (\kappa +\sin ^2\omega )}{\cos \omega }(\bar{\partial }^+\** +GH). \end{aligned}$$

It follows by inserting the above into (B.8) that

$$\begin{aligned}&\bar{\partial }^-\bar{\partial }^+\** =-\frac{\cos (2\omega )(\kappa +\sin ^2\omega )}{\cos ^2\omega }(\bar{\partial }^+\** +GH)\bar{\partial }^-\** \\&\qquad +\frac{\kappa +\sin ^2\omega }{\cos ^2\omega }(\bar{\partial }^+\** +GH)\bar{\partial }^+\** +[\bar{\partial }^+\** +\cos (2\omega )\bar{\partial }^-\** ]\bar{\partial }^+\** \\&\quad =\frac{\kappa +\sin ^2\omega }{\cos ^2\omega }(\bar{\partial }^+\** +GH) [\bar{\partial }^+\** -\cos (2\omega )\bar{\partial }^-\** ]\\&\qquad +[\bar{\partial }^+\** +\cos (2\omega )\bar{\partial }^-\** ]\bar{\partial }^+\** \\&\qquad =\frac{\kappa \bar{\partial }^+\** +(\kappa +\sin ^2\omega )GH}{\cos ^2\omega } [\bar{\partial }^+\** -\cos (2\omega )\bar{\partial }^-\** ]\\&\quad +\frac{\bar{\partial }^+\** }{\cos ^2\omega }[\bar{\partial }^+\** +\cos ^2 (2\omega )\bar{\partial }^-\** ], \end{aligned}$$

which is the first equation of (2.19).