SpringerLink
Log in

An Efficient Numerical Method for Fractional Advection–Diffusion–Reaction Problem with RLC Fractional Derivative

  • Published:
Mediterranean Journal of Mathematics Aims and scope Submit manuscript

Abstract

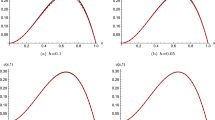
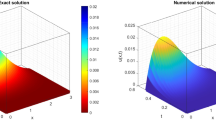
In this paper, we consider a two-point boundary-value problem with a Riemann–Liouville–Caputo fractional derivative of order \(\alpha \in (1,2)\). We solve this boundary-value problem in a sequence of processes, first using the shooting technique based on the secant iterative method, we convert the boundary-value problem into an initial-value problem, then the initial-value problem is transformed into an equivalent Volterra integral equation with weakly singular kernel. Finally, we find the approximate solution of the resultant equation by using a discretization scheme on a uniform mesh. The method’s convergence analysis has been thoroughly established, and it demonstrates that the scheme is first-order convergent. To show the effectiveness of the suggested approach, numerical results are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
EUR 32.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or Ebook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data Availability

Data sharing is not applicable to this article as no dataset were generated or analyzed during the current study.

References

  1. Al-Mdallal, Q.M., Syam, M.I., Anwar, M.N.: A collocation-shooting method for solving fractional boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 15(12), 3814–3822 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  2. Benson, D.A., Wheatcraft, S.W., Meerschaert, M.M.: Application of a fractional advection–dispersion equation. Water Resour. Res. 36(6), 1403–1412 (2000)

    Article  Google Scholar 

  3. Cen, Z., Huang, J., Xu, A.: An efficient numerical method for a two-point boundary value problem with a Caputo fractional derivative. J. Comput. Appl. Math. 336, 1–7 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cen, Z., Huang, J., Xu, A., Le, A.: A modified integral discretization scheme for a two-point boundary value problem with a Caputo fractional derivative. J. Comput. Appl. Math. 367, 112465, 10 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cen, Z., Liu, L.-B., Huang, J.: A posteriori error estimation in maximum norm for a two-point boundary value problem with a Riemann–Liouville fractional derivative. Appl. Math. Lett. 102, 106086, 8 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  6. Dahlquist, G., Björck, Å.: Numerical Methods in Scientific Computing, vol. I. SIAM, Philadelphia (2008)

    MATH  Google Scholar 

  7. del-Castillo-Negrete, D.: Fractional diffusion models of nonlocal transport. Phys. Plasmas 13(8), 082308, 16 (2006)

    Article  MathSciNet  Google Scholar 

  8. Diethelm, K.: The Analysis of Fractional Differential Equations. Lecture Notes in Mathematics, vol. 2004. Springer-Verlag, Berlin (2010)

    Book  MATH  Google Scholar 

  9. Diethelm, K., Ford, N.J.: Volterra integral equations and fractional calculus: do neighboring solutions intersect? J. Integr. Equ. Appl. 24(1), 25–37 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Diethelm, K., Walz, G.: Numerical solution of fractional order differential equations by extrapolation. Numer. Algorithms 16(3–4), 231–253 (1998). (1997)

    MathSciNet  MATH  Google Scholar 

  11. Dixon, J., McKee, S.: Weakly singular discrete Gronwall inequalities. Z. Angew. Math. Mech. 66(11), 535–544 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gracia, J.L., O’Riordan, E., Stynes, M.: Convergence analysis of a finite difference scheme for a two-point boundary value problem with a Riemann–Liouville–Caputo fractional derivative. BIT 60(2), 411–439 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hu, Y., Li, C., Li, H.: The finite difference method for Caputo-type parabolic equation with fractional Laplacian: one-dimension case. Chaos Soliton Fract. 102, 319–326 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. Huang, J., Cen, Z., Liu, L.-B., Zhao, J.: An efficient numerical method for a Riemann–Liouville two-point boundary value problem. Appl. Math. Lett. 103, 106201, 8 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  15. Jaishankar, A., McKinley, G. H.: Power-law rheology in the bulk and at the interface: quasi-properties and fractional constitutive equations. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 469(2149):20120284, 18 (2013)

  16. Jia, L., Chen, H., Ervin, V.J.: Existence and regularity of solutions to 1-D fractional order diffusion equations. Electron. J. Differ. Equ. 93, 21 (2019)

    MathSciNet  MATH  Google Scholar 

  17. Kelly, J.F., Sankaranarayanan, H., Meerschaert, M.M.: Boundary conditions for two-sided fractional diffusion. J. Comput. Phys. 376, 1089–1107 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  18. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier Science B.V, Amsterdam (2006)

    Google Scholar 

  19. Langlands, T.A.M., Henry, B.I.: The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 205(2), 719–736 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  20. Magin, R.L.: Fractional Calculus in Bioengineering, vol. 2. Begell House, Redding (2006)

    Google Scholar 

  21. Patie, P., Simon, T.: Intertwining certain fractional derivatives. Potential Anal. 36(4), 569–587 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  22. Shkhanukov, M.K.: On the convergence of difference schemes for differential equations with a fractional derivative. Dokl. Akad. Nauk 348(6), 746–748 (1996)

    MathSciNet  Google Scholar 

  23. Shkhanukov, M.K., Kerefov, A.A., Berezovskiĭ, A.A.: Boundary value problems for the heat equation with a fractional derivative in the boundary conditions, and difference methods for their numerical realization. Ukraïn. Mat. Zh. 45(9), 1289–1298 (1993)

    MathSciNet  MATH  Google Scholar 

  24. Waurick, M.: Homogenization in fractional elasticity. SIAM J. Math. Anal. 46(2), 1551–1576 (2014)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank the referees for their insightful comments and recommendations, which helped to make the article better. The first author would like to thank IIT Guwahati for their assistance with the fellowship and facilities during his research.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati, 781039, India

    Sandip Maji & Srinivasan Natesan

Authors
  1. Sandip Maji
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Srinivasan Natesan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.N proposed the research problem and methods to solve the equation. S.M. implemented the scheme and derived the error estimates and implemented the scheme in the computer. Both of us reviewed the manuscript.

Corresponding author

Correspondence to Srinivasan Natesan.

Ethics declarations

Conflict of Interest

The authors have no conflict of interest to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maji, S., Natesan, S. An Efficient Numerical Method for Fractional Advection–Diffusion–Reaction Problem with RLC Fractional Derivative. Mediterr. J. Math. 20, 297 (2023). https://doi.org/10.1007/s00009-023-02499-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00009-023-02499-8

Keywords

Mathematics Subject Classification

Search

Navigation