On size-dependent large-amplitude free oscillations of FGPM nanoshells incorporating vibrational mode interactions

Abstract

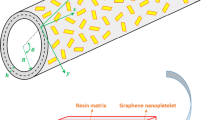
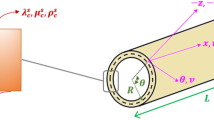
At nanoscale, surface free energies of the atoms located on the free surfaces of structures significantly affect their mechanical characteristics. In this study, nonlinear large-amplitude free vibration response of nanoshells prepared from functionally graded porous materials (FGPM) is investigated by taking into account surface stress size effects and vibrational mode interactions. Non-classical shell model is constructed on the basis of the Gurtin–Murdoch type of the surface theory of elasticity having the capability of capturing surface stress size dependency. The accuracy of nonlinear vibration analysis is improved by incorporating the interaction of the main vibration mode and the first, third and fifth symmetric oscillation modes. Moreover, the closed-cell Gaussian-Random field scheme is put to use to extract the mechanical characteristics of FGPM nanoshell. Multiple timescales technique is then applied to achieve surface stress elastic-based nonlinear frequency of FGPM nanoshell analytically for different interactions between vibrational modes. It is revealed that by incorporating the interactions of the main vibration mode and higher symmetric oscillation modes, the behavior of the backbone curves belongs to the nonlinear free oscillation response of FGPM nanoshells changes from hardening to softening schema. It is found that when only the main vibration mode is taken into account, surface elasticity effects makes an enhancement in the significance of the hardening schema. However, by considering the interactions of higher symmetric oscillation modes, surface elasticity effects makes a reduction in the significance of the softening schema.

Appendices

Appendix 1

$$c_{1} \left( t \right) = \eta \pi^{2} A_{1,n} /\left[ {\left( {\xi^{2} \eta^{2} \pi^{4} + \left( {\eta /\xi } \right)^{2} n^{4} } \right)\bar{\varGamma }_{1} + \eta^{2} \pi^{2} n^{2} \left( {\bar{\varGamma }_{2} - 2\bar{\varGamma }_{5} } \right)} \right]$$

$$c_{2} \left( t \right) = A_{1,0} /\left( {\xi^{2} \eta \pi^{2} \bar{\varGamma }_{1} } \right)$$

$$c_{3} \left( t \right) = A_{3,0} /\left( {9\xi^{2} \eta \pi^{2} \bar{\varGamma }_{1} } \right)$$

$$c_{4} \left( t \right) = A_{5,0} /\left( {25\xi^{2} \eta \pi^{2} \bar{\varGamma }_{1} } \right)$$

$$c_{5} \left( t \right) = n^{2} A_{1,n}^{2} /\left( {32\xi^{2} \pi^{2} \bar{\varGamma }_{1} } \right)$$

$$c_{6} \left( t \right) = \xi^{2} \pi^{2} A_{1,n} A_{1,0} /\left( {2n^{2} \bar{\varGamma }_{1} } \right)$$

$$ \begin{aligned}c_{7} \left( t \right) &= n^{2} \eta^{2} \pi^{2} A_{1,n} \left( {A_{1,0} - 9A_{3,0} } \right)/\\ &\quad\left[ {2\left( {16\xi^{2} \eta^{2} \pi^{4} + \left( {\eta /\xi } \right)^{2} n^{4} } \right)\bar{\varGamma }_{1} + 8\eta^{2} \pi^{2} n^{2} \left( {\bar{\varGamma }_{2} - 2\bar{\varGamma }_{5} } \right)} \right]\end{aligned} $$

$$ \begin{aligned}c_{8} \left( t \right) &= n^{2} \eta^{2} \pi^{2} A_{1,n} \left( {9A_{3,0} - 25A_{5,0} } \right)/\\ &\quad\left[ {2\left( {256\xi^{2} \eta^{2} \pi^{4} + \left( {\eta /\xi } \right)^{2} n^{4} } \right)\bar{\varGamma }_{1} + 32\eta^{2} \pi^{2} n^{2} \left( {\bar{\varGamma }_{2} - 2\bar{\varGamma }_{5} } \right)} \right]\end{aligned} $$

$$ \begin{aligned}c_{9} \left( t \right)& = 25n^{2} \eta^{2} \pi^{2} A_{1,n} A_{5,0} /\\ &\quad\left[ {2\left( {1296\xi^{2} \eta^{2} \pi^{4} + \left( {\eta /\xi } \right)^{2} n^{4} } \right)\bar{\varGamma }_{1} + 36\eta^{2} \pi^{2} n^{2} \left( {\bar{\varGamma }_{2} - 2\bar{\varGamma }_{5} } \right)} \right]\end{aligned} $$

$$c_{10} \left( t \right) = - \xi^{2} \pi^{2} A_{1,n}^{2} /\left( {32n^{2} \bar{\varGamma }_{1} } \right)$$

Appendix 2

For the second case of study, one will have

$$\left\{ {\begin{array}{*{20}l} \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{12} + \omega_{0}^{2} \fancyscript{q}_{12} & = - 2i\omega_{0} {\mathcal{A}}_{{,T_{2} }} e^{{i\omega_{0} T_{0} }} - 2i\xi_{1,n} \omega_{0}^{2} {\mathcal{A}}e^{{i\omega_{0} T_{0} }} - 3\bar{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left[ {\bar{\alpha }_{2} \bar{\beta }_{1} /\left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} + \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\omega_{1}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} - \alpha_{5} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} + {\text{NST}} + {\text{CC}} \\ \end{aligned} \hfill \\ \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{22} + \omega_{1}^{2} \fancyscript{q}_{22} & = - 2i\omega_{1} {\mathcal{B}}_{{,T_{2} }} e^{{i\omega_{1} T_{0} }} - 2i\xi_{1,0} \omega_{1}^{2} {\mathcal{B}}e^{{i\omega_{1} T_{0} }} - \bar{\beta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} \\ & \quad - \;\left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} \\ & \quad - \;2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]{\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} + {\text{NST}} + {\text{CC}} \\ \end{aligned} \hfill \\ \end{array} } \right.$$

(87)

where $NST$ is the non-secular terms.

Through elimination of the secular terms, one will have

$$\begin{aligned} & - 2i\omega_{0} {\mathcal{A}}_{{,T_{2} }} - 2i\xi_{1,n} \omega_{0}^{2} {\mathcal{A}} - 3\bar{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}} - \left[ {\bar{\alpha }_{2} \bar{\beta }_{1} /\left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}} + \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\omega_{1}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} - \left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} - \bar{\alpha }_{5} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} = 0 \\ \end{aligned}$$

$$\begin{aligned} & - 2i\omega_{1} {\mathcal{B}}_{{,T_{2} }} - 2i\xi_{1,0} \omega_{1}^{2} {\mathcal{B}} - \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{B}} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} - \bar{\beta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}} = 0 \\ \end{aligned}$$

(88)

After that, for the functions of $\left( {T_{2} } \right)$ and ${\mathcal{B}}\left( {T_{2} } \right)$, polar forms are assumed as

$${\mathcal{A}}\left( {T_{2} } \right) = a\left( {T_{2} } \right)e^{{i\varsigma \left( {T_{2} } \right)}} /2,\quad {\mathcal{B}}\left( {T_{2} } \right) = b\left( {T_{2} } \right)e^{{i\ell \left( {T_{2} } \right)}} /2$$

(89)

Eq. (89) is inserted in Eq. (88) to obtain a set of equations as

$$\left\{ {\begin{array}{*{20}l} {\fancyscript{a}_{{,T_{2} }} = - \xi_{1,n} \omega_{0} \fancyscript{a}} \hfill \\ \begin{aligned} & \fancyscript{a}\varsigma_{{,T_{2} }} - 3\bar{\alpha }_{1} \fancyscript{a}^{3} /\left( {8\omega_{0} } \right) - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{3} /\left[ {8\omega_{0} \left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right] + \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{3} /\left( {4\omega_{0} \omega_{1}^{2} } \right) \\ & \quad - \;\bar{\alpha }_{2}^{2} \fancyscript{a}\fancyscript{b}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{2}^{2} \fancyscript{a}\fancyscript{b}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\alpha }_{5} \fancyscript{a}\fancyscript{b}^{2} /\left( {8\omega_{0} } \right) = 0 \\ \end{aligned} \hfill \\ {\fancyscript{b}_{{,T_{2} }} + \xi_{1,0} \omega_{1} \fancyscript{b} = 0} \hfill \\ \begin{aligned} & \fancyscript{b}\ell_{{,T_{2} }} - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{2} b/\left[ {4\omega_{1} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{2} b/\left[ {4\omega_{1} \left( {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\beta }_{2} \fancyscript{a}^{2} b/\left( {8\omega_{1} } \right) = 0 \\ \end{aligned} \hfill \\ \end{array} } \right.$$

(90)

For the third case of study, one will have

$$\left\{ {\begin{array}{*{20}l} \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{12} + \omega_{0}^{2} \fancyscript{q}_{12} & = - 2i\omega_{0} {\mathcal{A}}_{{,T_{2} }} e^{{i\omega_{0} T_{0} }} - 2i\xi_{1,n} \omega_{0}^{2} {\mathcal{A}}e^{{i\omega_{0} T_{0} }} - 3\bar{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left[ {\bar{\alpha }_{2} \bar{\beta }_{1} /\left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} + \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\omega_{1}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} - \left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left[ {\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left( {4\omega_{0}^{2} - \omega_{3}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} + \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\omega_{3}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{3}^{2} /\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\omega_{0} T_{0} }} - \left( {\bar{\alpha }_{3}^{2} /\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{C}\bar{\mathcal{C}}\bar{\mathcal{C}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\alpha_{5} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} - \alpha_{6} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\omega_{0} T_{0} }} + {\text{NST}} + {\text{CC}} \\ \end{aligned} \hfill \\ \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{22} + \omega_{1}^{2} \fancyscript{q}_{22} & = - 2i\omega_{1} {\mathcal{B}}_{{,T_{2} }} e^{{i\omega_{1} T_{0} }} - 2i\xi_{1,0} \omega_{1}^{2} {\mathcal{B}}e^{{i\omega_{1} T_{0} }} - \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}} \\ & \quad - \;\left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} - \bar{\beta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} + {\text{NST}} + {\text{CC}} \\ \end{aligned} \hfill \\ \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{32} + \omega_{3}^{2} \fancyscript{q}_{32} & = - 2i\omega_{3} {\mathcal{C}}_{{,T_{2} }} e^{{i\omega_{3} T_{0} }} - 2i\xi_{3,0} \omega_{3}^{2} {\mathcal{C}}e^{{i\omega_{3} T_{0} }} - \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}} \\ & \quad - \;2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right]{\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\omega_{3} T_{0} }} - \bar{\vartheta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\omega_{3} T_{0} }} + {\text{NST}} + {\text{CC}} \\ \end{aligned} \hfill \\ \end{array} } \right.$$

(91)

Through elimination of the secular terms, one will have

$$\begin{aligned} & - 2i\omega_{0} {\mathcal{A}}_{{,T_{2} }} - 2i\xi_{1,n} \omega_{0}^{2} {\mathcal{A}} - 3\bar{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}} - \left[ {\bar{\alpha }_{2} \bar{\beta }_{1} /\left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}} \\ & \quad + \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\omega_{1}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}} - \left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} \\ & \quad - \left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} - \left[ {\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left( {4\omega_{0}^{2} - \omega_{3}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}} + \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\omega_{3}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}} \\ & \quad - \left( {\bar{\alpha }_{3}^{2} /\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{C}\bar{\mathcal{C}}} - \left( {\bar{\alpha }_{3}^{2} /\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{C}\bar{\mathcal{C}}} - \bar{\alpha }_{5} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} \\ \end{aligned}$$

$$\begin{aligned} & - 2i\omega_{1} {\mathcal{B}}_{{,T_{2} }} - 2i\xi_{1,0} \omega_{1}^{2} {\mathcal{B}} - \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{B}} \\ & \quad - \left( {\bar{\alpha }_{2}^{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} - \bar{\beta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}} = 0 \\ \end{aligned}$$

(92)

$$\begin{aligned} & - 2i\omega_{3} {\mathcal{C}}_{{,T_{2} }} - 2i\xi_{3,0} \omega_{3}^{2} {\mathcal{C}} - \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{C}} \\ & \quad - \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{C}} - \bar{\vartheta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}} = 0 \\ \end{aligned}$$

After that, for the functions of $\left( {T_{2} } \right)$, ${\mathcal{B}}\left( {T_{2} } \right)$, and ${\mathcal{C}}\left( {T_{2} } \right)$, polar forms are assumed as

$$ \begin{aligned}& {\mathcal{A}}\left( {T_{2} } \right) = \fancyscript{a}\left( {T_{2} } \right)e^{{i\varsigma \left( {T_{2} } \right)}} /2,\quad {\mathcal{B}}\left( {T_{2} } \right) = \fancyscript{b}\left( {T_{2} } \right)e^{{i\ell \left( {T_{2} } \right)}} /2,\quad \\ &{\mathcal{C}}\left( {T_{2} } \right) = \fancyscript{c}\left( {T_{2} } \right)e^{{i{\mathcal{J}}\left( {T_{2} } \right)}} /2\end{aligned} $$

(93)

Eq. (93) is inserted in Eq. (92) to obtain a set of equations as

$$\left\{ {\begin{array}{*{20}l} {\fancyscript{a}_{{,T_{2} }} + \xi_{1,n} \omega_{0} \fancyscript{a} = 0} \hfill \\ \begin{aligned} & \fancyscript{a}\varsigma_{{,T_{2} }} - 3\bar{\alpha }_{1} \fancyscript{a}^{3} /\left( {8\omega_{0} } \right) - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{3} /\left[ {8\omega_{0} \left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right] + \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{3} /\left( {4\omega_{0} \omega_{1}^{2} } \right) \\ & \quad - \;\bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{3} /\left[ {8\omega_{0} \left( {4\omega_{0}^{2} - \omega_{3}^{2} } \right)} \right] + \bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{3} /\left( {4\omega_{0} \omega_{3}^{2} } \right) - \bar{\alpha }_{2}^{2} \fancyscript{a}\fancyscript{b}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\alpha }_{2}^{2} \fancyscript{a}\fancyscript{b}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{3}^{2} \fancyscript{a}\fancyscript{c}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\alpha }_{3}^{2} \fancyscript{a}\fancyscript{c}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{5} \fancyscript{a}\fancyscript{b}^{2} /\left( {8\omega_{0} } \right) - \bar{\alpha }_{6} \fancyscript{a}\fancyscript{c}^{2} /\left( {8\omega_{0} } \right) = 0 \\ \end{aligned} \hfill \\ {\fancyscript{b}_{{,T_{2} }} + \xi_{1,0} \omega_{1} b = 0} \hfill \\ \begin{aligned} & \fancyscript{b}\ell_{{,T_{2} }} - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{2} \fancyscript{b}/\left[ {4\omega_{1} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{2} \fancyscript{b}/\left[ {4\omega_{1} \left( {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\beta }_{2} \fancyscript{a}^{2} b/\left( {8\omega_{1} } \right) = 0 \\ \end{aligned} \hfill \\ {\fancyscript{c}_{{,T_{2} }} + \xi_{3,0} \omega_{3} \fancyscript{c} = 0} \hfill \\ \begin{aligned} & \fancyscript{c}{\mathcal{J}}_{{,T_{2} }} - \bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{2} \fancyscript{c}/\left[ {4\omega_{3} \left( {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{2} \fancyscript{c}/\left[ {4\omega_{3} \left( {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\vartheta }_{2} \fancyscript{a}^{2} \fancyscript{c}/\left( {8\omega_{3} } \right) = 0 \\ \end{aligned} \hfill \\ \end{array} } \right.$$

(94)

For the forth case of study, one will have

$$\left\{ {\begin{array}{*{20}l} \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{12} + \omega_{0}^{2} \fancyscript{q}_{12} & = - 2i\omega_{0} {\mathcal{A}}_{{,T_{2} }} e^{{i\omega_{0} T_{0} }} - 2i\xi_{1,n} \omega_{0}^{2} {\mathcal{A}}e^{{i\omega_{0} T_{0} }} - 3\bar{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left[ {\bar{\alpha }_{2} \bar{\beta }_{1} /\left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} + \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\omega_{1}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} - \left[ {\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left( {4\omega_{0}^{2} - \omega_{3}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{2}^{2} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} + \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\omega_{3}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{3}^{2} /\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\omega_{0} T_{0} }} + \left( {2\bar{\alpha }_{4} \bar{\psi }_{1} /\omega_{5}^{2} } \right){\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{3}^{2} /\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\omega_{0} T_{0} }} - \left[ {\bar{\alpha }_{4} \bar{\psi }_{1} /\left( {4\omega_{0}^{2} - \omega_{5}^{2} } \right)} \right]{\mathcal{A}}^{2} {\bar{\mathcal{A}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{4}^{2} /\left[ {\left( {\omega_{5} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{F}\bar{\mathcal{F}}}e^{{i\omega_{0} T_{0} }} - \alpha_{5} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\left( {\bar{\alpha }_{4}^{2} /\left[ {\left( {\omega_{5} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\mathcal{F}\bar{\mathcal{F}}}e^{{i\omega_{0} T_{0} }} - \alpha_{6} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}e^{{i\omega_{0} T_{0} }} \\ & \quad - \;\alpha_{7} {\mathcal{A}\mathcal{F}\bar{\mathcal{F}}}e^{{i\omega_{0} T_{0} }} + NST + CC \\ \end{aligned} \hfill \\ \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{22} + \omega_{1}^{2} \fancyscript{q}_{22} & = - 2i\omega_{1} {\mathcal{B}}_{{,T_{2} }} e^{{i\omega_{1} T_{0} }} - \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} \\ & \quad - \;2i\xi_{1,0} \omega_{1}^{2} {\mathcal{B}}e^{{i\omega_{1} T_{0} }} - \left( {2\bar{\alpha }_{2} \bar{\beta }_{1} /\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} \\ & \quad - \;\bar{\beta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}e^{{i\omega_{1} T_{0} }} + NST + CC \\ \end{aligned} \hfill \\ \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{32} + \omega_{3}^{2} \fancyscript{q}_{32} & = - 2i\omega_{3} {\mathcal{C}}_{{,T_{2} }} e^{{i\omega_{3} T_{0} }} - \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\omega_{3} T_{0} }} \\ & \quad - \;2i\xi_{3,0} \omega_{3}^{2} {\mathcal{C}}e^{{i\omega_{3} T_{0} }} - \left( {2\bar{\alpha }_{3} \bar{\vartheta }_{1} /\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\omega_{3} T_{0} }} \\ & \quad - \;\bar{\vartheta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}e^{{i\omega_{3} T_{0} }} + NST + CC \\ \end{aligned} \hfill \\ \begin{aligned} {\mathcal{D}}_{0}^{2} \fancyscript{q}_{42} + \omega_{5}^{2} \fancyscript{q}_{42} & = - 2i\omega_{5} {\mathcal{F}}_{{,T_{2} }} e^{{i\omega_{5} T_{0} }} - \left( {2\bar{\alpha }_{4} \bar{\psi }_{1} /\left[ {\left( {\omega_{5} + \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{F}}e^{{i\omega_{5} T_{0} }} \\ & \quad - \;2i\xi_{5,0} \omega_{5}^{2} {\mathcal{F}}e^{{i\omega_{5} T_{0} }} - \left( {2\bar{\alpha }_{4} \bar{\psi }_{1} /\left[ {\left( {\omega_{5} - \omega_{0} } \right)^{2} - 1} \right]} \right){\mathcal{A}\bar{\mathcal{A}}\mathcal{F}}e^{{i\omega_{5} T_{0} }} \\ & \quad - \;\bar{\psi }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{F}}e^{{i\omega_{5} T_{0} }} + NST + CC \\ \end{aligned} \hfill \\ \end{array} } \right.$$

(95)

Through elimination of the secular terms, one will have

$$\begin{aligned} & - 2i\omega_{0} {\mathcal{A}}_{{,T_{2} }} - 2i\xi_{1,n} \omega_{0}^{2} {\mathcal{A}} - 3\bar{\alpha }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}} - \bar{\alpha }_{2} \bar{\beta }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}/\left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right) \\ & \quad + \;2\bar{\alpha }_{2} \bar{\beta }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}/\omega_{1}^{2} - \bar{\alpha }_{2}^{2} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}/\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right] \\ & \quad - \;\bar{\alpha }_{2}^{2} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}/\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right] - \bar{\alpha }_{3} \bar{\vartheta }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}/\left( {4\omega_{0}^{2} - \omega_{3}^{2} } \right) + 2\bar{\alpha }_{3} \bar{\vartheta }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}/\omega_{3}^{2} \\ & \quad - \;\bar{\alpha }_{3}^{2} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}/\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right] - \bar{\alpha }_{3}^{2} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}}/\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right] \\ & \quad - \;\bar{\alpha }_{4} \bar{\psi }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}/\left( {4\omega_{0}^{2} - \omega_{5}^{2} } \right) + 2\bar{\alpha }_{4} \bar{\psi }_{1} {\mathcal{A}}^{2} {\bar{\mathcal{A}}}/\omega_{5}^{2} - \bar{\alpha }_{4}^{2} {\mathcal{A}\mathcal{F}\bar{\mathcal{F}}}/\left[ {\left( {\omega_{5} + \omega_{0} } \right)^{2} - 1} \right] \\ & \quad - \;\bar{\alpha }_{4}^{2} {\mathcal{A}\mathcal{F}\bar{\mathcal{F}}}/\left[ {\left( {\omega_{5} - \omega_{0} } \right)^{2} - 1} \right] - \bar{\alpha }_{5} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}} - \alpha_{6} {\mathcal{A}\mathcal{C}\bar{\mathcal{C}}} - \alpha_{7} {\mathcal{A}\mathcal{F}\bar{\mathcal{F}}} = 0 \\ \end{aligned}$$

$$\begin{aligned} & - 2i\omega_{1} {\mathcal{B}}_{{,T_{2} }} - 2i\xi_{1,0} \omega_{1}^{2} {\mathcal{B}} - 2\bar{\alpha }_{2} \bar{\beta }_{1} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}}/\left[ {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right] \\ & \quad - \;\bar{\alpha }_{2}^{2} \bar{\beta }_{1} {\mathcal{A}\mathcal{B}\bar{\mathcal{B}}}/\left[ {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right] - \bar{\beta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{B}} = 0 \\ \end{aligned}$$

$$\begin{aligned} & - 2i\omega_{3} {\mathcal{C}}_{{,T_{2} }} - 2i\xi_{3,0} \omega_{3}^{2} {\mathcal{C}} - 2\bar{\alpha }_{3} \bar{\vartheta }_{1} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}/\left[ {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right] \\ & \quad - \;2\bar{\alpha }_{3} \bar{\vartheta }_{1} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}}/\left[ {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right] - \bar{\vartheta }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{C}} = 0 \\ \end{aligned}$$

(96)

$$\begin{aligned} & - 2i\omega_{5} {\mathcal{F}}_{{,T_{2} }} - 2i\xi_{5,0} \omega_{5}^{2} {\mathcal{F}} - 2\bar{\alpha }_{4} \bar{\psi }_{1} {\mathcal{A}\bar{\mathcal{A}}\mathcal{F}}/\left[ {\left( {\omega_{5} + \omega_{0} } \right)^{2} - 1} \right] \\ & \quad - \;2\bar{\alpha }_{4} \bar{\psi }_{1} {\mathcal{A}\bar{\mathcal{A}}\mathcal{F}}/\left[ {\left( {\omega_{5} - \omega_{0} } \right)^{2} - 1} \right] - \bar{\psi }_{2} {\mathcal{A}\bar{\mathcal{A}}\mathcal{F}} = 0 \\ \end{aligned}$$

After that, for the functions of $\left( {T_{2} } \right)$, ${\mathcal{B}}\left( {T_{2} } \right)$, ${\mathcal{C}}\left( {T_{2} } \right)$, and ${\mathcal{F}}\left( {T_{2} } \right)$, polar forms are assumed as

$${\mathcal{A}}\left( {T_{2} } \right) = \fancyscript{a}\left( {T_{2} } \right)e^{{i\varsigma \left( {T_{2} } \right)}} /2,\quad {\mathcal{B}}\left( {T_{2} } \right) = \fancyscript{b}\left( {T_{2} } \right)e^{{i\ell \left( {T_{2} } \right)}} /2$$

(97)

$${\mathcal{C}}\left( {T_{2} } \right) = \fancyscript{c}\left( {T_{2} } \right)e^{{i{\mathcal{J}}\left( {T_{2} } \right)}} /2,\quad {\mathcal{F}}\left( {T_{2} } \right) = \fancyscript{f}\left( {T_{2} } \right)e^{{i{\mathcal{K}}\left( {T_{2} } \right)}} /2$$

Equation (97) is inserted in Eq. (96) to obtain a set of equations as

$$\left\{ {\begin{array}{*{20}l} {\fancyscript{a}_{{,T_{2} }} + \xi_{1,n} \omega_{0} \fancyscript{a} = 0} \hfill \\ \begin{aligned} & \fancyscript{a}\varsigma_{{,T_{2} }} - 3\bar{\alpha }_{1} \fancyscript{a}^{3} /\left( {8\omega_{0} } \right) - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{3} /\left[ {8\omega_{0} \left( {4\omega_{0}^{2} - \omega_{1}^{2} } \right)} \right] + \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{3} /\left( {4\omega_{0} \omega_{1}^{2} } \right) \\ & \quad - \;\bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{3} /\left[ {8\omega_{0} \left( {4\omega_{0}^{2} - \omega_{3}^{2} } \right)} \right] + \bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{3} /\left( {4\omega_{0} \omega_{3}^{2} } \right) - \bar{\alpha }_{4} \bar{\psi }_{1} \fancyscript{a}^{3} /\left[ {8\omega_{0} \left( {4\omega_{0}^{2} - \omega_{5}^{2} } \right)} \right] \\ & \quad + \;\bar{\alpha }_{4} \bar{\psi }_{1} \fancyscript{a}^{3} /\left( {4\omega_{0} \omega_{5}^{2} } \right) - \bar{\alpha }_{2}^{2} \fancyscript{a}\fancyscript{b}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{5} \fancyscript{a}\fancyscript{b}^{2} /\left( {8\omega_{0} } \right) \\ & \quad - \;\bar{\alpha }_{2}^{2} \fancyscript{a}\fancyscript{b}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{1} - \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{3}^{2} \fancyscript{a}\fancyscript{c}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\alpha }_{6} \fancyscript{a}\fancyscript{c}^{2} /\left( {8\omega_{0} } \right) - \bar{\alpha }_{3}^{2} \fancyscript{a}\fancyscript{c}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{4}^{2} \fancyscript{a}\fancyscript{f}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{5} + \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\alpha }_{4}^{2} \fancyscript{a}\fancyscript{f}^{2} /\left[ {8\omega_{0} \left( {\left( {\omega_{5} - \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{7} \fancyscript{a}\fancyscript{f}^{2} /\left( {8\omega_{0} } \right) = 0 \\ \end{aligned} \hfill \\ {\fancyscript{b}_{{,T_{2} }} + \xi_{1,0} \omega_{1} b = 0} \hfill \\ \begin{aligned} & \fancyscript{b}\ell_{{,T_{2} }} - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{2} b/\left[ {4\omega_{1} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{2} \bar{\beta }_{1} \fancyscript{a}^{2} \fancyscript{b}/\left[ {4\omega_{1} \left( {\left( {\omega_{1} + \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\beta }_{2} \fancyscript{a}^{2} b/\left( {8\omega_{1} } \right) = 0 \\ \end{aligned} \hfill \\ {\fancyscript{c}_{{,T_{2} }} + \xi_{3,0} \omega_{3} \fancyscript{c} = 0} \hfill \\ \begin{aligned} & \fancyscript{c}{\mathcal{J}}_{{,T_{2} }} - \bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{2} c/\left[ {4\omega_{3} \left( {\left( {\omega_{3} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{3} \bar{\vartheta }_{1} \fancyscript{a}^{2} c/\left[ {4\omega_{3} \left( {\left( {\omega_{3} - \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\vartheta }_{2} \fancyscript{a}^{2} \fancyscript{c}/\left( {8\omega_{3} } \right) = 0 \\ \end{aligned} \hfill \\ {\fancyscript{f}_{{,T_{2} }} + \xi_{3,0} \omega_{5} \fancyscript{f} = 0} \hfill \\ \begin{aligned} & \fancyscript{f}{\mathcal{K}}_{{,T_{2} }} - \bar{\alpha }_{4} \bar{\psi }_{1} \fancyscript{a}^{2} f/\left[ {4\omega_{5} \left( {\left( {\omega_{5} + \omega_{0} } \right)^{2} - 1} \right)} \right] - \bar{\alpha }_{4} \bar{\psi }_{1} \fancyscript{a}^{2} f/\left[ {4\omega_{5} \left( {\left( {\omega_{5} - \omega_{0} } \right)^{2} - 1} \right)} \right] \\ & \quad - \;\bar{\psi }_{2} \fancyscript{a}^{2} f/\left( {8\omega_{5} } \right) = 0 \\ \end{aligned} \hfill \\ \end{array} } \right.$$

(98)