Epidemics control model with consideration of seven-segment population model

Abstract

This paper discusses a novel method for modeling the spread of an epidemic that facilitates the calculation of the optimal control policy. The proposed model considers seven compartments in the population as opposed to popular approaches based on three or four compartments. The usual compartments, i.e., susceptible, exposed, infected, and recovered individuals have been included in the seven compartment model with the addition of compartments pertaining to individuals under treatment, vaccinated individuals, and individuals in quarantine. The addition of new compartments allows for the incorporation of multiple control options such as treatment, quarantine, and vaccination. The mathematical expressions involved in the model have been described followed by a discussion on the calculation of optimal control policy. Finally, a simulation-based example has been included for demonstrating the effectiveness of the control policy resulting from the proposed model.

1 Introduction

Control of epidemic infections has been an active area of research in the past two decades or so [1] because it has the potential of saving lives with the minimal possible expense and timely efforts. Many control techniques have been developed for control in epidemiology [1, 2]. For example, predictive (or model predictive control based) techniques [15].

There are a few MDP and dynamics Bayesian network-based approaches available in the literature. For example [23] provides an approximate solution for graph-based MDPs but their approach is generic and not focus on the problem of control in epidemiology. Similarly, MDP for breast and ovarian cancer has been proposed in [10]. There has been some work on the stochastic prediction of the epidemic curve [24] as well as on the analysis of epidemics behavior under stochastic perturbations [6], delay [5], and geographical data [25]. A dynamic Bayesian network-based approach is proposed in [26] but this approach is specific to the prognosis of coronary heart disease. The game theory-based approach has been discussed in [27] in the context of the SIRV (Susceptible-Infected-Recovered-Vaccinated) model. MDP based three-compartment model has been discussed recently in [9]. A good reference on stochastic modeling and estimation for epidemics is [28]. An optimized nonlinear control based for SIR models is presented in [29] but the uncertainties involved in the process are not considered therein.

None of the previous MDP models discuss the seven-compartment approach. As discussed in the previous section, such an approach is more realistic and facilitates the control policy in making more informed decisions.

3 Problem formulation and MDP based stochastic model

In this section, we present our proposed MDP model for the following control problem.

Given the statistics and current status of various individuals in a population as infected, susceptible, recovered; device optimal control policy using vaccination, treatment, and isolation as means of preventing the spread of an epidemic disease.

Based on the above problem statement, the main objectives of the research are as follows

• Reduce the number of already infected individuals with the help of treatment

• Control the spread of the disease by using isolation

• Minimize the chances of disease spread using vaccination

• Keep the cost of treatment, vaccination, and isolation at a minimum possible value while meeting the above-mentioned objectives.

3.1 States

The state includes information that is available for decision making. For example, if the information available includes several infected individuals (I), number of individuals susceptible to the disease (S), number of vaccinated individuals (V), number of individuals under treatment (T), number of individuals exposed to the disease but not yet infected (E), number of individuals in quarantine (Q), and number of individuals recovered from the disease (R). The resulting state space becomes,

$$\begin{aligned} X & = \left\{ {x_{1} ,x_{2} , \ldots ,x_{n} } \right\}, \\ x_{i} & = \left\{ {S_{i} ,I_{i} ,R_{i} ,V_{i} ,T_{i} ,E_{i} ,Q_{i} } \right\},i \in \left\{ {1,2, \ldots ,n} \right\}, \\ S_{i} & \in \left\{ {0,1, \ldots ,N} \right\},I_{i} \in \left\{ {0,1, \ldots ,N} \right\},R_{i} \in \left\{ {0,1, \ldots ,N} \right\}, \\ V_{i} & \in \left\{ {0,1, \ldots ,N} \right\},T_{i} \in \left\{ {0,1, \ldots ,N} \right\},E_{i} \in \left\{ {0,1, \ldots ,N} \right\}, \\ Q_{i} & \in \left\{ {0,1, \ldots ,N} \right\},S_{i} + I_{i} + R_{i} + V_{i} + T_{i} + E_{i} + Q_{i} = N,\forall i. \\ \end{aligned}$$

(1)

Now, the number of states $n = \frac{{\left( {N + 6} \right)!}}{N!6!}$ (it is a solved problem in combinatorics that number of possible ways of placing N unlabeled objects in m labeled baskets is $\left( {\begin{array}{*{20}c} {N + m - 1} \\ N \\ \end{array} } \right)$. Each state is now a tuple of seven variables. However, to determine the state, it is enough to know the values of any six out of the seven variables in the tuple. One question that arises here is that of computational complexity and scalability of the representation concerning the population size.

3.1.1 Discussion on scalability

Whenever a problem is formulated as an MDP, the size of the state space has to be kept in check because of the curse of dimensionality involved in the methods used to calculate optimal control policy. Therefore, it is important to discuss the scalability of the proposed modeling. Figure 1 shows how the size of the state space varies as a function of population size. In this figure, m is the number of compartments (e.g. S, I, R, V, etc.) in the state space, N is the population size, and n is the size of the state space. The size of the state space is plotted in logarithm scale for clarity of representation. In the experience of the authors, a core i5 laptop with six gigabytes of random access memory can handle up to ten million states. This means that for a three-compartment model, we can handle a population size of about 3500. Whereas for five and seven compartment models, the limit on N is 120 and 40 respectively.

Fig. 1

Size of the state space versus population size

Population in real cities is of the order of several million. Even in small towns, the population is of the order of one hundred thousand. So the question arises that how an MDP model would handle such large numbers. A simple approach to this situation is state abstraction. Specifically, one unit of population in the state space may represent more than one person. In this way, a population size of 105,000 can be represented with 3500 units of population where each unit represents 30 persons. A drawback of such abstraction is that if any number of persons between one and thirty get infected, the unit will show either zero or thirty people being infected. This is similar to a well-known term quantization error in digital systems. The worst-case error is 15 persons for the case where each unit of the population represents 30 persons. Now if we represent this worst-case error as a percentage of the total population, it is merely 0.014% which should be acceptable for policy calculations. Handling models with five or seven compartments is still not easy. Extending the same example with a population of 105,000 to a seven compartment model with 40 units (instead of 3500), we get an error of 2.5% (as opposed to 0.014% in three-compartment cases). Further study can be done to explore ways of reducing effective computational complexity involved in the problem without incorporating prohibitive error. In this regard, the techniques in Approximate Dynamic Programming (ADP) [16, 30] may prove to be helpful. Specifically, [30] introduces a decomposition based Approximate Dynamic Programming approach that has been applied to a spacecrfat control problem but can be adapted for epidemics control problem discussed in this paper. The key is to decompose the population into appropriate subgroups.

3.2 Actions

There are three main types of actions in the epidemic infection problem i.e., vaccination, treatment, and isolation (or quarantine). Furthermore, within each type of action, there are divisions based on the number of individuals in the population upon which an action is applied. Consequently, we have $p_{1}$ vaccination actions, $p_{2}$ treatment actions, and $p_{3}$ isolation actions. This leads to the list of actions as

$$\begin{aligned} U & = \left\{ {u_{v1} , \ldots ,u_{vp1} ,u_{t1} , \ldots ,u_{tp2} ,u_{i1} , \ldots ,u_{ip3} ,NOOP} \right\}, \\ & \quad p_{1} ,p_{2} ,p_{3} \in \left\{ {1,2, \ldots ,N} \right\}. \\ \end{aligned}$$

(2)

Note that an additional action NOOP (no operation) has been included in the list of actions. This is to signify that it is not always desirable to vaccinate or isolate or treat somebody. For example, if the number of infected people is zero or the probability of infection spread is too low etc. Furthermore, the ideal value of $p_{1} , p_{2} ,p_{3}$ is N, but their actual value shall depend upon the available vaccination, treatment, and quarantine resources. For example, assume that there are five individuals in a population. Ideally, we should have $p_{1} = p_{2} = p_{3} = 5$ where $p_{1} = i$ means that we are vaccinating i, individuals, $p_{2} = j$ means we are starting treatment of j individuals etc. This would amount to a total of sixteen actions. But imagine that we only have two vaccines, three hospital beds (or treatment resources for three people at a time), and one isolation chamber. Then this would mean that $p_{1} = 2,p_{2} = 3,p_{3} = 1$.

3.3 State transitions

There are seven variables in the problem and evaluation of state transitions requires evaluation of the following joint probability distribution

$$P\left( {x^{\prime} |x,\mu } \right) = P\left( {S^{\prime},I^{\prime},R^{\prime},V^{\prime},E^{\prime},T^{\prime},Q^{\prime} |S,I,R,V,E,T,Q,\mu } \right)$$

(3)

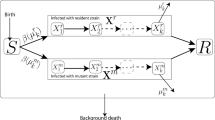
Assuming that the actions have a deterministic effect of transferring an individual from one compartment to another, we can remove $\mu$ from the above equation. Note that this assumption makes sense in the seven-compartment model because once a susceptible individual is vaccinated, it will deterministically shift from being susceptible to vaccinated regardless of whether the vaccination saves him from being infected or not. Similar arguments can be made for the actions of treatment and quarantine. Therefore, $P\left( {x^{\prime} |x,\mu } \right) = P\left( {x^{\prime} |x} \right)$. Furthermore, not all variables are dependent upon all other variables in our problem. We can construct a Bayesian network for the variables involved in the problem based on realistic assumptions as shown in Fig. 2. The doted links in Fig. 2 cater to the uncertainty involved in vaccination. This is to reflect that vaccination may not be 100% successful. Therefore, a vaccinated individual may be exposed or get infected. For practical implementation of the proposed approach, it would be required to know the a priori probabilities represented by directed links in the transition map which is a Bayesian Network. The advantage of having a Bayesian Network is that one does not need all the conditional and marginal distributions to calculate the joint distribution [16]. The joint conditional probability in (3) can be written as a product of less complicated probabilities using Bayesian network of Fig. 2 as

Fig. 2

Bayesian network for compartment transitions

$$\begin{aligned} P\left( {x^{\prime} |x} \right) & = \left( {P1} \right)\left( {P2} \right)\left( {P3} \right)\left( {P4} \right)\left( {P5} \right)\left( {P6} \right)\left( {P7} \right) \\ P1 & = P\left( {S^{\prime} |S} \right) \\ P2 & = P\left( {I^{\prime} |S,I,E,V} \right) \\ P3 & = P\left( {R^{\prime} |I,R,T,Q} \right) \\ P4 & = P\left( {V^{\prime} |S,V} \right) \\ P5 & = P\left( {E^{\prime} |S,V,E} \right) \\ P6 & = P\left( {T^{\prime} |I,T} \right) \\ P7 & = P(Q^{\prime}|I,Q) \\ \end{aligned}$$

(4)

3.4 Reward/cost function

First, we discuss the elements in the problem that have a positive or negative impact on the solution. The most important element in the cost is the number of infected individuals (I). Secondly, when the vaccination is available, the number of susceptible individuals should also be part of the cost function otherwise the optimal control would never use vaccination [9]. The purpose of vaccination is to build immunity among the susceptible individuals and once the immunity is created, a susceptible individual (S) is labeled as recovered (R) in the model. This is because the presence of immunity (or antibodies) against the disease is the only difference between the susceptible and recovered individuals. Having more recovered individuals is desirable because it reduces the chances of the spread of the disease. Therefore, it is important to have a cost function term associated with the susceptible individuals so that the optimal policy can justify spending money on vaccination. Next, kee** individuals in quarantine is costly and hence Q should be in the cost function. The cost of treatment and vaccination can be included by using either variable T and V or the cost can be included in the actions u_v and u_t for vaccination and treatment respectively. Finally, we must include the cost of exposed individuals (E) in the cost function since exposure leads to infection. The resulting cost function can be written as

$$C\left( {x,u} \right) = \alpha_{0} I + \alpha_{1} S + \alpha_{2} E + \alpha_{3} T + \alpha_{4} Q + \beta_{k} u_{vk} .$$

(5)

where $\alpha_{i}$ ($i \in \left\{ {0,1,2,3,4} \right\}$) and $\beta_{k}$ ($k \in \left\{ {1,2,..,N} \right\}$) are positive constants. Also $u_{vk}$ is kth vaccination action as presented in (2). Notice that the above cost function is an incremental cost. Total cost incorporated in an MDP problem is the expected sum of the cost over the whole decision horizon given as

$$C^{*} = \begin{array}{*{20}c} {min} \\ {u^{h} \in U} \\ \end{array} \left( {E\left[ {\mathop \sum \limits_{h = 0}^{\infty } \gamma^{h} C\left( {x^{h} ,u^{h} } \right)} \right]} \right).$$

(6)

In the above equation, h is the decision horizon i.e. the number of decisions to be made before the end of the problem. In (6), h varies from 0 to infinity indicating an infinite horizon. In general, the horizon can be finite rather in some cases, the horizon should be finite. Such cases arise in the problems where the deadline for decision making is predefined or the number of decisions allowed is limited such as in blackjack (cards game).

The cost function defined in (5) is a linear function of the variables in state and actions. In general, the cost does not have to be linear. A comparison of two different types of reward functions is discussed in [9]. For example, the cost of having patients may depend upon thresholds such as for the first few patients, the cost is low, then the number of patients above a certain threshold cost more and so on.

Furthermore, one could use exponential or quadratic functions instead of linear to reflect any real effect of the problem specific to the time and place (town/city) for which the optimal policy is to be calculated.

3.5 Calculation of the optimal control policy

In this section, we discuss the value iterations method for the calculation of optimal policy using an MDP model.

As the name suggests, value iteration is an iterative technique that is based on the value function of the states. The resulting control policy is optimal concerning the expected value of the criteria provided in (6). The decision making horizon h in value iteration is infinite. Value of each state is given by

$$V\left( x \right) = _{ u}^{max} \left( { - C\left( {x,u} \right) + \gamma \mathop \sum \limits_{x' \in X} P\left( {x^{\prime}|x,u} \right)V\left( {x^{\prime}} \right)} \right)$$

(7)

The value of a state depends upon the sum of the cost incurred by that state and the value of the states that it can lead to. This definition of the value function converges to the optimal value for each state via iterative calculations of the form

$$V_{h + 1} \left( x \right) \leftarrow _{ u}^{max} \left( { - C\left( {x,u} \right) + \gamma \mathop \sum \limits_{x' \in X} P\left( {x^{\prime}|x,u} \right)V_{h} \left( {x^{\prime}} \right)} \right)$$

(8)

Here $\gamma$ is the discount factor that ranges between zero and one. In case of epidemic infections, taking quick actions is desirable hence the discount factor value should be low e.g. between 0.5 and 0.8. Discount factor with value 0.5 means that the value of reaching the state decreases by half in each passing decision. A low discount factor results in less iteration before the convergence is achieved.

Once the optimal value is obtained, the optimal policy is calculated using the following expression

$$\varPi^{*} \left( x \right) = \mathop {\arg \hbox{max} }\limits_{u} \left( { - C\left( {x,u} \right) + \gamma \mathop \sum \limits_{{x^{\prime} \in X}} P(x^{\prime}|x,u)V^{*} \left( {x'} \right)} \right)$$

(9)

Here $V^{*} \left( {x'} \right)$ represents the optimal value of state $x'$ and $\varPi^{*} \left( x \right)$ represents an optimal policy for state $x$. Note that the optimal policy, in this case, is stationary, i.e., the optimal decision at each state is independent of the time at which the state is reached. This is because, in infinite decision horizon, time is irrelevant. The only factor affecting the early verses late decisions is the discount factor.

4 Case study

In this section, shows how the optimal policy can be summarized and analyzed parametrically. Also, the sample trajectory has been shown to demonstrate the performance of the optimal policy in terms of confining and diminishing the epidemic disease. The case study presented here involves 736,281 states where each state has four possible actions and each action can lead to one of the 384 possible next states (all possible combinations of the transitions as in Fig. 2). The values of the parameters used in the simulations are summarized in Table 1. Note that the values presented in the table are very important as the behavior of the optimal policy is directly related to these values. It is also important to understand that it is not the exact value that matters (as far as the optimal policy is concerned) rather, the key factor is the relative value of the parameters. For example, the cost of having an infected individual ($\alpha_{0} = 100$) is five times the cost of vaccination ($\beta = 20$). This provides a perspective of how important it is to avoid (or reduce) the infection among the individuals compared to using vaccination resources. Similarly, the cost ($\alpha_{1} = 40$) of having a susceptible (S) is less than that ($\alpha_{2} = 70$) of having an exposed individual (E) indicating that an exposed individual is relatively more undesirable compared to the susceptible one. A special piece-wise continuous value assignment has been associated with $\alpha_{3}$ (the cost of treatment) to emphasize that as the number of patients to be treated goes up, so does the cost of treatment. This assignment is realistic because as the demand for the supplies in the hospitals increases, the cost increases as well. Overall, the values in Table 1 have been selected to present a realistic approach. However, for specific diseases, the values may be estimated based on the actual cost of particular vaccination for the disease. The cost of hospitalization may also vary from country to country and even within a country, it may vary depending upon the type and standards of a particular hospital.

Table 1 Parameter values for the case study

The values related to the transition probabilities are presented in Table 2. The first column of the table shows the label transition (please refer to Fig. 2) for a single unit of population. The remaining four columns represent the corresponding probabilities of these transitions for each of the four possible actions. For example, the probability that a susceptible unit of population shall stay susceptible is 0.65 if no action (NOOP) is executed. Similarly, the probability of recovery of an infected individual is 0.1 for NOOP. The sum of all possible transitions from each of the seven variables is one. The probability values presented in this section have been inspired by the flu statistics¹ in the United States of America (USA). For example, about 20% of the population (in worst case) is infected by flu in the USA (the probability value of 0.25 in the second row of Table 2). Some values have been exaggerated a little bit to indicate that the disease is not easily recovered. The reason behind the selection of pessimistic probability values is to put the resulting optimal policy to a tough test.

Table 2 Transition Probabilities for a unit of population given against possible actions

The MDP for the seven-compartment model is solved using value iteration. The resulting optimal policy is summarized in Table 3. This table summarizes which actions are deemed optimal more often than the others i.e. it can be seen that vaccination and treatment are deemed optimal quite often.

Table 3 Summary of the optimal policy

A deeper parametric analysis of the policy is presented in Table 4. The values (or ranges) in this table present insights into the behavior of the optimal policy. For example, if the number of susceptible units of population (S) is greater than five, then it is not optimal to do nothing. Similarly, NOOP is not an optimal choice if the number of infected units in the population (I) is greater than two. Another interesting insight is that vaccination is no longer optimal when “I” is greater than ten. This means that when there are quite a few people infected, treating the infected individuals takes precedence over vaccinating the susceptible ones. In our case study, treatment is highly preferred over quarantine. This is because treatment yields a higher probability of recovering. In another setting where treatment is too costly or the spread probability of the infection is too high, quarantine may be preferable over treatment.

Table 4 Parametric analysis of the optimal policy

The traditional way of analyzing the control policy for epidemic infections is to show how it renders the susceptible and infected individuals to zero asymptotically. Therefore, a similar analysis of the proposed approach has also been presented. Figures 3 and 4 show the results of the optimal control policy with initially 20 units of population being susceptible and five units being infected. Exogenous events in these simulations have been selected using uniform distribution (an exogenous event refers to a possible state transition in the model given current state and action). Notice that the infected individuals recover after treatment and quarantine the susceptible units of the population are vaccinated. This kind of insight and those in Table 4 could be used to determine soft rules for epidemic control (the details of the development of such rules are beyond the scope of this paper.

Fig. 3

Results from the optimal policy with initial condition S = 20, I = 5

Fig. 4

Results from the optimal policy with initial condition S = 20, I = 5

5 Discussion of the results

A major advantage of the proposed approach over the existing approaches is the inclusion of more detailed information in the model. Although the case study has been designed using pessimistic values of recovery rate (see Table 2), still the numerical results (Figs. 3 and 4) indicate good control over the spread of the disease without a huge peak in the number of individuals under treatment or number of individuals being vaccinated or quarantined at any particular instant. Compared to the proposed approach, the SIR model-based approach [9] cannot depict how many individuals are currently being treated, and therefore, the decision to hospitalize another individual is less informed compared to the proposed approach. As a result, there is a risk that the optimal policy ends up chocking the medical support system. Similarly, the other approaches such as [

Notes

1. https://www.webmd.com/cold-and-flu/flu-statistics.