Introduction

In the latter part of 2019, Wuhan City in China witnessed the first public outbreak of the new corona virus COVID-19. SARS-CoV2 (severe acute respiratory syndrome coronavirus 2) is the source of the corona virus disease COVID-19. It is now widespread around the world with severe impact on 213 nations and territories by assuming the shape of a pandemic. On March 16th, 2020, the state like Odisha in India verified the first instance of COVID-19 pandemic. Initially contained inside the limits of the state capital, it has since grown to encompass the entire state, including the rural sectors and all 30 districts. The health and socioeconomic foundation of Odisha could be seriously hampered with the overall number of confirmed infection cases increases exponentially for an extended period of time (Parida and Das 2020). The first phase of the statewide shutdown in India was actioned from March 24 to May 31, 2020, with the intention of preventing the spread (Barku and Vibha 2020; Lancet 2020). The central and state governments implemented a number of multi-pronged methods and restrictive measures to stop the spread. Health systems have been largely concentrating on pandemic containment and critical care management since the start of COVID-19, which could have hampered normal preventive and curative services, including emergency care (Covid et al. 2020). Fever, cough, shortness of breath, loss of senses, chest pain and exhaustion are the main signs and symptoms of COVID-19. Numerous precautions are taken to stop the spread of viruses, including maintaining personal hygiene, routinely washing hands with soap and water, wearing face masks, and isolating oneself from social interactions. The first nationwide total lock-down was imposed by the Indian government from midnight March 24 to April 15 in an effort to break the COVID-19 transmission chain. Odisha is the first Indian state to have extended the second lock-down to April 30, 2020. By that point, the Indian government had enacted its second, third, and fourth lockdowns, with some services being relaxed, from the 16th of April 2020 to the 3rd of May 2020, the 4th of May 2020 to the 17th of May 2020, and the 18th of May 2020 to the 31st of May 2020, respectively. The critical problem facing civilization right now is how to stop the virus from spreading.

According to a government of India data (India COVID-19 Tracker 2020), Delhi has 1,07,051 instances, followed by Tamil Nadu with 1,26,581 cases and Maharashtra with 2,30,599 cases and 9667 deaths. India proclaims a national state of emergency to stem the infection's exponential spread to other nations including Italy. Due to COVID-19 the pandemic disease, migration and immigration of people provide a significant burden for all countries. The number of instances increased in the state due to the migration of workers across the nation with due approval of government of India. Odisha was the state with the least concern for COVID-19 up until May 6th, 2020, with fewer than 200 cases reported. However, the number unexpectedly increased after a large influx of migrants arrived during the third lock-down period from various hotspot areas, including Surat, Mumbai, Chennai, Kerala, West Bengal, New Delhi, and other regions of the country. By the May 18, 2020, almost 1.5 million migrants from various districts of states arrived in our state. Particularly the returnee migrants from Surat are found to have higher positive cases in the state, which increased the number of positive cases from 200 to over 800 in just one week. In this connection, Ganjam, Jajpur, Balasore, Bhadrak, Khurda, Kendrapara, Puri, Sundargarh, Cuttack, Anugul, and Mayurbhanj are hotspot districts in Odisha. Thus, if all the migrants enter into the state, it is extremely difficult to anticipate or forecast the spread of disease and how to prevent it.

Now, it is essential to construct a mathematical model to measure and forecast disease spread and control of COVID-19 for the state Odisha taking migrant inflow into account. Several researchers have developed various model such as: Chayu Yang et al. (Huang et al. 2020) implemented an SEIR mathematical model, Shilei Zao et al. (Zhao and Chen 2020) investigated the SUQC mathematical model, Rajesh Singh et al. (Singh and Adhikari 2020) suggested the SIR model, P. V. Khrapov et.al (Khrapov and Loginova 2020) emphasized a simple SIR model, Parash Ghosh et al. (Ghosh et al. 2020) investigated the federal contact rate, Kaustov Chatterjee et al. (Chatterjee et al. 2020) executed a SEIR model, R. Bhatanagra (Bhatnagar 2020) developed model on community and Kaushalendra Kumar et al. (Kumar et al. 2020) designed SIR model, Aswin Kumar Rauta et al. (Rauta et al. 2021) constructed stability analysis using mathematical modelling on influx of migrants, Santosh k Panda et al. (Panda et al. 2022) comparison the haematological and biochemical parameters of SARS-CoV-2-positive and negative neonates of COVID-19 mothers, Shreetam Behera et al. (Behera et al. 2022) investigate the impact of the influx of migrant labourers on the early spread, Singh et al. (Singh et al. 2021) make a statistical analysis.

In this paper, we have constructed a mathematical model based on Laplace Adomian Decomposition Technique (LADT) for numerical investigation of COVID-19 as infected migrants enter Odisha. We have constructed the model with quintic compartments of population namely susceptible, diagnoses, infected, quarantined and recovered. The model incorporates non-COVID-19 related deaths, COVID-19 related deaths, new births, and migration. The mathematical model contains a system of nonlinear differential equations. So, the model can only be solved approximately but not analytically. The present method is simple and provide a better solution that best fit to literature. Based on computational simulation results, it can be seen that changing some important model parameters drastically alters the dynamics of the model. The research conducted in this study is thus creative, real and original.

The paper is organized as follows: The literature study of COVID-19 of Odisha as introductory part is presented in “Introduction”. The construction of mathematical model of COVID-19 for special focus on Odisha is incorporated in “Mathematical modelling”. Existence of boundedness and positivity properties of model is handled in “Existence of boundedness and positivity”. The analysis and implementation of the method is analysed in “Analysis and implementation of the method”. Numerical experiments and results are reported in "Numerical experiments and results". The discussion is implemented in “Discussions”. The conclusions along with some remarks appear in “Conclusions”.

Mathematical modelling

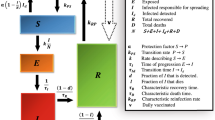
As an infectious disease is spreading, mathematical models can be implemented to tackle the situation. Here, we investigated a model where it split a fixed population into the following five groups: susceptible (\(S\)), diagnosed (\(D\)), infected (\(I\)), quarantined (\(Q\)) and recovered (\(R\)) population. \(S\) stands for the population at risk of infection or the most vulnerable group of people. Migrants who are examined at the checkpoint are indicated by \(D\). \(I\) identifies a group of people who have already infected by the disease and are capable of passing it on to people who are more susceptible to infection. Isolated population denoted as \(Q\) and \(R\) stands for the population members who have previously been infected but have since been eliminated from the infected category due to immunisation or death.

In the current scheme, the parameter description is employed as follows: \(\alpha \) is rate of contact, \(\lambda \) is rate of new born, \({\gamma }_{1}\) is the non COVID-19 death rate, \({\gamma }_{2}\) is the COVID-19 death rate, \(\rho \) is segment of Covid 19 in migrants, the rate of quarantined population due to infection is denoted by \(\mu \), the migrant population is represented by \(\sigma \) and \(\xi \) is the rate of recovered population by quarantine. The systematic presentation of the model is represented as follows:

figure a

COVID-19 quintic compartments mathematical model (Rauta et al. 2021) of Odisha is represented as follows:

$$\frac{dS}{dt}=\lambda -\alpha SI-{\gamma }_{1}S\equiv {G}_{1}$$
(1)
$$\frac{dD}{dt}=\sigma -\rho D-\left(1-\rho \right)D-{\gamma }_{1}D\equiv {G}_{2}$$
(2)
$$\frac{dI}{dt}=\alpha SI+\rho D-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\equiv {G}_{3}$$
(3)
$$\frac{dQ}{dt}=\left(1-\rho \right)D+\mu I-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\equiv {G}_{4}$$
(4)
$$\frac{dR}{dt}=\xi Q-{\gamma }_{1}R\equiv {G}_{5}$$
(5)

The initial conditions of present model are

$$S=S\left(0\right), D=D\left(0\right), I=I\left(0\right), Q=Q\left(0\right), R=R\left(0\right)$$
(6)

The values of parameters for the present model are

Parameter

Value (Rauta et al. 2021)

\(\alpha \)

\(0.045\)

\(\lambda \)

\(0.000054\)

\(\sigma \)

\(0.0089\)

\(\mu \)

\(0.047619\)

\(\rho \)

\(0.003\)

\(\xi \)

\(0.047619\)

\({\gamma }_{1}\)

\(0.000023\)

\({\gamma }_{2}\)

\(0.000083\)

Odisha is the only state in India have chosen a quarantine period of \(28\) days as opposed to \(14\) days, when the virus spread owing to immigrant entrance after the end of the second lockdown in India. Approximately \(4.5\) crore people live in the state as of right now. More than five lakh migrants have been registered for return to the state (https://covid19.odisha.gov.in) while being held in government custody. We have established the initial conditions for each department as per the directive (https://osdma.org; https://nrhmorissa.gov.in; https://ndma.org). The initial condition for diagnosed population in migrant individuals is therefore considered to be\(D\left(0\right)=600000\), whereas the initial conditions for the other populations are\(S\left(0\right)=45000000\),\(I\left(0\right)=695\),\(Q\left(0\right)=600052\),\(R\left(0\right)=220\). The initial values are scaled to unity for simplicity in plotting the graphs as\(S\left(0\right)=1\),\(D\left(0\right)=0.013333\),\(I\left(0\right)=0.00013\),\(Q\left(0\right)=0.013333\),\(R\left(0\right)=0.00061555\). The parameters are measured on a daily basis, or per unit of time i.e. per day. Odisha's contact rate \(\alpha \) ranges from \(0.01\) to\(0.13\). Since government imposes a \(21\)-day quarantine, therefore\(\xi =\frac{1}{21}=0.047619\). Given that the state's crude birth and mortality rates are respectively \(20\) and \(8.3\) per \(1000\) people. So,\(\lambda =\left(\frac{20}{1000}\right)/365=0.000054\),\({\gamma }_{1}=\left(\frac{3.8}{1000}\right)/365=0.000022\). Out of \(876\) confirmed infected cases over a \(55\)-day period, it has once again been reported that \(4\) deaths attributable to COVID-19 occurred; as a result, the disease death rate per day is\({\gamma }_{2}=\left(\frac{4}{876}\right)/55=0.000083\). It is anticipated that there are \(\sigma =10000000\) migrants overall and percentage of segment of infected migrant is\(\rho =0.0034\).

Existence of boundedness and positivity

The total population can be represented by

$$N=S+D+I+R+Q$$
$$\frac{dN}{dt}=\frac{dS}{dt}+\frac{dD}{dt}+\frac{dI}{dt}+\frac{dQ}{dt}+\frac{dR}{dt}$$
$$\frac{dN}{dt}=\lambda +\sigma -{\gamma }_{1}N-{\gamma }_{2}Q-{\gamma }_{2}I$$

For \({\gamma }_{2}=0\) i.e., if there is no diseases, \(\frac{dN}{dt}=\lambda +\sigma -{\gamma }_{1}N\).

When, \(\lambda \to \infty \) then \(N\to \frac{\lambda +\sigma }{{\gamma }_{1}}\)

The mathematical model for this purpose is imposed as,

$$\Omega =\left\{\left(S,D,I,R,Q\right)\in {R}_{+}^{5} :S+D+I+R+Q\le \left(\sigma +\lambda \right){{\gamma }_{1}}^{-1}\right\}$$

Analysis and implementation of the method

Now we, implement LADT to COVID-19 model in the actual scale.

Step 1

The nonlinear expression can be represented by single variable in the Covid-19 model as follows;

$$N=SI$$
(7)

The linear variables are expressed by infinite series as follows:

$$S=\sum_{n=0}^{\infty }{S}_{n}, D=\sum_{n=0}^{\infty }{D}_{n}, I=\sum_{n=0}^{\infty }{I}_{n} , Q=\sum_{n=0}^{\infty }{Q}_{n} , R=\sum_{n=0}^{\infty }{R}_{n}$$
(8)

Further, the nonlinear variable is expressed by infinite series as follows:

$$SI=\sum_{n=0}^{\infty }{A}_{n}\left(S,I\right)$$
(9)

Step 2

The nonlinear terms in Eq. (9) is tackled with the Adomian Decomposition Technique (ADT). The Adomian decomposition technique with nonlinear variables are represented in Eq. (10) as follows:

$${A}_{n}\left(S,I\right)=\frac{1}{k!}\frac{{d}^{k}}{d{\mu }^{k}}\left[\sum_{i=0}^{\infty }{\mu }^{i}{S}_{i}\sum_{i=0}^{\infty }{\mu }^{i}{I}_{i}\right] at \mu =0$$
(10)

In particular some terms are,

$${A}_{0}\left(S,I\right)={S}_{0}\left(t\right){I}_{0}\left(t\right)$$
$${A}_{1}\left(I,S\right)={S}_{0}\left(t\right){I}_{1}\left(t\right)+{S}_{1}\left(t\right){I}_{0}\left(t\right)$$

Proceeding in this manner, we can obtain more terms.

Step 3

In this step, we will employ the Laplace transform to the model Eqs. (1) to (5). Let us denote the vector dynamical variables of model as below,

$$\overrightarrow{U}=\left(S,D,I,Q,R\right)$$
$$\frac{d\overrightarrow{U}}{dt}=\overrightarrow{G}\left(\overrightarrow{U}\right)$$

where, \(\overrightarrow{G}=\left({G}_{1},{G}_{2},{G}_{3},{G}_{4},{G}_{5}\right)\) represents the vector field of the model Eqs. (1) to (5).

The Laplace transformation is now applied to both sides of the previous model.

$$\mathcal{L}\left(\frac{d\overrightarrow{U}}{dt}\right)=\mathcal{L}\left(\overrightarrow{G}\left(\overrightarrow{U}\right)\right)$$
(11)

The properties of derivative of Laplace transform is employed

$$s\mathcal{L}\left(\overrightarrow{U}\right)-\overrightarrow{U}\left(0\right)=\mathcal{L}\left(\overrightarrow{G}\left(\overrightarrow{U}\right)\right)$$
$$\mathcal{L}\left(\overrightarrow{U}\right)=\frac{1}{s}\overrightarrow{U}\left(0\right)+\frac{1}{s}\mathcal{L}\left(\overrightarrow{G}\left(\overrightarrow{U}\right)\right)$$
(12)

Then the model becomes,

$$\mathcal{L}\left[\sum_{n=0}^{\infty }{S}_{n}\left(t\right)\right]=\frac{1}{s}S\left(0\right)+\frac{1}{s}\mathcal{L}\left(\lambda \right)-\frac{1}{s}\alpha \mathcal{L}\left\{\sum_{n=0}^{\infty }{A}_{n}\left(S,I\right)\right\}-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left\{\sum_{n=0}^{\infty }{S}_{n}\left(t\right)\right\}$$
(13)
$$\mathcal{L}\left[\sum_{n=0}^{\infty }{D}_{n}\left(t\right)\right]=\frac{1}{s}D\left(0\right)+\frac{1}{s}\mathcal{L}\left(\sigma \right)-\frac{1}{s}\rho \mathcal{L}\left\{\sum_{n=0}^{\infty }{D}_{n}\left(t\right)\right\}-\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left\{\sum_{n=0}^{\infty }{D}_{n}\left(t\right)\right\}-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left\{\sum_{n=0}^{\infty }{D}_{n}\left(t\right)\right\}$$
(14)
$$\mathcal{L}\left[\sum_{n=0}^{\infty }{I}_{n}\left(t\right)\right]=\frac{1}{s}I\left(0\right)+\frac{1}{s}\alpha \mathcal{L}\left\{\sum_{n=0}^{\infty }{A}_{n}\left(S,I\right)\right\}+\frac{1}{s}\rho \mathcal{L}\left\{\sum_{n=0}^{\infty }{D}_{n}\left(t\right)\right\}-\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left\{\sum_{n=0}^{\infty }{I}_{n}\left(t\right)\right\}$$
(15)
$$\mathcal{L}\left[\sum_{n=0}^{\infty }{Q}_{n}\left(t\right)\right]=\frac{1}{s}Q\left(0\right)+\frac{1}{s}\mu \mathcal{L}\left\{\sum_{n=0}^{\infty }{I}_{n}\left(t\right)\right\}+\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left\{\sum_{n=0}^{\infty }{D}_{n}\left(t\right)\right\}-\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left\{\sum_{n=0}^{\infty }{Q}_{n}\left(t\right)\right\}$$
(16)
$$\mathcal{L}\left[\sum_{n=0}^{\infty }{R}_{n}\left(t\right)\right]=\frac{1}{s}R\left(0\right)+\frac{1}{s}\xi \mathcal{L}\left\{\sum_{n=0}^{\infty }{Q}_{n}\left(t\right)\right\}-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left\{\sum_{n=0}^{\infty }{R}_{n}\left(t\right)\right\}$$
(17)

Step 4

Comparing the terms on both side of model (13) to (17), we obtained

\(\mathcal{L}\left[{S}_{0}\left(t\right)\right]=\frac{1}{s}S\left(0\right)\), \(\mathcal{L}\left[{D}_{0}\left(t\right)\right]=\frac{1}{s}D\left(0\right)\), \(\mathcal{L}\left[{I}_{0}\left(t\right)\right]=\frac{1}{s}I\left(0\right)\), \(\mathcal{L}\left[Q\left(t\right)\right]=\frac{1}{s}Q\left(0\right)\) and \(\mathcal{L}\left[{R}_{0}\left(t\right)\right]=\frac{1}{s}R\left(0\right)\)

$$\mathcal{L}\left[{S}_{1}\left(t\right)\right]=\frac{1}{s}\mathcal{L}\left[\lambda \right]-\frac{1}{s}\alpha \mathcal{L}\left[{A}_{0}\left(S,I\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{S}_{0}\left(t\right)\right]$$
$$\mathcal{L}\left[{D}_{1}\left(t\right)\right]=\frac{1}{s}\mathcal{L}\left(\sigma \right)-\frac{1}{s}\rho \mathcal{L}\left[{D}_{0}\left(t\right)\right]-\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{0}\left(t\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{D}_{0}\left(t\right)\right]$$
$$\mathcal{L}\left[{I}_{1}\left(t\right)\right]=\frac{1}{s}\alpha \mathcal{L}\left[{A}_{0}\left(S,I\right)\right]+\frac{1}{s}\rho \mathcal{L}\left[{D}_{0}\left(t\right)\right]-\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{I}_{0}\left(t\right)\right]$$
$$\mathcal{L}\left[{Q}_{1}\left(t\right)\right]=\frac{1}{s}\mu \mathcal{L}\left[{I}_{0}\left(t\right)\right]+\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{0}\left(t\right)\right]-\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{Q}_{0}\left(t\right)\right]$$
$$\mathcal{L}\left[{R}_{1}\left(t\right)\right]=\frac{1}{s}\xi \mathcal{L}\left[{Q}_{0}\left(t\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{R}_{0}\left(t\right)\right]$$

Similarly,

$$\mathcal{L}\left[{S}_{2}\left(t\right)\right]=\frac{1}{s}\alpha \mathcal{L}\left[{A}_{1}\left(S,I\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{S}_{1}\left(t\right)\right]$$
$$\mathcal{L}\left[{D}_{2}\left(t\right)\right]=-\frac{1}{s}\rho \mathcal{L}\left[{D}_{1}\left(t\right)\right]-\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{1}\left(t\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{D}_{1}\left(t\right)\right]$$
$$\mathcal{L}\left[{I}_{2}\left(t\right)\right]=\frac{1}{s}\alpha \mathcal{L}\left[{A}_{1}\left(S,I\right)\right]+\frac{1}{s}\rho \mathcal{L}\left[{D}_{1}\left(t\right)\right]-\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{I}_{1}\left(t\right)\right]$$
$$\mathcal{L}\left[{Q}_{2}\left(t\right)\right]=\frac{1}{s}\mu \mathcal{L}\left[{I}_{1}\left(t\right)\right]+\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{1}\left(t\right)\right]-\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{Q}_{1}\left(t\right)\right]$$
$$\mathcal{L}\left[{R}_{2}\left(t\right)\right]=\frac{1}{s}\xi \mathcal{L}\left[{Q}_{1}\left(t\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{R}_{1}\left(t\right)\right]$$
$$\dots \dots $$
$$\mathcal{L}\left[{S}_{n+1}\left(t\right)\right]=\frac{1}{s}\alpha \mathcal{L}\left[{A}_{n}\left(S,I\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{S}_{n}\left(t\right)\right]$$
$$\mathcal{L}\left[{D}_{n+1}\left(t\right)\right]=-\frac{1}{s}\rho \mathcal{L}\left[{D}_{n}\left(t\right)\right]-\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{n}\left(t\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{D}_{n}\left(t\right)\right]$$
$$\mathcal{L}\left[{I}_{n+1}\left(t\right)\right]=\frac{1}{s}\alpha \mathcal{L}\left[{A}_{n}\left(S,I\right)\right]+\frac{1}{s}\rho \mathcal{L}\left[{D}_{n}\left(t\right)\right]-\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{I}_{n}\left(t\right)\right]$$
$$\mathcal{L}\left[{Q}_{n+1}\left(t\right)\right]=\frac{1}{s}\mu \mathcal{L}\left[{I}_{n}\left(t\right)\right]+\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{n}\left(t\right)\right]-\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{Q}_{n}\left(t\right)\right]$$
$$\mathcal{L}\left[{R}_{n+1}\left(t\right)\right]=\frac{1}{s}\xi \mathcal{L}\left[{Q}_{n}\left(t\right)\right]-\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{R}_{n}\left(t\right)\right]$$

Step 5

Now applying the inverse Laplace transform on both sides

$${S}_{0}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}S\left(0\right)\right]=S\left(0\right)=1$$

Similarly,

$${D}_{0}\left(t\right)=D\left(0\right)=0.013333$$
$${I}_{0}\left(t\right)=I\left(0\right)=0.000013$$
$${Q}_{0}\left(t\right)=Q\left(0\right)=0.0133$$
$${R}_{0}\left(t\right)=R\left(0\right)=0.0000061556$$
$${S}_{1}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\mathcal{L}\left[\lambda \right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{A}_{0}\left(S,I\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{S}_{0}\left(t\right)\right]\right]$$
$$={\mathcal{L}}^{-1}\left[\frac{1}{s}\mathcal{L}\left[\lambda \right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{S}_{0}\left(t\right){I}_{0}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{S}_{0}\left(t\right)\right]\right]$$
$$=\left[\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right]t$$
$${D}_{1}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\mathcal{L}\left(\sigma \right)\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\rho \mathcal{L}\left[{D}_{0}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{0}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{D}_{0}\left(t\right)\right]\right]$$
$$=\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t$$
$${I}_{1}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{A}_{0}\left(S,I\right)\right]\right]+{\mathcal{L}}^{-1}\left[\rho \mathcal{L}\left[{D}_{0}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{I}_{0}\left(t\right)\right]\right]$$
$$=\left[\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right]t$$
$${Q}_{1}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\mu \mathcal{L}\left[{I}_{0}\left(t\right)\right]\right]+{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{0}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{Q}_{0}\left(t\right)\right]\right]$$
$$=\left[\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right]t$$
$${R}_{1}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\xi \mathcal{L}\left[{Q}_{0}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{R}_{0}\left(t\right)\right]\right]$$
$$=\left[\xi Q\left(0\right)-{\gamma }_{1}R\left(0\right)\right]t$$
$${S}_{2}\left(t\right)=-{\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{A}_{1}\left(S,I\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{S}_{1}\left(t\right)\right]\right]$$
$$=-{\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{S}_{0}\left(t\right){I}_{1}\left(t\right)+{I}_{0}\left(t\right){S}_{1}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[\left[\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right]t\right]\right]$$
$$=\left[-\alpha S\left(0\right)\left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}-\alpha I\left(0\right)\left\{\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right\}-{\gamma }_{1}\left\{\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right\}\right]\frac{{t}^{2}}{2}$$
$${D}_{2}\left(t\right)=-{\mathcal{L}}^{-1}\left[\frac{1}{s}\rho \mathcal{L}\left[{D}_{1}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{1}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{D}_{1}\left(t\right)\right]\right]$$
$$=-{\mathcal{L}}^{-1}\left[\frac{1}{s}\rho \mathcal{L}\left[\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t\right]\right]$$
$$=\left[\rho \left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-\left(1-\rho \right)\left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-{\gamma }_{1}\left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}\right]\frac{{t}^{2}}{2}$$
$${I}_{2}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{A}_{1}\left(S,I\right)\right]\right]+{\mathcal{L}}^{-1}\left[\rho \mathcal{L}\left[{D}_{1}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{I}_{1}\left(t\right)\right]\right]$$
$${=\mathcal{L}}^{-1}\left[\frac{1}{s}\alpha \mathcal{L}\left[{S}_{0}\left(t\right){I}_{1}\left(t\right)+{I}_{0}\left(t\right){S}_{1}\left(t\right)\right]\right]+{\mathcal{L}}^{-1}\left[\rho \mathcal{L}\left[\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[\left[\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right]t\right]\right]$$
$$=\left[\alpha S\left(0\right)\left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}-\alpha I\left(0\right)\left\{\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right\}+\rho \left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}\right]\frac{{t}^{2}}{2}$$
$${Q}_{2}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\mu \mathcal{L}\left[{I}_{1}\left(t\right)\right]\right]+{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[{D}_{1}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[{Q}_{1}\left(t\right)\right]\right]$$
$$={\mathcal{L}}^{-1}\left[\frac{1}{s}\mu \mathcal{L}\left[\left[\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right]t\right]\right]+{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(1-\rho \right)\mathcal{L}\left[\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\mathcal{L}\left[\left[\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right]t\right]\right]$$
$$=\left[\mu \left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}+\left(1-\rho \right)\left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\left\{\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right\}\right]\frac{{t}^{2}}{2}$$
$${R}_{2}\left(t\right)={\mathcal{L}}^{-1}\left[\frac{1}{s}\xi \mathcal{L}\left[{Q}_{1}\left(t\right)\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[{R}_{1}\left(t\right)\right]\right]$$
$$={\mathcal{L}}^{-1}\left[\frac{1}{s}\xi \mathcal{L}\left[\left[\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right]t\right]\right]-{\mathcal{L}}^{-1}\left[\frac{1}{s}{\gamma }_{1}\mathcal{L}\left[\left[\xi Q\left(0\right)-{\gamma }_{1}R\left(0\right)\right]t\right]\right]$$
$$=\left[\xi \left\{\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right\}-{\gamma }_{1}\left\{\xi Q\left(0\right)-{\gamma }_{1}R\left(0\right)\right\}\right]\frac{{t}^{2}}{2}$$

Continuing in this manner, we obtain the required solution as follows:

$$S=\sum_{n=0}^{\infty }{S}_{n}=S\left(0\right)+\left[\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right]t+\left[-\alpha S\left(0\right)\left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}-\alpha I\left(0\right)\left\{\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right\}-{\gamma }_{1}\left\{\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right\}\right]\frac{{t}^{2}}{2}+\dots $$
$$D=\sum_{n=0}^{\infty }{D}_{n}=D\left(0\right)+\left[\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right]t+\left[\rho \left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-\left(1-\rho \right)\left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-{\gamma }_{1}\left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}\right]\frac{{t}^{2}}{2}+\dots $$
$$I=\sum_{n=0}^{\infty }{I}_{n}=I\left(0\right)+\left[\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right]t+\left[\alpha S\left(0\right)\left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}-\alpha I\left(0\right)\left\{\lambda -\alpha S\left(0\right)I\left(0\right)-{\gamma }_{1}S\left(0\right)\right\}+\rho \left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)\left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}\right]\frac{{t}^{2}}{2}+\dots $$
$$Q=\sum_{n=0}^{\infty }{Q}_{n}=Q\left(0\right)+\left[\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right]t+\left[\mu \left\{\alpha S\left(0\right)I\left(0\right)+\rho D\left(0\right)-\left(\mu +{\gamma }_{1}+{\gamma }_{2}\right)I\left(0\right)\right\}+\left(1-\rho \right)\left\{\sigma -\rho D\left(0\right)-\left(1-\rho \right)D\left(0\right)-{\gamma }_{1}D\left(0\right)\right\}-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)\left\{\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right\}\right]\frac{{t}^{2}}{2}+\dots $$
$$R=\sum_{n=0}^{\infty }{R}_{n}=R\left(0\right)+\left[\xi Q\left(0\right)-{\gamma }_{1}R\left(0\right)\right]t+\left[\xi \left\{\mu I\left(0\right)+\left(1-\rho \right)D\left(0\right)-\left(\xi +{\gamma }_{1}+{\gamma }_{2}\right)Q\left(0\right)\right\}-{\gamma }_{1}\left\{\xi Q\left(0\right)-{\gamma }_{1}R\left(0\right)\right\}\right]\frac{{t}^{2}}{2}+\dots $$

Numerical experiments and results

In this section the approximate solution for each compartment population of migrant is reported in tables (Tables 1, 2, 3, 4, 5) and plotted in 2D figures.

Table 1 Approximate study of susceptible population
Full size table
Table 2 Numerical study of diagnosed population
Full size table
Table 3 Estimate study of infected population
Full size table
Table 4 Numerical study of quarantined population
Full size table
Table 5 Approximate study of recovered population
Full size table

The initial conditions \(S\left(0\right)=1, I\left(0\right)=0.000013, D\left(0\right)=0.013333\) and the parameters \(\lambda =0.000054, {\gamma }_{1}=0.000023, {\gamma }_{2}=0.000083, \rho =0.003, \mu =0.047619\) are employed in Fig. 1.

Fig. 1
figure 1

Approximate study of susceptible population

Full size image

The initial condition \(D\left(0\right)=0.013333\) and the two parameters \(\sigma =0.0089\) and \({\gamma }_{1}=0.000023\) are applied in Fig. 2.

Fig. 2
figure 2

Approximate study of diagnosed population

Full size image

The initial conditions \(S\left(0\right)=1, I\left(0\right)=0.000013, D\left(0\right)=0.013333\) and parameters \(\lambda =0.000054, {\gamma }_{2}=0.000083, \rho =0.003, \mu =0.047619, \sigma =0.0089, \alpha =0.045\) are used in Fig. 3.

Fig. 3
figure 3

Approximate study of infected population

Full size image

The initial conditions \(S\left(0\right)=1, I\left(0\right)=0.000013, D\left(0\right)=0.013333, Q\left(0\right)=0.0133\) and parameters \({\gamma }_{1}=0.000023, \rho =0.003, \mu =0.047619, \alpha =0.045, \xi =0.047619\) are employed in Fig. 4.

Fig. 4
figure 4

Approximate study of quarantined population

Full size image

The initial conditions \(I\left(0\right)=0.000013, Q\left(0\right)=0.0133, R\left(0\right)=0.0000061556\) and the parameters \({\gamma }_{1}=0.000023, {\gamma }_{2}=0.000083, \rho =0.003, \mu =0.047619\) are used in Fig. 5.

Fig. 5
figure 5

Approximate study of recovered population

Full size image

Discussions

In this paper we introduce a procedure to evaluate and control the infectious disease of COVID-19 through the SDIQR pandemic model which consists of five compartments namely susceptible (\(S\)), diagnosed (\(D\)), infected (\(I\)), quarantined (\(Q\)) and recovered (\(R\)) population. We explore the model by the technique combining Laplace transform and Adomian decomposition and implement all the population rate with respect to the time level on the basis of increasing and decreasing parameter rate through two-dimensional plot. To validate the model, the numerical simulations for different population rate are plotted with suitable parameters. Figure 1 depicts the variations in susceptible population rate \(\left(S\right)\) with the increasing time (in one month and that one month partitioned into nine levels and the level increases per 3.3 days) with different rate of contact \(\alpha \). Figure 2 is the variations in rate of Diagnosed population \(\left(D\right)\) with respect to the \(\rho \) (the proportion of migrants detected COVID-19) with increasing time level. The Fig. 3 portray the fluctuation of the infected population rate \(\left(I\right)\) with increased \({\gamma }_{1}\) (non COVID-19 death rate). Figure 4 is the discrepancy in rate of quarantined population \(\left(Q\right)\) for isolated individuals with respect to the \({\gamma }_{2}\) (the death rate due to COVID-19). The variations in recovered population \(\left(R\right)\) with respect to the \(\xi \) with incremented time level is depicted in Fig. 5.

Conclusions

In this study, the time series behaviour is obtained to investigate changes in susceptible, diagnosed, infected, quarantined and recovered compartments with increase and fall of parameter values. Here, we explored the model by the Laplace Adomian decomposition technique and analytical power series to the SDIQR Covid-19 model to estimate the solution profiles of the dynamical variables. Each term in the series is derived from a polynomial produced by the power series expansion of an analytical function. The correct screening of immigrants, additional testing of those who are vulnerable, and contact tracing of infectives are proposed as necessary measures in addition to the quarantine policy and management technique. The approximate solution which strongly supports our method in each case is depicted in two dimensional profile with required initial conditions and various parameters. Therefore, the mathematical model developed during this work can be adopted for testing of disease behaviour in Odisha and further studies may be extended across the world.