Electroosmotic flow of pseudoplastic nanoliquids via peristaltic pum**

Abstract

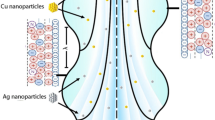
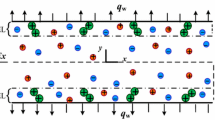
The study of electroosmotic flow of biorheological fluids has been employed in the advancement of diversified biomicrofluidics systems. To explore more in this field, a mathematical model is developed to investigate the electroosmotic flow of pseudoplastic aqueous nanoliquids in microchannel. A tangent hyperbolic fluid model is employed to describe the rheological behavior of the pseudoplastic fluid. Here, analytical solutions for potential distribution, temperature and nanoparticle fraction are derived and perturbation solution for stream function, pressure gradient and volumetric flow rate are obtained. The convective boundary condition is applied on the channel walls. The authentic assumptions of Debye–Hückel linearization, long wavelength and small Reynold’s number are employed in the dimensional conservative equations. The influences of various emerging parameters are graphically computed for axial velocity, pressure gradient, thermal temperature, nanoparticle volume fraction, skin friction coefficient and Nusselt profiles. To observe the thermal radiation effects, a thermal radiative flux model is also deployed. It is noticed that the heat transfer Biot number increases with increasing thermal temperature; however, a reversed behavior is reported for the nanoparticle volume fraction. Therefore, the present model does not only provide a deep theoretical insight to interpret the electroosmotic flow systems, but it will also be applicable in designing the emerging tool for biomicrofluidic devices/systems under peristalsis mechanisms.

Appendix

The following constants are utilized in the solution parts.

$$\gamma_{1} = \frac{{ - a_{2} + \sqrt {a_{2}^{2} - 4a_{3} } }}{2},\gamma_{2} = \frac{{ - a_{2} - \sqrt {a_{2}^{2} - 4a_{3} } }}{2},$$

$$A = \frac{{\cosh \left( {h\kappa } \right) + \sinh \left( {h\kappa } \right)}}{{2\sinh \left( {2h\kappa } \right)}},B = - \frac{{\cosh \left( {h\kappa } \right) - \sinh \left( {h\kappa } \right)}}{{2\sinh \left( {2h\kappa } \right)}},$$

$$C = \frac{{\left( {Bh - D\left( {Bh + \gamma_{2} } \right)\left( {\cosh (h\gamma_{2} ) + \sinh (h\gamma_{2} )} \right)} \right)\left( {\cosh (h\gamma_{1} ) - \sinh (h\gamma_{1} )} \right)}}{{Bh + \gamma_{1} }},$$

$$D = \frac{{Bh\left( {Bh - \gamma_{1} } \right)}}{{\left( \begin{aligned} \left( {Bh + \gamma_{2} } \right)\left( {\cosh (h(\gamma_{1} - \gamma_{2} )) - \sinh (h(\gamma_{1} - \gamma_{2} ))} \right) \hfill \\ - \left( {Bh - \gamma_{1} } \right)\left( {Bh - \gamma_{2} } \right)\left( {\cosh (h(\gamma_{1} - \gamma_{2} )) + \sinh (h(\gamma_{1} - \gamma_{2} ))} \right) \hfill \\ \end{aligned} \right)}},$$

$$E = \frac{1}{2} + \frac{{Nt\left( {C\cosh (\gamma_{1} h) + D\cosh (\gamma_{2} h)} \right)}}{Nb},$$

$$F = \frac{E}{h} - \frac{{CNt\left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right) - DNt\left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right)}}{hNb},$$

$$a_{1} = \frac{{Bh\left( {Nb + Nt} \right)}}{{2Nb\left( {hBh + 1} \right)}},a_{2} = \frac{{\Pr Bh\left( {Nb + Nt} \right)}}{{2\left( {hBh + 1} \right)\left( {\Pr Rn + 1} \right)}},a_{3} = \frac{\Pr \beta }{\Pr Rn + 1},a_{4} = \frac{AUhs}{{\kappa \left( {n - 1} \right)}},a_{5} = - \frac{BUhs}{{\kappa \left( {n - 1} \right)}},$$

$$a_{6} = \frac{CGr}{{\gamma_{1}^{3} \left( {n - 1} \right)}} - \frac{BrCNt}{{Nb\gamma_{1}^{3} \left( {n - 1} \right)}},a_{7} = \frac{DGr}{{\gamma_{2}^{3} \left( {n - 1} \right)}} - \frac{BrDNt}{{Nb\gamma_{2}^{3} \left( {n - 1} \right)}},a_{8} = \frac{Br}{{24\left( {n - 1} \right)}},$$

$$a_{9} = \frac{{F_{0} }}{2} - a_{10} h - a_{11} h^{2} - a_{12} h^{3} - a_{13} ,a_{10} = - 1 - 2a_{11} h - 3a_{12} h^{2} - a_{15} ,a_{11} = \frac{{a_{16} - a_{15} }}{4h},$$

$$a_{12} = \frac{{a_{13} - a_{14} - 2ha_{15} - 4h^{2} a_{11} - F_{0} - 2h}}{{4h^{3} }},$$

$$\begin{aligned} a_{13} & = a_{6} \left( {\cosh (\gamma_{1} h) + \sinh (\gamma_{1} h)} \right) + a_{7} \left( {\cosh (\gamma_{2} h) + \sinh (\gamma_{2} h)} \right) \\ & \quad + \,a_{4} \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) + a_{8} h^{4} + a_{5} \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right), \\ \end{aligned}$$

$$\begin{aligned} a_{14} & = a_{6} \left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right) + a_{7} \left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right) \\ & \quad + \,a_{5} \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) + a_{8} h^{4} + a_{4} \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right), \\ \end{aligned}$$

$$\begin{aligned} a_{15} = a_{6} \gamma_{1} \left( {\cosh (\gamma_{1} h) + \sinh (\gamma_{1} h)} \right) + a_{7} \gamma_{2} \left( {\cosh (\gamma_{2} h) + \sinh (\gamma_{2} h)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, - a_{5} \kappa \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right) + 4a_{8} h^{3} + a_{4} \kappa \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right), \hfill \\ \end{aligned}$$

$$\begin{aligned} a_{16} = a_{6} \gamma_{1} \left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right) + a_{7} \gamma_{2} \left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, - a_{5} \kappa \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) - 4a_{8} h^{3} + a_{4} \kappa \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right), \hfill \\ \end{aligned}$$

$$a_{17} = \frac{{n\left( {72a_{12}^{2} + 96a_{11} a_{8} } \right)}}{{24\left( {n - 1} \right)}},a_{18} = \frac{{864na_{12} a_{8} }}{120(n - 1)},a_{19} = \frac{{1328na_{8}^{2} }}{720(n - 1)},a_{20} = \frac{{n\kappa^{2} a_{4}^{2} }}{4(n - 1)},a_{21} = \frac{{n\kappa^{2} a_{5}^{2} }}{4(n - 1)},$$

$$a_{22} = \frac{{na_{6}^{2} }}{{4\gamma_{1}^{2} (n - 1)}},a_{23} = \frac{{na_{7}^{2} }}{{4\gamma_{2}^{2} (n - 1)}},a_{24} = \frac{{n\left( {4a_{11} a_{4} \kappa^{4} + 24a_{12} a_{9} \kappa^{3} + 48a_{8} a_{4} \kappa^{2} } \right)}}{{\kappa^{4} (n - 1)}},$$

$$a_{25} = \frac{{n\left( {4a_{11} a_{5} \kappa^{4} + 24a_{12} a_{5} \kappa^{3} + 48a_{8} a_{5} \kappa^{2} } \right)}}{{\kappa^{4} (n - 1)}},a_{26} = \frac{{n\left( {2a_{11} a_{6} \gamma_{1}^{4} + 24a_{12} a_{6} \gamma_{1}^{3} + 48a_{8} a_{6} \gamma_{1}^{2} } \right)}}{{\gamma_{1}^{4} (n - 1)}},$$

$$a_{27} = \frac{{n\left( {2a_{11} a_{7} \gamma_{2}^{4} + 24a_{12} a_{7} \gamma_{2}^{3} + 48a_{8} a_{7} \gamma_{2}^{2} } \right)}}{{\gamma_{2}^{4} (n - 1)}},a_{28} = \frac{{n\left( {12a_{12} a_{4} \kappa + 96a_{4} a_{8} } \right)}}{{\kappa^{2} (n - 1)}},$$

$$a_{29} = \frac{{n\left( {12a_{12} a_{5} \kappa - 96a_{5} a_{8} } \right)}}{{\kappa^{2} (n - 1)}},a_{30} = \frac{{n\left( {12a_{12} a_{6} \gamma_{1} + 96a_{6} a_{8} } \right)}}{{\gamma_{1}^{2} (n - 1)}},a_{31} = \frac{{n\left( {12a_{12} a_{7} \gamma_{2} + 96a_{7} a_{8} } \right)}}{{\gamma_{2}^{2} (n - 1)}},$$

$$a_{32} = \frac{{24na_{8} a_{4} }}{{\kappa^{2} (n - 1)}},a_{33} = \frac{{24na_{8} a_{5} }}{{\kappa^{2} (n - 1)}},a_{34} = \frac{{24na_{8} a_{6} }}{{\gamma_{1}^{2} (n - 1)}},a_{35} = \frac{{24na_{8} a_{7} }}{{\gamma_{2}^{2} (n - 1)}},a_{36} = \frac{{2na_{4} a_{6} \kappa^{2} \gamma_{1}^{2} }}{{(\kappa + \gamma_{1} )^{2} (n - 1)}},$$

$$a_{37} = \frac{{2na_{5} a_{6} \kappa^{2} \gamma_{1}^{2} }}{{(\kappa - \gamma_{1} )^{2} (n - 1)}},a_{38} = \frac{{2na_{5} a_{7} \kappa^{2} \gamma_{2}^{2} }}{{(\kappa - \gamma_{2} )^{2} (n - 1)}},a_{39} = \frac{{2na_{6} a_{7} \gamma_{2}^{2} \gamma_{1}^{2} }}{{(\gamma_{1} + \gamma_{2} )^{2} (n - 1)}},a_{40} = \frac{{2na_{4} a_{7} \gamma_{2}^{2} \kappa^{2} }}{{(\kappa + \gamma_{2} )^{2} (n - 1)}},$$

$$a_{41} = \frac{{F_{1} }}{2} - a_{42} h - a_{43} h^{2} - a_{44} h^{3} - a_{45} ,a_{42} = - 2a_{43} h - 3a_{44} h^{2} - a_{47} ,a_{43} = \frac{{a_{48} - a_{47} }}{4h},$$

$$a_{44} = \frac{{a_{45} - a_{46} - 2ha_{47} - 4h^{2} a_{43} - F_{1} }}{{4h^{3} }},$$

$$\begin{aligned} a_{45} & = a_{17} h^{4} + a_{18} h^{5} + a_{19} h^{6} + a_{20} \left( {\cosh (2\kappa h) + \sinh (2\kappa h)} \right) \\ & \quad + \,a_{21} \left( {\cosh (2\kappa h) - \sinh (2\kappa h)} \right) + a_{22} \left( {\cosh (2\gamma_{1} h) + \sinh (2\gamma_{1} h)} \right)\, + a_{23} \left( {\cosh (2\gamma_{2} h) + \sinh (2\gamma_{2} h)} \right) \\ & \quad + \,a_{24} \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) + a_{25} \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right) + a_{26} \left( {\cosh (\gamma_{1} h) + \sinh (\gamma_{1} h)} \right) \\ & \quad + \,a_{27} \left( {\cosh (\gamma_{2} h) + \sinh (\gamma_{2} h)} \right) + a_{28} \left( {\kappa h - 4} \right)\left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) \\ & \quad + \,a_{29} \left( {\kappa h + 4} \right)\left( {\cosh (\kappa h) - \sinh (\kappa h)} \right) + a_{30} \left( {\gamma_{1} h - 4} \right)\left( {\cosh (\gamma_{1} h) + \sinh (\gamma_{1} h)} \right) \\ & \quad + \,a_{31} \left( {\gamma_{2} h - 4} \right)\left( {\cosh (\gamma_{2} h) + \sinh (\gamma_{2} h)} \right) + a_{32} \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right)\left( {\kappa^{2} h^{2} - 8\kappa h + 12} \right) \\ & \quad + \,a_{33} \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right)\left( {\kappa^{2} h^{2} + 8\kappa h + 12} \right) + a_{34} \left( {\cosh (\gamma_{1} h) + \sinh (\gamma_{1} h)} \right)\left( {\gamma_{1}^{2} h^{2} - 8\gamma_{1} h + 12} \right) \\ & \quad + \,a_{35} \left( {\cosh (\gamma_{2} h) + \sinh (\gamma_{2} h)} \right)\left( {\gamma_{2}^{2} h^{2} - 8\gamma_{2} h + 12} \right) + a_{36} \left( {\cosh ((\gamma_{1} + \kappa )h) + \sinh ((\gamma_{1} + \kappa )h)} \right) \\ & \quad + \,a_{37} \left( {\cosh ((\gamma_{1} - \kappa )h) + \sinh ((\gamma_{1} - \kappa )h)} \right) + a_{38} \left( {\cosh ((\gamma_{2} - \kappa )h) + \sinh ((\gamma_{2} - \kappa )h)} \right) \\ & \quad + \,a_{39} \left( {\cosh ((\gamma_{1} + \gamma_{2} )h) + \sinh ((\gamma_{1} + \gamma_{2} )h)} \right) + a_{40} \left( {\cosh ((\gamma_{2} + \kappa )h) + \sinh ((\gamma_{2} + \kappa )h)} \right), \\ \end{aligned}$$

$$\begin{aligned} a_{46} & = a_{17} h^{4} - a_{18} h^{5} + a_{19} h^{6} + \,a_{20} \left( {\cosh (2\kappa h) - \sinh (2\kappa h)} \right) + a_{21} \left( {\cosh (2\kappa h) + \sinh (2\kappa h)} \right) \\ & \quad + \,a_{22} \left( {\cosh (2\gamma_{1} h) - \sinh (2\gamma_{1} h)} \right)\, + a_{23} \left( {\cosh (2\gamma_{2} h) - \sinh (2\gamma_{2} h)} \right) \\ & \quad + \,a_{24} \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right) + a_{25} \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) + a_{26} \left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right) \\ & \quad + \,a_{27} \left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right) - a_{28} \left( {\kappa h + 4} \right)\left( {\cosh (\kappa h) - \sinh (\kappa h)} \right) \\ & \quad + \,a_{29} \left( {4 - \kappa h} \right)\left( {\cosh (\kappa h) + \sinh (\kappa h)} \right) + a_{30} \left( {4 - \gamma_{1} h} \right)\left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right) \\ & \quad + \,a_{31} \left( {4 - \gamma_{2} h} \right)\left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right) + a_{32} \left( {\cosh (\kappa h) - \sinh (\kappa h)} \right)\left( {\kappa^{2} h^{2} + 8\kappa h + 12} \right) \\ & \quad + \,a_{33} \left( {\cosh (\kappa h) + \sinh (\kappa h)} \right)\left( {\kappa^{2} h^{2} - 8\kappa h + 12} \right) + a_{34} \left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right)\left( {\gamma_{1}^{2} h^{2} + 8\gamma_{1} h + 12} \right) \\ & \quad + \,a_{35} \left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right)\left( {\gamma_{2}^{2} h^{2} + 8\gamma_{2} h + 12} \right) + a_{36} \left( {\cosh ((\gamma_{1} + \kappa )h) - \sinh ((\gamma_{1} + \kappa )h)} \right) \\ & \quad + \,a_{37} \left( {\cosh ((\gamma_{1} - \kappa )h) - \sinh ((\gamma_{1} - \kappa )h)} \right) + a_{38} \left( {\cosh ((\gamma_{2} - \kappa )h) - \sinh ((\gamma_{2} - \kappa )h)} \right) \\ & \quad + \,a_{39} \left( {\cosh ((\gamma_{1} + \gamma_{2} )h) - \sinh ((\gamma_{1} + \gamma_{2} )h)} \right) + a_{40} \left( {\cosh ((\gamma_{2} + \kappa )h) - \sinh ((\gamma_{2} + \kappa )h)} \right), \\ \end{aligned}$$

$$\begin{aligned} a_{47} & = 4a_{17} h^{3} + 5a_{18} h^{4} + 6a_{19} h^{5} + a_{39} \left( {\gamma_{1} + \gamma_{2} } \right)\left( {\cosh ((\gamma_{1} + \gamma_{2} )h) + \sinh ((\gamma_{1} + \gamma_{2} )h)} \right) \\ & \quad - \,a_{34} \left( {\cosh (\gamma_{1} h) + \sinh (\gamma_{1} h)} \right)\left( { - 2h\gamma_{1}^{2} + 8\gamma_{1} } \right) - a_{35} \left( {\cosh (\gamma_{2} h) + \sinh (\gamma_{2} h)} \right)\left( { - 2h\gamma_{2}^{2} + 8\gamma_{2} } \right) \\ & \quad - \,a_{36} (\gamma_{1} + \kappa )\left( {\cosh (h(\gamma_{1} + \kappa )) + \sinh (h(\gamma_{1} + \kappa ))} \right) + a_{40} (\gamma_{2} + \kappa )\left( {\cosh (h(\gamma_{2} + \kappa )) + \sinh (h(\gamma_{2} + \kappa ))} \right) \\ & \quad - \,2a_{21} \kappa \left( {\cosh (2h\kappa ) - \sinh (2h\kappa )} \right) - 2a_{25} \kappa \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right) + a_{29} \kappa \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right) \\ & \quad - \,a_{32} \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right)( - 2h\kappa^{2} + 8\kappa ) + a_{37} \left( {\cosh (h(\gamma_{1} - \kappa )) + \sinh (h(\gamma_{1} - \kappa ))} \right)(\gamma_{1} - \kappa ) \\ & \quad + \,a_{38} \left( {\cosh (h(\gamma_{2} - \kappa )) + \sinh (h(\gamma_{2} - \kappa ))} \right)(\gamma_{2} - \kappa ) + a_{33} \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right)(2h\kappa^{2} + 8\kappa ) \\ & \quad + \,2a_{22} \gamma_{1} \left( {\cosh (2h\gamma_{1} ) + \sinh (2h\gamma_{1} )} \right) + a_{26} \gamma_{1} \left( {\cosh (h\gamma_{1} ) + \sinh (h\gamma_{1} )} \right) + a_{30} \gamma_{1} \left( {\cosh (h\gamma_{1} ) + \sinh (h\gamma_{1} )} \right) \\ & \quad + \,2a_{23} \gamma_{2} \left( {\cosh (2h\gamma_{2} ) + \sinh (2h\gamma_{2} )} \right) + a_{27} \gamma_{2} \left( {\cosh (h\gamma_{2} ) + \sinh (h\gamma_{2} )} \right) + a_{31} \gamma_{2} \left( {\cosh (h\gamma_{2} ) + \sinh (h\gamma_{2} )} \right) \\ & \quad + \,2a_{20} \kappa \left( {\cosh (2h\kappa ) + \sinh (2h\kappa )} \right) + (a_{24} + a_{28} )\kappa \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right) \\ & \quad + \,a_{34} \gamma_{1} \left( {\cosh (h\gamma_{1} ) + \sinh (h\gamma_{1} )} \right)\left( {\gamma_{1}^{2} h^{2} - 8\gamma_{1} h + 12} \right) + a_{35} \gamma_{2} \left( {\cosh (h\gamma_{2} ) + \sinh (h\gamma_{2} )} \right)\left( {\gamma_{2}^{2} h^{2} - 8\gamma_{2} h + 12} \right) \\ & \quad + \,a_{30} \gamma_{1} (\gamma_{1} h - 4)\left( {\cosh (h\gamma_{1} ) + \sinh (h\gamma_{1} )} \right) + a_{31} \gamma_{2} (\gamma_{2} h - 4)\left( {\cosh (h\gamma_{2} ) + \sinh (h\gamma_{2} )} \right) \\ & \quad + \,a_{28} \kappa (\kappa h - 4)\left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right) + a_{32} \kappa \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right)\left( {\kappa^{2} h^{2} - 8\kappa h + 12} \right) \\ & \quad - \,a_{29} \kappa \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right)(\kappa h + 4) - a_{33} \kappa \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right)(\kappa^{2} h^{2} + 8\kappa h + 12), \\ \end{aligned}$$

$$\begin{aligned} a_{48} & = - 4a_{17} h^{3} + 5a_{18} h^{4} - 6a_{19} h^{5} + a_{39} \left( {\gamma_{1} + \gamma_{2} } \right)\left( {\cosh ((\gamma_{1} + \gamma_{2} )h) - \sinh ((\gamma_{1} + \gamma_{2} )h)} \right) \\ & \quad - \,a_{34} \left( {\cosh (\gamma_{1} h) - \sinh (\gamma_{1} h)} \right)\left( {2h\gamma_{1}^{2} + 8\gamma_{1} } \right) - a_{35} \left( {\cosh (\gamma_{2} h) - \sinh (\gamma_{2} h)} \right)\left( {2h\gamma_{2}^{2} + 8\gamma_{2} } \right) \\ & \quad - \,a_{36} (\gamma_{1} + \kappa )\left( {\cosh (h(\gamma_{1} + \kappa )) - \sinh (h(\gamma_{1} + \kappa ))} \right) + a_{40} (\gamma_{2} + \kappa )\left( {\cosh (h(\gamma_{2} + \kappa )) - \sinh (h(\gamma_{2} + \kappa ))} \right) \\ & \quad - \,2a_{21} \kappa \left( {\cosh (2h\kappa ) + \sinh (2h\kappa )} \right) - 2a_{25} \kappa \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right) + a_{29} \kappa \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right) \\ & \quad - \,a_{32} \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right)(2h\kappa^{2} + 8\kappa ) + a_{37} \left( {\cosh (h(\gamma_{1} - \kappa )) - \sinh (h(\gamma_{1} - \kappa ))} \right)(\gamma_{1} - \kappa ) \\ & \quad + \,a_{38} \left( {\cosh (h(\gamma_{2} - \kappa )) - \sinh (h(\gamma_{2} - \kappa ))} \right)(\gamma_{2} - \kappa ) + a_{33} \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right)( - 2h\kappa^{2} + 8\kappa ) \\ & \quad + \,2a_{22} \gamma_{1} \left( {\cosh (2h\gamma_{1} ) - \sinh (2h\gamma_{1} )} \right) + a_{26} \gamma_{1} \left( {\cosh (h\gamma_{1} ) - \sinh (h\gamma_{1} )} \right) + a_{30} \gamma_{1} \left( {\cosh (h\gamma_{1} ) - \sinh (h\gamma_{1} )} \right) \\ & \quad + \,2a_{23} \gamma_{2} \left( {\cosh (2h\gamma_{2} ) - \sinh (2h\gamma_{2} )} \right) + a_{27} \gamma_{2} \left( {\cosh (h\gamma_{2} ) - \sinh (h\gamma_{2} )} \right) + a_{31} \gamma_{2} \left( {\cosh (h\gamma_{2} ) - \sinh (h\gamma_{2} )} \right) \\ & \quad + \,2a_{20} \kappa \left( {\cosh (2h\kappa ) - \sinh (2h\kappa )} \right) + (a_{24} + a_{28} )\kappa \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right) \\ & \quad + \,a_{34} \gamma_{1} \left( {\cosh (h\gamma_{1} ) - \sinh (h\gamma_{1} )} \right)\left( {\gamma_{1}^{2} h^{2} + 8\gamma_{1} h + 12} \right) + a_{35} \gamma_{2} \left( {\cosh (h\gamma_{2} ) - \sinh (h\gamma_{2} )} \right)\left( {\gamma_{2}^{2} h^{2} + 8\gamma_{2} h + 12} \right) \\ & \quad - \,a_{30} \gamma_{1} (\gamma_{1} h + 4)\left( {\cosh (h\gamma_{1} ) - \sinh (h\gamma_{1} )} \right) - a_{31} \gamma_{2} (\gamma_{2} h + 4)\left( {\cosh (h\gamma_{2} ) - \sinh (h\gamma_{2} )} \right) \\ & \quad - \,a_{28} \kappa (\kappa h + 4)\left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right) + a_{32} \kappa \left( {\cosh (h\kappa ) - \sinh (h\kappa )} \right)\left( {\kappa^{2} h^{2} + 8\kappa h + 12} \right) \\ & \quad - \,a_{29} \kappa \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right)( - \kappa h + 4) - a_{33} \kappa \left( {\cosh (h\kappa ) + \sinh (h\kappa )} \right)(\kappa^{2} h^{2} - 8\kappa h + 12), \\ \end{aligned}$$