Introduction

The optical properties of composite nanosystems that combine semiconductor quantum dots (SQDs) and plasmonic nanostructures, such as metallic nanoparticles (MNPs), have fascinated substantial interest in recent years [1,2,3,4,5,6]. These superstructures have outstanding capability and promising potential in optoelectronic devices [7], quantum computation [8], nanosensors [9], electrical DNA switches [10] and nanodevices [11]. The main phenomenon provoking these applications would be explained that MNPs could alter the optical properties of the semiconductor nanostructures noticeably by their localized surface plasmon resonances (LSPRs). Surface plasmons can increase the electric field experienced by SQDs, which cause the emission enhancement [12]. This process happens by increasing the radiative decay rates of excitons and enhancing the optical excitations of the SQDs. The hybrid systems is coherent coupling between excitons and plasmons so-called plexcitonic which such systems hold potential for tunable nanophotonic devices for sensing and switches [13]. The coupling can happen when these systems interact with coherent light sources, such as laser fields. Recently, several research groups have been studied SQD-MNP systems theoretically and experimentally [14, 15]. It was shown that the quantum coherence has a significant impact on the near fields of the LSPRs and this was done by showing that how the field enhancement factor changes with the center-to-center distance of the SQDs and MNPs for different intensities of the laser field intensities [5]. It was found that the power spectrum of metallic nanorod (MNR) in the SQD-MNR has two transparent states and they can be switched to one transparent state by the control field. Ultrafast switching and sensing nanodevices could be produced using this model; electrodynamic calculation of the near fields for the hybrid system based on the boundary element method was used in this study [16].

It was found that combined hybrid SQD-MNPs system could support a meta-molecular resonance. Such a resonance happens in the space/time domain and is associated with the time delay induced by the plasmonic effects in the response of the quantum dot to a time-dependent optical field. The results demonstrate generation of Rabi oscillation in quantum dots via plasmons and offer alternative ultrasensitive methods for sensing [17]. Four-wave mixing (FWM) response and optical bistability (OB) in a hybrid nanosystem composed of a metal nanoparticle (MNP) and a semiconductor quantum dot (SQD) coupled to a nanomechanical resonator are investigated theoretically [18]. Optical properties of a complex system including a closely spaced spherical SQD and a metal nanosphere were investigated [19]. It was shown that the system can manifest bistability and optical hysteresis [20]. Moreover, the resonant optical bistability condition induced by local-field effects was studied by considering the relationship between the population difference and the excitation field in a two-level system [21].

To the best of our knowledge, OB in coherent coupling of excitons and plasmons in nanoparticle systems consisting of SQDs and metallic nanospheres is recently studied [23], but for metallic nanorods (MNRs) it has not been considered. In this manuscript, we present a semianalytical model to investigate the coupling of an electronic excitation in a SQD to the LSPRs of a metal nanorod. This interaction can lead to resonance splittings in the scattering spectrum of metallic nanostructures and also to enhancement or quenching of the excited state population of SQD. It is shown that nonlinear optical response of this type of hybrid systems can possess more than one output state for a given input state. The modification of field inside SQD leads to some interesting nonlinear phenomena such as Kerr nonlinearity [22] and OB [23]. Besides, we further find that in the presence of quantum coherence SQD-MNR hybrid system, the intensity or polarization of the applied laser field, the distance between the MNR and SQD, the refractive index of the environment and the size of MNR can affect OB behavior dramatically. As an important result, we find that by selecting the better metal plasmonic material such as gold, copper, silver and aluminum, it is possible to achieve maximum or minimum the bistable region for a metal–semiconductor hybrid nanosystem that can be used in the many applications such as optical memory elements and quantum information.

Theoretical description

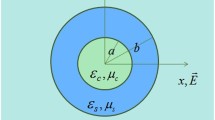
As a starting point for the problem, a brief description of the hybrid system is shown in Fig. 1. The SQD is considered as a two-level system, its ground state \(|1>\) and fundamental exciton state \(|2>\). The frequency of the \(|1> \rightarrow |2>\) transitions is denoted as optical transition dipole moment. It is assumed that the SQD is close enough to a MNR where its structure can be reasonably approximated by a nanorod (an ellipsoid with two equal semi-diameters). The MNR has semimajor and semiminor diameter b, and the corresponding aspect ratio is \(q = a/b\). SQD-MNR hybrid is surrounded by a homogeneous medium with dielectric constant \(\epsilon _{b}\). The center-to-center distance between the nanoparticles is denoted as R. It is treated quantum mechanically within the frame of the Maxwell–Bloch equations for the density matrix \(\rho \) representing a two-level atom which each element of the density matrix corresponds to a physical quantity. The interaction between SQD and MNR is described by the large electric dipole moments of SQD and plasmon resonance of the MNR. The frequency of the laser field \((\omega )\) is considered to be close to transition frequency between the ground and the first exciton state of the SQD \((\omega _{0})\). We also assume that the frequency of the MNR plasmon resonance is the same as the \(|1> \leftrightarrow |2>\) transition. The MNR is considered classically; the response of the MNP is explained by its frequency-dependent scalar polarizability within the point dipole approximation.

Fig. 1
figure 1

Schematics of the hybrid SQD-MNR system subjected to an external field with amplitude \(E_{0}\)

Full size image

The Bloch equations, which describe the dynamics of the system, are derived. Under the rotating wave approximation, the time evolution of the density matrix of the SQD can be obtained.

$$\begin{aligned} \dot{\rho }_{22}= & {} i\Omega \rho _{12}-i\Omega ^{*}\rho _{21}-\gamma \rho _{22}\nonumber \\ \dot{\rho }_{11}= & {} -i\Omega \rho _{12}+i\Omega ^{*}\rho _{21}+\gamma \rho _{22}\nonumber \\ \dot{\rho }_{21}= & {} -(i\varDelta +\varGamma )\rho _{21}+i\Omega (\rho _{11}-\rho _{22}) \end{aligned}$$
(1)

\(\rho _{22}\) and \(\rho _{11}\) are the exciton populations in the SQD excited and the SQD ground states, respectively. \(\rho _{21}=-(i/2)We^{(-i\omega t)}\) which W is the amplitude of the off-diagonal density matrix element and \(Z=\rho _{22} - \rho _{11}\) is the population difference between the SQD excited and the SQD ground states. We rewrite the density matrix equations for W and Z as:

$$\begin{aligned} \dot{Z}= & {} -\frac{1}{2}[\Omega W^{*}+\Omega ^{*}W]-\gamma (Z+1)\nonumber \\ \dot{W}= & {} -(i\varDelta +\varGamma )W+\Omega Z \end{aligned}$$
(2)

\(\gamma \) and \(\varGamma \) are the relaxation constant of the population and the dipole dephasing, respectively, \(\varDelta = \omega _{0} - \omega \) is the detuning of the driving field from the SQD resonance. \(\Omega = \mu E/\hbar \) is the effective electric field (in frequency units) acting inside the SQD. The field acting on the SQD is equal to the sum of the external field \({\mathbf{E}}_{0}\) and the field produced by the induced dipole moment \({\mathbf{P}}_{MNP}\) of the MNP. The effective or normalized Rabi frequency of the SQD is defined as

$$\begin{aligned} \Omega= & {} \tilde{\Omega }_{0} - iGR\nonumber \\ G= & {} \frac{a b^{2} S^{2}_{a} \mu ^{2}_{21}\gamma }{4\pi \epsilon _{b} \epsilon ^{2}_{eff} R^{6}} \end{aligned}$$
(3)

where \(\tilde{\Omega }_{0} = \Omega _{0} (1 + \frac{S_{a} \gamma a b^{2}}{R^{3}})\) and \(\Omega _{0} = \frac{\mu E}{2\hbar \epsilon _{eff}}\) refer to the Rabi frequency of the bare external field when the SQD is isolated. In addition, G denotes the self-interaction of the SQD, due to the creation of the hybrid exciton. \(|\tilde{\Omega }_{0}/ \Omega _{0}|^{2}\) represents the field enhancement factor caused by the MNP in the absence of quantum coherence.

In Eq. (3), \(\epsilon _{eff} = {(2\epsilon _{b} + \epsilon _{s})}/{3\epsilon _{b}}\), where \(\epsilon _{b}\) and \(\epsilon _{s}\) are the dielectric constant of the background material and dielectric constant of the SQD. The factor \(S_{a}\) refers to the polarization state of the system and has the value of \(2(-1)\) when the external fields are parallel (perpendicular) to the major axis of the hybrid system.

Geometric factor \(S_{a}\) is equal to \(2(-1)\) when E is parallel to the z(x, y) axis. The z direction corresponds to the axis of the hybrid system. \(\gamma = [\epsilon _{m}(\omega ) - \epsilon _{b}]/{[3\epsilon _{b} + 3\kappa (\epsilon _{m}(\omega ) - \epsilon _{b})]}\) corresponds to polarization of the MNP, which is called the depolarization factor of the MNR. In this study, since the amplitude of the incident electric field lies along the semimajor diameter a, the depolarization factor is considered the same for both polarizations. It is given by the following [24]

$$\begin{aligned} \kappa= & {} \frac{1-e^{2}}{e^{2}}\left[ \frac{1}{2e}\ln \left( \frac{1+e}{1-e}\right) - 1\right] \nonumber \\&\hbox {and} \nonumber \\ e= & {} \sqrt{1-1/q^{2}} \end{aligned}$$
(4)

We describe the MNP with the local dynamic dielectric function, according to the generalized Drude theory, the permittivity of a material can be written as follows [25]

$$\begin{aligned} \epsilon (\omega )=\epsilon (\omega )' + i\epsilon (\omega )'' = \epsilon _\mathrm{int} - \frac{\omega ^{2}_{p}}{\omega (\omega + i \varGamma )} \end{aligned}$$
(5)

\(\varGamma = 1/\tau \) , \(\tau \) is the relaxation time of conduction electrons in the metal, and \(\epsilon _\mathrm{int}\) is a contribution due to interband transitions; it is unity for the case of a perfectly free-electron gas.

The parameter G in Eq. (3) is the most prominent parameter and determines the nonlinear properties of the SQD response.

$$\begin{aligned} \frac{\hbox {d}W}{\hbox {d}t} = - [(\varGamma - G_{I} Z) + i (\varDelta + G_{R} Z)]W + \Omega Z \end{aligned}$$
(6)

where \(G_{R} = Re(G)\) and \(G_{I} = Im(G)\). From above equation, the SQD self-action leads to two renormalizations in the SQD resonance frequency \(\omega _{0} \rightarrow \omega _{0} + G_{R} Z\) and the dipole dephasing rate \(\varGamma \rightarrow \varGamma - G_{I}Z\). Both renormalized quantities depend on the population difference Z. The population dependence of the SQD resonance frequency and the dipole dephasing rate provide a feedback mechanism, which results in a number of fascinating effects.

In order to study the OB behavior, the rate equations should be analyzed under steady-state conditions \((\dot{Z} = \dot{W} = 0)\). The corresponding solutions read

$$\begin{aligned} \frac{|\Omega |^2}{\gamma \varGamma }= & {} -\frac{Z+1}{Z}\frac{|(\varGamma - G_{I} Z) + i(\varDelta + G_{R} Z)|^{2}}{\varGamma ^{2}}\nonumber \\ W= & {} \frac{Z\Omega }{(\varGamma - G_{I} Z) + i(\varDelta + G_{R} Z)} \end{aligned}$$
(7)

Equation (7) is of the third order in Z and consequently may have three real solutions, depending on the values of \(\varDelta ,\varGamma ,G_{R}, G_{I}\).

Results and discussion

In this section, we present the results of analytical calculations for the OB of the SQD-MNR hybrid system. It is assumed that the parameters used in our calculation are the transition energy \((\hbar \omega _{0} = 2.36\,\hbox {eV})\), \((\epsilon _{s} = 6.2)\), the SQD transition dipole moment \((\mu = 0.65\times 10^{-9}\,\hbox {e.m})\), the MNP radius \(d = 10\,\hbox {nm}\), the host dielectric constant \(\epsilon _{b} = 1\) and the relaxation constants \(\gamma \) and \(\varGamma \) are defined through \(1/\gamma = 0.8\,\hbox {ns}\).

We start with investigation the impact of the geometrical variation of the MNR on OB behavior of population inversion. For this purpose, we study how population inversion changes as a function of Rabi frequency of applied laser field \(|\Omega |^{2}\) for various aspect ratios (q). It is found that with increasing the aspect ratio parameter, the hysteresis loop of OB can be clearly expanded in comparison with the metal nanosphere (Fig. 2).

Fig. 2
figure 2

Population inversion Z as a function of intensity of applied laser field for a different values of q and b for metal nanorod (MNR) and metal nanosphere (MNS). The selected parameters are: \(\epsilon _{s} = 1, R = 20\,\hbox {nm}\)

Full size image

From these figures, one can see that the induced field inside the SQD dramatically changes by varying the q parameter. This means that the field experienced by the SQD in the presence of the MNP can be considerably different from that of the applied field. It is realized that the increase in the value of the aspect ratio (q) tends to widen the hysteresis loop in OB curve. Consequently, OB can happen in a wide range of input power of laser field. This result is unique and important, and no such consequence of hysteresis loops has been shown so far.

It is well known that a drastic reduction in the plasmon dephasing rate in nanorods happens as compared to small nanospheres due to a suppression of interband dam** [26]. The rods show very little radiation dam**, due to their small volumes. Therefore, it would imply large local-field enhancement factors and relatively high light-scattering efficiencies, making metal nanorods particularly interesting for optical applications. Comparison of the experimental results with theory shows that pure dephasing and interface dam** give small contributions to the total plasmon dephasing rate. It should be noted that by increasing q very much, the optical response of QD is entirely dependent on metallic nanorod and consequently, the optical bistability of QD would vanished

Here, to demonstrate the impact of the quantum coherence on the OB in the SQD, we also compare the results for different values of the center-to-center distance between the SQD and GNR in Fig. 3. It is shown that the effects of quantum coherence have vanished by increasing the distance in the other word; we will have a bare SQD in the long distance between SQD and GNR. Therefore, OB performance would be disappeared in SQD. It should be noticed that G parameter is proportional to \(\mathbf {R}^{-6}\). Consequently, by getting too close these two particles, induced SQD field enhances and nonlinear phenomena would be affected. So, this hybrid system does not show stability behavior and OB cannot be seen.

Fig. 3
figure 3

Population inversion Z as a function of intensity of applied laser field for different values of R. The selected parameters are: \(q=2, \epsilon _{b}=1\)

Full size image

In Fig. 4, we show the OB response for different values of \(\epsilon _{b}\). It is obvious that the behavior of bistability is influenced strongly by the background medium. As seen in this Fig. 3, by increasing \(\epsilon _{b}\), the OB becomes weaker and the widths of hysteresis loop become tighter. This effect can be explained by means of definition of induced field inside the SQD appropriately. From another perspective, the large \(\epsilon _{b}\) weaken the field enhancement factor and eventually cause the widening of the hysteresis loop.

Fig. 4
figure 4

Population inversion Z as a function of intensity of applied laser field for different values of \(\epsilon _{b}\). The selected parameters are: \(q=2, R = 20\,\hbox {nm}\)

Full size image

To study the impact of the MNR on OB, we show OB behavior for four different metal nanorods in Fig. 5. The OB as a function of intensity of applied laser field is shown for Au, Ag, Al and Cu for comparison, because these noble metals are good materials for plasmonic applications, while they are qualified to show bistability due to the their nonlinearity. Our results shows that by selecting the better metal plasmonic material, it is possible to achieve maximum or minimum the bistable region for a hybrid metal–semiconductor nanodimer that can be used in the many applications such as optical memory elements. However, these interesting findings for controlling optical hysteresis loops are very useful in practical applications.

Fig. 5
figure 5

Population inversion Z as a function of intensity of applied laser field for different metallic structures. The selected parameters are: \(q=2, \epsilon _{b}=1\)

Full size image

Conclusion

We investigate the OB in a SQD modulated by the surface plasmon of a MNR in a hybrid plexcitonic system formed by a SQD placed near a MNR. The SQD is assumed as a two-level atomic system, which is coupled to a classical metal nanorod by the dipole-dipole interaction, and this could modify the relevant decay rates of SQD. It is considered the interaction of the system with a weak probe electromagnetic field and present results from the solution of the relevant density matrix equations. These interaction effects in optical response of the SQD via the MNP, lead to population dependence of the SQD transition frequency and relaxation constant of the SQD dipole moment. This mechanism provides a positive feedback for the nanodimer and induces to the manifestation of OB in the optical response of SQD. Precisely, the total dipole moment of the system can be switched between its two stable states by the incoming field. The OB behavior is strongly dependent on the interparticle distance, and physical parameters of MNR such as aspect ratio (q) and the metal substance. It is especially important that the hysterical behaviors of the transmitted light rely on the refractive index of background medium, making this model to be a good candidate for tunable OB device, owing to the possibility of high adjustability of the embedding medium. Therefore, this model suggests such possible applications as optical memories and all-optical switches at the nanoscale.