1 Introduction

During these times, good quality product, satisfaction of customers’ requirements and existence in competitive marketplaces are elementary needs for any business. Indeed, these requirements have become business principles, prominent corporations to pursuit for different facets that influence the purchasing options of users. Subsequently, reverse logistics (RL) has become main feature for contributing to the desirable outcomes of several enterprises. RL comprises the actions related with the collection and succeeding retrieval of used products (Fattahi and Govindan 2017). The emerging implication of RL has supervised numerous enterprises to design and reconstruct procedures as a part of their sustainable development initiatives (Govindan et al. 2015; Banihashemi et al. 2019). Through RL, products are displaced from their final terminus to a new position, where their worth is considered and they are managed to the manufacturing line again or appropriately disposed (Tavana et al. 2016; Kannan et al. 2017). Furthermore, eco-conscious customers incline to give extra on eco-friendly products, increasing the revenue of those businesses that utilize RL to achieve with the needs of such consumers (Mavi et al. 2017; Zarbakhshnia et al. 2018).

RL management is one of the important issues in the SCM, which mostly emphases on backward flow of products and raw materials from users to suppliers (Mavi et al. 2017). Growing environmental responsiveness and prospective economic growth have determined ever more corporations to outsource their logistics operations to S3PRLPs (Mavi et al. 2017; Zarbakhshnia et al. 2018; Li et al. 2018). In order to achieve the objectives of cost savings and environmental sustainability, it is significant for the firms to select the best S3PRLPs option. In recent times, the assessment of 3PRLPs selection process has received great attentions from the researchers. Numerous scholarly articles have been presented for selecting the best 3PRLP alternative in the literature, however, more studies are required to manage the prioritizations of different expertise, different environments and knowledge levels on reverse logistics with the consideration of social, environmental and economic dimensions simultaneously. Because of increasing complexity and several constraints, it is not always possible to explore the priorities more proficiently and accurately in the best 3PRLPs selection.

The FSs doctrine (Zadeh 1965) has successfully been employed in diverse 3PRLPs selection problem and proved its powerful ability to tackle with imprecise and uncertain information. As an extension of FSs, the theory of FFSs (Senapati and Yager 2019a) has been proven as one of the powerful platforms to deal with the imprecise and uncertain information. The key characteristic of FFS is the cube addition of BD and NBD is less than or equal to 1. Thus, the FFSs theory is more superior tool than FSs, IFSs and PFSs. Based on its unique advantage, the paper focuses under the environment of FFSs for the assessment of S3PRLP selection. Inspired by the above studies and literature, we introduce Fermatean fuzzy-CRITIC-EDAS framework for assessing the S3PRLPs selection. Thus, this is the first study which proposes a hybrid framework under FFSs. The main contributions of the work are discussed as follows:

  1. 1.

    A New improved generalized score function (IGSF) is proposed for FFNs with their elegant properties.

  2. 2.

    An FF-CRITIC-EDAS framework is introduced to handle the MCDM problemon FFSs.

  3. 3.

    To determine the practicality and effectiveness of the introduced framework, a case study of S3PRLP selection is taken with FFNs.

  4. 4.

    A Comparative discussion is made with the extant models to validate of the developed framework.

The rest of paper is arranged as follows: Sect. 2 depicts a comprehensive review related to present study. Section 3 shows the basic notions on FFSs and proposes a new IGSF with its elegant properties. Section 4 introduces novel Fermatean fuzzy-CRITIC-EDAS approach to elucidate the MCDM problems. Section 5 deliberates a case study of S3PRLP selection and also discusses a comparative discussion with the extant models. Section 6 spectacles the conclusions and scope for future study.

2 Related works

In the current section, we present literature survey related to the present study.

2.1 3PRLP Selection

Various criteria are involved in the evaluation of 3PRLPs selection process, consequently, this selection process can be observed as a MCDM problem. Existing studies on 3PRLP selection problem confirm the emergent interest of scholars and manufacturers. Over the last few years, copious MCDM models have been established in the setting of 3PRLP assessment problem. Realistic reverse logistics outsourcing assessments are commonly prepared under imprecise and vague environment due to multiple indicators, like as partial ignorance, imprecise estimation, partial or inaccessible decision information (Saen 2010; Azadi and Saen 2011). Consequently, crisp values are usually inappropriate to model such type of practical decision conditions.

FS theory and their extensions have widely been employed to cope with uncertain and vague information occurred in realistic MCDM applications. Senthil et al. (2014) suggested a combined model with AHP and TOPSIS approaches for evaluating an ideal reverse logistics contractor. In a further study by Tajik et al. (2014), a decision-making framework was introduced for choosing most suitable 3PRLP alternative by taking all three aspects of sustainability on FSs. Later, Uygun et al. (2015) planned and selected an outsourcing provider for a telecommunications business by employing DEMATEL and ANP approaches. Tavana et al. (2016) suggested a conceptual analytic network model to thoroughly tackle the complex behavior of interactions among the 3PRLPs assessment factors. Mavi et al. (2017) presented SWARA method for weighting the assessment criteria of 3PRLP in the plastics industry and further, ranked the sustainable 3PRLP alternatives through MOORA model within FSs context. Tavana et al. (2018) suggested a combined method with the integration of ANP and grey superiority and inferiority methods on IFSs for the assessment of 3PRLPs selection process. Li et al. (2018) used a combined cumulative prospect doctrine with hybrid-information MCDM methodology for the evaluation of 3PRLPs from sustainability perspectives. Zarbakhshnia et al. (2018) weighted the assessment criteria through fuzzy SWARA method and ranked the sustainable 3PRLPs by employing COPRAS method under fuzzy environment. Liu et al. (2019) suggested the BWM to research the selection of 3PRLPs on IVPHFSs. Bai and Sarkis (2019) pioneered multi-stage, multi-method, and multi-metric decision-making tool based on TOPSIS, VIKOR and neighborhood rough set for the evaluation of 3PRLP selection decision. Recently, Zarbakhshnia et al. (2020) established a framework with the AHP and MOORA-G models for the assessment of 3PRLPs under FSs. Zhang and Su (2020) introduced the heterogeneous linguistic model with dominance degree to assess the best S3PRLP for a car manufacture industry.

2.2 Fermatean fuzzy sets

The theory of FSs has broadly been received great attention from the researchers for dealing with uncertain and imprecise information. In 1986, Atanassov (1986) presented the idea of IFS, which is termed as belongingness degree (BD), non-belongingness degree (NBD), and holds the condition that the addition of BD and NBD is less than or equal to 1. As an extension of IFSs, Yager (2014) initiated the notion of PFSs. The PFSs are more powerful tool than IFSs for handling the uncertain, vague and imprecise information arisen in the realistic problems. Recently, numerous researchers have explored the different concepts by considering the theoretical and practical aspects of PFSs. For instance, Rani et al. (2019) proposed the VIKOR approach-based on entropy and discrimination measures to handle the renewable energy resources assessment in India. Rani et al. (2020a) developed COPRAS method to select the pharmacological therapies for type-2 diabetes disease. Rani et al. (2020b) assessed and selected the healthcare waste treatment options using SWARA and ARAS methods.

However, in numerous practical concerns, a group of DMs may give the BD to which an alternative satisfies the attribute is 0.8 and the NBD to which an alternative dissatisfies the attribute is 0.7. Here, we observe that \(0.8+0.7>1\) and \({0.8}^{2}+{0.7}^{2}>1\), as a result, the IFS and PFS are incapable to tackle this concern. To handle such information, Senapati and Yager (2019a) gave the doctrine of Fermatean fuzzy set (FFS), which is termed as the BD and NBD and the constraint that the cube sum of BD and NBD is less than or equal to 1. Consequently, the FFS can efficiently solve the aforementioned concern. Also, FFSs can solve the MCDM problems with more effective way and handle the complex uncertain information. For example, Senapati and Yager (2019a) pioneered the doctrine of FFSs and proposed various basic concepts for solving decision-making problem. Senapati and Yager (2019b) discussed numerous aggregation operators with their elegant properties for FFSs and used WPM to solve the MCDM problems (Senapati and Yager 2019c). Garg et al. (2020) studied several Fermatean fuzzy aggregation operators and presented their application in COVID-19 facility selection. Aydemir and Gunduz (2020) proposed Dombi operators and their properties for FFSs. Recently, there is no study related to the S3PRLP assessment on FFSs context.

2.3 CRITIC method

In the MCDM process, various criteria weighting methods have been developed in the literature (Suh et al. 2019; Mishra et al. 2020a; Rani et al. 2020c). The criteria weight computation procedures are classified as objective weight and subjective weight (Peng 2019). The CRITIC approach (Diakoulaki et al. 1995) is one of the weighting models to estimate the objective weights of the attributes using the standard deviation and the correlation coefficient to quantify the value of each attribute and computes the attribute weights of MCDM procedure. Recently, several fusion models have been introduced by applying CRITIC with various other MCDM methods (Yalcin and Unlu 2018; Adali and Tus 2019). For example, Ghorabaee et al. (2017) discussed a hybrid model with CRITIC and WASPAS methods to solve the 3PRLPs with IT2FSs. Ghorabaee et al. (2018) presented a combined MCDM model with the CRITIC, EDAS and SWARA procedures. Peng et al. (2020) gave a CRITIC-CoCoSo method for 5G industry assessment on PFSs. Wei et al. (2020) initiated a hybrid model with GRA and CRITIC methods to assess and choose the suitable site for EVCSs under PULTSs environment. Peng and Huang (2020) discussed a hybrid model with CRITIC and CoCoSo methods for financial risk assessment problem. Liang (2020) gave a hybrid method with CRITIC and EDAS models under IFSs to solve the MCDM procedures.

2.4 EDAS method

The objective of MCDM procedure is to select the best option from a set of options under a set of various attributes. Currently, numerous MCDM approaches namely COPRAS (Kumari and Mishra 2020; Mishra et al. 2020a), CODAS (He et al. 2019; Zhou et al. 2020), ELECTRE (Fei et al. 2019; Mishra et al. 2020b), MULTIMOORA (Tian et al. 2017; Wu et al. 2020), TOPSIS (Aydemir and Gunduz 2020; Dammak et al. 2020), TODIM (Zindani et al. 2020; Mishra et al. 2020c), VIKOR (Rani et al. 2019; Krishankumar et al. 2020), WASPAS (Ghorabaee et al. 2017; Mishra and Rani 2018) and others have been discussed to solve the MCDM problems on different uncertain environments. Each MCDM procedure has been developed with different advantages and disadvantages, though, the scholars usually select an approach which is based on the nature and intricacy of the problem.

The EDAS method (Ghorabaee et al. 2015) is an original and efficient tool to solve the MCDM problem with conflicting attributes. It utilizes the AVS for prioritizing the options and describes the discrimination between the options and the AVS according to the measures PDA and NDA (Ghorabaee et al. 2016). Kahraman et al. (2017) used EDAS method for assessing solid waste disposal location on IFSs. Gundogdu et al. (2018) extended the EDAS model for assessing and choosing the suitable hospital under HFSs environment. Mi and Liao (2019) discussed a combined framework with BWM and EDAS method with HFSs to assess insurance projects. Zhang et al. (2019) extended the EDAS approach to select the best green supplier. Han and Wei (2020) gave multivalued neutrosophic EDAS model for dealing with the MCDM problems. Mishra et al. (2020d) discussed parametric discrimination measure-based EDAS framework for assessing the HCWD method on IFSs. In this study, we develop a combined framework with CRITIC and EDAS approaches for FFSs.

3 A new Fermatean fuzzy score function

This section introduces a new score function for Fermatean Fuzzy Numbers (FFNs) which avoids the shortcoming of existing score function (Senapati & Yager, 2019a,b). Here, the first subsection presents the concept, score and accuracy functions, and operational laws of FFSs. Based on this concept, an improved score function for FFNs is developed in the next subsection.

3.1 Prerequisites

Definition 3.1.

Let \(\Delta\) be a limited universe of discourse. In 2019, Senapati and Yager (2019a) firstly presented the concept of FFS, which is mathematically expressed as.

$$T\, = \,\left\{ {\left. {\left\langle {t_{i} ,\left( {b_{T} (t_{i} ),\,n_{T} (t_{i} )} \right)} \right\rangle } \right|\,t_{i} \, \in \,\Delta } \right\},$$

wherein \(b_{T} :\,\Delta \, \to \,\left[ {0,\,1} \right]\) represent the belongingness degree (BD) of an element \(t_{i} \, \in \,\Delta\) in FFS and \(n_{T} \,:\,\Delta \, \to \,\left[ {0,\,1} \right]\) signify the non-belongingness degree (NBD) of an element \(t_{i} \, \in \,\Delta\) in FFS. For every \(t_{i} \, \in \,\Delta ,\) it satisfies the condition \(0\, \le \,\left( {b_{T} (t_{i} )} \right)^{3} \, + \,\left( {n_{T} (t_{i} )} \right)^{3} \, \le \,1.\) The indeterminacy degree of FFS is expressed by \(\pi_{T} \left( {t_{i} } \right) = \,\sqrt[3]{{1\, - \,b_{T}^{3} \left( {t_{i} } \right) - \,n_{T}^{3} \left( {t_{i} } \right)}},\,\,\,\forall \,t_{i} \, \in \,\Delta .\) For simplicity, Senapati and Yager (2019a) called \(\left( {b_{T} (t_{i} ),\,n_{T} (t_{i} )} \right)\) as a Fermatean fuzzy number (FFN), given by \(\lambda = \left( {b_{\lambda } ,\,n_{\lambda } } \right)\) where \(b_{\lambda } ,\,n_{\lambda } \in \,\left[ {0,\,1} \right],\) \(\pi _{\lambda } = \,\sqrt[3]{{1\, - \,b_{\lambda }^{3} - \,n_{\lambda }^{3} }}\) and \(0\, \le \,b_{\lambda }^{3} \, + \,n_{\lambda }^{3} \, \le \,1.\)

Definition 3.2.

Let \(\lambda = \left( {b_{\lambda } ,\,n_{\lambda } } \right)\) be a FFN. Then, the score and accuracy functions of \(\lambda\) are defined as follows (Senapati and Yager 2019a, b):

\(\wp_{s} \left( \lambda \right) = \left( {b_{\lambda } } \right)^{3} - \left( {n_{\lambda } } \right)^{3}\) and \(\Im_{a} \left( \lambda \right) = \left( {b_{\lambda } } \right)^{3} + \left( {n_{\lambda } } \right)^{3} ,\) where \(- 1\, \le \,\wp_{s} \left( \lambda \right)\, \le \,1\) and \(0\, \le \,\Im_{a} \left(\lambda \right)\, \le \,1.\)

Thus, to rank two FFNs \(\lambda_{1} = \left( {b_{{\lambda_{1} }} ,\,n_{{\lambda_{1} }} } \right)\) and \(\lambda_{2} = \left( {b_{{\lambda_{2} }} ,\,n_{{\lambda_{2} }} } \right)\), we have the following comparative scheme (Senapati and Yager 2019a, b):

  1. (i)

    If \(\wp_{s} \left( {\lambda_{1} } \right)\, > \,\wp_{s} \left( {\lambda_{2} } \right),\) then \(\lambda_{1}\) is larger than \(\lambda_{2} ,\) denoted by \(\lambda_{1} \succ \lambda_{2} ;\)

  2. (ii)

    If \(\wp_{s} \left( {\lambda_{1} } \right)\, = \,\wp_{s} \left( {\lambda_{2} } \right),\) then

  3. (iii)

    if \(\Im_{a} \left( {\lambda_{1} } \right)\, > \,\Im_{a} \left( {\lambda {}_{2}} \right),\) then \(\lambda_{1}\) is larger than \(\lambda_{2} ,\) denoted by \(\lambda_{1} \succ \lambda_{2} ;\)

  4. (iv)

    if \(\Im_{a} \left( {\lambda_{1} } \right)\, < \,\Im_{a} \left( {\lambda {}_{2}} \right),\) then \(\lambda_{1}\) is smaller than \(\lambda_{2} ,\) denoted by \(\lambda_{1} \, \prec \lambda_{2} ;\)

  5. (v)

    if \(\Im_{a} \left( {\lambda_{1} } \right)\, = \,\Im_{a} \left( {\lambda {}_{2}} \right),\) then \(\lambda_{1}\) is identical with \(\lambda_{2} ,\) denoted by \(\lambda_{1} =\lambda_{2} .\)

Definition 3.3.

Assume that \(\lambda = \left( {b_{\lambda } ,\,n_{\lambda } } \right),\) \(\lambda_{1} = \left( {b_{{\lambda_{1} }} ,\,n_{{\lambda_{1} }} } \right)\) and \(\lambda_{2} =\left( {b_{{\lambda_{2} }} ,\,n_{{\lambda_{2} }} } \right)\) are three FFNs. Now, the operational laws are summarized as follows:

  1. 1)

    \(\lambda^{c} \, = \left( {n_{\lambda } ,\,b_{\lambda } } \right);\)

  2. 2)

    \(\lambda_{1} \, \cap \,\lambda_{2} \, = \left( {\min \left\{ {b_{{\lambda_{1} }} \,,\,b_{{\lambda_{2} }} } \right\},\,\,\,\max \left\{ {n_{{\lambda_{1} }} \,,\,n_{{\lambda_{2} }} } \right\}} \right);\)

  3. 3)

    \(\lambda_{1} \, \cup \lambda_{2} \, = \left( {\max \left\{ {b_{{\lambda_{1} }} ,\,b_{{\lambda_{2} }} } \right\},\,\,\,\min \left\{ {n_{{\lambda_{1} }} ,\,n_{{\lambda_{2} }} } \right\}} \right);\)

  4. 4)

    \(\lambda_{1} \, \oplus \,\lambda_{2} \, = \left( {\sqrt[3]{{b_{{\lambda_{1} }}^{3} \, + \,b_{{\lambda_{2} }}^{3} \, - \,b_{{\lambda_{1} }}^{3} \,b_{{\lambda_{2} }}^{3} }},\,n_{{\lambda_{1} }} n_{{\lambda_{2} }} } \right);\)

  5. 5)

    \(\lambda_{1} \, \otimes \,\lambda_{2} \, = \left( {b_{{\lambda_{1} }} b_{{\lambda_{2} }} ,\,\sqrt[3]{{\nu_{{\lambda_{1} }}^{3} \, + \,\nu_{{\lambda_{2} }}^{3} \, - \,\nu_{{\lambda_{1} }}^{3} \,\nu_{{\lambda_{2} }}^{3} }}} \right);\)

  6. 6)

    \(\lambda_{1} \,\Theta \lambda_{2} \, = \,\left\{ \begin{gathered} \left( {\sqrt[3]{{\frac{{b_{{\lambda_{1} }}^{3} - b_{{\lambda_{2} }}^{3} }}{{1 - b_{{\lambda_{2} }}^{3} }}}},\,\frac{{n_{{\lambda_{1} }} \,}}{{n_{{\lambda_{2} }} }}\,} \right),\,\,b_{{\lambda_{1} }} \ge \,b_{{\lambda_{2} }} ,\,n_{{\lambda_{1} }} \le \min \left\{ {n_{{\lambda_{2} }} ,\,\frac{{n_{{\lambda_{2} }} \,\pi_{{\lambda_{1} }} }}{{\pi_{{\lambda_{2} }} }}} \right\} \hfill \\ \left( {0,1\,} \right),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{otherwise;}}\,\, \hfill \\ \end{gathered} \right.\)

  7. 7)

    \(\iota \,\lambda \, = \left( {\sqrt[3]{{1 - \left( {1 - \,b_{\lambda }^{3} } \right)^{\iota } }}\,,\,\left( {n_{\lambda } } \right)^{\iota } } \right),\,\,\iota \, > \,0;\)

  8. 8)

    \(\lambda^{\iota } \, = \,T\left( {\left( {b_{\lambda } } \right)^{\iota } ,\,\sqrt[3]{{1 - \left( {1 - \,n_{\lambda }^{3} } \right)^{\iota } }}} \right),\,\,\iota \, > \,0.\)

3.2 Improved generalized score function (IGSF) for FFN

This section develops an IGSF for any FFN \(\lambda_{j} = \left( {b_{j} ,\,n_{j} } \right),\) and is presented as

$$\wp_{s}^{*} \left( {\lambda_{j} } \right) = \,b_{j}^{3} \left[ {1 + \left( {\gamma_{1} \, + \gamma_{2} } \right)\left( {1 - \,b_{j}^{3} - \,n_{j}^{3} } \right)} \right].$$
(1)

Here, \(\gamma_{1} \,,\,\gamma_{2} > 0\) signifies the performance of the proposed IGSF and \(\gamma_{1} \, + \gamma_{2} = 1\). In addition, \(\gamma_{1}\) and \(\gamma_{2}\) provide the weighted average of the indeterminacy degree between the BD and NBD.

Theorem 3.1:

For a FFN \(\lambda_{j} = \left( {b_{j} ,\,n_{j} } \right),\) the IGSF \(\wp_{s}^{*} \left( . \right)\) satisfies the following:

  1. p1.

    \(\wp_{s}^{*} \left( {\left( {0,1} \right)} \right) = 0\) and \(\wp_{s}^{*} \left( {\left( {1,0} \right)} \right) = 1.\)

  2. p2.

    An IGSF \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) is increasing monotonically w. r. t. \(b_{j}\) and is decreasing monotonically w. r. t. \(n_{j} .\)

Proof

p1. When \(\lambda_{j} = \left( {0,\,1} \right)\) or \(\lambda_{j} = \left( {1,\,0} \right),\) then according to Eq. (1), the IGSF \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) attains the least value ‘0′ or utmost value ‘1′, respectively. It follows that \(0 \le \wp_{s}^{*} \left( {\lambda_{j} } \right) \le \,1.\)

p2. To prove this part, differentiate Eq. (1) partially w.r.t. bj, then we have

$$\begin{aligned} \frac{{\partial \,\wp_{s}^{*} \left( {\lambda_{j} } \right)}}{{\partial \,b_{j} }}\, =& \,3\,b_{j}^{2} \left( {1\, + \,\left( {\gamma_{1} \, + \,\gamma_{2} } \right)\,\left( {1 - b_{j}^{3} - \,n_{j}^{3} } \right)} \right)\, \\ &- \,3\,b_{j}^{5} \,\left( {\gamma_{1} \, + \,\gamma_{2} } \right)\,\, \ge \,0. \end{aligned}$$

In the similar way, the first partial derivative of Eq. (1) w.r.t. nj is presented as follows:

$$\frac{{\partial \,\wp_{s}^{*} \left( {\lambda_{j} } \right)}}{{\partial \,n_{j} }}\, = \, - 3\,b_{j}^{3} \,n_{j}^{2} \,\left( {\gamma_{1} \, + \,\gamma_{2} } \right)\,\, \le \,0.$$

Thus, the theorem is proved.

Remark 3.1

When we comparing any two FFNs \(\lambda_{1} = \,\left( {0.5,\,0.5} \right)\) and \(\lambda_{2} = \,\left( {0.4,\,0.4} \right)\), we can observe that the score function given by Definition 3.2 (Senapati and Yager 2019a, b) is unable to distinguish the difference between the given FFNs because \(\wp_{s} \left( {\lambda_{1} } \right) = \,\wp_{s} \left( {\lambda_{2} } \right)\, = \,0\), whilst the developed IGSF (1) can successfully deal with this example and therefore, we have \(\wp_{s}^{*} \left( {\lambda_{1} } \right) = \,0.2188\) and \(\wp_{s}^{*} \left( {\lambda_{2} } \right) = \,0.1198.\) Hence, \(\lambda_{1} \, \succ \,\lambda_{2} .\) This verifies the validity of the proposed score function over the existing one.

Here, Fig. 1 presents the value of score function \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) w. r. t. \(\gamma_{1} \,,\,\gamma_{2} > 0,\,\,\gamma_{1} \, + \gamma_{2} = 1\) and at \(\left( {b_{j} ,\,n_{j} } \right) = \left( {0.8,\,0.7} \right).\) The color of each pair \(\,\left( {\gamma_{1} \,,\,\gamma_{2} } \right)\) on the simplex demonstrates the score value of the fixed Fermatean fuzzy numbers. As the value of \(\,\gamma_{1}\) and \(\gamma_{2}\) become larger, the value of \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) becomes better. Similarly, Fig. 2 presents the value of score function \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) w.r.t. \(b_{j}\) and \(n_{j}\) at \(\gamma_{1} = \gamma_{2} = 0.5.\) The color of each pair \(\,\left( {b_{j} \,,\,n_{j} } \right)\) on the simplex presents the deviation on score function of the fixed Fermatean fuzzy numbers. As the value of \(\,b_{j}\) become larger, the value of \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) becomes superior.

Fig. 1
figure 1

IGSF \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) w.r.t. parameters \(\,\gamma_{1} \,,\,\gamma_{2} ,\) at \(\,\left( {b_{j} ,\,\,n_{j} } \right) = \left( {0.8,0.7} \right).\)

Full size image
Fig. 2
figure 2

The function \(\wp_{s}^{*} \left( {\lambda_{j} } \right)\) w.r.t. parameters \(b_{j} \,,\,n_{j} ,\) at \(\gamma_{1} \, = \,\gamma_{2} \, = \,0.5\)

Full size image

Alternatively, the effects of diverse values of \(\gamma_{1}\) and \(\gamma_{2}\) on the preference order of the FFNs has been examined and their equivalent score values are summarized in Fig. 1 and Fig. 2. From the Figs. 1 and 2, it has been concluded that with the increase of \(\gamma_{1}\) from 0 to 1 (or simultaneously decreasing the value of \(\gamma_{2}\) from 1 to 0) the relative score of the FFNs increases. Also, from Remark 3.1, relative score of the FFNs increases but the overall ranking of the FFNs remain unaltered. Thus, based on these different parameter values, system analysis or decision maker may possess the power to alter the ranks of the FFNs.

4 Novel Fermatean fuzzy-based decision making method

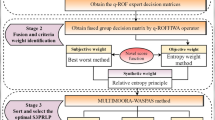
Ghorabaee et al. (2015) originated the notion of EDAS method as an effective tool for solving MCDM problems with conflicting criteria. In this method, the optimal solution is estimated based on the distance from average solution. Therefore, there is no need to estimate the ideal and anti-ideal solutions. This is the key benefit of the EDAS approach. As FFS is one of the new ways to deal with the uncertainty of real-life applications. So, in this section, we combine the CRITIC and EDAS approaches with FFSs for solving complicated decision-making problems and named as Fermatean fuzzy CRITIC-EDAS (FF-CRITIC-EDAS) (see Fig. 3).

Fig. 3
figure 3

Proposed decision making method

Full size image

Step 1. Problem description

Consider that \(\left\{ {K_{1} ,\,K_{2} ,\,...,\,K_{p} } \right\}\) be a set of options and \(\left\{ {N_{1} ,\,N_{2} ,\,...,\,N_{q} } \right\}\) be a criterion set. Let us suppose that a group of decision makers (DMs) \(\left\{ {O_{1} ,\,O_{2} ,\,...,\,O_{r} } \right\}\) presents their judgments on each option \(K_{i}\) concerning a criterion \(N_{j}\) in terms of FFNs. Assume that \(M_{k} \, = \,\left( {\beta_{ij}^{(k)} } \right)\,(i\, = 1,\,2,\,...,p,\,j\, = 1,\,2,\,...,q)\) be the Fermatean fuzzy decision matrix (FF-DM) offered by the kth DM, in which \(\beta_{ij}^{(k)}\) signifies the evaluation information of an option \(K_{i}\) w.r.t. criterion \(N_{j}\) in the form of FFNs.

Step 2. Determination of DMs’ weights

In order to compute the significance degrees of DMs, first of all, consider the significance degrees of the DMs in term of FFNs. Now, suppose \(W = \left( {b_{k} ,\,n_{k} } \right)\) be the importance rating of kth DM expressed by an authority in terms of FFN, then the formula for the computation of kth DM’s weight is presented as follows:

$$\psi_{k} = \frac{{b_{k}^{3} \left[ {1 + \left( {\gamma_{1} \, + \gamma_{2} } \right)\left( {1 - b_{k}^{3} - n_{k}^{3} } \right)} \right]}}{{\sum\limits_{k = 1}^{r} {\left( {b_{k}^{3} \left[ {1 + \left( {\gamma_{1} \, + \gamma_{2} } \right)\left( {1 - b_{k}^{3} - n_{k}^{3} } \right)} \right]} \right)} }},\,\,k = 1,\,2,\,...,r,\,\gamma_{1} \, + \gamma_{2} = 1,\,\gamma_{1} \,,\,\gamma_{2} > 0.$$
(2)

Here, \(\psi_{k} \ge 0\) and \(\sum\limits_{k = 1}^{r} {\psi_{k} \, = \,1.}\)

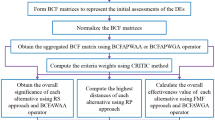
Step 3. Aggregate the individual opinions of DMs

In the MCDM problem, it is important to merge all the individuals’ opinions of DMs into a collective opinion to form the aggregated Fermatean fuzzy decision matrix (A-FFDM). To facilitate this, FF-weighted averaging operator (FFWAO) is employed on FF-DM and let \(Z = \left( {z_{ij} } \right)_{p\, \times \,q} ,\)\((i = 1,\,2,\,...,\,p,\)\(j = 1,2,\,...,\,q)\) be the A-FFDM, where

$$z_{ij} = \left( {\sqrt[3]{{1 - \prod\limits_{k = 1}^{r} {\left( {1 - \left( {b_{ij}^{k} } \right)^{3} } \right)^{{\psi_{k} }} \,} }}\prod\limits_{k = 1}^{r} {\left( {n_{ij}^{k} } \right)^{{\psi_{k} }} } } \right).$$
(3)

Step 4. Evaluate the criteria weight by employing CRITIC technique

Firstly, consider that \({\rm X} = \left( {\varpi_{1} ,\,\varpi_{2} ,...,\,\varpi_{q} } \right)^{T}\) be the weight of the criterion set with \(\varpi_{j} \in \left[ {0,\,\,1} \right]\) and \(\sum\limits_{j = 1}^{q} {\varpi_{j} } \, = 1\). Now, the computation procedure of CRITIC method is presented in the following steps:

Step 4.1. Evaluate the score matrix \(\** = \left( {\kappa_{ij} } \right)_{p\, \times \,q} ,\,\) wherein

$$\kappa_{ij} = \,b_{ij}^{3} \left[ {1 + \left( {\gamma_{1} \, + \gamma_{2} } \right)\left( {1 - b_{ij}^{3} - n_{ij}^{3} } \right)} \right],$$
(4)

Step 4.2. Switch the score matrix \(\**\) into a standard Fermatean fuzzy matrix \(\tilde{\** } = \left( {\tilde{\kappa }_{ij} } \right)_{p\, \times \,q}\)

$$\tilde{\kappa }_{ij} = \left\{ \begin{gathered} \frac{{\kappa_{ij} - \,\kappa_{j}^{ - } }}{{\kappa_{j}^{ + } - \,\kappa_{j}^{ - } }},\,\,\,\,\,\,j \in N_{b} , \hfill \\ \frac{{\kappa_{j}^{ + } - \,\kappa_{ij} }}{{\kappa_{j}^{ + } - \,\kappa_{j}^{ - } }},\,\,\,\,\,\,j \in N_{n} , \hfill \\ \end{gathered} \right.$$
(5)

where \(\kappa_{j}^{ - } = \mathop {\min }\limits_{i} \kappa_{ij}\) and \(\kappa_{j}^{ + } = \mathop {\max }\limits_{i} \,\kappa_{ij} .\)

Step 4.3. Estimate the criteria standard deviations with the use of following formula:

$$\sigma_{j} = \sqrt {\frac{{\sum\limits_{i = 1}^{p} {\left( {\tilde{\kappa }_{ij} - \overline{\kappa }_{j} } \right)^{2} } }}{p}} ,$$
(6)

where \(\overline{\kappa }_{j} = \,\sum\limits_{i = 1}^{p} {{{\tilde{\kappa }_{ij} } \mathord{\left/ {\vphantom {{\tilde{\kappa }_{ij} } p}} \right. \kern-\nulldelimiterspace} p}} .\)

Step 4.4. Calculate the correlation between criteria with the use of following formula:

$$r_{jt} = \frac{{\sum\limits_{i = 1}^{p} {\left( {\tilde{\kappa }_{ij} - \overline{\kappa }_{j} } \right)\left( {\tilde{\kappa }_{it} - \overline{\kappa }_{t} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^{p} {\left( {\tilde{\kappa }_{ij} - \overline{\kappa }_{j} } \right)^{2} \sum\limits_{i = 1}^{p} {\left( {\tilde{\kappa }_{it} - \overline{\kappa }_{t} } \right)^{2} } } } }}.$$
(7)

Step 4.5. Evaluate the quantity of information of each criterion by using

$$\upsilon_{j} = \sigma_{j} \,\sum\limits_{t = 1}^{q} {\left( {1 - r_{jt} } \right)} .$$
(8)

The better the cj is, the more information an attribute contains, consequently the weight of evaluation attribute is superior than that of other attributes.

Step 4.6. Calculate the weight of each criterion as follows:

$$\varpi_{j} = \frac{{\upsilon_{j} }}{{\sum\limits_{j = 1}^{q} {\upsilon_{j} } }}.$$
(9)

Step 5. Assess the average solution (AVS) associated to the criteria

$$\diamondsuit_{i} = \left[ {\varepsilon_{i} } \right]_{1 \times q} = \frac{1}{p}\mathop \oplus \limits_{i = 1}^{p} z_{ij} ,\,\,i = 1,\,2,\,...,p,\,\,j = 1,\,2,\,...,q.$$
(10)

Step 6. Estimate the positive distance and the negative distance from average solution matrix according as the benefit and cost criteria

If \(N_{b}\) and \(N_{n}\) are the set of benefit and cost criteria, respectively, then the positive distance from average (PDA) and the negative distancefrom average (NDA) are computed as below:

$$\Lambda_{PDA} = \left[ {h_{ij} } \right]_{p\,\, \times \,q} \;{\text{and}}\;\Lambda_{NDA} = \left[ {\chi_{ij} } \right]_{p\,\, \times \,q},$$
(11)

such that

$$h_{ij} = \left\{ \begin{aligned} \frac{{\max \left( {0,\,z_{ij} \,\Theta \,\varepsilon_{i} } \right)}}{{\wp_{s}^{*} \left( {\varepsilon_{i} } \right)}},\,\,{\rm if}\,\,j \in N_{b} \\ \frac{{\max \left( {0,\,\varepsilon_{i} \,\Theta \,z_{ij} } \right)}}{{\wp_{s}^{*} \left( {\varepsilon_{i} } \right)}},\,\,{\rm if}\,\,j \in N_{n}\end{aligned} \right.\; {\rm and} \;\;\;\chi_{ij} = \left\{ \begin{aligned} \,\frac{{\max \left( {0,\,\varepsilon_{i} \,\Theta \,z_{ij} } \right)}}{{\wp_{s}^{*} \left( {\varepsilon_{i} } \right)}},\,\,{\rm if}\,\,j \in N_{b} \\ \frac{{\max \left( {0,\,z_{ij} \,\Theta \,\varepsilon_{i} } \right)}}{{\wp_{s}^{*} \left( {\varepsilon_{i} } \right)}},\,\,{\rm if}\,\,j \in N_{n} , \end{aligned} \right.$$
(12)

wherein \(h_{ij}\) and \(\chi_{ij}\) describe the positive and the negative distances of assessment degrees of ith option from the AVS on jth criterion, respectively, and \(\wp_{s}^{*} \left( {\varepsilon_{i} } \right)\) shows the score value of AVS.

Step 7. Compute the weighted sum of PDA \(\left( {{\mathbb{Z}}_{i}^{\left( + \right)} } \right)\) and weighted sum of NDA \(\left( {{\mathbb{Z}}_{i}^{\left( - \right)} } \right)\) for all options by using the following formulae:

$${\mathbb{Z}}_{i}^{\left( + \right)} = \mathop \oplus \limits_{j = 1}^{q} \varpi_{j} \,h_{ij} ,$$
(13)
$${\mathbb{Z}}_{i}^{\left( - \right)} = \mathop \oplus \limits_{j = 1}^{q} \varpi_{j} \,\chi_{ij} .$$
(14)

Step 8. For all options, determine the normalize values of \({\mathbb{Z}}_{i}^{\left( + \right)}\) and \({\mathbb{Z}}_{i}^{\left( - \right)}\), given as

$${\mathbb{N}}_{i}^{\left( + \right)} = \frac{{{\mathbb{Z}}_{i}^{\left( + \right)} }}{{\max_{i} \left[ {\wp_{s}^{*} \left( {{\mathbb{Z}}_{i}^{\left( + \right)} } \right)} \right]}},$$
(15)
$${\mathbb{N}}_{i}^{\left( - \right)} = 1 - \frac{{{\mathbb{Z}}_{i}^{\left( - \right)} }}{{\max_{i} \left[ {\wp_{s}^{*} \left( {{\mathbb{Z}}_{i}^{\left( - \right)} } \right)} \right]}}.$$
(16)

Here, the terms ‘\(\wp_{s}^{*} \left( {{\mathbb{Z}}_{i}^{\left( + \right)} } \right)\)’ and ‘\(\wp_{s}^{*} \left( {{\mathbb{Z}}_{i}^{\left( - \right)} } \right)\)’ denote the score values of weighted sum of PDA and NDA, respectively.

Step 9. Evaluate the appraisal score for all options, given as

$${\mathbb{C}}_{i} = \frac{1}{2}\left( {{\mathbb{N}}_{i}^{\left( + \right)} \oplus {\mathbb{N}}_{i}^{\left( - \right)} } \right),\,\,i = 1,\,2,\,...,p.$$
(17)

Step 10. Based on the score values \(\wp_{s}^{*} \left( {{\mathbb{C}}_{i} } \right)\) of appraisal scores \({\mathbb{C}}_{i} \,\left( {i = 1,\,2,\,...,p} \right),\) determine the ranking of the alternatives. As a result, the alternative with the highest appraisal score is the most appropriate choice among the others.

Step 11. End.

5 Case study: S3PRLP selection problem

In this section, we present an illustrative example of Indian electronics manufacturing firm to reveal the effectiveness and potentiality of the proposed FF-CRITIC-EDAS methodology. The considered manufacturing firm is situated in Gurugram, India and at present, this firm has five S3PRLP options (K1, K2, K3, K4, K5), correspondingly. In order to process the present decision-making problem, we form a group of three skilled decision makers (\(O_{1} ,\,O_{2} ,\,O_{3}\)). The given S3PRLP options are evaluated on the basis of following 13 attributes/criteria: Cost of pollution control (N1), Cost of green product and eco-design (N2), Green warehousing (N3), Green R & D and innovation (N4), Environmental management system (N5), Costs (N6), Flexibility (N7), Quality (N8), Technology capability (N9), Health and safety practices (N10), Social responsibility (N11), Education Infrastructure (N12) and Employment Practices (N13). The preferred criteria in this study are taken from different resources. The descriptions of these attributes are shown in Table 1. In this study, the criteria N1, N2 and N6 are of cost type and remaining others are of benefit type.

Table 1 Descriptions of the criteria for S3PRLP assessment
Full size table

The implementation procedures of FF-CRITIC-EDAS method for the evaluation of S3PRLPs are as given below:

Step 1. Let us assume that the importance ratings of DMs’ judgements are given in the form of FFNs which as {(0.80, 0.50, 0.7133), (0.85, 0.45, 0.6655), (0.75, 0.55, 0.7440)}. Now, the FF-DM is constructed in Table 2.

Table 2 Fermatean fuzzy decision matrix for S3PRLPs assessment
Full size table

Steps 2–3: As the weights ofthe DMs’ as expressed by the experts are conveyed in the form of FFNs. Next, with the use of Eq. (2), the DMs’ weights are obtained in the following crisp form: {\(\Psi_{1} =\) 0.3341, \(\Psi_{2} =\) 0.3807, \(\Psi_{3} =\) 0.2852}. Further, the evaluation opinions provided by three DMs are aggregated with the use of Eq. (3) and then required A-FFDM are presented in Table 3.

Table 3 A-FFDM and AVS matrix for S3PRLP assessment
Full size table

Step 4. In the step, the criteria weights are determined by CRITIC approach, which as

Step 4.1. First, with the use of Eq. (4) and Table 3, the score values of A-FFDM are evaluated.

Step 4.2. Convert the score matrix \(\** = \left( {\kappa_{ij} } \right)_{p\, \times \,q}\) into the standard FF-matrix \(\tilde{\** } = \left( {\tilde{\kappa }_{ij} } \right)_{p\, \times \,q}\) by employing the Eq. (5).

Steps 4.3–4.6. With the use of Eqs. (6)–(8), the standard deviation, correlation coefficient and quantity of information of each factor are computed and presented in Table 4. By employing Eq. (9), the criteria weights (\(\varpi_{j}\)) are estimated and then shown in Table 4.

Table 4 The standard FF-matrix \(\tilde{\** } = \left( {\tilde{\kappa }_{ij} } \right)_{p\, \times \,q} ,\) SD, quantity of information and weight value for each factor
Full size table

Steps 5–9. By employing Eq. (10) and Table 3, the AVS matrix is computed and shown in Table 3. With the use of formulae (11)-(17), the PDA and NDA based on types of criteria, weighted sum of PDA and NDA for all alternatives, the normalize values of weighted sum of PDA and NDA and the appraisal score \(\left( {{\mathbb{C}}_{i} } \right)\) for all options are estimated and presented in Tables 5, 6, respectively.

Table 5 PDA and NDA matrices for S3PRLP selection
Full size table
Table 6 Evaluation parameters of FF-CRITIC-EDAS approach for S3PRLP selection
Full size table

Step 10. On the basis of score function \(\wp_{s}^{*} \left( {{\mathbb{C}}_{i} } \right)\) of appraisal score \(\left( {{\mathbb{C}}_{i} } \right),\) the option K3 is the most optimal choice and the ranking order of the S3PRLP alternatives is \(K_{3} \, \succ \,K_{4} \, \succ \,K_{5} \, \succ K_{1} \, \succ \,K_{2} .\,\)

5.1 Comparative analysis

In this section, a comparison with Fermatean Fuzzy-TOPSIS (Senapati & Yager, 2019a) and Fermatean Fuzzy-WPM (Senapati & Yager, 2019b) is presented to verify the robustness of the proposed methodology.

5.1.1 Fermatean fuzzy-TOPSIS (Senapati and Yager 2019a) method

The Fermatean Fuzzy-TOPSIS method involves the following calculation procedures:

Steps 1–4. Same as FF-CRITIC-EDAS framework.

Step 5. In the present case study, N1, N2 and N6 are cost criteria and rest all are benefit criteria, therefore, there is a need to normalize the A-FFDM.

Step 6. Estimate the Fermatean fuzzy positive and negative ideal solutions, presented as \(x^{ + }\) = {(0.578,0.688), (0.441, 0.722), (0.548, 0.477),(0.701, 0.563), (0.681, 0.556), (0.533, 0.777), (0.707, 0.635), (0.705, 0.556), (0.685, 0.588), (0.685, 0.554), (0.710, 0.604),(0.755, 0.638), (0.724, 0.581)} and \(x^{ - }\) = {(0.437, 0.753), (0.616, 0.712), (0.693, 0.544),(0.619, 0.530), (0.641, 0.547), (0.615, 0.764), (0.671, 0.654), (0.658, 0.538), (0.631, 0.564), (0.664, 0.672), (0.657, 0.610), (0.701, 0.655), (0.625, 0.714)}, respectively.

Now, find out the distances between the alternatives Ki and the Fermatean fuzzy positive and negative ideal solutions over the attribute Nj.

Step 7. The relative closeness to the Fermatean fuzzy positive ideal solution is determined by utilizing

$$R\left( {K_{i} } \right) = \frac{{\Upsilon_{i}^{ - } }}{{\Upsilon_{i}^{ + } + \,\Upsilon_{i}^{ - } }},$$

where \(\Upsilon_{i}^{ + } = \,dis\left( {z_{ij} ,\,x^{ + } } \right) = \sum\limits_{j = 1}^{n} {\varpi_{j} \sqrt {\frac{1}{2}\left[ {\left( {\left( {b_{ij} } \right)^{3} - \left( {b_{j}^{ + } } \right)^{3} } \right)^{2} + \left( {\left( {n_{ij} } \right)^{3} - \left( {n_{j}^{ + } } \right)^{3} } \right)^{2} + \left( {\left( {\pi_{ij} } \right)^{3} - \left( {\pi_{j}^{ + } } \right)^{3} } \right)^{2} } \right]} }\) and

$$\Upsilon_{i}^{ - } = dis\left( {z_{ij} ,\,x^{ - } } \right) = \sum\limits_{j = 1}^{q} {\varpi_{j} \sqrt {\frac{1}{2}\left[ {\left( {\left( {b_{ij} } \right)^{3} - \left( {b_{j}^{ - } } \right)^{3} } \right)^{2} + \left( {\left( {n_{ij} } \right)^{3} - \left( {n_{j}^{ - } } \right)^{3} } \right)^{2} + \left( {\left( {\pi_{ij} } \right)^{3} - \left( {\pi_{j}^{ - } } \right)^{3} } \right)^{2} } \right]} } .$$

Therefore, the obtained values are \(R\left( {K_{1} } \right)\) = 0.589, \(R\left( {K_{2} } \right)\) = 0.343, \(R\left( {K_{3} } \right)\) = 0.499, \(R\left( {K_{4} } \right)\) = 0.472, \(R\left( {K_{5} } \right)\) = 0.480.

Step 8: The preference order of S3PRLP options are \(K_{1} \succ K_{3} \succ K_{5} \succ K_{4} \succ K_{2} ,\) thus, the option K1 is the best S3PRLP.

5.1.2 Fermatean fuzzy-WPM (Senapati and Yager 2019b) method

Steps 1–5. Same as FF-CRITIC-EDAS approach.

Step 6. Based on Weighted Product Model (WPM), the total relative significance of option Ki is calculated using \(\delta \left( {K_{i} } \right) = \mathop \otimes \limits_{j = 1}^{q} \,\varpi_{j} \,z_{ij} ,\,\,\,i = 1,\,2,\,...,p.\) Thus, we have \(\delta \left( {K_{i} } \right)\) = {(0.654, 0.594), (0.660, 0.630), (0.690, 0.605), (0.677, 0.609), (0.672, 0.598).

Step 7. The score values of relative importance degree of options are calculated as \(\wp_{s}^{*} \left( {\delta \left( {K_{1} } \right)} \right) = \,0.422,\), \(\wp_{s}^{*} \left( {\delta \left( {K_{2} } \right)} \right) = \, 0.421,\), \(\wp_{s}^{*} \left( {\delta \left( {K_{3} } \right)} \right) = \,0.476,\), \(\wp_{s}^{*} \left( {\delta \left( {K_{4} } \right)} \right) = \,0.454\) and \(\wp_{s}^{*} \left( {\delta \left( {K_{5} } \right)} \right) = \,0.450.\) The preference order of options are as \(K_{3} \succ K_{4} \succ K_{5} \succ K_{1} \succ K_{2} .\) Hence, the alternative K3 is the best choice among the given S3PRLPoptions.

Based on Fermatean fuzzy-TOPSIS method, the preference ordering of the S3PRLP alternatives is \(K_{1} \succ K_{3} \succ K_{5} \succ K_{4} \succ K_{2} ,\) and thus, the option K1 is the best choice. Similarly, with the use of Fermatean fuzzy-WPM, the final ranking of the S3PRLP alternatives is \(K_{3} \succ K_{4} \succ K_{5} \succ K_{1} \succ K_{2}\) and thus, K3 is the most desirable option. Figure 4 presents the graphical representation of ranking of the options by different approaches. Consequently, we can see that the desirable S3PRLP alternative, i.e., (K3) is same by using Fermatean fuzzy-WPM and introduced approach, whereas the ranking result somewhat differ by Fermatean fuzzy-TOPSIS approach and the desirable choice is K1. Also, by comparing with Tavana et al. (2018) and Li et al. (2018) approaches, the final ranking order of the S3PRLP alternatives is \(K_{3} \succ K_{5} \succ K_{4} \succ K_{2} \succ K_{1}\) and \(K_{3} \succ K_{4} \succ K_{5} \succ K_{2} \succ K_{1} ,\) respectively, therefore, the most appropriate choice is K3 among all other S3PRLPs.

Fig. 4
figure 4

The significance degrees of alternatives over different methods

Full size image

The introduced methodology discussed in this study is found proficient for solving the MCDM problems with conflicting criteria. The main advantages of the proposed method are listed as below:

  • To deal with the ambiguity in the MCDM problems, all input variables are taken into account as uncertain issues described by Fermatean fuzzy numbers. The indeterminacy degree is considered necessary independently in the whole method and the options are put in rank utilizing trade-off values of all three parameters, unlike Tavana et al. (2018) wherein the IFSs have been applied, and Li et al. (2018) wherein the FSs have been used a particular case of the FFSs.

  • In the proposed method, the optimal criteria weights are evaluated using the CRITIC approach, which combines the individual contrast intensity and conflict between criteria, thus provides more accurate results, whereas the criteria weights are randomly chosen in Fermatean fuzzy-TOPSIS (Senapati and Yager 2019a) and Fermatean fuzzy-WPM (Senapati and Yager 2019b), and Tavana et al. (2018) applies ANP model to evaluate subjective weights of the criteria and Li et al. (2018) utilizes PCA-AHP model to compute the criteria weights.

  • As compared to the Fermatean fuzzy-TOPSIS (Senapati and Yager 2019a) and fuzzy-TOPSIS (Tavana et al. 2018) approaches, in which the “positive ideal solution” and “negative ideal solution” are calculated by the experts as per their own facts, whilst in EDAS method, Fermatean fuzzy weighted averaging operator is employed for the determination of AVS, which is simple and free from the impact of human concerns. Furthermore, the subtraction procedure and IGSF of Fermatean fuzzy numbers is used to estimate the “PDA” and the “NDA” of each alternative. It can fruitfully evade the selecting distance measure which needs to add or reduce the number of objects of FFSs and lead to the distortion of information.

  • The developed FF-CRITIC-EDAS framework is not only appropriate for evaluating the MCDM problems under FFSs context, but can also successfully tackle with the MCDM problems under fuzzy sets, intuitionistic fuzzy sets and Pythagorean fuzzy sets contexts. The introduce methodology has the benefits of easy computation process and fast information processing.

Some limitations of the proposed method are as follows:

  • In the proposed FF-CRITIC-EDAS method, all criteria are assumed to be independent. In reality, there are interrelationships among the criteria.

  • This method has limitation in order to deal with a large number of criteria.

5.2 Discussions

The past period has witnessed ever-increasing issue about the disposal of customer goods, since numerous of these materials comprise both large quantities of waste and considerable amounts of toxic heavy metals. Manufacturers have faced intensifying pressure from both governments and environmentally concentrated committee to ‘reduce’, ‘recycle’, and ‘reuse’ their industrial waste. Presently, RL has been considered as a main concern. The operative management of RL is useful to environmental safety, and it can carry the evident economic benefits to organizations. Many corporations do not hold sufficient resource or capability to accomplish their RL activities, thus they have to select the S3PRLP to those activities.

In this study, a novel FF-CRITIC-EDAS method was used to choose the suitable S3PRLPs for Indian manufacturing company located in Gurugram, India. A case study is taken to display some important insights regarding assessment criteria and prominent S3PRLP options. To do this, proposed IGSF is applied to compute the DMs’ weights, CRITIC model is used to assess the importance value of criteria and proposed EDAS method is implemented to rank the S3PRLP options. The obtained results by proposed method show that the option K3 is the most appropriate provider for this case. Moreover, the comparative discussion with extant models is also presented to elucidate the rationality of the introduced method. Thus, we found that K3 is the most suitable choice among a set of S3PRLPs. As a consequence, the proposed model has significant information that can be utilized by administrators in taking strategic or operational decisions in S3PRLPs evaluation.

Without loss of generality, the proposed framework would be correspondingly appropriate to other concerns and different organizations. It can also be applied as a standard procedure for service providers in guiding their modifications to the processes and strategic instructions, so that they can well assistance with client and societal potentials. Simultaneously, administrations and governing bodies can employ the introduced method to study the relationships among economic, environmental, and social concerns, and utilize the outcomes to influence and reassure stronger law and strategy execution on the sustainability.

6 Conclusions

The assessment of S3PRLP has become one of important decisions for the enterprises in the modern competitive market. The objective of this study is to introduce a MCDM methodology for assessing and selecting the optimal S3PRLP option on FFSs. To do this, firstly novel IGSF has been proposed to compare the options. Secondly, a hybrid framework based on CRITIC and EDAS methods with FFSs has been developed to solve the MCDM problems, wherein the DMs and attribute weights are completely unknown. In this framework, IGSF-based procedure has been proposed to compute the DMs’ weights and the attribute weights have been calculated by applying CRITIC approach. Further, a case study of S3PRLP selection has been taken to elucidate the practicality and effectiveness of the introduced framework. For this, an evaluation index process for S3PRLPs has been organized, which comprises three prime aspects. These aspects are characterized into five, four and four criteria, respectively, which are broadly deliberated according to the existing literatures. The CRITIC approach determines the weights of the considered criteria, which as Education infrastructure (0.1183), Flexibility (0.1097), Cost of green product and eco-design (0.1013), Green R & D and innovation (0.0975), Green warehousing (0.0745), Quality (0.0731), Environmental management system (0.0680), Technology capability (0.0644), Health and safety practices (0.0605), Costs (0.0603), Social responsibility (0.0587), Cost of pollution control (0.0569) and Employment practices (0.0567). Next, by employing the EDAS method, the priority order of S3PRLPs is obtained as \(K_{3} \, \succ \,K_{4} \, \succ \,K_{5} \, \succ K_{1} \, \succ \,K_{2} .\,\) Next, comparison with extant models has been made to validate the introduced framework. The outcomes verify that the introduced model has good proficiency and strength than the extant models. In addition, the introduced approach not only offers the priority order of the S3PRLP options but also illustrates the attributes performances in the S3PRLP selection.

In future, we will work on diverse MCDM approaches (namely, CoCoSo, WASPAS, MULTIMOORA or DNMA) to select the optimal S3PRLP under FFSs context. Also, we will implement the introduced framework to the different problems, namely, EVCS site evaluation, HCWD method assessment, green supplier assessment, and other decision-making problems.