A novel simple technique for determining the geogrid geometry affecting the bearing capacity of reinforced cohesive-frictional soil

Abstract

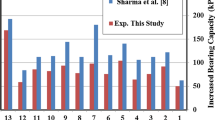
In this study, a developed simple new expression is suggested to analyze an impact of geometric dimensions of geogrid and its influences on increasing soil bearing capacity under the strip footing. The longitudinal and transverse elements in the reinforcement geogrid perform an essential function in resisting tensile stresses in reinforced soil. Therefore, the geogrid passive tensile strength is evaluated by the general shear failure pattern of Terzaghi’s theory. Since the failure in reinforced soil takes place as a result of increased stress affecting the tensile strength of the geogrid transverse and longitudinal ribs, the passive bearing mobilized strength is calculated according to the general shear failure of the theory of Terzaghi. The impact of bearing member rigidity, characteristic of geogrid surface, and the shearing mechanism inside the soil mass reinforced through the geometric proportions of the reinforcing element was investigated. A series of 22 numbers of experimental tests were carried out on both reinforced and non-reinforced soils. One type of fine sand and geogrid reinforcement were utilized in small-scale physical modeling. The influence of embedment depth of the first geogrid layer, vertical distance between two geogrid layers, and geogrid’s length was investigated by conducting different footing widths of plate load tests. The arrangement of the geogrid layers was also investigated to demonstrate how they affected parameters study and the results. Parameters affecting soil tolerance equation include interior friction angle of soil, coherence, geogrid tensile modulus, geogrid opening dimensions, thickness and length of longitudinal and transverse elements, soil unit weight, and footing width. The results were compared with some previous research findings. Then, new simple metric criteria were used for evaluation of quantitative expression of errors of new bearing capacity equation by regression analyses. The calculations indicate that the median error rate is less than 8%. As a result, the laboratory study confirms high-grade compatibility with a new bearing capacity expression.

Appendix. An example of a computational process (all the parameters used in the formula are from this study)

Example 1:

• 1) B = 0.1 m, c = 13.5 kPa, ϕ = 29.33°, γ = 15 kN/m³, z/B = u/B = 0.3, h/B = 0.4, L/B = 5, a = 0.01m, t = 0.0033m, n = 51.

• 2) ϕ = 29.33°, c =13.5 kN/m², t = 3.33 mm, D₅₀ = 0.34 mm.

N_q = 17.06, N_c = 28.58, N_γ = 16.7.

$$ {\displaystyle \begin{array}{c}{N}_{qg}=1.2\ \left(\frac{20-\frac{t_B}{D_{50}}}{10}\right).\left({e}^{\left(\left(\frac{\pi }{2}+\varnothing \right)\tan \varnothing \right)}\right).\tan \left(45+\frac{\varnothing }{2}\right)=1.74\kern0.5em {\mathrm{N}}_{\mathrm{qg}}=1.74\\ {}{\alpha}_q=\frac{1.2\ \left(\frac{20-\frac{t_B}{D_{50}}}{10}\right).\left({e}^{\left(\varnothing -\frac{\pi }{2}\right)\tan \varnothing}\right)}{\mathit{\tan}\left(45+\frac{\varnothing }{2}\right)}=0.102\end{array}} $$

${\alpha}_c=\frac{\left({N}_{qg}-1\right)}{\left({N}_q-1\right)}=0.046\kern0.5em$. Then, the results are α_c = 0.046, α_q = 0.102.

• 3) γ = 15 kN/m³, B = 0.1 m, z = u = 0.3B, h = 0.4B, and n = 51

  $$ {\displaystyle \begin{array}{c}{\alpha}_r=\sum \limits_{i=1}^N\frac{4n.t.\left[u+\left(i-1\right)h\right]}{B^2}=4.755\\ {}{q}^{\ast }=\left(1+\sum \limits_{i=1}^N\frac{4n.t.\left[u+\left(i-1\right)h\right]}{B^2}\times {\alpha}_c\right)\ c.{N}_c+\frac{1}{2}\gamma .B.{N}_{\gamma }=1.219\times 13.5\times 28.58+0.5\times 15\times 0.1\times 16.7=470.33+12.525=482\ \mathrm{kPa}.\end{array}} $$

• 4) γ = 15 kN/m³, z = u = 0.3B, h = 0.4B, a = 0.01 m, t = 0.0033 m, n = 51.

  $$ {q}_r=\frac{\left(1+\sum \limits_{i=1}^N\frac{4n.t.\left[u+\left(i-1\right)h\right]}{B^2}\times {\alpha}_c\right)\ c.{N}_c+\frac{1}{2}\gamma .B.{N}_{\gamma }}{\left(1-\frac{1}{\pi}\sum \limits_{i=1}^N\frac{4n.t.\left[u+\left(i-1\right)h\right]}{B^2}\ \left[{\tan}^{-1}\frac{2z}{B-2x}-{\tan}^{-1}\frac{2z}{B+2x}-\frac{4 Bz\left(4{x}^2-4{z}^2-{B}^2\right)}{{\left(4{x}^2+4{z}^2-{B}^2\right)}^2+16{B}^2{z}^2}\right].{\alpha}_q.{N}_q\right)}=\frac{482}{\left(1-\Big(0.0172\right)\times 0.102\times 17.06\Big)}=497\ \mathrm{kPa}. $$