“A multi-tier sustainable food supplier selection model under uncertainty”

Abstract

Supplier selection in food supply chains (FSCs) is not much explored due to the inherent difficulties, complexities and nature of food industry. Food security and quality are top row topics in today’s world health scenario. During sudden food crisis, it needs extra attention where producers, suppliers, and stakeholders play the most vital roles. This paper puts forward a two-phase sustainable multi-tier supplier selection model for FSC based on an integrated decision analysis under multi-criteria perspectives considering sustainability criteria, suppliers and sub-suppliers. In the first phase, the model estimates supplier selection criteria weights using a combined version of step-wise weight assessment ratio analysis (SWARA) and level based weight assessment (LBWA) in conjunction with D-numbers. In the second phase, Measurement of Alternatives and Ranking according to the COmpromise Solution (MARCOS)-D method is applied to obtain a ranking pre-order of different tier suppliers. Moreover, several sensitivity analyses are carried out in order to examine model reliability. To check application practicability, the proposed model is implemented in a case study of WineSol Corporation in Spain. The proposed model is expected to serve as a kickoff point for develo** advanced decision-making models for effectually address multi-tier supplier selection problems under uncertain environment.

1 Introduction

Global market and trade utterly need integrated supply chain management systems (SCMSs) to enable organizations to effectively react to increased customer satisfaction. SCM is interpreted as a process establishing network of firms, suppliers, transportation systems, logistics hubs and production units. The major concerns of any SCM is to coordinate and efficiently control material flow, information and finances in order to meet customer demands and overall business objectives (Meredith and Shafer 2019; Saberi et al. 2019). The main concern of SC managers is to ensure a harmonic balance among all elements in the SCM network. This harmony can be defined in terms of safety, security, stability, sustainability and cooperation between the elements during entire product life cycle. In many aspects, suppliers as the main operating engine can accelerate the system or negatively affect system efficiency.

Supplier relationship and development initiatives coupled with a capable and competent supplier network always play a decisive role for any enterprise in order to remain competitive in the worldwide market for drawing out maximum value through such relationships. Food SCM (FSCM) provides crucial support to any country’s socio-economic development and emphasize on precise development of producer–consumer relationships and transparency with regard to production practices. Nowadays, food and agricultural consumers are highly keen to be kept informed about the different processes which food products go through from farm level to market level. In other words, consumers are interested in being informed about the procurement quality, safety, production and packaging methods, hygiene and other related standards which strongly affect their willingness to buy products (Redmond and Griffith 2003). According to Wognum et al. (2011), food and agricultural organizations have to consider such parameters in their SC operations in order to meet consumer requirements and satisfaction. Apart from social considerations, an appropriately designed FSCM also requires efficient and effective SC operations in terms of economic and environmental considerations. For example, León-Bravo et al. (2019) investigated that there is a strong relationship between sustainability practices and its operational performances in an FSCM, especially, roles of multi-tier suppliers in food sector can not be neglected. In an FSCMS, multi-tier SC includes more than one level of manufacturers or suppliers to produce or supply products or services. There are numerous relationships happening between buyers and suppliers within the entire SC. In many real time situations, this process may involve number of different suppliers to bring products to customers. Wilhelm et al. (2016) believed that involvement of multi-tier suppliers is an essential requirement in achieving sustainability compliance in the entire SCMS, failing of which may put focal organizations at a risk of degraded brand value and unsolicited legal issues. Real time examples have already been observed for many well reputed supermarkets due to the delinquency of second and (1 + n)^th-tier suppliers (Viswanadham and Samvedi 2013; Sawik 2020). These sub-suppliers are basically the extended parts of the SC and remain on the far side of direct control of the focal organizations. In spite of such incidents, most of the conventional approaches have disregarded organizational responsibilities for unfavorable consequences arising due to improper sub-level supplier selection including first phase of raw material extraction and environmental impacts in the SC. Moreover, past researchers have not paid much attention beyond the implied evaluation of straightforward first-tier suppliers. Dedicated studies in FSC are also limited in the literature due to its inherent complication and particularized nature of product characteristics. According to Rong et al. (2011), the most significant parameters in an FSC include product quality, security and safety. Global food industry currently struggles with multiple competitive primitivenesses along with new challenges of green production and safe delivery to end users. Even in pandemic crisis like COVID-19, the basic food supply system in many develo** countries have been severely interrupted due to lack of access to workers, failure of operating systems, supplier disruptions, transportation restrictions and production breakdown (WHO 2020). FSC industries usually face unexpected variations in operations, breakdowns, quality issues and other unpredicted events like supply disasters. A failure in supplier performance potentially liberates negative consequences for further upstream or downstream of FSC. One of the most promising elements in FSC is supplier performance, the potential interaction of which may totally collapse or enhance the overall efficiency (Diabat et al. 2012; Grimm et al. 2014; Pamucar 2020).

Suppliers are vital elements of any SCMS and their functional capacity and performance directly or indirectly affect the fluency of the system including manufacturing, service or food industries (Ahmed et al. 2020). Transportation companies, logistics services and raw material providers are parts of a SC network for any typical enterprise. Evaluating performance and quality of suppliers should be configured and programmed in long horizons. Development of such plans greatly reduces risk and vulnerability of SC and helps to progress toward a smoother production system (Tidy et al. 2016). Earlier studies have demonstrated the important role of supplier performance measurement on productivity of SCMSs (Narasimhan et al. 2008; Kim et al. 2018); healthcare centers (Liu et al. 2019); agriculture (Kamble et al. 2020); food industry (Govindan 2018; Yazdani et al. 2020) and logistics (Khan et al. 2019b; Khan et al. 2020a). Interested readers are referred to a comprehensive literature review on sustainable supply chain management recently published by Khan et al. (2021).

One of the important applications of SC operations is found in perishable products like food items. FSC is defined as an integrated operation starting from production farms to manufacturers to distribution centers which finally delivers agricultural products to the customers (Allaoui et al. 2018). In other words, FSC is a series of operations that has an important position in global SC networks with respect to the fact that food products are considered as the main demand of human beings. Furthermore, FSC is not only targeting to fulfill food demands of human beings, but also, it is one of the potential industries for job creation, economic growth, environmental and social effects (Vermeulen et al. 2012; Khan and Qianli 2017; Govindan 2018; Khan and Yu 2020; Khan et al. 2020b). Unlike other applications of SCM, the FSCM is always under surveillance of different environmental, social and economic organizations who support and propose consumption policies with respect to societal characteristics. Therefore, FSCM and its operational functions are very pragmatic and should deliberately be addressed in order to maximize customer satisfaction and organizational profits.

In one of the very first studies, Jedvall (1999) premeditated FSCM with respect to its effect on economy and environment in order to make SC operations more efficient and sustainable. Smith (2008) presented a framework to analyze the important factors for sustainable FSCs with a focus on suppliers, manufacturers, distributors, governmental and non-governmental organizations. Wognum et al. (2011) addressed FSCM using information systems in terms of transparency which has an important role in customer’s trust and brand loyalty. Cojocariu (2012) studied SCMS of modern agriculture and manufacturing technologies with emphasize on logistics considering green factors. Garnett (2013) studied FSCM policies and operations in terms of environmental aspects of production, consumption, and socio-economic challenges. Kaipa et al. (2013) presented a descriptive analysis of FSC for material and information flows in milk and fish companies. Li et al. (2014) presented a review for FSCM considering sustainable development goals in order to highlight the research gaps in applied methods. Govindan (2018) proposed a conceptual framework for sustainable production and consumption policies in FSC. This study presented a comprehensive literature review of sustainable SC and FSC. In this study, the author developed a framework for FSC by highlighting important indicators, drivers and barriers in FSC.

As discussed above, FSC is one of the significant SC networks which aims to deliver food products from farms to consumers before their expiration times. Thus, organizations are required to develop reliable and well-designed decision making models for facilitating the decision making process for different operations and functions. Decision making process in FSC has turned to be very difficult and at the same time, critical due to the presence of high number of decision factors and barriers. To overcome these, researchers have developed different decision making models using simulation, mathematical optimization, data mining, machine learning algorithms and multi-criteria decision making (MCDM) methods to address its complexities. Ting et al. (2014) proposed an association rule mining (ARM) and Dempster's rule of combination-based decision support system to increase the power of DMs in FSC to devise reliable plans for logistics section. The proposed decision support model was investigated for a real case study of wine industry in Hong Kong. Meneghetti and Monti (2015) developed an optimization model using constraint programming for sustainable network design of cold food products. In this model, they focused on important factors like facility location, storage temperature of warehouses, additional costs caused by temperature, energy use, and harmful greenhouse emissions. Bortolini et al. (2016) proposed a multi-objective optimization (MOO) model using mixed integer programming (MIP) for a FSC problem in multi-produce, multi-model, and multi-level distribution network environment. The proposed model was applied for an Italian fresh fruits and vegetable distribution network case study. In a similar study, Mohammed and Wang (2017) used a multi-objective mixed integer programming (MOMIP) model for a FSC problem considering green factors. In order to consider real life parametric changes, the proposed optimization model was implemented under fuzzy set theory (FST). The main focus of this study was to address facility location, transportation cost, CO₂ emissions, and transportation time for a meat industry in the United Kingdom. Varsei and Polyakovskiy (2017) developed another MOMIP model to optimize facility location process, transportation costs, production costs, purchasing costs, CO₂ emissions and social impact of wine SC network in Australia. Tabrizi et al. (2018) formulated a mathematical model for fish SC using a bi-level optimization model using Nash-Stackelberg equilibrium. A brief literature summary on decision-making models in FSC is tabulated Table 1.

Table 1 Decision-making models in FSCM

2.2 MCDM methods for supplier selection

Supplier selection problem is one of the crucial processes in SC operations for any organization. Operational entities spend great amount of time and materials along with professionals to make SC operations more efficient. Supplier selection problem is performed in initial stages of SC operations where organizations are required to make one of the most important decisions through SC networks since supplier selection has a noticeable effect on the rest of operations. In order to make an appropriate decision and select best supplier among several suppliers, manufacturing centers come up with several comprehensive factors which highly contribute to DM’s opinion while assessing potential suppliers. Supplier selection factors differ broadly from an industry to another so that companies try to make more accurate definition on the factors that they define in order to evaluate all suppliers. Factors or criteria play a very crucial part in supplier selection problem. In other words, preferences of suppliers in supplier selection problem strongly rely on the criteria are introduced and defined. Sustainability has emerged as one of most important subjects that organizations aim to integrate within their policies and strategies. Under sustainability, along with technical criteria, economic, environmental and social criteria are also used to assess suppliers. Sustainability is now an integral part in most of the industries worldwide.

In supplier selection process, manufacturing industries aim to develop decision-making frameworks to compare potential candidate suppliers under several factors in order to identify the best alternative for yielding maximum benefits. However, supplier selection problem is a very complicated and difficult process and DMs require reliable methods in making appropriate assessments. MCDM methods are among such frequently adopted methods for supplier selection problems which can efficiently deal with multiple decision factors simultaneously. MCDM methods are used in two main ways to address supplier selection problem. First, methods such as best–worst method (BWM) (Rezaei 2015; Ecer and Pamucar 2020; Torkayesh et al. 2020a), step‐wise weight assessment ratio analysis (SWARA) (Zolfani et al. 2018), CRiteria Importance Through Intercriteria Correlation (CRITIC) (Diakoulaki et al. 1995; Ghorabaee et al. 2017), entropy (Lee and Chang 2018; Torkayesh et al. 2020b), analytic hierarchy process (AHP) (Yazdani et al. 2020; Sambasivam et al. 2020), analytic network process (ANP) (Asadabadi et al. 2019), quality function deployment (QFD) (Yazdani et al. 2017), data envelopment analysis (DEA) (Kumar et al. 2014; Chu et al. 2019), decision making trial and evaluation laboratory (DEMATEL) (Si et al. 2018) are used to obtain the importance of decision criteria or to find the relationship between them. On other hand, ranking MCDM methods such as ELimination Et Choix Traduisant la REalité (ELECTRE) (Govindan and Jepsen 2016), Viekriterijumsko Kompromisno Rangiranje (VIKOR) (Opricovic and Tzeng 2004), TODIM (an acronym in Portuguese of interactive and multi-criteria decision-making) (Bai et al. 2019), technique for order preference by similarity to ideal solution (TOPSIS) (Behzadian et al. 2012; Ramakrishnan and Chakraborty 2020), combined compromise solution (CoCoSo) (Yazdani et al. 2019a, b), measurement of alternatives and ranking according to compromise solution (MARCOS) (Stević et al. 2020; Chakraborty et al. 2020), Grey rational analysis (GRA) (Kuo and Liang 2011), preference ranking organization method for enrichment evaluations (PROMETHEE) (Brans and Smet 2016) are used to prioritize a set of suppliers based on defined decision criteria. In Table 2, MCDM methods for supplier selection problems in different industries are listed.

Table 2 Review of supplier selection methods

2.3 MCDM in food supplier selection

As discussed above, FSCM operations and functions are considered as important global concerns since they are dealing with fulfilling demands of human beings. Considering nutrition-based characteristics of food products, food manufacturing industries are dealing with an important challenge to select the most suitable supplier in order to get the best input raw materials that would benefit the consumers in several ways. However, the literature of food supplier selection problem is very limited and only a few studies have proposed a solution framework.

Grimm et al. (2014) addressed FSC problem by highlighting the significance of supplier management. They reviewed FSC studies to highlight the critical success factors for supplier management in terms of firm-related, relationship-related, partner-related, and context-related factors to integrate them with sustainable SC factors. Validi et al. (2014) developed a hybrid decision making model using genetic algorithm (GA) and TOPSIS method for selection of suitable distributor for diary production considering green factors. Banaeian et al. (2015) studied supplier selection problem in FSC under fuzzy environment. This study focused on identification of green factors in food supplier selection problem using Delphi, AHP, and Grey relational analysis (GRA) methods. Amorim et al. (2016) proposed a stochastic programming model for food supplier selection problem by considering the uncertainty in demand and supplier operation. Govindan et al. (2017) applied PROMETHEE method to address supplier selection problem for an Indian food industry considering green decision factors. Frej et al. (2017) utilized FI Trade off method for a Brazilian food supplier selection problem in terms of price, freight, accuracy, quality, flexibility, lead time, promptness factors. Miranda-Ackerman et al. (2017) proposed a hybrid decision making model by integrating life cycle analysis (LCA), TOPSIS, and MOO model for food supplier selection problem in an orange juice industry. Ma et al. (2017) studied food supplier selection in terms of safety risk factors using a MCDM-based interval intuitive fuzzy tool. Wang et al. (2018) developed a fuzzy AHP (FAHP) and fuzzy data envelopment analysis (FDEA) methods for supplier selection problem considering sustainable factors in an edible oil production industry. In this study, FAHP method was used to determine weights of supplier selection criteria, while FDEA was used to prioritize alternative suppliers. Allaoui et al. (2018) used AHP and ordered weighted averaging (OWA) methods to select the most suitable partner in food industry. Shi et al. (2018) developed an MCDM model using GRA and TOPSIS methods for food supplier selection problem considering green factors. The developed model was formulated under interval valued intuitionstic linguistic sets. Fu (2019) proposed a multi-choice goal programming model using AHP and additive ratio assessment (ARAS) methods for food supplier selection in catering industry. Lau et al. (2020) used a game theory based decision making model using fuzzy AHP, TOPSIS and ELECTRE methods for organic food supplier selection problem in Hong Kong. It considered different selection criteria like product quality, organic safety, monitoring cost, price, delivery, availability of services, commercial position, supplier relationship, risk factors and corporate social responsibility factors. It has been observed that none of the above studies have considered any combined weighting structure, nor used D-numbers. This paper takes an endeavour to structure a new decision making model to fill this gap. Table 3 lists MCDM methods for food supplier selection problems in a comprehensive way.

Table 3 MCDM methods for food supplier selection problems

2.4 Research motivations, gaps, objectives and contributions

It is well know that multi-tier food supplier selection process in sustainable environment is highly influenced by the built-in uncertainties like lack of perfect information, incompatible historical data, adoption of advanced technologies, complex network relationship with customers, supply capacity contraints, supply quality, delivery issues, unavailability of items, logistics and transportation bottlenecks, social and cross-culturalism, virtuous compromise, demand unpredictability and information misinterpretation. Inaccuracis in data can directly influence system outcomes and misdirect DMs to incorrect strategic decisions regarding supplier selection. Therefore, development of such models which can support DMs while confronting ambiguous situations to overcome uncertainties becomes one of the frontier objectives and motivations for SC practitioners and researchers. The fundamental concept of overcoming uncertainties in decision making processes is to utilize fuzzy set (FS) approach. Several fuzzy-based decision making methods have been developed for supplier selection problems in the literuare. However, there exists a serious problem in resolving uncertain information using fuzzy logic. Unlike the fuzzy logic, D-numbers empower us to use linguistic variables without intersection with each other. Therefore, the assessment process for supplier selection problem could be performed in an efficient way as experts can express their judgments using D-number linguistic variables. As intersection between linguistc variables in reality is inevitable, D-numbers can be of high significance for supplier selection problem in such cases. On the other hand, SC of agricultural product such as wine industry are due to manifold risks and factors which make the assessment process very tough and difficult. However, applying D-number-based decision making model can overcome such issues.

Based on the above notions, this paper proposes a novel MCDM model which is based on the application of fuzzy linguistic variables and D-numbers to represent uncertainty. D-numbers basically represent a universal approach for intending uncertainty and imprecision in expert decisions. D-numbers can easily be combined with crisp numbers as well as with all so far known uncertainty theories like fuzzy numbers, Z-numbers (Zadeh 2011; Ghoushchi et al. 2020a, b; Reza et al. 2020), G-numbers (Ghoushchi and Khazaeili 2019) and R-numbers (Seiti et al. 2019a, b). Interval numbers which include fuzzy numbers, Z-numbers, G-numbers, R-numbers and grey numbers are used to express uncertainty based on predefined interval criteria values. Some of these approaches use one, two or more membership functions (MFs) to represent uncertainties. By introducing D-numbers, existing intervals of MFs are additionally corrected depending on the probability of choosing criterion value.

In the proposed model, criteria weights are defined by integrating LBWA (Zizovic and Pamucar 2019) and SWARA methods (Keršuliene et al. 2010). LBWA and SWARA methods are extended in D-number environment. Also, the obtained criteria weights are integrated through a function that enables variable integration of values while simultaneously exploiting advantages of both methods. Extensions of LBWA and SWARA methods using D-numbers (LBWA-D and SWARA-D) contribute to a more rational processing of expert preferences for defining criteria weights. Moreover, combination of two MCDM models for weight determination would definitely enhance reliability and robustness of the derived weights for decision factors. In the proposed multi-criteria model, evaluation and selection of alternatives are performed using MARCOS method (Stević et al. 2020). Extension of MARCOS method using linguistic variables and D-numbers enables a realistic recognition of existing uncertainties during expert evaluation of alternatives. The proposed model provides a new multi-criteria framework for supplier selection and processing of complex information in uncertain conditions. In addition, it enables reasoning and processing of uncertain information using D-numbers-based algorithm which contributes to rational decision making.

In order to illustrate the effectiveness of the proposed model, an empirical case study is presented in which application of the proposed model is presented. The set objectives are:

• i. Proposing a novel decision making model using D-numbers for a multi-tier supplier selection problem,

• ii. Enriching decision-making domain through model development to aid DMs in solving complex multi-tier supplier selection problems.

• iii. In order to illustrate the effectiveness of the proposed model, an empirical case study for a wine industry is presented in which application of the proposed model is presented.

• iv. Assessing suppliers (wine producers) under uncertainty and controlling quality and performance.

The proposed decision making model contributes to:

• ✔ A real case study of wine sector that operates in beverage market since many years,

• ✔ Establishing an efficient decision support model with participation of several experts that offers judgment of supplier performance under qualitative values. We offer a chance to experts to present their opinion by probability scale,

• ✔ The proposed model combining D-numbers, MARCOS and a new integrated weighting method (LBWA-SWARA) is applied for the first time,

• ✔ The model can easily be adopted with the relevant and few changes to other food supply sector including olive oil, fruits and vegetables, horticulture to name a few.

3 Preliminaries

3.1 D-numbers

Dempster-Shafer (DS) evidence theory (Dempster 1967; Shafer 1978) is a powerful method for processing uncertain information. As DS theory enables the development of algorithms for objective reasoning, so it has found wide applications in the field of artificial intelligence (AI). Deng (2012) introduced the concept of D-numbers in order to express uncertain information and judgments. Several MCDM models combined D-numbers in order to empower DM to express their opinions, information, and judgment not only by crisp numbers. Deng et al. (2014c) proposed an extended version of AHP method under D-numbers for supplier selection problem. Fan et al. (2016) integrated D-numbers with AHP method in order to determine weight of criteria in a curtain grouting efficiency evaluation problem. Mo and Deng (2018) developed an MCDM model for vehicle selection problems using D-numbers. In a similar study, ** a novel risk-based MCDM approach based on D-numbers and fuzzy information axiom and its applications in preventive maintenance planning. Appl Soft Comput 82:105559" href="/article/10.1007/s12063-021-00186-z#ref-CR107" id="ref-link-section-d240739926e2379">b) utilized fuzzy axiomatic design principles under D-numbers for preventive maintenance planning problem. Further, for eliminating the shortcomings of DS theory, Deng et al. (2014a, b) developed the concept of D-numbers. Deng et al. (2014a) singled out a key problem which is overcome by D-numbers through the elimination of exclusivity of elements in reasoning. Problem of exclusivity is explained in the appendix section through an example of medical diagnostics comprehensively. The basic characteristic of D-numbers is that it enables additional expression of the uncertainty that exists in expert preferences, which cannot be expressed by the existing uncertainty theories. D-numbers enable the fusion of expert decisions through a special reasoning algorithm, so their application in group decision-making is recommended. Based on the above properties, we can highlight the following advantages of D-numbers:

• 1 D-numbers represent a tool for additional expression of uncertainty in expert preferences, which is based on the introduction of the probability of choosing the appropriate criterion value;

• 2 D-numbers can be used to represent uncertainty in expert preferences whether the criterion values are expressed in crisp numbers or some other uncertainty theories (fuzzy numbers, Z-numbers, G-numbers, R-numbers and Grey numbers);

• 3 By applying a special algorithm for reasoning with D-numbers, the probability of expressing uncertainty of criterion value provides additional correction in interval value of fuzzy number, Z-number, G-number and other interval theories;

• 4 Through the algorithm of combining D-numbers, traditional theories for representing uncertainty are further strengthened, thus creating a powerful methodology that contributes to a more objective and rational decision-making in a dynamic environment;

• 5 D-numbers in relation to other popoular uncertainty theories have the ability to aggregate expert decisions based on combination and fusion algorithms of D-numbers.

• 6 On the other hand, existing uncertainty theories do not have any special algorithms for aggregation of expert decisions, but use other tools like mathematical operators for value aggregation.

• 7 Application of D-numbers eliminates the stated shortcomings of DS theory as the exclusive property of the elements in the frame of discernment is not required and completeness constraint is released if necessary. By eliminating this shortcoming using D-numbers, it is possible to apply DS theory to process uncertainty in an objective way. The basic mathematical concept of D-numbers is presented in the next section.

Fig. 1

Proposed decision making model

Definition 1

Let Ω be a finite nonempty set, and a D-number is a map** that $D:\Omega\rightarrow\left[0,1\right]$ , with

$$\sum_{A\subseteq\Omega}D\left(A\right)\leq1and\;D\left(\varnothing\right)=0$$

(1)

where Ø is an empty set and A is any subset of Ω. As emphasized within the advantages of D-numbers, D-number theory requires set of elements Ω to be mutually exclusive and completely constraint. Information is considered complete if it is$\sum_{A\subseteq\Omega}D\left(A\right)=1$ , or if it is $\sum_{A\subseteq\Omega}D\left(A\right)<1$  the information is incomplete.

Definition 2

(Deng and Jiang 2019). Let two D-numbers be given $D_1=\{\left(b_1,\;v_1\right),...,\left(b_i,\;v_i\right),...,\left(b_n,\;v_n\right)\}$ and $D_2=\{\left(b_n,\;v_n\right),...,\left(b_i,\;v_i\right),...,\left(b_1,\;v_1\right)\}$, then a combination of D-numbers D = D₁ʘD₂ can be defined as:

$$\begin{aligned}&\left\{\begin{array}{l}D\left(\varnothing\right)=0\\D\left(B\right)=\frac1{1-K_D}\sum_{B_1\cap B_2=B}D_1\left(B_1\right)D_2\left(B_2\right),\;B\neq\varnothing\end{array}\right.\\&with\\&K_D=\frac1{Q_1Q_2}\sum_{B_1\cap B_2=\varnothing}D_1\left(B_1\right)D_2\left(B_2\right)\\&Q_1=\sum_{B_1\subseteq\Omega}D_1\left(B_1\right)\\&Q_2=\sum_{B_2\subseteq\Omega}D_2\left(B_2\right)\end{aligned}$$

(2)

Equation (2) represents a generalization of DS rules. If complete information is presented through D-numbers (D₁ and D₂), that is, if $Q_1=1$  and  $Q_2=1$ , then rule (2) is transformed into DS rule. Rule (2) is a basic tool for fusing uncertain information contained in D-numbers.

Property 1

(Permutation invariability). If there are two D-numbers that are represented as $D_1=\left\{\left(b_1,\;v_1\right),...,\left(b_i,\;v_i\right),...,\left(b_n,\;v_n\right)\right\}$ and $D_2=\left\{\left(b_n,\;v_n\right),...,\left(b_i,\;v_i\right),...,\left(b_1,\;v_1\right)\right\}$$\left(b_i,\;v_i\right)\;,\;\left(b_j,\;v_j\right)...\left(b_n,\;v_n\right)\}$, then we have $D_1\Leftrightarrow D_2$ , where „⇔ “ means „equal to “.

Example 2

If there are two D-numbers that are represented as: $D_1=\left\{\left(2,\;0.3\right),\left(5,\;0.35\right),\left(9,\;0.35\right)\right\}$ and  $D_2=\left\{\left(5,\;0.35\right),\left(2,\;0.3\right),\left(9,\;0.35\right)\right\}$, then we can say that it is $D_1\Leftrightarrow D_2$.

Property 2

(Integration). For discrete D-number $D=\left\{\left(b_1,v_1\right),\left(b_2,v_2\right)...\left(b_i,v_i\right),\left(b_j,v_j\right)...\left(b_n,v_n\right)\right\}$ we can define the integration operator as follows

$$I(D) = \sum\limits_{i = 1}^n {{d_i}{v_i}}$$

(3)

where $d_i\in R^+,v_i>0$ and $\sum\nolimits_{i=1}^nv_i\leq1$.

Example 3

For discrete D-number $D=\left\{\left(2,\;0.3\right),\;\left(5,\;0.35\right),\;\left(9,\;0.35\right)\right\}$, then we can define its integration operator as $I\left(D\right)=2\cdot0.3\;+\;5\cdot0.35\;+\;9\cdot0.35=5.5$.

3.2 Transformation of the uncertain linguistic information to the trapezoidal fuzzy numbers

It is assumed that the DMs perform qualitative assessments of the alternatives using appropriate set of linguistic variables. Let $S=\left\{\left.s_i\right|\;i=0,1,\dots,T-1\right\}$ represents a set of linguistic variables, where $s_i$ represents a linguistic variable, while T represents odd D-numbers. Based on the settings shown, we can define the following linguistic examples:

$$\begin{aligned}S=\left({s_0},{s_1},{s_2}\right)=\left(poor,\;fair,\;good\right),\\S=\left({s_0},{s_1},{s_2},{s_3},{s_4}\right)=\left(very\;poor,\;poor,\;fair,\;good,\;very\;good\right),\\S=\left(s_0,s_1,s_2,s_3,s_4,s_5,s_6\right)=\left(very\;poor,\;poor,\;slightly\;poor,\;fair,\;slightly\;good,\;good,\;very\;good\right),\end{aligned}$$

Each linguistic variable $s_i$ can be represented by triangular fuzzy numbers (TFN) $A_i=\left(a_i^L,a_i^M,a_i^U\right),\;\left(a_i^L\leq a_i^M\leq a_i^U\right)$, which is further represented by the following membership function (MF) (Pamucar and Ecer 2020):

$$\mu_{A_i}\left(x\right)=\left\{\begin{array}{l}\frac{x-a_i^L}{a_i^M-a_i^L} a_i^L\leq x\leq\,a_i^M\\\frac{a_i^U-x}{a_i^U-a_i^M} a_i^M\leq x\leq\,a_i^U\\0 x\in\left(-\infty,a_i^L\right)\cup\left(a_i^U,\infty\right)\end{array}\right.$$

(4)

Transformation of linguistic variables into TFNs can be performed using Eq. (5)

$$A_i=\left\{\begin{array}{l}a_0=0\\a_i^L=\frac{i-1}{T-1}\left(1\leq i\leq T-1\right)\\a_i^M=\frac i{T-1}\left(0\leq i\leq T-1\right)\\a_i^U=\frac{i+1}{T-1}\left(0\leq i\leq T-2\right)\\a_{L-1}^U=1\end{array}\right.$$

(5)

Lets suppose there are $A_i=\left(a_i^L,a_i^M,a_i^U\right)$  and $B_i=\left(b_i^L,b_i^M,b_i^U\right)$  two TFNs, then we can define the following arithmetic rules for operations with TFNs.

$$A_i+B_i=\left(a_i^L+b_i^L,a_i^M+b_i^M,a_i^U+b_i^U\right)$$

(6)

$$A_i-B_i=\left(a_i^L-b_i^U,a_i^M-b_i^M,a_i^U-b_i^L\right)$$

(7)

$${A_i}{B_i}=\left({a_i^L}{b_i^L},{a_i^M}{b_i^M},{a_i^U}{b_i^U}\right)$$

(8)

$${A_i}/{B_i}=\left({a_i^L}/{b_i^U},{a_i^M}/{b_i^M},{a_i^U}/{b_i^L}\right)$$

(9)

$$\lambda{A_i}=\left(\lambda{a_i^L},\lambda{a_i^M},\lambda{a_i^U}\right)$$

(10)

Definition 3

Lets suppose there are $A_i=\left(a_i^L,a_i^M,a_i^U\right)$ and $B_i=\left(b_i^L,b_i^M,b_i^U\right)$  two TFNs, then we can compare them as follows:

• i) If $a_i^L\geq b_i^L,\;a_i^M\geq b_i^M,\;a_i^U\geq b_i^U$ then $A_i\geq B_i$.

• ii) If this three conditions $a_i^L\geq b_i^L,\;a_i^M\geq b_i^M,\;a_i^U\geq b_i^U$ are not met, but $\left(a_i^L+a_i^M+a_i^U\right)/3\geq\left(b_i^L+b_i^M+b_i^U\right)/3$ is met, then $A_i\geq B_i$.

4 Proposed decision making model

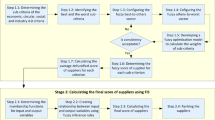
In this section, mathematical formulations of the proposed decision making model based on fuzzy linguistic descriptors and D-numbers are presented. The proposed model enables easy processing of uncertainties in expert preferences that are represented by linguistic variables and probabilities. Different phases of this model are shown in Fig. 1. In the first phase, criteria weights are determined using LBWA-D and SWARA-D methods, while in the second phase, alternative suppliers are evaluated using fuzzy linguistic MARCOS-D method.

This model is based on the integration of LBWA-D and SWARA-D methods which are used to determine criteria weights. The fuzzy linguistic MARCOS-D method is used in this model to evaluate alternative suppliers. Detail steps of the proposed model are presented in the next sections.

4.1 Phase- I: Determination of criteria weights

In the proposed model, criteria weights are determined by integration of LBWA and SWARA methods to overcome the limitations of unilateral application of these two methods to use the advantages of both weighting methods. Since either of these two methods has its inherent advantages and disadvantages, an integrated determination of criteria weights seems to be more pragmatic. The combinative weighting can conform to different situtaions where a group of experts are involved and have different knowledge and experince levels. One more advantage of integrated weights is that it not only benefits from the DMs’ expertise but also involves end users in the whole decision-making process more functionally. In addition, combined criteria weights also consider the influence of both LBWA and SWARA methods in ranking pre-orders of the considered alternatives. The motivation behind selecting LBWA and SWARA methods are presented below:

LBWA method requires smaller number of pairwise criteria comparisons and has a rational and logical mathematical algorithm (Zizovic and Pamucar 2019). From the group of subjective criteria weighting methods, LBWA stands out due to the following advantages (Bozanic et al. 2020): i) small number of comparisons; ii) algorithm does not become complicated with increase in number of criteria, thus making it suitable for complex MCDM problems; and iii) it allows DMs a logical algorithm to present their preferences while prioritizing criteria. This eliminates inconsistencies in expert preferences.

On the other hand, SWARA method stands out due to the following advantages: i) this method can be successfully used to coordinate and collect data from experts; ii) it has simple mathematics; iii) easily applicable in the case of larger group of criteria; iv) any suitable scale can be used to express expert preferences. These features give significant flexibility to SWARA method, making it an automatic choice for complex problems.

Kee** in mind all the above mentioned advantages of LBWA and SWARA methods and the fact that they have not still been explored in conjunction with DS theory, this paper aims to present extensions of LBWA and SWARA methods by applying D-numbers to address uncertainties, dilemmas and subjectivity for criteria comparisons.

a) LBWA-D method

Zizovic and Pamucar (2019) developed LBWA method for weight estimation in MCDM environment. This method empowers n optimal arrangement of experts’ judgement without increasing the complexity of the multiple criteria problem. The procedural steps of LBWA-D method are as follows:

Step 1: Determining the most important criterion from a set of criteria.

Suppose there is a group of k experts who are divided into two homogeneous groups. Also, suppose that the experts defined a set of $C=\left\{C_1,\;C_2,\dots,\;C_n\right\}$ criteria, where n represents the total number of criteria. Experts decide on the selection of the most influential criterion from set C. Suppose that experts decide that $C_1$S is the most influential criterion from set C.

Step 2: Grou** criteria by levels of significance.

Experts group the criteria according to the levels of significance using the following rules:

Level $S_1$ :

At the level of $S_1$, group the criteria from the set S whose significance is equal to the significance of criterion $C_1$ or is up to twice less than the significance of the criterion $C_1$;

Level $S_2$ :

At the level, group the criteria from the set whose significance is exactly twice less than the significance of the criterion $C_1$ or up to three times less than the significance of the criterion $C_1$;

Level $S_3$ :

At the level S, group the criteria from the set whose significance is exactly k times less than the significance of the criteria $C_1$ or is up to $k+1$ times less than the significance of the criteria $C_1$.

By applying the previously presented rules, experts establish a rough classification of the observed criteria, i.e. group the criteria according to the levels of significance. If the significance of a criterion $C_j$ is denoted by $s(C_j)$, where $j\in\left\{1,2,\dots,n\right\}$, then we have $S=S_1\cup S_2\cup\dots\cup S_k$, where for each level $i\in\left\{1,2,\dots,k\right\}$, we have

$$S_i=\left\{C_{i_1},C_{i_2,}\dots,C_{i_s}\right\}=\left\{C_j\in S\,:\,\,i\leq s(C_j)<i+1\right\}$$

(11)

Also, for each $p,q\in\left\{1,2,\dots,k\right\}$ such that $p\neq q$  holds $S_p\cap S_q=\varnothing$.

Step 3: Comparison of criteria by significance. After grou** the criteria by their significance levels, it is necessary to compare them in pairs. The comparison in pairs is made in relation to the best criterion. Within the formed subsets (levels), each expert group compares the criteria according to their significance. Each criterion $C_{i_p}\in S_i$ within a subset $C_i=\left\{C_{i_1},C_{i_2,},\dots,C_{i_s}\right\}$ is assigned the value $I_{i_p}=\left\{\left(b_{i_p(1)},v_{i_p(1)}\right),\dots,\left(b_{i_p(i)},v_{i_p(i)}\right),\dots,\left(b_{i_p(m)},v_{i_p(m)}\right)\right\}$,$b_{i_p}\in\left[0,r\right],v_{i_p}\leq1$, so that the most important criterion $C_1$ is assigned the value $b_1=0$. Also, if $C_{i_p}$ is more significant than $C_{i_q}$ then $b_p<b_q$, and if $C_{i_p}$ is equivalent to $C_{i_q}$ then $b_p=b_q$. Maximum value of the scale for criteria comparison is defined by Eq. (12)

$$r = \max \left\{ {\left| {S_1} \right|,\,\left| {S_2} \right|, \ldots ,\left| {S_k} \right|} \right\}$$

(12)

Since we have two homogeneous groups of experts, for each group of experts we get the values $I_{i_p}$, i.e. we get $I_{i_p}^1$ and $I_{i_p}^2$. Thus, for each position $I_{i_p}^1$ and $I_{i_p}^2$, the D-number$I_{i_p}=\left\{\left(b_{i_p(1)},v_{i_p(1)}\right),\dots,\left(b_{i_p(i)},v_{i_p(i)}\right),\dots,\left(b_{i_p(m)},v_{i_p(m)}\right)\right\}$ is defined. In order to obtain a unique value that compares the j^th criterion with the most influential criterion ($I_{i_p}$), it is necessary to fuse the uncertainties presented in the initial expert preferences. Accordingly, by applying combination rule of D-numbers $I_{i_p}=I_{i_p}^1\odot I_{i_p}^2$, analysis and fusion of uncertainties from D-numbers $I_{i_p}^1=\left\{\left(b_{i_p(1)}^1,v_{i_p(1)}^1\right),\left(b_{i_p(2)}^1,v_{i_p(2)}^1\right),\dots,\left(b_{i_p(m)}^1,v_{i_p(m)}^1\right)\right\}$ and $I_{i_p}^2=\left\{\left(b_{i_p(1)}^2,v_{i_p(1)}^2\right),\left(b_{i_p(2)}^2,v_{i_p(2)}^2\right),\dots,\left(b_{i_p(m)}^2,v_{i_p(m)}^2\right)\right\}$ are performed. After the fusion of uncertainty, the final values $I_{i_p}=\left\{\left(b_{i_p(1)},v_{i_p(1)}\right),\left(b_{i_p(2)},v_{i_p(2)}\right),\dots,\left(b_{i_p(m)},v_{i_p(m)}\right)\right\}$  are defined. By applying integration operator of Eq. (3), the uncertainties represented by D-numbers are integrated into a unique value ${\overline I}_{i_p}$.

Step 4: Defining the coefficient of elasticity. In order to calculate the criterion influence function using Eq. (13), it is necessary to define the value of coefficient of elasticity ($\varphi$). Based on the defined maximum value of the scale for comparing criteria (r) using Eq. (12), the coefficient of elasticity $\varphi\in N$ (where N represents a set of real numbers) should satisfy the condition $\varphi>r$, where $r=\text{max}\left\{\left|S_1\right|,\left|S_2\right|,\dots,\left|S_k\right|\right\}$.

Step 5. Calculation of the criterion influence function. The criterion influence function is used in Eq. (14) to calculate optimal values of criteria weights. The influence function $f:S\rightarrow R$ is defined in the following way. For each criterion$C_{i_p}\in C_i$, we can define influence function of the criterion as:

$$f({C_{i_p}}) = \frac{\varphi }{{i \cdot \varphi + {{\overline I }_{i_p}}}}$$

(13)

where i represents the number of levels/subsets where the criterion is classified, $\varphi$ represents the coefficient of elasticity, while ${\overline I}_{i_p}$ represents the value assigned to the criterion $C_{i_p}$ within the observed level.

Step 6. Calculation of optimal values of weight coefficients of criteria. Using Eq. (14), weight coefficient of the most influential criterion is calculated:

$${\xi_1} = \frac{1}{{1 + f({C_2}) + \cdots + f({C_n})}}$$

(14)

where $\xi_1$ represents value of weight coefficient of the most influential criterion, while $f\left(C_n\right)$ represents function of the influence of criterion defined in Step 5.

The values of the weighting coefficients of the remaining criteria are obtained by applying Eq. (15)

$${\xi_j} = f({C_j}) \cdot {\xi_1}$$

(15)

where $j=2,3,\dots,n$, and n represents the total number of criteria.

b) SWARA-D method

Keršuliene et al. (2010) introduced SWARA method to determine criteria weights for MCDM problems. Since then this method has been applied for many real life solutions. Zolfani and Saparauskas (2013) used SWARA method for analyzing and assessing the sustainability factors of energy systems. Dehnavi et al. (2015) developed a decision making model using SWARA and adaptive neuro-fuzzy inference system for landslide hazard assessment for a case study in Iran. In this study, SWARA method was used to determine the importance of each landslide decision factors. Valipour et al. (2017) developed an integrated MCDM model based on SWARA and COPRAS methods for risk assessment of in foundation excavation projects. This study identified important decision factors for risk assessment in excavation industry and then determined the importance of the criteria via SWARA method. Zolfani et al. (2018) proposed a new version of SWARA method with a focus on improving criteria prioritization process which was achieved by integrating the reliability evaluation of expert judgments. Zolfani and Chatterjee (2019) constructed a decision making model using BWM and SWARA methods for sustainable design of household furnishing materials. Balki et al. (2020) combined SWARA and ARAS methods for an optimization problem of spark ignition (SI) engines where MCDM methods were supposed to select the best fuel alternative. SWARA was used to obtain the importance of energy criteria and then fuel alternatives were prioritized based on ARAS method. In a similar study, Ghenai et al. (2020) used SWARA and ARAS methods for prioritization of renewable energies such as wind, fuel cell and solar photo voltaic cell under sustainability factors. SWARA-D method has the following simple steps:

Step 1. Defining criteria significance. Suppose, there is a group of k experts who are divided into two homogeneous groups and the experts have defined a set of criteria $C=\left\{C_1,C_2,\dots,C_n\right\}$, where n represents the total number of criteria. After that, an expert assessment is performed, i.e.comparative significance of the criteria is defined as $s_j=\left\{\left(b_{j(1)},v_{j(1)}\right),\dots,\left(b_{j(i)},v_{j(i)}\right),\dots,\left(b_{j(m)},v_{j(m)}\right)\right\}$, $b_j\in\left[0,e\right]$, $v_j\leq1$, (where e represents the upper limit of the scale for comparing the criteria). In order to obtain a unique value of criteria significance ${\overline s}_j$ , it is necessary to perform fusion of the criteria significance, represented by D-numbers. By applying combination rule of D-numbers ${\overline s}_j=\overset1{s_j}$ ʘ $\overset2{s_j}$, fusion of D-numbers is performed $s_j^1=\left\{\left(b_{j(1)}^1,v_{j(1)}^1\right),\left(b_{j(2)}^1,v_{j(2)}^1\right),\dots,\left(b_{j(m)}^1,v_{j(m)}^1\right)\right\}$ and $s_j^2=\left\{\left(b_{j(1)}^2,v_{j(1)}^2\right),\left(b_{j(2)}^2,v_{j(2)}^2\right),\dots,\left(b_{j(m)}^2,v_{j(m)}^2\right)\right\}$. By applying integration operator of Eq. (3), the uncertainties represented by D-numbers are integrated into a unique value ${\overline s}_j$.

Korak 2. Calculation of criteria weights. Criteria weights are obtained by using Eq. (16).

$${\zeta_j} = \left\{ \begin{gathered} 1\;\;\;\;\;j = 1 \\ \frac{{{\zeta_{j - 1}}}}{{{{\overline s }_{j + 1}}}}\;j > 1 \\ \end{gathered} \right.$$

(16)

By applying Eq. (17), $\zeta_j$ values are translated into the interval [0,1] so that they fulfill the condition $\sum_{j=1}^n\zeta'_j=1$.

$${\zeta}_{j}^{\prime} = \frac{{\zeta_j}}{{\sum\limits_{j = 1}^n {\zeta_j} }}$$

(17)

where $\zeta'_j$  represents criterion weights, as obtained from SWARA-D method.

Finally, based on LBWA-D and SWARA-D criteria weights, aggregated weights are calculated using Eq. (18):

$${w_j} = \delta \cdot {\xi_j} + \left( {1 - \delta } \right) \cdot {\zeta_j}$$

(18)

where $w_j$ ($j=1,2,\dots,n$) represents final criteria weights, $\xi_j$ represents criteria weights obtained using LBWA-D method, $\zeta_j$  represents criteria weights obtained using SWARA-D method, while the coefficient $\delta\in\left[0,1\right]$ defines the percentage share of weights.

It is recommended to use $\delta=0.5$  value for initial ranking of alternatives, since both methods equally participate in this value while defining final criteria weights. For other values in the range of $0.5<\delta\leq1$_, LBWA-D method has advantage over SWARA-D, while SWARA-D method is favored for values $0\leq\delta<0.5$ . It is also recommended that during the validation of final results, an analysis of impact of parameter $\delta$ on final ranking should always be performed.

4.2 Phase- II: Fuzzy linguistic MARCOS-D method

Stević et al. (2020) introduced MARCOS method to prioritize alternatives with help of anti-ideal and idea solutions for supplier selection in a heathcare application. Other applications of this method include evaluation of human resources for transport company (Stević and Brković 2020), evaluation of project management software (Puška et al. 2020) and road traffic risk analysis (Stanković et al. 2020) to mention a few. The procedural steps of fuzzy linguistic MARCOS-D method are explained below:

Step 1. Forming an initial decision-making matrix . In the Y$={\left[{\overline y}_{ij}\right]}_{b\times n}$matrix, experts express their preferences using predefined fuzzy linguistic variables $S=\left\{S_i\left|i=0,1,...,T-1\right.\right\}$. Expert evaluation of alternatives in relation to the criteria from the set $C=\left\{C_1,C_2,\dots,C_n\right\}$ was performed using D-numbers and is presented as $D_{y_{ij}}=\left\{\left(b_{y_{ij}}^1,v_{y_{ij}}^1\right),...,\left(b_{y_{ij}}^1,v_{y_{ij}}^1\right),\dots,\left(b_{y_{ij}}^m,v_{y_{ij}}^m\right)\right\}$, where $b_{y_{ij}}^1$  represents the fuzzy linguistic variable (FLV) from the set S, and $v_{y_{ij}}^1$  represents the probability of choosing FLV.

Since the experts are grouped into two homogeneous groups, each group of experts evaluates the alternatives. Thus, we get one initial decision matrix for each expert group, i.e. $Y^1={\left[D_{y_{ij}(1)}\right]}_{b\times n}$  and $Y^2={\left[D_{y_{ij}(2)}\right]}_{b\times n}$  where                                                                                        $D_{y_{ij}(1)}=\left\{\left(b_{y_{ij}(1)}^1,v_{y_{ij}(1)}^1\right),...,\left(b_{y_{ij}(1)}^1,v_{y_{ij}(1)}^1\right),\dots,\left(b_{y_{ij}(1)}^m,v_{y_{ij}(1)}^m\right)\right\}$ and $D_{y_{ij}(2)}=\left\{\left(b_{y_{ij}(1)}^1,v_{y_{ij}(2)}^1\right),...,\left(b_{y_{ij}(1)}^1,v_{y_{ij}(2)}^1\right),\dots,\left(b_{y_{ij}(1)}^m,v_{y_{ij}(2)}^m\right)\right\}$  represent the elements of the initial matrices $Y^1$ and $Y^2$ . In order to obtain a unique initial decision matrix Y, a fusion of the uncertainties represented by matrices $Y^1$ and $Y^2$ is performed by applying combination rule of D-numbers $D_{y_{ij}=}D_{y_{ij}(1)\;}\odot D_{y_{ij}(2)}$  using Eq. (2). Since individual D-numbers represent uncertainties at the intersection of two FLVs (Fig. 6), FLV is transformed into fuzzy numbers using using Eq. (4).

Thus, the unique values of D-numbers are defined by applying Eqs. (19) and (20). FLV transformation is performed based on the ratio of the surfaces at the intersection $s_{i,i+1}$ .

$${D_{FLV}}({s_i}) = D({s_i}) + D({s_i},{s_{i + 1}})\frac{{\frac{{{s_{i,i + 1}}}}{{s_i}}}}{{\frac{{{s_{i,i + 1}}}}{{s_i}} + \frac{{{s_{i,i + 1}}}}{{{s_{i + 1}}}}}}$$

(19)

$${D_{FLV}}({s_{i + 1}}) = D({s_{i + 1}}) + D({s_i},{s_{i + 1}})\frac{{\frac{{{s_{i,i + 1}}}}{{{s_{i + 1}}}}}}{{\frac{{{s_{i,i + 1}}}}{{s_i}} + \frac{{{s_{i,i + 1}}}}{{{s_{i + 1}}}}}}$$

(20)

where $s_{i,i+1}$  represents the intersection of linguistic variables $s_i$  and $s_{i+1}$  respectively, while $s_i$  and $s_{i+1}$  represent the area of the linguistic variable $s_i$  and $s_{i+1}$ , respectively.

By aggregating the unique values of D-numbers of Eq. (3), an aggregated initial initial decision matrix $Y={\left[{\overline y}_{ij}\right]}_{b\times n}$ is obtained with transformed FLV into fuzzy numbers, where $\;{\overline y}_{ij}$  represents fuzzy values.

Step 2: Formation of an extended initial fuzzy matrix. The extension of the initial fuzzy matrix is performed by defining the fuzzy ideal $\widetilde A(ID)$  and fuzzy anti-ideal $\widetilde A(AI)$  solution.

$$X = \begin{array}{*{20}{c}} \begin{gathered} A\left( {AI} \right) \hfill \\ \;{A_1} \hfill \\ \end{gathered} \\ {{A_{2\quad }}} \\ {...\quad } \\ \begin{gathered} {A_m} \hfill \\ A\left( {ID} \right) \hfill \\ \end{gathered} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {C_1}&{C_2}&{...}&{C_n} \end{array}} \\ {\left[ {\begin{array}{*{20}{c}} \begin{gathered} {{\tilde x}_{ai1}} \hfill \\ {{\tilde x}_{11}} \hfill \\ \end{gathered} &\begin{gathered} {{\tilde x}_{ai2}} \hfill \\ {{\tilde x}_{12}} \hfill \\ \end{gathered} &\begin{gathered} ... \hfill \\ ... \hfill \\ \end{gathered} &\begin{gathered} {{\tilde x}_{ain}} \hfill \\ {{\tilde x}_{1n}} \hfill \\ \end{gathered} \\ {{{\tilde x}_{21}}}&{{{\tilde x}_{22}}}&{...}&{{{\tilde x}_{2n}}} \\ {...}&{...}&{...}&{...} \\ \begin{gathered} {{\tilde x}_{b1}} \hfill \\ {{\tilde x}_{id1}} \hfill \\ \end{gathered} &\begin{gathered} {{\tilde x}_{b2}} \hfill \\ {{\tilde x}_{id2}} \hfill \\ \end{gathered} &\begin{gathered} ... \hfill \\ ... \hfill \\ \end{gathered} &\begin{gathered} {{\tilde x}_{bn}} \hfill \\ {{\tilde x}_{idn}} \hfill \\ \end{gathered} \end{array}} \right]} \end{array}$$

(21)

The fuzzy anti-ideal solution $A(AI)$  is the worst alternative while the fuzzy ideal solution $A(ID)$  is an alternative with the best characteristic. Depending on the nature of the criteria, $A(AI)$  and $A(ID)$  are defined by Eq. (22) as follows:

$$\begin{gathered} A\left( {AI} \right) = \mathop {\min }\limits_i {{\tilde x}_{ij}}\quad if\;j \in \;B\quad and\quad \mathop {\max }\limits_i {{\tilde x}_{ij}}\quad if\;j \in C \hfill \\ A\left( {ID} \right) = \mathop {\max }\limits_i {{\tilde x}_{ij}}\quad if\;j \in \;B\quad and\quad \mathop {\min }\limits_i {{\tilde x}_{ij}}\quad if\;j \in C \hfill \\ \end{gathered}$$

(22)

where B represents benefit criteria and C represents cost criteria.

Step 3: Creating a normalized fuzzy matrix. The elements of the normalized fuzzy matrix $N={\left[{\widetilde n}_{ij}\right]}_{b\times n}$  are obtained by applying Eq. (23):

$${\tilde n_{ij}} = \left( {n_{ij}^l,n_{ij}^m,n_{ij}^u} \right) = \left\{ \begin{gathered} \left( {\frac{{x_{idj}^l}}{{x_{ij}^u}},\frac{{x_{idj}^l}}{{x_{ij}^m}},\frac{{x_{idj}^l}}{{x_{ij}^l}}} \right)\quad if\;j \in \;C \hfill \\ \left( {\frac{{x_{ij}^l}}{{x_{idj}^u}},\frac{{x_{ij}^m}}{{x_{idj}^u}},\frac{{x_{ij}^u}}{{x_{idj}^u}}} \right)\quad if\;j \in \;B \hfill \\ \end{gathered} \right.$$

(23)

where elements ${\widetilde\chi}_{ij}=\left(\chi_{{}_{ij}}^l,\chi_{{}_{ij}}^m,\chi_{{}_{ij}}^u\right)$ and ${\widetilde\chi}_{idj}=\left(\chi_{{}_{idj}}^l,\chi_{{}_{idj}}^m,\chi_{{}_{idj}}^u\right)$ represent the elements of the matrix X.

Normalized fuzzy matrix is used in the next step to calculate the elements of the weighted fuzzy matrix.

Step 4: Determination of weighted fuzzy matrix $V=\;{\left[{\widetilde v}_{ij}\right]}_{b\times n}$. The weighted matrix V is obtained by multiplying the normalized fuzzy matrix N with the fuzzy weight coefficients of the criterion $w_j$, as shown in Eq. (24).

$${\tilde v_{ij}} = \left( {v_{ij}^l,v_{ij}^m,v_{ij}^u} \right) = {\tilde n_{ij}} \otimes {w_j} = \left( {n_{ij}^l \times {w_j},n_{ij}^m \times {w_j},n_{ij}^u \times {w_j}} \right)$$

(24)

Weighted fuzzy matrix elements are used to calculate the ${\widetilde S}_i$ fuzzy matrix elements in Step 5.

Step 5: Calculation of ${\widetilde S}_i$  fuzzy matrix using the following expression:

$${\tilde S_i} = \sum\limits_{i = 1}^n {{{\tilde v}_{ij}}}$$

(25)

where ${\widetilde S}_i\left(S_{{}_i}^l,S_{{}_i}^m,S_{{}_i}^u\right)$  represents the sum of the elements of the weighted fuzzy matrix $V$ .

Elements of fuzzy matrix ${\widetilde S}_i$  are used to calculate the utility degree of alternatives, which is explained in the next step.

Step 6: Calculation of the utility degree of alternatives ${\widetilde K}_i$. By applying Eqs. (26) and (27), utility degrees of an alternative in relation to the anti-ideal and ideal solution are calculated.

$${\tilde K_i}^- = \frac{{{{\tilde S}_i}}}{{{{\tilde S}_{ai}}}} = \left( {\frac{s_i^l}{{s_{ai}^u}},\frac{s_i^m}{{s_{ai}^m}},\frac{s_i^u}{{s_{ai}^l}}} \right)$$

(26)

$${\tilde K_i}^+ = \frac{{{{\tilde S}_i}}}{{{{\tilde S}_{id}}}} = \left( {\frac{s_i^l}{{s_{id}^u}},\frac{s_i^m}{{s_{id}^m}},\frac{s_i^u}{{s_{id}^l}}} \right)$$

(27)

In the next step, the utility degree of alternatives is used to calculate the utility functions $f\left(\widetilde K_i^+\right)$ and $f\left(\widetilde K_i^-\right)$.

Step 7. Determination of utility functions in relation to the ideal $f\left(\widetilde K_i^+\right)$ and anti-ideal $f\left(\widetilde K_i^-\right)$ solution. They are determined by applying Eqs. (28) and (29).

$$f\left( {\tilde K_i^+ } \right) = \frac{\tilde K_i^- }{d} = \left( {\frac{{k_i^{ - l}}}{d},\frac{{k_i^{ - m}}}{d},\frac{{k_i^{ - u}}}{d}} \right)$$

(28)

$$f\left( {\tilde K_i^- } \right) = \frac{\tilde K_i^+ }{d} = \left( {\frac{{k_i^{ + l}}}{d},\frac{{k_i^{ + m}}}{d},\frac{{k_i^{ + u}}}{d}} \right)$$

(29)

where $d=\underset i{\text{max}}\left\{\sum_{i=1}^b\left(\widetilde K_i^-+\widetilde K_i^+\right)\right\}=\underset i{\text{max}}\left\{\sum_{i=1}^b\left(\widetilde K_i^{-u}+\widetilde K_i^{+u}\right)\right\}$.

Utility functions in relation to the ideal $f\left(\widetilde K_i^+\right)$ and anti-ideal $f\left(\widetilde K_i^-\right)$ solution are used in Eq. (30) to calculate the utility function of alternatives $f\left(K_i\right)$  and final rank of alternatives.

Step 8: Determination of the utility function of alternatives $f\left(K_i\right)$. Utility function is a compromised value of the observed alternative in relation to fuzzy ideal and fuzzy anti-ideal solutions. Utility functions of the alternatives are defined by Eq. (30).

$$f\left( {K_i} \right) = \frac{K_i^+ + K_i^- }{{1 + \frac{{1 - f\left( {K_i^+ } \right)}}{{f\left( {K_i^+ } \right)}} + \frac{{1 - f\left( {K_i^- } \right)}}{{f\left( {K_i^- } \right)}}}};$$

(30)

where $K_i^+$, $K_i^-$, $f\left(K_i^+\right)$ and $f\left(K_i^-\right)$ represents defuzzified values of Eqs. (26)-(29). Defuzzified values are obtained by applying Eq. (31)

$${d_{crisp}} = {{\left( {l + 4m + u} \right)} \mathord{\left/ {\vphantom {{\left( {l + 4m + u} \right)} 6}} \right. \kern-\nulldelimiterspace} 6}$$

(31)

Step 9: Ranking the alternatives. Ranking of the alternatives is based on the final values of utility functions. It is desirable that an alternative has the highest possible value of the utility function.

5 Model implementation and results

5.1 Case study

In Spanish food and agriculture industry, one of the largest sectors is Winery units. In 2019 Spain has produced 12,333 tons of wine and olive oil. The quantity every year is increasing and many corporations are trying to join and bring high quality brands to the market. WineSol Corporation¹ is a cooperation company that distributes the ecological wine in Castilla-la-Mancha zone, one of the greatest wine region in whole Spain and Europe. It has more than 180 employees all around the country and drives transportation and distribution of wines in high volumes. The company is originated from a family business with years of experiences in wine production. The company has grown drastically and is trying to penetrate in new and emerging markets. Its global aim is to extend wine production fields and employ and educate people due to its traditional policy and social responsibility. They are currently directing a wine school in several cities tfor better promotion. The company mission is to gather best tasty and ecological wines for the loyalty of its clients. Long-term strategy is to keep competition of price in one side and constant relation to wine producers and control their products, performance and activities. WineSol is a known brand in the wine market which receives various types of bottled wines in a range of qualities. WineSol has a wide distribution system and network of sellers in Europe and Spain. Its major clients are supermarkets, restaurants, hotels, cruiser, and wine shops all over the country. Indeed, it has some first-tier suppliers that act as a bridge between WineSol (buyer) and upstream suppliers. The upstream suppliers can be farmers, focal and rural wine producers that directly provide wines in different factories. We study the performance of our “first-tier suppliers” that directly deliver WineSol the completed products packed for selling. The main task of WineSol is to contract with two or three of them as significant first-tier suppliers. This is an opportunity to enhance efficiency by controlling a wider group of products. Consequently, WineSol can vouch that ecological wines are going under a very strict control and the process assures no pesticides and chemicals ingredients being used.

In the company, one of the concerns of investors is to make wines from organic grapes. It has been decided to control and observe the performance of first-tier suppliers every six months and an initiative is also endeavored to provide a pre-approved list of sub-suppliers to its first-tier suppliers to understate sustainability hazards arising from the lower-level suppliers. WineSol collects ecological wine produced from five first-tier suppliers (S₁,…S₅) who further procure the bottles from three second-tier suppliers (SS₁, SS₂ and SS₃). WineSol finally hack the blended brand, pack and distribute through its wide distribution channels. Couple of meetings and phone call conversation with company owners and experts resulted the characteristics that define the quality of a wine. Together with expert opinion and an exhaustive literature review, the following criteria are found predominant for sustainable and ecological wine production systems: 1. plant environment (C₁) including climate and weather conditions (continental, maritime and mediterranean), temperature involving cool, mild, warm, hot, sunlight and soil condition; 2. quality and appropriateness of species and varieties that are originating from North America (C₂); 3. viticulture practices, training and trellising, pruning, canopy management and harvest (mechanical or manual) (C₃). It basically involves practices for soil preparation and tilling, growing and planting of varieties, trellising and pruning of vines, and combating diseases; 4. ecological practices (oxygen, sulfur dioxide and oak emission) (C₄); 5. flexibility of delivery (C₅); 6. offered price (C₆); 7. environmental management system and pollution control (C₇) and 8. social responsibility and sustainability of the suppliers (C₈). Two groups of decision experts (D) are consulted to fill a set of questionnaire by them. They are responsible to visit wine providers’ sites, compare the importance of criteria and interpret the performance of suppliers. The experts are from chemical engineering backgrounds and have good experience and knowledge in wine sector. Group 1 (G1) is composed of 3 experts with more than 10 years of experiences in food and beverage sector, studied engineering in bachelor and master degree and consulting to several firms to keep quality standards. In other side, Group 2 (G2) is also having 3 SC executives with masters in environemmtal and agriculture and ecology sciences.

5.2 Application of the proposed model

5.2.1 First-tier supplier selection

The proposed model is now implemented for the first-tier supplier selection through the previously scripted two phases. The first phase involves determination of criteria weights using LBWA-D and SWARA-D methods. In the second phase, alternatives are evaluated using fuzzy linguistic MARCOS-D method, as already explained in Fig. 2.

Fig. 2

Influence of varying weights in score functions of fuzzy linguistic MARCOS-D method

Phase I—Determination of criteria weights

a) Application of LBWA-D method

This section describes the detail procedure for defining criteria weights using LBWA-D method.

Step 1. Identification of the most important criterion from the set of given criteria $S=\left\{C_1,C_2,\dots,C_8\right\}$. Expert groups defined criterion $C_5$ as the most significant/influential criterion.

Step 2. Grou** criteria by levels of significance. In accordance with expert preferences, the criteria are grouped into the following levels:

$$\begin{gathered} {S_1} = \left\{ {{C_5},{C_4},{C_6},{C_7}} \right\}, \hfill \\ {S_2} = \left\{ {{C_8},{C_1},{C_2}} \right\}, \hfill \\ {S_3} = \left\{ {C_3} \right\}. \hfill \\ \end{gathered}$$

Step 3. Based on Eq. (12), maximum value of criteria comparison scale is defined, as shown below:

$$\left. \begin{gathered} {S_1} = \left\{ {{C_5},{C_4},{C_6},{C_7}} \right\}, \hfill \\ {S_2} = \left\{ {{C_8},{C_1},{C_2}} \right\}, \hfill \\ {S_3} = \left\{ {C_3} \right\}. \hfill \\ \end{gathered} \right\} \Rightarrow r = \max \left\{ {\left| {S_1} \right|,\left| {S_2} \right|,\left| {S_3} \right|} \right\} = 4$$

Based on the maximum value of comparison scale, it can be concluded this scale ranges in the interval $I_{i_p}\in\left[0,4\right]$. Comparisons of criteria performed by expert groups G1 and G2 are shown in Table 4.

Table 4 Comparisons of criteria by levels of significance

In order to obtain unique comparisons of criteria by significance levels, a fusion of uncertainties is now performed. Using combination rule of D-numbers (Eq. (2)), unique D-numbers within the levels are obtained, as exhibited in Table 5.

Table 5 Preferences represented by D-numbers

By fusing the uncertainties obtained in Table 5, integrated values of preferences are obtained using Eq. (3):

$${\overline I_{i_p}} = \begin{array}{*{20}{l}} {C1} \\ {C2} \\ {C3} \\ {C4} \\ {C5} \\ {C6} \\ {C7} \\ {C8} \end{array}\left\{ {\begin{array}{*{20}{r}} {1.76} \\ {2.26} \\ {2.89} \\ {0.50} \\ {0.00} \\ {0.56} \\ {2.26} \\ {1.08} \end{array}} \right\}$$

Step 4. Based on r value and the condition that the coefficient of elasticity $\varphi>r$, $r=\text{max}\left\{\left|S_1\right|,\left|S_2\right|,\dots,\left|S_k\right|\right\}$, in this study, the value $\varphi=5$ is taken as the coefficient of elasticity.

Step 5. Define influence function of the criteria. By applying Eq. (13), influence functions of the considered criteria are calculated as follows:

$$f({C_j}) = \begin{array}{*{20}{l}} {C1} \\ {C2} \\ {C3} \\ {C4} \\ {C5} \\ {C6} \\ {C7} \\ {C8} \end{array}\left\{ {\begin{array}{*{20}{r}} {0.43} \\ {0.41} \\ {0.28} \\ {0.91} \\ {1.00} \\ {0.90} \\ {0.69} \\ {0.45} \end{array}} \right\}$$

Thus, for criterion C₁, we obtained a value $f\left(C_j\right)=5/\left(2\cdot5+1.76\right)=0.43$  using Eq. (13). In a similar way, the remaining values of criteria influence functions are obtained.

Step 6. Calculation of optimal criteria weights.

Weight coefficient of the best criterion (C5) is obtained using Eq. (14), as shown below: ${\xi_{C5}} = \frac{1}{1 + 0.43 + 0.41 + 0.28 + ... + 0.45} = 0.198$

Weights of remaining criteria are obtained using Eq. (15), as given below:

$$\begin{aligned}\xi_{C1}=f\left(C_1\right)\cdot\xi_{C5}=0.084; \xi_{C2}=f\left(C_2\right)\cdot\xi_{C5}=0.081;\\\xi_{C3}=f\left(C_3\right)\cdot\xi_{C5}=0.055; \xi_{C4}=f\left(C_4\right)\cdot\xi_{C5}=0.180\\\xi_{C6}=f\left(C_6\right)\cdot\xi_{C5}=0.178; \xi_{C7}=f\left(C_7\right)\cdot\xi_{C5}=0.136\\\xi_{C8}=f\left(C_8\right)\cdot\xi_{C5}=0.089.\end{aligned}$$

b) Application of SWARA-D method

This section presents application of the SWARA-D method for estimating criteria weights as follows:

Step 1. Define criteria significance.

The experts evaluated the criteria and defined comparative significance of the criteria, as shown in Table 6.

Table 6 Comparative significance of the first-tier supplier selection criteria

Based on the data presented in Table 6, it can be concluded that there is a dilemma when experts defined their preferences over the criteria. For example, for criterion C₁, we noticed that experts in G1 have a dilemma between the values of 0.15, 0.2, and 0.25. Experts from G1 are 20% sure that the significance of criterion C₁ is 0.15, so this dilemma is presented as (0.15, 0.2). Also, experts from the G1 group are 55% convinced that the significance of criterion C₇ is 0.2, so this dilemma is presented as (0.2, 0.55). In addition to the above two dilemmas, G1 experts are 35% sure that the degree of significance is 0.25, so this dilemma is presented as (0.25, 0.35). Finally, all the uncertainties in G1 are represented with D-number D₁ = {(0.5,0.3),(0.5; 1,0.35),(1.5,0.35)}. D-numbers for the remaining values shown in Table 5 are formed in the similar way.

In order to obtain a unique value of criteria significance ${\overline s}_j$, a fusion of the significance is performed by applying combination rules of D-numbers ${\overline s}_j=\overset1{s_j}\odot\overset2{s_j}$. After applying these rules and synthesis of uncertainties, the following unique D-numbers are obtained (Table 7).

Table 7 Expert preferences represented by D-numbers

.

Now, using integration operator of Eq. (3), uncertainties represented by D-numbers are integrated into a unique value ${\overline s}_j$:

$${\overline s_j} = \begin{array}{*{20}{l}} {C5} \\ {C6} \\ {C4} \\ {C7} \\ {C8} \\ {C2} \\ {C1} \\ {C3} \end{array}\left\{ {\begin{array}{*{20}{l}} - \\ {0.570} \\ {0.500} \\ {0.470} \\ {0.291} \\ {0.170} \\ {0.151} \\ {0.090} \end{array}} \right\}$$

Step 2. Criteria weight estimation.

Using Eq. (16), the estimated criteria significance values are given below.

For example, significance value of criterion C₁ is estimated as follows: $\zeta_{C1}=0.191/\left(0.151+1\right)=0.166$.

$${\zeta_j} = \begin{array}{*{20}{l}} {C5} \\ {C6} \\ {C4} \\ {C7} \\ {C8} \\ {C2} \\ {C1} \\ {C3} \end{array}\left\{ {\begin{array}{*{20}{r}} {1.000} \\ {0.637} \\ {0.425} \\ {0.289} \\ {0.224} \\ {0.191} \\ {0.166} \\ {0.152} \end{array}} \right\}$$

In a similar way we get the remaining values $\zeta_j$. By normalizing these values using Eq. (17), final criteria weights are obtained as follows:

$${\zeta}_{j}^{\prime} = \begin{array}{*{20}{l}} {C1} \\ {C2} \\ {C3} \\ {C4} \\ {C5} \\ {C6} \\ {C7} \\ {C8} \end{array}\left\{ {\begin{array}{*{20}{r}} {0.054} \\ {0.062} \\ {0.049} \\ {0.138} \\ {0.324} \\ {0.207} \\ {0.094} \\ {0.073} \end{array}} \right\}$$

Based on the obtained weights according to LBWA-D and SWARA-D methods, aggregated criteria weights are finally computed using Eq. (17), as shown in Table 8.

Table 8 Aggregated criteria weights

To obtain aggregated values of weighting coefficients, a value $\delta=0.5$ is considered here, in which both LBWA-D and SWARA-D methods equally participated in the weight calculation process.

Phase II—Evaluation of alternatives using fuzzy linguistic MARCOS-D method

After calculation of criteria weights, expert evaluation of the alternatives $A_i=\left(i=1,2,\dots,5\right)$ is performed. Evaluation of alternatives $A_i=\left(i=1,2,\dots,5\right)$ is performed on the basis of the eight considered criteria $C_j$ $\left(j=1,2,\dots,8\right)$.

Step 1. Construction of initial decision matrix (Y).

For the expert evaluation of alternatives, linguistic variables from the set $S=\left\{\left.s_i\right|i=0,1,\dots,6\right\}$  are used, i.e.

$$S=\left(s_0,s_1,s_2,s_3,s_4,s_5,s_6\right)=\left(very\,poor,\,poor,\,slightly\,poor,\,fair,\,slightly\,good,\,good,\,very\,good\right).$$

Expert groups evaluated alternatives based on a set of linguistic variables, as shown in Table 13. In order to obtain a unique initial decision matrix Y, fusion of uncertainties is then performed by applying combination rules of D-numbers. Aggregated values of the linguistic variables after fusion are exhibited in Table 9. In D-numbers D = {(s₃,0.1), (s₃;s₄,0.1)} and D = {(s₃,0.5), (s₃;s₄,0.13), (s₄,0.37)}, we did not obtain unique values of linguistic variables in all positions. In the first D-number, unique linguistic variable s₃ is obtained in the first position, while in the second position, value between the linguistic variables s₃ and s₄, i.e. “s₃;s₄” is obtained. It is similar with the second D-number D = {(s₃,0.5), (s₃;s₄,0.13), (s₄,0.37)}. The unique linguistic variables s₃ and s₄ are obtained at the first and third positions, while the value between linguistic variables s₃ and s₄ is obtained at the second position. Now to determine a unique linguistic value, Eq. (5) is applied and the linguistic variables s₃ and s₄ are transformed into TFNs as follows: $s_3=\left(0.333,0.500,0.667\right)$ and $s_4=\left(0.500,0.667,0.833\right)$ . Unique values of D-numbers are then defined using Eqs. (19) and (20), as: C₂-A₂: D = {(s₃,0.157),(s₄,0.843)} and C₂-A₄: D = {(s₃,0.572),(s₄,0.428)}.

Table 9 Aggregated values of linguistic variables

Now, by aggregating the unique values of D-numbers, an aggregated linguistic initial initial decision matrix is obtained, as shown below:

$$\begin{gathered} \begin{array}{*{20}{c}} { \, A1}&{ \, A2}&{ \, A3}&{ \, A4}&{ \, A5} \end{array} \hfill \\ \overline Y = \begin{array}{*{20}{l}} {C1} \\ {C2} \\ {C3} \\ {C4} \\ {C5} \\ {C6} \\ {C7} \\ {C8} \end{array}\left[ {\begin{array}{*{20}{l}} {{s_{2.83}}}&{{s_{3.26}}}&{{s_{2.20}}}&{{s_{2.77}}}&{{s_{2.48}}} \\ {{s_{2.85}}}&{{s_{3.84}}}&{{s_{4.20}}}&{{s_{3.43}}}&{{s_{3.20}}} \\ {{s_{4.33}}}&{{s_{2.10}}}&{{s_{4.75}}}&{{s_{1.90}}}&{{s_{3.00}}} \\ {{s_{2.77}}}&{{s_{4.22}}}&{{s_{2.00}}}&{{s_{3.90}}}&{{s_{3.20}}} \\ {{s_{2.53}}}&{{s_{3.88}}}&{{s_{3.00}}}&{{s_{4.73}}}&{{s_{3.00}}} \\ {{s_{3.73}}}&{{s_{2.88}}}&{{s_{3.43}}}&{{s_{2.00}}}&{{s_{5.00}}} \\ {{s_{5.70}}}&{{s_{2.71}}}&{{s_{2.41}}}&{{s_{3.00}}}&{{s_{4.12}}} \\ {{s_{4.50}}}&{{s_{3.80}}}&{{s_{3.00}}}&{{s_{3.54}}}&{{s_{2.00}}} \end{array}} \right] \hfill \\ \end{gathered}$$

An aggregated value for position C₁-A₁ is thus obtained using Eq. (3), as follows: $y_{11}=s_2\cdot0.17+s_3\cdot0.83=s_{2.83}$. In a similar way, remaining values from matrix $\overline Y$ are calculated. Next, the linguistic variables from matrix $\overline Y$ are transformed into triangular fuzzy numbers using Eq. (5), thus obtaining an aggregated initial initial decision matrix Y.

$$\begin{aligned}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A5\\Y=\begin{array}{c}C1\\C2\\C3\\C4\\C5\\C6\\C7\\C8\end{array}\begin{bmatrix}\left(0.306,0.472,0.639\right)&\left(0.376,0.543,0.709\right)&\left(0.201,0.367,0.534\right)&\left(0.295,0.462,0.628\right)&\left(0.247,0.414,0.580\right)\\\left(0.308,0.475,0.642\right)&\left(0.474,0.640,0.807\right)&\left(0.534,0.701,0.867\right)&\left(0.405,0.571,0.738\right)&\left(0.367,0.533,0.700\right)\\\left(0.556,0.722,0.889\right)&\left(0.183,0.350,0.517\right)&\left(0.625,0.792,0.958\right)&\left(0.150,0.317,0.483\right)&\left(0.333,0.500,0.667\right)\\\left(0.295,0.462,0.628\right)&\left(0.537,0.704,0.870\right)&\left(0.167,0.333,0.500\right)&\left(0.483,0.650,0.817\right)&\left(0.367,0.533,0.700\right)\\\left(0.256,0.422,0.589\right)&\left(0.479,0.646,0.813\right)&\left(0.333,0.500,0.667\right)&\left(0.621,0.788,0.955\right)&\left(0.333,0.500,0.667\right)\\\left(0.455,0.621,0.788\right)&\left(0.314,0.481,0.647\right)&\left(0.405,0.571,0.738\right)&\left(0.167,0.333,0.500\right)&\left(0.667,0.833,1.000\right)\\\left(0.783,0.950,1.117\right)&\left(0.285,0.451,0.618\right)&\left(0.235,0.402,0.568\right)&\left(0.333,0.500,0.667\right)&\left(0.520,0.687,0.853\right)\\\left(0.583,0.750,0.917\right)&\left(0.467,0.633,0.800\right)&\left(0.333,0.500,0.667\right)&\left(0.424,0.591,0.757\right)&\left(0.167,0.333,0.500\right)\end{bmatrix}\end{aligned}$$

Step 2 and 3: Formation of extended initial fuzzy matrix (EIFM) and normalization of EIFM elements. The fuzzy matrix is extended and elements of this extended matrix are normalized using Eq. (22).

$$\begin{aligned}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;AA1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A2\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A3\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\N=\begin{array}{c}C1\\C2\\C3\\C4\\C5\\C6\\C7\\C8\end{array}\left[\begin{array}{cccc}\left(0.283,0.518,0.753\right)&\left(0.431,0.666,0.901\right)&\left(0.530,0.765,1.000\right)&\left(0.283,0.518,0.753\right)\\\left(0.355,0.548,0.740\right)&\left(0.355,0.548,0.740\right)&\left(0.546,0.738,0.930\right)&\left(0.616,0.808,1.000\right)\\\left(0.157,0.330,0.504\right)&\left(0.580,0.754,0.928\right)&\left(0.191,0.365,0.539\right)&\left(0.652,0.826,1.000\right)\\\left(0.191,0.383,0.574\right)&\left(0.339,0.530,0.722\right)&\left(0.617,0.809,1.000\right)&\left(0.191,0.383,0.574\right)\\\left(0.268,0.442,0.617\right)&\left(0.268,0.442,0.617\right)&\left(0.502,0.677,0.851\right)&\left(0.349,0.524,0.698\right)\\\left(0.167,0.200,0.167\right)&\left(0.212,0.268,0.367\right)&\left(0.257,0.347,0.531\right)&\left(0.226,0.292,0.412\right)\\\left(0.210,0.360,0.509\right)&\left(0.701,0.851,1.000\right)&\left(0.255,0.404,0.553\right)&\left(0.210,0.360,0.509\right)\\\left(0.182,0.364,0.545\right)&\left(0.636,0.818,1.000\right)&\left(0.509,0.691,0.873\right)&\left(0.364,0.545,0.727\right)\end{array}\cdots\right]\end{aligned}$$

$$\begin{aligned}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;A5\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;AID\\N=\begin{array}{c}C1\\C2\\C3\\C4\\C5\\C6\\C7\\C8\end{array}\left[\cdots\begin{array}{ccc}\left(0.416,0.651,0.886\right)&\left(0.348,0.583,0.818\right)&\left(0.530,0.765,1.000\right)\\\left(0.467,0.659,0.851\right)&\left(0.423,0.615,0.807\right)&\left(0.616,0.808,1.000\right)\\\left(0.157,0.330,0.504\right)&\left(0.348,0.522,0.696\right)&\left(0.652,0.826,1.000\right)\\\left(0.555,0.747,0.938\right)&\left(0.421,0.613,0.804\right)&\left(0.617,0.809,1.000\right)\\\left(0.651,0.825,1.000\right)&\left(0.349,0.524,0.698\right)&\left(0.651,0.825,1.000\right)\\\left(0.333,0.500,1.000\right)&\left(0.167,0.200,0.250\right)&\left(0.333,0.500,1.000\right)\\\left(0.299,0.448,0.597\right)&\left(0.466,0.615,0.764\right)&\left(0.701,0.851,1.000\right)\\\left(0.462,0.644,0.826\right)&\left(0.182,0.364,0.545\right)&\left(0.636,0.818,1.000\right)\end{array}\right]\end{aligned}$$

Step 4 and 5: Determination of weighted fuzzy matrix and calculation of ${\widetilde S}_i$ fuzzy matrix.

By multiplying criteria weights of Table 8 with the elements of matrix N, weighted fuzzy matrix is computed. Thereafter, elements of fuzzy matrix are obtained using Eq. (25), as follows:

$${\tilde{S}_i} = \begin{array}{*{20}{l}} {AAI} \\ {A1} \\ {A2} \\ {A3} \\ {A4} \\ {A5} \\ {AID} \end{array}\left[ {\begin{array}{*{20}{l}} {\left( {0.223,0.379,0.523} \right)} \\ {\left( {0.400,0.561,0.729} \right)} \\ {\left( {0.435,0.601,0.784} \right)} \\ {\left( {0.314,0.476,0.648} \right)} \\ {\left( {0.451,0.630,0.870} \right)} \\ {\left( {0.336,0.493,0.652} \right)} \\ {\left( {0.581,0.761,1.000} \right)} \end{array}} \right]$$

Step 6: Calculation of utility degree of alternatives ${\widetilde K}_i$.

By applying Eqs. (26) and (27), utility degrees of the considered alternatives are calculated:

$$\begin{gathered} \, K_i^- \, K_i^+ \hfill \\ \begin{array}{*{20}{l}} {AAI} \\ {A1} \\ {A2} \\ {A3} \\ {A4} \\ {A5} \\ {AID} \end{array}\left[ {\begin{array}{*{20}{l}} {\left( {0.426,1.000,2.349} \right)}&{\left( {0.223,0.498,0.901} \right)} \\ {\left( {0.765,1.480,3.270} \right)}&{\left( {0.400,0.737,1.254} \right)} \\ {\left( {0.831,1.586,3.519} \right)}&{\left( {0.435,0.790,1.349} \right)} \\ {\left( {0.600,1.256,2.906} \right)}&{\left( {0.314,0.626,1.114} \right)} \\ {\left( {0.861,1.664,3.903} \right)}&{\left( {0.451,0.829,1.497} \right)} \\ {\left( {0.643,1.300,2.925} \right)}&{\left( {0.336,0.647,1.122} \right)} \\ {\left( {1.110,2.008,4.488} \right)}&{\left( {0.581,1.000,1.721} \right)} \end{array}} \right] \hfill \\ \end{gathered}$$

For example, $\widetilde K_1^-$ and $\widetilde K_1^-$ values of alternative A1, are obtained as follows:

$${\tilde K_1}^- = \frac{{\left( {0.400,0.561,0.729} \right)}}{{\left( {0.223,0.379,0.523} \right)}} = \left( {\frac{0.400}{{0.523}},\frac{0.561}{{0.379}},\frac{0.729}{{0.223}}} \right) = \left( {0.765,1.480,3.270} \right)$$

$${\tilde K_i}^+ = \frac{{\left( {0.400,0.561,0.729} \right)}}{{\left( {0.581,0.761,1.000} \right)}} = \left( {\frac{0.400}{{1.000}},\frac{0.561}{{0.761}},\frac{0.729}{{0.581}}} \right) = \left( {0.400,0.737,1.254} \right)$$

Step 7. Determination of utility functions in relation to ideal $f\left(\widetilde K_i^+\right)$ and anti-ideal $f\left(\widetilde K_i^-\right)$ solutions. Using Eqs. (28) and (29), values of $f\left(\widetilde K_i^+\right)$ and $f\left(\widetilde K_i^-\right)$ are obtained.

$$\begin{gathered} \, f\left( {K_i^- } \right) \, f\left( {K_i^+ } \right) \hfill \\ \begin{array}{*{20}{l}} {A1} \\ {A2} \\ {A3} \\ {A4} \\ {A5} \end{array}\left[ {\begin{array}{*{20}{l}} {\left( {0.142,0.274,0.606} \right)}&{\left( {0.074,0.136,0.232} \right)} \\ {\left( {0.154,0.294,0.652} \right)}&{\left( {0.081,0.146,0.250} \right)} \\ {\left( {0.111,0.233,0.538} \right)}&{\left( {0.058,0.116,0.206} \right)} \\ {\left( {0.159,0.308,0.723} \right)}&{\left( {0.083,0.153,0.277} \right)} \\ {\left( {0.119,0.241,0.542} \right)}&{\left( {0.062,0.120,0.208} \right)} \end{array}} \right] \hfill \\ \end{gathered}$$

For example, $f\left(\widetilde K_i^+\right)$ and $f\left(\widetilde K_i^-\right)$ values of alternative A1 are estimated as follows:

$$f\left( {\tilde K_1^+ } \right) = \frac{{\left( {0.400,0.737,1.254} \right)}}{5.339} = \left( {\frac{0.400}{{5.339}},\frac{0.737}{{5.339}},\frac{1.254}{{5.339}}} \right) = \left( {0.074,0.136,0.232} \right)$$

$$f\left( {\tilde K_i^- } \right) = \frac{{\left( {0.765,1.480,3.270} \right)}}{5.339} = \left( {\frac{0.765}{{5.339}},\frac{1.480}{{5.339}},\frac{3.270}{{5.339}},} \right) = \left( {0.142,0.274,0.606} \right)$$

where $d=\underset i{\text{max}}\left\{\sum_{i=1}^5\left(\widetilde K_i^-+\widetilde K_i^+\right)\right\}=\underset i{\text{max}}=\left\{1.312;2.492;5.399\right\}=5.399$.

Step 8: Determination of utility function of alternatives $f\left(K_i\right)$ and subsequent ranking of the alternatives.

After defuzzification of $\widetilde K_1^-$, $\widetilde K_1^+$, $f\left(\widetilde K_1^+\right)$ and $f\left(\widetilde K_1^-\right)$ values, Eq. (30) is used to obtain utility functions of the alternatives, as shown in Table 10:

Table 10 Utility functions and corresponding ranking of the alternatives

For example, utility function of alternative A₁ is calculated as follows:

$$f\left( {K_1} \right) = \frac{0.767 + 1.659}{{1 + \frac{1 - 0.142}{{0.142}} + \frac{1 - 0.307}{{0.307}}}} = 0.261$$

In the same way, $f\left(K_i\right)$ values of the remaining alternatives are computed. The considered alternatives are ranked according to the descending values of the utility functions. From Table 10, it is clear that A₄ is the best first-tier supplier, followed by A₂, whereas A₃ emerges out as the worst alternative supplier.

5.2.2 Second-tier supplier selection

In this section, the proposed model is now used for evaluation of the three second-tier suppliers (SS₁, SS₂ and SS₃). Use of hazardous materials (SC₁), green management and design (SC₂), health and safety issues (SC₃), manufacturing and technological capability (SC₄) and social responsibility (SC₅) are considered as the evaluating criteria. The second-tier suppliers are the one that produce bottle for wine producers. We have requested the same experts to visit the relevant suppliers and provide us their opinions. Similar to the previous stage of evaluating first-tier suppliers, criteria weights for second-tier supplier selection are calculated by both LBWA-D and SWARA-D methods and finally, the aggregated weights are estimated, as shown in Table 11. Health and safety (SC₃) emerges to be the highest important criterion in the considered supplier evaluation process according to expert opinions.

Table 11 Aggregated criteria weights

The next step in finding the most suitable second-tier supplier is to develop the performance matrix using aggregated expert preferences, as adopted in Sect. 5.2.1. This matrix is shown in Table 14. Thereafter, by aggregating the unique values of D-numbers, an aggregated linguistic initial initial-decision matrix is obtained, as shown below:

$$\begin{gathered} \begin{array}{*{20}{c}} { \, SS1}&{SS2}&{SS3} \end{array} \hfill \\ \overline Y = \begin{array}{*{20}{c}} {SC1} \\ {SC2} \\ {SC3} \\ {SC4} \\ {SC5} \end{array}\left[ {\begin{array}{*{20}{l}} {{s_{2.21}}}&{{s_{3.13}}}&{{s_{2.03}}} \\ {{s_{2.23}}}&{{s_{3.81}}}&{{s_{2.57}}} \\ {{s_{2.45}}}&{{s_{5.06}}}&{{s_{3.00}}} \\ {{s_{2.51}}}&{{s_{5.28}}}&{{s_{2.53}}} \\ {{s_{5.36}}}&{{s_{3.80}}}&{{s_{2.85}}} \end{array}} \right] \hfill \\ \end{gathered}$$

Now, the utility functions and rank of the alternatives are obtained using Eqs. (19)-(31), as shown in Table 12. From this table, it is observed SS₂ with highest utility score of 0.424 emerges out as the best alternative second-tier supplier for enhancing quality of the wine bottles regarding the pre-defined criteria.

Table 12 Utility functions and corresponding ranking of the alternatives

6 Sensitivity analysis and discussion

Sensitivity analysis and validation of the results are now performed in three distinct phases. In the second phase of sensitivity analysis, influence of changes in parameter δ in criteria function values is analyzed. The third phase presents a comparison of ranking results between the fuzzy linguistic MARCOS-D method with three other D-number-based MCDM methods. Due to space limitations, sensitivity analyses for first-tier suppliers are shown here.

6.1 Changing the weights of the criteria

In the first phase, analysis of influence of changing criteria weights on ranking results is performed. Changes in criteria weights are considered in relation to the change in weight (w₅) of the most influential criterion (C₅). 50 scenarios are considered using Eq. (31) in which changes in w₅ are simulated (Pamucar et al. 2017). At the same time, weights of other criteria are proportionally adjusted.

$${\varpi_{n\beta }} = \left( {1 - {\varpi_{n\alpha }}} \right)\frac{{w_\beta }}{{\left( {1 - {w_n}} \right)}}$$

(32)

where $\varpi_{n\beta}$ represents adjusted value of the criterion, $\varpi_{n\alpha}$ represents reduced value of the best criterion (C₅), $w_\beta$ represents original value of the criterion and $w_n$ represents original value of the best criterion (C₅).

In the first scenario, value of criterion C₅ is reduced by 1%, while the values of remaining criteria are proportionally adjusted using Eq. (31). In each subsequent scenarios, value of criterion C₅ is changed by 2% while the values of remaining criteria are adjusted so as to satisfy the condition ${\textstyle\sum_{j=1}^8}w_j=1$. Changes in criteria weights for all the 50 scenarios are shown in Fig. 7.

Fig. 3

Influence of parameter $\delta\in\left[0,1\right]$ on alternative ranking

After the formation of new 50 weight vectors, score functions for all the alternatives are again estimated for fuzzy linguistic MARCOS-D method, as shown in Fig. 2.

From Fig. 2, it is observed that changes in weights of criterion C5 slightly affect criterion function values in fuzzy linguistic MARCOS-D method and thus, no changes in ranking of the alternatives are observed. Consequently, it can be concluded that the two alternatives {A₄, A₂} are indicated as good solutions, with the confirmed advantage of alternative A₄ over A2.

6.2 Change of parameter δ in the function for aggregation of weight coefficients

As stated in Sect. 3.1, parameter δ affects the final values of criteria weights as it indicates the influence of LBWA-D and SWARA-D methods in the final weights. The initial ranks of the alternatives are derived at δ = 0.50 value. In this section, an analysis on the influence of varying δ values on criteria weights is performed to observe its effects on the final ranking results. Changes in δ values in the interval $\delta\in\left[0,1\right]$ is simulated. The complete interval is divided into 100 equal sequences, i.e. 100 scenarios are formed. In the first scenario, δ is assumed to be of zero value, while for each subsequent scenario, value of δ is increased by 0.01. Thus, 100 new weight vectors are formed, through which the influence of these changes on final ranking are analyzed, as exhibited through Fig. 3.

From Fig. 3, it is distinctly noticed that changes in δ values in the interval $\delta\in\left[0,1\right]$ affects criterion function values in fuzzy linguistic MARCOS-D method. However, despite such changes during the 100 scenarios, there is no change in the positions of the first three dominant alternatives {A₄, A₂, A₁}. However, few minor changes are observed for alternatives A₅ and A₃ when δ > 0.15. From the presented analysis, it can be concluded that parameter δ has an impact on ranking of the alternatives, but these changes are insufficient to cause any major changes. However, it should be noted that such an analysis should always be performed as an indispensable step before making a final decision.

6.3 Comparison with fuzzy MCDM methodologies

To best of the knowledge, there are only few papers on application of D-numbers to extend traditional MCDM methods (Fei et al.

7 Conclusions, research implication and future directions

Supplier management becomes a strategic topic in SCM for industrial organizations. Therefore, accuracy of supplier performance measurement is a fundamental requirement for an efficient and smooth SCMS. Food sector during the recent pandemic has suffered immensely. Agricultures, corporations, manufacturers, distributers and suppliers are highly disturbed and hurrmed due to lack of planned strategies in unpredicted and disruption conditions. The necessity of establishing a stable SCM is vital in environmental, social, and economic crisis. Policy makers in FSC must recognize minor changes in SC performance which can lead to negative consequences. Therefore, implementation of supplier selectio with respect to sustianble and ecological objectives has become strategic responsibility to managers in this sector. This paper develops an integrated LBWA and SWARA model coupled with D-numbers for estimating criteria weights under multi-tier supplier selection environment. Such integrated structure permits experts to offer a more rational processing of preferences when they weight the criteria. In the proposed multiple criteria model, supplier selection is carried out using MARCOS method under fuzzy linguistic variables and D-numbers. Ecological practices (oxygen, sulfur dioxide and oak emission) and flexibility of delivery emerged out as the most predominant criteria for the first-tier supplier selection the considered wine industry case study. Viticulture practices, training and trellising, pruning, canopy management and harvest (mechanical or manual) criterion received the least importance according to the experts’ evaluations. Health and safety issues and social responsibility emerged out as the best and least important criteria for the second tier suppliers. It signifies that lower tier suppliers potentially violate social and environmental standards which can result adversely to upper tier suppleirs. Both the manufacturer and upper tier suppliers should exert effort to improve the responsibility of the lower tier suppliers. In the context of global sustainable multi-tier SCs, involvement of first-tier suppliers has become instrumental to achieve socio-econimiocally and environmentally viable SCM systems. Findings from the presented analytical outcomes reveal that the lead organizations should motivate and encourage the role of different tiers separately to reduce information asymmetries, particularly at lower tier levels.

Results assert that the proposed decision making model eliminates uncertainties that exist in supplier performance assessment. By designing several sensitivity analyses, preciousness and capability of the model is also tested. In this paper, several criteria are considered to assess the wine producers (suppliers) for the considered case study. Authors believe that the proposed model with some modifications and adjustments can be adopted to other type of studies where supplier performance is a major concern. This paper has some limitations also in terms of data collection in wine sector which is not an easy task to perform. Any technical and chemical processes require special observations and may be time consuming also. As a future research scope, other MCDM methods like CoCoSo, EDAS and MABAC can be further extended using D-numbers and their results can be compareD. Use of quality function deployment (QFD) along with D-numbers in supplier selection can be a novel research theme. Inspite of having several advantages like overcoming exclusiveness hypothesis and completeness constraint, D-numbers also have some associated limitations in terms of operations and use of combination rules to fulfil associative properties. Once the combination algorithm is used, D-numbers are transformed into triangular fuzzy numbers for further multiplications and divisions as such algorithms for D numbers are not definitive. To overcome such operational issues, further researches are required for development of improved combination algorithms like multiplicative and additive forms so that multiple D-numbers can be combined efficiently.

Appendix

1.1 Problem of exclusivity

Example: Suppose a patient has symptoms of fever, polypnea, and cough. Two doctors examined the patient and assumed that it was flu (F), bacterial or fungal pneumonia (B) or COVID-19 (C). The first doctor submitted a report stating that the 35% probability is that the patient has an F or B (m₁{F,B} = 0.35), while the probability of 55% that the patient has C (m₁{C} = 0.55), the remaining probability of 10% refers to the unknown. Another doctor stated in his report that he was 45% sure that the patient had F (m₂{F} = 0.45) and that 45% was sure that the patient had C (m₂{C} = 0.50), the other 10% were not sure which disease the patient had. The problem that doctors need to solve is to define exactly which disease the patient has. Using DS theory, the following results were obtained: m{F} = 0.340; m{C} = 0.584; m{F,B} = 0.059 and m{F,B,C} = 0.017. As can be seen from the results, a hypothesis emerges that covers all other diseases that cause the symptoms of fever, polypnea and cough. This hypothesis is presented as {F,B,C}. However, this hypothesis is not covered by the doctor's report. It is obvious that this hypothesis is not rational from the aspect of medical diagnostics. The appearance of the irrational hypothesis is a consequence of the problem of the exclusivity of the elements in DS theory (Fig. 5), in our case of diagnosed diseases. From this real world example we can conclude that this limitation of DS theory limits its application for solving certain real problems.

Fig. 5

Frame of discernment in DS theory and domain in D-numbers

Fig. 6

Fuzzy linguistic variables

Fig. 7

Varying criteria weights through 50 scenarios

Table 13 Experts' evaluation of alternatives

Table 14 Expert’s preference matrix for second tier supplier evaluation