SpringerLink
Log in

Singularity analysis of Jeffcott rotor-magnetic bearing with time delays

  • Published:
Applied Mathematics-A Journal of Chinese Universities Aims and scope Submit manuscript

Abstract

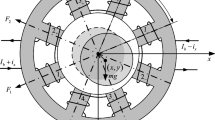
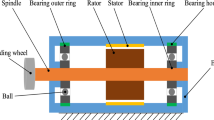
A Jeffcott rotor-magnetic bearing with time delays is investigated in this paper. Firstly, it is found that the characteristic equation of the system satisfies the conditions of the singularity. Secondly, the center manifold reduction and normal form are employed to study the bifurcation from simple zero and zero-purely imaginary singularities. The results of this paper will help to understand the influence of the time delays in feedback loop on the dynamics of rotor-magnetic bearing system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. T Faria, L T Magalhaes. Normal forms for retarded functional differential equations and applications to Bogdanov-Takens singularity, J Differential Equations, 1995, 122(2): 201–224.

    Article  MathSciNet  MATH  Google Scholar 

  2. J Hale. Theory of Functional Differential Equations, Springer, New York, 1977.

    Book  MATH  Google Scholar 

  3. J C Ji, C H Hansen. Non-linear oscillations of a rotor in active magnetic bearings, J Sound Vibration, 2001, 240(4): 599–612.

    Article  Google Scholar 

  4. J C Ji. Stability and bifurcation in an electromechanical system with time delays, Mech Res Comm, 2003, 30(3): 217–225.

    Article  MATH  Google Scholar 

  5. J C Ji. Stability and Hopf bifurcation of a magnetic bearing system with time delay, J Sound Vibration, 2003, 259(4): 845–856.

    Article  MathSciNet  MATH  Google Scholar 

  6. J C Ji. Dynamics of a Jeffcott rotor-magnetic bearing system with time delays, Internat J Non-Linear Mech, 2003, 38(9): 1387–1401.

    Article  MathSciNet  MATH  Google Scholar 

  7. J C Ji, C H Hansen. Hopf bifurcation of a magnetic bearing system with time delay, J Vib Acoust, 2005, 127(4): 362–369.

    Article  MathSciNet  Google Scholar 

  8. W H Jiang, J J Wei. Bifurcation analysis in van der Pol’s oscillator with delayed feedback, J Comput Appl Math, 2008, 213(2): 604–615.

    Article  MathSciNet  MATH  Google Scholar 

  9. W H Jiang, Y Yuan. Bogdanov-Takens singularity in van der Pol’s oscillator with delayed feedback, Phys D, 2007, 227(2): 149–161.

    Article  MathSciNet  MATH  Google Scholar 

  10. S J Kim, C W Lee. On-line identification of current and position stiffness by LMS algorithm in active magnetic bearing system equipped with force transducers, Mech Syst Signal Pr, 1999, 13(5): 681–690.

    Article  Google Scholar 

  11. D Laier, R Markert. Nonlinear oscillations of magnetically suspended rotors, In: Proceedings of the Second European Nonlinear Oscillation Conference, vol I, Academy of Science of the Czech Republic, Prague, 1996, 239–242.

    Google Scholar 

  12. D J Peel, C M Bringham, D Howe. Simplified characteristics of active magnetic bearings, P IMech Eng C J Mec, 2002, 216(5): 623–628.

    Article  Google Scholar 

  13. S Ruan, J Wei. On the zeros of transcendental functions with applications to stability of delay differential equations with two delays, Dynam Contin Discrete Impuls Systems, 2003, 10(6): 863–874.

    MathSciNet  MATH  Google Scholar 

  14. A Tonoli, H J Bornemann. Analysis of losses due to rotor vibrations in a high-Tc superconducting flywheel system, J Sound Vibration, 1998, 212: 649–662.

    Article  Google Scholar 

  15. L Virgin, T F Walsh, J D Knight. Nonlinear behavior of a magnetic bearing system, J Eng Gas Turbines Power, 1995, 117(3): 582–588.

    Article  Google Scholar 

  16. C C Wang. Application of a hybrid numerical method to the nonlinear dynamic analysis of a micro gas bearing system, Nonlinear Dynam, 2010, 59(4): 695–710.

    Article  MATH  Google Scholar 

  17. C C Wang, H Yau. Theoretical analysis of high speed spindle air bearings by a hybrid numerical method, Appl Math Comput, 2010, 217(5): 2084–2096.

    Article  MathSciNet  MATH  Google Scholar 

  18. C C Wang. Application of a hybrid method to the bifurcation analysis of a relative short gas journal bearing system with herringbone grooves, Ind Lubr Tribol, 2011, 63(5): 307–319.

    Article  Google Scholar 

  19. C C Wang. Bifurcation analysis of an aerodynamic journal bearing system considering the effect of stationary herringbone grooves, Chaos Solitons Fractals, 2007, 33(5): 1532–1545.

    Article  MATH  Google Scholar 

  20. H B Wang, J Q Liu. Stability and bifurcation analysis in a magnetic bearing system with time delays, Chaos Solitons Fractals, 2005, 26(3): 813–825.

    Article  MathSciNet  MATH  Google Scholar 

  21. H B Wang, W H Jiang. Multiple stabilities analysis in a magnetic bearing system with time delays, Chaos Solitons Fractals, 2006, 27(3): 789–799.

    Article  MathSciNet  MATH  Google Scholar 

  22. Y Yuan, J J Wei. Singularity Analysis on a Planar System with Multiple Delays, J Dynam Differential Equations, 2007, 19(2): 437–456.

    Article  MathSciNet  MATH  Google Scholar 

  23. B Zhen, J Xu. Simple zero singularity analysis in a coupled FitzHugh-Nagumo neural system with delay, Neurocomputing, 2010, 73(4–6): 874–882.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Heilongjiang Institute of Science and Technology, Harbin, 150027, China

    **u-yan Xu

  2. Department of Mathematics, Harbin Institute of Technology, Harbin, 150001, China

    Wei-hua Jiang

Authors
  1. **u-yan Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wei-hua Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to **u-yan Xu.

Additional information

Supported by the Heilongjiang Province Department of Education Science and Technology Project (11544048).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xu, Xy., Jiang, Wh. Singularity analysis of Jeffcott rotor-magnetic bearing with time delays. Appl. Math. J. Chin. Univ. 27, 419–427 (2012). https://doi.org/10.1007/s11766-012-2752-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11766-012-2752-8

MR Subject Classification

Keywords

Search

Navigation