Mold Simulator Study of Heat Transfer Phenomenon During the Initial Solidification in Continuous Casting Mold

Abstract

In this paper, mold simulator trials were firstly carried out to study the phenomena of the initial shell solidification of molten steel and the heat transfer across the initial shell to the infiltrated mold/shell slag film and mold. Second, a one-dimensional inverse heat transfer problem for solidification (1DITPS) was built to determine the temperature distribution and the heat transfer behavior through the solidifying shell from the measured shell thickness. Third, the mold wall temperature field was recovered by a 2DIHCP mathematical model from the measured in-mold wall temperatures. Finally, coupled with the measured slag film thickness and the calculations of 1DITPS and 2DIHCP, the thermal resistance and the thickness of liquid slag film in the vicinity of the meniscus were evaluated. The experiment results show that: the total mold/shell thermal resistance, the mold/slag interfacial thermal resistance, the liquid film thermal resistance, and the solid film thermal resistance is 8.0 to 14.9 × 10⁻⁴, 2.7 to 4.8 × 10⁻⁴, 1.5 to 4.6 × 10⁻⁴, and 3.9 to 6.8 × 10⁻⁴ m² K/W, respectively. The percentage of mold/slag interfacial thermal resistance, liquid film thermal resistance, and solid film thermal resistance over the total mold/shell thermal resistance is 27.5 to 34.4, 17.2 to 34.0, and 38.5 to 48.8 pct, respectively. The ratio of radiation heat flux is around 14.1 to 51.9 pct in the liquid slag film.

Introduction

Mold flux is usually added on the top of liquid steel surface that protects the steel meniscus from oxidation, inhibits heat loss from steel, and absorbs the inclusions rising from liquid steel.[1] The liquid slag from the top molten slag layer infiltrates into the mold/shell gap and lubricates the newly formed shell. Then the liquid slag is getting cooled quickly and leads to the formation of a solid slag film (1 to 2 mm thick)[2] with glass, crystal, or a mixture of both phases, and a liquid slag film (~0.1 mm thick) next to the solidified steel shell.[3,4,5,6] Lubrication of liquid slag film throughout the shell is preferred to prevent the sticking of the shell to the mold and decrease the occurrences of the longitudinal surface cracks and the star cracks.[6] Jenkins[3] pointed out that the liquid film slag thickness could be estimated from 1/(3V ^0.5_c ). As the liquid slag film travels with the strand, the average thickness of liquid slag film can be estimated from the slag consumption by assuming that the solid slag film remains stuck to the mold. The calculated thickness of liquid slag film would be thicker than that of the exact value as the solid slag could be dragged intermittently downward at an average speed slower than the casting speed.[7,8] In this study, a novel method for estimating the liquid slag film thickness is proposed.

Occurrences of shell surface longitudinal cracks and off squareness are accelerated when the heat flux at the meniscus area exceeds a critical value (depending on the steel grade).[9,10,11] Hence the decrease of heat flux is expected to alleviate the longitudinal facial cracks and the off squareness, especially for the hypo-peritectic steels. The major heat transfer mechanism across the slag film is heat conduction and radiation, where the conduction dominates the heat transfer in the solid slag and the radiative heat transfer plays an important role in the transparent glassy and the liquid layer.[2] The control of the heat flux through the mold can be achieved by adjusting the slag film thickness (controlled by slag break temperature and viscosity etc), the fraction of crystals, and the optical properties of slag.[4,12,13,14,15] Generally, the high basicity mold flux (high tendency for crystallization) is applied to the crack-sensitive steel grades to optimize the mold heat flux and the liquid/glassy slag film with transition metal oxides is desired to suppress the radiative heat transfer and provide the lubrication.[16,49] However, there is little literature to report the measurement of the liquid slag film thickness below the meniscus.

For investigating the mold/slag interfacial thermal resistance, several techniques have been developed, which includes the pouring experiment,[29] the parallel-sided plate experiment,[24,30,31] the infrared emitter technique,[50,51] and the dip experiment.[52,53,54,55] However, all above techniques for the measurement of thermal resistance cannot represent the real scenario of continuous casting mold where the mold/slag thermal resistance varies with the position below the meniscus. A pilot caster[2,56] had been used to investigate the heat transfer across the slag film, while the thermal resistance of slag film along the casting direction was difficult to be calculated due to the complex and transient heat transfer in the vicinity of the meniscus. Recently, works by Wang et al.[54,55] on the dip experiment have shown the extended use of the mold simulator for investigating the influence of the mold oscillation on the mold/slag interfacial thermal resistance. The mold simulator[19,57,58,59,60,61,62] has the ability to replicate the initial solidification phenomena of an actual continuous casting mold under laboratory conditions, including the initial shell solidification and the lubrication of liquid mold flux.

In this study, mold simulator trials were carried out to study the initial solidification phenomena of continuous casting, then the initial shell and the infiltrated mold/shell slag film were obtained. Second, an one-dimensional inverse heat transfer problem for solidification (1DITPS) was built to determine the heat transfer of solidifying shell from the measured shell thickness. Third, the mold wall temperature field was recovered by a 2DIHCP mathematical model[63] from the measured temperature of the two columns of thermocouples at different depths inside the mold. Finally coupled with the measured slag film thickness and the calculations of 1DITPS and 2DIHCP, the thermal resistance and the thickness of liquid slag film in the vicinity of meniscus were evaluated.

Experiment Setup and Process

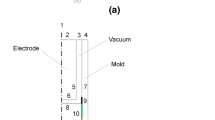
The mold simulator applied to this study is an inverse-type copper mold with the size of 30 mm × 50 mm × 350 mm, and is shown in Figure 1, which includes induction furnace, water-cooled mold, and extractor. The mold with water-cooling grooves is manufactured inside a copper plate and 16 thermocouples (Figure 2) are embedded inside the mold. The mold equipped with an extractor only makes one face of mold expose to the liquid melt. As the liquid steel contacts the mold, it would form an initial shell. Then the extractor withdraws the solidifying shell downward during the solidification process. The responding temperatures could be measured by the thermocouples at the frequency of 60 Hz through the data acquisition system. As shown in Figure 2, the distribution of thermocouples in the mold is represented by the dots that give the fixed locations of thermocouples. Along the middle position of the mold, there are two columns of thermocouples, and they are 3 mm (hot) and 8 mm (cold) away from the mold hot surface, respectively.

Fig. 1

Schematic figure of the mold simulator and the experiment process

Fig. 2

Location of the thermocouples and the computational domain

During the test, 25 kg ultra-low carbon steel ([C]: 0.0011 wt pct, [Si]: 0.004 wt pct, [Mn]: 0.107 wt pct, [P]: 0.0093 wt pct, [S]: 0.0048 wt pct) was firstly melted in the induction furnace. After the charge was molten, the temperature of the melt was adjusted to the target superheat, the mold flux designed for low carbon steel (about 0.3 kg, composition is shown in Table I) was added to the surface of liquid bath, so that there would be a layer of 9-mm-thick molten flux on the top of liquid steel. Then, the copper mold covered with extractor descended inside the melt, while the mold was kept oscillating. The mold and extractor were lowered to the preset depth into the melt bath, where the liquid mold flux surface and the meniscus of liquid steel were located in the mold thermocouple-measuring zone. After the mold and the extractor reached the target depth, it was held for 5 seconds to form an initial shell on the water-cooled copper mold, to ensure that the initial shell is strong enough to prevent tearing during extraction. Then the casting started. The extractor withdrew the solidifying shell downward at a constant speed to simulate the continuous casting. The mold is moved upward at a certain speed to compensate for the rise of mold level, so that the liquid mold flux surface and the meniscus could be kept at the same position with respect to the mold. When casting was completed for the desired length, the mold and the extractor were withdrawn out of the melt and then cooled in air. From the moment the mold was lowered into the bath to the completion of casting and the mold kept oscillating in sinusoidal pattern (oscillation parameters are listed in Table II). At last, the position of the shell tip with respect to the mold was measured and then the solidified shell and the slag film adjacent to copper mold were obtained for further study.

Table I Chemical Compositions of Mold Fluxes (Weight Percent)

Table II Mold Oscillation Setting and Casting Conditions

One example of the responding temperature evolution of the two columns of thermocouples during the period of casting simulation in one trial is shown in Figure 3, where the temperatures of thermocouples 3 mm away from hot surface, TC-hot, are about 6 K to 10 K (6 °C to 10 °C) higher than those thermocouples that are 8 mm away from hot surface, i.e., TC-cold. The detailed information about the responding temperature variations can be found in our previous papers.[38,61]

Fig. 3

Measured in-mold wall temperatures during experiment: (a) temperature of thermocouples at hot side, and (b) temperature of thermocouples at cold side

Figure 4 shows the measured shell thickness and the measured thickness of the slag film (liquid slag film plus solid slag film) between the mold and the solidified shell.[38,61] The shell thickness (s) is measured and fitted into a square root raw equation, v = K × t ^1/2_s , where the solidification time (t _s, minute) is calculated using the equation t _s = l/V _c (l is the distance from the shell tip and V _c is casting speed). Then the solidification factor K, is found to be 19.6 mm min^1/2, and the shell thickness is 3.26 mm at 18 mm below the shell tip. The thickness of the slag film in between mold and solidified shell is in the range of 0.8 to 3.0 mm. The detailed similar information can be found in previous papers.[38,61]

Fig. 4

Thicknesses of the shell and the mold flux film in mold/shell gap

Mathematical Model for Analyzing Experimental Data

In this section, a partial differential equation (PDE)-based direct problem model is first built to determine the temperature field during the liquid steel solidification. Based on the PDE direct problem model, an one-dimensional inverse heat transfer problem for solidification (1DITPS) is built to determine the heat transfer across solidifying shell from the measured shell thickness. Finally, the 1DITPS is solved using the Levenberg–Marquardt iterative method.

Inverse Heat Transfer Problem for Solidification

Direct problem

Figure 2 shows the solidifying shell is withdrawn downward, and the liquid slag infiltrates into the mold/shell gap and solidifies on the mold to provide lubrication and the control of horizontal heat transfer. The heat transfer across the solidifying shell is assumed as one dimensional by neglecting the heat transferring upward into the mold top slag, the fluid flow of melt, and the z-axis heat conduction in steel, due to the large Péclet number: Pe = V _c × shell length × ρ _steel × c/k _s ≈ 0.01 × 0.018 × 7400 × 820/35 = 31.2. Thus the computed domain {(x)|0 ≤ x ≤ l} is a heat transfer bar with a finite length through the liquid steel and the solidifying shell. Then, the computed domain moves downward at the casting speed for the simulation of the liquid steel solidification. The initial temperature of steel is T ₀, and the boundary conditions are set as heat flux q(t) = 0 at x = 0 side and is insulated at x = l side due to the liquid steel is in contact with the wall of furnace (MgO). The mathematical formula of this problem is governed by,

$$ \rho \frac{\partial E}{\partial t} = \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right), \, x \in \left[ {0,l} \right], \, t \in \left[ {0,t_{\text{f}} } \right], $$

(1a)

$$ - k\frac{\partial T(0,t)}{\partial x} = q\left( t \right), $$

(1b)

$$ - k\frac{\partial T(l,t)}{\partial x} = 0, $$

(1c)

$$ T\left( {x,0} \right) = T_{0}, $$

(1d)

where the E = c·T − L _a·f _s, is enthalpy,[64] in J/kg. The solid fraction f _s is zero in the liquid steel, and it equals to (T _l − T)/(T _l − T _s) in the mushy zone, and is one in the solidified steel. Solidification front in the mushy zone is defined at the position where f _s is 0.8. The enthalpy method that includes both sensible and latent heat of steel is adopted to solve heat transfer problem of solidification.[65,66]

The heat flux at the mold side q(t), with a function of time t, is assumed to be the linear superposition of a group known as orthogonal functions C _j (t) (e.g., polynomial, trigonometric function), and each orthogonal function has a parameter P _j . In this study the heat flux is assumed as a fifth-order polynomial equation.

$$ q(t) = \sum\limits_{k = 1}^{N} {p_{k} C_{k} (t)} $$

(2)

Inverse problem

Obviously, the direct problem could be solved only when all of the parameters, P = [P ₁, P ₂, …, P _N ], are specified. Therefore, an inverse problem is constructed to determine the parameter vector P, such that the calculated shell thicknesses from direct problem would approach to the measured one from the experiment. The solution of inverse problem is based on the minimization of the sum of the squares of the deviations between the calculated shell thickness and the measured shell thickness. The objective function of inverse problem is

$$ s({\mathbf{P}}) = \sum\limits_{j = 1}^{M} {\left[ {v_{j} - u_{j} ({\mathbf{P}})} \right]^{2} }, $$

(3)

where M is the number of measurement, v _j and u _j (P) are the measured and the calculated shell thickness at the time of j, respectively. u = [u ₁, u ₂, …, u _M ]^T and v = [v ₁, v ₂, …,v _M ]^T.

Solution to the inverse problem

Levenberg–Marquardt iterative method is used to minimize the objective function of inverse problem Eq. [3], where the derivatives of s(P) with respect to each of the unknown parameter, P = [P ₁, P ₂, …, P _N ], are set to zero, then Eq. [4] is obtained as the following.

$$ \frac{{\partial s({\mathbf{P}})}}{{\partial p_{1} }} = \frac{{\partial s({\mathbf{P}})}}{{\partial p_{2} }} = \cdots = \frac{{\partial s({\mathbf{P}})}}{{\partial p_{N} }} = 0 $$

(4)

Equation [4] is rewritten in the matrix form by setting the gradient of s(P) with respect to the vector of parameters P to zero.

$$ \left[ {\nabla s\left( {\mathbf{P}} \right)} \right]_{k} = - 2\sum\limits_{j = 1}^{M} {\frac{{\partial u_{j} }}{{\partial p_{k} }}\left[ {v_{j} - u_{j} ({\mathbf{P}})} \right]} = 0\quad k = { 1},\; 2,\; 3,\; \ldots ,\;N. $$

(5)

Defining the sensitivity coefficient matrix, it then becomes:

$$ {\mathbf{J}}({\mathbf{P}}) = \left| {\begin{array}{*{20}c} {\frac{{\partial u_{1} }}{{\partial p_{1} }} \, \frac{{\partial u_{1} }}{{\partial p_{2} }} \cdots \frac{{\partial u_{1} }}{{\partial p_{N} }}} \\ {\frac{{\partial u_{2} }}{{\partial p_{1} }} \, \frac{{\partial u_{2} }}{{\partial p_{2} }} \cdots \frac{{\partial u_{2} }}{{\partial p_{N} }}} \\ { \vdots \, \vdots \, \vdots } \\ {\frac{{\partial u_{M} }}{{\partial p_{1} }} \, \frac{{\partial u_{M} }}{{\partial p_{2} }} \cdots \frac{{\partial u_{M} }}{{\partial p_{N} }}} \\ \end{array} } \right| $$

(6)

The element of the sensitivity coefficient matrix J(P) is called the sensitivity coefficients J _jk , and a forward difference is used for estimating the sensitivity coefficients with respect to parameter P _k , that is,

$$ J_{jk} = \left[ {\frac{{\partial u_{j} }}{{\partial p_{k} }}} \right]^{\text{T}} \cong \frac{{u_{j} (p_{1} ,p_{2} , \ldots ,p_{k} + \xi p_{k} , \ldots ,p_{N} ) - u_{j} (p_{1} ,p_{2} , \ldots ,p_{k} , \ldots ,p_{N} )}}{{\xi p_{k} }}, $$

(7)

where the ξ is a small number (10⁻³ to 10⁻⁶).

Using the sensitivity coefficient matrix J(P), Eq. [5] becomes,

$$ - 2{\mathbf{J}}^{T} ({\mathbf{P}})(\varvec{v} - \varvec{u}) = 0 $$

(8)

The solution to Eq. [8] needs an iterative procedure that was obtained by line raring the vector u with a Taylor series expansion around the current solution P ⁱ.

$$ \varvec{u}({\mathbf{P}}^{i + 1} )\varvec{ = u}({\mathbf{P}}^{i} )\varvec{ + }{\mathbf{J}}^{i} (\varvec{u} - \varvec{u}^{i} ) $$

(9)

Substituting Eq. [9] into [8], then the following iterative procedure is obtained for estimating the vector P,

$$ {\mathbf{P}}^{i + 1} = {\mathbf{P}}^{i} + [({\mathbf{J}}^{i} )^{\text{T}} {\mathbf{J}}^{i} ]^{ - 1} ({\mathbf{J}}^{i} )^{\text{T}} (\varvec{v} - \varvec{u}^{i} ) $$

(10)

In the above calculation, if the determinant of J ^T J is very small, the parameters P cannot be determined using the iterative procedure of Eq. [10]. Then the Levenberg–Marquardt method could be used to alleviate such difficulties by utilizing an iterative procedure in the following form.

$$ {\mathbf{P}}^{i + 1} = {\mathbf{P}}^{i} + \left\{ {({\mathbf{J}}^{i} )^{\text{T}} {\mathbf{J}}^{i} + \mu^{i} {\text{diag}}[({\mathbf{J}}^{i} )^{\text{T}} {\mathbf{J}}^{i} ]} \right\}^{ - 1} ({\mathbf{J}}^{i} )^{\text{T}} (\varvec{v} - \varvec{u}^{i} ), $$

(11)

where diag means taking the diagonal terms of the matrix. μ ⁱ is a positive scalar dam** parameter whose magnitude is dynamically adjusted to the condition of the iterative process. μ ⁱ, initially with a larger number at the beginning of iterative, is gradually reduced as the iterative procedure advances.

The following criteria are used to stop the iterative procedure of the Levenberg–Marquardt method,[67]

$$ s({\mathbf{P}}^{i + 1} ) < \varepsilon_{1}, $$

(12a)

$$ \left\| {\left( {{\mathbf{J}}^{i} } \right)^{T} (\varvec{v} - \varvec{u}^{i} )} \right\| < \varepsilon_{2}, $$

(12b)

$$ \left\| {{\mathbf{P}}^{i + 1} - {\mathbf{P}}^{i} } \right\| < \varepsilon_{3}, $$

(12c)

where ε ₁, ε ₂, and ε ₃ are the pre-chosen tolerances, and $\left\| \cdot \right\|$ is the vector Euclidean norm. The Levenberg–Marquardt algorithm procedure for solving the inverse problem is summarized in the Table III. The algorithm is achieved using MATLAB™.

Table III Algorithm for Solving 1DITPS by Levenberg–Marquardt Method

Validations for Direct and Inverse Problem

Validation for direct problem

Equation [1] is solved using finite difference (FD) method with explicit scheme, where the stable condition should satisfy:

$$ \Delta t < {{\Delta x^{2} } \mathord{\left/ {\vphantom {{\Delta x^{2} } {2\alpha }}} \right. \kern-0pt} {2\alpha }}, $$

(13)

where Δt is time step, Δx is discrete space step, and α (= k/(ρ × c)) is thermal diffusion coefficient.

The numeric method for solving direct problem is verified through comparison with a Stefan condition solidification problem that a melt of pure substance (temperature is T ₀) is solidifying against a mold wall with a constant temperature T _mld. By assuming a constant shell surface temperature and constant substance properties, the analytical solution of the Stefan condition solidification problem could be obtained and the temperatures in the solid (T _S) and the liquid (T _L) are,[68]

$$ \frac{{T_{\text{S}} - T_{\text{mld}} }}{{T_{\text{p}} - T_{\text{mld}} }} = \frac{{{\text{erf}}\left( {{x \mathord{\left/ {\vphantom {x {2\sqrt {\alpha_{\text{s}} t} }}} \right. \kern-0pt} {2\sqrt {\alpha_{\text{s}} t} }}} \right)}}{{{\text{erf}}(\eta )}},\quad \frac{{T_{\text{L}} - T_{0} }}{{T_{\text{mld}} - T_{0} }} = \frac{{{\text{erfc}}\left( {{x \mathord{\left/ {\vphantom {x {2\sqrt {\alpha_{\text{l}} t} }}} \right. \kern-0pt} {2\sqrt {\alpha_{\text{l}} t} }}} \right)}}{{{\text{erfc}}\left( {\eta \sqrt {{{\alpha_{\text{s}} } \mathord{\left/ {\vphantom {{\alpha_{\text{s}} } {\alpha_{\text{l}} }}} \right. \kern-0pt} {\alpha_{\text{l}} }}} } \right)}} $$

(14)

The thickness of the solid is,

$$ v = 2\eta \sqrt {\alpha_{\text{s}} t}, $$

(15)

where α _l and α _s are the thermal diffusion coefficients for the liquid and the solid, respectively. The η is a constant that could be determined by the following equation,

$$ \frac{{\exp ( - \eta^{2} )}}{{{\text{erf}}(\eta )}} + \frac{{k_{\text{l}} }}{{k_{\text{s}} }}\sqrt {\frac{{\alpha_{\text{s}} }}{{\alpha_{\text{l}} }}} \frac{{T_{\text{p}} - T_{0} }}{{T_{\text{p}} - T_{\text{mld}} }}\frac{{\exp ( - \eta^{2} {{\alpha_{\text{s}} } \mathord{\left/ {\vphantom {{\alpha_{\text{s}} } {\alpha_{\text{l}} }}} \right. \kern-0pt} {\alpha_{\text{l}} }})}}{{{\text{erfc}}(\eta \sqrt {{{\alpha_{\text{s}} } \mathord{\left/ {\vphantom {{\alpha_{\text{s}} } {\alpha_{\text{l}} }}} \right. \kern-0pt} {\alpha_{\text{l}} }}} )}} = \frac{{\eta L_{\text{a}} \sqrt \pi }}{{c(T_{\text{p}} - T_{\text{mld}} )}} $$

(16)

For numeric solution of direct problem Eq. [1], five different space steps (Δx) 0.05, 0.1, 0.2, 0.5, and 1.0 mm are used, and the time step (Δt) equals to Δx ²/3α. For validation, the physical properties, such as density, specific heat, latent heat, thermal conductivity, melting point, and initial melt temperature, etc are listed in Table IV.

Table IV Physical Properties Used in Analytical Solution and Numeric Solution

Figure 5(a) shows the shell thickness calculated by FD method that is in good agreement with the calculated value by analytical solution. The thickness growth by FD method matches the results by the analytical solution, no matter what the length of space step is used. Figure 5(b) shows the shell temperature distribution of FD method with Δx being 0.1 mm, and it is observed that the results are consistent with the ones obtained by analytical solution, which suggests that the direct problem solved by FD method is accurate.

Fig. 5

Comparison of the analytical solution and the numeric solution: (a) solidified shell growth, and (b) evolution of the temperature

Validations for inverse problem

In this section, a numeric test problem is designed to provide simulated experimental data for the verification of the 1DITPS model. First, assign the heat flux q(t) at x = 0 side (Figure 2) for direct problem Eq. [1], which is:

$$ q(t) = a_{0} + a_{1} t + a_{2} t^{2} + a_{3} t^{3} + a_{4} t^{4} + a_{5} t^{5} $$

(17)

where a ₀, a ₁, a ₂, a ₃, a ₄, and a ₅ are 1 × 10⁴, 2 × 10⁴, −3 × 10⁴, 4 × 10⁴, −5 × 10⁴ and 6 × 10⁴, respectively. Second, substituting q(t) into direct problem Eq. [1], then the exact thickness of shell growth within 18 seconds is obtained in Figure 6(a), and thickness measurement is taken every 0.2 seconds. Third, the Gaussian noise signals ωσ are added to the exact thickness of the shell to mimic the thickness measurement error for the further testing of the anti-noise ability of 1DITPS model, where the standard deviation of noise σ is set as 0, 0.02, 0.05, and 0.1, respectively, and ω is a random variable within −2.576 to 2.576 for a 99 pct confidence bound. Next, the exact thickness of the shell is delivered to the 1DITPS model for the back calculation of the heat flux at x = 0 side. Finally, those recovered shell thickness and the recovered heat flux at x = 0 side from 1DITPS are compared with the exact thickness of shell and the exact heat flux of Eq. [17], respectively. If the exact shell thickness contains the measurement errors, the recovered shell thickness still shows good agreement with the exact thickness of shell (Figure 6(a)), and also the recovered shell surface heat flux agrees well with the exact heat flux (Figure 6(b)). This suggests that the 1DITPS is capable of recovering the shell surface heat flux from the measured shell thickness data.

Fig. 6

Recovered results: (a) shell thickness, and (b) surface heat fluxes

The mean absolute percentage error (MAPE) is defined to investigate the accuracy of 1DITPS model for determining the heat flux from the measured shell thicknesses with different measurement errors.

$$ {\text{MAPE}} = \frac{100\% }{M}\sum\limits_{i = 1}^{M} {\left| {\frac{{A_{i} - C_{i} }}{{A_{i} }}} \right|} $$

(18)

in which A _i is exact heat flux used to calculate shell thickness and C _i is the recovered heat flux at time j.

Figure 7 shows the MAPE of 1DITPS model for determining the heat flux at x = 0 side under three different noise levels σ. It could be seen that the accuracy of 1DITPS model is improved with the decrease of measurement error in shell thickness where the standard deviation of noise σ is 0, 0.02, 0.05, and 0.1, and the corresponding MAPE is 4.54, 18.27, 20.77, and 22.18 pct, respectively.

Fig. 7

Effect of the measurement error on the mean absolute percentage error of recovered heat flux

Results and Discussion

In this section, the mold wall temperature field was recovered by a 2DIHCP[63] mathematical model from the temperature of the two columns of thermocouples at different depths inside the mold. The 2DIHCP is capable of restructuring the mold wall temperature and the heat flux at mold surface from the in-mold temperature measurement, and shows a good anti-interference ability of inverse results to the temperature measurement noise.[63] Subsequently, 1DITPS was applied to estimate the heat transfer across solidifying shell from the measured shell thickness. Next, coupled with the measured slag film thickness and the calculations of 1DITPS and 2DIHCP, the thermal resistance and the thickness of the liquid slag film in the vicinity of the meniscus were evaluated.

Recovered Results from 1DITPS and 2DIHCP

Thermal field of mold determined by 2DIHCP

The measured mold wall temperatures during casting simulation (Figure 3) are delivered into the 2DIHCP,[63] then one mold oscillation cycle of the temperature and the heat flux at the mold surface are recovered and shown in Figure 8, where Z = 0 mm represents the location of the shell tip, and the time of 63.633, 63.733, 63.833, 63.933, and 64.133 seconds are corresponding to the oscillating location of mold at crest, midway, trough, midway, and crest, respectively. It could be observed that the temperature and heat flux at the mold surface, T _mold and q _int, increase below the shell tip and reach the maximum values of 374 K (101 °C) and 2.1 MW/m² at the position 7 to 8 mm below the shell tip (corresponding to the thinnest slag film, Figure 4), which is due to the fact that the thermal resistance between the mold and shell in this range is lowest (Figure 12). Then both of them decrease with the addition of total thermal resistance, as shown in Figure 12. The mean heat flux through mold surface is 1.66 MW/m² at the shell tip and 1.44 MW/m² at 18 mm below the shell tip. The mean temperature of mold surface is 367.0 K (93.9 °C) at the shell tip and 364.9 K (91.5 °C) at 18 mm below the shell tip. During one single oscillation cycle, it can be observed that the heat flux increases with the mold down-stroke (include negative strip time), which is associated with the enhancement of liquid flux infiltration in between mold/shell gap during negative strip time.[47] Meanwhile, the deformation of the meniscus makes the meniscus get further close to the mold,[46] leading to the heat flux pickup at early positive strip time. The result is consistent with previous studies.[38,46,47,58,61,63]

Fig. 8

One cycle of the results calculated by 2DIHCP. (a) mold surface heat flux, and (b) mold surface heat flux temperature

Thermal field of solidifying shell determined by 1DITPS

The measured shell thickness values (Figure 4) are delivered into the 1DITPS (Physical properties of steel are listed in Table V), then the thermal field of the shell solidification is recovered. Figure 9 shows the recovered temperature (T _sh) and heat flux (q _shell) at the solidifying shell surface. The shell surface temperature T _sh is 1803 K (1530 °C) at the shell tip, and rapidly decreases for the location 0 to 5.4 mm below the shell tip, as the growth of the shell thickness (from 0 to 1.9 mm thick) causes the additional thermal barriers for the heat transfer to isolate the direct heating from the molten bath. The heat flux of shell surface, q _shell, also decreases sharply due to the growth of initial shell. At the location of 5.4 mm below the shell tip, T _sh reaches the minimal value of 1523 K (1250 °C), then it begins to increase for the location of 5.4 to 15.7 mm below the shell tip, and reaches a maximal value of 1617 K (1344 °C). Afterwards, T _sh decreases slightly and becomes 1604 K (1331 °C) at 18 mm. This could be explained by the heat accumulated at the solidification front that was introduced by the difference between the q _shell and q _int, which is clearly shown in Figure 9. Finally, once the heat flux difference is getting closer, T _sh would decrease with the increase of the total thermal resistance (R _tot + R _shell) and the reduction of q _int.

Table V Physical Properties of Ultra-low Carbon Steel

Fig. 9

Mold surface temperature and heat flux

For the heat flux of shell surface, q _shell continues to decrease as the shell thickness grows, and attenuates from 12.9 MW/m² at the shell tip to 2.0 MW/m² at 14 mm below the shell tip. Finally it stabilizes around 2.5 MW/m². It can be seen that the heat flux at solidifying shell surface (q _shell) is higher than that of heat flux across the mold surface (q _int), especially for the location 0 to 6 mm below the shell tip. There is no surprise for this: the shell solidification near the meniscus area is multi-dimensional heat transfer including heat convection, and heat conduction along both vertical and horizontal directions. For 1DITPS calculation, the heat flux across the solidifying shell surface whether in vertical or horizontal direction would be classified into the horizontal heat flux, as 1DITPS neglects the heat convection and heat conduction transferring upward into the mold top slag and the vertical heat conduction in steel shell. The mold surface heat flux (q _int) recovered by 2DIHCP is the heat flux perpendicular to the mold surface. Thus, the heat flux across the mold surface (q _int) could be regarded as the horizontal component of heat flux across the solidifying shell surface (q _shell). Along the casting direction, the difference between q _int and q _shell gets smaller, which implies that the two-dimensional heat transfer of shell solidification tends to attenuate and the one-dimensional (horizontal) heat transfer becomes dominant in the shell solidification.

When the mold oscillating position is at midway, the temperature field of the mold wall is restructured by 2DIHCP and the temperature field in the solidifying steel is recovered by 1DITPS as shown in Figure 10. The temperature of solidifying shell surface decreases rapidly for the location 0 to 5.4 mm below the shell tip, and reaches the minimal value of 1523 K (1250 °C) at 5.4 mm below the shell tip. The maximum values of the mean temperature [374 K (101 °C)] and the mean heat flux (2.1 MW/m²) of the mold surface heated by the hot steel occurred at about 7 to 8 mm below the shell tip. This is due to the fact that the total thermal resistance between mold and shell is smallest (Figure 12) for the position 7 to 8 mm below the shell tip.

Fig. 10

Temperature fields across the mold to the melt

Heat Transfer in the Slag Film During the Mold Simulator Trial

In this section the heat transfer model of slag film was built, then the thermal resistance and the liquid slag film thickness were evaluated based on the measured slag film thickness and the calculations of 1DITPS and 2DIHCP were carried out.

Shell/mold heat transfer model near the meniscus area

Figure 11 shows the thermal resistances between the mold and the shell. The total thermal resistance R _tot between shell and mold includes the mold/slag interfacial thermal resistance R _int and slag film thermal resistance R _film (contains the conductive and radiative parts). The slag film thermal resistance R _film consists of solid slag film thermal resistance R _s and liquid slag film thermal resistance R _l. For the simplification of heat transfer calculation in the slag film, the following three assumptions are made: (1) the liquid slag temperature at shell side equals to the shell surface temperature, (2) the latent heat during the solid–liquid transition of liquid slag film is neglected, and (3) the heat transfer in slag film is at steady state, owing to the fact that the heat transfer from shell to mold q _int is much larger than the heat accumulated in the slag film: q _int/(ρ _slag × C _slag × slag cooling rate × liquid slag film thickness) ≈ [1.44 − 2.1 MW/m²]/(1000 × 2500 × [(1800 − 1600)/2 K/s] × [0.5 mm]) = 11.6 to 16.8. According to the superposition principle, the mold surface heat flux (q _int) would be regarded as the horizontal component of heat flux across the slag film. Therefore the total thermal resistance R _tot could be estimated from the average mold surface heat flux q _int (Figure 8(a)), the shell surface temperature T _sh (Figure 9), and the average mold surface temperature T _mld (Figure 8(b)),

Fig. 11

Thermal resistances between the mold and the shell

$$ R_{\text{tot}} = \frac{{T_{\text{sh}} - T_{\text{mld}} }}{{q_{\text{int}} }} $$

(19)

$$ R_{\text{tot}} = R_{\text{int}} + R_{\text{film}} = R_{\text{int}} + R_{\text{s}} + R_{\text{l}} $$

(20)

The liquid slag film thermal resistance R _l could be obtained from the average mold surface heat flux q _int (Figure 8(a)), and the shell surface temperature T _sh (Figure 9) and T _sol, where T _sol is the interfacial temperature between the crystal and liquid layers and equals to the crystallization temperature that is obtained through an experiment by SHTT.[54,69,70]

$$ R_{\text{l}} = \frac{{T_{\text{sh}} - T_{\text{sol}} }}{{q_{\text{int}} }} $$

(21)

The liquid slag film thermal resistance R _l consists of the conductive thermal resistance R _lc and the radiative thermal resistance 1/h _lr, that is,

$$ R_{\text{l}} = \frac{1}{{{1 \mathord{\left/ {\vphantom {1 {R_{\text{lc}} }}} \right. \kern-0pt} {R_{\text{lc}} }} + h_{\text{lr}} }}, $$

(22)

where R _lc equals to d _l/k _sl and the radiative thermal resistance is as following,[5]

$$ \frac{1}{{h_{\text{lr}} }} = \frac{{0.75\varphi_{\text{l}} d_{\text{l}} + \varepsilon_{\text{sh}}^{ - 1} + \varepsilon_{\text{cry}}^{ - 1} - 1}}{{m^{2} \sigma_{\text{B}} (T_{\text{sh}}^{2} + T_{\text{sol}}^{2} )(T_{\text{sh}} + T_{\text{sol}} )}} $$

(23)

The liquid slag film thickness d _l is calculated from Eqs. [21] through [23], then the solid slag film thickness d _s could be obtained from the measured slag film thickness d _m (Figure 4).

$$ d_{\text{s}} + d_{\text{l}} = d_{\text{m}} $$

(24)

Knowing the mold/slag interfacial thermal resistance R _int, the temperature of slag surface at mold side T _ss could be computed from the average mold surface heat flux q _int (Figure 8(a)) and the average mold surface temperature T _mld (Figure 8(b)),

$$ T_{\text{ss}} = T_{\text{mld}} + R_{\text{int}} q_{\text{int}} $$

(25)

The slag film from the mold simulator trials consists of crystals, glass, air gap, and cracks, which are also found in the industrial caster ones.[56] Thus it is very hard to determine the physical properties of the solid slag, and the simple heat transfer model of gray body is not suitable for studying the heat transfer process in solid slag film which is a discontinuous medium.[55,71] For simplification, an effective thermal conductivity k _eff[2] that takes both the conductive and the radiative heat transfers into account is used here to investigate the heat transfer in the solid slag film. Then the mold/slag interfacial thermal resistance R _int and the slag surface temperature at mold side T _ss could be computed from Eqs. [26] and [27], respectively. During the calculation, the physical properties of mold flux, such as shell emission ε _sh, thermal conductivity and crystallization temperature T _sol etc, are listed in Table VI.

Table VI Physical Properties of Mold Flux

$$ R_{\text{s}} = \frac{{d_{\text{s}} }}{{k_{\text{eff}} }} $$

(26)

$$ q_{\text{int}} = \frac{{T_{\text{sol}} - T_{\text{ss}} }}{{R_{\text{s}} }} = \frac{{T_{\text{ss}} - T_{\text{mld}} }}{{R_{\text{int}} }} $$

(27)

Analysis of shell/mold heat transfer

Figure 12 shows the total shell/mold thermal resistance, and R _tot is 13.7 × 10⁻⁴ m² K/W at the location of shell tip (Z = 0 mm), and decreases to the minimum (8.0 × 10⁻⁴ m² K/W) at 8 mm below the shell tip due to the reduction of slag film thickness (Figure 4), then it begins to increase and finally becomes 14.9 × 10⁻⁴ m² K/W at 18 mm below the shell tip due to the increases of the slag film thickness, the mold/slag interfacial thermal resistance R _int, and the slag film thermal resistance R _film. The solid slag film thermal resistance R _s is 5.3 × 10⁻⁴ m² K/W at the location of shell tip (Z = 0 mm), and decreases to the minimum (3.9 × 10⁻⁴ m² K/W) at 8 mm below the shell tip, then it begins to increase and finally becomes 6.8 × 10⁻⁴ m² K/W at 18 mm below the shell tip due to the further crystallization of mold flux. The thermal resistance of solid slag film R _s is about 1.4 to 2.8 times larger than that of the thermal resistance in the liquid slag film R _l. The mold/slag interfacial thermal resistance R _int is 3.8 × 10⁻⁴ m² K/W at the location of shell tip (Z = 0 mm), and decreases to the minimum (2.7 × 10⁻⁴ m² K/W) at 8 mm below the shell tip, then begins to increase and finally reaches 4.8 × 10⁻⁴ m² K/W at 18 mm below the shell tip. The mold/slag interfacial thermal resistance R _int increases with the addition of the slag film thickness (Figures 4 and 12), which is consistent with the study of Cho.[30] The value of R _int has the same magnitude as the values studied by Nakato et al.[74] (3 to 9 × 10⁻⁴ m² K/W) and Yamauchi et al.[24] (4 to 8 × 10⁻⁴ m² K/W). Supposing R _int is the result of the air gap formation between the mold and the slag film, then the equivalent air gap size (R _int × k _a ) could be calculated as 12.0 μm at the location of shell tip (Z = 0 mm), and decreases to the minimum (8.6 μm) at 8 mm below the shell tip, then it increases and finally becomes 15.3 μm at 18 mm below the shell tip.

Fig. 12

Thermal resistance between the mold and shell along the continuous casting direction

Figure 13 shows the percentage of the mold/slag interfacial thermal resistance R _int, the liquid film thermal resistance R _l, and the solid film thermal resistance R _s over the total mold/shell thermal resistance, and they are 27.5 to 34.4 pct (R _int/R _tot), 17.2 to 34.0 pct (R _l/R _tot), and 38.5 to 48.8 pct (R _s/R _tot), respectively. Therefore, the interfacial thermal resistance, R _int, and the solid film thermal resistance, R_s, are regarded as the dominant factors to control the heat transfer from the shell to the mold.

Fig. 13

Percentage of the resistance in total

There are conductive and radiative heat transfers in the liquid slag film. The conductive thermal resistance of liquid layer R _lc (=d _l/k _sl) is proportional to the thickness of liquid slag layer, d _l. As Figure 14 shows the conductive thermal resistance of the liquid thickness R _lc, and it is 9.6 × 10⁻⁴ m² K/W at the location of shell tip (Z = 0 mm), then decreases to 1.7 × 10⁻⁴ m² K/W at 6 mm below the shell tip, then begins to increase and finally is 5.0 × 10⁻⁴ m² K/W at 18 mm below the shell tip. According to Eq. [23], both the shell surface temperature T _sh and the thickness of liquid slag layer d _l have effects on the radiative thermal resistance 1/h _lr. The radiative thermal resistance 1/h _lr is about 1.8 to 5 times larger than that of the conductive thermal resistance R _lc in liquid slag film. The radiative thermal resistance 1/h _lr is 8.9 × 10⁻⁴ m² K/W at the location of shell tip (Z = 0 mm), and increases for the location 0 to 6 mm below the shell tip and is 10.6 × 10⁻⁴ m² K/W at 6 mm below the shell tip, the main reason for this is the decreasing of the shell surface temperature (Figure 9); afterwards 1/h _lr stabilizes around 10.2 × 10⁻⁴ m² K/W due to the combination effects of the increase of liquid slag film thickness and the variation of shell surface temperature. The thermal resistance of liquid slag film R _l varies with the changes of the conductive thermal resistance R _lc and the radiative thermal resistance 1/h _lr, and R _l is 4.6 × 10⁻⁴ m² K/W at the location of shell tip (Z = 0 mm) and decreases to the minimum (1.5 × 10⁻⁴ m² K/W) at 7 mm below the shell tip, then increase and approaches 3.4 × 10⁻⁴ m² K/W at 18 mm below the shell tip.

Fig. 14

Rate of the radiative heat transfer in the liquid flux film

The heat transfer across the liquid slag is the function of the shell surface temperature and the thickness of liquid slag film. Figure 15 shows that the rate of heat transfer by radiation in the liquid slag film is 51.9 pct at the location of shell tip (Z = 0 mm) and decreases to 14.1 pct at 6 mm below the shell tip; the main reason for this is due to the reduction of the shell surface temperature, then the rate begins to increase and finally becomes 32.9 pct at 18 mm below the shell tip. The rate of heat transfer by conduction in the liquid slag film is 48.1 pct at the location of shell tip (Z = 0 mm) and increases to 85.9 pct at 6 mm below the shell tip, then the rate begins to decrease and finally reaches 67.1 pct at 18 mm below the shell tip; the main reason for this is due to the increase of the liquid slag thickness 6 mm below the shell tip.

Fig. 15

Thermal resistances in the liquid flux film

Figure 16 shows the measured mold/shell slag film thickness from experiment d _m (=d _s + d _l), and the calculated solid slag film thickness d _s and the liquid slag film thickness d _l. The liquid slag film thickness d _l is 1.2 mm at the location of shell tip (Z = 0 mm), and decreases to the minimum (0.2 mm) for the location about 6 mm below the shell tip due to the reduction of shell surface temperature (Figure 9), then it begins to increase and finally becomes 0.6 mm at 18 mm below the shell tip with the increase of the shell surface temperature. The main reason for the variation of liquid slag film thickness is due to the change of the shell surface temperature, T _sh (Figure 9). Cramb,[4] Mills[1] estimated the liquid slag film thickness to be about 0.1 mm. According to Jenkins[3] equation 1/(3V ^0.5_c ), the liquid slag film thickness is calculated as 0.43 mm.

Fig. 16

Thicknesses of the solid film and liquid film between the mold and shell

Conclusions

Combining the calculations of a one-dimensional inverse heat transfer problem for solidification (1DITPS) and 2DIHCP, a novel method to evaluate the temperature distribution and heat transfer phenomena across the initial shell to the mold flux film and copper mold has been successfully developed based on the mold simulator trials. The specific conclusions are made as follows:

• 1. A partial differential equation (PDE)-based direct problem model is first built to determine the temperature field during the liquid steel solidification, then a one-dimensional inverse heat transfer problem for solidification (1DITPS) is successfully developed to determine the heat transfer across solidifying shell based on the PDE direct problem model.

• 2. Through the calculation of 2DIHCP, the temperature and heat flux at the mold surface, T _mld and q _int, increase below the shell tip and reach the maximum values of 374 K (101 °C) and 2.1 MW/m² at the position 7 to 8 mm below the shell tip, which is due to the fact that the thermal resistance between the mold and shell in this range is lowest. Then both of them decrease with the addition of total thermal resistance. The mean heat flux through mold surface is 1.66 MW/m² at the shell tip and 1.44 MW/m² at 18 mm below the shell tip. The mean temperature of mold surface is 367.0 K (93.9 °C) at the shell tip and 364.9 K (91.5 °C) at 18 mm below the shell tip.

• 3. Through the calculation of 1DITPS, the recovered temperature (T _sh) and heat flux (q _shell) at the solidifying shell surface are obtained. The shell surface temperature T _sh is 1803 K (1530 °C) at the shell tip, and rapidly decreases for the location 0 to 5.4 mm below the shell tip. At the location of 5.4 mm below the shell tip, T _sh reaches the minimal value of 1523 K (1250 °C), then it begins to increase for the location of 5.4 to 15.7 mm below the shell tip, and reaches a maximal value of 1617 K (1344 °C). Afterwards, T _sh decreases slightly and becomes 1604 K (1331 °C) at 18 mm. The heat flux of shell surface, q _shell, continues to decrease as the growth of the shell thickness, and attenuates from 12.9 MW/m² at the shell tip to 2.0 MW/m² at 14 mm below the shell tip. Finally it stabilizes around 2.5 MW/m².

• 4. The total mold/shell thermal resistance, interfacial thermal resistance, the liquid film thermal resistance, and the solid film thermal resistance are 8.0 to 14.9 × 10⁻⁴, 2.7 to 4.8 × 10⁻⁴, 1.5 to 4.6 × 10⁻⁴, and 3.9 to 6.8 × 10⁻⁴ m² K/W, respectively. The percentage of the interfacial thermal resistance between mold/slag, the liquid film thermal resistance and the solid film thermal resistance in total mold/shell thermal resistance are 27.5 to 34.4, 17.2 to 34.0, and 38.5 to 48.8 pct, respectively.

• 5. The solid slag film thermal resistance R _s is about 1.4 to 2.8 times larger than that of thermal resistance in liquid slag film R _l. Both the solid slag film thermal resistance R _s and the mold/slag interfacial thermal resistance dominate the heat transfer from the shell to mold. For the liquid slag film, the radiative thermal resistance is about 1.8 to 5 times larger than that of the conductive thermal resistance, and the rate of heat transfer by radiation is 14.1 to 51.9 pct.

• 6. The liquid slag film thickness d _l is 1.2 mm at the location of shell tip, and decreases to the minimum (0.2 mm) at the location 6 mm below the shell tip due to the reduction of the shell surface temperature, then it begins to increase and becomes 0.6 mm at 18 mm below the shell tip due to the increasing of the shell surface temperature.